Правоаголен пресек.
Правоаголен пресек има две оски на симетрија, а главните централни оски Cx и Cy минуваат низ средните точки на паралелните страни.
Главен централен момент на инерција околу x-оската

Во овој случај, елементарната површина dA може да се претстави како лента со целата ширина на пресекот и дебелина dy, што значи dA=b*dy. Да ја замениме вредноста dA под знакот интегрален и да се интегрираме на целата површина, т.е. во границите на промена на ординатата y од –h/2 во +h/2, добиваме
Конечно

Слично на тоа, ја добиваме формулата за главниот централен момент на инерција на правоаголник во однос на y-оската:

Тркалезен дел

За круг, главните централни моменти на инерција за оските x и y се еднакви.
Затоа, од еднаквоста 




Триаголник





2. Промена на моментите на инерција при преминот од централните оски во паралелните:

J x1 =J x + a 2 A;
J y1 =J y + b 2 A;
Моментот на инерција за која било оска е еднаков на моментот на инерција околу централната оска паралелна на дадената, плус производот од плоштината на фигурата и квадратот на растојанието помеѓу оските. J y 1 x 1 =J yx + abF;
(„а“ и „б“ се заменуваат во формулата земајќи го предвид нивниот знак).

3. Промена на моментите на инерција при вртење на оските
J x1 =J x cos 2 + J y sin 2 - J xy sin2;
J y1 =J y cos 2 + J x sin 2 + J xy sin2;
J x1y1 =(J x - J y)sin2 + J xy cos2 ; Агол >0, ако преминот од стариот координатен систем во новиот се случи спротивно од стрелките на часовникот. J y1 + J x1 = J y + J xСе нарекуваат екстремни (максимални и минимални) вредности на моменти на инерција главните моменти на инерција. Се нарекуваат оските околу кои аксијалните моменти на инерција имаат екстремни вредности главните оски на инерција. Главните оски на инерција се меѓусебно нормални. Центрифугална  моменти на инерција
моменти на инерција
во однос на главните оски = 0, т.е. главни оски на инерција - оски околу кои центрифугалниот момент на инерција = 0. Ако една од оските се совпаѓаат или двете се совпаѓаат со оската на симетрија, тогаш тие се главните. Агол што ја дефинира положбата на главните оски: , Ако 0 >0 оските се вртат спротивно од стрелките на часовникот. Максималната оска секогаш прави помал агол со оној на оските во однос на кои моментот на инерција има поголема вредност. Главните оски што минуваат низ центарот на гравитација се нарекуваат 
J max + J min = J x + J y. Центрифугалниот момент на инерција во однос на главните централни оски на инерција е еднаков на 0. Ако се познати главните моменти на инерција, тогаш формулите за премин кон ротирани оски се:
J x 1 =J max cos 2 + J min sin 2 ;
J y 1 =J max cos 2 + J min sin 2 ; J x 1 y 1 =(J max - J min)sin2;
4.Класификација на конструктивни елементиПрачката
повикани Геом тела кај кои едната големина е многу поголема од другите.Чинии или школки<< других
– ова е геом на телата кои имаат една од големинитеМасивни тела
- сите големини се со ист редослед
5.Основни претпоставки за својствата на материјалот
Хомогена - заљубена. точка материјалите се исти. физичко-хемиски светци;
Континуираната средина е кристална. структура и микроскопски дефектите не се земаат предвид;
Изотропно - механички. својствата не зависат од насоката на вчитување;
6. Идеална еластичност - целосно ја враќа формата и големината по отстранувањето на товарот.
Видови потпори

а) Со шарки - фиксна (двојно поврзана) потпора: Прима и вертикални и хоризонтални сили (сили под агол).
б) Шарки - подвижна потпора - перцепира само вертикални оптоварувања. Реакцијата за поддршка е секогаш насочена по должината на потпорната шипка, нормално на потпорната површина
в) Цврста заптивка (три-поврзани)

7. Реакциите во потпорите се одредуваат од состојбата на рамнотежа (статичка равенка).
Класификација на оптоварување
По локација
Површински и волуметриски
а) концентрирана сила 
б) распоредена сила
правоаголна Rq= qa
триаголен Rq= ½ qa
в) концентриран момент
виткање
извртување
г) дистрибуиран момент
Rmz= mz a – рамнотежа
По времетраење
Постојана и привремена
Според природата на дејството
Статични и динамични
По природа на настанување
8. Активни (познати) и реактивни (непознати)
Основни принципи на курсот што се изучува При пресметување на комплексен отпор, се користипринцип на самостојно дејствување на силите
. Комплексен тип на товарење е претставен како систем на едноставни типови на товарење кои дејствуваат независно еден од друг. Решението за сложена отпорност се добива со додавање на решенијата добиени за едноставни типови на оптоварување.
Принципот Сен Венан
9. на доволно растојание од местото каде што се нанесува товарот, природата на неговото влијание не зависи од начинот на неговото нанесување, туку зависи од големината на резултатот.

Внатрешни напори. Метод на пресек (метод ROZU)
Nz=∑z (pi) нормално со
Qx=∑x (pi) попречно со
Mz=∑mz (pi) вртежен момент
Mx=∑mx (pi) свиткување
Сечење на мисловното тело рамно
Отфрламе една од внатрешните сили
Заменете со внатрешни напори
10. Правило на знаци на внатрешни напори
Правило за знаци на попречни сили при свиткување:

Вртежен момент
Против итни случаи кога се гледа од страна +
Правило за знаци на моменти на свиткување:

Правило за проверка на исправноста на конструирање дијаграми за оптоварување:
Во пресеците на гредата каде што се применуваат надворешни концентрирани оптоварувања на дијаграмот d.b. скок во големината на овој товар.
11. Дијаграми на внатрешни сили
КОГА СТЕНЗИЈА-КОМПРЕСИЈА

ТОРЗИОНАЛЕН

на прав свиок

12.Диференцијални зависности при свиткување
 ;
;
 ;
;
13. Последици од диференцијални зависности
Ако нема распределба на оптоварување во областа (q = 0), тогаш попречната сила во оваа област има постојана брзина, а дијаграмите на свиткување се менуваат според линеарниот закон
На полигонот каде што е присутна дистрибуцијата на топлина, постот е интензивен. Попречната сила се менува според правата, а дијаграмите според законот за квадратни параболи. Покрај тоа, дијаграмот на mx секогаш е насочен кон оптоварувањето на дистрибуцијата. Каде што Qy е еднакво на 0, дијаграмот mx има екстрем. Ако Qy е еднакво на 0 низ целата област, тогаш mx е константна вредност
4. Во областа каде што Qy>0 mx дијаграмот се зголемува од лево кон десно
5. Во тој дел. каде што се применува централна сила, дијаграмот Qy има скок на брзината на оваа сила. На местото каде што моментот е центриран, дијаграмот mx има скок за вредноста на овој момент
Тела мпо квадрат на растојание гпомеѓу оските:
J = J c + m d 2, (\displaystyle J=J_(c)+md^(2),)Каде м- вкупна телесна тежина.
На пример, моментот на инерција на прачка во однос на оската што минува низ нејзиниот крај е еднаков на:
J = J c + m d 2 = 1 12 m l 2 + m (l 2) 2 = 1 3 m l 2.(\displaystyle J=J_(c)+md^(2)=(\frac (1)(12))ml^(2)+m\left((\frac (l)(2))\десно)^ (2)=(\frac (1)(3))ml^(2).)
| во однос на некои оски на ротација | Тело | Опис Положба на оската | а Момент на инерција |
|---|---|---|---|
| Ј а м | Материјална точка маса На далечинар | ||
| од точка, неподвижна На далечинаШуплив тенкоѕиден цилиндар или прстен со радиус м | и масите | Оска на цилиндарот | |
| m r 2 (\displaystyle mr^(2)) На далечинаШуплив тенкоѕиден цилиндар или прстен со радиус м | и масите | Цврст цилиндар или диск со радиус | |
| 1 2 m r 2 (\displaystyle (\frac (1)(2))mr^(2)) мШуплив масен цилиндар со дебели ѕидови На далечинасо надворешен радиус На далечина 1 | и масите | 2 и внатрешен радиус | |
| m r 2 2 + r 1 2 2 (\displaystyle m(\frac (r_(2)^(2)+r_(1)^(2))(2))) Цврста должина на цилиндаротл На далечинаШуплив тенкоѕиден цилиндар или прстен со радиус м | , радиус | ||
| 1 4 m ⋅ r 2 + 1 12 m ⋅ l 2 (\стил на прикажување (1 \над 4)m\cточка r^(2)+(1 \над 12)m\cточка l^(2)) Цврста должина на цилиндаротл На далечинаШуплив тенкоѕиден цилиндар или прстен со радиус м | Должина на шупливи тенкоѕидни цилиндри (прстен). | Оската е нормална на цилиндерот и минува низ нејзиниот центар на маса | |
| 1 2 m ⋅ r 2 + 1 12 m ⋅ l 2 (\стил на приказ (1 \над 2)m\cточка r^(2)+(1 \над 12)m\cточка l^(2)) Цврста должина на цилиндаротШуплив тенкоѕиден цилиндар или прстен со радиус м | Оската е нормална на шипката и минува низ нејзиниот центар на маса | 1 12 m l 2 (\displaystyle (\frac (1)(12))ml^(2)) | |
| 1 2 m ⋅ r 2 + 1 12 m ⋅ l 2 (\стил на приказ (1 \над 2)m\cточка r^(2)+(1 \над 12)m\cточка l^(2)) Цврста должина на цилиндаротШуплив тенкоѕиден цилиндар или прстен со радиус м | Оската е нормална на шипката и минува низ нејзиниот крај | 1 3 m l 2 (\displaystyle (\frac (1)(3))ml^(2)) | |
| Сфера со радиус со тенок ѕид На далечинаШуплив тенкоѕиден цилиндар или прстен со радиус м | Оската поминува низ центарот на сферата | 2 3 m r 2 (\displaystyle (\frac (2)(3))mr^(2)) | |
| Топка со радиус На далечинаШуплив тенкоѕиден цилиндар или прстен со радиус м | Оската поминува низ центарот на топката | 2 5 m r 2 (\displaystyle (\frac (2)(5))mr^(2)) | |
| Конус на радиус На далечинаШуплив тенкоѕиден цилиндар или прстен со радиус м | Конусна оска | 3 10 m r 2 (\displaystyle (\frac (3)(10))mr^(2)) | |
| Рамнокрак триаголник со надморска височина ч, основа Положба на оскатаи маса м | Оската е нормална на рамнината на триаголникот и минува низ темето | 1 24 m (а 2 + 12 ч 2) (\стил на приказ (\frac (1)(24)) m(a^(2)+12h^(2))) | |
| Правилен триаголник со страна Положба на оскатаи маса м | Оската е нормална на рамнината на триаголникот и минува низ центарот на масата | 1 12 m a 2 (\displaystyle (\frac (1)(12))ma^(2)) | |
| Квадрат со страна Положба на оскатаи маса м | Оската е нормална на рамнината на квадратот и минува низ центарот на масата | 1 6 m a 2 (\displaystyle (\frac (1)(6))ma^(2)) | |
| Правоаголник со страни Положба на оскатаИ би маса м | Оската е нормална на рамнината на правоаголникот и минува низ центарот на масата | 1 12 m (a 2 + b 2) (\стил на приказ (\frac (1)(12)) m(a^(2)+b^(2))) | |
| Регуларен n-гон со радиус На далечинаи маса м | Оската е нормална на рамнината и минува низ центарот на масата | m r 2 6 [ 1 + 2 cos (π / n) 2 ] (\стил на приказ (\frac (mr^(2))(6))\лево) | |
| Торус (шуплив) со радиус на водечки круг Р, радиус на генерирачкиот круг На далечинаи маса м | Оската е нормална на рамнината на кружниот круг на торусот и минува низ центарот на масата | I = m (3 4 r 2 + R 2) (\приказ I=m\лево((\frac (3)(4))\,r^(2)+R^(2)\десно)) |
Изведување формули
Цилиндар со тенкоѕиди (прстен, обрач)
Изведување на формулата
Моментот на инерција на телото е еднаков на збирот на моментите на инерција на неговите составни делови. Дозволете ни да го поделиме цилиндарот со тенкоѕиди на елементи со маса dmи моменти на инерција dJ i. Потоа
J = ∑ d J i = ∑ R i 2 d m .(1) .
(\displaystyle J=\sum dJ_(i)=\sum R_(i)^(2)dm.\qquad (1).)Бидејќи сите елементи на цилиндарот со тенкоѕиди се на исто растојание од оската на ротација, формулата (1) се трансформира во форма
Изведување на формулата
J = ∑ R 2 d m = R 2 ∑ d m = m R 2 . Р(\displaystyle J=\sum R^(2)dm=R^(2)\sum dm=mR^(2).) РЦилиндар со дебел ѕид (прстен, обрач) чНека има хомоген прстен со надворешен радиус , внатрешен радиус 1, дебел На далечинаи густина ρ. Ајде да го скршиме на тенки прстени дебели
d m = ρ d V = ρ ⋅ 2 π r h d r ;d J = r 2 d m = 2 π ρ h r 3 d r.
(\displaystyle dm=\rho dV=\rho \cdot 2\pi rhdr;\qquad dJ=r^(2)dm=2\pi \rho hr^(3)dr.) Да го најдеме моментот на инерција на дебелиот прстен како интегралJ = ∫ R 1 R d J = 2 π ρ h ∫ R 1 R r 3 d r = (\displaystyle J=\int _(R_(1))^(R)dJ=2\pi \rho h\int _ (R_(1))^(R)r^(3)dr=)
= 2 π ρ h r 4 4 |R 1 R = 1 2 π ρ h (R 4 − R 1 4) = 1 2 π ρ h (R 2 − R 1 2) (R 2 + R 1 2) .
(\displaystyle =2\pi \rho h\left.(\frac (r^(4))(4))\десно|_(R_(1))^(R)=(\frac (1)(2 ))\pi \rho h\лево(R^(4)-R_(1)^(4)\десно)=(\frac (1)(2))\pi \rho h\left(R^(2 )-R_(1)^(2)\десно)\лево(R^(2)+R_(1)^(2)\десно).)Бидејќи волуменот и масата на прстенот се еднакви
Изведување на формулата
V = π (R 2 − R 1 2) h ; Р m = ρ V = π ρ (R 2 − R 1 2) h , (\displaystyle V=\pi \left(R^(2)-R_(1)^(2)\right)h;\qquad m= \rho V=\pi \rho \лево(R^(2)-R_(1)^(2)\десно)h,)
ја добиваме конечната формула за моментот на инерција на прстенотJ = 1 2 m (R 2 + R 1 2) .
Изведување на формулата
(\дисплеј стил J=(\frac (1)(2))m\лево(R^(2)+R_(1)^(2)\десно).) Хомоген диск (цврст цилиндар)Сметајќи цилиндар (диск) како прстен со внатрешен радиус нула (
1 = 0 ), ја добиваме формулата за моментот на инерција на цилиндерот (диск):Каде Р J = 1 2 m R 2 . (\displaystyle J=(\frac (1)(2))mR^(2).)Цврст конус чАјде да го скршиме конусот на тенки дискови со дебелина
dh, нормално на оската на конусот. Радиусот на таков диск е еднаков на
r = R h H , (\displaystyle r=(\frac (Rh)(H)),)- радиус на конусната основа,
Изведување на формулата
Х Хомоген диск (цврст цилиндар), нормално на оската на ротација. Радиусот на таков диск лоциран на височина чод центарот на сферата, ја наоѓаме користејќи ја формулата
r = R 2 − h 2 .(\displaystyle r=(\sqrt (R^(2)-h^(2))).)
Масата и моментот на инерција на таков диск ќе бидат d m = ρ d V = ρ ⋅ π r 2 d h ;(\displaystyle dm=\rho dV=\rho \cdot \pi r^(2)dh;)
d J = 1 2 r 2 d m = 1 2 π ρ r 4 d h = 1 2 π ρ (R 2 − h 2) 2 d h = 1 2 π ρ (R 4 − 2 R 2 h 2 + h 4) d h .(\displaystyle dJ=(\frac (1)(2))r^(2)dm=(\frac (1)(2))\pi \rho r^(4)dh=(\frac (1)( 2))\pi \rho \лево(R^(2)-h^(2)\десно)^(2)dh=(\frac (1)(2))\pi \rho \лево(R^( 4)-2R^(2)h^(2)+h^(4)\десно)dh.)
Изведување на формулата
Го наоѓаме моментот на инерција на топката со интеграција: Р :
J = ∫ − R R d J = 2 ∫ 0 R d J = π ρ ∫ 0 R (R 4 − 2 R 2 h 2 + h 4) d h = = π ρ (R 4 h − 2 3 R 2 h 3 + 1 5 ч 5) |0 R = π ρ (R 5 − 2 3 R 5 + 1 5 R 5) = 8 15 π ρ R 5 = = (4 3 π R 3 ρ) ⋅ 2 5 R 2 = 2 5 m R 2 . (\displaystyle (\begin(порамнет)J&=\int _(-R)^(R)dJ=2\int _(0)^(R)dJ=\pi \rho \int _(0)^(R )\лево(R^(4)-2R^(2)h^(2)+h^(4)\десно)dh=\\&=\pi \rho \лево.\лево(R^(4) h-(\frac (2)(3))R^(2)h^(3)+(\frac (1)(5))h^(5)\десно)\десно|_(0)^( R)=\pi \rho \лево(R^(5)-(\frac (2)(3))R^(5)+(\frac (1)(5))R^(5)\десно) =(\frac (8)(15))\pi \rho R^(5)=\\&=\left((\frac (4)(3))\pi R^(3)\rho \десно) \cdot (\frac (2)(5))R^(2)=(\frac (2)(5))mR^(2).\end(порамнет))) .
Сфера со тенкоѕидиЗа да го изведеме ова, ја користиме формулата за моментот на инерција на хомогена топка со радиус
Изведување на формулата
J 0 = 2 5 M R 2 = 8 15 π ρ R 5 . , внатрешен радиус(\displaystyle J_(0)=(\frac (2)(5))MR^(2)=(\frac (8)(15))\pi \rho R^(5).)
Дозволете ни да пресметаме колку моментот на инерција на топката ќе се промени ако, при постојана густина ρ, неговиот радиус се зголеми за бесконечно мала количина, нормално на оската на конусот. Радиусот на таков диск е еднаков на
J = ∫ − l / 2 l / 2 d J = 2 ∫ 0 l / 2 d J = 2 m l ∫ 0 l / 2 r 2 d r = 2 m l r 3 3 |0 l / 2 = 2 m l l 3 24 = 1 12 m l 2 .
Изведување на формулата
(\дисплеј стил J=\int _(-l/2)^(l/2)dJ=2\int _(0)^(l/2)dJ=(\frac (2m)(l))\int _ (0)^(l/2)r^(2)dr=(\frac (2m)(l))\лево.(\frac (r^(3))(3))\десно|_(0) ^(l/2)=(\frac (2m)(l))(\frac (l^(3))(24))=(\frac (1)(12))ml^(2.) Тенка прачка (оската поминува низ крајот)Кога оската на ротација се движи од средината на шипката до нејзиниот крај, центарот на гравитација на шипката се движи во однос на оската за растојание
l ⁄ 2. Според теоремата на Штајнер, новиот момент на инерција ќе биде еднаков на
J = J 0 + m r 2 = J 0 + m (l 2) 2 = 1 12 m l 2 + 1 4 m l 2 = 1 3 m l 2 . На далечинаШуплив тенкоѕиден цилиндар или прстен со радиус м (\displaystyle J=J_(0)+mr^(2)=J_(0)+m\left((\frac (l)(2))\десно)^(2)=(\frac (1)( 12))ml^(2)+(\frac (1)(4))ml^(2)=(\frac (1)(3))ml^(2.)Бездимензионални моменти на инерција на планети и сателити Нивните бездимензионални моменти на инерција се од големо значење за проучување на внатрешната структура на планетите и нивните сателити. Бездимензионален момент на инерција на тело со радиуседнаков на односот На далечинанеговиот момент на инерција во однос на оската на ротација до моментот на инерција материјална точкаистата маса во однос на фиксната оска на ротација која се наоѓа на растојание (еднакво наг
2). Оваа вредност ја одразува распределбата на масата преку длабочина. Еден од методите за негово мерење во близина на планети и сателити е да се одреди доплеровото поместување на радио сигналот што го пренесува AMS што лета во близина на дадена планета или сателит. За сфера со тенкоѕиди, бездимензионалниот момент на инерција е еднаков на 2/3 (~ 0,67), за хомогена топка - 0,4, а воопшто помалку,
голема маса
Телото е концентрирано во неговиот центар. На пример, Месечината има бездимензионален момент на инерција блиску до 0,4 (еднакво на 0,391), па се претпоставува дека е релативно хомогена, нејзината густина малку се менува со длабочината. Бездимензионалниот момент на инерција на Земјата е помал од оној на хомогена топка (еднакво на 0,335), што е аргумент во прилог на постоењето на густо јадро. Центрифугален момент на инерција J y z = ∫ (m) y z d m = ∫ (V) y z ρ d V , (\displaystyle J_(yz)=\int \limits _((m))yzdm=\int \limits _((V))yz\ rho dV,)Каде x , yИ z- координати на мал тело елемент со волумен dV, густина ρ и маса dm .
Се нарекува оската OX главната оска на инерција на телото, ако центрифугалните моменти на инерција J xyИ J xzсе истовремено еднакви на нула. Низ секоја точка на телото може да се повлечат три главни оски на инерција. Овие оски се меѓусебно нормални една на друга. Моменти на инерција на телоторелативно три главниоски на инерција нацртани на произволна точка Отелата се нарекуваат главните моменти на инерцијана ова тело.
Се нарекуваат главните оски на инерција кои минуваат низ центарот на масата на телото главните централни оски на инерција на телото, а моментите на инерција околу овие оски се негови главни централни моменти на инерција. Оската на симетрија на хомогено тело е секогаш една од неговите главни централни оски на инерција.
Геометриски моменти на инерција
Геометриски момент на инерција на волумен
J V a = ∫ (V) r 2 d V , (\displaystyle J_(Va)=\int \limits _((V))r^(2)dV,)каде, како и досега На далечина- растојание од елементот dVдо оската Положба на оската .
Геометриски момент на инерција на површинаво однос на оската - геометриска карактеристика на телото, изразена со формулата:
J S a = ∫ (S) r 2 d S , (\displaystyle J_(Sa)=\int \limits _((S))r^(2)dS,)каде што се врши интеграција преку површината С, А dS- елемент на оваа површина.
Димензија JSa- должина до четврта сила ( d i m J S a = L 4 (\displaystyle \mathrm (мрачно) J_(Sa)=\mathrm (L^(4)) )), соодветно, мерната единица SI е 4. Во градежните пресметки, литературата и асортиманот на валани метали, често се означува во cm 4.
Моментот на отпор на пресекот се изразува преку геометрискиот момент на инерција на областа:
W = J S a r m a x.(\displaystyle W=(\frac (J_(Sa))(r_(max))).) Еве rmax
| - максимално растојание од површината до оската. | |
|---|---|
| Геометриски моменти на инерција на областа на некои фигури Висина на правоаголник h (\displaystyle h) и ширина: | b (\displaystyle b)
J y = b h 3 12 (\displaystyle J_(y)=(\frac (bh^(3))(12))) |
| J z = h b 3 12 (\displaystyle J_(z)=(\frac (hb^(3))(12))) Правоаголен дел од кутијата со висина и ширина по надворешните контури H (\displaystyle H) И B (\displaystyle B) Висина на правоаголник H (\displaystyle H) и ширина, и за внатрешни | соодветно
J y = H B 3 12 − h b 3 12 = 1 12 (H B 3 − h b 3) (\displaystyle J_(y)=(\frac (HB^(3))(12))-(\frac (hb^( 3))(12))=(\frac (1)(12))(HB^(3)-hb^(3))) |
| Дијаметар на кругот d (\displaystyle d) | J y = J z = π d 4 64 (\displaystyle J_(y)=J_(z)=(\frac (\pi d^(4))(64))) |
Момент на инерција во однос на рамнината
Момент на инерција солиднаво однос на некоја рамнина се нарекува скаларна количина, еднаков на збирот на производите од масата на секоја точка на телото по квадратот на растојанието од оваа точка до предметната рамнина.
Ако преку произволна точка O (\displaystyle O)спроведе координатни оски x , y , z (\приказ на стил x,y,z), потоа моментите на инерција во однос на координатни рамнини x O y (\displaystyle xOy), y O z (\displaystyle yOz) H (\displaystyle H) z O x (\displaystyle zOx)ќе се изрази со формулите:
J x O y = ∑ i = 1 n m i z i 2 , (\displaystyle J_(xOy)=\sum _(i=1)^(n)m_(i)z_(i)^(2)\ ,) J y O z = ∑ i = 1 n m i x i 2 , (\displaystyle J_(yOz)=\sum _(i=1)^(n)m_(i)x_(i)^(2)\ ,) J z O x = ∑ i = 1 n m i y i 2 .(\displaystyle J_(zOx)=\sum _(i=1)^(n)m_(i)y_(i)^(2)\ .)
Во случај на цврсто тело, сумирањето се заменува со интеграција.
Во случај на цврсто тело, сумирањето се заменува со интеграција. (Централен момент на инерција) момент на инерција за точката О, момент на инерција за полот, поларен момент на инерција J O (\displaystyle J_(O))
е количината определена со изразот:J a = ∫ (m) r 2 d m = ∫ (V) ρ r 2 d V , (\displaystyle J_(a)=\int \limits _((m))r^(2)dm=\int \limits _((V))\rho r^(2)dV,)
Централниот момент на инерција може да се изрази во однос на главните аксијални моменти на инерција, како и во однос на моментите на инерција за рамнините: J O = 1 2 (J x + J y + J z) , (\displaystyle J_(O)=(\frac (1)(2))\left(J_(x)+J_(y)+J_(z) \десно))J O = J x O y + J y O z + J x O z.
(\displaystyle J_(O)=J_(xOy)+J_(yOz)+J_(xOz).) Тензор на инерција и елипсоид на инерцијаМоментот на инерција на тело во однос на произволна оска што минува низ центарот на масата и има насока одредена од единечниот вектор
s → = ‖ s x, s y, s z ‖ T, | (1)s → | 3 × 3 (\стил на приказ 3\пати 3)и се состои од компоненти на центрифугални моменти:
(\displaystyle J_(xx)=\int \limits _((m))(y^(2)+z^(2))dm,\quad J_(yy)=\int \limits _((m)) (x^(2)+z^(2))dm,\quad J_(zz)=\int \limits _((m))(x^(2)+y^(2))dm.) Со избирање на соодветниот координатен систем, матрицата на тензорот на инерција може да се сведе во дијагонална форма. За да го направите ова, треба да го решите проблемот со сопствената вредност за матрицата на тензорите:
Каде J ^ d = ‖ J X 0 0 0 J Y 0 0 0 J Z ‖ , (\displaystyle (\hat (J))_(d)=\left\Vert (\begin(array)(ccc)J_(X)&0&0\ \0&J_(Y)&0\\0&0&J_(Z)\крај (низа))\десно\Vert ,) Q ^ (\displaystyle (\hat (Q))) - ортогонална матрица на премин кон сопствената основа на тензорот на инерција. Во соодветна основа, координатните оски се насочени по главните оски на тензорот на инерција, а исто така се совпаѓаат со главните полуоски на елипсоидот на инерцискиот тензор. Количини J X, J Y, J Z (\стил на дисплеј J_(X), J_(Y), J_(Z))
I s = J X ⋅ s x 2 + J Y ⋅ s y 2 + J Z ⋅ s z 2 , (\приказ I_(s)=J_(X)\cdot s_(x)^(2)+J_(Y)\cdot s_(y )^(2)+J_(Z)\cточка s_(z)^(2),) од кој ја добиваме равенката на елипсоидот во сопствените координати. Поделувајќи ги двете страни на равенката со
(s x I s) 2 ⋅ J X + (s y I s) 2 ⋅ J Y + (s z I s) 2 ⋅ J Z = 1 (\displaystyle \left((s_(x) \over (\sqrt (I_(s))) ))\десно)^(2)\cdot J_(X)+\left((s_(y) \over (\sqrt (I_(s))))\десно)^(2)\cdot J_(Y) +\left((s_(z) \over (\sqrt (I_(s))))\десно)^(2)\cdot J_(Z)=1)
и правење замени:ја добиваме канонската форма на елипсоидната равенка во координати ξ η ζ (\displaystyle \xi \eta \zeta ):
ξ 2 ⋅ J X + η 2 ⋅ J Y + ζ 2 ⋅ J Z = 1. (\displaystyle \xi ^(2)\cdot J_(X)+\eta ^(2)\cdot J_(Y)+\zeta ^( 2)\cточка J_(Z)=1.)Растојанието од центарот на елипсоидот до одредена точка е поврзано со вредноста на моментот на инерција на телото по права линија што минува низ центарот на елипсоидот и оваа точка.
Имајќи ги предвид во претходните делови наједноставните типови на деформации - аксијално напнатост и компресија, дробење, распарчување - дознавме дека нивната отпорност дејствувачка силапропорционално само на димензиите на пресечната површина на елементот на кој дејствува силата. Значи, со иста површина на пресек, истиот материјал и истата сила дејствува на секоја од прачките прикажани на сл. 9.14, во нив ќе се појават еднакви напрегања.
Продолжете да учите други повеќе сложени видовидеформации (торзија, свиткување, ексцентрична компресија итн.), ќе видиме дека во овие случаи отпорот на конструктивниот елемент на надворешни сили зависи не само од неговата површина на пресек, туку и од распределбата на оваа област во пресекот рамнина, односно на обликот на делот.
Од секојдневното искуство е јасно дека свиткувањето на прачката 4 во вертикална насока е потешко од шипката 5, а шипката 6 има уште поголема цврстина, иако пресечните површини на сите овие прачки се исти (сл. 9.14).
Параметри кои карактеризираат геометриски својстваРазни фигури на рамнини, покрај плоштината, се: статични моменти, моменти на инерција, моменти на отпор и радиуси на инерција.
Статички момент на областа. Ајде да замислиме зрак со произволна форма на пресек со површина Ф, во чија рамнина е нацртана оската X(Сл. 9.15). Изберете го елементот област dF, кој се наоѓа на далечина наод оската X.. Статичкиот момент на елементарна платформа, во однос на оската x, е производ на оваа платформа и нејзиното растојание до оската:
Статички момент на целата област Фво однос на оската Xеднаков на збирот на статичките моменти на сите елементарни области што може да се идентификуваат на површината што се разгледува:
Од теоретската механика е познато дека координатите на центарот на гравитација на областа на фигурата се одредуваат со формулите:
Според тоа, статичниот момент на фигура со површина Фво однос на која било оска е еднаква на производот од областа и растојанието од центарот на гравитација на фигурата до оваа оска. Димензијата на статичкиот момент е единица должина во коцка (,).
Оските што минуваат низ тежиштето на делот се нарекуваат централни Ако фигурата има оска на симетрија, тогаш таа секогаш минува низ центарот на гравитација на фигурата, односно оските на симетрија се исто така централни оски.
Исто така, ќе имаме на ум дека статичкиот момент на сложена фигура во однос на некоја оска е еднаков на збирот на статичките моменти во однос на истата оска на едноставни фигури на кои може да се подели оригиналната сложена фигура:
Ориз. 9.16. Шема за одредување на координатите на тежиштето на сложена фигура.
За да го решиме овој проблем, избираме две координатни оски X H (\displaystyle H) на, што се совпаѓа со страните на фигурата. Дозволете ни да ја поделиме фигурата, чиишто димензии мора да бидат познати, на елементарни делови - правоаголници - чии координати на центрите на гравитација се очигледни, бидејќи овие делови се симетрични. Сега да составиме изрази за пресметување на статичкиот момент на целата област, на пример во однос на оската на. Ова може да се направи на два начина:
а) земете го збирот на статичките моменти на одделни области
Во овие изрази Ф- површина на целата фигура;
- координата на неговиот центар на гравитација;
- областите на одделни делови на фигурата и - координатите на нивните тежишта. XИзедначувајќи ги формулите напишани погоре една со друга, добиваме равенка со една непозната:
Слично на тоа, растојанието на центарот на гравитација на фигурата од оската може да се изрази вака::
Составувајќи интеграл во кој интеграндот е производ на елементот плоштина и квадратот на растојанието до потеклото (сл. 9.17), добиваме dFполарен момент на инерција
Да забележиме уште една карактеристика во која страницата множи со производот на координатиОваа количина се нарекува
центрифугален момент на инерција . Дадените моменти на инерција се мерат во единици за должина земени до четвртата моќност (,).Аксијалните и поларните моменти на инерција на фигурата се позитивни величини и не можат да бидат еднакви на нула. Центрифугалниот момент на инерција, во зависност од положбата на оските, може да биде позитивен или негативен, како и еднаков на нула.
Две меѓусебно нормални оски околу кои центрифугалниот момент на инерција е нула се нарекуваат
Исто како и за статичкиот момент, моментот на инерција на сложена фигура е еднаков на збирот на моментите на инерција на фигурите што ја формираат. Нагласуваме дека горенаведеното е точно во случај кога сите моменти на инерција се пресметани во однос на истата оска.
За моменти на инерција, постои уште едно правило кое често се користи во пресметките. Во однос на аксијалните моменти, тој е формулиран на следниов начин: момент на инерција на фигураво однос на оската паралелна на централната, еднаква на моментот на инерција во однос на централната оска плус производот на површината на фигурата множи со квадратот на растојанието помеѓу оските (слика 9.18):
За центрифугалните моменти на инерција, соодветното правило во аналитичка форма изгледа вака:
За да се добие вредноста на моментот на инерција на одредена фигура, во принцип, неопходно е да се реши соодветниот интеграл над површината на оваа бројка. Меѓутоа, за да се олеснат инженерските пресметки, ваквите интеграли за најчестите облици на попречен пресек на градежните елементи веќе се решени и резултатите од решенијата во форма на формули се претставени во табели, од кои едната е ставена во Додаток 3. .
Дополнително, стандардите ГОСТ за сите стандардни валани профили произведени во нашата земја (агли, I-зраци, итн.) даваат вредности на аксијални моменти на инерција и други геометриски карактеристики за секоја стандардна големина на валани производи (види Додаток 4).
Конечно, за пресеците со сложени форми, моментите на инерција се одредуваат користејќи ги двете правила наведени погоре: додавање на моменти на инерција и претворање на моменти на инерција околу една оска во други оски.
Момент на отпор. Аксијален момент на отпор рамна фигураво однос на која било оска што лежи во рамнината на сликата, количникот на делење на моментот на инерција во однос на истата оска со растојанието до најоддалечената точка на сликата се нарекува (види Сл. 9.17):
Моментите на отпор имаат димензија на должина во коцка (,).
Формулите за пресметување на аксијалните моменти на отпорност на најчесто појавуваните бројки се дадени во Додаток 3, а специфичните вредности на оваа карактеристика за валани челични профили се дадени во ГОСТ (Додаток 4). Забележете дека, за разлика од моментите на инерција, моментите на отпор не можат да се додадат.
Радиус на инерција. Радиусот на вртење е вредноста добиена од формулата
и за круг со дијаметар градиусот на вртење во однос на оската што минува низ центарот на кругот е еднаков на
Обемот на примена на геометриските карактеристики на пресеците дискутирани погоре ќе се открие при проучувањето на типовите на деформации, кои се дискутирани во следните подделови од ова поглавје.
Во пресметковната практика, деловите често се наоѓаат во форма на едноставни фигури (правоаголници, кругови, триаголници итн.) или нивни комбинации. При пресметување на моментите на инерција на таквите бројки, обично се користат претходно изведени пресметковни формули. Ајде да погледнеме некои од бројките.
Правоаголник и паралелограм (сл. 6.4). Дозволете ни да избереме елементарна лента со површина dF= bdyи заменете ја оваа вредност dF под интегралниот знак (6.5):
Моментите на инерција на овие бројки во однос на оските што минуваат низ основата се пронајдени со формулата (6.13):
|
|
Моменти на инерција на правоаголник околу неговите оски yв H (\displaystyle H) yсе пресметуваат со користење на формулите (6.16) и (6.17), каде бсе заменува со ч, А чна б:
Пресметувајќи го моментот на инерција на триаголникот во однос на централната оска паралелна со основата користејќи ги формулите за пренос, добиваме

Обично, димензиите на кружен пресек се изразени во однос на дијаметарот ги брои Јасстрспоред формулата
Централни оски y H (\displaystyle H) zподелете го кругот на четири целосно идентични делови со еднакви моменти на инерција околу овие оски. Следствено, моментите на инерција на кругот и полукругот во однос на оските y H (\displaystyle H) zмора да биде еднаква на, соодветно, четирикратни и удвоени моменти на инерција околу истите оски од една четвртина од кругот. Од горенаведеното произлегува дека моментите на инерција на полукругот во однос на оската на симетрија yи оски z, минување низ неговата основа (сл. 6.2) ќе биде идентично и еднакво на половина од моментот на инерција на кругот,
и моментите на инерција од четвртина круг
Основен курспредавања за јачина на материјали, теорија, пракса, задачи.
1. Геометриски карактеристики на пресеците.1.3. Моменти на инерција на едноставни пресеци.
1. Правоаголник(Сл. 1.5, а). Дозволете ни да го пресметаме моментот на инерција на пресекот во однос на оската X0 што минува низ центарот на гравитација паралелно со основата.
За dA ја земаме областа на бесконечно тенок слој dA = bdy. 
Потоа ![]() (1.11)
(1.11)
Значи, ![]() (1.12)
(1.12)
Слично, добиваме 2. Заокружете ![]()
(Сл. 1.5,б). Прво го одредуваме поларниот момент на инерција во однос на центарот на кругот ![]()
За dA ја земаме областа на бескрајно тенок прстен со дебелина dp 
Потоа
(1.13)
Оттука,
(1.14)
Сега можеме лесно да го најдеме Ixo. Навистина, за круг, според формулата (1.9.), имаме Iр = 2Iхо = 2Iуо, од каде 2. Прстен  (1.15)
(1.15)
(Сл. 1.5, в). Аксијалниот момент на инерција во овој случај е еднаков на разликата помеѓу моментите на инерција на надворешните и внатрешните кругови
каде што c = d/D.  (1.16)
(1.16)
Слично на тоа, поларниот момент на инерција 2. Триаголник ![]()
За dA ја земаме плоштината на бескрајно тенок трапез KBDE, чија површина може да се смета еднаква површинаправоаголник:
DA = со dy,
Каде што е должината на правоаголникот.
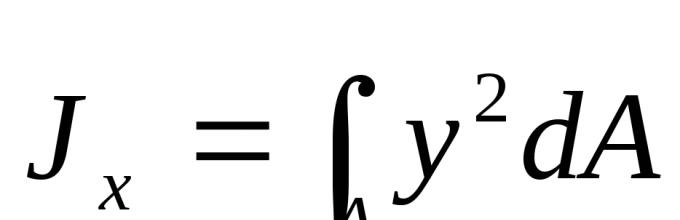
 .
.






