На оваа страница ќе ги најдете сите основни тригонометриски формули кои ќе ви помогнат да решите многу вежби, значително поедноставувајќи го самиот израз.
Тригонометриски формули - математички еднаквости за тригонометриски функции, кои се извршуваат за сите валидни вредности на аргументот.
Формулите ја поставуваат врската помеѓу главните тригонометриски функции - синус, косинус, тангента, котангента.
Синус на агол е y-координата на точка (ордината) на единица круг. Косинусот на аголот е х-координати на точка (абциса).
Тангента и котангента се, соодветно, односот на синус и косинус и обратно.
`sin\\alpha,\cos\\alpha`
`tg \ \alpha=\frac(sin\ \alpha)(cos \\alpha),` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`ctg \ \alpha=\frac(cos\ \alpha)(sin\ \alpha),` ` \alpha\ne\pi+\pi n, \ n \in Z`
И две што се користат поретко - секант, косекант. Тие означуваат сооднос од 1 спрема косинус и синус.
`sec \ \alpha=\frac(1)(cos\ \alpha),` ` \alpha\ne\frac\pi2+\pi n,\ n \in Z`
`cosec \ \alpha=\frac(1)(sin \ \alpha),` ` \alpha\ne\pi+\pi n,\ n \in Z`
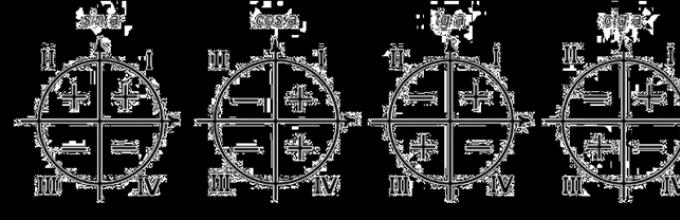
Од дефинициите на тригонометриските функции, можете да видите какви знаци имаат во секоја четвртина. Знакот на функцијата зависи само од тоа во кој квадрант е аргументот.

При промена на знакот на аргументот од „+“ во „-“, само функцијата косинус не ја менува својата вредност. Тоа се нарекува дури. Неговиот график е симетричен во однос на y-оската.
Останатите функции (синус, тангента, котангента) се непарни. Кога знакот на аргументот се менува од „+“ во „-“, нивната вредност исто така се менува во негативна. Нивните графикони се симетрични во однос на потеклото.
`sin(-\alpha)=-sin \ \alpha`
`cos(-\alpha)=cos \ \alpha`
`tg(-\alpha)=-tg \ \alpha`
`ctg(-\alpha)=-ctg \ \alpha`
Основни тригонометриски идентитети
Основните тригонометриски идентитети се формули кои воспоставуваат врска помеѓу тригонометриските функции на еден агол (`sin \\alpha, \ cos \\alpha, \ tg \\alpha, \ ctg \ \alpha`) и кои ви дозволуваат да го пронајдете вредноста на секоја од овие функции преку која било позната друга.
`sin^2 \alpha+cos^2 \alpha=1`
`tg \ \alpha \cdot ctg \ \alpha=1, \ \alpha\ne\frac(\pi n) 2, \ n \in Z`
`1+tg^2 \alpha=\frac 1(cos^2 \alpha)=sec^2 \alpha,` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`1+ctg^2 \alpha=\frac 1(sin^2 \alpha)=cosec^2 \alpha,` ` \alpha\ne\pi n, \ n \in Z`
Формули за збир и разлика на агли на тригонометриски функции
Формулите за собирање и одземање аргументи ги изразуваат тригонометриските функции на збирот или разликата на два агли во однос на тригонометриските функции на овие агли.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alpha+\beta)=\frac(tg \\alpha+tg \\beta)(1-tg \\alpha\ tg \\beta)`
`tg(\alpha-\beta)=\frac(tg \\alpha-tg \\beta)(1+tg \\alpha \ tg \\beta)`
`ctg(\alpha+\beta)=\frac(ctg \\alpha \ ctg \\beta-1)(ctg \\beta+ctg \\alpha)`
`ctg(\alpha-\beta)=\frac(ctg \\alpha\ ctg \\beta+1)(ctg \\beta-ctg \\alpha)`
Формули со двоен агол
`sin \ 2\alpha=2 \ sin \ \alpha \ cos \ \alpha=` `\frac (2 \ tg \ \alpha)(1+tg^2 \alpha)=\frac (2 \ ctg \ \alpha )(1+ctg^2 \alpha)=` `\frac 2(tg \\alpha+ctg \\alpha)`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \ sin^2 \alpha=2 \ cos^2 \alpha-1=` `\frac(1-tg^ 2\алфа)(1+tg^2\алфа)=\frac(ctg^2\алфа-1)(ctg^2\алфа+1)=` `\frac(ctg \\алфа-tg \\алфа) (ctg \\ алфа + tg \\ алфа)`
`tg \ 2\alpha=\frac(2 \ tg \\alpha)(1-tg^2 \alpha)=` `\frac(2 \ ctg \\alpha)(ctg^2 \alpha-1)=` `\frac 2( \ ctg \ \alpha-tg \ \alpha)`
`ctg \ 2\alpha=\frac(ctg^2 \alpha-1)(2 \ ctg \\alpha)=` `\frac ( \ ctg \ \alpha-tg \ \alpha)2`
Формули со троен агол
`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \\alpha`
`tg \ 3\alpha=\frac(3 \ tg \\alpha-tg^3 \alpha)(1-3 \ tg^2 \alpha)`
`ctg \ 3\alpha=\frac(ctg^3 \alpha-3 \ ctg \\alpha)(3 \ ctg^2 \alpha-1)`
Формули со половина агол
`sin \ \frac \alpha 2=\pm \sqrt(\frac (1-cos \ \alpha)2)`
`cos \ \frac \alpha 2=\pm \sqrt(\frac (1+cos \\alpha)2)`
`tg \ \frac \alpha 2=\pm \sqrt(\ frac (1-cos \ \alpha)(1+cos \\alpha))=` `\frac (sin \ \alpha)(1+cos \\ алфа)=\frac (1-cos \ \alpha)(sin \ \alpha)`
`ctg \ \frac \alpha 2=\pm \sqrt(\frac (1+cos \\alpha)(1-cos \\alpha))=` `\frac (sin \ \alpha)(1-cos \\ алфа)=\frac (1+cos \ \alpha)(sin \ \alpha)`
Половина, двоен и троен аргумент ги изразуваат функциите `sin, \cos, \tg, \ctg` на тие аргументи (`\frac(\alpha)2, \ 2\alpha, \ 3\alpha,… `) во условите на истите овие функции на аргументот `\alpha`.
Нивниот излез може да се добие од претходната група (собирање и одземање на аргументи). На пример, идентитетите со двоен агол лесно се добиваат со замена на `\beta` со `\alpha`.
Формули за намалување
Формулите на квадрати (коцки, итн.) на тригонометриски функции ви дозволуваат да преминете од 2,3, ... степени до тригонометриски функции од прв степен, но повеќе агли (`\алфа, \ 3\алфа, \ ... ` или `2\алфа, \ 4\алфа, \...`).
`sin^2 \alpha=\frac(1-cos \ 2\alpha)2,` ` (sin^2 \frac \alpha 2=\frac(1-cos \\alpha)2)`
`cos^2 \alpha=\frac(1+cos \ 2\alpha)2,` ` (cos^2 \frac \alpha 2=\frac(1+cos \\alpha)2)`
`sin^3 \alpha=\frac(3sin \\alpha-sin \ 3\alpha)4`
`cos^3 \alpha=\frac(3cos \\alpha+cos \ 3\alpha)4`
`sin^4 \alpha=\frac(3-4cos \ 2\alpha+cos \ 4\alpha)8`
`cos^4 \alpha=\frac(3+4cos \ 2\alpha+cos \ 4\alpha)8`
Формули за збир и разлика на тригонометриски функции
Формулите се трансформации на збирот и разликата на тригонометриските функции на различни аргументи во производ.
`sin \ \alpha+sin \ \beta=` `2 \ sin \frac(\alpha+\beta)2 \ cos \frac(\alpha-\beta)2`
`sin \ \alpha-sin \ \beta=` `2 \ cos \frac(\alpha+\beta)2 \ sin \frac(\alpha-\beta)2`
`cos \ \alpha+cos \ \beta=` `2 \ cos \frac(\alpha+\beta)2 \ cos \frac(\alpha-\beta)2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac(\alpha+\beta)2 \ sin \frac(\alpha-\beta)2=` `2 \ sin \frac(\alpha+\ бета)2\sin\frac(\бета-\алфа)2`
`tg \ \alpha \pm tg \ \beta=\frac(sin(\alpha \pm \beta))(cos \\alpha \ cos \\beta)`
`ctg \ \alpha \pm ctg \ \beta=\frac(sin(\beta \pm \alpha))(sin \\alpha \ sin \\beta)`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac(cos(\alpha \mp \beta))(cos \ \alpha \ sin \ \beta)`
Овде собирањето и одземањето на функциите на еден аргумент се претвораат во производ.
`cos \ \alpha+sin \ \alpha=\sqrt(2) \ cos (\frac(\pi)4-\alpha)`
`cos \ \alpha-sin \ \alpha=\sqrt(2) \sin (\frac(\pi)4-\alpha)`
`tg \ \alpha+ctg \ \alpha=2 \cosec \2\alpha;` `tg \ \alpha-ctg \ \alpha=-2 \ctg \2\alpha`
Следниве формули го претвораат збирот и разликата на единица и тригонометриска функција во производ.
`1+cos \ \alpha=2 \ cos^2 \frac(\alpha)2`
`1-cos \ \alpha=2 \ sin^2 \frac(\alpha)2`
`1+sin \ \alpha=2 \ cos^2 (\frac (\pi) 4-\frac(\alpha)2)`
`1-sin \ \alpha=2 \ sin^2 (\frac (\pi) 4-\frac(\alpha)2)`
`1 \pm tg \ \alpha=\frac(sin(\frac(\pi)4 \pm \alpha))(cos \frac(\pi)4 \ cos \\alpha)=` `\frac(\sqrt (2) sin(\frac(\pi)4 \pm \alpha))(cos \\alpha)`
`1 \pm tg \ \alpha \ tg \ \beta=\frac(cos(\alpha \mp \beta))(cos \ \alpha \ cos \ \beta);` ` \ctg \ \alpha \ ctg \ \ бета \pm 1=\frac(cos(\alpha \mp \beta))(sin \\alpha \ sin \\beta)`
Формули за конверзија на функции
Формули за претворање на производот на тригонометриските функции со аргументи `\alpha` и `\beta` во збир (разлика) на овие аргументи.
`sin \ \alpha \ sin \ \beta =` `\frac(cos(\alpha - \beta)-cos(\alpha + \beta))(2)`
`sin\alpha \ cos\beta =` `\frac(sin(\alpha - \beta)+sin(\alpha + \beta))(2)`
`cos \ \alpha \ cos \ \beta =` `\frac(cos(\alpha - \beta)+cos(\alpha + \beta))(2)`
`tg \ \алфа \ tg \ \бета =` `\frac(cos(\алфа - \бета)-cos(\алфа + \бета))(cos(\алфа - \бета)+cos(\алфа + \ бета)) =` `\frac(tg \ \алфа + tg \\бета)(ctg \\алфа + ctg \\бета)`
`ctg \ \алфа \ ctg \ \бета =` `\frac(cos(\алфа - \бета)+cos(\алфа + \бета))(cos(\алфа - \бета)-cos(\алфа + \ бета)) =` `\frac(ctg \\алфа + ctg \\бета)(tg \\алфа + tg \\бета)`
`tg \ \алфа \ ctg \ \бета =` `\frac(sin(\алфа - \бета)+sin(\алфа + \бета))(sin(\алфа + \бета)-sin(\алфа - \ бета))`
Универзална тригонометриска замена
Овие формули изразуваат тригонометриски функции во однос на тангента на половина агол.
`sin \ \alpha= \frac(2tg\frac(\alpha)(2))(1 + tg^(2)\frac(\alpha)(2)),` ` \alpha\ne \pi +2\ pi n, n \во Z`
`cos \ \алфа= \frac(1 - tg^(2)\frac(\алфа)(2))(1 + tg^(2)\frac(\алфа)(2)),` ` \алфа \ ne \pi +2\pi n, n \in Z`
`tg \ \alpha= \frac(2tg\frac(\alpha)(2))(1 - tg^(2)\frac(\alpha)(2)),` ` \alpha \ne \pi +2\ pi n, n \in Z,` ` \alpha \ne \frac(\pi)(2)+ \pi n, n \in Z`
`ctg \ \алфа = \frac(1 - tg^(2)\frac(\алфа)(2))(2tg\frac(\алфа)(2),` ` \alpha \ne \pi n, n \во Z,` `\алфа \ne \pi + 2\pi n, n \во Z`
Формули за лиење
Формулите за редукција може да се добијат со користење на такви својства на тригонометриските функции како периодичност, симетрија, својство на поместување по даден агол. Тие дозволуваат произволните функции на аголот да се претворат во функции чиј агол е помеѓу 0 и 90 степени.
За агол (`\frac (\pi)2 \pm \alpha`) или (`90^\circ \pm \alpha`):
`sin(\frac (\pi)2 - \alpha)=cos \\alpha;` ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha`
`cos(\frac (\pi)2 - \alpha)=sin \ \alpha;` ` cos(\frac (\pi)2 + \alpha)=-sin \ \alpha`
`tg(\frac (\pi)2 - \alpha)=ctg \ \alpha;` ` tg(\frac (\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (\pi)2 - \alpha)=tg \ \alpha;` ` ctg(\frac (\pi)2 + \alpha)=-tg \ \alpha`
За агол (`\pi \pm \alpha`) или (`180^\circ \pm \alpha`):
`sin(\pi - \alpha)=sin \ \alpha;`` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi - \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi - \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi - \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
За агол (`\frac (3\pi)2 \pm \alpha`) или (`270^\circ \pm \alpha`):
`sin(\frac (3\pi)2 - \alpha)=-cos \ \alpha;` ` sin(\frac (3\pi)2 + \alpha)=-cos \ \alpha`
`cos(\frac (3\pi)2 - \alpha)=-sin \ \alpha;` ` cos(\frac (3\pi)2 + \alpha)=sin \ \alpha`
`tg(\frac (3\pi)2 - \alpha)=ctg \ \alpha;` ` tg(\frac (3\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (3\pi)2 - \alpha)=tg \ \alpha;` ` ctg(\frac (3\pi)2 + \alpha)=-tg \ \alpha`
За агол (`2\pi \pm \alpha`) или (`360^\circ \pm \alpha`):
`sin(2\pi - \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi - \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi - \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi - \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Изразување на некои тригонометриски функции во однос на други
`sin \ \alpha=\pm \sqrt(1-cos^2 \alpha)=` `\frac(tg \\alpha)(\pm \sqrt(1+tg^2 \alpha))=\frac 1( \pm \sqrt(1+ctg^2 \alpha))`
`cos \ \alpha=\pm \sqrt(1-sin^2 \alpha)=` `\frac 1(\pm \sqrt(1+tg^2 \alpha))=\frac (ctg \ \alpha)( \pm \sqrt(1+ctg^2 \alpha))`
`tg \ \alpha=\frac (sin \ \alpha)(\pm \sqrt(1-sin^2 \alpha))=` `\frac (\pm \sqrt(1-cos^2 \alpha))( cos \ \alpha)=\frac 1(ctg \ \alpha)`
`ctg \ \alpha=\frac (\pm \sqrt(1-sin^2 \alpha))(sin \\alpha)=` `\frac (cos \\alpha)(\pm \sqrt(1-cos^ 2 \алфа))=\frac 1(tg \\алфа)`
Тригонометријата буквално се преведува како „мерење на триаголници“. Почнува да се изучува на училиште, а подетално продолжува на универзитетите. Затоа, потребни се основните формули за тригонометрија, почнувајќи од 10-то одделение, како и за полагање на испитот. Тие означуваат врски помеѓу функциите, и бидејќи има многу од овие врски, постојат неколку и самите формули. Запомнувањето на сите нив не е лесно и не е неопходно - доколку е потребно, сите тие можат да се заклучат.
Тригонометриските формули се користат во интегрално пресметување, како и во тригонометриски поедноставувања, пресметки и трансформации.
Вежбајте.
Најдете ја вредноста на x во.
Решение.
Да се најде вредноста на функцискиот аргумент, при кој е еднаков на некоја вредност, значи да се одреди за кои аргументи вредноста на синусот ќе биде точно иста како што е наведено во условот.
Во овој случај, треба да откриеме во кои вредности вредноста на синусот ќе биде еднаква на 1/2. Ова може да се направи на неколку начини.
На пример, користете , со што ќе се одреди при кои вредности на x синусната функција ќе биде еднаква на 1/2.
Друг начин е да се користи. Дозволете ми да ве потсетам дека вредностите на синусите лежат на оската Ој.
Најчестиот начин е да се користи, особено кога станува збор за такви стандардни вредности за оваа функција како 1/2.
Во сите случаи, не треба да се заборави за една од најважните својства на синусот - нејзиниот период.
Ајде да ја најдеме вредноста 1/2 за синусот во табелата и да видиме кои аргументи одговараат на тоа. Аргументите за кои не интересира се Pi / 6 и 5Pi / 6.
Ги запишуваме сите корени што задоволуваат дадена равенка. За да го направите ова, го запишуваме непознатиот аргумент x од нас и една од вредностите на аргументот добиен од табелата, односно Pi / 6. Ајде да запишеме за тоа, земајќи го предвид синусниот период, сите вредности на аргументот:
![]()
Да ја земеме втората вредност и да ги следиме истите чекори како во претходниот случај:
![]()
Целосното решение на оригиналната равенка ќе биде: ![]() И
И ![]()
qможе да ја земе вредноста на кој било цел број.
Во тригонометријата, многу формули се полесно да се заклучат отколку да се запаметат. Косинусот на двоен агол е прекрасна формула! Ви овозможува да ги добиете формулите за намалување и формулите за половина агол.
Значи, ни треба косинус на двојниот агол и тригонометриската единица:
Тие се дури и слични: во формулата на косинус на двоен агол - разликата помеѓу квадратите на косинус и синус, а во тригонометриската единица - нивниот збир. Ако го изразиме косинусот од тригонометриската единица:
и го замениме во косинус на двојниот агол, добиваме:
Ова е уште една формула за косинус со двоен агол:
Оваа формула е клучот за добивање формула за намалување:
Значи, формулата за намалување на степенот на синус е:
![]()
Ако во него аголот алфа се замени со половина агол алфа на половина, а двојниот агол два алфа се замени со аголот алфа, тогаш ја добиваме формулата за половина агол за синусот:
![]()
Сега, од тригонометриската единица, го изразуваме синусот:
Заменете го овој израз во формулата за косинус на двоен агол:
![]()
Добивме друга формула за косинус на двоен агол:
Оваа формула е клучот за пронаоѓање на формулата за намалување на косинус и половина агол за косинус.
Така, формулата за намалување на степенот на косинус е:
![]()
Ако го замениме α со α/2 во него, а 2α со α, тогаш ја добиваме формулата за половина аргумент за косинус:
![]()
Бидејќи тангентата е односот на синус и косинус, формулата за тангента е:
![]()
Котангента е односот на косинус и синус. Значи формулата за котангенсот е:
![]()
Се разбира, во процесот на поедноставување тригонометриски изразинема смисла да се изведуваат формули со полуаголни формули или да се намалува степенот секој пат. Многу е полесно да ставите лист со формули пред вас. И поедноставувањето ќе напредува побрзо, а визуелната меморија ќе се вклучи за меморирање.
Но, сепак вреди да се изведат овие формули неколку пати. Тогаш ќе бидете апсолутно сигурни дека за време на испитот, кога нема начин да користите лист за мамење, можете лесно да ги добиете ако се појави потреба.