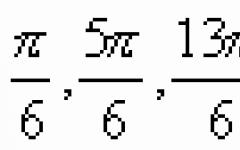Во механиката, надворешните сили во однос на даден систем на материјални точки (т.е. таков збир на материјални точки во кои движењето на секоја точка зависи од позициите или движењата на сите други точки) се оние сили кои го претставуваат дејството на другите тела на овој систем (други системи на материјални точки) кои не се вклучени од нас во овој систем. Внатрешните сили се сили на интеракција помеѓу поединечни материјални точки на даден систем. Поделбата на силите на надворешни и внатрешни е целосно условена: кога се менува дадениот состав на системот, некои сили кои претходно биле надворешни можат да станат внатрешни и обратно. Така, на пример, кога се размислува
движењето на системот кој се состои од земјата и нејзиниот сателит месечината, силите на интеракцијата помеѓу овие тела ќе бидат внатрешни сили за овој систем, а гравитационите сили на сонцето, преостанатите планети, нивните сателити и сите ѕвезди ќе бидат надворешни сили во однос на наведениот систем. Но, ако го промениме составот на системот и го сметаме движењето на сонцето и сите планети како движење на една заеднички систем, потоа надворешен силите ќе бидат само силите на привлекување што ги вршат ѕвездите; сепак, силите на интеракција помеѓу планетите, нивните сателити и сонцето стануваат внатрешни сили за овој систем. На ист начин, ако, кога се движи парната локомотива, го избереме клипот на цилиндерот за пареа како посебен системматеријални точки предмет на нашето разгледување, тогаш притисокот на пареата врз клипот во однос на него ќе биде надворешна сила, а истиот парен притисок ќе биде еден од внатрешните сили, ако го земеме предвид движењето на целата локомотива како целина; во овој случај, надворешните сили во однос на целата локомотива, земени како еден систем, ќе бидат: триење помеѓу шините и тркалата на локомотивата, гравитацијата на локомотивата, реакцијата на шините и отпорот на воздухот; внатрешните сили ќе бидат сите сили на интеракција помеѓу деловите на локомотивата, на пример. силите на интеракција помеѓу пареата и клипот на цилиндерот, помеѓу лизгачот и неговите паралели, помеѓу поврзувачката шипка и иглата на чудакот итн. Како што гледаме, во суштина нема разлика помеѓу надворешните и внатрешните сили, релативната разлика меѓу нив се одредува само во зависност од тоа кои тела ги вклучуваме во системот што се разгледува и кои сметаме дека не се вклучени во системот. Сепак, посочената релативна разлика во силите е многу значајна кога се проучува движењето на даден систем; според третиот закон на Њутн (за еднаквост на дејство и реакција), внатрешните сили на интеракција помеѓу секоја две материјални точки на системот се еднакви по големина и насочени по истата права линија во спротивни насоки; Благодарение на ова, кога се решаваат различни прашања за движењето на системот на материјални точки, можно е да се исклучат сите внатрешни сили од равенките на движење на системот и со тоа да се овозможи проучување на движењето на целиот систем. Овој метод на елиминирање на внатрешните, во повеќето случаи непознати, сили на спојување е од суштинско значење за изведување на различни закони на механиката на системот.
Апсолутно еластично влијание- судир на две тела, како резултат на кој не остануваат никакви деформации во двете тела кои учествуваат во судирот и целата кинетичка енергија на телата пред ударот по ударот повторно се претвора во првобитната кинетичка енергија (забележете дека ова е идеализирана случај).
За апсолутно еластично влијание, законот за зачувување на кинетичката енергија и законот за зачувување на импулсот се задоволени.
Да ги означиме брзините на топчињата со маси m 1 и m 2 пред ударот ν 1И ν 2, по удар - преку ν 1"И ν 2"(сл. 1). За директно централно влијание, векторите на брзината на топчињата пред и по ударот лежат на права линија што минува низ нивните центри. Проекциите на векторите на брзина на оваа линија се еднакви на модулите за брзина. Ќе ги земеме предвид нивните насоки користејќи знаци: позитивните ќе бидат поврзани со движење надесно, негативните со движење налево.
Сл.1
Според овие претпоставки, законите за заштита имаат форма
(1)
(2)
Откако ги направивме соодветните трансформации во изразите (1) и (2), добиваме
(3)
(4)
Решавајќи ги равенките (3) и (5), наоѓаме
(7)
Ајде да погледнеме неколку примери.
1. Кога ν 2=0
(8) 
(9)
Да ги анализираме изразите (8) во (9) за две топчиња со различна маса:
а) m 1 = m 2. Ако втората топка висеше неподвижна пред ударот ( ν 2=0) (сл. 2), потоа по ударот првата топка ќе застане ( ν 1"=0), а втората ќе се движи со иста брзина и во иста насока во која се движела првата топка пред ударот ( ν 2"=ν 1);
Сл.2
б) m 1 > m 2. Првата топка продолжува да се движи во иста насока како и пред ударот, но со помала брзина ( ν 1"<ν 1). Брзината на втората топка по ударот е поголема од брзината на првата топка по ударот ( ν 2">ν 1") (сл. 3);
Сл.3
в) m 1
Сл.4
г) m 2 >>m 1 (на пример, судир на топка со ѕид). Од равенките (8) и (9) произлегува дека ν 1"= -ν 1; ν 2"≈ 2 m 1 ν 2"/m2.
2. Кога m 1 =m 2 изразите (6) и (7) ќе имаат форма ν 1"= ν 2; ν 2"= ν 1; односно топките со еднаква маса се чини дека разменуваат брзини.
Апсолутно нееластично влијание- судир на две тела, како резултат на што телата се поврзуваат, движејќи се понатаму како единствена целина. Апсолутно нееластичен удар може да се докаже со помош на топчиња од пластелин (глина) кои се движат една кон друга (сл. 5).
Сл.5
Ако масите на топчињата се m 1 и m 2, нивните брзини пред ударот ν 1И ν 2, тогаш, користејќи го законот за зачувување на моментумот
Каде v- брзината на движење на топчињата по ударот. Потоа
(15.10)
Ако топчињата се движат една кон друга, тие заедно ќе продолжат да се движат во насока во која топката се движела со голема динамика. Во конкретниот случај, ако масите на топчињата се еднакви (m 1 = m 2), тогаш
Дозволете ни да одредиме како се менува кинетичката енергија на топчињата при централно апсолутно нееластично влијание. Бидејќи при судир на топки меѓу нив има сили кои зависат од нивните брзини, а не од самите деформации, имаме работа со дисипативни сили слични на силите на триење, затоа законот за зачувување на механичката енергија во овој случај не треба да се почитува. . Поради деформација доаѓа до намалување на кинетичката енергија која преминува во топлинска или во други форми на енергија. Ова намалување може да се определи со разликата во кинетичката енергија на телата пред и по ударот:
Користејќи го (10), добиваме
Ако погоденото тело првично било неподвижно (ν 2 =0), тогаш
Кога m 2 >>m 1 (масата на неподвижното тело е многу голема), тогаш ν <<ν 1и практично целата кинетичка енергија на телото се претвора во други форми на енергија при удар. Затоа, на пример, за да се добие значителна деформација, наковалната мора да биде многу помасивна од чеканот. Напротив, кога зачукувате клинци во ѕид, масата на чеканот треба да биде многу поголема (m 1 >>m 2), потоа ν≈ν 1 и речиси целата енергија се троши на поместување на шајката што е можно повеќе. а не на резидуална деформација на ѕидот.
Целосно нееластично влијание е пример за губење на механичка енергија под влијание на силите на дисипација.
1. Работа со променлива сила.
Да разгледаме материјална точка која се движи под влијание на силата P во права линија. Ако ефективна силае константна и насочена по права линија, а поместувањето е еднакво на s, тогаш, како што е познато од физиката, работата А на оваа сила е еднаква на производот Ps. Сега да изведеме формула за пресметување на работата направена од променлива сила.
Нека точка се движи по оската Ox под влијание на сила, чија проекција на оската Ox е функција од f од x. Во овој случај ќе претпоставиме дека f е континуирана функција. Под влијание на оваа сила, материјалната точка се пресели од точката М (а) до точката М (б) (сл. 1, а). Да покажеме дека во овој случај работата на А се пресметува со формулата
(1)
Да го поделиме сегментот [a; b] во n сегменти со иста должина Тоа се отсечките [a; x 1 ], ,..., (сл. 1.6). Работа на сила на целиот сегмент [a; b] е еднаков на збирот на работата направена од оваа сила на добиените сегменти. Бидејќи f е континуирана функција на x, за доволно мал сегмент [a; x 1 ] работата што ја врши силата на оваа отсечка е приближно еднаква на f (a) (x 1 -a) (го занемаруваме фактот дека f се менува на отсечката). Слично на тоа, работата што ја врши силата на вториот сегмент е приближно еднаква на f (x 1) (x 2 - x 1), итн.; работата што ја врши силата на n-тиот сегмент е приближно еднаква на f (x n-1)(b - x n-1). Следствено, работата на сила на целиот сегмент [a; b] е приближно еднаква на:
а точноста на приближната еднаквост е поголема, толку пократки се отсечките на кои е поделена отсечката [a;b] Секако, оваа приближна еднаквост станува точна ако претпоставиме дека n→∞:
Бидејќи A n се стреми кон интегралот на функцијата што се разгледува од a до b како n →∞, се добива формула (1).
2. Моќ.
Моќта P е стапката на извршената работа,
Тука v е брзина материјална точка, на кој се применува силата
Сите сили што се среќаваат во механиката обично се поделени на конзервативни и неконзервативни.
Силата што дејствува на материјална точка се нарекува конзервативна (потенцијална) ако работата што ја врши оваа сила зависи само од почетната и крајната положба на точката. Работата на конзервативната сила не зависи ниту од типот на траекторијата ниту од законот за движење на материјалната точка долж траекторијата (види слика 2): 
.
Промената на правецот на движење на точка по мала површина на спротивна предизвикува промена на знакот на елементарната работа, затоа, . Затоа, работата на конзервативна сила долж затворена траекторија 1 а 2б 1 е еднакво на нула: 
.
Точки 1 и 2, како и делови од затворена траекторија 1 а 2 и 2 б 1 може да се избере сосема произволно. Така, работата на конзервативна сила долж произволна затворена траекторија L на точката на нејзината примена е еднаква на нула:
Во оваа формула, кругот на интегралниот знак покажува дека интеграцијата се изведува по затворена патека. Често затворена траекторија Лнаречен затворена јамка Л(сл. 3). Обично се одредува со насоката на преминување на контурата Лво насока на стрелките на часовникот. Насоката на векторот на елементарното поместување се совпаѓа со насоката на преминувањето на контурата Л. Во овој случај, формулата (5) вели: циркулацијата на векторот по затворена јамка L е еднаква на нула.
Треба да се забележи дека силите на гравитација и еластичност се конзервативни, а силите на триење се неконзервативни. Всушност, бидејќи силата на триење е насочена во насока спротивна на поместувањето или брзината, работата на силите на триење по затворена патека е секогаш негативна и, според тоа, не е еднаква на нула.
Дисипативен систем(или дисипативна структура, од лат. дисипација- „растури, уништи“) е отворен систем кој работи далеку од термодинамичка рамнотежа. Со други зборови, ова е стабилна состојба која се јавува во нерамнотежна средина под услов на дисипација (дисипација) на енергијата што доаѓа однадвор. Понекогаш се нарекува и дисипативен систем стационарни отворен систем или нерамнотежен отворен систем.
Дисипативниот систем се карактеризира со спонтан изглед на сложена, често хаотична структура. Карактеристична карактеристикатакви системи - незачувување на волуменот во фазен простор, односно неисполнување на Лиувиловата теорема.
Едноставен примерТаков систем се Бенардовите клетки. Колку повеќе сложени примеринаречени ласери, реакцијата Белоусов-Жаботински и биолошкиот живот.
Терминот „дисипативна структура“ беше воведен од Илја Пригожин.
Неодамнешните истражувања во областа на „дисипативните структури“ ни овозможуваат да заклучиме дека процесот на „самоорганизација“ се случува многу побрзо во присуство на надворешен и внатрешен „шум“ во системот. Така, ефектите од бучавата доведуваат до забрзување на процесот на „самоорганизација“.
Кинетичка енергија
енергија механички систем, во зависност од брзината на движење на неговите точки. К.е. Тматеријалната точка се мери со половина производ од масата мод оваа точка по квадратот на неговата брзина υ, т.е. Т = 1/ 2 mυ 2 . К.е. механички систем е еднаков на аритметичка сумаК.е. сите негови точки: Т =Σ 1/2 m k υ 2 k.Изразот K. e. системи може да се претстават и во форма Т = 1 / 2 Mυ s 2 + Tc,Каде М- маса на целиот систем, υ в- брзина на центарот на масата, Tc - К.е. систем во своето движење околу центарот на масата. К.е. солидна, движејќи се преведувачки, се пресметува на ист начин како и K. e. точка со маса еднаква на масатацело тело. Формули за пресметување на K. e. на тело што ротира околу фиксна оска, види чл. Ротационо движење.
Промена во K. e. систем кога се поместува од својата позиција (конфигурација) 1
да се позиционира 2
се јавува под влијание на надворешни и внатрешни сили кои се применуваат на системот и е еднаков на збирот на работата 
.
Оваа еднаквост ја изразува теоремата за промена на динамичката енергија, со чија помош се решаваат многу проблеми на динамиката.
При брзини блиски до брзината на светлината, К.е. материјална точка
Каде m 0- маса на точка во мирување, Со- брзина на светлината во вакуум ( m 0 s 2- енергија на точка во мирување). при мали брзини ( υ<< c ) последната релација оди во вообичаената формула 1/2 mυ 2.
Кинетичка енергија.
Кинетичка енергија - енергија на тело во движење. (Од грчкиот збор кинема - движење). По дефиниција, кинетичката енергија на телото во мирување во дадена референтна рамка исчезнува.
Оставете го телото да се движи под влијание константнасила во насока на силата.
Потоа: 
.
Бидејќи движењето подеднакво се забрзува, тогаш: .
Оттука: 
.
- кинетичка енергија се нарекува
Силите кои дејствуваат на која било точка на механичкиот систем се поделени на внатрешни и надворешни.
Фи- внатрешна сила
Fe- надворешна сила
Внатрешнасе нарекуваат сили со кои точките вклучени во системот делуваат една на друга.
Надворешенсе нарекуваат сили кои се применуваат на точки однадвор, односно од други точки или тела кои не се вклучени во системот. Поделбата на силите на внатрешни и надворешни е условена.
mg – надворешна сила
Ftr - внатрешна сила
Механички систем. Надворешни и внатрешни сили.
Механички систем на материјални точки или тела е збир од нив во кој положбата или движењето на секоја точка (или тело) зависи од положбата и движењето на сите други.
Материјалното апсолутно цврсто тело ќе го разгледаме и како систем на материјални точки кои го формираат ова тело и се меѓусебно поврзани на таков начин што растојанијата меѓу нив не се менуваат и остануваат постојани цело време.
Класичен пример за механички систем е Сончевиот систем, во кој сите тела се поврзани со сили на взаемна привлечност. Друг пример за механички систем е секоја машина или механизам во кој сите тела се поврзани со шарки, прачки, кабли, ремени итн. (т.е. различни геометриски врски). Во овој случај, телата на системот се предмет на меѓусебни сили на притисок или напнатост што се пренесуваат преку врски.
Збирка тела меѓу кои нема сили на интеракција (на пример, група авиони кои летаат во воздух) не формира механички систем.
Во согласност со кажаното, силите што дејствуваат на точките или телата на системот можат да се поделат на надворешни и внатрешни.
Надворешните сили се оние кои дејствуваат на точките на системот од точките или телата кои не се дел од дадениот систем.
Внатрешните сили се оние кои дејствуваат на точките на системот од други точки или тела од истиот систем. Надворешните сили ќе ги означиме со симболот - , а внатрешните сили со - .
И надворешните и внатрешните сили, за возврат, можат да бидат или активни или реакции на врски.
Реакциите на врските, или едноставно реакциите, се сили кои го ограничуваат движењето на точките во системот (нивните координати, брзината итн.). Во статиката тоа беа сили кои ги заменуваат врските. Во динамиката, за нив се воведува поопшта дефиниција.
Сите други сили се нарекуваат активни или дадени сили, сè освен реакции.
Неопходноста од оваа класификација на силите ќе стане јасна во следните поглавја.
Поделбата на силите на надворешни и внатрешни е условена и зависи од движењето на кој систем на тела го разгледуваме. На пример, ако го земеме предвид движењето на целиот Сончев систем како целина, тогаш силата на привлекување на Земјата кон Сонцето ќе биде внатрешна; при проучување на движењето на Земјата во нејзината орбита околу Сонцето, истата сила ќе се смета за надворешна.
Внатрешните сили ги имаат следниве својства:
1. Геометрискиот збир (главен вектор) на сите внатрешни сили F12 и F21 на системот е еднаков на нула. Всушност, според третиот закон за динамика, кои било две точки на системот (сл. 31) делуваат една на друга со еднакви по големина и спротивно насочени сили и чиј збир е еднаков на нула. Бидејќи сличен резултат важи за кој било пар точки во системот, тогаш
2. Збирот на моменти (главен момент) на сите внатрешни сили на системот во однос на кој било центар или оска е еднаков на нула. Навистина, ако земеме произволен центар О, тогаш од Сл. 18 е јасно дека . Сличен резултат ќе се добие и при пресметување на моментите околу оската. Затоа, за целиот систем ќе има:
Меѓутоа, од докажаните својства не произлегува дека внатрешните сили се меѓусебно избалансирани и не влијаат на движењето на системот, бидејќи овие сили се применуваат на различни материјални точки или тела и можат да предизвикаат меѓусебни движења на овие точки или тела. Внатрешните сили ќе бидат избалансирани кога системот што се разгледува е апсолутно цврсто тело.
30 Теорема за движење на центарот на масата.
Тежина на системот е еднаков на алгебарскиот збир на масите на сите точки или тела на системот во еднообразно гравитационо поле, за кое тежината на која било честичка од телото е пропорционална на нејзината маса. Според тоа, распределбата на масите во едно тело може да се определи со положбата на неговиот центар на гравитација - геометриската точка C, чии координати се нарекуваат центар на маса или центар на инерција на механички систем
Теорема за движењето на центарот на масата на механички систем : центарот на масата на механичкиот систем се движи како материјална точка чија маса е еднаква на масата на системот и на која се применуваат сите надворешни сили кои делуваат на системот
Заклучоци:
Механички систем или круто тело може да се смета за материјална точка во зависност од природата на неговото движење, а не од нејзината големина.
Внатрешните сили не се земени предвид со теоремата за движење на центарот на масата.
Теоремата за движењето на центарот на масата не го карактеризира ротационото движење на механичкиот систем, туку само преводното
Закон за зачувување на движењето на центарот на масата на системот:
1. Ако збирот на надворешните сили (главниот вектор) е постојано еднаков на нула, тогаш центарот на масата на механичкиот систем е во мирување или се движи рамномерно и праволиниско.
2. Ако збирот на проекциите на сите надворешни сили на која било оска е еднаков на нула, тогаш проекцијата на брзината на центарот на масата на системот на истата оска е константна вредност.
Равенката ја изразува теоремата за движењето на центарот на масата на системот: производот од масата на системот и забрзувањето на неговиот центар на маса е еднаков на геометрискиот збир на сите надворешни сили што делуваат на системот. Споредувајќи се со равенката на движење на материјална точка, добиваме уште еден израз на теоремата: центарот на масата на системот се движи како материјална точка, чија маса е еднаква на масата на целиот систем и на која сите надворешни се применуваат сили кои делуваат на системот.
Ако изразот (2) е ставен во (3), имајќи го предвид фактот дека добиваме:
(4’) – ја изразува теоремата за движењето на центарот на масата на системот: центарот на масата на системот се движи како материјална точка на која дејствуваат сите сили на системот.
Заклучоци:
1. Внатрешните сили не влијаат на движењето на центарот на масата на системот.
2. Ако , движењето на центарот на масата на системот се случува со константна брзина.
3., тогаш движењето на центарот на масата на системот во проекција на оската се случува со постојана брзина.
Овие равенки се диференцијални равенки на движење на центарот на масата во проекции на оските на Декартовиот координатен систем.
Значењето на докажаната теорема е следново.
1) Теоремата дава оправдување за методите на динамика на точки. Од равенките јасно се гледа дека решенијата што ги добиваме со разгледување на дадено тело како материјална точка го одредуваат законот за движење на центарот на масата на ова тело, т.е. имаат многу специфично значење.
Особено, ако телото се движи транслативно, тогаш неговото движење е целосно определено со движењето на центарот на масата. Така, преводно подвижно тело секогаш може да се смета како материјална точка со маса еднаква на масата на телото. Во други случаи, телото може да се смета за материјална точка само кога, практично, за да се одреди положбата на телото доволно е да се знае положбата на неговиот центар на маса.
2) Теоремата дозволува, при одредување на законот за движење на центарот на масата на кој било систем, да се исклучат од разгледување сите претходно непознати внатрешни сили. Ова е неговата практична вредност.
Така, движењето на автомобилот на хоризонтална рамнина може да се случи само под влијание на надворешни сили, сили на триење кои дејствуваат на тркалата од патот. И сопирањето на автомобилот е исто така можно само со овие сили, а не со триење помеѓу влошките на сопирачките и барабанот на сопирачката. Ако патот е мазен, тогаш колку и да ги сопирате тркалата, тие ќе се лизгаат и нема да го запрат автомобилот.
Или по експлозијата на летечки проектил (под влијание на внатрешните сили), неговите делови, фрагменти, ќе се распрснат така што нивниот центар на маса ќе се движи по истата траекторија.
Теоремата за движењето на центарот на масата на механичкиот систем треба да се користи за решавање на проблемите на механиката кои бараат:
Користејќи ги силите што се применуваат на механички систем (најчесто на цврсто тело), утврдете го законот за движење на центарот на масата;
Според дадениот закон за движење на телата вклучени во механички систем, најдете ги реакциите на надворешните врски;
Врз основа на даденото меѓусебно движење на телата вклучени во механичкиот систем, определи го законот за движење на овие тела во однос на некој фиксен референтен систем.
Користејќи ја оваа теорема, можете да создадете една од равенките на движење на механички систем со неколку степени на слобода.
При решавање на проблеми, често се користат последиците од теоремата за движењето на центарот на масата на механичкиот систем.
Заклучок 1. Ако главниот вектор на надворешните сили што се применуваат на механички систем е еднаков на нула, тогаш центарот на масата на системот мирува или се движи рамномерно и праволиниско. Бидејќи забрзувањето на центарот на масата е нула, .
Заклучок 2. Ако проекцијата на главниот вектор на надворешни сили на која било оска е нула, тогаш центарот на масата на системот или не ја менува својата положба во однос на оваа оска или се движи рамномерно во однос на него.
На пример, ако две сили почнат да дејствуваат на тело, формирајќи пар сили (сл. 38), тогаш неговиот центар на маса C ќе се движи по истата траекторија. И самото тело ќе ротира околу центарот на масата. И не е важно каде се применуваат неколкуте сили.
Механички системе збир на материјални точки или тела во кои положбата или движењето на секоја точка или тело зависи од положбата и движењето на сите други. Така, на пример, кога го проучуваме движењето на Земјата и Месечината во однос на Сонцето, севкупноста на Земјата и Месечината е механички систем кој се состои од две материјални точки кога проектилот се распаѓа на фрагменти, ги сметаме фрагментите како; механички систем. Механички систем е секој механизам или машина.
Ако растојанијата помеѓу точките на механичкиот систем не се менуваат кога системот се движи или мирува, тогаш таквиот механички систем се нарекува непроменливи.
Концептот на непроменлив механички систем ни овозможува да го проучуваме произволното движење на цврстите тела во динамика. Во овој случај, како и во статиката и кинематиката, со круто тело ќе разбереме материјално тело во кое растојанието помеѓу секоја две точки не се менува кога телото се движи или мирува. Секое цврсто тело може ментално да се подели на доволно голем број доволно мали делови, чија целина приближно може да се смета како механички систем. Бидејќи цврстото тело формира континуирано продолжување, за да се утврдат неговите точни (и не приближни) својства, неопходно е да се изврши ограничувачка транзиција, крајна фрагментација на телото, кога големините на разгледуваните делови од телото истовремено имаат тенденција да нула.
Така, познавањето на законите за движење на механичките системи ни овозможува да ги проучуваме законите за произволно движење на цврсти тела.
Сите сили што дејствуваат на точките на механичкиот систем се поделени на надворешни и внатрешни сили.
Надворешните сили во однос на даден механички систем се сили кои дејствуваат на точките на овој систем од материјални точки или тела кои не се вклучени во системот.Ознаки: - надворешна сила применета на та точка; 
-главниот вектор на надворешни сили; 
- главниот момент на надворешните сили во однос на полот.
Внатрешни сили се силите со кои материјалните точки или телата вклучени во даден механички систем дејствуваат на точки или тела од истиот систем.Со други зборови, внатрешните сили се сили на интеракција помеѓу точките или телата на даден механички систем. Ознаки: - внатрешна сила применета на та точка; 
-главниот вектор на внатрешните сили; 
- главниот момент на внатрешните сили во однос на полот.
3.2 Својства на внатрешните сили.
Првиот имот.Главниот вектор на сите внатрешни сили на механичкиот систем е еднаков на нула, т.е
. (3.1)
Втор имот.Главниот момент на сите внатрешни сили на механичкиот систем во однос на кој било пол или оска е еднаков на нула, т.е.
, 
. (3.2)
|
За да ги докажеме овие својства, забележуваме дека со оглед на тоа што внатрешните сили се сили на интеракција на материјалните точки вклучени во системот, тогаш според третиот закон на Њутн, кои било две точки на системот (сл. 17) дејствуваат една на друга со сили и еднакви во големина и спротивен во насока. Така, за секоја внатрешна сила постои директно спротивна внатрешна сила и, според тоа, внатрешните сили формираат одреден сет на парно спротивни сили. Но, геометрискиот збир на две директно спротивни сили е нула, така
.
Како што беше прикажано во статиката, геометрискиот збир на моментите на две директно спротивни сили во однос на истиот пол е еднаков на нула, затоа
.
Сличен резултат се добива при пресметување на главниот момент околу оската
.
3.3 Диференцијални равенки на движење на механички систем.
Да разгледаме механички систем кој се состои од материјални точки чии маси се . За секоја точка ја применуваме основната равенка на динамиката на точките
, 
,
, (3.3)
de е резултат на надворешните сили применети на та точка и е резултат на внатрешните сили.
Се нарекува системот на диференцијални равенки (3.3). диференцијални равенки на движење на механички систем во векторска форма.
Проектирајќи ги векторските равенки (3.3) на правоаголни Декартови координатни оски, ги добиваме диференцијални равенки на движење на механички систем во координатна форма:
,
, (3.4)
,
.
Овие равенки се систем на обични диференцијални равенки од втор ред. Следствено, за да се најде движењето на механичкиот систем според дадените сили и почетните услови за секоја точка од овој систем, потребно е да се интегрира систем на диференцијални равенки. Интегрирањето на системот на диференцијални равенки (3.4), општо земено, е поврзано со значителни, честопати непремостливи, математички тешкотии. Меѓутоа, во теоретската механика, развиени се методи кои овозможуваат да се заобиколат главните тешкотии што се јавуваат при користење на диференцијални равенки на движење на механички систем во форма (3.3) или (3.4). Тие вклучуваат методи кои обезбедуваат општи теореми за динамиката на механичкиот систем, воспоставувајќи ги законите на промена во некои вкупни (интегрални) карактеристики на системот како целина, а не моделите на движење на неговите поединечни елементи. Тоа се таканаречените мерки на движење - главниот вектор на импулсот; главен момент на моментум; кинетичка енергија. Знаејќи ја природата на промената на овие количини, можно е да се формира делумна, а понекогаш и целосна слика за движењето на механичкиот систем.
IV. ОСНОВНИ (ОПШТИ) ТЕОРЕМИ НА ДИНАМИКА НА ТОЧКА И СИСТЕМ
4.1 Теорема за движењето на центарот на масата.
4.1.1 Центар на маса на механички систем.
Да разгледаме механички систем кој се состои од материјални точки чии маси се .
Масата на механичкиот систем,што се состои од материјални точки, збирот на масите на точките на системот ќе го наречеме:
Дефиниција.Центарот на масата на механичкиот систем е геометриска точка, чиј вектор на радиус се одредува со формулата:
каде е векторот на радиусот на центарот на масата; -радиус вектори на системски точки; -нивните маси (сл. 18).
; 
; . (4.1")
Центарот на маса не е материјална точка, туку геометриски. Може да не се совпаѓа со која било материјална точка на механичкиот систем. Во еднообразно гравитационо поле, центарот на масата се совпаѓа со центарот на гравитација. Сепак, ова не значи дека концептите на центар на маса и центар на гравитација се исти. Концептот на центар на маса е применлив за сите механички системи, а концептот на центар на гравитација е применлив само за механички системи кои се под влијание на гравитацијата (односно привлекување кон Земјата). Така, на пример, во небесната механика, кога се разгледува проблемот со движењето на две тела, на пример Земјата и Месечината, може да се земе предвид центарот на масата на овој систем, но не може да се земе предвид центарот на гравитација.
Така, концептот центар на маса е поширок од концептот центар на гравитација.
4.1.2. Теорема за движењето на центарот на масата на механички систем.
Теорема. Центарот на масата на механичкиот систем се движи како материјална точка, чија маса е еднаква на масата на целиот систем и на која се применуваат сите надворешни сили кои делуваат на системот, т.е.
.
(4.2)
Еве -главниот вектор на надворешни сили.
Доказ. Да разгледаме механички систем, чии материјални точки се движат под влијание на надворешни и внатрешни сили. е резултат на надворешните сили кои се применуваат на та точка и е резултат на внатрешните сили. Според (3.3), равенката на движење на та точка има форма
, .
Додавајќи ја левата и десната страна на овие равенки, добиваме
.
Бидејќи главниот вектор на внатрешните сили е еднаков на нула (дел 3.2, прво својство), тогаш
.
Ајде да ја трансформираме левата страна на оваа еднаквост. Од формулата (4.1), која го одредува векторот на радиусот на центарот на масата, следува:
.
Во текот на следново ќе претпоставиме дека се разгледуваат само механички системи со постојан состав, односно и . Да го земеме вториот извод во однос на времето од двете страни на оваа еднаквост
Бидејќи 
, -
забрзување на центарот на масата на системот, потоа, конечно,
.
Проектирајќи ги двете страни на оваа векторска еднаквост на координатните оски, добиваме:
,
, (4.3)
,
каде , , се проекции на сила;
Проекции на главниот вектор на надворешни сили на координатните оски.
Равенки (4.3) - диференцијални равенки на движење на центарот на масата на механички систем во проекции на Декартови координатни оски.
Од равенките (4.2) и (4.3) произлегува дека Само внатрешните сили не можат да ја променат природата на движењето на центарот на масата на механичкиот систем.Внатрешните сили можат да имаат индиректно влијание врз движењето на центарот на маса само преку надворешни сили. На пример, во автомобил, внатрешните сили развиени од моторот влијаат на движењето на центарот на масата низ силите на триење на тркалата и патот.
4.1.3. Закони за зачувување на движењето на центарот на масата
(последици од теоремата).
Од теоремата за движењето на центарот на масата може да се добијат следните последици.
Заклучок 1.Ако главниот вектор на надворешните сили што дејствуваат на системот е нула, тогаш неговиот центар на маса е во мирување или се движи праволиниски и рамномерно.
Навистина, ако главниот вектор на надворешни сили е , тогаш од равенката (4.2):
Ако, особено, почетната брзина на центарот на маса е , тогаш центарот на маса е во мирување. Ако почетната брзина е , тогаш центарот на масата се движи праволиниско и рамномерно.
Заклучок 2.Ако проекцијата на главниот вектор на надворешни сили на која било фиксна оска е нула, тогаш проекцијата на брзината на центарот на масата на механичкиот систем на оваа оска не се менува.
Оваа последица произлегува од равенките (4.3). Нека, на пример, тогаш
,
од тука. Ако во почетниот момент, тогаш:
односно проекцијата на центарот на масата на механичкиот систем на оската во овој случај нема да се движи по оската. Ако , тогаш проекцијата на центарот на масата на оската се движи рамномерно.
4.2 Количина на движење на точка и систем.
Теорема за промена на моментумот.
4.2.1. Количината на движење на точка и систем.
Дефиниција.Количеството на движење на материјалната точка е вектор еднаков на производот од масата на точката и нејзината брзина, т.е.
. (4.5)
Вектор колинеарна со векторот и насочена тангенцијално на траекторијата на материјалната точка (сл. 19).
Импулсот на точка во физиката често се нарекува импулс на материјална точка.
Димензијата на моментумот во SI-kg·m/s или N·s.
Дефиниција.Количеството на движење на механички систем е вектор еднаков на векторскиот збир на количините на движења (главниот вектор на количините на движења) на поединечните точки вклучени во системот, т.е.
(4.6)
Проекции на импулсот на правоаголните Декартови координатни оски:
Вектор на моментум на системот за разлика од векторот на моментум на точка, тој нема точка на примена. Векторот на импулсот на точката се применува на најдвижечката точка, а векторот е слободен вектор.
Лема на количества на движење.Импулсот на механичкиот систем е еднаков на масата на целиот систем помножена со брзината на неговиот центар на маса, т.е.
Доказ. Од формулата (4.1), која го одредува векторот на радиусот на центарот на масата, следува:
.
Да го земеме временскиот дериват на двете страни
, или 
.
Од тука добиваме
, што требаше да се докаже.
Од формулата (4.8) е јасно дека ако телото се движи на таков начин што неговиот центар на маса останува неподвижен, тогаш моментумот на телото е еднаков на нула. На пример, количината на движење на тело што ротира околу фиксна оска што минува низ неговиот центар на маса (сл. 20),
, бидејќи
Ако движењето на телото е рамно-паралелно, тогаш количината на движење нема да го карактеризира ротациониот дел од движењето околу центарот на масата. На пример, за тркало што се тркала (сл. 21), без оглед на тоа како тркалото се врти околу центарот на масата. Количината на движење го карактеризира само преводниот дел од движењето заедно со центарот на масата.
4.2.2. Теорема за промена на импулсот на механички систем
во диференцијална форма.
Теорема.Временскиот дериват на импулсот на механичкиот систем е еднаков на геометрискиот збир (главниот вектор) на надворешните сили што дејствуваат на овој систем, т.е.
.
(4.9)
Доказ. Да разгледаме механички систем кој се состои од материјални точки чии маси се ; -резултант на надворешните сили применети на та точка. Во согласност со лемата на импулсот, формула (4.8):
Да го земеме дериватот во однос на времето од двете страни на оваа еднаквост
.
Десната страна на оваа еднаквост од теоремата за движење на центарот на масата е формулата (4.2):
.
Конечно:
а теоремата е докажана .
Во проекции на правоаголни Декартови координатни оски:
; 
; 
, (4.10)
односно временскиот дериват на проекцијата на импулсот на механичкиот систем на која било координатна оска е еднаков на збирот на проекциите (проекцијата на главниот вектор) на сите надворешни сили на системот на истата оска.
4.2.3. Закони за зачувување на импулсот
(последици од теоремата)
Заклучок 1.Ако главниот вектор на сите надворешни сили на механичкиот систем е еднаков на нула, тогаш количината на движење на системот е константна по големина и насока.
Навистина, ако 
,
тогаш од теоремата за промената на импулсот, односно од еднаквоста (4.9) произлегува дека
Заклучок 2.Ако проекцијата на главниот вектор на сите надворешни сили на механичкиот систем на одредена фиксна оска е еднаква на нула, тогаш проекцијата на моментумот на системот на оваа оска останува константна.
Нека проекцијата на главниот вектор на сите надворешни сили на оската е еднаква на нула: 
. Потоа од првата еднаквост (4.10):
4.2.4. Теорема за промена на импулсот на механички систем
во интегрална форма.
Елементарен импулс на силасе нарекува векторска големина еднаква на производот на векторот на сила и елементарен временски интервал
. (4.11)
Насоката на елементарниот импулс се совпаѓа со насоката на векторот на силата.
Присилувајте импулс во одреден временски периодеднаков на одреден интеграл на елементарниот моментум
. (4.12)
Ако силата е константна по големина и насока (), тогаш нејзиниот импулс со текот на времето е еднакво на:
Проекции на импулсот на силата на координатните оски:
Да ја докажеме теоремата за промената на импулсот на механички систем во интегрална форма.
Теорема.Промената на моментумот на механичкиот систем во одреден временски период е еднаква на геометрискиот збир на импулсите на надворешните сили на системот во истиот временски период, т.е.
(4.14)
Доказ. Нека во моментот количината на движење на механичкиот систем е еднаква, а во моментот на времето -; - импулс на надворешна сила која делува на та точка во времето.
Ја користиме теоремата за промена на импулсот во диференцијална форма - еднаквост (4.9):
.
Помножувајќи ги двете страни на оваа еднаквост со и интегрирајќи ги во опсегот од до , добиваме
, 
, 
.
Докажано е теоремата за промена на импулсот во интегрална форма.
Во проекциите на координатните оски според (4.14):
,
, (4.15)
.
4.3. Теорема за промена на аголниот моментум.
4.3.1. Кинетички момент на точка и систем.
Во статиката, концептите на моменти на сила во однос на полот и оската беа воведени и широко користени. Бидејќи моментумот на материјалната точка е вектор, можно е да се одредат неговите моменти во однос на полот и оската на ист начин како што се одредуваат моментите на сила.
Дефиниција. во однос на столбот се нарекува момент на неговиот вектор на импулс во однос на истиот пол, т.е.
. (4.16)
Моментум на материјална точка во однос на полот е вектор (сл. 22) насочен нормално на рамнината што ги содржи векторот и полот во насока од која векторот е во однос на полот видливи во спротивна насока од стрелките на часовникот. Векторски модул
еднаква на производот на модулот и кракот - должината на нормалната спуштена од столбот на линијата на дејство на векторот:
Аголниот моментум во однос на полот може да се претстави како векторски производ: аголниот момент на материјална точка во однос на полот е еднаков на векторскиот производ на радиусот на векторот извлечен од полот до точката со векторот на импулсот:
(4.17)
Дефиниција.Кинетички момент на материјална точкарелативно оска се нарекува моментот на неговиот вектор на импулс во однос на истата оска, т.е.
. (4.18)
Кинетички момент на материјална точка во однос на оската (сл. 23) е еднаков на производот од проекцијата на векторот земен со знак плус или минус на рамнина нормална на оската , на рамото на оваа проекција:
каде што рамо е должината на нормалната испуштена од точката крстосници на оските со рамнината на линијата на дејство на проекцијата и ако гледајќи кон оската , видлива е проекцијата во однос на точката насочен спротивно од стрелките на часовникот и на друг начин.
Димензијата на кинетичкиот момент во SI-kg m 2 /s, или N m s.
Дефиниција.Кинетичкиот момент или главниот момент на импулсот на механички систем во однос на полот е вектор еднаков на геометрискиот збир на кинетичките моменти на сите материјални точки на системот во однос на овој пол:
.
(4.19)
Дефиниција.Кинетичкиот момент или главниот момент на импулсот на механичкиот систем во однос на оската е алгебарскиот збир на кинетичките моменти на сите материјални точки на системот во однос на оваа оска:
. (4.20)
Кинетичките моменти на механички систем во однос на пол и оската што минува низ овој пол се поврзани со истата зависност како и главните моменти на системот на сили во однос на полот и оската:
-проекција на кинетичкиот момент на механички систем во однос на полот на оската ,минување низ овој пол е еднакво на аголниот моментум на системот во однос на оваа оска, т.е.
. (4.21)
4.3.2. Теореми за промена на кинетичкиот момент на механички систем.
Да разгледаме механички систем кој се состои од материјални точки чии маси се . Да докажеме теоремата за промената на аголниот моментум на механички систем во однос на полот.
Теорема.Временскиот дериват на кинетичкиот момент на механички систем во однос на фиксен пол е еднаков на главниот момент на надворешните сили на системот во однос на истиот пол, т.е.
.
(4.22)
Доказ. Ајде да избереме фиксен столб . Кинетичкиот момент на механичкиот систем во однос на овој пол, по дефиниција, е еднаквост (4.19):
.
Ајде да го разликуваме овој израз во однос на времето:
Да ја погледнеме десната страна на овој израз. Пресметување на дериватот на производот:
, (4.24)
Овде се зема предвид дека . Вектори и имаат иста насока, нивниот векторски производ е еднаков на нула, според тоа, првиот збир во еднаквост (4.24).
Надворешните сили се оние кои дејствуваат на телото од точки или тела кои не се дел од даденото тело или систем. Внатрешните сили се оние со кои точките на даденото тело делуваат една на друга.
Уништувањето или дури и едноставното откажување на структурниот елемент е можно само со зголемување на внатрешните сили и кога тие минуваат низ одредена ограничувачка бариера. Удобно е да се пресмета висината на оваа бариера од нивото што одговара на отсуството на надворешни сили. Во суштина, треба да се земат предвид само дополнителни внатрешни сили кои се појавуваат само во присуство на надворешни сили. Во механиката, овие дополнителни внатрешни сили едноставно се нарекуваат внатрешни сили во тесна, механичка смисла.
Внатрешните сили се одредуваат со помош на „метод на пресеци“, кој се заснова на прилично очигледна изјава: ако телото како целина е во рамнотежа, тогаш кој било дел изолиран од него е исто така во оваа состојба.
Слика 2.1.5
Да разгледаме прачка во рамнотежа под дејство на систем на надворешни сили, Сл. 2.1.5, а. Дозволете ни ментално да го поделиме на два дела користејќи го делот AB, Сл. 2.1.5, б. На секој од пресеците AB од левиот и десниот дел ќе примениме систем на сили што одговара на внатрешните сили што дејствуваат во вистинско тело, Сл. 1.7, в. Така, користејќи го методот на пресеци, внатрешните сили се претвораат во надворешни сили во однос на секој од отсечените делови на телото, што овозможува да се одредат од условите за рамнотежа на секој од овие делови посебно.
Делот AB може да се ориентира на кој било начин, но пресекот нормален на надолжната оска на шипката се покажува како попогоден за понатамошна дискусија.
Да ја воведеме следната нотација:
главни вектори и главни моменти на надворешни и внатрешни сили кои се применуваат на левиот пресечен дел. Земајќи ја предвид воведената нотација, условите за рамнотежа на ова тело може да се напишат како:
0, + =0 (2.1.1)
Слични изрази може да се состават за десниот отсечен дел од шипката. По едноставни трансформации можете да добиете:
=- , =- (2.1.1)
што може да се толкува како последица на познатиот закон на механиката: дејството е секогаш придружено со еднаква и спротивна реакција.
Во случај на решавање на проблемот на динамичко дејство на прачка, може да се свртиме кон добро познатиот принцип на d’Alembert, според кој на надворешните сили се додаваат инерцијални сили, што повторно го сведува проблемот на рамнотежни равенки. Затоа, постапката на методот на секција останува
Вредностите и не зависат од ориентацијата на делот AB (види Сл. 2.1.5). Сепак, во практични пресметки се чини најзгодно да се користи пресек. Во овој случај, нормалата на делот се совпаѓа со надолжната оска на шипката. Понатаму, главниот вектор и главниот момент на внатрешните сили обично се претставени во форма на нивните проекции на ортогоналните координатни оски, при што една од оските (на пример, оската x) е порамнета со споменатата нормала, види Сл. 2.1.6.
Слика 2.1.6
Да ги прошириме векторите , , , по координатните оски, Сл. 2.1.6, а-д. Компонентите на главниот вектор и главниот момент имаат општоприфатени имиња. Силата N x нормална на рамнината на пресекот се нарекува нормална (надолжна) сила, а Q x и Q y се нарекуваат попречни (сечење) сили. Моменти за секирите наИ z, т.е. M y и M z ќе бидат свиткување и моментот во однос на надолжната оска X, т.е. M x - вртежен момент.
Компонентите на главниот момент на внатрешните сили во отпорот на материјалите најчесто се прикажани како што е прикажано на сл. 2.1.6, г и ѓ.
Равенките за векторска рамнотежа може да се претстават како проекција на координатните оски:
Така, секоја компонента на главниот вектор за главниот момент на внатрешните сили се пресметува како збир на проекциите на сите надворешни сили на соодветната оска или како збир на моментите на сите надворешни сили во однос на оваа оска (земајќи ја предвид прифатеното правило за знак), кое се наоѓа на едната страна од делот.
Проекцијата на векторот на координатната оска, како скаларна големина, може да биде или позитивна или негативна. Ова зависи од тоа дали насоката на проекцијата се совпаѓа со позитивната или негативната насока на оската, соодветно. За внатрешните сили ова правило се почитува само за случајот кога нормално Xе надворешен, како што беше случајот со левиот отсечен дел на Сл. 2.1.6. Во ситуација кога нормално Xе внатрешен, видете го десниот отсечен дел на сл. 2.1.6, знакот на внатрешната сила се зема позитивен кога нејзината насока се совпаѓа со негативната насока на оската. На сл. 2.1.6 сите проекции на внатрешните сили N x , Q x , Q y , M x , M y и M z (и оние поврзани со левиот и оние поврзани со десните отсечени делови) се прикажани како позитивни.
Деформација, сила и цврстина.Јакоста на материјалите е дел од механиката која се занимава со дизајнирање на конструктивни елементи за цврстина, крутост и стабилност.
Јачината на материјалите се заснова на познавање на теоретската механика. Но, ако предметот на теоретската механика е апсолутно цврсто тело, тогаш силата на материјалите ги смета деформабилните цврсти материи.
Во пракса, вистинските делови од машините и конструкциите се изложени на различни видови сили. Под влијание на овие сили доаѓа до деформација на телата, т.е. промена на релативниот распоред на материјалните честички. Ако силите се доволно силни, можно е уништување на телото.
Способноста на телото да апсорбира товари без уништување и големи деформации се нарекува соодветно цврстина и ригидност.
Некои состојби на рамнотежа на телата и структурите се нестабилни, т.е. оние во кои помалите механички влијанија, обично од случајна природа, може да доведат до значителни отстапувања од овие услови. Ако отстапувањата се исто така мали, тогаш таквите состојби на рамнотежа се нарекуваат стабилни.
Надворешни сили.Надворешните сили што дејствуваат на структурата вклучуваат активни сили (оптоварувања) и реакции на надворешни врски. Постојат неколку видови на товари.
Концентрирана сила применета во точка. Се воведува наместо вистински сили кои делуваат на мала површина од површината на структурен елемент, чии димензии може да се занемарат.
Дистрибуирани сили. На пример, силите на притисокот на течноста на дното на садот се однесуваат на оптоварувањата распоредени по површината и се мерат во единици, а силите на тежината се однесуваат на оптоварувањата распределени над волуменот и измерени во единици. Во некои случаи, се внесува оптоварување распределено по должината на линијата, чиј интензитет се мери во
Една од опциите за оптоварување е концентриран момент (пар сили).
Внатрешни сили во шипката.Најчест структурен елемент е прачката, па затоа во цврстината на материјалите и се посветува главно внимание.
Надолжната оска и пресекот се главните геометриски елементи на шипката. Се претпоставува дека пресеците на шипката
нормално на надолжната оска, а надолжната оска поминува низ центрите на гравитација на пресеците.
Внатрешните сили на шипката се силите на интеракција помеѓу нејзините поединечни делови кои произлегуваат под влијание на надворешни сили (се претпоставува дека во отсуство на надворешни сили, внатрешните сили се еднакви на нула).
Да разгледаме прачка која е во рамнотежа под дејство на некој систем на надворешни сили (сл. 1, а). Ајде ментално да нацртаме произволен пресек кој ја дели шипката на два дела L и P. На десниот дел P од шипката од левиот дел L дејствува систем на сили распоредени по површината на пресекот - внатрешни сили во однос на прачката како целина. Овој систем на сили може да се сведе на главниот вектор и главниот момент М, земајќи го центарот на гравитација на пресекот - точка О - како центар на редукција.
Внатрешни фактори на моќност.Ајде да избереме координатен систем, поставувајќи ги оските x, y во пресекот и оската нормална на него и да го разложиме M на компоненти долж овие оски: (сл. 1, б).
Овие шест големини се нарекуваат фактори на внатрешна сила на шипката (или внатрешни сили) во делот што се разгледува. Секоја од овие сили има свое име, што одговара на неговата насока или одреден тип на деформација на шипката, што е предизвикано од оваа сила. Силите се нарекуваат попречни (смолкнување) сили, а се нарекуваат нормална (надолжна) сила. Моментите се нарекуваат моменти на свиткување и вртежен момент.
