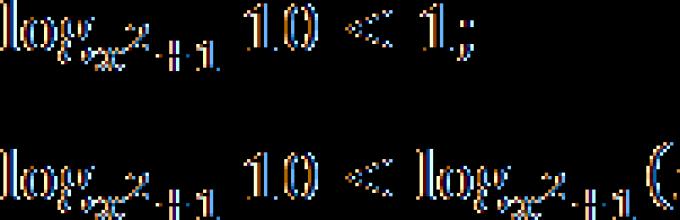Меѓу целата разновидност на логаритамски неравенки, неравенките со променлива основа се проучуваат одделно. Тие се решаваат со помош на специјална формула, која поради некоја причина ретко се учи на училиште:
log k (x) f (x) ∨ log k (x) g (x) ⇒ (f (x) − g (x)) (k (x) − 1) ∨ 0
Наместо полето за избор „∨“, можете да ставите кој било знак за нееднаквост: повеќе или помалку. Главната работа е дека и во двете нееднаквости знаците се исти.
На овој начин се ослободуваме од логаритмите и го сведуваме проблемот на рационална нееднаквост. Последново е многу полесно да се реши, но кога се отфрлаат логаритми, може да се појават дополнителни корени. За да ги отсечете, доволно е да го пронајдете опсегот на прифатливи вредности. Ако сте го заборавиле ODZ на логаритам, силно препорачувам да го повторите - видете „Што е логаритам“.
Сè што е поврзано со опсегот на прифатливи вредности мора да се запише и реши одделно:
f(x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1.
Овие четири нееднаквости сочинуваат систем и мора да се исполнат истовремено. Кога ќе се најде опсегот на прифатливи вредности, останува само да се пресече со решението на рационалната нееднаквост - и одговорот е готов.
Задача. Решете ја неравенството:
Прво, да го напишеме ODZ на логаритамот:
Првите две неравенки се задоволуваат автоматски, но последната ќе треба да се отпише. Бидејќи квадратот на број е нула ако и само ако самиот број е нула, имаме:
x 2 + 1 ≠ 1;
x2 ≠ 0;
x ≠ 0.
Излегува дека ODZ на логаритмот се сите броеви освен нула: x ∈ (−∞ 0)∪(0; +∞). Сега ја решаваме главната нееднаквост:

Го правиме преминот од логаритамска нееднаквост во рационална. Оригиналната неравенка има знак „помалку од“, што значи дека добиената неравенка мора да има и знак „помалку од“. Ние имаме:
(10 − (x 2 + 1)) · (x 2 + 1 − 1)< 0;
(9 − x 2) x 2< 0;
(3 − x) · (3 + x) · x 2< 0.
Нулите на овој израз се: x = 3; x = −3; x = 0. Згора на тоа, x = 0 е корен од второто множество, што значи дека при поминување низ него, знакот на функцијата не се менува. Ние имаме:

Добиваме x ∈ (−∞ −3)∪(3; +∞). Ова множество е целосно содржано во ODZ на логаритмот, што значи дека ова е одговорот.
Конвертирање на логаритамски неравенки
Честопати првичната нееднаквост е различна од горенаведената. Ова може лесно да се коригира користејќи ги стандардните правила за работа со логаритми - видете „Основни својства на логаритмите“. Имено:
- Секој број може да се претстави како логаритам со дадена основа;
- Збирот и разликата на логаритми со исти основи може да се заменат со еден логаритам.
Одделно, би сакал да ве потсетам за опсегот на прифатливи вредности. Бидејќи може да има неколку логаритми во првобитната нееднаквост, потребно е да се најде VA на секој од нив. Така, општа шемаРешенијата на логаритамските неравенки се како што следува:
- Најдете го VA на секој логаритам вклучен во неравенството;
- Намалете ја нееднаквоста на стандардна користејќи ги формулите за собирање и одземање логаритми;
- Решете ја добиената неравенка користејќи ја шемата дадена погоре.
Задача. Решете ја неравенството:
Ајде да го најдеме доменот на дефиниција (DO) на првиот логаритам:
Решаваме со методот на интервал. Наоѓање на нулите на броителот:
3x − 2 = 0;
x = 2/3.
Потоа - нулите на именителот:
x − 1 = 0;
x = 1.
Обележуваме нули и знаци на координатната стрелка:

Добиваме x ∈ (−∞ 2/3)∪(1; +∞). Вториот логаритам ќе го има истиот VA. Ако не верувате, можете да проверите. Сега го трансформираме вториот логаритам така што основата е две:
Како што можете да видите, тројките во основата и пред логаритамот се намалени. Добивме два логаритами со истата основа. Ајде да ги собереме:

дневник 2 (x − 1) 2< 2;
дневник 2 (x − 1) 2< log 2 2 2 .
Ја добивме стандардната логаритамска неравенка. Се ослободуваме од логаритмите користејќи ја формулата. Бидејќи првобитната нееднаквост содржи знак „помалку од“, како резултат рационално изразувањеисто така мора да биде помал од нула. Ние имаме:
(f (x) − g (x)) (k (x) − 1)< 0;
((x − 1) 2 − 2 2) (2 − 1)< 0;
x 2 − 2x + 1 − 4< 0;
x 2 − 2x − 3< 0;
(x − 3)(x + 1)< 0;
x ∈ (−1; 3).
Добивме два сета:
- ODZ: x ∈ (−∞ 2/3)∪(1; +∞);
- Одговор на кандидатот: x ∈ (−1; 3).
Останува да ги пресечеме овие множества - го добиваме вистинскиот одговор:

Ние сме заинтересирани за пресекот на множества, затоа избираме интервали кои се засенчени на двете стрелки. Добиваме x ∈ (−1; 2/3)∪(1; 3) - сите точки се пробиени.
Со нив се внатре логаритми.
Примери:
\(\log_3x≥\log_39\)
\(\log_3 ((x^2-3))< \log_3{(2x)}\)
\(\log_(x+1)((x^2+3x-7))>2\)
\(\lg^2((x+1))+10≤11 \lg((x+1))\)
Како да се решат логаритамските неравенки:
Треба да се стремиме да ја намалиме секоја логаритамска нееднаквост во формата \(\log_a(f(x)) ˅ \log_a(g(x))\) (симболот \(˅\) значи кој било од ). Овој тип ви овозможува да се ослободите од логаритмите и нивните основи, правејќи премин кон нееднаквоста на изразите под логаритми, односно до формата \(f(x) ˅ g(x)\).
Но, кога се прави оваа транзиција, постои една многу важна суптилност:
\(-\) ако е број и е поголем од 1, знакот за неравенство останува ист за време на транзицијата,
\(-\) ако основата е број поголем од 0, но помал од 1 (се наоѓа помеѓу нула и еден), тогаш знакот за нееднаквост треба да се промени во спротивното, т.е.
|
\(\log_2((8-x))<1\) Решение: |
\(\log\)\(_(0,5)\) \((2x-4)\)≥\(\log\)\(_(0,5)\) \(((x+ 1))\) Решение: |
Многу важно!Во која било неравенка, преминот од формата \(\log_a(f(x)) ˅ \log_a(g(x))\) кон споредување на изрази под логаритми може да се направи само ако:
Пример . Решавање на неравенка: \(\log\)\(≤-1\)
Решение:
|
\(\log\) \(_(\frac(1)(3))(\frac(3x-2)(2x-3))\)\(≤-1\) |
Ајде да го испишеме ОДЗ. |
|
ODZ: \(\frac(3x-2)(2x-3)\) \(>0\) |
|
|
\(\frac(3x-2-3(2x-3))(2x-3)\)\(≥\) \(0\) |
Ги отвораме заградите и носиме . |
|
\(\frac(-3x+7)(2x-3)\) \(≥\) \(0\) |
Ја множиме неравенството со \(-1\), не заборавајќи да го смениме знакот за споредба. |
|
\(\frac(3x-7)(2x-3)\) \(≤\) \(0\) |
|
|
\(\frac(3(x-\frac(7)(3)))(2(x-\frac(3)(2)))\)\(≤\) \(0\) |
Ајде да конструираме бројна права и да ги означиме точките \(\frac(7)(3)\) и \(\frac(3)(2)\) на неа. Ве молиме имајте предвид дека точката е отстранета од именителот, и покрај фактот што нееднаквоста не е строга. Факт е дека оваа точка нема да биде решение, бидејќи кога ќе се замени со нееднаквост ќе не доведе до делење со нула. |
|
|
Сега го исцртуваме ODZ на истата нумеричка оска и го запишуваме како одговор интервалот што спаѓа во ODZ. |
|
|
Го запишуваме конечниот одговор. |
Пример . Решете ја неравенката: \(\log^2_3x-\log_3x-2>0\)
Решение:
|
\(\log^2_3x-\log_3x-2>0\) |
Ајде да го испишеме ОДЗ. |
|
ODZ: \(x>0\) |
Ајде да дојдеме до решението. |
|
Решение: \(\log^2_3x-\log_3x-2>0\) |
Овде имаме типична квадратно-логаритамска неравенка. Ајде да го направиме тоа. |
|
\(t=\log_3x\) |
Ја прошируваме левата страна на неравенката во . |
|
\(D=1+8=9\) |
|
|
Сега треба да се вратиме на оригиналната променлива - x. За да го направите ова, да одиме до , кој го има истото решение и да ја направиме обратната замена. |
|
|
\(\лево[ \почеток(собрано) t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2\\\log_3x<-1 \end{gathered} \right.\) |
Трансформирајте \(2=\log_39\), \(-1=\log_3\frac(1)(3)\). |
|
\(\лево[ \почеток(собрано) \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) |
Ајде да продолжиме со споредување аргументи. Основите на логаритмите се поголеми од \(1\), така што знакот на неравенките не се менува. |
|
\(\лево[ \почеток(собрано) x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) |
Дозволете ни да го споиме решението на неравенката и ODZ во една слика. |
|
|
Ајде да го запишеме одговорот. |
Меѓу целата разновидност на логаритамски неравенки, неравенките со променлива основа се проучуваат одделно. Тие се решаваат со помош на специјална формула, која поради некоја причина ретко се учи на училиште. Во презентацијата се претставени решенија за задачите В3 од Единствениот државен испит - 2014 година по математика.
Преземи:
Преглед:
За да користите прегледи на презентации, креирајте сметка на Google и најавете се на неа: https://accounts.google.com
Наслов на слајд:
Решавање логаритамски неравенки кои содржат променлива во основата на логаритамот: методи, техники, еквивалентни транзиции, наставник по математика, СОУ бр.143 Књазкина Т.В.
Меѓу целата разновидност на логаритамски неравенки, неравенките со променлива основа се проучуваат одделно. Тие се решаваат со помош на посебна формула, која поради некоја причина ретко се учи во училиште: log k (x) f (x) ∨ log k (x) g (x) ⇒ (f (x) − g (x)) ( k ( x) − 1) ∨ 0 Наместо полето за избор „∨“, можете да ставите кој било знак за нееднаквост: повеќе или помалку. Главната работа е дека и во двете нееднаквости знаците се исти. На овој начин се ослободуваме од логаритмите и го сведуваме проблемот на рационална нееднаквост. Последново е многу полесно да се реши, но кога се отфрлаат логаритми, може да се појават дополнителни корени. За да ги отсечете, доволно е да го пронајдете опсегот на прифатливи вредности. Не заборавајте на ODZ на логаритамот! Сè што е поврзано со опсегот на прифатливи вредности мора да се запише и реши одделно: f (x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1. Овие четири неравенки сочинуваат систем и мора да се задоволат истовремено. Кога ќе се најде опсегот на прифатливи вредности, останува само да се пресече со решението на рационалната нееднаквост - и одговорот е готов.
Решете ја неравенката: Решение Прво, ајде да го запишеме OD на логаритмот Првите две неравенки се задоволуваат автоматски, но последната ќе треба да се запише. Бидејќи квадратот на број е еднаков на нула ако и само ако самиот број е еднаков на нула, имаме: x 2 + 1 ≠ 1; x2 ≠ 0; x ≠ 0. Излегува дека ODZ на логаритам се сите броеви освен нула: x ∈ (−∞0)∪(0 ;+ ∞). Сега ја решаваме главната неравенка: Го правиме преминот од логаритамската неравенка во рационалната. Оригиналната неравенка има знак „помалку од“, што значи дека добиената неравенка мора да има и знак „помалку од“.
Имаме: (10 − (x 2 + 1)) · (x 2 + 1 − 1)
Трансформирање на логаритамски неравенки Честопати првобитната неравенка е различна од горенаведената. Ова може лесно да се коригира со користење на стандардни правила за работа со логаритми. Имено: Секој број може да се претстави како логаритам со дадена основа; Збирот и разликата на логаритми со исти основи може да се заменат со еден логаритам. Одделно, би сакал да ве потсетам за опсегот на прифатливи вредности. Бидејќи може да има неколку логаритми во првобитната нееднаквост, потребно е да се најде VA на секој од нив. Така, општата шема за решавање на логаритамски неравенки е следна: Најдете ја VA на секој логаритам вклучен во неравенката; Намалете ја нееднаквоста на стандардна користејќи ги формулите за собирање и одземање логаритми; Решете ја добиената неравенка користејќи ја шемата дадена погоре.
Решавање на неравенството: Решение Да го најдеме доменот на дефиниција (DO) на првиот логаритам: Решаваме со методот на интервали. Најдете ги нулите на броителот: 3 x − 2 = 0; x = 2/3. Тогаш - нулите на именителот: x − 1 = 0; x = 1. Означи нули и знаци на координатната права:
Добиваме x ∈ (−∞ 2/3) ∪ (1; +∞). Вториот логаритам ќе го има истиот VA. Ако не верувате, можете да проверите. Сега да го трансформираме вториот логаритам така што во основата има два: Како што можете да видите, тројките во основата и пред логаритам се откажани. Добивме два логаритами со иста основа. Соберете ги: лог 2 (x − 1) 2
(f (x) − g (x)) (k (x) − 1)
Ние сме заинтересирани за пресекот на множества, затоа избираме интервали кои се засенчени на двете стрелки. Добиваме: x ∈ (−1; 2/3) ∪ (1; 3) - сите точки се дупнати. Одговор: x ∈ (−1; 2/3)∪(1; 3)
Решавање задачи USE-2014 тип C3
Решете го системот на неравенки Решение. ОДЗ: 1) 2)
Решете го системот на неравенки 3) -7 -3 - 5 x -1 + + + − − (продолжение)
Решете го системот на неравенки 4) Заедничка одлука: и -7 -3 - 5 x -1 -8 7 дневник 2 129 (продолжение)
Решете ја неравенката (продолжение) -3 3 -1 + − + − x 17 + -3 3 -1 x 17 -4
Решете ја неравенката Решение. ОДЗ:
Решете ја неравенството (продолжува)
Решете ја неравенката Решение. ОДЗ: -2 1 -1 + − + − x + 2 -2 1 -1 x 2
Дали мислите дека има уште време до обединет државен испит и ќе имате време да се подготвите? Можеби ова е така. Но, во секој случај, колку порано студентот започне со подготовка, толку поуспешно ги положува испитите. Денес решивме да посветиме статија на логаритамските неравенки. Ова е една од задачите, што значи можност да се добие дополнителен кредит.
Дали веќе знаете што е логаритам? Навистина се надеваме дека е така. Но, дури и да немате одговор на ова прашање, тоа не е проблем. Да се разбере што е логаритам е многу едноставно.

Зошто 4? Треба да го подигнете бројот 3 на оваа моќност за да добиете 81. Откако ќе го разберете принципот, можете да продолжите со посложени пресметки.
Поминавте низ нееднаквости пред неколку години. И оттогаш постојано ги среќавате во математиката. Ако имате проблеми со решавање на нееднаквости, проверете го соодветниот дел.
Сега кога се запознавме со концептите поединечно, да продолжиме да ги разгледуваме воопшто.
Наједноставната логаритамска неравенка.

Наједноставните логаритамски неравенки не се ограничени на овој пример; има уште три, само со различни знаци. Зошто е ова потребно? За подобро разбирање како да се решаваат неравенки со логаритми. Сега да дадеме поприменлив пример, сè уште прилично едноставен; сложените логаритамски неравенки ќе ги оставиме за подоцна.

Како да се реши ова? Се започнува со ОДЗ. Вреди да знаете повеќе за тоа ако сакате секогаш лесно да ја решавате секоја нееднаквост.
Што е ОДЗ? ODZ за логаритамски неравенки
Кратенката значи опсег на прифатливи вредности. Често се појавува во задачите за обединетиот државен испит. оваа формулација. ODZ ќе ви биде корисен не само во случај на логаритамски неравенки.
Погледнете го повторно горниот пример. Ќе го разгледаме ODZ врз основа на него, за да го разберете принципот, а решавањето на логаритамските неравенки не поставува прашања. Од дефиницијата за логаритам произлегува дека 2x+4 мора да биде поголемо од нула. Во нашиот случај тоа значи следново.

Овој број, по дефиниција, мора да биде позитивен. Решете ја нееднаквоста претставена погоре. Ова може да се направи дури и усно, овде е јасно дека X не може да биде помал од 2. Решението за неравенството ќе биде дефинирање на опсегот на прифатливи вредности.
Сега да преминеме на решавање на наједноставната логаритамска неравенка.

Самите логаритми ги отфрламе од двете страни на неравенката. Што ни останува како резултат? Едноставна нееднаквост.

Не е тешко да се реши. X мора да биде поголем од -0,5. Сега ги комбинираме двете добиени вредности во систем. Така,

Ова ќе биде опсегот на прифатливи вредности за логаритамската нееднаквост што се разгледува.
Зошто воопшто ни треба ОДЗ? Ова е можност да ги отстраните неточните и невозможни одговори. Ако одговорот не е во опсегот на прифатливи вредности, тогаш одговорот едноставно нема смисла. Ова вреди да се запамети долго време, бидејќи на Единствениот државен испит честопати има потреба да се бара ОДЗ, а тоа се однесува не само на логаритамските неравенки.
Алгоритам за решавање на логаритамска неравенка
Решението се состои од неколку фази. Прво, треба да го пронајдете опсегот на прифатливи вредности. Ќе има две значења во ОДЗ, за ова разговаравме погоре. Следно, треба да ја решите самата нееднаквост. Методите на решение се како што следува:
- метод за замена на мултипликатор;
- распаѓање;
- метод на рационализација.
Во зависност од ситуацијата, вреди да се користи еден од горенаведените методи. Да преминеме директно на решението. Дозволете ни да го откриеме најпопуларниот метод, кој е погоден за решавање на задачите за унифициран државен испит во скоро сите случаи. Следно ќе го разгледаме методот на распаѓање. Може да помогне ако наидете на особено незгодна нееднаквост. Значи, алгоритам за решавање на логаритамска нееднаквост.
Примери на решенија :

Не за џабе ја зедовме токму оваа нееднаквост! Обрнете внимание на основата. Запомнете: ако е поголем од еден, знакот останува ист кога се наоѓа опсегот на прифатливи вредности; во спротивно, треба да го промените знакот за нееднаквост.
Како резултат, ја добиваме нееднаквоста:

Сега ја намалуваме левата страна на формата на равенката еднаква на нула. Наместо знакот „помалку од“ ставаме „еднакво“ и ја решаваме равенката. Така, ќе го најдеме ОДЗ. Се надеваме дека со решение за ова едноставна равенканема да имате никакви проблеми. Одговорите се -4 и -2. Тоа не е се. Треба да ги прикажете овие точки на графиконот, ставајќи ги „+“ и „-“. Што треба да се направи за ова? Заменете ги броевите од интервалите во изразот. Онаму каде што вредностите се позитивни, таму ставаме „+“.
Одговори: x не може да биде поголем од -4 и помал од -2.
Го најдовме опсегот на прифатливи вредности само за левата страна; сега треба да го најдеме опсегот на прифатливи вредности за десната страна. Ова е многу полесно. Одговор: -2. Ние ги пресекуваме двете добиени области.
И дури сега почнуваме да се осврнуваме на самата нееднаквост.

Ајде да го поедноставиме што е можно повеќе за полесно да се реши.

Повторно го користиме методот интервал во решението. Ајде да ги прескокнеме пресметките, сè е веќе јасно со тоа од претходниот пример. Одговори.

Но, овој метод е погоден ако логаритамската неравенка ги има истите основи.
Решавањето на логаритамски равенки и неравенки со различни основи бара почетно намалување на иста основа. Следно, користете го методот опишан погоре. Но, има повеќе тежок случај. Да го разгледаме еден од најпознатите сложени видовилогаритамски неравенки.
Логаритамски неравенки со променлива основа
Како да се решат неравенки со такви карактеристики? Да, и такви луѓе може да се најдат на обединетиот државен испит. Решавањето на нееднаквостите на следниот начин исто така ќе ви користи образовен процес. Да го разгледаме прашањето подетално. Да ја отфрлиме теоријата и да одиме директно на пракса. За да ги решите логаритамските неравенки, доволно е еднаш да се запознаете со примерот.

За да се реши логаритамска нееднаквост на претставената форма, потребно е да се намали десната страна на логаритам со иста основа. Принципот наликува на еквивалентни транзиции. Како резултат на тоа, нееднаквоста ќе изгледа вака.

Всушност, останува само да се создаде систем на неравенки без логаритми. Користејќи го методот на рационализација, преминуваме кон еквивалентен систем на неравенки. Ќе го разберете самото правило кога ќе ги замените соодветните вредности и ќе ги следите нивните промени. Системот ќе ги има следните нееднаквости.

Кога го користите методот на рационализација при решавање на неравенки, треба да го запомните следново: еден мора да се одземе од основата, x, по дефиниција на логаритамот, се одзема од двете страни на неравенката (десно од лево), два изрази се множат и се постави под оригиналниот знак во однос на нула.
Понатамошното решение се изведува со методот на интервал, сè е едноставно овде. Важно е да ги разберете разликите во методите на решение, тогаш сè ќе почне лесно да функционира.
Има многу нијанси во логаритамските неравенки. Наједноставните од нив се прилично лесни за решавање. Како можете да го решите секој од нив без проблеми? Веќе ги добивте сите одговори во оваа статија. Сега имате долга пракса пред вас. Постојано вежбајте да решавате различни проблеми на испитот и ќе успеете да го добиете највисок резултат. Среќно за вас во вашата тешка задача!