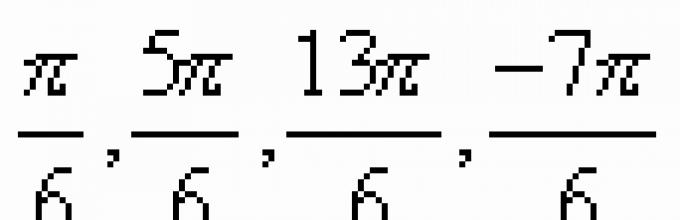Инверзни тригонометриски функции. Арксин, аркозин - својства, графикони, формули Тригонометрија на лак функции

Проблемите поврзани со инверзните тригонометриски функции често се нудат на училишните завршни испити и на приемните испити на некои универзитети. Детално проучување на оваа тема може да се постигне само во изборни часови или изборни предмети. Предложениот курс е дизајниран да ги развие способностите на секој студент што е можно поцелосно и да ја подобри неговата математичка подготовка.

Курсот трае 10 часа:

1.Функции arcsin x, arccos x, arctg x, arcctg x (4 часа).

2.Операции на инверзни тригонометриски функции (4 часа).

3. Инверзни тригонометриски операции на тригонометриски функции (2 часа).

Лекција 1 (2 часа) Тема: Функции y = arcsin x, y = arccos x, y = arctan x, y = arcctg x.

Цел: целосно покривање на ова прашање.

1.Функција y = arcsin x.

а) За функцијата y = sin x на отсечка има инверзна (едновредносна) функција, која се договоривме да ја наречеме лаксин и да ја означиме на следниот начин: y = arcsin x. Графикот на инверзната функција е симетричен со графикот на главната функција во однос на симетралата на координатните агли I - III.

Својства на функцијата y = arcsin x.

1) Домен на дефиниција: сегмент [-1; 1];

2) Област на промена: сегмент;

3)Функција y = arcsin x непарен: arcsin (-x) = - arcsin x;

4)Функцијата y = arcsin x монотоно се зголемува;

5) Графикот ги пресекува оските Ox, Oy на почетокот.

Пример 1. Најдете a = arcsin. Овој пример може детално да се формулира на следниов начин: најдете аргумент a, кој лежи во опсегот од до, чиј синус е еднаков на.

Решение. Постојат безброј аргументи чиј синус е еднаков на, на пример: итн. Но, нас не интересира само аргументот што е на сегментот. Ова би бил аргументот. Значи,.

Пример 2. Најдете .Решение.Расправајќи се на ист начин како во Пример 1, добиваме .

б) орални вежби. Најдете: arcsin 1, arcsin (-1), arcsin, arcsin(), arcsin, arcsin(), arcsin, arcsin(), arcsin 0. Примерок одговор: , бидејќи . Дали изразите имаат смисла: ; лаксин 1,5; ?

в) Подредете по растечки редослед: лаксин, лаксин (-0,3), лаксин 0,9.

II. Функции y = arccos x, y = arctg x, y = arcctg x (слично).

Час 2 (2 часа) Тема: Инверзни тригонометриски функции, нивните графикони.

Цел: во оваа лекција потребно е да се развијат вештини за одредување на вредностите на тригонометриските функции, за конструирање графикони на инверзни тригонометриски функции користејќи D (y), E (y) и потребните трансформации.

Во оваа лекција комплетирајте вежби кои вклучуваат наоѓање на доменот на дефиниција, доменот на вредност на функциите од типот: y = arcsin, y = arccos (x-2), y = arctg (tg x), y = arccos.

Треба да конструирате графикони на функциите: а) y = arcsin 2x; б) y = 2 лаксин 2x; в) y = лаксин;

г) y = лаксин; д) y = лаксин; д) y = лаксин; е) y = | лаксин | .

Пример.Ајде да зацртаме y = arccos

Можете да ги вклучите следните вежби во вашата домашна задача: изградете графикони на функции: y = arccos, y = 2 arcctg x, y = arccos | x | .

Графикони на инверзни функции

Лекција бр. 3 (2 часа) Тема:

Операции на инверзни тригонометриски функции.

Цел: да се прошири математичкото знаење (ова е важно за оние кои влегуваат во специјалности со зголемени барања за математичка обука) со воведување на основни односи за инверзни тригонометриски функции.

Материјал за лекцијата.

Неколку едноставни тригонометриски операции на инверзни тригонометриски функции: sin (arcsin x) = x , i xi ? 1; cos (arсcos x) = x, i xi? 1; tg (arctg x)= x, x I R; ctg (arcctg x) = x, x I R.

Вежби.

а) tg (1,5 + arctg 5) = - ctg (arctg 5) = .

ctg (arctg x) = ; tg (arcctg x) = .

б) cos ( + arcsin 0,6) = - cos (arcsin 0,6). Нека arcsin 0,6 = a, sin a = 0,6;

cos (arcsin x) = ; грев (arccos x) = .

Забелешка: го земаме знакот „+“ пред коренот бидејќи a = arcsin x задоволува .

в) грев (1,5 + arcsin Одговор: ;

г) ctg ( + arctg 3) Одговор: ;

д) tg ( – arcctg 4) Одговор: .

д) cos (0,5 + arccos). Одговор:.

Пресметајте:

а) грев (2 арктан 5) .

Нека арктан 5 = а, потоа син 2 а = или грев (2 арктан 5) = ;

б) cos ( + 2 arcsin 0,8 Одговор: 0,28).

в) arctg + arctg.

Нека a = арктан, b = арктан,

тогаш tg(a + b) = .

г) грев (arcsin + arcsin).

д) Докажи дека за сите x I [-1; 1] вистински arcsin x + arccos x = .

Доказ:

arcsin x = – arccos x

грев (arcsin x) = грев ( – arccos x)

x = cos (arccos x)

За да го решите сами: sin (arccos), cos (arcsin), cos (arcsin ()), sin (arctg (- 3)), tg (arccos), ctg (arccos).

За домашно решение: 1) грев (арцин 0,6 + арктан 0); 2) arcsin + arcsin ; 3) ctg ( – arccos 0,6); 4) cos (2 arcctg 5) ; 5) грев (1,5 – arcsin 0,8); 6) arctg 0,5 – arctg 3.

Час бр.4 (2 часа) Тема: Операции на инверзни тригонометриски функции.

Цел: Во оваа лекција, демонстрирајте ја употребата на соодноси при трансформирање на посложени изрази.

Материјал за лекцијата.

УСНО:

а) sin (arccos 0,6), cos (arcsin 0,8);

б) tg (arcсtg 5), ctg (arctg 5);

в) sin (arctg -3), cos (arcсtg());

г) tg (arccos), ctg (arccos()).

ПИСМЕНО:

1) cos (arcsin + arcsin + arcsin).

2) cos (arctg 5–arccos 0,8) = cos (arctg 5) cos (arccos 0,8) + sin (arctg 5) sin (arccos 0,8) =

3) tg ( - arcsin 0,6) = - tg (arcsin 0,6) =

4)

Независната работа ќе помогне да се идентификува нивото на владеење на материјалот.

1) tg (arctg 2 - arctg) 2) cos( - арктан2) 3) arcsin + arccos	1) cos (arcsin + arcsin) 2) грев (1,5 - арктан 3) 3) arcctg3 – arctg 2

За домашна работа можете да предложите:

1) ctg (arctg + arctg + arctg); 2) грев 2 (arctg 2 – arcctg ()); 3) sin (2 arctg + tan (arcsin )); 4) грев (2 арктан); 5) tg ((арцин))

Час бр.5 (2 часа) Тема: Инверзни тригонометриски операции на тригонометриски функции.

Цел: да се формира разбирање на учениците за инверзните тригонометриски операции на тригонометриските функции, фокусирајќи се на зголемување на разбирањето на теоријата што се изучува.

При проучувањето на оваа тема, се претпоставува дека обемот на теоретскиот материјал што треба да се запамети е ограничен.

Материјал за лекција:

Можете да започнете да учите нов материјал со проучување на функцијата y = arcsin (sin x) и исцртување на нејзиниот график.

3. Секој x I R е поврзан со y I, т.е.<= y <= такое, что sin y = sin x.

4. Функцијата е непарна: sin(-x) = - sin x; arcsin(sin(-x)) = - arcsin(sin x).

6. Графикон y = arcsin (sin x) на:

а) 0<= x <= имеем y = arcsin(sin x) = x, ибо sin y = sin x и <= y <= .

б)<= x <= получим y = arcsin (sin x) = arcsin ( - x) = - x, ибо

sin y = грев ( – x) = грев x , 0<= - x <= .

Значи,

Откако го конструиравме y = arcsin (sin x) на , продолжуваме симетрично во однос на потеклото на координатите на [- ; 0], со оглед на необичноста на оваа функција. Користејќи периодичност, продолжуваме по целата нумеричка линија.

Потоа запишете неколку врски: arcsin (грев а) = a ако<= a <= ; arccos (cos а ) = a ако 0<= a <= ; arctg (tg a) = a ако< a < ; arcctg (ctg a) = a , если 0 < a < .

И направете ги следните вежби:а) arccos(sin 2).Одговор: 2 - ; б) arcsin (cos 0,6) Одговор: - 0,1; в) arctg (tg 2) Одговор: 2 - ;

г) arcctg(tg 0.6).Одговор: 0.9; д) arccos (cos ( - 2) Одговор: 2 - ; д) арксин (грев (-0,6)). Одговор: - 0,6; g) arctg (tg 2) = arctg (tg (2 - )). Одговор: 2 - ; ж) аrcctg (tg 0,6). Одговор: - 0,6; - арктан x; д) arccos + arccos

Инверзни тригонометриски функции(кружни функции, лак функции) - математички функции кои се инверзни на тригонометриските функции.

лаксин(означено како arcsin x; arcsin x- ова е аголот гревотнеговите еднакви x).

лаксин (y = arcsin x) - инверзна тригонометриска функција до гревот (x = грев y), кој има домен и збир на вредности . Со други зборови, го враќа аголот според неговата вредност гревот.

Функција y=sin xе континуирана и ограничена по целата нејзина бројна права. Функција y=arcsin x- строго се зголемува.

Својства на функцијата arcsin.

Арксин заговор.

Добивање на функцијата arcsin.

Има функција y = грев x. Во текот на целиот негов домен на дефиниција, таа е делумна монотона, а со тоа и обратна кореспонденција y = arcsin xне е функција. Затоа, го разгледуваме сегментот на кој само се зголемува и ја зема секоја вредност од опсегот на вредности - . Бидејќи за функција y = грев xна интервалот, сите вредности на функцијата се добиваат со само една вредност на аргументот, што значи дека на овој интервал има инверзна функција y = arcsin x, чиј график е симетричен со графикот на функцијата y = грев xна релативно исправен сегмент y = x.

Дефиниција и нотација

Арксин (y = arcsin x) е инверзна функција на синус (x = грешни -1 ≤ x ≤ 1и множеството вредности -π /2 ≤ y ≤ π/2.
sin(arcsin x) = x ;
arcsin(sin x) = x .

Арксинот понекогаш се означува на следниов начин:
.

График на функцијата на лак

График на функцијата y = arcsin x

Графикот на лак се добива од синусниот график ако се заменети оските на апсцисата и ординатите. За да се елиминира двосмисленоста, опсегот на вредности е ограничен на интервалот во кој функцијата е монотона. Оваа дефиниција се нарекува главна вредност на лакот.

Аркозин, аркос

Дефиниција и нотација

Лачен косинус (y = arccos x) е инверзна функција на косинус (x = cos y). Има опсег -1 ≤ x ≤ 1и многу значења 0 ≤ y ≤ π.
cos(arccos x) = x ;
arccos(cos x) = x .

Аркозинот понекогаш се означува на следниов начин:
.

График на косинус функција на лакот

График на функцијата y = arccos x

Косинусниот график на лакот се добива од косинусниот график ако се заменуваат оските на апсцисата и ординатите. За да се елиминира двосмисленоста, опсегот на вредности е ограничен на интервалот во кој функцијата е монотона. Оваа дефиниција се нарекува главна вредност на лакот косинус.

Паритет

Функцијата на лак е непарна:
arcsin(- x) = arcsin(-sin arcsin x) = arcsin(sin(-arcsin x)) = - arcsin x

Косинусот на лакот не е парен или непарен:
arccos(- x) = arccos(-cos arccos x) = arccos(cos(π-arccos x)) = π - arccos x ≠ ± arccos x

Својства - екстремни, зголемување, намалување

Функциите arcsine и arccosine се континуирани во нивниот домен на дефиниција (види доказ за континуитет). Главните својства на арксин и аркозин се претставени во табелата.

	y= arcsin x	y= arccos x
Опсег и континуитет	- 1 ≤ x ≤ 1	- 1 ≤ x ≤ 1
Опсег на вредности
Растечки, опаѓачки	монотоно се зголемува	монотоно се намалува
Високи
Минимумите
Нули, y = 0	x = 0	x = 1
Пресечни точки со ординатна оска, x = 0	y= 0	y = π/ 2

Табела на арксини и аркосини

Оваа табела ги прикажува вредностите на арксини и аркосини, во степени и радијани, за одредени вредности на аргументот.

x	arcsin x		arccos x
	град	мило.	град	мило.
- 1	- 90 °	-	180°	π
-	- 60 °	-	150°
-	- 45 °	-	135°
-	- 30 °	-	120°
0	0°	0	90°
	30°		60°
	45°		45°
	60°		30°
1	90°		0°	0

≈ 0,7071067811865476
≈ 0,8660254037844386

Формули

Видете исто така: Изведување на формули за инверзни тригонометриски функции

Формули за збир и разлика

на или

на и

на и

на или

на и

на и

на

на

на

на

Изрази преку логаритми, сложени броеви

Видете исто така: Изведување формули

Изрази преку хиперболични функции

Деривати

;
.
Видете Изведување на арксин и деривати на аркозин > > >

Деривати од повисок ред:
,
каде е полином на степен .
;
;
.

Се одредува со формулите:

Видете Изведување на деривати од повисок ред на арксин и аркозин > > >

Интеграли Ја правиме замената x =грев т ., Интегрираме по делови, имајќи предвид дека -π/:
.

2 ≤ t ≤ π/2
.

цена t ≥ 0

Ајде да изразиме лак косинус преку лачен синус:< 1 Проширување на серијата
;
.

Кога |x|

се случува следното распаѓање:

Инверзни функции
sin(arcsin x) = x
cos(arccos x) = x .

Инверзните на арксин и аркозин се синус и косинус, соодветно.
arcsin(sin x) = xСледниве формули важат во целиот домен на дефиниција:
arccos(cos x) = xСледниве формули важат само за множеството вредности на арксин и аркозин:

на
во .

Користена литература:

И.Н. Бронштајн, К.А. Семендјаев, Прирачник за математика за инженери и студенти, „Лан“, 2009 година. Видете исто така:Бидејќи тригонометриските функции се периодични, нивните инверзни функции не се единствени. Значи, равенката y = грев х, за дадено , има бескрајно многу корени. Навистина, поради периодичноста на синусот, ако x е таков корен, тогаш тоа е x + 2πn(каде n е цел број) исто така ќе биде коренот на равенката. Така, Видете исто така:инверзните тригонометриски функции се повеќевредни Видете исто така:. За полесно да се работи со нив, се воведува концептот на нивните главни значења. Размислете, на пример, синус: y = ..

Ако аргументот x го ограничиме на интервалот , тогаш на него функцијата y =

се зголемува монотоно. Затоа, има единствена инверзна функција, која се нарекува лак: x = arcsin y arcsin xОсвен ако не е поинаку наведено, под инверзни тригонометриски функции ги подразбираме нивните главни вредности, кои се одредени со следните дефиниции. Арксин ( грешни
y= arcsin y arccos x) е инверзна функција на синус ( Арксин ( cos y x =
лак косинус ( arcsin y ) е инверзна функција на косинус (), имајќи домен на дефиниција и збир на вредности. Арксин ( Арктангент ( x =
арктан x arcsin y ) е инверзна функција на тангента ( tg y Арксин ( аркотангента ( arcctg x

) е инверзна функција на котангента (

ctg y

arcsin y arcsin x

arcsin y arccos x

arcsin y ) е инверзна функција на косинус (

arcsin y ) е инверзна функција на тангента (

), имајќи домен на дефиниција и збир на вредности.

Графикони на инверзни тригонометриски функции

arcsin(sin x) = xСледниве формули важат во целиот домен на дефиниција:
sin(arcsin x) = x
arccos(cos x) = xСледниве формули важат во целиот домен на дефиниција:
cos(arccos x) = x

арктан(tg x) = xСледниве формули важат во целиот домен на дефиниција:
tg(arctg x) = x
arcctg(ctg x) = xСледниве формули важат во целиот домен на дефиниција:
ctg(arcctg x) = x

Формули кои ги поврзуваат инверзните тригонометриски функции

Видете исто така: Изведување на формули за инверзни тригонометриски функции

Формули за збир и разлика

на или

на и

на и

на или

на и

на и

на

на

на

на

на

на

на

на

на

на

на
во .

Функциите sin, cos, tg и ctg секогаш се придружени со арксин, аркозин, арктангенс и аркотангенс. Едното е последица на другото, а паровите функции се подеднакво важни за работа со тригонометриски изрази.

Размислете за цртеж на единечен круг, кој графички ги прикажува вредностите на тригонометриските функции.

Ако ги пресметаме лаците OA, arcos OC, arctg DE и arcctg MK, тогаш сите тие ќе бидат еднакви на вредноста на аголот α. Формулите подолу ја одразуваат врската помеѓу основните тригонометриски функции и нивните соодветни лаци.

За да се разбере повеќе за својствата на лак, неопходно е да се разгледа неговата функција. Распоред има форма на асиметрична крива што минува низ координатниот центар.

Својства на арксин:

Ако ги споредиме графиконите гревотИ лаксин, две тригонометриски функции можат да имаат заеднички обрасци.

лак косинус

Arccos на број е вредноста на аголот α, чиј косинус е еднаков на a.

Крива y = arcos xго отсликува графикот arcsin x, со единствената разлика што минува низ точката π/2 на оската OY.

Ајде да ја разгледаме функцијата на косинус на лакот подетално:

1. Функцијата е дефинирана на интервалот [-1; 1].
2. ОДЗ за лакови - .
3. Графикот е целосно лоциран во првата и втората четвртина, а самата функција не е ниту парна ниту непарна.
4. Y = 0 на x = 1.
5. Кривата се намалува по целата должина. Некои својства на лачниот косинус се совпаѓаат со косинусната функција.

Некои својства на лачниот косинус се совпаѓаат со косинусната функција.

Можеби на учениците ќе им биде непотребно такво „детално“ проучување на „лакови“. Меѓутоа, во спротивно, некои елементарни стандардни испитни задачи може да ги доведат студентите во ќорсокак.

Задача 1.Наведете ги функциите прикажани на сликата.

Одговор:оризот. 1 – 4, слика 2 – 1.

Во овој пример, акцентот е ставен на малите нешта. Вообичаено, учениците се многу невнимателни кон градењето графикони и изгледот на функциите. Навистина, зошто да се сеќавате на типот на кривата ако секогаш може да се нацрта со помош на пресметани точки. Не заборавајте дека во услови на тест, времето поминато на цртање за едноставна задача ќе биде потребно за решавање на посложени задачи.

Арктангенс

ArctgБроевите a се вредноста на аголот α така што неговата тангента е еднаква на a.

Ако го земеме предвид графикот на арктангента, можеме да ги истакнеме следниве својства:

1. Графикот е бесконечен и дефиниран на интервалот (- ∞; + ∞).
2. Арктангенсот е непарна функција, затоа, арктан (- x) = - арктан x.
3. Y = 0 на x = 0.
4. Кривата се зголемува низ целиот дефинитивен регион.

Да претставиме кратка компаративна анализа на tg x и arctg x во форма на табела.

Аркотангента

Arcctg на број - зема вредност α од интервалот (0; π) така што неговиот котангенс е еднаков на a.

Својства на функцијата на лак котангента:

1. Интервалот за дефиниција на функцијата е бесконечност.
2. Опсегот на прифатливи вредности е интервалот (0; π).
3. F(x) не е ниту парен ниту непарен.
4. Во текот на целата нејзина должина, графикот на функцијата се намалува.

Многу е едноставно да се споредат ctg x и arctg x, само треба да направите два цртежи и да го опишете однесувањето на кривите.

Задача 2.Поврзете го графикот и формата на нотација на функцијата.

Ако размислуваме логично, од графиконите е јасно дека и двете функции се зголемуваат. Според тоа, двете фигури прикажуваат одредена арктан функција. Од својствата на арктангенсот се знае дека y=0 при x = 0,

Одговор:оризот. 1 – 1, сл. 2 – 4.

Тригонометриски идентитети arcsin, arcos, arctg и arcctg

Претходно, веќе ја идентификувавме врската помеѓу лакови и основните функции на тригонометријата. Оваа зависност може да се изрази со голем број формули кои овозможуваат да се изрази, на пример, синусот на аргументот преку неговиот лаксин, аркозин или обратно. Познавањето на таквите идентитети може да биде корисно при решавање на конкретни примери.

Исто така, постојат врски за arctg и arcctg:

Друг корисен пар формули ја поставува вредноста за збирот на arcsin и arcos, како и arcctg и arcctg од истиот агол.

Примери за решавање проблеми

Задачите за тригонометрија можат да се поделат во четири групи: да се пресмета нумеричката вредност на одреден израз, да се конструира график на дадена функција, да се најде нејзиниот домен на дефиниција или ODZ и да се извршат аналитички трансформации за да се реши примерот.

Кога го решавате првиот тип на проблем, мора да се придржувате до следниот акционен план:

Кога работите со графикони на функции, главната работа е познавање на нивните својства и изгледот на кривата. Решавањето на тригонометриски равенки и неравенки бара идентитетски табели. Колку повеќе формули ученикот запомни, толку полесно е да го најде одговорот на задачата.

Да речеме, во Обединетиот државен испит треба да го најдете одговорот за равенката како што е:

Ако правилно го трансформирате изразот и го доведете до посакуваната форма, тогаш неговото решавање е многу едноставно и брзо. Прво, да го преместиме arcsin x на десната страна на еднаквоста.

Ако се сеќавате на формулата arcsin (sin α) = α, тогаш можеме да го намалиме пребарувањето за одговори на решавање на систем од две равенки:

Ограничувањето на моделот x произлезе, повторно од својствата на лаксинот: ODZ за x [-1; 1]. Кога a ≠0, дел од системот е квадратна равенка со корени x1 = 1 и x2 = - 1/a. Кога a = 0, x ќе биде еднаква на 1.