Правоаголна нормална. Нормална симетрала. Пресечна точка на симетрали на триаголници

Дајте идеја за нова класа на проблеми - изградба геометриски формикористејќи компас и линијар без поделби на скала.

Воведување на концептот на GMT.

Дефинирајте ја нормалната симетрала, научете како да ја изградите и докажете ја теоремата за нормалната симетрала, како и нејзината инверзна.

Користејќи го компјутерскиот систем за цртање „Компас-3Д“, изведете геометриски конструкции, кои се препорачуваат да се изведат на курс по геометрија со помош на компас и линијар.

Материјали (Прилог бр. 1)

Проблемите кои вклучуваат изградба со компаси и линијар без поделби најчесто се решаваат според одредена шема:

Јас. Анализа: Шематски нацртајте ја саканата слика и воспоставете врски помеѓу податоците за задачата и потребните елементи.

II. Градба: Според планираниот план, изградбата се изведува со компас и линијар.

III. Доказ: Докажете дека конструираната фигура ги задоволува условите на проблемот.

IV. Студија: Направете студија за да видите дали проблемот има решение за даден податок и, ако има, колку решенија има (не се спроведуваат во сите проблеми).

Еве неколку примери на елементарни градежни задачи што ќе ги разгледаме:

1. Одвојте отсечка еднаква на дадената (проучена претходно).

2. Конструкција на нормална симетрала на отсечка:

конструира средина на даден сегмент;
конструирај права што минува низ дадена точка и е нормална на дадена права (точката може или не може да лежи на дадена права).

3. Конструкција на симетралата на аголот.

4. Конструирање на агол еднаков на дадениот.

Нормална симетраладо сегментот.

Дефиниција: Нормална симетрала на отсечка е права што минува низ средината на отсечката и е нормална на неа.

Задача: „Конструирај ја нормалната симетрала на отсечката“. Презентација

О - среден АБ

Опис на изградбата ( слајд број 4):

Зрак a; А – почеток на зракот

Обем (A; r =m)

Заокружи a = B; AB = m

Круг 1 (A; r 1 > m/2)

Круг 2 (B; r 1)

Заокружи 1 Круг 2 =

MN; MN AB = 0, (MN = L)

каде MN AB, O – средината на AB

III. Доказ(слајд бр. 5, 6)

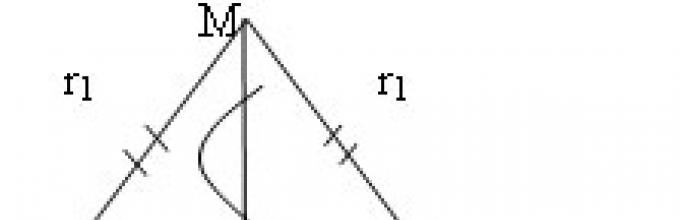
1. Размислете за AMN и BNM:

AM = MB=BN=AN=r 2, затоа AM = BN, AN = BM MN – заедничка страна

(Слика 3)

Затоа, AMN = BNM (на 3 страни),

Оттука

1= 2 (по дефиниција за еднакво)

3= 4 (по дефиниција за еднакво)

2. MAN и NBM се рамнокраки (по дефиниција) ->

1 = 4 и 3 = 2 (по рамнокрак својство)

3. Од точките 1 и 2 -> 1 = 3 затоа MO е симетрала на рамнокрак AMB

4. Така докажавме дека MN е нормална симетрала на отсечката AB

IV. Студија

Оваа задача има единствена одлука, бидејќи која било отсечка има само една средна точка, а низ дадена точка може да се повлече една права права нормална на дадената.

Дефиниција: Геометриски сетпоени (GMT) е збир на точки кои имаат одредено својство. (Прилог бр. 2)

GMT што ги знаете:

Нормална симетрала на отсечка е множество точки на еднакво растојание од краевите на отсечката.
Симетрала на агол - збир на точки еднакво оддалечени од страните на аголот

Значи, да ја докажеме теоремата:

Теорема: „Секоја точка на нормалната симетрала на отсечка е еднакво оддалечена од краевите на оваа отсечка“.

(Слика 4)

Дадени: AB; MO – нормална симетра

Докажи: AM = VM

Доказ:

1. MO – нормална симетрала (по услов) -> O – средна точка на отсечката AB, MOAB

2. Размислете за AMO и VMO - правоаголни

МО – општа нога

AO = VO (O – средината на AB) -> AMO = VMO (на 2 краци) -> AM = VM (по дефиниција за еднакви триаголници, како соодветни страни)

Q.E.D

Домашна задача: „Докажете ја инверзната теорема на оваа“

Теорема: „Секоја точка еднакво оддалечена од краевите на отсечката лежи на нормалната симетрала на оваа отсечка“.

(Слика 5)

Дадени: AB; MA=MV

Доказ: Точката М лежи на нормалната симетрала

Доказ:

Тоа. MO е нормална симетрала која ги содржи сите точки еднакво оддалечени од краевите на отсечката.

Својство на нормални симетрали на страните на триаголникот

Тие се вкрстуваат во една точка и оваа точка е центар на опишаната кружница околу триаголникот, која ќе ја проучуваме во осмо одделение.

Работилница

Материјална и техничка опрема:

Дистрибуција: 29.574 KB

ОС: Windows 9x/2000/XP

Веб-страница: http://www.ascon.ru

Сега да ја пренесеме конструкцијата во графичката околина на компјутерот (слајд бр. 7)

Претходно стекнатото знаење и вештини мора да се применат на одредена задача. Ќе видите дека изградбата нема да ви одземе повеќе време од изградбата во тетратка. Меѓу другото, интересно е да се види како компјутерското опкружување ги извршува човечките команди за конструирање на фигури на авиони. Еве Додаток бр. 3, кој детално ги опишува вашите чекори за изградба. Вчитајте ја програмата и отворете нов цртеж ( слајд број 8, 9).

Нацртајте ги геометриските објекти наведени во изјавата за проблемот: ray Апочнувајќи од точка Аа отсечката е еднаква м- произволна должина ( слајд број 10).

Внесете ја ознаката на зракот, сегментот, почетокот на зракот во цртежот користејќи го јазичето „Алатки" текст.

Конструирај круг со радиус еднаков на отсечката мцентриран на темето во дадена точка А (слајд број 11).

мсо центар на темето дадена точка А ( слајд бр. 12, 13).

Конструирај круг со радиус еднаков на отсечка поголема од 1/2 мЗа да го направите ова, изберете ја ставката „ во контекстното мени RMB Помеѓу 2 поени“ (слајд бр. 14, 15, 16).

Преку пресечните точки на кругови М и Нповлече права линија ( слајд бр.17,18).

Користени книги:

Угринович Н.Д. „Информатика. Основен курс„7-мо одделение. - М.: БИНОМ – 2008 – 175 стр.
Угринович Н.Д. „Работилница за компјутерски науки и информациска технологија" Упатство. – М.: БИНОМ, 2004-2006. -
Угринович Н.Д. „Настава на курсот „Информатика и ИКТ“ во основните и средношколските одделенија 8-11 М.: Лабораторија на знаење БИНОМ, 2008. - 180 стр.
Угринович Н.Д. Компјутерска работилница на ЦД-РОМ. – М.: БИНОМ, 2004-2006.
Богуславски А.А., Третјак Т.М. Фарафонов А.А. „Компас - 3D v 5.11-8.0 Работилница за почетници“ - М.: СОЛОН - ПРЕС, 2006 - 272 стр.
Атанасјан Л.С., Бутузов В.Ф., Кадомцев С.Б., и други „Геометрија 7-9. Учебник за средни училишта“ – М: Образование 2006 – 384 стр.
Атанасјан Л.С., Бутузов В.Ф., Кадомцев С.Б., и други „Изучување геометрија 7-9 одделение. Методолошки препораки за учебникот“ - М: Образование 1997 - 255 стр.
Афанасиева Т.Л., Тапилина Л.А. „Планови за часови базирани на учебникот за 8-мо одделение од Атанасјан Л.С.“ - Волгоград „Учител“ 2010 година, 166 стр.

Додаток бр.1

План за решавање на проблеми кои вклучуваат изградба со компас и линијар.

Анализа.
Градба.
Доказ.
Студија.

Објаснување

При вршење на анализа шематски се исцртува саканата слика и се воспоставува врска помеѓу податоците за задачата и бараните елементи.
Според планираниот план, изградбата се изведува со помош на компаси и линијар.
Тие докажуваат дека конструираната фигура ги задоволува условите на проблемот.
Тие спроведуваат студија: дали проблемот има решение за даден податок, и ако има, колку решенија?

Примери на елементарни градежни проблеми

Одвојте отсечка еднаква на дадената.
Конструирај ја нормалната симетрала на отсечката.
Конструирај ја средната точка на отсечката.
Конструирај права што минува низ дадена точка, нормална на дадена права (Точката може или не може да лежи на дадена права).
Конструирај симетрала на аголот.
Конструирај агол еднаков на дадениот.

Додаток бр.2

Геометрискиот локус на точки (GLP) е збир на точки кои имаат одредено својство.

Примери за GMT:

Нормална симетрала на отсечка е множество точки на еднакво растојание од краевите на отсечката.
Круг е збир на точки на еднакво растојание од дадена точка– центарот на кругот.
Симетралата на аголот е множество точки на еднакво растојание од страните на аголот.

Секоја точка на нормалната симетрала на отсечката е еднакво оддалечена од краевите на таа отсечка.

Речник на поими за планиметрија- Овде се собрани дефиниции на поими од планиметријата. Референците на термините во овој речник (на оваа страница) се со закосени букви. # A B C D E E E F G H I J K L M N O P R S ... Википедија

Колинеарни точки

Конкурентни директно- Овде се собрани дефиниции на поими од планиметријата. Референците на термините во овој речник (на оваа страница) се со закосени букви. # A B C D E E F G H I J K L M N O P R S T U V ... Википедија

Круг Аполонија- Овде се собрани дефиниции на поими од планиметријата. Референците на термините во овој речник (на оваа страница) се со закосени букви. # A B C D E E F G H I J K L M N O P R S T U V ... Википедија

Трансформација на авион- Овде се собрани дефиниции на поими од планиметријата. Референците на термините во овој речник (на оваа страница) се со закосени букви. # A B C D E E F G H I J K L M N O P R S T U V ... Википедија

Цевиана- Овде се собрани дефиниции на поими од планиметријата. Референците на термините во овој речник (на оваа страница) се со закосени букви. # A B C D E E F G H I J K L M N O P R S T U V ... Википедија

Речник на планиметрија- Оваа страница е речник. Видете ја и главната статија: Планиметрија Дефинициите на термините од планиметријата се собрани овде. Врските до термините во овој речник (на оваа страница) се со курзив... Википедија

Проблемот на Аполониј- Проблемот на Аполониј е да изгради круг тангента на три дадени кругови со помош на компас и линијар. Според легендата, проблемот бил формулиран од Аполониј од Перга околу 220 година п.н.е. д. во книгата „Допир“, која беше изгубена ... Википедија

Проблемот на Аполониј- Проблемот на Аполониј е да изгради круг тангента на три дадени кругови со помош на компас и линијар. Според легендата, проблемот бил формулиран од Аполониј од Перга околу 220 година п.н.е. д. во книгата „Допирање“, која беше изгубена, но беше... ... Википедија

Вороној дијаграм- случаен множество точки на рамнината Вороноевиот дијаграм на конечно множество точки S на рамнината претставува поделба на рамнината таква што ... Википедија

Во претходната лекција, ги разгледавме својствата на симетралата на аголот, и двете затворени во триаголник и слободни. Триаголникот вклучува три агли и за секој од нив се зачувани разгледаните својства на симетралата.

Теорема:

Симетралите AA 1, BB 1, СС 1 на триаголникот се сечат во една точка O (сл. 1).

Ориз. 1. Илустрација за теоремата

Доказ:

Прво да разгледаме две симетрали BB 1 и CC 1. Тие се сечат, пресечната точка О постои. За да го докажеме ова, да го претпоставиме спротивното: дадените симетрали да не се сечат, во тој случај тие се паралелни. Тогаш правата линија BC е секанта, а збирот на аглите е , ова е во спротивност со фактот дека во целиот триаголник збирот на аглите е .

Значи, точката О на пресекот на две симетрали постои. Ајде да ги разгледаме неговите својства:

Точката O лежи на симетралата на аголот, што значи дека е еднакво оддалечена од нејзините страни BA и BC. Ако OK е нормално на BC, OL е нормално на BA, тогаш должините на овие нормални се еднакви - . Исто така, точката O лежи на симетралата на аголот и е еднакво оддалечена од нејзините страни CB и CA, перпендикуларите OM и OK се еднакви.

Ги добивме следните еднаквости:

, односно сите три нормални спуштени од точката О на страните на триаголникот се еднакви една со друга.

Ние сме заинтересирани за еднаквоста на перпендикуларите OL и OM. Оваа еднаквост вели дека точката O е подеднакво оддалечена од страните на аголот, следува дека лежи на нејзината симетрала AA 1.

Така, докажавме дека сите три симетрали на триаголникот се сечат во една точка.

Покрај тоа, триаголникот се состои од три отсечки, што значи дека треба да ги земеме предвид својствата на поединечен сегмент.

Дадена е отсечката AB. Секоја отсечка има средна точка, а низ неа може да се повлече нормална - да ја означиме како стр. Така, p е нормална симетрала.

Ориз. 2. Илустрација за теоремата

Секоја точка што лежи на нормалната симетрала е еднакво оддалечена од краевите на отсечката.

Докажи дека (сл. 2).

Доказ:

Размислете за триаголници и . Тие се правоаголни и еднакви, бидејќи имаат заедничка нога ОМ, а катетите АО и ОБ се еднакви по услов, така што имаме две правоаголен триаголник, еднакви на две нозе. Следи дека и хипотенусите на триаголниците се еднакви, односно она што се барало да се докаже.

Конверзната теорема е вистинита.

Секоја точка еднакво оддалечена од краевите на отсечката лежи на нормалната симетрала на оваа отсечка.

Дадена е отсечка AB, нејзината нормална симетрала p и точка М еднакво оддалечена од краевите на отсечката. Докажете дека точката M лежи на нормалната симетрала на отсечката (сл. 3).

Ориз. 3. Илустрација за теоремата

Доказ:

Размислете за триаголник. Тоа е рамнокрак, според состојбата. Размислете за медијаната на триаголникот: точката O е средината на основата AB, OM е медијаната. Според имотот рамнокрак триаголник, медијаната навлечена до нејзината основа е и висината и симетралата. Го следи тоа . Но правата p е исто така нормална на AB. Знаеме дека во точката O е можно да се нацрта една нормална на отсечката AB, што значи дека правите OM и p се совпаѓаат, следува дека точката M припаѓа на правата p, што ни требаше да го докажеме.

Директно и обратна страна на теорематаможе да се генерализира.

Точка лежи на нормалната симетрала на отсечката ако и само ако е еднакво оддалечена од краевите на оваа отсечка.

Значи, да повториме дека има три отсечки во еден триаголник и својството на нормална симетрала важи за секоја од нив.

Теорема:

Нормалните симетрали на триаголникот се сечат во една точка.

Даден е триаголник. Перпендикулари на неговите страни: P 1 на страната BC, P 2 на страната AC, P 3 на страната AB.

Докажете дека перпендикуларите P 1, P 2 и P 3 се сечат во точката O (сл. 4).

Ориз. 4. Илустрација за теоремата

Доказ:

Да разгледаме две нормални симетрали P 2 и P 3, тие се сечат, пресечната точка O постои. Да го докажеме овој факт со контрадикторност - нека се паралелни нормалните P 2 и P 3. Тогаш аголот е обратен, што е во спротивност со фактот дека збирот на трите агли на триаголникот е . Значи, постои точка О на пресекот на две од трите нормални симетрали. Својства на точката O: лежи на нормалната симетрала на страната AB, што значи дека е еднакво оддалечена од краевите на отсечката AB: . Лежи и на нормалната симетрала на страната AC, што значи . Ги добивме следните еднаквости.

Теорема:

Симетралите AA 1, BB 1, СС 1 на триаголникот се сечат во една точка O (сл. 1).

Ориз. 1. Илустрација за теоремата

Доказ:

Значи, точката О на пресекот на две симетрали постои. Ајде да ги разгледаме неговите својства:

Ги добивме следните еднаквости:

, односно сите три нормални спуштени од точката О на страните на триаголникот се еднакви една со друга.

Така, докажавме дека сите три симетрали на триаголникот се сечат во една точка.

Ориз. 2. Илустрација за теоремата

Секоја точка што лежи на нормалната симетрала е еднакво оддалечена од краевите на отсечката.

Докажи дека (сл. 2).

Доказ:

Размислете за триаголници и . Тие се правоаголни и еднакви, бидејќи имаат заедничка катета OM, а катетите AO и OB се еднакви по услов, така што имаме два правоаголни триаголници, еднакви во две катети. Следи дека и хипотенусите на триаголниците се еднакви, односно она што се барало да се докаже.

Конверзната теорема е вистинита.

Секоја точка еднакво оддалечена од краевите на отсечката лежи на нормалната симетрала на оваа отсечка.

Ориз. 3. Илустрација за теоремата

Доказ:

Размислете за триаголник. Тоа е рамнокрак, според состојбата. Размислете за медијаната на триаголникот: точката O е средината на основата AB, OM е медијаната. Според својството на рамнокрак триаголник, медијаната навлечена до неговата основа е и надморска височина и симетрала. Го следи тоа . Но правата p е исто така нормална на AB. Знаеме дека во точката O е можно да се нацрта една нормална на отсечката AB, што значи дека правите OM и p се совпаѓаат, следува дека точката M припаѓа на правата p, што ни требаше да го докажеме.

Директната и обратната теорема може да се генерализираат.

Теорема:

Нормалните симетрали на триаголникот се сечат во една точка.

Даден е триаголник. Перпендикулари на неговите страни: P 1 на страната BC, P 2 на страната AC, P 3 на страната AB.

Докажете дека перпендикуларите P 1, P 2 и P 3 се сечат во точката O (сл. 4).

Ориз. 4. Илустрација за теоремата

Доказ:

Нормална симетрала (средна нормалнаили медијатрикс) - права линија нормална на даден сегмент и минува низ нејзината средина.

Својства

p_a=\tfrac(2aS)(a^2+b^2-c^2), p_b=\tfrac(2bS)(a^2+b^2-c^2), p_c=\tfrac(2cS)( a^2-b^2+c^2),

каде што подлогата ја означува страната на која е нацртана нормалната,

С

е плоштината на триаголникот, а исто така се претпоставува дека страните се поврзани со неравенки

a\geqslant b\geqslant в.

p_a\geq p_b

p_c\geq p_b.

Со други зборови, најмалата перпендикуларна симетрала на триаголникот припаѓа на средниот сегмент.

Напишете рецензија за написот „Перпендикуларна симетрала“

Белешки

Извадок што ја карактеризира нормалната симетрала

Кутузов, запирајќи да џвака, изненадено зјапа во Волцоген, како да не разбираше што му се зборува. Волцоген, забележувајќи ја возбудата на des alten Herrn, [стариот господин (Германец)] рече со насмевка:
– Не сметав дека имам право да го кријам од вашиот господар тоа што го видов... Војниците се во целосен неред...
- Дали сте виделе? Видовте?.. – викна Кутузов, намуртено, брзо стана и напредувајќи кон Волцоген. „Како... како се осмелуваш!..“, извикал, правејќи заканувачки гестови со ракување и гушење. - Како се осмелуваш, драг господине, да ми го кажеш ова? Ти ништо не знаеш. Кажете му на генералот Баркли од мене дека неговите информации се неточни и дека вистинскиот тек на битката мене, врховниот командант, подобро ми е познат отколку него.
Волцоген сакаше да приговара, но Кутузов го прекина.
- Непријателот е одбиен од лево и поразен на десното крило. Ако не сте виделе добро, почитуван господине, тогаш не дозволувајте да го кажувате она што не го знаете. Ве молам, одете кај генералот Баркли и следниот ден пренесете му ја мојата апсолутна намера да го нападнам непријателот“, строго рече Кутузов. Сите молчеа, а се слушаше само тешкото дишење на задишениот стар генерал. „Тие беа одбиени насекаде, за што му благодарам на Бога и на нашата храбра војска“. Непријателот е поразен, а утре ќе го избркаме од светата руска земја“, рече Кутузов прекрстувајќи се; и одеднаш заплака од солзите што дојдоа. Волцоген, кревајќи ги рамениците и стискајќи ги усните, тивко се оддалечи на страна, прашувајќи се uber diese Eingenommenheit des alten Herrn. [на оваа тиранија на стариот господин. (германски)]
„Да, еве го, мојот херој“, му рече Кутузов на полничкиот, убав, црномурест генерал, кој во тоа време влегуваше во тумбата. Тоа беше Раевски, кој го помина целиот ден на главната точка на полето Бородино.
Раевски извести дека трупите се цврсто на своите места и дека Французите повеќе не се осмелуваат да нападнат. Откако го слушна, Кутузов на француски рече:
– Vous ne pensez donc pas comme lesautres que nous sommes obliges de nous пензионер? [Тогаш, не мислите, како и другите, дека треба да се повлечеме?]