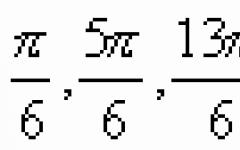W artykule szczegółowo wyjaśniono definicje, znaczenie geometryczne pochodna z zapisem graficznym. Równanie stycznej zostanie omówione na przykładach, znalezione zostaną równania stycznej do krzywych drugiego rzędu.
Definicja 1Kąt nachylenia prostej y = k x + b nazywany jest kątem α i mierzonym od dodatniego kierunku osi x do prostej y = k x + b w kierunku dodatnim.
Na rysunku kierunek x jest oznaczony zieloną strzałką i zielonym łukiem, a kąt nachylenia czerwonym łukiem. Niebieska linia odnosi się do linii prostej.
Definicja 2
Nachylenie prostej y = k x + b nazywa się współczynnikiem liczbowym k.
Współczynnik kątowy jest równy tangensowi prostej, czyli k = t g α.
- Kąt nachylenia prostej jest równy 0 tylko wtedy, gdy jest równoległa względem x, a nachylenie jest równe zero, ponieważ tangens zera jest równy 0. Oznacza to, że równanie będzie miało postać y = b.
- Jeżeli kąt nachylenia prostej y = k x + b jest ostry, to warunek 0 jest spełniony< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение nachylenie k uważa się za liczbę dodatnią, gdyż wartość tangensa spełnia warunek t g α > 0, a na wykresie następuje wzrost.
- Jeśli α = π 2, to położenie prostej jest prostopadłe do x. Równość jest określona przez x = c, gdzie wartość c jest liczbą rzeczywistą.
- Jeżeli kąt nachylenia prostej y = k x + b jest rozwarty, to odpowiada warunkom π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает wartość ujemna, a wykres maleje.
Sieczna to prosta przechodząca przez 2 punkty funkcji f (x). Innymi słowy, sieczna to linia prosta poprowadzona przez dowolne dwa punkty na wykresie dana funkcja.

Rysunek pokazuje, że AB jest sieczną, a f (x) jest czarną krzywą, α jest czerwonym łukiem, wskazującym kąt nachylenia siecznej.
Kiedy współczynnik kątowy linii prostej jest równy tangensowi kąta nachylenia, jasne jest, że tangens trójkąta prostokątnego A B C można znaleźć poprzez stosunek przeciwnej strony do sąsiedniej.
Definicja 4
Otrzymujemy wzór na znalezienie secansu postaci:
k = t g α = B C A C = f (x B) - f x A x B - x A, gdzie odcięte punktów A i B są wartościami x A, x B i f (x A), f (x B) są funkcjami wartości w tych punktach.
Oczywiście współczynnik kątowy siecznej wyznacza się za pomocą równości k = f (x B) - f (x A) x B - x A lub k = f (x A) - f (x B) x A - x B , a równanie należy zapisać jako y = f (x B) - f (x A) x B - x A x - x A + f (x A) lub
y = fa (x ZA) - fa (x B) x A - x B x - x B + fa (x B) .
Sieczna dzieli wykres wizualnie na 3 części: na lewo od punktu A, od A do B, na prawo od B. Poniższy rysunek pokazuje, że istnieją trzy sieczne, które uważa się za pokrywające się, to znaczy wyznacza się je za pomocą podobne równanie.

Z definicji jasne jest, że linia prosta i jej sieczna w tym przypadku pokrywają się.
Sieczna może przecinać wykres danej funkcji wielokrotnie. Jeżeli dla siecznej istnieje równanie w postaci y = 0, to liczba punktów przecięcia z sinusoidą jest nieskończona.
Definicja 5
Styczna do wykresu funkcji f (x) w punkcie x 0 ; f (x 0) jest linią prostą przechodzącą przez dany punkt x 0; f (x 0), z obecnością segmentu, który ma wiele wartości x bliskich x 0.
Przykład 1
Przyjrzyjmy się bliżej poniższemu przykładowi. Wtedy widać, że prostą wyznaczoną funkcją y = x + 1 uważa się za styczną do y = 2 x w punkcie o współrzędnych (1; 2). Dla jasności należy wziąć pod uwagę wykresy o wartościach bliskich (1; 2). Funkcja y = 2 x jest zaznaczona kolorem czarnym, niebieska linia to styczna, a czerwona kropka to punkt przecięcia.

Oczywiście y = 2 x łączy się z linią y = x + 1.
Aby wyznaczyć styczną, powinniśmy rozważyć zachowanie stycznej A B, gdy punkt B zbliża się do punktu A w nieskończoność. Dla przejrzystości przedstawiamy rysunek.

Sieczna A B, oznaczona niebieską linią, zmierza do położenia samej stycznej, a kąt nachylenia siecznej α zacznie zmierzać do kąta nachylenia samej stycznej α x.
Definicja 6
Styczną do wykresu funkcji y = f (x) w punkcie A uważa się za położenie graniczne siecznej A B, ponieważ B dąży do A, czyli B → A.
Przejdźmy teraz do rozważenia geometrycznego znaczenia pochodnej funkcji w punkcie.
Przejdźmy do rozważenia siecznej A B dla funkcji f (x), gdzie A i B o współrzędnych x 0, f (x 0) i x 0 + ∆ x, f (x 0 + ∆ x), i ∆ x wynoszą oznaczane jako przyrost argumentu. Teraz funkcja przyjmie postać ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Dla jasności podamy przykład rysunku.

Rozważ powstały trójkąt prostokątny A B C. Do rozwiązania używamy definicji stycznej, czyli otrzymujemy relację ∆ y ∆ x = t g α . Z definicji stycznej wynika, że lim ∆ x → 0 ∆ y ∆ x = t g α x . Zgodnie z zasadą pochodnej w punkcie mamy, że pochodna f (x) w punkcie x 0 nazywana jest granicą stosunku przyrostu funkcji do przyrostu argumentu, gdzie ∆ x → 0 , oznaczamy to jako f (x 0) = lim ∆ x → 0 ∆ y ∆ x .
Wynika z tego, że f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, gdzie k x oznacza się jako nachylenie stycznej.
Oznacza to, że stwierdzamy, że f ' (x) może istnieć w punkcie x 0 i podobnie jak styczna do danego wykresu funkcji w punkcie styczności równej x 0, f 0 (x 0), gdzie wartość nachylenie stycznej w punkcie jest równe pochodnej w punkcie x 0 . Wtedy otrzymujemy, że k x = f " (x 0) .
Znaczenie geometryczne pochodnej funkcji w punkcie polega na tym, że daje ona pojęcie o istnieniu stycznej do wykresu w tym samym punkcie.
Aby zapisać równanie dowolnej linii prostej na płaszczyźnie, konieczne jest posiadanie współczynnika kątowego z punktem, przez który ona przechodzi. Przyjmuje się, że jego zapis wynosi x 0 na przecięciu.
Równanie styczne do wykresu funkcji y = f (x) w punkcie x 0, f 0 (x 0) przyjmuje postać y = f "(x 0) x - x 0 + f (x 0).
Oznacza to, że końcową wartość pochodnej f” (x 0) można wykorzystać do określenia położenia stycznej, czyli w pionie, pod warunkiem, że lim x → x 0 + 0 f „ (x) = ∞ i lim x → x 0 - 0 f " (x ) = ∞ lub w ogóle nieobecny pod warunkiem lim x → x 0 + 0 fa " (x) ≠ lim x → x 0 - 0 f " (x) .
Położenie stycznej zależy od wartości jej współczynnika kątowego k x = f "(x 0). Gdy równolegle do osi o x otrzymujemy, że k k = 0, gdy równolegle do około y - k x = ∞, oraz postać równanie styczne x = x 0 rośnie wraz z k x > 0, maleje wraz z k x< 0 .
Przykład 2
Ułóż równanie stycznej do wykresu funkcji y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 w punkcie o współrzędnych (1; 3) i wyznacz kąt nachylenia.
Rozwiązanie
Pod warunkiem mamy, że funkcja jest zdefiniowana dla wszystkich liczby rzeczywiste. Stwierdzamy, że punkt o współrzędnych określonych warunkiem (1; 3) jest punktem styczności, wówczas x 0 = - 1, f (x 0) = - 3.
Należy znaleźć pochodną w punkcie o wartości - 1. Rozumiemy to
y " = mi x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = mi x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = mi x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = mi - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3
Wartość f' (x) w punkcie styczności jest nachyleniem stycznej, która jest równa stycznej nachylenia.
Następnie k x = t g α x = y " (x 0) = 3 3
Wynika z tego, że α x = a r do t sol 3 3 = π 6
Odpowiedź: równanie styczne przyjmuje postać
y = fa " (x 0) x - x 0 + fa (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3
Dla przejrzystości podajemy przykład na ilustracji graficznej.
Kolorem czarnym oznaczono wykres oryginalnej funkcji, kolor niebieski przedstawia styczną, a czerwona kropka oznacza punkt styczności. Rysunek po prawej stronie przedstawia widok w powiększeniu.

Przykład 3
Ustalić istnienie stycznej do wykresu danej funkcji
y = 3 · x - 1 5 + 1 w punkcie o współrzędnych (1 ; 1) . Napisz równanie i określ kąt nachylenia.
Rozwiązanie
Pod warunkiem mamy, że za dziedzinę definicji danej funkcji uważa się zbiór wszystkich liczb rzeczywistych.
Przejdźmy do znalezienia pochodnej
y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5
Jeśli x 0 = 1, to f' (x) jest nieokreślone, ale granice są zapisywane jako lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ i lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞, co oznacza istnienie stycznej pionowej w punkcie (1; 1).
Odpowiedź: równanie przyjmie postać x = 1, gdzie kąt nachylenia będzie równy π 2.
Dla jasności przedstawmy to graficznie.

Przykład 4
Znajdź punkty na wykresie funkcji y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, gdzie
- Nie ma stycznej;
- Styczna jest równoległa do x;
- Styczna jest równoległa do prostej y = 8 5 x + 4.
Rozwiązanie
Należy zwrócić uwagę na zakres definicji. Pod warunkiem mamy, że funkcja jest zdefiniowana na zbiorze wszystkich liczb rzeczywistych. Rozbudowujemy moduł i rozwiązujemy układ o przedziałach x ∈ - ∞ ; 2 i [- 2; + ∞) . Rozumiemy to
y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)
Konieczne jest różniczkowanie funkcji. Mamy to
y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)
Gdy x = - 2, to pochodna nie istnieje, ponieważ jednostronne granice nie są w tym punkcie równe:
lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3
Obliczamy wartość funkcji w punkcie x = - 2, gdzie to otrzymujemy
- y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, czyli styczna w punkcie ( - 2; - 2) nie będzie istnieć.
- Styczna jest równoległa do x, gdy nachylenie wynosi zero. Następnie k x = t g α x = f "(x 0). Oznacza to, że konieczne jest znalezienie wartości takiego x, gdy pochodna funkcji zamienia ją na zero. To znaczy wartości f ' (x) będą punktami styczności, gdzie styczna jest równoległa do x .
Kiedy x ∈ - ∞ ; - 2, wówczas - 1 5 (x 2 + 12 x + 35) = 0, a dla x ∈ (- 2; + ∞) otrzymujemy 1 5 (x 2 - 4 x + 3) = 0.
1 5 (x 2 + 12 x + 35) = 0 re = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 re = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞
Oblicz odpowiednie wartości funkcji
y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3
Stąd - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 są uważane za wymagane punkty wykresu funkcji.
Rozważmy obraz graficzny rozwiązania.

Czarna linia to wykres funkcji, czerwone kropki to punkty styczności.
- Gdy linie są równoległe, współczynniki kątowe są równe. Następnie należy wyszukać punkty na wykresie funkcji, w których nachylenie będzie równe wartości 8 5. Aby to zrobić, musisz rozwiązać równanie postaci y "(x) = 8 5. Następnie, jeśli x ∈ - ∞; - 2, otrzymujemy to - 1 5 (x 2 + 12 x + 35) = 8 5, a jeśli x ∈ ( - 2 ; + ∞), to 1 5 (x 2 - 4 x + 3) = 8 5.
Pierwsze równanie nie ma pierwiastków, ponieważ dyskryminator jest mniejszy od zera. Zapiszmy to
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0
Zatem inne równanie ma dwa rzeczywiste pierwiastki
1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 re = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞
Przejdźmy do znalezienia wartości funkcji. Rozumiemy to
y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3
Punkty o wartościach - 1; 4 15, 5; 8 3 to punkty, w których styczne są równoległe do prostej y = 8 5 x + 4.
Odpowiedź: linia czarna – wykres funkcji, linia czerwona – wykres y = 8 5 x + 4, linia niebieska – styczne w punktach - 1; 4 15, 5; 8 3.

Możliwe istnienie nieskończona liczba tangensy dla danych funkcji.
Przykład 5
Zapisz równania wszystkich dostępnych stycznych funkcji y = 3 cos 3 2 x - π 4 - 1 3, które leżą prostopadle do prostej y = - 2 x + 1 2.
Rozwiązanie
Aby skompilować równanie styczne, należy znaleźć współczynnik i współrzędne punktu stycznego, w oparciu o warunek prostopadłości linii. Definicja jest następująca: iloczyn współczynników kątowych prostopadłych do prostych jest równy -1, czyli zapisywany jako k x · k ⊥ = - 1. Z warunku mamy, że współczynnik kątowy leży prostopadle do prostej i jest równy k ⊥ = - 2, wówczas k x = - 1 k ⊥ = - 1 - 2 = 1 2.
Teraz musisz znaleźć współrzędne punktów dotyku. Musisz znaleźć x, a następnie jego wartość dla danej funkcji. Należy zauważyć, że z geometrycznego znaczenia pochodnej w punkcie
x 0 otrzymujemy, że k x = y "(x 0). Z tej równości znajdujemy wartości x dla punktów styku.
Rozumiemy to
y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - grzech 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 grzech 3 2 x 0 - π 4 3 2 = - 9 2 grzech 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 grzech 3 2 x 0 - π 4 = 1 2 ⇒ grzech 3 2 x 0 - π 4 = - 1 9
Ten równanie trygonometryczne zostaną użyte do obliczenia współrzędnych punktów stycznych.
3 2 x 0 - π 4 = a r do sin - 1 9 + 2 πk lub 3 2 x 0 - π 4 = π - a r do grzech - 1 9 + 2 πk
3 2 x 0 - π 4 = - a r do grzech 1 9 + 2 πk lub 3 2 x 0 - π 4 = π + za r do grzech 1 9 + 2 πk
x 0 = 2 3 π 4 - za r do sin 1 9 + 2 πk lub x 0 = 2 3 5 π 4 + za r do sin 1 9 + 2 πk , k ∈ Z
Z jest zbiorem liczb całkowitych.
znaleziono x punktów kontaktowych. Teraz musisz przejść do wyszukiwania wartości y:
y 0 = 3 cos 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - grzech 2 3 2 x 0 - π 4 - 1 3 lub y 0 = 3 - 1 - grzech 2 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - - 1 9 2 - 1 3 lub y 0 = 3 - 1 - - 1 9 2 - 1 3
y 0 = 4 5 - 1 3 lub y 0 = - 4 5 + 1 3
Z tego otrzymujemy, że 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r do grzech 1 9 + 2 πk ; - 4 5 + 1 3 to punkty styczności.
Odpowiedź: niezbędne równania zostaną zapisane jako
y = 1 2 x - 2 3 π 4 - za r do grzech 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + za r do grzech 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z
Aby uzyskać reprezentację wizualną, rozważ funkcję i styczną na linii współrzędnych.
Z rysunku wynika, że funkcja znajduje się na przedziale [-10; 10 ], gdzie czarna linia to wykres funkcji, niebieskie linie to styczne, które leżą prostopadle do danej prostej postaci y = - 2 x + 1 2. Czerwone kropki to punkty dotykowe.

Równania kanoniczne krzywych drugiego rzędu nie są funkcjami jednowartościowymi. Równania styczne dla nich są zestawiane według znanych schematów.
Styczna do okręgu
Aby zdefiniować okrąg ze środkiem w punkcie x środek t e r ; y c e n t e r i promień R, zastosuj wzór x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .
Równość tę można zapisać jako sumę dwóch funkcji:
y = R 2 - x - x do mi n t mi r 2 + y do mi n t e r y = - R 2 - x - x do mi n t mi r 2 + y do mi n t mi r
Pierwsza funkcja znajduje się na górze, a druga na dole, jak pokazano na rysunku.

Aby skompilować równanie okręgu w punkcie x 0; y 0 , który znajduje się w górnym lub dolnym półkolu, powinieneś znaleźć równanie wykresu funkcji postaci y = R 2 - x - x c e n t e r 2 + y c e n t e r lub y = - R 2 - x - x c e n t e r 2 + centrum we wskazanym punkcie.
Kiedy w punktach x cent e r ; y c e n t e r + R i x c e n t e r ; y c e n t e r - R styczne można wyrazić za pomocą równań y = y c e n t e r + R i y = y c e n t e r - R oraz w punktach x c e n t e r + R ; y centrum i
x środek t e r - R ; y c e n t e r będzie równoległe do o y, wówczas otrzymamy równania postaci x = x c e n t e r + R i x = x c e n t e r - R .

Styczna do elipsy
Gdy elipsa ma środek w xcenter r ; y centrum t e r z półosiami a i b, to można to określić za pomocą równania x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.
Elipsę i okrąg można oznaczyć poprzez połączenie dwóch funkcji, a mianowicie górnej i dolnej półelipsy. Wtedy to zrozumiemy
y = b za · za 2 - (x - x do e n t mi r) 2 + y do mi n t e r y = - b a · za 2 - (x - x do mi n t e r) 2 + y do mi n t mi r

Jeśli styczne znajdują się na wierzchołkach elipsy, to są one równoległe względem x lub y. Poniżej, dla jasności, rozważ rysunek.

Przykład 6
Zapisz równanie stycznej do elipsy x - 3 2 4 + y - 5 2 25 = 1 w punktach o wartościach x równych x = 2.
Rozwiązanie
Konieczne jest znalezienie punktów stycznych odpowiadających wartości x = 2. Podstawiamy do istniejącego równania elipsy i znajdujemy to
x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5
Następnie 2; 5 3 2 + 5 i 2; - 5 3 2 + 5 to punkty styczne należące do górnej i dolnej półelipsy.
Przejdźmy do znalezienia i rozwiązania równania elipsy względem y. Rozumiemy to
x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2
Oczywiście górną półelipsę określa się funkcją w postaci y = 5 + 5 2 4 - x - 3 2, a dolną półelipsę y = 5 - 5 2 4 - x - 3 2.
Zastosujmy standardowy algorytm do utworzenia równania stycznej do wykresu funkcji w punkcie. Napiszmy, że równanie dla pierwszej stycznej w punkcie 2; 5 3 2 + 5 będzie wyglądać
y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5
Stwierdzamy, że równanie drugiej stycznej z wartością w punkcie
2; - 5 3 2 + 5 przyjmuje formę
y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5
Graficznie styczne są oznaczone w następujący sposób:

Styczna do hiperboli
Gdy hiperbola ma środek w punkcie x środek ; y środek i wierzchołki x środek t e r + α ; y centrum t i x cen t e r - α; y c e n t e r , nierówność x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 ma miejsce, jeśli z wierzchołkami x c e n t e r ; y c e n t e r + b i x c e n t e r ; y c e n t e r - b , wówczas określa się je za pomocą nierówności x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Hiperbolę można przedstawić jako dwie połączone funkcje formy
y = b za · (x - x do e n t e r) 2 - za 2 + y do mi n t e r y = - b a · (x - x do mi n t e r) 2 - za 2 + y c e n t e r lub y = b a · (x - x c e n t e r) 2 + za 2 + y do e n t e r y = - b a · (x - x c e n t e r) 2 + za 2 + y c e n t e r

W pierwszym przypadku mamy, że styczne są równoległe do y, a w drugim są równoległe do x.
Wynika z tego, że aby znaleźć równanie stycznej do hiperboli, należy dowiedzieć się, do jakiej funkcji należy punkt styczności. Aby to ustalić, należy podstawić równania i sprawdzić identyczność.
Przykład 7
Napisz równanie stycznej do hiperboli x - 3 2 4 - y + 3 2 9 = 1 w punkcie 7; - 3 3 - 3 .
Rozwiązanie
Konieczne jest przekształcenie zapisu rozwiązania w celu znalezienia hiperboli za pomocą 2 funkcji. Rozumiemy to
x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 i y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3
Konieczne jest określenie, do jakiej funkcji należy Do dany punkt o współrzędnych 7; - 3 3 - 3 .
Oczywiście do sprawdzenia pierwszej funkcji potrzebne jest y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, wtedy punkt nie należy do wykresu, ponieważ równość nie zachodzi.
Dla drugiej funkcji mamy, że y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, co oznacza, że punkt należy do danego wykresu. Stąd powinieneś znaleźć zbocze.
Rozumiemy to
y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3
Odpowiedź: równanie styczne można przedstawić jako
y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3
Jest to wyraźnie przedstawione w ten sposób:

Styczna do paraboli
Aby utworzyć równanie stycznej do paraboli y = a x 2 + b x + c w punkcie x 0, y (x 0), należy użyć standardowego algorytmu, wówczas równanie przybierze postać y = y ”(x 0) x - x 0 + y ( x 0). Taka styczna w wierzchołku jest równoległa do x.
Powinieneś zdefiniować parabolę x = a y 2 + b y + c jako sumę dwóch funkcji. Dlatego musimy rozwiązać równanie dla y. Rozumiemy to
x = za y 2 + b y + do ⇔ za y 2 + b y + do - x = 0 re = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a
Graficznie przedstawiony jako:

Aby dowiedzieć się czy punkt x 0, y (x 0) należy do funkcji, postępuj delikatnie według standardowego algorytmu. Taka styczna będzie równoległa do oy względem paraboli.
Przykład 8
Zapisz równanie stycznej do wykresu x - 2 y 2 - 5 y + 3 gdy mamy kąt styczny równy 150°.
Rozwiązanie
Rozwiązanie zaczynamy od przedstawienia paraboli jako dwóch funkcji. Rozumiemy to
2 lata 2 - 5 lat + 3 - x = 0 re = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4
Wartość nachylenia jest równa wartości pochodnej w punkcie x 0 tej funkcji i jest równa tangensowi kąta nachylenia.
Otrzymujemy:
k x = y "(x 0) = t sol α x = t g 150 ° = - 1 3
Stąd określamy wartość x dla punktów styku.
Pierwsza funkcja zostanie zapisana jako
y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3
Oczywiście nie ma prawdziwych pierwiastków, ponieważ otrzymaliśmy wartość ujemną. Dochodzimy do wniosku, że dla takiej funkcji nie ma stycznej o kącie 150°.
Druga funkcja zostanie zapisana jako
y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4
Mamy, że punktów styku jest 23 4 ; - 5 + 3 4 .
Odpowiedź: równanie styczne przyjmuje postać
y = - 1 3 x - 23 4 + - 5 + 3 4
Przedstawmy to graficznie w ten sposób:

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter
Dowód
Jeśli cięciwa jest średnicą, wówczas twierdzenie jest oczywiste.
Rysunek 287 przedstawia okrąg o środku O, M jest punktem przecięcia średnicy CD i cięciwy AB, CD ⊥ AB. Musimy udowodnić, że AM = MB.
Narysujmy promienie OA i OB. W trójkącie równoramiennym AOB (OA = OB) odcinek OM jest wysokością, a zatem medianą, czyli AM = MB.
Twierdzenie 20.2
Średnica okręgu dzielącego cięciwę inna niż średnica na pół jest prostopadła do tej cięciwy.
Udowodnij to twierdzenie sam. Zastanów się, czy to stwierdzenie byłoby prawdziwe, gdyby cięciwa miała średnicę.
Rysunek 288 pokazuje wszystkie możliwe przypadki położenie względne linia prosta i okrąg. Na ryc. 288 a nie mają punktów wspólnych, na ryc. 288, b - mają dwa punkty wspólne, na ryc. 288, c - jeden.
|
Ryż. 288 |
||
|
|
|
|
Definicja
Prostą, która ma tylko jeden punkt wspólny z okręgiem, nazywamy styczną do okręgu.
Styczna do okręgu ma tylko jeden punkt wspólny z okręgiem ograniczonym przez ten okrąg. Na rysunku 288 linia a jest styczna do okręgu o środku w punkcie O, A jest punktem styczności.
Jeśli odcinek (prosta) należy do stycznej do okręgu i ma z tym okręgiem punkt wspólny, to mówimy, że ten odcinek (prosta) jest styczny do okręgu. Na przykład Rysunek 289 przedstawia odcinek AB, który styka się z okręgiem w punkcie C.
Twierdzenie 20.3
(właściwość styczna)
Styczna do okręgu jest prostopadła do promienia poprowadzonego do punktu styczności.
Dowód
Rysunek 290 przedstawia okrąg o środku O, A jest punktem stycznym prostej a i okręgu. Musimy udowodnić, że OA ⊥ a.
|
Ryż. 289 |
Ryż. 290 |
Ryż. 291 |
|
|
|
|
Załóżmy, że tak nie jest, czyli odcinek OA jest nachylony do prostej a. Następnie z punktu O obniżamy prostopadłą OM do linii prostej a (ryc. 291). Ponieważ punkt A jest jedynym punktem wspólnym prostej a i okręgu o środku O, to punkt M nie należy do tego okręgu. Stąd OM = MB + OB, gdzie punkt B jest punktem przecięcia okręgu i prostopadłej OM. Odcinki OA i OB są równe promieniom okręgu. Zatem OM > OA.
Otrzymaliśmy sprzeczność: prostopadła OM jest większa niż ukośna OA. Dlatego OA ⊥ a.
Twierdzenie 20.4
(znak stycznej do okręgu)
Dowód
|
Jeżeli prosta przechodząca przez punkt na okręgu jest prostopadła do promienia poprowadzonego do tego punktu, to ta prosta jest styczna do tego okręgu. |
|
|
Rysunek 290 przedstawia okrąg o środku w punkcie O, odcinek OA jest jego promieniem, punkt A należy do prostej a, OA ⊥ a. Udowodnijmy, że prosta a jest styczna do okręgu.
Niech prosta a nie będzie styczna, ale będzie miała inny punkt wspólny B z okręgiem (ryc. 292). Wtedy ∆ AOB jest równoramienne (OA = OB jako promień). Stąd ∠ OBA = ∠ OAB = 90°. Otrzymujemy sprzeczność: trójkąt AOB ma dwa kąty proste. Zatem prosta a jest styczna do okręgu.
Konsekwencja
Jeżeli odległość środka okręgu od pewnej prostej jest równa promieniowi okręgu, to ta prosta jest styczna do tego okręgu.
|
Ryż. 293 |
|
|
Udowodnij tę konkluzję samodzielnie.
Zadanie. Udowodnij, że jeśli przez dany punkt poprowadzono dwie styczne do okręgu, to odcinki styczne łączące ten punkt z punktami styczności są równe.
Rozwiązanie. Rysunek 293 przedstawia okrąg o środku O. Linie AB i AC są stycznymi, a punkty B i C są punktami stycznymi. Musimy udowodnić, że AB = AC.
Narysujmy promienie OB i OC do punktów styku. Z własności stycznej OB ⊥ AB i OC ⊥ AC. W trójkątach prostokątnych AOB i AOC ramiona OB i OC są równe promieniom jednego okręgu, a AO jest wspólną przeciwprostokątną. Dlatego trójkąty AOB i AOC są równe pod kątem przeciwprostokątnej i nogi. Stąd AB = AC.

- Jak średnica prostopadła do niej dzieli cięciwę?
- Jaki jest kąt między cięciwą inny niż średnica i średnica dzieląca tę cięciwę na pół?
- Opisz wszystkie możliwe przypadki względnego położenia prostej i okręgu.
- Jaką prostą nazywamy styczną do okręgu?
- Jaką właściwość ma promień poprowadzony do punktu styczności prostej i okręgu?
- Sformułuj test na styczną do okręgu.
- Jaką właściwość mają styczne poprowadzone do okręgu przez jeden punkt?

Zadania praktyczne

507. Narysuj okrąg o środku O, narysuj cięciwę AB. Za pomocą kwadratu podziel ten akord na pół.
508. Narysuj okrąg ze środkiem O, narysuj cięciwę CD. Za pomocą linijki ze skalą narysuj średnicę prostopadle do cięciwy CD.
509. Narysuj okrąg, zaznacz na nim punkty A i B. Za pomocą linijki i kwadratu narysuj linie proste, które stykają się z okręgiem w punktach A i B.
510. Narysuj linię a i zaznacz na niej punkt M. Za pomocą kwadratu, linijki i kompasu narysuj okrąg o promieniu 3 cm, który styka się z linią a w punkcie M. Ile takich okręgów można narysować?

Ćwiczenia
511. Na rysunku 294 punkt O jest środkiem okręgu, średnica CD jest prostopadła do cięciwy AB. Udowodnić, że ∠AOD = ∠BOD.
512. Udowodnić, że równe cięciwy okręgu są w jednakowej odległości od jego środka.
513. Udowodnij, że jeśli cięciwy okręgu są w równej odległości od jego środka, to są sobie równe.
514. Czy prawdą jest, że prosta prostopadła do promienia okręgu styka się z tym okręgiem?
515. Prosty CD styka się z okręgiem o środku O w punkcie A, odcinek AB jest cięciwą okręgu, ∠ BAD = 35° (ryc. 295). Znajdź ∠AOB.
516. Prosty CD styka się z okręgiem o środku O w punkcie A, odcinek AB jest cięciwą okręgu, ∠ AOB = 80° (patrz rys. 295). Znajdź ∠BAC.
517. Mając okrąg o średnicy 6 cm, linia a jest oddalana od jego środka o: 1) 2 cm; 2) 3 cm; 3) 6 cm W jakim przypadku linia jest styczna do okręgu?
518. W trójkącie ABC wiemy, że ∠ C = 90°. Udowodnij, że:
1) proste BC jest styczna do okręgu, którego środek A przechodzi przez punkt C;
2) proste AB nie jest styczna do okręgu, którego środek C przechodzi przez punkt A.

519. Udowodnić, że średnica okręgu jest większa od cięciwy innej niż średnica.
520. W okręgu o środku O cięciwa AB jest poprowadzona przez środek promienia, prostopadle do niego. Udowodnić, że ∠ AOB = 120°.
521. Znajdź kąt zawarty między promieniami OA i OB okręgu, jeśli odległość środka O koła od cięciwy AB jest 2 razy mniejsza niż: 1) długość cięciwy AB; 2) promień okręgu.
522. Na okręgu narysowano średnicę AB oraz cięciwy AC i CD w taki sposób, że AC = 12 cm, ∠ BAC = 30°, AB ⊥ CD. Znajdź długość akordu CD.
523. Przez punkt M do okręgu o środku O rysujemy styczne MA i MB, A i B są punktami styczności, ∠ OAB = 20°. Znajdź ∠AMB.
524. Przez końce cięciwy AB równe promieniowi okręgu poprowadzono dwie styczne przecinające się w punkcie C. Znajdź ∠ ACB.
525. Przez punkt Z okręgu o środku O rysujemy styczną do tego okręgu, AB jest średnicą okręgu. Z punktu A prostopadła AD została spuszczona na styczną. Udowodnić, że promień AC jest dwusieczną kąta BAD.
526. Prosty AC dotyka okręgu o środku O w punkcie A (ryc. 296). Udowodnić, że kąt BAC jest 2 razy mniejszy od kąta AOB.
|
Ryż. 294 |
Ryż. 295 |
Ryż. 296 |
|
|
|
|
527. Segmenty AB i BC to odpowiednio cięciwa i średnica okręgu, ∠ ABC = 30°. Przez punkt A poprowadź styczną do okręgu przecinającego linię BC w punkcie D. Udowodnij, że ∆ ABD jest równoramienne.
528. Wiadomo, że średnica AB przecina cięciwę CD na pół, ale nie jest do niej prostopadła. Udowodnić, że CD jest również średnicą.

529. Znajdować umiejscowienieśrodki okręgów stykających się z daną linią w danym punkcie.
530. Znajdź miejsce środków okręgów stykających się z obiema stronami danego kąta.
531. Znajdź miejsce środków okręgów stykających się z daną linią.
532. Proste styczne do okręgu o środku O w punktach A i B przecinają się w punkcie K, ∠ AKB = 120°. Udowodnić, że AK + BK = OK.
533. Okrąg dotyka boku AB trójkąta ABC w punkcie M i dotyka przedłużenia pozostałych dwóch boków. Udowodnić, że suma długości odcinków BC i BM jest równa połowie obwodu trójkąta ABC.
|
Ryż. 297 |
|
|
534. Przez punkt C to styczne AC i BC do okręgu, A i B to punkty styczności (ryc. 297). Na okręgu wzięliśmy dowolny punkt M leżący w tej samej półpłaszczyźnie z punktem C względem prostej AB i poprowadziliśmy przez niego styczną do okręgu przecinającego proste AC i BC odpowiednio w punktach D i E. Udowodnić, że obwód trójkąta DEC nie zależy od wyboru punktu M.
Ćwiczenia do powtórzenia
535. Udowodnić, że środek M odcinka, którego końce należą do dwóch prostych równoległych, jest środkiem dowolnego odcinka przechodzącego przez punkt M i którego końce należą do tych prostych.
536. Segmenty AB i CD leżą na tej samej prostej i mają wspólny środek. Punkt M został wybrany w taki sposób, że trójkąt AMB jest równoramienny o podstawie AB. Udowodnić, że ∆ CMD jest również równoramienne z podstawą CD.
537. Ubocznie MK trójkąta MPK oznaczyli punkty E i F tak, że punkt E leży pomiędzy punktami M i F, ME = EP, PF = FK. Znajdź kąt M, jeśli ∠ EPF = 92°, ∠ K = 26°.
538. W ostry trójkąt ABC, rysujemy dwusieczną BM, z punktu M na bok BC rysujemy prostopadłą MK, ∠ ABM = ∠ KMC. Udowodnij to trójkąt ABC- równoramienne.
Obserwuj, rysuj, projektuj, fantazjuj
539. Ustal wzór kształtów figur pokazanych na rycinie 298. Którą figurę ustawić jako następną?
|
Ryż. 298 |
Bezpośredni ( MN), mający tylko jeden punkt wspólny z okręgiem ( A), zwany tangens do kręgu.
W tym przypadku nazywany jest punkt wspólny punkt kontaktowy.
Możliwość istnienia tangens, a ponadto przeciągnięta przez dowolny punkt koło, jako punkt styczności, udowadnia się w następujący sposób twierdzenie.
Niech będzie to wymagane do wykonania koło z centrum O tangens przez punkt A. Aby to zrobić od razu A, jak od środka, opisujemy łuk promień AO, i od razu O, jako środek, przecinamy ten łuk w punktach B I Z rozwiązanie kompasu równe średnicy danego koła.
Po spędzeniu wtedy akordy O.B. I system operacyjny, połącz kropkę A z kropkami D I mi, w którym cięciwy te przecinają się z danym okręgiem. Bezpośredni OGŁOSZENIE I AE - styczne do okręgu O. Rzeczywiście, z konstrukcji wynika, że trójkąty AOB I AOC równoramienny(AO = AB = AC) z podstawami O.B. I system operacyjny równy średnicy okręgu O.
Ponieważ OD I OE- zatem promienie D - środek O.B., A mi- środek system operacyjny, Oznacza OGŁOSZENIE I AE - mediany, przeniesiony do baz trójkąty równoramienne, a więc prostopadle do tych podstaw. Jeśli prosto DA I EA prostopadle do promieni OD I OE, wtedy oni - styczne.
Konsekwencja.
Dwie styczne poprowadzone z jednego punktu do okręgu są równe i tworzą równe kąty z linią prostą łączącą ten punkt ze środkiem.
Więc AD=AE i ∠ OAD = ∠OAE ponieważ trójkąty prostokątne AOD I Obszar działania, mając wspólne przeciwprostokątna AO i równe nogi OD I OE(jako promienie) są równe. Zauważ, że tutaj słowo „styczna” w rzeczywistości oznacza „ odcinek styczny” od danego punktu do punktu styku.
Linia prosta względem okręgu może znajdować się w trzech następujących pozycjach:- Odległość środka okręgu od prostej jest większa od promienia. W tym przypadku wszystkie punkty linii leżą poza okręgiem.
- Odległość środka okręgu od prostej jest mniejsza niż promień. W tym przypadku linia prosta ma punkty leżące wewnątrz okręgu, a ponieważ linia prosta jest nieskończona w obu kierunkach, przecina ją okrąg w 2 punktach.
- Odległość środka okręgu od prostej jest równa promieniowi. Linia prosta jest styczna.
Prostą, która ma tylko jeden punkt wspólny z okręgiem, nazywa się tangens do kręgu.
W tym przypadku nazywany jest punkt wspólny punkt kontaktowy.
Możliwość istnienia stycznej, a ponadto poprowadzonej przez dowolny punkt okręgu jako punkt styczności, udowadnia następujące twierdzenie.
Twierdzenie. Jeżeli prosta jest prostopadła do promienia na końcu leżącego na okręgu, to ta prosta jest styczną.
Niech O (rys.) będzie środkiem jakiegoś okręgu, a OA częścią jego promienia. Przez jego koniec A przeciągamy MN ^ OA.
Należy wykazać, że prosta MN jest styczna, tj. że prosta ta ma tylko jeden punkt wspólny A z okręgiem.

Załóżmy odwrotnie: niech MN ma inny punkt wspólny z okręgiem, na przykład B.
Wtedy linia prosta OB byłaby promieniem, a zatem równa OA.
Ale tak nie może być, gdyż jeśli OA jest prostopadła, to OB musi być nachylona do MN, a nachylona jest większa od prostopadłej.
Twierdzenie odwrotne. Jeżeli prosta jest styczna do okręgu, to promień poprowadzony do punktu styczności jest do niej prostopadły.
Niech MN będzie styczną do okręgu, A punktem styczności, a O środkiem okręgu.
Należy udowodnić, że OA^MN.
Załóżmy odwrotnie, tj. Załóżmy, że prostopadła rzucona z O do MN nie będzie OA, ale inną prostą, np. OB.
Weźmy BC = AB i wykonajmy OS.
Wtedy OA i OS będą nachylone, jednakowo oddalone od prostopadłej OB, a zatem OS = OA.
Wynika z tego, że okrąg, biorąc pod uwagę nasze założenie, będzie miał dwa punkty wspólne z prostą MN: A i C, tj. MN nie będzie styczną, ale sieczną, co jest sprzeczne z warunkiem.
Konsekwencja. Przez dowolny punkt na okręgu można poprowadzić styczną do tego okręgu i tylko jedną, gdyż przez ten punkt można poprowadzić prostopadłą i tylko jedną do wciągniętego w niego promienia.
Twierdzenie. Styczna równoległa do cięciwy dzieli łuk, na którym opiera się cięciwa, na pół w punkcie styku.
Niech prosta AB (rys.) dotyka okręgu w punkcie M i jest równoległa do cięciwy CD.
Musimy udowodnić, że ÈCM = ÈMD.

Rysując średnicę ME przez punkt styczności, otrzymujemy: EM ^ AB, a zatem EM ^ CB.
Zatem CM=MD.
Zadanie. Przez dany punkt poprowadź styczną do danego okręgu.
Jeżeli dany punkt leży na okręgu, to poprowadź przez niego promień i prostą prostopadłą przez koniec promienia. Ta linia będzie pożądaną styczną.
Rozważmy przypadek, gdy punkt jest dany poza okręgiem.
Niech będzie wymagane (ryc.) narysowanie stycznej do okręgu o środku O przez punkt A.
W tym celu z punktu A jako środek opisujemy łuk o promieniu AO, a z punktu O jako środek przecinamy ten łuk w punktach B i C z otworem kompasu równym średnicy danego okręgu .
Po narysowaniu cięciw OB i OS łączymy punkt A z punktami D i E, w których cięciwy te przecinają się z danym okręgiem.
Linie AD i AE są styczne do okręgu O.

Rzeczywiście z konstrukcji jasno wynika, że rury AOB i AOC są równoramienne (AO = AB = AC), których podstawy OB i OS są równe średnicy koła O.
Ponieważ OD i OE są promieniami, wówczas D jest środkiem OB, a E jest środkiem OS, co oznacza, że AD i AE to środkowe poprowadzone do podstaw rur równoramiennych, a zatem prostopadłe do tych podstaw. Jeżeli proste DA i EA są prostopadłe do promieni OD i OE, to są styczne.
Konsekwencja. Dwie styczne poprowadzone z jednego punktu do okręgu są równe i tworzą równe kąty z linią prostą łączącą ten punkt ze środkiem.
Zatem AD=AE i ÐOAD = ÐOAE (ryc.), ponieważ prostokątne tr-ki AOD i AOE, mające wspólną przeciwprostokątną AO i równe ramiona OD i OE (jako promienie), są równe.
Należy zauważyć, że tutaj słowo „styczna” oznacza rzeczywisty „odcinek styczny” od danego punktu do punktu styku.
Zadanie. Narysuj styczną do danego okręgu O, równoległą do danej prostej AB (rys.).
Opuszczamy prostopadłą OS do AB ze środka O i przez punkt D, w którym ta prostopadła przecina okrąg, rysujemy EF || AB.
Styczna, której szukamy, będzie EF.

Rzeczywiście, ponieważ OS ^ AB i EF || AB, następnie EF ^ OD, a prosta prostopadła do promienia na jego końcu leżąca na okręgu jest styczną.
Zadanie. Narysuj wspólną styczną do dwóch okręgów O i O 1 (ryc.).

Analiza. Załóżmy, że problem został rozwiązany.
Niech AB będzie wspólną styczną, A i B punktami styczności.
Oczywiście, jeśli znajdziemy jeden z tych punktów, na przykład A, to bez problemu znajdziemy drugi.
Narysujmy promienie OA i O 1 B. Promienie te, prostopadłe do wspólnej stycznej, są do siebie równoległe.
Zatem jeśli z O 1 wyciągniemy O 1 C || BA, wówczas rurociąg OCO 1 będzie prostokątny w wierzchołku C.
W rezultacie, jeśli opiszemy okrąg z O jako środek o promieniu OS, to będzie on dotykał prostej O 1 C w punkcie C.
Promień tego okręgu pomocniczego jest znany: jest równy OA – CA = OA – O 1 B, tj. jest równa różnicy promieni tych okręgów.
Budowa. Ze środka O opisujemy okrąg o promieniu równym różnicy tych promieni.
Z O 1 rysujemy styczną O 1 C do tego okręgu (w sposób wskazany w poprzednim zadaniu).
Przez punkt styczny C rysujemy promień OS i kontynuujemy go, aż dotrze do zadanego okręgu w punkcie A. Na koniec z A rysujemy AB równolegle do CO 1.
Dokładnie w ten sam sposób możemy skonstruować kolejną wspólną styczną A 1 B 1 (ryc.). Wywoływane są linie bezpośrednie AB i A 1 B 1 zewnętrzny wspólne styczne.
Możesz wydać jeszcze dwa wewnętrzny styczne w następujący sposób:

Analiza. Załóżmy, że problem został rozwiązany (ryc.). Niech AB będzie pożądaną styczną.
Narysujmy promienie OA i O 1 B do punktów stycznych A i B. Ponieważ oba te promienie są prostopadłe do wspólnej stycznej, są one do siebie równoległe.
Zatem jeśli z O 1 wyciągniemy O 1 C || BA i kontynuuj OA do punktu C, następnie OS będzie prostopadły do O 1 C.
W rezultacie okrąg opisany promieniem OS z punktu O jako środka dotknie prostej O 1 C w punkcie C.
Promień tego okręgu pomocniczego jest znany: jest równy OA+AC = OA+O 1 B, tj. jest równa sumie promieni danych okręgów.
Budowa. Od O jako środka opisujemy okrąg o promieniu równym sumie tych promieni.
Z O 1 rysujemy styczną O 1 C do tego okręgu.
Łączymy punkt styku C z O.
Wreszcie przez punkt A, w którym OS przecina dany okrąg, rysujemy AB = O 1 C.
W podobny sposób możemy skonstruować kolejną styczną wewnętrzną A 1 B 1.
Ogólna definicja stycznej
Niech styczna AT i sieczna AM zostaną poprowadzone przez punkt A do okręgu o środku (rys.).
Obróćmy tę sieczną wokół punktu A tak, aby drugi punkt przecięcia B zbliżał się coraz bardziej do A.

Wtedy prostopadła OD, obniżona od środka do siecznej, będzie coraz bardziej zbliżać się do promienia OA, a kąt AOD może stać się mniejszy niż dowolny mały kąt.
Kąt MAT utworzony przez sieczną i styczną wynosi równy kątowi AOD (ze względu na prostopadłość ich boków).
Dlatego też, gdy punkt B zbliża się do A w nieskończoność, kąt MAT może również stać się dowolnie mały.
Wyraża się to innymi słowami:
styczna jest pozycją graniczną, do której zmierza sieczna przeprowadzona przez punkt styczności, gdy drugi punkt przecięcia zbliża się do punktu styczności w nieskończoność.
Ta właściwość jest traktowana jako definicja stycznej, gdy mówimy o dowolnej krzywej.

Zatem styczna do krzywej AB (rys.) jest pozycją graniczną MT, do której dąży sieczna MN, gdy punkt przecięcia P zbliża się do M bez ograniczeń.
Należy pamiętać, że tak zdefiniowana styczna może mieć więcej niż jedno połączenie z krzywą. wspólny punkt(jak widać na ryc.)
Zachowanie Twojej prywatności jest dla nas ważne. Z tego powodu opracowaliśmy Politykę prywatności, która opisuje, w jaki sposób wykorzystujemy i przechowujemy Twoje dane. Zapoznaj się z naszymi praktykami dotyczącymi prywatności i daj nam znać, jeśli masz jakiekolwiek pytania.
Gromadzenie i wykorzystywanie danych osobowych
Dane osobowe to dane, które można wykorzystać do identyfikacji konkretnej osoby lub skontaktowania się z nią.
Możesz zostać poproszony o podanie swoich danych osobowych w dowolnym momencie kontaktu z nami.
Poniżej znajduje się kilka przykładów rodzajów danych osobowych, które możemy gromadzić i sposobu, w jaki możemy je wykorzystywać.
Jakie dane osobowe zbieramy:
- Kiedy składasz wniosek na stronie, możemy zbierać różne informacje, w tym Twoje imię i nazwisko, numer telefonu, adres e-mail itp.
Jak wykorzystujemy Twoje dane osobowe:
- Zebrane przez nas dane osobowe pozwala nam kontaktować się z Tobą i informować Cię o wyjątkowych ofertach, promocjach i innych wydarzeniach oraz nadchodzących wydarzeniach.
- Od czasu do czasu możemy wykorzystywać Twoje dane osobowe do wysyłania ważnych powiadomień i komunikatów.
- Możemy również wykorzystywać dane osobowe do celów wewnętrznych, takich jak przeprowadzanie audytów, analiza danych i różnych badań w celu ulepszenia świadczonych przez nas usług i przedstawienia rekomendacji dotyczących naszych usług.
- Jeśli bierzesz udział w losowaniu nagród, konkursie lub podobnej promocji, możemy wykorzystać podane przez Ciebie informacje w celu administrowania takimi programami.
Ujawnianie informacji osobom trzecim
Nie udostępniamy otrzymanych od Państwa informacji osobom trzecim.
Wyjątki:
- Jeżeli jest to konieczne – zgodnie z prawem, procedurą sądową, postępowaniem sądowym i/lub na podstawie żądań publicznych lub żądań od agencje rządowe na terytorium Federacji Rosyjskiej – ujawnij swoje dane osobowe. Możemy również ujawnić informacje o Tobie, jeśli uznamy, że takie ujawnienie jest konieczne lub odpowiednie ze względów bezpieczeństwa, egzekwowania prawa lub innych celów ważnych dla społeczeństwa.
- W przypadku reorganizacji, fuzji lub sprzedaży możemy przekazać zebrane dane osobowe odpowiedniej następczej stronie trzeciej.
Ochrona danych osobowych
Podejmujemy środki ostrożności – w tym administracyjne, techniczne i fizyczne – aby chronić Twoje dane osobowe przed utratą, kradzieżą i niewłaściwym wykorzystaniem, a także nieuprawnionym dostępem, ujawnieniem, zmianą i zniszczeniem.
Szanowanie Twojej prywatności na poziomie firmy
Aby zapewnić bezpieczeństwo Twoich danych osobowych, przekazujemy naszym pracownikom standardy dotyczące prywatności i bezpieczeństwa oraz rygorystycznie egzekwujemy praktyki dotyczące prywatności.