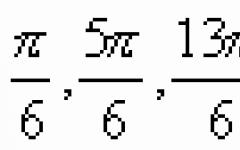Podczas przekształcania ułamkowego wyrażenia algebraicznego, którego mianownik jest zapisany irracjonalne wyrażenie, zwykle starają się przedstawić ułamek tak, aby jego mianownik był wymierny. Jeśli A,B,C,D,... są pewnymi wyrażeniami algebraicznymi, to możesz określić reguły, za pomocą których możesz pozbyć się znaków pierwiastkowych w mianowniku wyrażeń postaci

We wszystkich tych przypadkach uwolnienie od irracjonalności osiąga się poprzez pomnożenie licznika i mianownika ułamka przez tak dobrany współczynnik, aby jego iloczyn przez mianownik ułamka był racjonalny.

1) Aby pozbyć się irracjonalności w mianowniku ułamka formy . Mnożąc licznik i mianownik przez

Przykład 1. .

2) W przypadku ułamków postaci . Pomnóż licznik i mianownik przez niewymierny współczynnik

odpowiednio, tj. do sprzężonego wyrażenia irracjonalnego.

Znaczenie ostatniej akcji polega na tym, że w mianowniku iloczyn sumy i różnicy przekształca się w różnicę kwadratów, co będzie już wyrażeniem wymiernym.

Przykład 2. Uwolnij się od irracjonalności w mianowniku wyrażenia:

Rozwiązanie, a) Pomnóż licznik i mianownik ułamka przez wyrażenie . Otrzymujemy (pod warunkiem, że)

3) W przypadku wyrażeń typu

mianownik jest traktowany jako suma (różnica) i mnożona przez częściowy kwadrat różnice (sumy), aby otrzymać sumę (różnicę) kostek ((20.11), (20.12)). Licznik jest również mnożony przez ten sam współczynnik.

Przykład 3. Uwolnij się od irracjonalności w mianowniku wyrażeń:

Rozwiązanie a) Rozważając mianownik tego ułamka jako sumę liczb i 1, pomnóż licznik i mianownik przez częściowy kwadrat różnicy tych liczb:

lub wreszcie:

W niektórych przypadkach konieczne jest wykonanie transformacji o odwrotnym charakterze: uwolnienie ułamka od irracjonalności w liczniku. Odbywa się to dokładnie w ten sam sposób.

Przykład 4. Uwolnij się od irracjonalności w liczniku ułamka.

W tym temacie rozważymy wszystkie trzy grupy granic z irracjonalnością wymienione powyżej. Zacznijmy od granic zawierających niepewność postaci $\frac(0)(0)$.

Ujawnienie niepewności $\frac(0)(0)$.

Rozwiązanie standardowych przykładów tego typu zwykle składa się z dwóch kroków:

Pozbywamy się irracjonalności, która powodowała niepewność, mnożąc przez tak zwane wyrażenie „koniugatowe”;
Jeśli to konieczne, uwzględnij wyrażenie w liczniku lub mianowniku (lub obu);
Redukujemy czynniki prowadzące do niepewności i obliczamy pożądaną wartość granicy.

Stosowany powyżej termin „wyrażenie koniugatu” zostanie szczegółowo wyjaśniony w przykładach. Na razie nie ma powodu się nad tym szczegółowo rozwodzić. Ogólnie rzecz biorąc, możesz pójść w drugą stronę, bez użycia wyrażenia sprzężonego. Czasami dobrze dobrany zamiennik może wyeliminować irracjonalność. Takie przykłady są rzadkością w standardzie testy dlatego w celu zastosowania zamiany rozważymy tylko jeden przykład nr 6 (patrz druga część tego tematu).

Będziemy potrzebować kilku formuł, które napiszę poniżej:

\begin(równanie) a^2-b^2=(a-b)\cdot(a+b) \end(równanie) \begin(równanie) a^3-b^3=(a-b)\cdot(a^2 +ab+b^2) \end(równanie) \begin(równanie) a^3+b^3=(a+b)\cdot(a^2-ab+b^2) \end(równanie) \begin (równanie) a^4-b^4=(a-b)\cdot(a^3+a^2 b+ab^2+b^3)\end(równanie)

Ponadto zakładamy, że czytelnik zna wzory na rozwiązywanie równań kwadratowych. Jeśli $x_1$ i $x_2$ są pierwiastkami trójmian kwadratowy$ax^2+bx+c$, to można to rozłożyć na czynniki za pomocą następującego wzoru:

\begin(równanie) ax^2+bx+c=a\cdot(x-x_1)\cdot(x-x_2) \end(równanie)

Wzory (1)-(5) w zupełności wystarczą do rozwiązania standardowych problemów, do czego teraz przejdziemy.

Przykład nr 1

Znajdź $\lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)$.

Ponieważ $\lim_(x\to 3)(\sqrt(7-x)-2)=\sqrt(7-3)-2=\sqrt(4)-2=0$ i $\lim_(x\ to 3) (x-3)=3-3=0$, to w danej granicy mamy niepewność postaci $\frac(0)(0)$. Różnica $\sqrt(7-x)-2$ uniemożliwia ujawnienie tej niepewności. Aby pozbyć się takich irracjonalności, stosuje się mnożenie przez tzw. „Wyrażenie sprzężone”. Przyjrzymy się teraz, jak działa takie mnożenie. Pomnóż $\sqrt(7-x)-2$ przez $\sqrt(7-x)+2$:

$$(\sqrt(7-x)-2)(\sqrt(7-x)+2)$$

Aby otworzyć nawiasy zastosuj , podstawiając $a=\sqrt(7-x)$, $b=2$ po prawej stronie wspomnianego wzoru:

$$(\sqrt(7-x)-2)(\sqrt(7-x)+2)=(\sqrt(7-x))^2-2^2=7-x-4=3-x .$$

Jak widać, jeśli pomnożysz licznik przez $\sqrt(7-x)+2$, to pierwiastek (tj. irracjonalność) w liczniku zniknie. To wyrażenie $\sqrt(7-x)+2$ będzie miało postać sprzężony do wyrażenia $\sqrt(7-x)-2$. Nie możemy jednak po prostu pomnożyć licznika przez $\sqrt(7-x)+2$, ponieważ spowoduje to zmianę ułamka $\frac(\sqrt(7-x)-2)(x-3)$ poniżej limitu . Musisz pomnożyć jednocześnie licznik i mianownik:

$$ \lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)= \left|\frac(0)(0)\right|=\lim_(x\to 3)\frac((\sqrt(7-x)-2)\cdot(\sqrt(7-x)+2))((x-3)\cdot(\sqrt(7-x)+2)) $$

Teraz pamiętaj, że $(\sqrt(7-x)-2)(\sqrt(7-x)+2)=3-x$ i otwórz nawiasy. A po otwarciu nawiasów i małej transformacji $3-x=-(x-3)$ zmniejszamy ułamek o $x-3$:

$$ \lim_(x\to 3)\frac((\sqrt(7-x)-2)\cdot(\sqrt(7-x)+2))((x-3)\cdot(\sqrt( 7-x)+2))= \lim_(x\to 3)\frac(3-x)((x-3)\cdot(\sqrt(7-x)+2))=\\ =\lim_ (x\to 3)\frac(-(x-3))((x-3)\cdot(\sqrt(7-x)+2))= \lim_(x\to 3)\frac(-1 )(\sqrt(7-x)+2) $$

Niepewność $\frac(0)(0)$ zniknęła. Teraz możesz łatwo uzyskać odpowiedź ten przykład:

$$ \lim_(x\to 3)\frac(-1)(\sqrt(7-x)+2)=\frac(-1)(\sqrt(7-3)+2)=-\frac( 1)(\sqrt(4)+2)=-\frac(1)(4).$$

Zauważam, że wyrażenie sprzężone może zmieniać swoją strukturę, w zależności od tego, jaki rodzaj irracjonalności ma usunąć. W przykładach nr 4 i nr 5 (patrz druga część tego tematu) zostanie użyty inny typ wyrażenia koniugatu.

Odpowiedź: $\lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)=-\frac(1)(4)$.

Przykład nr 2

Znajdź $\lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))$.

Ponieważ $\lim_(x\to 2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=\sqrt(2^2+5)-\sqrt(7\cdot 2 ^ 2-19)=3-3=0$ i $\lim_(x\to 2)(3x^2-5x-2)=3\cdot2^2-5\cdot 2-2=0$, wtedy my mają do czynienia z niepewnością w postaci $\frac(0)(0)$. Pozbądźmy się irracjonalności mianownika tego ułamka. Aby to zrobić, dodajemy licznik i mianownik ułamka $\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))$ do wyrażenie $\sqrt(x^ 2+5)+\sqrt(7x^2-19)$ koniuguj do mianownika:

$$ \lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=\left|\frac(0 )(0)\right|= \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19))) ((\sqrt(x^2+5)-\sqrt(7x^2-19))(\sqrt(x^2+5)+\sqrt(7x^2-19))) $$

Ponownie, jak w przykładzie nr 1, aby rozwinąć, musisz użyć nawiasów. Podstawiając $a=\sqrt(x^2+5)$, $b=\sqrt(7x^2-19)$ po prawej stronie wspomnianego wzoru, otrzymujemy następujące wyrażenie na mianownik:

$$ \left(\sqrt(x^2+5)-\sqrt(7x^2-19)\right)\left(\sqrt(x^2+5)+\sqrt(7x^2-19)\ prawo)=\\ =\lewo(\sqrt(x^2+5)\prawo)^2-\lewo(\sqrt(7x^2-19)\prawo)^2=x^2+5-(7x ^2-19)=-6x^2+24=-6\cdot(x^2-4) $$

Wróćmy do naszego limitu:

$$ \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)))((\sqrt(x ^2+5)-\sqrt(7x^2-19))(\sqrt(x^2+5)+\sqrt(7x^2-19)))= \lim_(x\do 2)\frac( (3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)))(-6\cdot(x^2-4))=\\ =-\ frac(1)(6)\cdot \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)) )(x^2-4) $$

W przykładzie nr 1, niemal natychmiast po pomnożeniu przez wyrażenie koniugatu, ułamek został zmniejszony. Tutaj przed redukcją będziesz musiał rozłożyć na czynniki wyrażenia $3x^2-5x-2$ i $x^2-4$, a dopiero potem przystąpić do redukcji. Aby rozłożyć wyrażenie $3x^2-5x-2$, musisz użyć . Najpierw zdecydujmy równanie kwadratowe$3x^2-5x-2=0$:

$$ 3x^2-5x-2=0\\ \begin(aligned) & D=(-5)^2-4\cdot3\cdot(-2)=25+24=49;\\ & x_1=\ frac(-(-5)-\sqrt(49))(2\cdot3)=\frac(5-7)(6)=-\frac(2)(6)=-\frac(1)(3) ;\\ & x_2=\frac(-(-5)+\sqrt(49))(2\cdot3)=\frac(5+7)(6)=\frac(12)(6)=2. \end(wyrównane) $$

Podstawiając $x_1=-\frac(1)(3)$, $x_2=2$ do , będziemy mieli:

$$ 3x^2-5x-2=3\cdot\lewo(x-\lewo(-\frac(1)(3)\prawo)\prawo)(x-2)=3\cdot\lewo(x+\ frac(1)(3)\prawo)(x-2)=\lewo(3\cdot x+3\cdot\frac(1)(3)\prawo)(x-2) =(3x+1)( x-2). $$

Teraz czas na rozkład na czynniki wyrażenia $x^2-4$. Użyjmy , podstawiając do niego $a=x$, $b=2$:

$$ x^2-4=x^2-2^2=(x-2)(x+2) $$

Wykorzystajmy uzyskane wyniki. Ponieważ $x^2-4=(x-2)(x+2)$ i $3x^2-5x-2=(3x+1)(x-2)$, to:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2 -19)))(x^2-4) =-\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(x-2)(\sqrt(x ^2+5)+\sqrt(7x^2-19)))((x-2)(x+2)) $$

Redukując przez nawias $x-2$ otrzymujemy:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(x-2)(\sqrt(x^2+5)+\sqrt(7x^ 2-19)))((x-2)(x+2)) =-\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(\sqrt( x^2+5)+\sqrt(7x^2-19)))(x+2). $$

Wszystko! Niepewność zniknęła. Jeszcze jeden krok i dochodzimy do odpowiedzi:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(\sqrt(x^2+5)+\sqrt(7x^2-19)) )(x+2)=\\ =-\frac(1)(6)\cdot\frac((3\cdot 2+1)(\sqrt(2^2+5)+\sqrt(7\cdot 2 ^2-19)))(2+2)= -\frac(1)(6)\cdot\frac(7(3+3))(4)=-\frac(7)(4). $$

Odpowiedź: $\lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=-\frac(7)( 4)$.

W następnym przykładzie rozważmy przypadek, w którym irracjonalność będzie obecna zarówno w liczniku, jak i mianowniku ułamka.

Przykład nr 3

Znajdź $\lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9 ))$.

Ponieważ $\lim_(x\to 5)(\sqrt(x+4)-\sqrt(x^2-16))=\sqrt(9)-\sqrt(9)=0$ i $\lim_( x \to 5)(\sqrt(x^2-3x+6)-\sqrt(5x-9))=\sqrt(16)-\sqrt(16)=0$, wtedy mamy niepewność postaci $ \frac (0)(0)$. Ponieważ w tym przypadku pierwiastki występują zarówno w mianowniku, jak i liczniku, aby pozbyć się niepewności, będziesz musiał pomnożyć przez dwa nawiasy jednocześnie. Najpierw do wyrażenia $\sqrt(x+4)+\sqrt(x^2-16)$ skoniuguj z licznikiem. A po drugie, wyrażenie $\sqrt(x^2-3x+6)-\sqrt(5x-9)$ skoniuguj do mianownika.

$$ \lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9 ))=\left|\frac(0)(0)\right|=\\ =\lim_(x\to 5)\frac((\sqrt(x+4)-\sqrt(x^2-16) )(\sqrt(x+4)+\sqrt(x^2-16))(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((\sqrt(x^2 -3x+6)-\sqrt(5x-9))(\sqrt(x^2-3x+6)+\sqrt(5x-9))(\sqrt(x+4)+\sqrt(x^2 -16))) $$ $$ -x^2+x+20=0;\\ \begin(aligned) & D=1^2-4\cdot(-1)\cdot 20=81;\\ & x_1=\frac(-1-\sqrt(81))(-2)=\frac(-10)(-2)=5;\\ & x_2=\frac(-1+\sqrt(81))( -2)=\frac(8)(-2)=-4. \end(aligned) \\ -x^2+x+20=-1\cdot(x-5)(x-(-4))=-(x-5)(x+4). $$

Dla wyrażenia $x^2-8x+15$ otrzymujemy:

$$ x^2-8x+15=0;\\ \begin(aligned) & D=(-8)^2-4\cdot 1\cdot 15=4;\\ & x_1=\frac(-(- 8)-\sqrt(4))(2)=\frac(6)(2)=3;\\ & x_2=\frac(-(-8)+\sqrt(4))(2)=\frac (10)(2)=5. \end(aligned)\\ x^2+8x+15=1\cdot(x-3)(x-5)=(x-3)(x-5). $$

Podstawiając powstałe rozwinięcia $-x^2+x+20=-(x-5)(x+4)$ i $x^2+8x+15=(x-3)(x-5)$ do granicy pod uwagę będziemy mieli:

$$ \lim_(x\to 5)\frac((-x^2+x+20)(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((x^2 -8x+15)(\sqrt(x+4)+\sqrt(x^2-16)))= \lim_(x\to 5)\frac(-(x-5)(x+4)(\ sqrt(x^2-3x+6)+\sqrt(5x-9)))((x-3)(x-5)(\sqrt(x+4)+\sqrt(x^2-16)) )=\\ =\lim_(x\to 5)\frac(-(x+4)(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((x-3) (\sqrt(x+4)+\sqrt(x^2-16)))= \frac(-(5+4)(\sqrt(5^2-3\cdot 5+6)+\sqrt(5 \cdot 5-9)))((5-3)(\sqrt(5+4)+\sqrt(5^2-16)))=-6. $$

Odpowiedź: $\lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9 ))=-6$.

W kolejnej (drugiej) części rozważymy jeszcze kilka przykładów, w których wyrażenie koniugatu będzie miało inną formę niż w poprzednich zadaniach. Najważniejszą rzeczą do zapamiętania jest to, że celem użycia wyrażeń sprzężonych jest pozbycie się irracjonalności, która powoduje niepewność.

Wyrażenia, konwersja wyrażeń

Jak uwolnić się od irracjonalności w mianowniku? Metody, przykłady, rozwiązania

W ósmej klasie na lekcjach algebry, w ramach tematu transformacji wyrażeń irracjonalnych, rozmowa schodzi na wyzwolenie od irracjonalności w mianowniku ułamka. W tym artykule przeanalizujemy, jaki to rodzaj transformacji, zastanowimy się, jakie działania pozwalają uwolnić się od irracjonalności w mianowniku ułamka i podamy rozwiązania typowych przykładów ze szczegółowymi wyjaśnieniami.

Nawigacja strony.

Co to znaczy uwolnić się od irracjonalności w mianowniku ułamka?

Najpierw musisz zrozumieć, czym jest irracjonalność w mianowniku i co to znaczy uwolnić się od irracjonalności w mianowniku ułamka. Pomogą nam w tym informacje z podręczników szkolnych. Na uwagę zasługują następujące punkty.

Jeżeli zapis ułamka zawiera pierwiastek (pierwiastek) w mianowniku, to mówimy, że w mianowniku znajduje się irracjonalność. Prawdopodobnie wynika to z faktu, że liczby pisane za pomocą pierwiastka są często . Jako przykład podajemy ułamki , , oczywiście mianowniki każdego z nich zawierają znak pierwiastka, a zatem irracjonalność. W szkole średniej nieuniknione jest spotkanie ułamków, których irracjonalność w mianownikach wprowadzają nie tylko znaki pierwiastki kwadratowe, ale także ślady pierwiastków sześciennych, czwartych itp. Oto przykłady takich ułamków: , .

Biorąc pod uwagę podane informacje i znaczenie słowa „bezpłatny”, bardzo naturalna jest następująca definicja:

Definicja.

Wyzwolenie od irracjonalności w mianowniku ułamka to przekształcenie, w którym ułamek mający niewymierność w mianowniku zostaje zastąpiony przez identycznie równy ułamek, który nie zawiera pierwiastka w mianowniku.

Często można usłyszeć, jak ludzie mówią, żeby się nie uwolnić, ale pozbyć się irracjonalności w mianowniku ułamka. Znaczenie się nie zmienia.

Przykładowo, jeśli przejdziemy od ułamka do ułamka, którego wartość jest równa wartości ułamka pierwotnego i którego mianownik nie zawiera pierwiastka, to możemy stwierdzić, że uwolniliśmy się od irracjonalności w mianowniku ułamek. Inny przykład: zastąpienie ułamka identycznym ułamkiem w mianowniku ułamka następuje wyzwolenie od irracjonalności.

Tak więc otrzymano wstępne informacje. Pozostaje dowiedzieć się, co należy zrobić, aby uwolnić się od irracjonalności w mianowniku ułamka.

Sposoby uwolnienia się od irracjonalności, przykłady

Zwykle, aby pozbyć się irracjonalności, w mianowniku ułamka używa się dwóch. konwersje ułamków: Mnożenie licznika i mianownika przez niezerową liczbę lub wyrażenie i przekształcanie wyrażenia w mianowniku. Poniżej przyjrzymy się, jak w prosty sposób wykorzystuje się konwersje ułamków, aby usunąć irracjonalność z mianownika ułamka. Poruszmy następujące przypadki.

W najprostszych przypadkach wystarczy przekształcić wyrażenie w mianownik. Przykładem jest ułamek, którego mianownikiem jest pierwiastek z dziewięciu. W takim przypadku zastąpienie go wartością 3 uwalnia mianownik od irracjonalności.

W więcej trudne przypadki musisz najpierw pomnożyć licznik i mianownik ułamka przez jakąś niezerową liczbę lub wyrażenie, co później pozwala na przekształcenie mianownika ułamka do postaci niezawierającej znaków pierwiastkowych. Na przykład po pomnożeniu licznika i mianownika ułamka przez , ułamek przyjmuje postać , a następnie wyrażenie w mianowniku można zastąpić wyrażeniem bez znaków pierwiastka x+1. Zatem po uwolnieniu od irracjonalności w mianowniku ułamek przyjmuje postać .

Jeśli mówimy o przypadku ogólnym, to aby pozbyć się irracjonalności w mianowniku ułamka, należy uciekać się do różnych dopuszczalnych przekształceń, czasem dość specyficznych.

A teraz szczegółowo.

Zamiana wyrażenia na mianownik ułamka

Jak już wspomniano, jednym ze sposobów pozbycia się irracjonalności mianownika ułamka jest jego przekształcenie. Spójrzmy na rozwiązania przykładów.

Przykład.

Pozbądź się irracjonalności w mianowniku ułamka .

Rozwiązanie.

Otwierając nawiasy w mianowniku, dochodzimy do wyrażenia . Następnie pozwalają przejść do ułamków . Po obliczeniu wartości pod znakami pierwiastków mamy . Oczywiście w wynikowym wyrażeniu jest to możliwe, co daje ułamek równy 1/16. W ten sposób pozbyliśmy się irracjonalności w mianowniku.

Zwykle rozwiązanie jest pisane krótko bez wyjaśnień, ponieważ wykonane czynności są dość proste:

Odpowiedź:

Przykład.

Rozwiązanie.

Kiedy mówiliśmy o przekształcaniu wyrażeń irracjonalnych za pomocą własności pierwiastków, zauważyliśmy, że dla dowolnego wyrażenia A z parzystym n (w naszym przypadku n=2) wyrażenie można zastąpić wyrażeniem |A| na całym ODZ zmiennych dla oryginalnego wyrażenia. Można zatem wykonać następującą transformację danego ułamka:

Odpowiedź:

, co uwalnia nas od irracjonalności w mianowniku.

Mnożenie licznika i mianownika przez pierwiastek Gdy wyrażenie w mianowniku ułamka ma postać , gdzie wyrażenie A nie zawiera znaków pierwiastka, to pomnożenie licznika i mianownika przez pozwala pozbyć się niewymierności w mianowniku. Ta akcja jest możliwa, ponieważ nie znika w zmiennych zmiennych oryginalnego wyrażenia. W tym przypadku mianownik tworzy wyrażenie, które można łatwo przekształcić do postaci bez radykalnych znaków:

Przykład.

Uwolnij się od irracjonalności w mianowniku ułamka: a), b) .

Rozwiązanie.

a) Mnożenie licznika i mianownika ułamka przez pierwiastek kwadratowy z trzech, otrzymujemy .

b) Aby pozbyć się pierwiastka kwadratowego z mianownika, pomnóż licznik i mianownik ułamka przez , a następnie wykonaj przekształcenia w mianowniku:

Odpowiedź:

a) , b) .

W przypadku, gdy w mianowniku znajdują się czynniki lub , gdzie m i n są liczbami naturalnymi, licznik i mianownik należy pomnożyć przez taki współczynnik, aby po tym wyrażenie w mianowniku można było przekształcić do postaci lub , gdzie k jest jakąś liczbę naturalną. Wtedy łatwo jest przejść do ułamka pozbawionego irracjonalności w mianowniku. Zademonstrujmy zastosowanie opisanej metody pozbycia się irracjonalności w mianowniku na przykładach.

Przykład.

Uwolnij się od irracjonalności w mianowniku ułamka: a), b) .

Rozwiązanie.

a) Najbliższa liczba naturalna większa od 3 i podzielna przez 5 to 5. Aby wykładnik sześciu stał się równy pięć, wyrażenie w mianowniku należy pomnożyć przez. W konsekwencji uwolnienie się od irracjonalności mianownika ułamka ułatwi wyrażenie, przez które należy pomnożyć licznik i mianownik:

b) Oczywiście najbliższa liczba naturalna, która przekracza 15 i jest podzielna przez 4 bez reszty, to 16. Aby wykładnik w mianowniku był równy 16, należy pomnożyć wyrażenie przez. Zatem pomnożenie licznika i mianownika ułamka pierwotnego przez (uwaga, wartość tego wyrażenia nie jest równa zeru dla żadnego rzeczywistego x) pozbędzie się irracjonalności mianownika:

Odpowiedź:

A) , B) .

Mnożenie przez koniugat

Poniższa metoda pozbycia się niewymierności w mianowniku ułamka obejmuje przypadki, gdy w mianowniku znajdują się wyrażenia w postaci , , , lub . W takich przypadkach, aby uwolnić się od irracjonalności mianownika ułamka, należy pomnożyć licznik i mianownik ułamka przez tzw. wyrażenie sprzężone.

Pozostaje dowiedzieć się, które wyrażenia są sprzężone z powyższym. W przypadku wyrażenia wyrażeniem sprzężonym jest , a w przypadku wyrażenia wyrażeniem sprzężonym jest . Podobnie dla wyrażenia koniugatem jest , a dla wyrażenia koniugatem jest . A dla wyrażenia koniugatem jest , a dla wyrażenia koniugatem jest . Zatem wyrażenie sprzężone z tym wyrażeniem różni się od niego znakiem przed drugim terminem.

Zobaczmy, co daje pomnożenie wyrażenia przez jego koniugat. Weźmy na przykład pod uwagę pracę . Można go zastąpić różnicą kwadratów, czyli , skąd możemy następnie przejść do wyrażenia a−b, które nie zawiera znaków pierwiastków.

Teraz staje się jasne, jak pomnożenie licznika i mianownika ułamka przez sprzężenie wyrażenia do mianownika pozwala uwolnić się od irracjonalności mianownika ułamka. Spójrzmy na rozwiązania typowych przykładów.

Przykład.

Wyobraź sobie wyrażenie jako ułamek, którego mianownik nie zawiera pierwiastka: a) , b) .

Rozwiązanie.

a) Wyrażenie sprzężone z mianownikiem to . Pomnóżmy przez to licznik i mianownik, co pozwoli nam uwolnić się od irracjonalności w mianowniku ułamka:

b) Koniugat wyrażenia to . Mnożąc przez to licznik i mianownik, otrzymujemy

Można było najpierw usunąć znak minus z mianownika, a dopiero potem pomnożyć licznik i mianownik przez sprzężenie wyrażenia do mianownika:

Odpowiedź:

A) , B) .

Uwaga: mnożąc licznik i mianownik ułamka przez wyrażenie ze zmiennymi sprzężonymi z mianownikiem, należy uważać, aby nie zniknął on dla żadnego zbioru wartości zmiennych z ODZ dla pierwotnego wyrażenia.

Przykład.

Uwolnij się od irracjonalności w mianowniku ułamka.

Rozwiązanie.

Najpierw znajdźmy zakres dopuszczalnych wartości (APV) zmiennej x. Wyznaczają ją warunki x≥0 i , z których wnioskujemy, że ODZ jest zbiorem x≥0.

Wyrażenie sprzężone z mianownikiem to . Możemy pomnożyć przez niego licznik i mianownik ułamka pod warunkiem, że , co na ODZ jest równoznaczne z warunkiem x≠16. W tym przypadku mamy

I przy x=16 mamy .

Zatem dla wszystkich wartości zmiennej x z ODZ, z wyjątkiem x=16, , i dla x=16 mamy .

Odpowiedź:

Korzystanie ze wzorów na sumę kostek i różnicę kostek

Z poprzedniego akapitu dowiedzieliśmy się, że mnożenie licznika i mianownika ułamka przez sprzężenie wyrażenia do mianownika odbywa się w celu późniejszego zastosowania wzoru na różnicę kwadratów i tym samym uwolnienia się od irracjonalności mianownika. W niektórych przypadkach inne skrócone wzory na mnożenie są przydatne, aby pozbyć się irracjonalności mianownika. Na przykład wzór na różnicę kostek za 3 −b 3 =(a−b)·(a 2 +a·b+b 2) pozwala pozbyć się irracjonalności, gdy mianownik ułamka zawiera wyrażenia z pierwiastkami sześciennymi postaci lub , gdzie A i B to liczby lub wyrażenia. W tym celu licznik i mianownik ułamka mnoży się przez częściowy kwadrat sumy lub odpowiednio przez różnicę. Wzór na sumę kostek stosuje się w ten sam sposób. za 3 +b 3 =(a+b)·(a 2 −a·b+b 2).

Przykład.

Uwolnij się od irracjonalności w mianowniku ułamka: a), b) .

Rozwiązanie.

a) Łatwo zgadnąć, że w tym przypadku pomnożenie licznika i mianownika przez niepełny kwadrat sumy liczb i pozwala uwolnić się od irracjonalności w mianowniku, ponieważ w przyszłości pozwoli to przekształcić wyrażenie w mianowniku stosując wzór na różnicę sześcianów:

b) Wyrażenie w mianowniku ułamka można przedstawić w postaci , z czego wyraźnie widać, że jest to niepełny kwadrat różnicy między liczbami 2 i . Zatem jeśli licznik i mianownik ułamka pomnożymy przez sumę, to mianownik można przeliczyć korzystając ze wzoru na sumę kostek, co uwolni nas od irracjonalności mianownika ułamka. Można to zrobić pod warunkiem, który jest równoważny dalszemu warunkowi x≠−8:

A po podstawieniu x=−8 do ułamka pierwotnego mamy .

Zatem dla wszystkich x z ODZ dla ułamka pierwotnego (w tym przypadku jest to zbiór R), z wyjątkiem x=−8, mamy , i dla x=8 mamy .

Odpowiedź:

Używanie różnych metod

W bardziej skomplikowanych przykładach zazwyczaj nie da się uwolnić od irracjonalności mianownika w jednym działaniu, ale trzeba konsekwentnie stosować metodę za metodą, łącznie z tymi omówionymi powyżej. Czasami konieczne mogą okazać się rozwiązania niestandardowe. Wystarczająco ciekawe zadania na omawiany temat można znaleźć w podręczniku autorstwa Yu. N. Kolyagina. Referencje.

Algebra: podręcznik dla 8 klasy. wykształcenie ogólne instytucje / [Yu. N. Makaryczew, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edytowany przez SA Telyakovsky. - wyd. 16. - M.: Edukacja, 2008. - 271 s. : chory. - ISBN 978-5-09-019243-9.
Mordkovich A.G. Algebra. 8 klasa. O 14:00 Część 1. Podręcznik dla studentów instytucje edukacyjne/ A. G. Mordkovich. - wyd. 11, usunięte. - M.: Mnemosyne, 2009. - 215 s.: il. ISBN 978-5-346-01155-2.
Algebra i zaczął analiza matematyczna. Klasa 10: podręcznik. dla edukacji ogólnej instytucje: podstawowe i profilowe. poziomy / [Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; edytowany przez A. B. Żyżczenko. - wyd. 3. - M.: Edukacja, 2010. - 368 s. : chory - ISBN 978-5-09-022771-1.

Danny’ego Perica Campany

Jeszcze jedno ciekawa książka dla dzieci w wieku szkolnym zainteresowanych, niestety nie przetłumaczonych na język rosyjski, jest to książka „Przygody matematyczne Daniela” (Las Aventuras Matemáticas de Daniel) autorstwa chilijskiego nauczyciela matematyki Danny'ego Pericha Campany, bardzo niezwykłej i interesującej osoby. Nie tylko uczy dzieci, ale także pisze piosenki i publikuje w Internecie różne materiały edukacyjne na temat matematyki. Można je znaleźć na YouTube oraz na stronie http://www.sectormatematica.cl/ (oczywiście wszystkie materiały są w języku hiszpańskim).

Tutaj zamieszczam jeden rozdział z książki Danniego Perica. Uważam, że jest to całkiem interesujące i przydatne dla uczniów. Aby było jasne o czym mówimy, powiem, że Daniel i Camila pracują w szkole, są nauczycielami.

Sekret pozbycia się irracjonalności

„Camila, mam teraz wiele problemów, kiedy próbuję wyjaśnić, dlaczego to, przez co przechodzimy na zajęciach, zostaje wykorzystane” – powiedział Daniel.

- Nie bardzo rozumiem, o czym mówisz.

– Mówię o tym, co jest w każdym podręczniki szkolne a nawet książki uniwersyteckie. Wciąż mam wątpliwości: dlaczego musimy pozbyć się irracjonalności w mianowniku? I nienawidzę mówić ludziom tego, czego od tak dawna nie rozumiem” – poskarżył się Daniel.

„Ja też nie wiem, skąd to się bierze i dlaczego jest potrzebne, ale musi być na to jakieś logiczne wyjaśnienie.

— Czytałem kiedyś w czasopiśmie naukowym, że pozbycie się irracjonalności w mianowniku pozwala uzyskać wynik z większą dokładnością, ale nigdy więcej się z tym nie spotkałem i nie jestem pewien, czy to prawda.

- Dlaczego tego nie sprawdzimy? – zapytała Kamila.

– Masz rację – zgodził się Daniel. — Zamiast narzekać, spróbuj wyciągnąć własne wnioski. Więc pomóż mi...

- Oczywiście, teraz sam jestem tym zainteresowany.

„Musimy wziąć kilka wyrażeń i pozbyć się irracjonalności w mianowniku, następnie zastąpić pierwiastek jego wartością i znaleźć wynik wyrażenia przed i po pozbyciu się irracjonalności mianownika i zobaczyć, czy coś się zmieni”.

– Oczywiście – zgodziła się Camila. - Zróbmy to.

„Weźmy na przykład to wyrażenie” – powiedział Daniel i wziął kartkę papieru, aby zapisać, co się dzieje. - Pomnóż licznik i mianownik przez i otrzymaj .

„Będzie poprawne i pomoże nam wyciągnąć wnioski, jeśli uznamy inne irracjonalne wyrażenia za równe temu” – zasugerowała Camila.

„Zgadzam się” – powiedział Daniel. „Podzielę licznik i mianownik przez , a ty pomnożysz je przez ”.

- Zrobiłem to. A ty?

„Tak” – odpowiedział Daniel. - Teraz obliczmy pierwotne wyrażenie i powstałe, zastępując je jego wartością ze wszystkimi miejscami po przecinku, które podaje kalkulator. Otrzymujemy:

„Nie widzę nic szczególnego” – stwierdziła Camila. „Spodziewałem się jakiejś różnicy, która uzasadniałaby pozbycie się irracjonalności”.

„Jak już mówiłem, kiedyś czytałem o tym w związku z podejściem. Co powiesz, jeśli zastąpimy go mniej precyzyjną liczbą, np. ?

- Spróbujmy zobaczyć, co się stanie.

Tokariew Cyryl

Praca pomaga nauczyć się wyciągać pierwiastek kwadratowy z dowolnej liczby bez użycia kalkulatora i tabeli kwadratów oraz uwolnić mianownik ułamka od irracjonalności.

Uwolnienie się od irracjonalności mianownika ułamka

Istota tej metody polega na pomnożeniu i podzieleniu ułamka przez wyrażenie, które wyeliminuje irracjonalność (pierwiastki kwadratowe i sześcienne) z mianownika i uprości sprawę. Następnie łatwiej jest sprowadzić ułamki do wspólnego mianownika i ostatecznie uprościć oryginalne wyrażenie.

Wyciąganie pierwiastka kwadratowego z przybliżeniem do danej cyfry.

Załóżmy, że musimy wziąć pierwiastek kwadratowy z liczba naturalna 17358122 i wiadomo, że korzeń jest ekstrahowany. Aby znaleźć wynik, czasami wygodnie jest skorzystać z reguły opisanej w pracy.

Pobierać:

Zapowiedź:

Aby skorzystać z podglądu utwórz konto Google i zaloguj się na nie: https://accounts.google.com

Zapowiedź:

Aby skorzystać z podglądu prezentacji utwórz konto Google i zaloguj się na nie: https://accounts.google.com

Podpisy slajdów:

Rodnik. Uwolnienie się od irracjonalności mianownika ułamka. Wyodrębnij pierwiastek kwadratowy z określonym stopniem dokładności. Uczeń klasy 9B Miejskiej Szkoły Oświatowej nr 7, Salsk Kirill Tokarev

PYTANIE PODSTAWOWE: Czy można wyciągnąć pierwiastek kwadratowy z dowolnej liczby z zadaną dokładnością, bez konieczności posiadania kalkulatora i tabeli kwadratów?

CELE I ZADANIA: Rozważ przypadki rozwiązywania wyrażeń z pierwiastkami, które nie są badane kurs szkolny matematyka, ale niezbędna do zdania jednolitego egzaminu państwowego.

HISTORIA KORZENIA Znak korzenia pochodzi od małej litery łacińskiej r (inicjał w łacińskim słowie radix - root), połączonej z indeksem górnym. W dawnych czasach zamiast obecnego nawiasu używano wyrażenia podkreślającego, więc jest to po prostu zmodyfikowany starożytny sposób pisania czegoś podobnego. Zapis ten został po raz pierwszy użyty przez niemieckiego matematyka Thomasa Rudolfa w 1525 roku.

WOLNOŚĆ OD IRRRACJONALNOŚCI mianownika ułamka Istota metody polega na pomnożeniu i podzieleniu ułamka przez wyrażenie, które wyeliminuje irracjonalność (pierwiastki kwadratowe i sześcienne) z mianownika i uprości sprawę. Następnie łatwiej jest sprowadzić ułamki do wspólnego mianownika i ostatecznie uprościć oryginalne wyrażenie. ALGORYTM UWOLNIENIA OD IRAJNORODNOŚCI W mianowniku ułamka: 1. Podziel mianownik ułamka na czynniki. 2. Jeżeli mianownik ma postać lub zawiera dzielnik, to licznik i mianownik należy pomnożyć przez. Jeżeli mianownik ma postać lub zawiera czynnik tego typu, to licznik i mianownik ułamka należy pomnożyć odpowiednio przez lub przez. Liczby nazywane są koniugatami. 3. Jeśli to możliwe, przelicz licznik i mianownik ułamka, a następnie zmniejsz powstały ułamek.

a) b) c) d) = - Wyzwolenie od irracjonalności w mianowniku ułamka.

WYCIĄGANIE PIERZENIA KWADRATOWEGO Z PRZYBLIŻENIEM DO OKREŚLONEJ CYFRY. 1) -1 100 96 400 281 11900 11296 24 4 281 1 2824 4 16 135 81 5481 4956 52522 49956 81 1 826 6 8326 6 2) Metoda starożytnego Babilonu: Przykład: Znajdź. Aby rozwiązać problem podany numer rozkłada się na sumę dwóch wyrazów: 1700 = 1600 + 100 = 40 · 2 + 100, z których pierwszy to idealny kwadrat. Następnie stosujemy formułę. Sposób algebraiczny:

WYCIĄGANIE PIERZENIA KWADRATOWEGO Z PRZYBLIŻENIEM DO OKREŚLONEJ CYFRY. , 4 16 8 . 1 1 1 3 5 1 8 1 5 4 8 1 8 2 + 66 4 9 5 6 6 5 2 5 2 2 + 8 3 2 66 4 9 9 5 6 6 + 8 3 3 2 33 2 5 6 6 0 0 , 3

Literatura 1. Zbiór problemów matematycznych dla osób rozpoczynających naukę na uniwersytetach, pod red. M.I.Skanavi. V. K. Egerev, B. A. Kordemsky, V. V. Zaitsev, „ONICS 21st century”, 2003 2. Algebra i funkcje elementarne. R. A. Kalnin, „Nauka”, 1973 3. Matematyka. Materiały referencyjne. V. A. Gusiew, A. G. Mordkovich, wydawnictwo „Prosveshcheniye”, 1990. 4. Dzieci w wieku szkolnym o matematyce i matematykach. Opracowane przez M.M. Limana, Enlightenment, 1981.