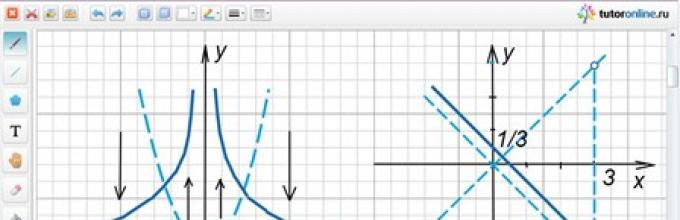
1. Ułamkowa funkcja liniowa i jej wykres
Funkcja w postaci y = P(x) / Q(x), gdzie P(x) i Q(x) są wielomianami, nazywana jest ułamkową funkcją wymierną.
Prawdopodobnie znasz już pojęcie liczb wymiernych. Podobnie funkcje racjonalne to funkcje, które można przedstawić jako iloraz dwóch wielomianów.
Jeżeli ułamkowa funkcja wymierna jest ilorazem dwóch funkcji liniowych - wielomianów pierwszego stopnia, tj. funkcja formy
y = (ax + b) / (cx + d), wówczas nazywa się to linią ułamkową.
Należy zauważyć, że w funkcji y = (ax + b) / (cx + d), c ≠ 0 (w przeciwnym razie funkcja staje się liniowa y = ax/d + b/d) oraz że a/c ≠ b/d (w przeciwnym razie funkcja jest stała). Liniowa funkcja ułamkowa jest zdefiniowana dla wszystkich liczb rzeczywistych z wyjątkiem x = -d/c. Wykresy ułamkowych funkcji liniowych nie różnią się kształtem od znanego Ci wykresu y = 1/x. Krzywą będącą wykresem funkcji y = 1/x nazywa się hiperbola. Przy nieograniczonym wzroście x wartości bezwzględnej funkcja y = 1/x maleje w sposób nieograniczony w wartości bezwzględnej i obie gałęzie wykresu zbliżają się do odciętej: prawa od góry, lewa od dołu. Linie, do których zbliżają się gałęzie hiperboli, nazywane są jej asymptoty.
Przykład 1.
y = (2x + 1) / (x – 3).
Rozwiązanie.
Wybierzmy całą część: (2x + 1) / (x – 3) = 2 + 7/(x – 3).
Teraz łatwo zauważyć, że wykres tej funkcji otrzymuje się z wykresu funkcji y = 1/x poprzez następujące przekształcenia: przesunięcie o 3 odcinki jednostkowe w prawo, rozciągnięcie wzdłuż osi Oy 7 razy i przesunięcie o 2 segmenty jednostkowe w górę.
Dowolny ułamek y = (ax + b) / (cx + d) można zapisać w podobny sposób, podkreślając „część całkowitą”. W konsekwencji wykresy wszystkich ułamkowych funkcji liniowych są hiperbolami, przesuniętymi w różny sposób wzdłuż osi współrzędnych i rozciągniętymi wzdłuż osi Oy.
Aby skonstruować wykres dowolnej funkcji ułamkowo-liniowej, wcale nie jest konieczne przekształcanie ułamka definiującego tę funkcję. Skoro wiemy, że graf jest hiperbolą, wystarczy znaleźć proste, do których zbiegają się jego gałęzie – asymptoty hiperboli x = -d/c i y = a/c.
Przykład 2.
Znajdź asymptoty wykresu funkcji y = (3x + 5)/(2x + 2).
Rozwiązanie.
Funkcja nie jest zdefiniowana, przy x = -1. Oznacza to, że prosta x = -1 służy jako asymptota pionowa. Aby znaleźć asymptotę poziomą, dowiedzmy się, do czego zbliżają się wartości funkcji y(x), gdy argument x wzrasta do wartości bezwzględnej.
Aby to zrobić, podziel licznik i mianownik ułamka przez x:
y = (3 + 5/x) / (2 + 2/x).
Gdy x → ∞ ułamek będzie miał tendencję do 3/2. Oznacza to, że asymptotą poziomą jest linia prosta y = 3/2.
Przykład 3.
Naszkicuj funkcję y = (2x + 1)/(x + 1).
Rozwiązanie.
Wybierzmy „całą część” ułamka:
(2x + 1) / (x + 1) = (2x + 2 – 1) / (x + 1) = 2(x + 1) / (x + 1) – 1/(x + 1) =
2 – 1/(x + 1).
Teraz łatwo zauważyć, że wykres tej funkcji otrzymuje się z wykresu funkcji y = 1/x poprzez następujące przekształcenia: przesunięcie o 1 jednostkę w lewo, symetryczne przedstawienie względem Ox i przesunięcie o 2 segmenty jednostkowe w górę wzdłuż osi Oy.
Dziedzina D(y) = (-∞; -1)ᴗ(-1; +∞).
Zakres wartości E(y) = (-∞; 2)ᴗ(2; +∞).
Punkty przecięcia z osiami: c Oy: (0; 1); c Wół: (-1/2; 0). Funkcja rośnie w każdym przedziale dziedziny definicji.
Odpowiedź: Rysunek 1.
2. Ułamkowa funkcja wymierna
Rozważmy ułamkową funkcję wymierną postaci y = P(x) / Q(x), gdzie P(x) i Q(x) są wielomianami stopnia wyższego niż pierwszy.
Przykłady takich funkcji wymiernych:
y = (x 3 – 5x + 6) / (x 7 – 6) lub y = (x – 2) 2 (x + 1) / (x 2 + 3).
Jeśli funkcja y = P(x) / Q(x) reprezentuje iloraz dwóch wielomianów o stopniu wyższym od pierwszego, to jej wykres będzie z reguły bardziej złożony i czasami może być trudno go dokładnie skonstruować , ze wszystkimi szczegółami. Często jednak wystarczy zastosować techniki podobne do tych, które przedstawiliśmy już powyżej.
Niech ułamek będzie ułamkiem właściwym (n< m). Известно, что любую несократимую рациональную дробь можно представить, и притом единственным образом, в виде суммы конечного числа элементарных дробей, вид которых определяется разложением знаменателя дроби Q(x) в произведение действительных сомножителей:
P(x)/Q(x) = A 1 /(x – K 1) m1 + A 2 /(x – K 1) m1-1 + … + A m1 /(x – K 1) + …+
L 1 /(x – K s) ms + L 2 /(x – K s) ms-1 + … + L ms /(x – K s) + …+
+ (B 1 x + C 1) / (x 2 +p 1 x + q 1) m1 + … + (B m1 x + C m1) / (x 2 +p 1 x + q 1) + …+
+ (M 1 x + N 1) / (x 2 +p t x + q t) m1 + … + (M m1 x + N m1) / (x 2 +p t x + q t).
Oczywiście wykres ułamkowej funkcji wymiernej można otrzymać jako sumę wykresów ułamków elementarnych.
Rysowanie wykresów ułamkowych funkcji wymiernych
Rozważmy kilka sposobów konstruowania wykresów ułamkowej funkcji wymiernej.
Przykład 4.
Narysuj wykres funkcji y = 1/x 2 .
Rozwiązanie.
Korzystając z wykresu funkcji y = x 2, konstruujemy wykres y = 1/x 2 i stosujemy technikę „dzielenia” wykresów.
Dziedzina D(y) = (-∞; 0)ᴗ(0; +∞).
Zakres wartości E(y) = (0; +∞).
Nie ma punktów przecięcia z osiami. Funkcja jest parzysta. Zwiększa się dla wszystkich x z przedziału (-∞; 0), maleje dla x od 0 do +∞.
Odpowiedź: Rysunek 2.
Przykład 5.
Naszkicuj funkcję y = (x 2 – 4x + 3) / (9 – 3x).
Rozwiązanie.
Dziedzina D(y) = (-∞; 3)ᴗ(3; +∞).
y = (x 2 – 4x + 3) / (9 – 3x) = (x – 3)(x – 1) / (-3(x – 3)) = -(x – 1)/3 = -x/ 3 + 1/3.
Tutaj zastosowaliśmy technikę faktoryzacji, redukcji i redukcji do funkcji liniowej.
Odpowiedź: Rysunek 3.

Przykład 6.
Naszkicuj funkcję y = (x 2 – 1)/(x 2 + 1).
Rozwiązanie.
Dziedziną definicji jest D(y) = R. Ponieważ funkcja jest parzysta, wykres jest symetryczny względem rzędnej. Zanim zbudujemy wykres, przekształćmy wyrażenie jeszcze raz, podkreślając całą część:
y = (x 2 – 1)/(x 2 + 1) = 1 – 2/(x 2 + 1).
Należy pamiętać, że izolowanie części całkowitej we wzorze ułamkowej funkcji wymiernej jest jedną z głównych podczas konstruowania wykresów.
Jeśli x → ±∞, to y → 1, tj. linia prosta y = 1 jest asymptotą poziomą.
Odpowiedź: Rysunek 4.
Przykład 7.
Rozważmy funkcję y = x/(x 2 + 1) i spróbujmy dokładnie znaleźć jej największą wartość, tj. najwyższy punkt w prawej połowie wykresu. Aby dokładnie skonstruować ten wykres, dzisiejsza wiedza nie wystarczy. Oczywiście nasza krzywa nie może „wznieść się” bardzo wysoko, ponieważ mianownik szybko zaczyna „przewyższać” licznik. Zobaczmy, czy wartość funkcji może być równa 1. Aby to zrobić, musimy rozwiązać równanie x 2 + 1 = x, x 2 – x + 1 = 0. Równanie to nie ma pierwiastków rzeczywistych. Oznacza to, że nasze założenie jest błędne. Aby znaleźć największą wartość funkcji, musisz dowiedzieć się, przy jakim największym A równanie A = x/(x 2 + 1) będzie miało rozwiązanie. Zastąpmy pierwotne równanie równaniem kwadratowym: Ax 2 – x + A = 0. Równanie to ma rozwiązanie, gdy 1 – 4A 2 ≥ 0. Stąd znajdujemy największą wartość A = 1/2. 
Odpowiedź: Rysunek 5, max y(x) = ½.
Nadal masz pytania? Nie wiesz jak wykreślić funkcje?
Aby uzyskać pomoc korepetytora zarejestruj się.
Pierwsza lekcja jest bezpłatna!
stronie internetowej, przy kopiowaniu materiału w całości lub w części wymagany jest link do źródła.
Jedną z najbardziej znanych funkcji wykładniczych w matematyce jest wykładnik. Reprezentuje liczbę Eulera podniesioną do określonej potęgi. W Excelu istnieje oddzielny operator, który pozwala to obliczyć. Zobaczmy jak można to wykorzystać w praktyce.
Wykładnik to liczba Eulera podniesiona do danej potęgi. Sama liczba Eulera wynosi w przybliżeniu 2,718281828. Czasami nazywana jest także liczbą Napiera. Funkcja wykładnicza wygląda następująco:
gdzie e jest liczbą Eulera, a n jest stopniem podniesienia.
Aby obliczyć ten wskaźnik w programie Excel, używany jest oddzielny operator - DO POTĘGI. Dodatkowo funkcję tę można wyświetlić w formie wykresu. O pracy z tymi narzędziami porozmawiamy dalej.
Metoda 1: Oblicz wykładnik, ręcznie wprowadzając funkcję
EXP(liczba)
Oznacza to, że ta formuła zawiera tylko jeden argument. Jest to dokładnie potęga, do której należy podnieść liczbę Eulera. Argument ten może być wartością liczbową lub odwołaniem do komórki zawierającej wykładnik.


Metoda 2: Korzystanie z Kreatora funkcji
Chociaż składnia obliczania wykładnika jest niezwykle prosta, niektórzy użytkownicy wolą z niej korzystać Kreator funkcji. Spójrzmy, jak to się robi na przykładzie.


Jeśli jako argument zostanie użyte odwołanie do komórki zawierające wykładnik, należy umieścić kursor w tym polu "Numer" i po prostu wybierz tę komórkę na arkuszu. Jego współrzędne zostaną natychmiast wyświetlone w polu. Następnie, aby obliczyć wynik, kliknij przycisk "OK".

Metoda 3: kreślenie
Dodatkowo w programie Excel istnieje możliwość skonstruowania wykresu wykorzystującego jako podstawę wyniki uzyskane z obliczenia wykładnika. Aby skonstruować wykres, arkusz musi mieć już obliczone wartości wykładnika różnych potęg. Można je obliczyć za pomocą jednej z metod opisanych powyżej.
W dziedzinie definicji funkcji potęgowej y = x p obowiązują następujące wzory:
;
;
;
;
;
;
;
;
.
Własności funkcji potęgowych i ich wykresy
Funkcja potęgi z wykładnikiem równym zero, p = 0
Jeżeli wykładnik funkcji potęgowej y = x p jest równy zero, p = 0, to funkcja potęgowa jest zdefiniowana dla wszystkich x ≠ 0 i jest stałą równą jedności:
y = x p = x 0 = 1, x ≠ 0.
Funkcja potęgi z naturalnym wykładnikiem nieparzystym, p = n = 1, 3, 5, ...
Rozważmy funkcję potęgową y = x p = x n z naturalnym nieparzystym wykładnikiem n = 1, 3, 5, ... . Wskaźnik ten można również zapisać w postaci: n = 2k + 1, gdzie k = 0, 1, 2, 3, ... jest nieujemną liczbą całkowitą. Poniżej znajdują się właściwości i wykresy takich funkcji.
Wykres funkcji potęgi y = x n z naturalnym wykładnikiem nieparzystym dla różnych wartości wykładnika n = 1, 3, 5, ....
Domena: -∞ < x < ∞
Wiele znaczeń: -∞ < y < ∞
Parytet: nieparzyste, y(-x) = - y(x)
Monotonia: monotonicznie wzrasta
Skrajności: NIE
Wypukły:
przy -∞< x < 0
выпукла вверх
o 0< x < ∞
выпукла вниз
Punkty przegięcia: x = 0, y = 0
x = 0, y = 0
Limity:
;
Wartości prywatne:
przy x = -1,
y(-1) = (-1) n ≡ (-1) 2k+1 = -1
przy x = 0, y(0) = 0 n = 0
dla x = 1, y(1) = 1 n = 1
Funkcja odwrotna:
dla n = 1 funkcja jest jej odwrotnością: x = y
dla n ≠ 1 funkcją odwrotną jest pierwiastek stopnia n:
Funkcja potęgi z naturalnym parzystym wykładnikiem, p = n = 2, 4, 6, ...
Rozważmy funkcję potęgową y = x p = x n z naturalnym parzystym wykładnikiem n = 2, 4, 6, ... . Wskaźnik ten można również zapisać w postaci: n = 2k, gdzie k = 1, 2, 3, ... - naturalny. Poniżej podano właściwości i wykresy takich funkcji.
Wykres funkcji potęgi y = x n z naturalnym parzystym wykładnikiem dla różnych wartości wykładnika n = 2, 4, 6, ....
Domena: -∞ < x < ∞
Wiele znaczeń: 0 ≤ r< ∞
Parytet: parzysty, y(-x) = y(x)
Monotonia:
dla x ≤ 0 maleje monotonicznie
dla x ≥ 0 rośnie monotonicznie
Skrajności: minimum, x = 0, y = 0
Wypukły: wypukły w dół
Punkty przegięcia: NIE
Punkty przecięcia z osiami współrzędnych: x = 0, y = 0
Limity:
;
Wartości prywatne:
przy x = -1, y(-1) = (-1) n ≡ (-1) 2k = 1
przy x = 0, y(0) = 0 n = 0
dla x = 1, y(1) = 1 n = 1
Funkcja odwrotna:
dla n = 2, pierwiastek kwadratowy:
dla n ≠ 2, pierwiastek stopnia n:
Funkcja potęgi z ujemnym wykładnikiem całkowitym, p = n = -1, -2, -3, ...
Rozważmy funkcję potęgową y = x p = x n z całkowitym ujemnym wykładnikiem n = -1, -2, -3, ... . Jeśli umieścimy n = -k, gdzie k = 1, 2, 3, ... jest liczbą naturalną, to można to przedstawić jako:
Wykres funkcji potęgi y = x n z ujemnym wykładnikiem całkowitym dla różnych wartości wykładnika n = -1, -2, -3, ... .
Wykładnik nieparzysty, n = -1, -3, -5, ...
Poniżej znajdują się właściwości funkcji y = x n z nieparzystym wykładnikiem ujemnym n = -1, -3, -5, ....
Domena: x ≠ 0
Wiele znaczeń: y ≠ 0
Parytet: nieparzyste, y(-x) = - y(x)
Monotonia: monotonicznie maleje
Skrajności: NIE
Wypukły:
o x< 0
:
выпукла вверх
dla x > 0: wypukły w dół
Punkty przegięcia: NIE
Punkty przecięcia z osiami współrzędnych: NIE
Podpisać:
o x< 0, y < 0
dla x > 0, y > 0
Limity:
; ; ;
Wartości prywatne:
dla x = 1, y(1) = 1 n = 1
Funkcja odwrotna:
gdy n = -1,
o godz< -2
,
Wykładnik parzysty, n = -2, -4, -6, ...
Poniżej znajdują się właściwości funkcji y = x n z parzystym wykładnikiem ujemnym n = -2, -4, -6, ....
Domena: x ≠ 0
Wiele znaczeń: y > 0
Parytet: parzysty, y(-x) = y(x)
Monotonia:
o x< 0
:
монотонно возрастает
dla x > 0: maleje monotonicznie
Skrajności: NIE
Wypukły: wypukły w dół
Punkty przegięcia: NIE
Punkty przecięcia z osiami współrzędnych: NIE
Podpisać: y > 0
Limity:
; ; ;
Wartości prywatne:
dla x = 1, y(1) = 1 n = 1
Funkcja odwrotna:
przy n = -2,
o godz< -2
,
Funkcja potęgowa z wykładnikiem wymiernym (ułamkowym).
Rozważmy funkcję potęgi y = x p z wykładnikiem wymiernym (ułamkowym), gdzie n jest liczbą całkowitą, m > 1 jest liczbą naturalną. Co więcej, n, m nie mają wspólnych dzielników.
Mianownik wskaźnika ułamkowego jest nieparzysty
Niech mianownik wykładnika ułamkowego będzie nieparzysty: m = 3, 5, 7, ... . W tym przypadku funkcja potęgi x p jest zdefiniowana zarówno dla dodatnich, jak i ujemnych wartości argumentu x. Rozważmy właściwości takich funkcji potęgowych, gdy wykładnik p mieści się w pewnych granicach.
Wartość p jest ujemna, p< 0
Niech wykładnik wymierny (z nieparzystym mianownikiem m = 3, 5, 7, ...) będzie mniejszy od zera: .
Wykresy funkcji potęgowych z wymiernym wykładnikiem ujemnym dla różnych wartości wykładnika, gdzie m = 3, 5, 7, ... jest nieparzyste.
Licznik nieparzysty, n = -1, -3, -5, ...
Przedstawiamy własności funkcji potęgowej y = x p z wymiernym wykładnikiem ujemnym, gdzie n = -1, -3, -5, ... jest nieparzystą liczbą całkowitą ujemną, m = 3, 5, 7 ... jest liczbą całkowitą nieparzysta liczba całkowita naturalna.
Domena: x ≠ 0
Wiele znaczeń: y ≠ 0
Parytet: nieparzyste, y(-x) = - y(x)
Monotonia: monotonicznie maleje
Skrajności: NIE
Wypukły:
o x< 0
:
выпукла вверх
dla x > 0: wypukły w dół
Punkty przegięcia: NIE
Punkty przecięcia z osiami współrzędnych: NIE
Podpisać:
o x< 0, y < 0
dla x > 0, y > 0
Limity:
; ; ;
Wartości prywatne:
przy x = -1, y(-1) = (-1) n = -1
dla x = 1, y(1) = 1 n = 1
Funkcja odwrotna:
Licznik parzysty, n = -2, -4, -6, ...
Własności funkcji potęgowej y = x p z wymiernym wykładnikiem ujemnym, gdzie n = -2, -4, -6, ... jest parzystą ujemną liczbą całkowitą, m = 3, 5, 7 ... jest nieparzystą liczbą naturalną .
Domena: x ≠ 0
Wiele znaczeń: y > 0
Parytet: parzysty, y(-x) = y(x)
Monotonia:
o x< 0
:
монотонно возрастает
dla x > 0: maleje monotonicznie
Skrajności: NIE
Wypukły: wypukły w dół
Punkty przegięcia: NIE
Punkty przecięcia z osiami współrzędnych: NIE
Podpisać: y > 0
Limity:
; ; ;
Wartości prywatne:
przy x = -1, y(-1) = (-1) n = 1
dla x = 1, y(1) = 1 n = 1
Funkcja odwrotna:
Wartość p jest dodatnia, mniejsza niż jeden, 0< p < 1
Wykres funkcji potęgowej z wykładnikiem wymiernym (0< p < 1 ) при различных значениях показателя степени , где m = 3, 5, 7, ... - нечетное.
Licznik nieparzysty, n = 1, 3, 5, ...
< p < 1 , где n = 1, 3, 5, ... - нечетное натуральное, m = 3, 5, 7 ... - нечетное натуральное.
Domena: -∞ < x < +∞
Wiele znaczeń: -∞ < y < +∞
Parytet: nieparzyste, y(-x) = - y(x)
Monotonia: monotonicznie wzrasta
Skrajności: NIE
Wypukły:
o x< 0
:
выпукла вниз
dla x > 0: wypukły w górę
Punkty przegięcia: x = 0, y = 0
Punkty przecięcia z osiami współrzędnych: x = 0, y = 0
Podpisać:
o x< 0, y < 0
dla x > 0, y > 0
Limity:
;
Wartości prywatne:
przy x = -1, y(-1) = -1
przy x = 0, y(0) = 0
dla x = 1, y(1) = 1
Funkcja odwrotna:
Licznik parzysty, n = 2, 4, 6, ...
Przedstawiono właściwości funkcji potęgowej y = x p z wykładnikiem wymiernym w zakresie 0< p < 1 , где n = 2, 4, 6, ... - четное натуральное, m = 3, 5, 7 ... - нечетное натуральное.
Domena: -∞ < x < +∞
Wiele znaczeń: 0 ≤ r< +∞
Parytet: parzysty, y(-x) = y(x)
Monotonia:
o x< 0
:
монотонно убывает
dla x > 0: rośnie monotonicznie
Skrajności: minimum przy x = 0, y = 0
Wypukły: wypukły w górę dla x ≠ 0
Punkty przegięcia: NIE
Punkty przecięcia z osiami współrzędnych: x = 0, y = 0
Podpisać: dla x ≠ 0, y > 0
Limity:
;
Wartości prywatne:
przy x = -1, y(-1) = 1
przy x = 0, y(0) = 0
dla x = 1, y(1) = 1
Funkcja odwrotna:
Indeks p jest większy niż jeden, p > 1
Wykres funkcji potęgi z wykładnikiem wymiernym (p > 1) dla różnych wartości wykładnika, gdzie m = 3, 5, 7, ... - nieparzyste.
Licznik nieparzysty, n = 5, 7, 9, ...
Własności funkcji potęgowej y = x p z wykładnikiem wymiernym większym od jedności: . Gdzie n = 5, 7, 9, ... - dziwne naturalne, m = 3, 5, 7 ... - dziwne naturalne.
Domena: -∞ < x < ∞
Wiele znaczeń: -∞ < y < ∞
Parytet: nieparzyste, y(-x) = - y(x)
Monotonia: monotonicznie wzrasta
Skrajności: NIE
Wypukły:
przy -∞< x < 0
выпукла вверх
o 0< x < ∞
выпукла вниз
Punkty przegięcia: x = 0, y = 0
Punkty przecięcia z osiami współrzędnych: x = 0, y = 0
Limity:
;
Wartości prywatne:
przy x = -1, y(-1) = -1
przy x = 0, y(0) = 0
dla x = 1, y(1) = 1
Funkcja odwrotna:
Licznik parzysty, n = 4, 6, 8, ...
Własności funkcji potęgowej y = x p z wykładnikiem wymiernym większym od jedności: . Gdzie n = 4, 6, 8, ... - nawet naturalne, m = 3, 5, 7 ... - dziwne naturalne.
Domena: -∞ < x < ∞
Wiele znaczeń: 0 ≤ r< ∞
Parytet: parzysty, y(-x) = y(x)
Monotonia:
o x< 0
монотонно убывает
dla x > 0 rośnie monotonicznie
Skrajności: minimum przy x = 0, y = 0
Wypukły: wypukły w dół
Punkty przegięcia: NIE
Punkty przecięcia z osiami współrzędnych: x = 0, y = 0
Limity:
;
Wartości prywatne:
przy x = -1, y(-1) = 1
przy x = 0, y(0) = 0
dla x = 1, y(1) = 1
Funkcja odwrotna:
Mianownik wskaźnika ułamkowego jest parzysty
Niech mianownik wykładnika ułamkowego będzie parzysty: m = 2, 4, 6, ... . W tym przypadku funkcja potęgi x p nie jest zdefiniowana dla ujemnych wartości argumentu. Jej właściwości pokrywają się z właściwościami funkcji potęgowej z niewymiernym wykładnikiem (patrz następny rozdział).
Funkcja potęgowa z wykładnikiem niewymiernym
Rozważmy funkcję potęgową y = x p z niewymiernym wykładnikiem p. Właściwości takich funkcji różnią się od omówionych powyżej tym, że nie są zdefiniowane dla ujemnych wartości argumentu x. W przypadku dodatnich wartości argumentu właściwości zależą tylko od wartości wykładnika p i nie zależą od tego, czy p jest liczbą całkowitą, wymierną czy irracjonalną.

y = x p dla różnych wartości wykładnika p.
Funkcja potęgowa z wykładnikiem ujemnym p< 0
Domena: x > 0
Wiele znaczeń: y > 0
Monotonia: monotonicznie maleje
Wypukły: wypukły w dół
Punkty przegięcia: NIE
Punkty przecięcia z osiami współrzędnych: NIE
Limity: ;
Znaczenie prywatne: Dla x = 1, y(1) = 1 p = 1
Funkcja potęgowa z wykładnikiem dodatnim p > 0
Wskaźnik mniejszy niż jeden 0< p < 1
Domena: x ≥ 0
Wiele znaczeń: y ≥ 0
Monotonia: monotonicznie wzrasta
Wypukły: wypukły ku górze
Punkty przegięcia: NIE
Punkty przecięcia z osiami współrzędnych: x = 0, y = 0
Limity:
Wartości prywatne: Dla x = 0, y(0) = 0 p = 0 .
Dla x = 1, y(1) = 1 p = 1
Wskaźnik jest większy niż jeden p > 1
Domena: x ≥ 0
Wiele znaczeń: y ≥ 0
Monotonia: monotonicznie wzrasta
Wypukły: wypukły w dół
Punkty przegięcia: NIE
Punkty przecięcia z osiami współrzędnych: x = 0, y = 0
Limity:
Wartości prywatne: Dla x = 0, y(0) = 0 p = 0 .
Dla x = 1, y(1) = 1 p = 1
Bibliografia:
W. Bronstein, KA Semendyaev, Podręcznik matematyki dla inżynierów i studentów, „Lan”, 2009.
Wykładnik jest oznaczony jako , lub .
Numer mi
Podstawą stopnia wykładnika jest numer e. To liczba niewymierna. Jest mniej więcej równa
mi ≈ 2,718281828459045...
Liczbę e wyznacza się poprzez granicę ciągu. Jest to tzw drugi wspaniały limit:
.
Liczbę e można również przedstawić jako serię:
.
Wykres wykładniczy
Wykres wykładniczy, y = mi x .Wykres pokazuje wykładniczy mi do pewnego stopnia X.
y (x) = mi x
Z wykresu wynika, że wykładnik rośnie monotonicznie.
Formuły
Podstawowe wzory są takie same jak dla funkcji wykładniczej o podstawie stopnia e.
;
;
;
Wyrażenie funkcji wykładniczej o dowolnej podstawie stopnia a poprzez wykładniczą:
.
Wartości prywatne
Niech y (x) = mi x. Następnie
.
Właściwości wykładnika
Wykładnik ma właściwości funkcji wykładniczej o podstawie potęgowej mi > 1 .
Dziedzina, zbiór wartości
Wykładnik y (x) = mi x zdefiniowane dla wszystkich x.
Jego dziedzina definicji:
- ∞ < x + ∞
.
Ma wiele znaczeń:
0
< y < + ∞
.
Ekstremalności, rosnące, malejące
Funkcja wykładnicza jest funkcją rosnącą monotonicznie, więc nie ma ekstremów. Jego główne właściwości przedstawiono w tabeli.
Funkcja odwrotna
Odwrotnością wykładnika jest logarytm naturalny.
;
.
Pochodna wykładnika
Pochodna mi do pewnego stopnia X równy mi do pewnego stopnia X
:
.
Pochodna n-tego rzędu:
.
Wyprowadzanie wzorów > > >
Całka
Liczby zespolone
Operacje na liczbach zespolonych wykonuje się za pomocą Wzory Eulera:
,
gdzie jest jednostka urojona:
.
Wyrażenia poprzez funkcje hiperboliczne
;
;
.
Wyrażenia wykorzystujące funkcje trygonometryczne
;
;
;
.
Rozszerzanie szeregu potęgowego
Bibliografia:
W. Bronstein, KA Semendyaev, Podręcznik matematyki dla inżynierów i studentów, „Lan”, 2009.
Długość odcinka na osi współrzędnych określa wzór:
Długość odcinka w płaszczyźnie współrzędnych oblicza się ze wzoru:
Aby znaleźć długość odcinka w trójwymiarowym układzie współrzędnych, użyj następującego wzoru:
Współrzędne środka odcinka (dla osi współrzędnych stosuje się tylko pierwszy wzór, dla płaszczyzny współrzędnych - dwa pierwsze wzory, dla trójwymiarowego układu współrzędnych - wszystkie trzy wzory) oblicza się za pomocą wzorów:
Funkcjonować– jest to zgodność formy y= F(X) pomiędzy wielkościami zmiennymi, dzięki czemu każda rozważana wartość jakiejś zmiennej wielkości X(argument lub zmienna niezależna) odpowiada określonej wartości innej zmiennej, y(zmienna zależna, czasami tę wartość nazywa się po prostu wartością funkcji). Należy pamiętać, że funkcja przyjmuje wartość jednego argumentu X może odpowiadać tylko jedna wartość zmiennej zależnej Na. Jednak ta sama wartość Na można uzyskać różnymi X.
Dziedzina funkcji– są to wszystkie wartości zmiennej niezależnej (argument funkcji, zwykle this X), dla którego zdefiniowano funkcję, tj. jego znaczenie istnieje. Wskazany jest obszar definicji D(y). Ogólnie rzecz biorąc, znasz już tę koncepcję. Dziedzina definicji funkcji nazywana jest inaczej dziedziną wartości dopuszczalnych lub VA, którą już dawno udało ci się znaleźć.
Zakres funkcji są wszystkimi możliwymi wartościami zmiennej zależnej danej funkcji. Wyznaczony mi(Na).
Funkcja wzrasta na przedziale, w którym większa wartość argumentu odpowiada większej wartości funkcji. Funkcja jest malejąca na przedziale, w którym większa wartość argumentu odpowiada mniejszej wartości funkcji.
Przedziały znaku stałego funkcji- są to przedziały zmiennej niezależnej, w których zmienna zależna zachowuje swój znak dodatni lub ujemny.
Zera funkcji– są to wartości argumentu, przy których wartość funkcji jest równa zeru. W tych punktach wykres funkcji przecina oś odciętych (oś OX). Bardzo często potrzeba znalezienia zer funkcji oznacza konieczność prostego rozwiązania równania. Często też potrzeba znalezienia przedziałów stałości znaku oznacza konieczność prostego rozwiązania nierówności.
Funkcjonować y = F(X) są nazywane nawet X
![]()
Oznacza to, że dla dowolnych przeciwnych wartości argumentu wartości funkcji parzystej są równe. Wykres funkcji parzystej jest zawsze symetryczny względem osi rzędnych wzmacniacza operacyjnego.
Funkcjonować y = F(X) są nazywane dziwne, jeśli jest zdefiniowany na zbiorze symetrycznym i dla dowolnego X z dziedziny definicji równość zachodzi:
![]()
Oznacza to, że dla dowolnych przeciwnych wartości argumentu wartości funkcji nieparzystej są również przeciwne. Wykres funkcji nieparzystej jest zawsze symetryczny względem początku.
Suma pierwiastków funkcji parzystych i nieparzystych (punktów przecięcia osi x OX) jest zawsze równa zeru, ponieważ dla każdego pierwiastka dodatniego X ma pierwiastek ujemny - X.
Ważne jest, aby pamiętać: niektóre funkcje nie muszą być parzyste lub nieparzyste. Istnieje wiele funkcji, które nie są ani parzyste, ani nieparzyste. Takie funkcje nazywane są funkcje ogólne, i dla nich żadna z podanych powyżej równości ani właściwości nie jest spełniona.
Funkcja liniowa jest funkcją, którą można wyrazić wzorem:
Wykres funkcji liniowej jest linią prostą i w ogólnym przypadku wygląda tak (przykład podano dla przypadku, gdy k> 0, w tym przypadku funkcja jest rosnąca; z okazji k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону - слева направо):

Wykres funkcji kwadratowej (Parabola)
Wykres paraboli jest określony funkcją kwadratową:
Funkcja kwadratowa, jak każda inna funkcja, przecina oś OX w punktach będących jej pierwiastkami: ( X 1 ; 0) i ( X 2; 0). Jeśli nie ma pierwiastków, to funkcja kwadratowa nie przecina osi OX; jeśli jest tylko jeden pierwiastek, to w tym punkcie ( X 0 ; 0) funkcja kwadratowa dotyka tylko osi OX, ale jej nie przecina. Funkcja kwadratowa przecina zawsze oś OY w punkcie o współrzędnych: (0; C). Wykres funkcji kwadratowej (paraboli) może wyglądać następująco (na rysunku przedstawiono przykłady, które nie wyczerpują wszystkich możliwych typów paraboli):

W której:
- jeśli współczynnik A> 0, w funkcji y = topór 2 + bx + C, wówczas gałęzie paraboli są skierowane w górę;
- Jeśli A < 0, то ветви параболы направлены вниз.
Współrzędne wierzchołka paraboli można obliczyć za pomocą następujących wzorów. Szczyty X (P- na zdjęciach powyżej) parabole (czyli punkt, w którym trójmian kwadratowy osiąga największą lub najmniejszą wartość):
Igrek górą (Q- na rysunkach powyżej) parabole lub maksimum, jeśli ramiona paraboli są skierowane w dół ( A < 0), либо минимальное, если ветви параболы направлены вверх (A> 0), wartość trójmianu kwadratowego:
Wykresy innych funkcji
Funkcja zasilania
Oto kilka przykładów wykresów funkcji potęgowych:

Odwrotnie proporcjonalny jest funkcją określoną wzorem:
W zależności od znaku liczby k Wykres zależności odwrotnie proporcjonalny może mieć dwie podstawowe opcje:

Asymptota jest linią, do której wykres funkcji zbliża się nieskończenie blisko, ale się nie przecina. Asymptotami wykresów odwrotnej proporcjonalności pokazanych na powyższym rysunku są osie współrzędnych, do których wykres funkcji zbliża się nieskończenie blisko, ale ich nie przecina.
Funkcja wykładnicza z bazą A jest funkcją określoną wzorem:
A Wykres funkcji wykładniczej może mieć dwie podstawowe opcje (podajemy również przykłady, patrz poniżej):

Funkcja logarytmiczna jest funkcją określoną wzorem:
W zależności od tego, czy liczba jest większa, czy mniejsza od jedności A Wykres funkcji logarytmicznej może mieć dwie podstawowe opcje:

Wykres funkcji y = |X| następująco:

Wykresy funkcji okresowych (trygonometrycznych).
Funkcjonować Na = F(X) jest nazywany okresowy, jeśli istnieje taka liczba różna od zera T, Co F(X + T) = F(X), dla kazdego X z dziedziny funkcji F(X). Jeśli funkcja F(X) jest okresowy z kropką T, to funkcja:
Gdzie: A, k, B są liczbami stałymi, oraz k nierówny zeru, także okresowy z kropką T 1, co określa się wzorem:
Większość przykładów funkcji okresowych to funkcje trygonometryczne. Przedstawiamy wykresy głównych funkcji trygonometrycznych. Poniższy rysunek przedstawia część wykresu funkcji y= grzech X(cały wykres ciągnie się w nieskończoność w lewo i w prawo), wykres funkcji y= grzech X zwany sinusoida:

Wykres funkcji y=co X zwany cosinus. Wykres ten pokazano na poniższym rysunku. Ponieważ wykres sinusoidalny przebiega w nieskończoność wzdłuż osi OX w lewo i w prawo:

Wykres funkcji y= tg X zwany styczna. Wykres ten pokazano na poniższym rysunku. Podobnie jak wykresy innych funkcji okresowych, ten wykres powtarza się w nieskończoność wzdłuż osi OX w lewo i w prawo.

I na koniec wykres funkcji y=ctg X zwany kotangentoid. Wykres ten pokazano na poniższym rysunku. Podobnie jak wykresy innych funkcji okresowych i trygonometrycznych, ten wykres powtarza się w nieskończoność wzdłuż osi OX w lewo i w prawo.

- Z powrotem
- Do przodu
Jak skutecznie przygotować się do tomografii komputerowej z fizyki i matematyki?
Aby skutecznie przygotować się do egzaminu TK z fizyki i matematyki, należy spełnić trzy najważniejsze warunki:
- Zapoznaj się ze wszystkimi tematami i wykonaj wszystkie testy i zadania podane w materiałach edukacyjnych na tej stronie. Aby to zrobić, nie potrzebujesz niczego, a mianowicie: poświęcaj trzy do czterech godzin dziennie na przygotowanie się do CT z fizyki i matematyki, studiowanie teorii i rozwiązywanie problemów. Faktem jest, że CT to egzamin, na którym nie wystarczy znać tylko fizykę czy matematykę, trzeba także umieć szybko i bezbłędnie rozwiązać dużą liczbę problemów o różnej tematyce i o różnym stopniu złożoności. Tego ostatniego można się nauczyć jedynie rozwiązując tysiące problemów.
- Naucz się wszystkich wzorów i praw fizyki oraz wzorów i metod matematyki. W rzeczywistości jest to również bardzo proste; w fizyce jest tylko około 200 niezbędnych formuł, a w matematyce jeszcze trochę mniej. W każdym z tych przedmiotów istnieje kilkanaście standardowych metod rozwiązywania problemów o podstawowym poziomie złożoności, których również można się nauczyć, a co za tym idzie, całkowicie automatycznie i bez trudności rozwiązując większość CT we właściwym czasie. Potem będziesz musiał myśleć tylko o najtrudniejszych zadaniach.
- Weź udział we wszystkich trzech etapach próbnych testów z fizyki i matematyki. Każdy RT można odwiedzić dwukrotnie, aby zdecydować się na obie opcje. Ponownie na CT oprócz umiejętności szybkiego i sprawnego rozwiązywania problemów oraz znajomości wzorów i metod trzeba także umieć odpowiednio zaplanować czas, rozłożyć siły i co najważniejsze poprawnie wypełnić formularz odpowiedzi, bez myląc liczbę odpowiedzi i problemów lub własne nazwisko. Ponadto podczas RT ważne jest, aby przyzwyczaić się do stylu zadawania pytań w problemach, który może wydawać się bardzo nietypowy dla nieprzygotowanej osoby w DT.
Pomyślne, sumienne i odpowiedzialne wdrożenie tych trzech punktów, a także odpowiedzialne przestudiowanie końcowych testów szkoleniowych, pozwoli Ci wykazać się na CT doskonałym wynikiem, maksymalnie do czego jesteś zdolny.
Znalazłeś błąd?
Jeśli uważasz, że znalazłeś błąd w materiałach szkoleniowych, napisz o tym e-mailem (). W piśmie podaj temat (fizyka lub matematyka), nazwę lub numer tematu lub testu, numer zadania lub miejsce w tekście (stronie), w którym Twoim zdaniem znajduje się błąd. Opisz również, na czym polega podejrzewany błąd. Twój list nie pozostanie niezauważony, błąd zostanie poprawiony lub zostaniesz wyjaśniony, dlaczego nie jest to błąd.