Aksjomatyczna konstrukcja teorii liczb naturalnych. IV. Aksjomatyczna konstrukcja układu liczb naturalnych. Odejmowanie i dzielenie liczb naturalnych

Umowa na wykorzystanie materiałów serwisu

Prosimy o wykorzystywanie opublikowanych w serwisie utworów wyłącznie do celów osobistych. Zabrania się publikowania materiałów na innych stronach.
Ta praca (i wszystkie inne) jest dostępna do pobrania całkowicie bezpłatnie. Możesz w myślach podziękować jego autorowi i zespołowi serwisu.

Wyślij swoją dobrą pracę do bazy wiedzy jest prosta. Skorzystaj z poniższego formularza

Studenci, doktoranci, młodzi naukowcy, którzy wykorzystują bazę wiedzy w swoich studiach i pracy, będą Państwu bardzo wdzięczni.

Podobne dokumenty

Dodawanie i mnożenie liczb całkowitych p-adycznych, definiowane jako dodawanie i mnożenie ciągów wyraz po wyrazie. Pierścień liczb całkowitych p-adycznych, badanie własności ich podziału. Wyjaśnianie danych liczb poprzez wprowadzanie nowych obiektów matematycznych.

praca na kursie, dodano 22.06.2015


Jak ludzie nauczyli się liczyć, pojawienie się liczb, liczb i systemów liczbowych. Tabliczka mnożenia na „palcach”: technika mnożenia liczb 9 i 8. Przykłady szybkiego liczenia. Sposoby pomnożenia liczby dwucyfrowej przez 11, 111, 1111 itd. i trzycyfrowy numer 999.

praca na kursie, dodano 22.10.2011


Nowy sposób mnożenia liczb. Podobieństwo między macierzą liczb utworzoną podczas obliczeń a trójkątem jest względne, ale nadal istnieje, zwłaszcza przy mnożeniu liczb trzycyfrowych i wyższych. Macierz trójkątna.

artykuł, dodano 02.06.2005


streszczenie, dodano 13.01.2011


Charakterystyka historii badań znaczenia liczb pierwszych w matematyce poprzez opisanie metod ich znajdowania. Wkład Pietro Cataldiego w rozwój teorii liczb pierwszych. Metoda Eratostenesa zestawiania tablic liczb pierwszych. Przyjazność liczb naturalnych.

test, dodano 24.12.2010


Zbiór nieujemnych liczb rzeczywistych jako interpretowalny podzbiór R. Podzielność w półgrupach multiplikatywnych. Struktura numerycznych gcd i lcd półgrup. Badanie multiplikatywnych półgrup nieujemnych liczb rzeczywistych z 0 i 1.

teza, dodana 27.05.2008


Własności liczb rzeczywistych, ich rola w rozwoju matematyki. Analiza konstrukcji zbioru liczb rzeczywistych w aspekcie historycznym. Podejścia do konstruowania teorii liczb rzeczywistych według Cantora, Weierstrassa, Dedekinda. Ich nauka w ramach zajęć szkolnych.

prezentacja, dodano 10.09.2011


Podstawowe elementy matematyki. Własności liczb naturalnych. Pojęcie teorii liczb. Ogólne własności porównań i równań algebraicznych. Działania arytmetyczne z porównaniami. Podstawowe prawa arytmetyki. Sprawdzanie wyników działań arytmetycznych.

praca na kursie, dodano 15.05.2015

Jako podstawowa koncepcja, kiedy
aksjomatyczna konstrukcja arytmetyki
Liczby naturalne przyjmują stosunek
„bezpośrednio podążaj” podane dalej
zbiór niepusty N.
Element bezpośrednio następujący
element a, oznacz a”.

Aksjomat 1. W zbiorze N istnieje
element, który nie następuje bezpośrednio po którymkolwiek
za którym elementem tego zestawu. Będziemy
nazwijmy to jednostką.
Aksjomat 2. Dla każdego elementu a N
jest tylko jeden element a”,
bezpośrednio po a.

Aksjomat 3. Dla każdego elementu a N
istnieje co najwyżej jeden element na
po którym następuje bezpośrednio a.
Aksjomat 4. Każdy podzbiór M
zbiór N, ma następujące właściwości:
1) jednostka należy do zbioru M;
2) z faktu, że a jest zawarte w M wynika, że
że a” jest zawarte w M, to M pokrywa się z
zestaw N.

Definicja liczby naturalnej

Zbiór N, dla którego elementów ustalana jest relacja
„bezpośrednio podążaj”, spełniając aksjomaty 1-4,
nazywa się zbiorem liczb naturalnych, a jego elementy są liczbami naturalnymi.

Dodatek

Definicja. Dodawanie liczb naturalnych nazywa się
operacja algebraiczna o następujących właściwościach:
1) (Ɐa ∈ N) za + 1 = za”,
2) (Ɐa, b ∈ N) a + b"=(a+b)".
Liczbę a+b nazywamy sumą liczb a i b oraz samych liczb a i b
warunki.
Uzgodnijmy następujący zapis:
1" = 2; 2" = 3; 3” = 4; 4” = 5 itd.

Właściwości dodatku

Twierdzenie 3. Dodawanie liczb naturalnych istnieje i istnieje
tylko
Twierdzenie 4. (Ɐ a, b, do ∈ N)(a + b) + do = a + (b + c)
Twierdzenie 5. (Ɐ a, b ∈ N) a+b = b+a

Mnożenie

Mnożenie liczb naturalnych nazywa się algebraicznym
operację o następujących właściwościach:
1)(Ɐ za ∈ N) a·1 =a;
2)(Ɐ a, b ∈ N) a·b" = a·b + a.
Liczbę a b nazywamy iloczynem liczb a i b oraz samych liczb a i
b - mnożniki

Właściwości mnożenia

Twierdzenie 7. Istnieje mnożenie liczb naturalnych i to
tylko.
Twierdzenie 8. (Ɐ a, b, c ∈ N)(a + b) c = ac + b do - rozdzielność
po prawej stronie względem dodawania.
Twierdzenie 9. (Ɐ a, b, c ∈ N) a·(b + c) = + a·c – rozdzielność lewa
odnośnie dodawania.
Twierdzenie 10. (Ɐ a, b, c ∈ N) (a b) c = a (b c) - łączność
mnożenie.
Twierdzenie 11. (Ɐ a, b ∈ N) a·b = a·b - przemienność mnożenia

Pytania autotestowe

1. Czy aksjomat 3 można sformułować następująco: „Dla każdego elementu
i po N następuje pojedynczy element
powinien?
2. Kontynuuj definicję liczby naturalnej: „Liczba naturalna
nazywa się elementem zbioru…”
3. Czy prawdą jest, że każdą liczbę naturalną otrzymujemy z poprzedniej?
dodając jeden?
4. Jakie właściwości mnożenia można wykorzystać przy znajdowaniu
znaczenie wyrażeń:
a) 5·(10 + 4); b) 125·15·6; c) (8·379)·125?

Literatura

Stoilova L.P.
Matematyka: Podręcznik dla studentów. wyższy pe. podręcznik zakłady.
M.: Ośrodek Wydawniczy „Akademia”. 2002. - 424 s.

Metoda aksjomatyczna w matematyce.

Podstawowe pojęcia i relacje aksjomatycznej teorii szeregu naturalnego. Definicja liczby naturalnej.

Dodawanie liczb naturalnych.

Mnożenie liczb naturalnych.

Własności zbioru liczb naturalnych

Odejmowanie i dzielenie liczb naturalnych.

Metoda aksjomatyczna w matematyce

W aksjomatycznej konstrukcji dowolnej teorii matematycznej przestrzegane są następujące zasady: pewne zasady:

1. Niektóre koncepcje teorii zostały wybrane jako główny i są akceptowane bez definicji.

2. Są sformułowane aksjomaty, które w tej teorii są akceptowane bez dowodu, ujawniają właściwości pojęć podstawowych.

3. Podano każde pojęcie teorii, które nie jest zawarte na liście pojęć podstawowych definicja wyjaśnia jego znaczenie za pomocą pojęć głównych i poprzedzających.

4. Każde twierdzenie teorii, które nie jest zawarte w liście aksjomatów, musi zostać udowodnione. Takie propozycje nazywane są twierdzenia i udowodnij je na podstawie aksjomatów i twierdzeń poprzedzających rozważane.

System aksjomatów powinien wyglądać następująco:

a) spójne: musimy być pewni, że wyciągając wszystkie możliwe wnioski z danego systemu aksjomatów, nigdy nie dojdziemy do sprzeczności;

b) niezależny: żaden aksjomat nie powinien być konsekwencją innych aksjomatów tego systemu.

V) pełny, jeśli w jego ramach zawsze da się udowodnić albo dane twierdzenie, albo jego zaprzeczenie.

Za pierwsze doświadczenie konstrukcji teorii aksjomatycznej można uznać przedstawienie geometrii przez Euklidesa w jego „Elementach” (III wiek p.n.e.). Znaczący wkład w rozwój aksjomatycznej metody konstruowania geometrii i algebry wniósł N.I. Łobaczewskiego i E. Galois. Pod koniec XIX wieku. Włoski matematyk Peano opracował system aksjomatów arytmetycznych.

Podstawowe pojęcia i relacje aksjomatycznej teorii liczb naturalnych. Definicja liczby naturalnej.

Jako pojęcie podstawowe (nieokreślone) w pewnym zbiorze N jest zaznaczona postawa , a także posługuje się pojęciami teorii mnogości, a także regułami logiki.

Element bezpośrednio następujący po elemencie A, oznaczać A".

Relacja „bezpośrednio podążaj” spełnia następujące aksjomaty:

Aksjomaty Peano:

Aksjomat 1. W obfitości N istnieje element bezpośrednio nie następny nie dla żadnego elementu tego zestawu. Zadzwońmy do niego jednostka i oznaczone symbolem 1 .

Aksjomat 2. Dla każdego elementu A z N jest tylko jeden element A" , zaraz po A .

Aksjomat 3. Dla każdego elementu A z N istnieje co najwyżej jeden element, po którym następuje bezpośrednio A .

Aksjomat 4. Dowolny podzbiór M zestawy N zbiega się z N , jeżeli posiada następujące właściwości: 1) 1 zawarte w M ; 2) z tego, że A zawarte w M , wynika, że A" zawarte w M.

Definicja 1. Pęczek N , dla których elementów ustalana jest relacja „bezpośrednio podążaj", spełniający aksjomaty 1-4, nazywa się zbiór liczb naturalnych, a jego elementy są liczby naturalne.

Definicja ta nie mówi nic o naturze elementów zbioru N . Więc to może być wszystko. Do wyboru jako zestaw N jakiś konkretny zbiór, na którym podana jest konkretna relacja „bezpośrednio wynika”, spełniająca aksjomaty 1-4, otrzymujemy modelu tego układu aksjomat.

Standardowy model systemu aksjomatów Peano to ciąg liczb, który powstał w procesie historycznego rozwoju społeczeństwa: 1,2,3,4,... Szereg naturalny zaczyna się od liczby 1 (aksjomat 1); po każdej liczbie naturalnej następuje bezpośrednio pojedyncza liczba naturalna (aksjomat 2); każda liczba naturalna następuje bezpośrednio po co najwyżej jednej liczbie naturalnej (aksjomat 3); zaczynając od liczby 1 i przechodząc w kierunku następujących po sobie liczb naturalnych, otrzymujemy cały zbiór tych liczb (aksjomat 4).

Zaczęliśmy więc aksjomatyczną konstrukcję systemu liczb naturalnych od wyboru podstawy relacja „bezpośrednio podążaj”. i aksjomaty opisujące jego właściwości. Dalsza konstrukcja teorii wymaga rozważenia znanych właściwości liczb naturalnych i operacji na nich. Muszą być one ujawnione w definicjach i twierdzeniach, tj. wywodzą się czysto logicznie z relacji „bezpośrednio podążaj” i aksjomatów 1-4.

Pierwszym pojęciem, które wprowadzimy po zdefiniowaniu liczby naturalnej, jest postawa „bezpośrednio poprzedza” , który jest często używany przy rozważaniu właściwości szeregu naturalnego.

Definicja 2. Jeśli liczba naturalna B bezpośrednio następuje Liczba naturalna A, ten numer A zwany Bezpośrednio poprzedzającym(lub poprzedni) numer b .

Relacja „poprzedza” ma szereg nieruchomości.

Twierdzenie 1. Jednostka nie ma poprzedzającej liczby naturalnej.

Twierdzenie 2. Każda liczba naturalna A, inny niż 1, ma pojedynczą liczbę poprzedzającą B, takie, że B"= A.

Ani w szkołach podstawowych, ani średnich nie rozważa się aksjomatycznej konstrukcji teorii liczb naturalnych. Jednakże te własności relacji „bezpośrednio wynikają”, które znajdują odzwierciedlenie w aksjomatach Peano, są przedmiotem badań w początkowym toku matematyki. Już w pierwszej klasie, rozważając liczby pierwszej dziesiątki, staje się jasne, w jaki sposób można uzyskać każdą liczbę. Używane są pojęcia „następuje” i „poprzedza”. Każda nowa liczba stanowi kontynuację badanego odcinka naturalnego ciągu liczb. Studenci są przekonani, że po każdej liczbie następuje następna i to tylko jedna rzecz, że naturalny ciąg liczb jest nieskończony.

Dodawanie liczb naturalnych

Zgodnie z zasadami konstruowania teorii aksjomatycznej definicję dodawania liczb naturalnych należy wprowadzić wykorzystując jedynie relację „bezpośrednio podążaj” i koncepcje "Liczba naturalna" I „poprzedni numer”.

Przedmówmy definicję dodawania następującymi rozważaniami. Jeśli do dowolnej liczby naturalnej A dodaj 1, otrzymamy liczbę A", zaraz po A, tj. A+ 1= a” i dlatego otrzymujemy regułę dodawania 1 do dowolnej liczby naturalnej. Ale jak dodać do liczby A Liczba naturalna B, różni się od 1? Wykorzystajmy następujący fakt: jeśli wiemy, że 2 + 3 = 5, to suma wynosi 2 + 4 = 6, co bezpośrednio następuje po liczbie 5. Dzieje się tak, ponieważ w sumie 2 + 4 drugim wyrazem jest liczba bezpośrednio następująca liczba 3. Zatem 2 + 4 =2+3 " =(2+3)". Generalnie mamy , .

Fakty te stanowią podstawę definicji dodawania liczb naturalnych w teorii aksjomatycznej.

Definicja 3. Dodawanie liczb naturalnych jest operacją algebraiczną mającą następujące właściwości:

Numer a + b zwany suma liczb A I B , i same liczby A I B - warunki.

Przy aksjomatycznym konstruowaniu teorii przestrzegane są pewne zasady:

niektóre koncepcje teorii są wybierane jako podstawowy, i są akceptowane bez definicji i nazywane są niedefiniowalnymi.

formułowane są aksjomaty - twierdzenia, które w danej teorii są akceptowane bez dowodu; ujawniają właściwości podstawowych pojęć;

podane jest każde pojęcie teorii, które nie jest zawarte na liście pojęć podstawowych definicja, wyjaśnia jego znaczenie za pomocą pojęć podstawowych i poprzedzających;

każde twierdzenie teorii, które nie jest zawarte w liście aksjomatów, musi zostać udowodnione; twierdzenia takie nazywane są twierdzeniami i dowodzi się ich na podstawie aksjomatów i twierdzeń poprzedzających rozważane.

W aksjomatycznej konstrukcji teorii zasadniczo wszystkie twierdzenia wyprowadza się poprzez dowód z aksjomatów. Dlatego na system aksjomatów nakładane są specjalne wymagania. Przede wszystkim musi być spójny i niezależny.

Nazywa się system aksjomatów spójny, jeśli nie można z niego logicznie wywnioskować dwóch wzajemnie wykluczających się zdań.

Spójny system aksjomatów nazywa się niezależny, jeśli żaden z aksjomatów tego układu nie jest konsekwencją innych aksjomatów tego układu.

Aksjomaty z reguły są odzwierciedleniem wielowiekowych praktycznych działań ludzi i to decyduje o ich ważności.

Za podstawowe pojęcie w aksjomatycznej konstrukcji arytmetyki liczb naturalnych przyjmuje się relację „bezpośrednio podążaj”, zdefiniowaną na niepustym zbiorze N. Za dobrze znane uważa się także pojęcia zbioru, elementu zbioru oraz inne pojęcia z zakresu teorii mnogości, a także reguły logiki.

Element bezpośrednio następujący po elemencie A, oznaczać A". Istotę relacji „bezpośrednio podążaj” ujawniają następujące aksjomaty zaproponowane przez włoskiego matematyka G. Peano w 1891 roku.

Aksjomat 1. W obfitości N istnieje element, który nie następuje bezpośrednio po żadnym elemencie tego zbioru. Nazywa się to jednostką i jest oznaczone symbolem 1.

Aksjomat 2. Dla każdego elementu A z N jest tylko jeden element A", zaraz po A.

Aksjomat 3. Dla każdego elementu a N istnieje co najwyżej jeden element, po którym następuje bezpośrednio A.

Aksjomat 4. (Aksjomat indukcji). Dowolny podzbiór M zestawy N pokrywa się z N, jeśli ma następujące właściwości: 1) 1 jest zawarty w M; 2) z faktu, że dowolny element A zawarte w M, wynika, że A" zawarte w M.

Sformułowane aksjomaty nazywane są często aksjomatami Peano, a aksjomat czwarty nazywany jest aksjomatem indukcji.

Zapiszmy te aksjomaty w formie symbolicznej.

A 1 )( 1  N)( A N)A"  1;

A 2 )( A N)( !B N)A"=b

A 3 ) ( A,B,Z N)c = a" c = b"  A= b;

4) M N 1  M (A M A"  M)  M=N

Korzystając z relacji „natychmiast podążaj” i aksjomatów Peano 1-4, możemy podać następującą definicję liczby naturalnej.

Definicja 1. Zbiór N., dla którego elementów ustalono relację „bezpośrednio wynikającą”, spełniającą aksjomaty 1-4, nazywa się zbiorem liczb naturalnych, a jego elementy liczby naturalne.

___________________________________________________________________

Definicja 2 . Jeśli liczba naturalnaBbezpośrednio następuje po liczbie a, wówczas liczbę a nazywa się liczbą bezpośrednio poprzedzającą (poprzedzającą).B.

______________________________________________________________________________________________

Twierdzenie 1. Jednostka nie ma poprzedzającej liczby naturalnej (prawdziwość twierdzenia wynika bezpośrednio z aksjomatu A 1 ).

Twierdzenie 2. Każda liczba naturalna A, różny od jednego ma poprzedzającą liczbę b , takie, że b " = A.

Definicja liczby naturalnej nie mówi nic o naturze elementów zbioru N. Więc to może być wszystko. Standardowy model systemu aksjomatów Peano to ciąg liczb, które pojawiły się w procesie historycznego rozwoju społeczeństwa:

1, 2, 3, 4, 5 ,..,

Każdy numer w tej serii ma swoje własne oznaczenie i nazwę, które uznamy za znane.

Warto zauważyć, że przy definicji liczby naturalnej nie można pominąć żadnego z aksjomatów.

1 A B C D

    …

B

Ryż. 16 Ryż. 17

Zadanie 1.

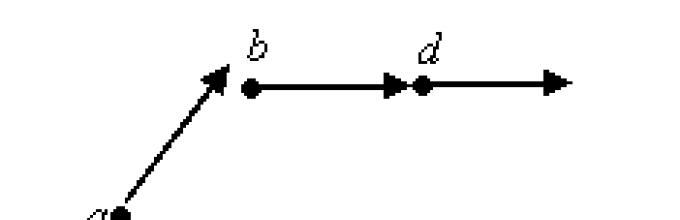
Na rysunkach każdy element jest połączony strzałką z elementem następującym po nim.

Określ, które ze zbiorów pokazanych na rysunkach 15 i 16 są modelami układu aksjomatów Peano.

1. Na ryc. Rysunek 16 przedstawia zbiór, w którym spełnione są aksjomaty 2 i 3, ale aksjomat 1 nie jest spełniony.

Aksjomat 4 nie będzie miał sensu, ponieważ w zbiorze nie ma elementu, który nie następuje bezpośrednio po innym.

2. Na ryc. Rysunek 17 przedstawia zbiór, w którym spełnione są aksjomaty 1, 2, 3, ale aksjomat 4 nie jest spełniony - zbiór punktów leżących na półprostej zawiera 1, a wraz z każdą liczbą zawiera liczbę bezpośrednio po niej następującą, ale tak nie jest nie pokrywają się z całością nastaw pokazanych na rysunku. Wniosek: żaden z zestawów pokazanych na ryc. Rys. 16 i 17 nie można uważać za modele systemu aksjomatów Peano.

Zadanie 2.

Udowodnijmy, że każda liczba naturalna różni się od liczby naturalnej znajdującej się bezpośrednio po niej, tj. ( X )X X"

Dowód

Korzystamy z aksjomatu indukcji - A 4 .

Pozwalać M=(x/x , X X"}, ponieważ . X  M N.

Dowód składa się z dwóch części.

Udowodnijmy to 1  M, te. 1  1" . Wynika to z A 1 .

Udowodnijmy to X M=> X" M. Pozwalać  X M te. X X". Udowodnijmy to X" M, tj. X"  (X")". I aksjomaty A 3 powinien X" (X")". Rzeczywiście, według A 3 , jeśli x" = (x)", to x = x", i odtąd poprzez propozycję indukcyjną x  M, wtedy x  X", W rezultacie dochodzimy do sprzeczności. Oznacza, X" (X")" ,  X" M.

Zastosowano tu zasadę kontrapozycji (PC), powszechnie stosowaną w dowodach sprzecznych.

Więc mamy:

M N (1  M (x M => x"  M))  M = N, tj. stwierdzenie x  x” jest prawdziwe dla dowolnej liczby naturalnej.

Pytania kontrolne

Jaka jest istota konstrukcji teorii aksjomatycznej?

Wymień podstawowe pojęcia szkolnego kursu planimetrii. Zapamiętaj system aksjomatów z tego kursu. Właściwości jakich pojęć są w nich opisane?

Sformułuj i zapisz aksjomaty Peano w formie symbolicznej. "

Sformułuj aksjomatyczną definicję liczby naturalnej.

Kontynuuj definicję liczby naturalnej: „Liczba naturalna jest elementem zbioru N,... » .

Podaj przykłady z podręczników do matematyki dla klas podstawowych, w których:

a) nowa (dla studentów) liczba stanowi kontynuację powstałego odcinka ciągu naturalnego;

b) ustalono, że po każdej liczbie naturalnej następuje bezpośrednio tylko jedna inna liczba naturalna.

Ćwiczenia

285. Elementami zbioru są grupy myślników (I, II, III, IIII,...). Czy ten zbiór spełnia aksjomaty Peano? Jak zdefiniowano tutaj, zdefiniowano tutaj relację „bezpośrednio podążaj”. Rozważ te same pytania dla zbioru (0, 00, 000, 0000,...).

Ryż. 17

286. Na ryc. 17 a) każdy element jest połączony strzałką z elementem następującym po nim. Czy zbiór można uznać za model układu aksjomatów Peano? Te same pytania dla zbiorów z ryc. 17 b), c), d).

287. Czy zbiór liczb (1, 2, 3) spełnia aksjomaty Peano P, ...), jeśli relacja sekwencji jest w nim zdefiniowana w następujący sposób:

1 3  5 7….

2  4  6 8….

288. Podaj przykłady zadań z podręczników matematyki dla klas podstawowych, w których poprawność wykonania zadań wyjaśniają aksjomaty Peano.

MATEMATYKA OZO Rok 1, semestr 2

Przykład 1: Uzasadnijmy wybór działania przy rozwiązywaniu problemu: „Kupiliśmy 4 paczki kolorowego papieru i 3 paczki białego papieru więcej. Ile paczek białego papieru kupiłeś?

Rozwiązanie. Problem dotyczy dwóch zestawów. Niech A będzie zbiorem paczek kolorowego papieru, B będzie zbiorem paczek białego papieru. Warunkowo znana jest liczba paczek kolorowego papieru, tj. n(A)=4 i trzeba znaleźć rozmiar zbioru B. Dodatkowo, zgodnie z warunkami zadania, w zbiorze B możemy wybrać podzbiór C, którego liczba wynosi 3, tj. n(C)=3. Zróbmy to na przykład tak, jak pokazano na ryc. 1.

Obrazek 1

Wtedy różnica B \ C = B 1 będzie równa zbiorowi A, tj. n(B1) = n(A).

Zatem zbiór B jest sumą zbiorów B 1 i C, gdzie B 1 C=Æ.

Problem sprowadza się do określenia wielkości sumy dwóch zbiorów rozłącznych i rozwiązuje się go poprzez dodanie: n(B) = n(B 1 C) = n(B 1) + n(C); n(B) = 4+3 = 7.

Przykład 2: Wykorzystując pojęcie liczby jako miary wielkości uzasadnimy wybór działań przy rozwiązywaniu zadania: „Na spódnicę zużyto 3 m materiału, na bluzkę 2 m. Ile metrów materiału poszło na cały garnitur?

Rozwiązanie: Problem dotyczy ilości - długości, którą mierzy się w jednostce 1 metr, ponieważ długość jest ciągła, wówczas wyjaśnimy wybór działań przy rozwiązywaniu problemu za pomocą segmentów (ryc. 2).

Niech e=1m, odcinek a pokazuje długość materiału użytego na spódnicę, a=3e. Odcinek b pokazuje długość materiału użytego do bluzki, b = 2e. Ponieważ W zadaniu musisz sprawdzić ilość całego użytego materiału, wówczas segment c wskaże ilość całego użytego materiału: c = a + b.

Rysunek 2

a=3e b=2e m mi (c)= m mi (a)+m mi (c) m mi (c) = 2+3 m mi (c) = 5 Odpowiedź: 5 m.

Przykład 3: Wykorzystując pojęcie liczby jako miary wielkości uzasadnimy wybór działania przy rozwiązywaniu zadania: „W pierwszym pudełku było 12 kg ciastek, a w drugim było ich o 3 kg mniej. Ile kilogramów ciasteczek znajdowało się w drugim pudełku?

Rozwiązanie: Problem dotyczy wielkości masy, której jednostką miary jest 1 kilogram, e = 1 kg, ponieważ ilość, masa jest ciągła, wówczas wyjaśnimy wybór działań przy rozwiązywaniu problemu za pomocą segmentów (ryc. 3).

Niech e = 1kg, odcinek a pokazuje, ile kilogramów ciasteczek znajdowało się w pierwszym pudełku, a = 12e.

Odcinek b pokazuje, o ile kilogramów ciastek było w drugim pudełku mniej niż w pierwszym, b = 3e.

Segment c pokazuje, ile kilogramów ciasteczek znajdowało się w drugim polu, m e (c) - ? Wiadomo, że w drugim pudełku znajduje się o 3 kg ciastek mniej niż w pierwszym, tj. to samo, ale o 3 mniej.

Niech d=a, następnie c = d – b. a = 12e, co oznacza d = 12e. m mi (c)= m mi (d)-m mi (c) m mi (c)=12-3 m mi (c)=9

Rysunek 3

Odpowiedź: W drugim pudełku było 9 kilogramów ciasteczek.