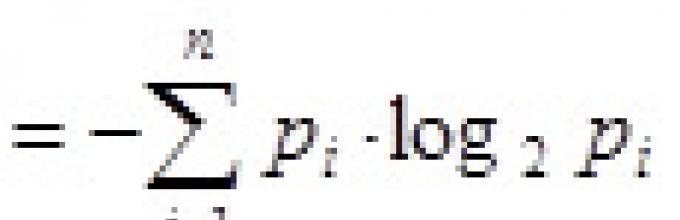Pojęcie Entropia
po raz pierwszy wprowadzony w 1865 r. przez R. Clausiusa do termodynamiki w celu określenia miary nieodwracalnego rozpraszania energii. Entropia wykorzystywana jest w różnych dziedzinach nauki, m.in. w teorii informacji, jako miara niepewności każdego doświadczenia, testu, który może mieć różne wyniki. Te definicje entropii są głębokie awiofon. Tak więc, na podstawie pomysłów na temat informacji, można wydedukować wszystkie najważniejsze przepisy fizyka statystyczna. [BĄDZ S. Fizyka. M: Wielka Encyklopedia Rosyjska, 1998].
Ilość ta jest również nazywana średnia entropia wiadomości. Entropia we wzorze Shannona wynosi charakterystyka średnia – oczekiwanie matematyczne rozkłady zmiennej losowej.
Na przykład w sekwencji liter tworzących zdanie w języku rosyjskim: różne litery pojawiają się z różną częstotliwością, więc niepewność wystąpienia jest w przypadku niektórych liter mniejsza niż w przypadku innych.
W 1948 roku badając problematykę racjonalnego przekazywania informacji poprzez szum kanał komunikacyjny Claude Shannon zaproponował rewolucyjne probabilistyczne podejście do zrozumienia komunikacji i stworzył pierwszą prawdziwie matematyczną teorię entropii. Jego sensacyjne pomysły szybko stały się podstawą rozwoju teorii informacji, która wykorzystuje pojęcie prawdopodobieństwa. Pojęcie entropii jako miary losowości zostało wprowadzone przez Shannona w jego artykule „A Mathematical Theory of Communication”, opublikowanym w dwóch częściach w Bell System Technical Journal w 1948 roku.
W przypadku równie prawdopodobnych zdarzeń ( szczególny przypadek), gdy wszystkie opcje są jednakowo prawdopodobne, zależność pozostaje jedynie od liczby rozważanych opcji, a wzór Shannona jest znacznie uproszczony i pokrywa się ze wzorem Hartleya, który po raz pierwszy zaproponował amerykański inżynier Ralpha Hartleya w 1928 roku jako jedno z naukowych podejść do oceny przekazów:
, gdzie I to ilość przesłanej informacji, p to prawdopodobieństwo zdarzenia, N to możliwa liczba różnych (równie prawdopodobnych) komunikatów.Zadanie 1. Dla zdarzeń równie prawdopodobnych.
W talii znajduje się 36 kart. Ile informacji zawiera wiadomość o tym, że z talii została pobrana karta z portretem „asa”; „As pik”?
Prawdopodobieństwo p1 = 4/36 = 1/9 i p2 = 1/36. Korzystając ze wzoru Hartleya mamy:
Odpowiedź: 3,17; 5,17 bita
Zauważ (z drugiego wyniku), że do zakodowania wszystkich kart potrzeba 6 bitów.
Z wyników wynika również, że im mniejsze prawdopodobieństwo zdarzenia, tym więcej informacji ono zawiera. (Ta właściwość nazywa się monotonia)
Zadanie 2. Dla zdarzeń nierówno prawdopodobnych
W talii znajduje się 36 kart. Spośród nich 12 to karty z „portretami”. Jedna po drugiej, jedna z kart jest wyjmowana z talii i pokazywana, aby ustalić, czy przedstawia portret. Karta wraca do talii. Określ ilość informacji przesyłanych za każdym razem, gdy zostanie pokazana jedna karta.
Amerykański inżynier i matematyk
twórca teorii informacji,
te. teorie przetwarzania, transmisji
i przechowywanie informacji
Claude'a Shannona jako pierwszy zinterpretował przesyłane komunikaty i szum w kanałach komunikacyjnych ze statystycznego punktu widzenia, biorąc pod uwagę zarówno skończone, jak i ciągłe zbiory komunikatów. Nazywa się Claude Shannon „ojciec teorii informacji”.
Jeden z najbardziej sławnych prace naukowe Claude Shannon to jego artykuł „Matematyczna teoria komunikacji”, wydany w 1948 r.
W tej pracy Shannon, badając problem racjonalnego przesyłania informacji przez zaszumiony kanał komunikacyjny, zaproponował probabilistyczne podejście do rozumienia komunikacji, stworzył pierwszą prawdziwie matematyczną teorię entropii jako miary losowości i wprowadził miarę dyskretnego rozkładu P prawdopodobieństwa zbioru alternatywnych stanów nadawcy i odbiorcy komunikatów.
Shannon ustalił wymagania dotyczące pomiaru entropii i wyprowadził wzór, który stał się podstawą ilościowej teorii informacji:
H(p)![]() .
.
Tutaj N- liczba znaków, z których można ułożyć wiadomość (alfabet), H - informacyjna entropia binarna .
W praktyce wartości prawdopodobieństwa Liczba Pi w powyższym wzorze zastępuje się je szacunkami statystycznymi: Liczba Pi - częstotliwość względna I znak w wiadomości, gdzie N- ilość wszystkich znaków w wiadomości, N ja- częstotliwość bezwzględna I znak w wiadomości, tj. numer wystąpienia I znak w wiadomości.
We wstępie do swojego artykułu „Matematyczna teoria komunikacji” Shannon zauważa, że w tym artykule rozszerza teorię komunikacji, której główne postanowienia zawarte są w ważne dzieła Nyquista I Hartleya.
 Harry Nyquist (1889-1976) -
Harry Nyquist (1889-1976) - Amerykański szwedzki inżynier
pochodzenia, jeden z pionierów
teoria informacji
Wczesne wyniki Nyquista w określeniu szerokości zakresu częstotliwości wymaganej do transmisji informacji położyły podwaliny pod późniejsze sukcesy Claude'a Shannona w rozwoju teorii informacji.
W 1928 roku Hartley wprowadził logarytmiczną miarę informacji H = K dziennik 2 N, którą często nazywa się ilością informacji Hartleya.
Hartley ma następujące ważne twierdzenie o wymaganej ilości informacji: jeśli w danym zbiorze M, składający się z N elementy, zawiera element X, o którym wiadomo tylko, że należy do tego zbioru M, a następnie znaleźć X, należy uzyskać ilość informacji o tym zbiorze równą log 2 N fragment.
Swoją drogą, zwróćcie uwagę na tytuł FRAGMENT pochodzi od angielskiego skrótu BIT - Cyfra binarna. Termin ten został po raz pierwszy zaproponowany przez amerykańskiego matematyka Johna Tukeya w 1946 r. Hartley i Shannon wykorzystali ten bit jako jednostkę informacji.
Ogólnie rzecz biorąc, entropia Shannona jest entropią zbioru prawdopodobieństw P 1 , P 2 ,…, p.n.
 Ralph Vinton Lyon Hartley (1888-1970)
Ralph Vinton Lyon Hartley (1888-1970) - Amerykański naukowiec zajmujący się elektroniką
Ściśle mówiąc, jeśli X P 1 , P 2 ,…, p.n- prawdopodobieństwo wszystkich jego możliwych wartości, a następnie funkcja H (X)![]() w tym przypadku określa entropię tej zmiennej losowej X i nie jest argumentem entropii, możemy napisać H (X)
w tym przypadku określa entropię tej zmiennej losowej X i nie jest argumentem entropii, możemy napisać H (X)![]() .
.
Podobnie, jeśli Y jest skończoną dyskretną zmienną losową, oraz Q 1 , Q 2 ,…, Q m jest prawdopodobieństwem wszystkich możliwych wartości, wówczas dla tej zmiennej losowej możemy napisać H (Y)![]() .
.
 Johna Wildera Tukeya (1915-2000) -
Johna Wildera Tukeya (1915-2000) - Amerykański matematyk. Tukey wybrany
bit wskazujący jedną cyfrę
w binarnym systemie liczbowym
Shannon nazwała tę funkcję H(X)![]() entropia za radą Johna von Neumanna.
entropia za radą Johna von Neumanna.
Neumann był przekonany: tę funkcję należy nazwać entropią „z dwóch powodów. Po pierwsze, Twoja funkcja niepewności była używana w mechanice statystycznej pod tą nazwą, więc ma już nazwę. Po drugie, co ważniejsze, nikt nie wie, czym właściwie jest entropia, więc zawsze będziesz mieć przewagę w debacie”..
Należy założyć, że ta rada Neumanna nie była zwykłym żartem. Najprawdopodobniej zarówno John von Neumann, jak i Claude Shannon wiedzieli o informacyjnej interpretacji entropii Boltzmanna jako wielkości charakteryzującej niekompletność informacji o układzie.
W definicji Shannon entropia- jest to ilość informacji przypadająca na jeden elementarny komunikat ze źródła generującego komunikaty statystycznie niezależne.
7. Entropia Kołmogorowa
 Andriej Nikołajewicz
Andriej Nikołajewicz Kołmogorow (1903-1987) -
Radziecki naukowiec, jeden z największych
matematycy XX wieku
JAKIŚ. Kołmogorow Uzyskano podstawowe wyniki z wielu dziedzin matematyki, w tym z teorii złożoności algorytmów i teorii informacji.
W szczególności odegrał kluczową rolę w przekształceniu teorii informacji, sformułowanej przez Claude'a Shannona jako dyscyplina techniczna, w rygorystyczną naukę matematyczną oraz w budowaniu teorii informacji na zasadniczo odmiennych podstawach niż teoria Shannona.
W swoich pracach nad teorią informacji oraz w dziedzinie teorii układów dynamicznych A.N. Kołmogorow uogólnił koncepcję entropii na procesy losowe ergodyczne poprzez graniczny rozkład prawdopodobieństwa. Aby zrozumieć sens tego uogólnienia, należy poznać podstawowe definicje i pojęcia teorii procesów losowych.
Wartość entropii Kołmogorowa (tzw K-entropia) określa szacunkową szybkość utraty informacji i może być interpretowany jako miara „pamięci” systemu lub miara szybkości „zapominania” warunków początkowych. Można go również uznać za miarę chaosu systemu.
8. Entropia Renyiego
 Alfred Renyi (1921-1970) -
Alfred Renyi (1921-1970) - Węgierski matematyk, twórca
Instytut Matematyczny w Budapeszcie,
teraz noszący jego imię
Wprowadzono jednoparametrowe widmo entropijne Renyi'ego.
Z jednej strony entropia Rényi jest uogólnieniem entropii Shannona. Z drugiej strony stanowi jednocześnie uogólnienie odległości (rozbieżności) Kullbacka-Leiblera. Zauważmy również, że to Rényi był odpowiedzialny za pełny dowód twierdzenia Hartleya o wymaganej ilości informacji.
Odległość Kullbacka-Leiblera(rozbieżność informacji, entropia względna) jest asymetryczną miarą odległości od siebie dwóch rozkładów prawdopodobieństwa.
Zwykle jeden z porównywanych rozkładów jest rozkładem „prawdziwym”, a drugi rozkładem jest rozkładem oszacowanym (testowanym), będącym przybliżeniem pierwszego.
Pozwalać X, Y- są to skończone dyskretne zmienne losowe, dla których zakresy możliwych wartości należą do zadanego zbioru i znane są funkcje prawdopodobieństwa: P (X = ja) = Liczba Pi I P (Y = ja) = qi.
Następnie ze wzorów oblicza się wartość DKL odległości Kullbacka-Leiblera
DKL (X, Y) =, DKL (Y, X) = .
W przypadku absolutnie ciągłych zmiennych losowych X, Y, biorąc pod uwagę ich gęstości rozkładu, we wzorach obliczania wartości odległości Kullbacka-Leiblera sumy zastępuje się odpowiednimi całkami.
Odległość Kullbacka-Leiblera jest zawsze liczbą nieujemną i równa zero DKL(X, Y) = 0 wtedy i tylko wtedy, gdy dla danych zmiennych losowych równość jest prawdziwa prawie wszędzie X = Y.
W 1960 roku Alfred Rényi zaproponował uogólnienie entropii.
Entropia Renyiego reprezentuje rodzinę funkcjonałów ilościowej różnorodności losowości układu. Rényi zdefiniował swoją entropię jako moment rzędu α miary ε-podziału (pokrycia).
Niech α będzie dane prawdziwy numer, spełniający wymagania α ≥ 0, α ≠ 1. Następnie entropię Rényiego rzędu α wyznacza się ze wzoru H α = H α ( X)![]() , Gdzie Liczba Pi = P (X = x ja) to prawdopodobieństwo zdarzenia polegające na tym, że dyskretna zmienna losowa X będzie równa odpowiadającej jej możliwej wartości, N- całkowita liczba różnych możliwych wartości zmiennej losowej X.
, Gdzie Liczba Pi = P (X = x ja) to prawdopodobieństwo zdarzenia polegające na tym, że dyskretna zmienna losowa X będzie równa odpowiadającej jej możliwej wartości, N- całkowita liczba różnych możliwych wartości zmiennej losowej X.
Aby zapewnić równomierną dystrybucję, gdy P 1 = P 2 =…= p.n =1/N, wszystkie entropie Renyi są równe H α ( X) = log N.
W przeciwnym razie wartości entropii Renyi'ego nieznacznie maleją wraz ze wzrostem wartości parametru α. Entropie Rényi odgrywają ważną rolę w ekologii i statystyce jako wskaźniki różnorodności.
Entropia Rényiego jest również ważna w informacji kwantowej i może być stosowana jako miara złożoności.
Rozważmy kilka szczególnych przypadków entropii Rényiego dla określonych wartości rzędu α:
1. Entropia Hartleya : H 0 = H 0 (X) = log N, Gdzie N- potęga obszaru możliwych wartości skończonej zmiennej losowej X, tj. liczba różnych elementów należących do zbioru możliwych wartości;
2. Entropia informacji Shannona : H 1 = H 1 (X) = H 1 (P) (zdefiniowana jako granica α → 1, którą łatwo znaleźć np. korzystając z reguły L'Hopitala);
3. Entropia korelacji Lub zderzenie entropii: H 2 = H 2 (X)= - ln ( X = Y);
4. Min-entropia : H ∞ = H ∞ (X).
Należy zauważyć, że dla dowolnej nieujemnej wartości rzędu (α ≥ 0) nierówności zawsze zachodzą: H ∞ (X) ≤ H α ( X). Oprócz, H 2 (X) ≤ H 1 (X) I H ∞ (X) ≤ H 2 (X) ≤ 2· H ∞ (X).
Alfred Rényi przedstawił nie tylko swoje entropie absolutne (1,15), ale także zdefiniował spektrum miar dywergencji, które uogólniają rozbieżności Kullbacka-Leibnera.
Niech α będzie daną liczbą rzeczywistą spełniającą wymagania α > 0, α ≠ 1. Wtedy w zapisie służącym do określenia wartości DKL odległości Kullbacka-Leiblera, wartość rozbieżności Rényiego rzędu α wyznacza się ze wzorów
D α ( X, Y) , D α ( X, Y)
, D α ( X, Y) .
.
Rozbieżność Renyi jest również nazywana dywergencją Renyi alfa-dywergencja lub α-dywergencja. Sam Rényi używał logarytmu o podstawie 2, ale jak zawsze wartość podstawy logarytmu jest zupełnie nieistotna.
9. Entropia Tsallisa
 Constantino Tsallis (ur. 1943) -
Constantino Tsallis (ur. 1943) - Brazylijski fizyk
Pochodzenie greckie
W 1988 roku zaproponował nowe uogólnienie entropii, które jest wygodne do zastosowania przy rozwijaniu teorii termodynamiki nieliniowej.
Być może zaproponowane przez niego uogólnienie entropii może w najbliższej przyszłości odegrać znaczącą rolę w fizyce teoretycznej i astrofizyce.
Entropia Tsallisa Plac, często nazywana nieekstensywną (nieaddytywną) entropią, jest zdefiniowana dla N mikrostany według następującego wzoru:
Plac = Plac (X) = Plac (P) = K· , ![]() .
.
Tutaj K- stała wymiarowa, jeśli wymiar odgrywa ważną rolę w zrozumieniu problemu.
Tsallis i jego zwolennicy proponują rozwinięcie „nierozszerzonej mechaniki statystycznej i termodynamiki” jako uogólnienia tych klasycznych dyscyplin na przypadek układów z długą pamięcią i/lub siłami dalekiego zasięgu.
Ze wszystkich innych typów entropii, m.in. a od entropii Renyi entropia Tsallisa różni się tym, że nie jest addytywna. To zasadnicza i istotna różnica.
Tsallis i jego zwolennicy uważają, że ta cecha umożliwia zbudowanie nowej termodynamiki i nowej teorii statystycznej, która może w prosty i poprawny sposób opisać układy o długiej pamięci oraz układy, w których każdy element oddziałuje nie tylko ze swoimi bezpośrednimi sąsiadami, ale z całym systemem jako całość lub jej duże części.
Przykład takich układów, a co za tym idzie możliwy przedmiot badań wykorzystujących nowa teoria, to kosmiczne układy grawitacyjne: gromady gwiazd, mgławice, galaktyki, gromady galaktyk itp.
Od 1988 roku, kiedy Constantino Tsallis zaproponował swoją entropię, pojawiło się wiele zastosowań termodynamiki układów anomalnych (z pamięcią długości i/lub siłami dalekiego zasięgu), m.in. w dziedzinie termodynamiki układów grawitacyjnych.
10. Entropia kwantowa von Neumanna
 Jan (Janos) von Neumann (1903-1957) -
Jan (Janos) von Neumann (1903-1957) - Amerykański matematyk i fizyk
pochodzenia węgierskiego
Entropia von Neumanna odgrywa ważną rolę w: Fizyka kwantowa oraz w badaniach astrofizycznych.
Johna von Neumanna wniósł znaczący wkład w rozwój takich dziedzin nauki jak fizyka kwantowa, logika kwantowa, analiza funkcjonalna, teoria mnogości, informatyka i ekonomia.
Był członkiem Projektu Manhattan na rzecz rozwoju bronie nuklearne, jeden z twórców matematycznej teorii gier i koncepcji automatów komórkowych, a także twórca nowoczesnej architektury komputerowej.
Entropia von Neumanna, jak każda entropia, jest powiązana z informacją: w tym przypadku z informacją o układ kwantowy. I pod tym względem pełni rolę podstawowego parametru, który ilościowo charakteryzuje stan i kierunek ewolucji układu kwantowego.
Obecnie entropia von Neumanna jest szeroko stosowana w różne formy(entropia warunkowa, entropia względna itp.) w obrębie teoria kwantowa Informacja.
Różne miary splątania są bezpośrednio powiązane z entropią von Neumanna. Jednakże ostatnio pojawiło się wiele prac poświęconych krytyce entropii Shannona jako miary informacji i jej możliwej niedokładności, a w konsekwencji nieadekwatności entropii von Neumanna jako uogólnienia entropii Shannona.
Przegląd (niestety pobieżny i czasami niewystarczająco rygorystyczny matematycznie) ewolucji poglądy naukowe na pojęciu entropii pozwala udzielić odpowiedzi na ważne pytania związane z prawdziwą istotą entropii i perspektywami wykorzystania podejścia entropijnego w badaniach naukowych i praktycznych. Ograniczmy się do rozważenia odpowiedzi na dwa takie pytania.
Pierwsze pytanie: Czy liczne typy entropii, zarówno omówione, jak i nie omówione powyżej, mają ze sobą coś wspólnego poza tą samą nazwą?
To pytanie pojawia się naturalnie, jeśli weźmiemy pod uwagę różnorodność charakteryzującą różne istniejące koncepcje entropii.
Dziś społeczność naukowa nie opracowała jednej, powszechnie akceptowanej odpowiedzi na to pytanie: niektórzy naukowcy odpowiadają na to pytanie twierdząco, inni - negatywnie, a jeszcze inni traktują wspólność entropii różnych typów z zauważalnym stopniem wątpliwości. .
Clausius najwyraźniej był pierwszym naukowcem przekonanym o uniwersalnym charakterze entropii i uważał, że we wszystkich procesach zachodzących we Wszechświecie odgrywa ona ważną rolę, w szczególności wyznaczając kierunek ich rozwoju w czasie.
Nawiasem mówiąc, to Rudolf Clausius wymyślił jedno z sformułowań drugiej zasady termodynamiki: „Niemożliwy jest proces, którego jedynym skutkiem byłoby przeniesienie ciepła z ciała zimniejszego do cieplejszego”.
To sformułowanie drugiej zasady termodynamiki nazywa się Postulat Clausiusa , a nieodwracalnym procesem omawianym w tym postulatie jest Proces Clausiusa .
Od czasu odkrycia drugiej zasady termodynamiki procesy nieodwracalne odgrywają wyjątkową rolę w fizycznym obrazie świata. Tak więc słynny artykuł z 1849 r Williama Thompsona, który zawierał jedno z pierwszych sformułowań drugiej zasady termodynamiki, nosił tytuł „O powszechnej tendencji w przyrodzie do rozpraszania energii mechanicznej”.
Należy również zauważyć, że Clausius był zmuszony użyć języka kosmologicznego: „Entropia Wszechświata dąży do maksimum”.
 Ilja Romanowicz Prigogine (1917-2003) -
Ilja Romanowicz Prigogine (1917-2003) - Belgijsko-amerykański fizyk i
chemik pochodzenia rosyjskiego,
laureat nagroda Nobla
z chemii 1977
Doszedłem do podobnych wniosków Ilja Prigożin. Prigogine uważa, że zasada entropii odpowiada za nieodwracalność czasu we Wszechświecie i być może odgrywa ważną rolę w zrozumieniu znaczenia czasu jako zjawiska fizycznego.
Do chwili obecnej przeprowadzono wiele badań i uogólnień entropii, w tym z punktu widzenia ścisłej teorii matematycznej. Jednak zauważalna aktywność matematyków w tym obszarze nie jest jeszcze pożądana w zastosowaniach, z możliwym wyjątkiem dzieł Kołmogorow, Renyi I Tsallis.
Niewątpliwie entropia jest zawsze miarą (stopniem) chaosu, nieporządku. To właśnie różnorodność przejawów zjawiska chaosu i nieporządku decyduje o nieuchronności różnorodności modyfikacji entropii.
Drugie Pytanie: Czy zakres stosowania podejścia entropijnego można uznać za szeroki, czy też wszystkie zastosowania entropii i drugiej zasady termodynamiki ograniczają się do samej termodynamiki i pokrewnych dziedzin nauk fizycznych?
Fabuła badania naukowe entropia oznacza, że entropia jest zjawiskiem naukowym odkrytym w termodynamice, a następnie z powodzeniem przeniesionym do innych nauk, a przede wszystkim do teorii informacji.
Niewątpliwie entropia odgrywa ważną rolę w prawie wszystkich obszarach nowoczesne nauki przyrodnicze: w termofizyce, fizyce statystycznej, kinetyce fizycznej i chemicznej, biofizyce, astrofizyce, kosmologii i teorii informacji.
Mówiąc o matematyce stosowanej, nie sposób nie wspomnieć o zastosowaniach zasady maksymalnej entropii.
Jak już wspomniano, ważnymi obszarami zastosowań entropii są obiekty mechaniki kwantowej i relatywistyczne. W fizyce kwantowej i astrofizyce takie zastosowania entropii cieszą się dużym zainteresowaniem.
Wspomnijmy tylko o jednym oryginalnym wyniku termodynamiki czarnych dziur: entropia czarna dziura równy jednej czwartej jego powierzchni (obszar horyzontu zdarzeń).
W kosmologii uważa się, że entropia Wszechświata jest równa liczbie reliktowych kwantów promieniowania na nukleon.
Zatem zakres stosowania podejścia entropijnego jest bardzo szeroki i obejmuje bardzo różnorodne gałęzie wiedzy, począwszy od termodynamiki, przez inne dziedziny nauk fizycznych, informatykę, a skończywszy na przykład na historii i ekonomii.
AV Seagala, lekarz nauki ekonomiczne, Uniwersytet Krymski imienia V.I. Wernadski
Informacja i entropia
Omawiając pojęcie informacji, nie sposób nie poruszyć innego, pokrewnego mu pojęcia – entropii. Pojęcia entropii i informacji po raz pierwszy połączył K. Shannon.
| Claude Elwood Shannon ( Claude'a Elwooda Shannona), 1916-2001 - daleki krewny Thomasa Edisona, amerykańskiego inżyniera i matematyka, był pracownikiem Bell Laboratories od 1941 do 1972. W swojej pracy „Mathematical Theory of Communications” (http://cm.bell-labs.com /cm/ms /what/shannonday/), opublikowana w 1948 roku, jako pierwsza zdefiniowała miarę zawartości informacyjnej każdego przekazu oraz pojęcie kwantu informacji – bit. Idee te stworzyły podstawę teorii współczesnej komunikacji cyfrowej. Inna praca Shannona, Communication Theory of Secrecy Systems, opublikowana w 1949 r., przyczyniła się do rozwoju kryptografii w dyscyplina naukowa. On jest założycielem teoria informacji, który znalazł zastosowanie w nowoczesnych, zaawansowanych technologicznie systemach komunikacyjnych. Shannon wniósł ogromny wkład w teorię obwodów probabilistycznych, teorię automatów i teorię systemów sterowania - nauk, które łączy koncepcja „cybernetyki”. |
Fizyczna definicja entropii
Pojęcie entropii zostało po raz pierwszy wprowadzone przez Clausiusa w 1865 roku jako funkcja stanu termodynamicznego układu
gdzie Q to ciepło, T to temperatura.
Fizyczne znaczenie entropii objawia się jako część energii wewnętrznej układu, której nie można przekształcić w pracę. Clausius uzyskał tę funkcję empirycznie, eksperymentując z gazami.
L. Boltzmann (1872), korzystając z metod fizyki statystycznej, wyprowadził teoretyczne wyrażenie na entropię
gdzie K jest stałą; W – prawdopodobieństwo termodynamiczne (liczba przegrupowań cząsteczek gazu doskonałego, która nie wpływa na makrostan układu).
Entropię Boltzmanna wyprowadzono dla gazu doskonałego i interpretowano ją jako miarę nieporządku, miarę chaosu układu. W przypadku gazu doskonałego entropie Boltzmanna i Clausiusa są identyczne. Formuła Boltzmanna stała się tak sławna, że została wpisana jako epitafium na jego grobie. Istnieje opinia, że entropia i chaos to jedno i to samo. Pomimo tego, że entropia opisuje jedynie gazy doskonałe, bezkrytycznie zaczęto ją stosować do opisu bardziej złożonych obiektów.
Sam Boltzmann w 1886 r próbował użyć entropii, aby wyjaśnić, czym jest życie. Według Boltzmanna życie jest zjawiskiem zdolnym do zmniejszania swojej entropii. Według Boltzmanna i jego zwolenników wszystkie procesy we Wszechświecie zmieniają się w kierunku chaosu. Wszechświat zmierza w stronę śmierci cieplnej. Ta ponura prognoza zdominowała naukę na długi czas. Jednak pogłębianie wiedzy o otaczającym świecie stopniowo podważało ten dogmat.
Klasycy nie łączyli entropii z informacją.
Entropia jako miara informacji
Należy pamiętać, że pojęcie „informacji” jest często interpretowane jako „informacja”, a przekazywanie informacji odbywa się za pomocą komunikacji. K. Shannon uważał entropię za miarę przydatna informacja w procesach przesyłania sygnałów przewodami.
Aby obliczyć entropię, Shannon zaproponował równanie przypominające klasyczne wyrażenie na entropię znalezione przez Boltzmanna. Rozważane jest niezależne zdarzenie losowe X przy N możliwych stanach i p i -prawdopodobieństwo i-tego stanu. Następnie entropia zdarzenia X

Wielkość ta nazywana jest również średnią entropią. Na przykład możemy mówić o przekazywaniu wiadomości w języku naturalnym. Przesyłając różne litery, przekazujemy różne ilości Informacja. Ilość informacji przypadająca na literę jest powiązana z częstotliwością używania tej litery we wszystkich wiadomościach tworzonych w danym języku. Im rzadszy list przekazujemy, tym więcej zawiera informacji.
Ogrom
H ja = P ja log 2 1/P ja = -P i log 2 P ja ,
nazywa się entropią częściową, charakteryzującą jedynie stan i-e.
 Wyjaśnijmy na przykładach. Podczas rzucania monetą pojawiają się orły lub reszki, jest to pewna informacja o wyniku rzutu.
Wyjaśnijmy na przykładach. Podczas rzucania monetą pojawiają się orły lub reszki, jest to pewna informacja o wyniku rzutu.
W przypadku monety liczba równie prawdopodobnych możliwości wynosi N = 2. Prawdopodobieństwo wypadnięcia orła (reszki) wynosi 1/2.
Rzucając kostką otrzymujemy informację o określonej liczbie punktów (np. trzy). W którym przypadku otrzymamy więcej informacji?
W przypadku kości liczba równie prawdopodobnych możliwości wynosi N = 6. Prawdopodobieństwo zdobycia trzech punktów wynosi 1/6. Entropia wynosi 2,58. Uświadomienie sobie mniej prawdopodobnego zdarzenia dostarcza więcej informacji. Im większa niepewność przed otrzymaniem komunikatu o zdarzeniu (rzut monetą, kostką), tym większa ilość informacji otrzymanych po odebraniu komunikatu.
Takie podejście do ilościowego wyrażania informacji jest dalekie od uniwersalnego, ponieważ przyjęte jednostki nie uwzględniają tak ważnych właściwości informacji, jak jej wartość i znaczenie. Abstrakcja od specyficznych właściwości informacji (jej znaczenia, wartości) o realnych obiektach, jak się później okazało, umożliwiła identyfikację ogólnych wzorców informacji. Jednostki (bity) zaproponowane przez Shannona do pomiaru ilości informacji nadają się do oceny wszelkich komunikatów (narodziny syna, wynik meczu sportowego itp.). W dalszej kolejności próbowano znaleźć miary ilości informacji, które uwzględniałyby jej wartość i znaczenie. Jednakże uniwersalność została natychmiast utracona: różne procesy mają różne kryteria wartości i znaczenia. Ponadto definicje znaczenia i wartości informacji są subiektywne, a miara informacji zaproponowana przez Shannona jest obiektywna. Na przykład zapach niesie dla zwierzęcia ogromną ilość informacji, ale jest nieuchwytny dla człowieka. Ucho ludzkie nie odbiera sygnałów ultradźwiękowych, ale jak na delfina niosą one wiele informacji itp. Dlatego zaproponowana przez Shannona miara informacji nadaje się do badania wszelkiego rodzaju procesów informacyjnych, niezależnie od „smaków” informacji konsument.
Informacje pomiarowe
Z kursu fizyki wiesz to przed zmierzeniem wartości jakiejkolwiek wielkość fizyczna, należy wprowadzić jednostkę miary. Informacja również ma taką jednostkę - trochę, ale jej znaczenie jest inne w zależności od różnych podejść do definiowania pojęcia „informacja”.
Istnieje kilka różnych podejść do problemu pomiaru informacji.
Entropia (teoria informacji)
Entropia (informacyjna)- miara chaosu informacyjnego, niepewności pojawienia się dowolnego symbolu alfabetu pierwotnego. W przypadku braku strat informacyjnych jest ona liczbowo równa ilości informacji przypadającej na symbol przesyłanej wiadomości.
Na przykład w ciągu liter tworzących zdanie w języku rosyjskim różne litery pojawiają się z różną częstotliwością, więc niepewność wystąpienia niektórych liter jest mniejsza niż innych. Jeśli weźmiemy pod uwagę, że niektóre kombinacje liter (w tym przypadku mówimy o entropii N-tego rzędu, patrz) są bardzo rzadkie, wówczas niepewność jest jeszcze bardziej zmniejszona.
Aby zilustrować pojęcie entropii informacyjnej, można także odwołać się do przykładu z dziedziny entropii termodynamicznej, zwanego demonem Maxwella. Pojęcia informacji i entropii są ze sobą głęboko powiązane, mimo to rozwój teorii mechaniki statystycznej i teorii informacji zajął wiele lat, zanim stały się ze sobą spójne.
Definicje formalne
| Ustalenie na podstawie własnych informacji |
|
Można również określić entropię zmiennej losowej, wprowadzając najpierw koncepcję rozkładu zmiennej losowej X mający ostateczny numer wartości: I(X) = - log P X (X).Następnie entropię zdefiniujemy jako: Jednostka miary informacji i entropii zależy od podstawy logarytmu: bit, nat lub hartley. |
Entropia informacyjna dla niezależnych zdarzeń losowych X Z N możliwe stany (od 1 do N) oblicza się ze wzoru:

Ilość ta jest również nazywana średnia entropia wiadomości. Ilość nazywa się entropia prywatna, tylko charakteryzujący I-nieruchomość.
Zatem entropia zdarzenia X jest sumą o przeciwnym znaku wszystkich iloczynów względnych częstotliwości występowania zdarzenia I, pomnożone przez ich własne logarytmy binarne (podstawę 2 wybrano jedynie dla wygody pracy z informacjami przedstawionymi w postaci binarnej). Tę definicję dyskretnych zdarzeń losowych można rozszerzyć do funkcji rozkładu prawdopodobieństwa.
Ogólnie B-ary entropia(Gdzie B równa się 2, 3, ...) źródło z oryginalnym alfabetem i dyskretnym rozkładem prawdopodobieństwa gdzie P I jest prawdopodobieństwo A I (P I = P(A I) ) wyznacza się ze wzoru:

Definicja entropii Shannona jest powiązana z pojęciem entropii termodynamicznej. Boltzmann i Gibbs włożyli wiele pracy w termodynamikę statystyczną, co przyczyniło się do przyjęcia słowa „entropia” w teorii informacji. Istnieje związek pomiędzy entropią termodynamiczną i informacyjną. Na przykład demon Maxwella również kontrastuje entropię termodynamiczną z informacją, a zdobycie dowolnej ilości informacji równa się utracie entropii.
Alternatywna definicja
Innym sposobem zdefiniowania funkcji entropii jest H jest tego dowodem H jest jednoznacznie określona (jak stwierdzono wcześniej) wtedy i tylko wtedy, gdy H spełnia warunki:
Nieruchomości
Należy pamiętać, że entropia to wielkość zdefiniowana w kontekście probabilistycznego modelu źródła danych. Na przykład rzut monetą ma entropię - 2(0,5log 2 0,5) = 1 bit na rzut (zakładając, że jest niezależny). Źródło generujące ciąg składający się wyłącznie z liter „A” ma zerową entropię: ![]() . Można więc na przykład ustalić eksperymentalnie tę entropię angielski tekst wynosi 1,5 bita na znak, co oczywiście będzie się różnić dla różnych tekstów. Stopień entropii źródła danych oznacza średnią liczbę bitów na element danych wymaganych do jego zaszyfrowania bez utraty informacji, przy optymalnym kodowaniu.
. Można więc na przykład ustalić eksperymentalnie tę entropię angielski tekst wynosi 1,5 bita na znak, co oczywiście będzie się różnić dla różnych tekstów. Stopień entropii źródła danych oznacza średnią liczbę bitów na element danych wymaganych do jego zaszyfrowania bez utraty informacji, przy optymalnym kodowaniu.
- Niektóre bity danych mogą nie przenosić informacji. Na przykład struktury danych często przechowują nadmiarowe informacje lub mają identyczne sekcje niezależnie od informacji zawartych w strukturze danych.
- Wielkość entropii nie zawsze jest wyrażana jako całkowita liczba bitów.
Właściwości matematyczne
Efektywność
Oryginalny alfabet spotykany w praktyce ma rozkład prawdopodobieństwa odległy od optymalnego. Gdyby oryginalny alfabet miał N znaków, wówczas można go porównać do „zoptymalizowanego alfabetu”, którego rozkład prawdopodobieństwa jest równomierny. Stosunek entropii alfabetu oryginalnego i zoptymalizowanego to wydajność alfabetu oryginalnego, którą można wyrazić procentowo.
Wynika z tego, że skuteczność oryginalnego alfabetu z N symbole można po prostu zdefiniować jako równe N-ary entropia.
Entropia ogranicza maksymalną możliwą bezstratną (lub prawie bezstratną) kompresję, którą można zrealizować przy użyciu teoretycznie typowego kodowania zbiorowego lub w praktyce kodowania Huffmana, kodowania Lempela – Ziv – Welcha lub kodowania arytmetycznego.
Odmiany i uogólnienia
Entropia warunkowa
Jeśli sekwencja znaków alfabetu nie jest niezależna (na przykład w Francuski po literze „q” prawie zawsze następuje „u”, a po słowie „redakcja” w gazetach radzieckich zwykle następowało słowo „produkcja” lub „praca”), ilość informacji niesiona przez sekwencję takich symboli (a zatem entropia) jest oczywiście mniejsza. Aby uwzględnić takie fakty, stosuje się entropię warunkową.
Entropia warunkowa pierwszego rzędu (podobna do modelu Markowa pierwszego rzędu) to entropia alfabetu, w którym znane jest prawdopodobieństwo wystąpienia jednej litery po drugiej (tj. prawdopodobieństwa kombinacji dwuliterowych):
Gdzie I jest stanem zależnym od poprzedzającego znaku, oraz P I (J) - takie jest prawdopodobieństwo J, pod warunkiem że I był poprzednią postacią.
Tak więc dla języka rosyjskiego bez litery „”.
Straty informacji podczas transmisji danych w zaszumionym kanale są w pełni opisane za pomocą częściowych i ogólnych entropii warunkowych. W tym celu tzw macierze kanałów. Tak więc, aby opisać straty po stronie źródła (to znaczy wysłany sygnał jest znany), uwzględnia się warunkowe prawdopodobieństwo otrzymania symbolu przez odbiornik B J pod warunkiem, że znak został wysłany A I. W tym przypadku macierz kanału ma następującą postać:
| B 1 | B 2 | … | B J | … | B M | |
|---|---|---|---|---|---|---|
| A 1 | … | … | ||||
| A 2 | … | … | ||||
| … | … | … | … | … | … | … |
| A I | … | … | ||||
| … | … | … | … | … | … | … |
| A M | … | … |
Oczywiście prawdopodobieństwa umieszczone wzdłuż przekątnej opisują prawdopodobieństwo poprawnego odbioru, a suma wszystkich elementów kolumny da prawdopodobieństwo pojawienia się odpowiedniego symbolu po stronie odbiorcy - P(B J) . Straty na przesyłany sygnał A I, są opisane poprzez częściową entropię warunkową:
Aby obliczyć straty przesyłowe wszystkich sygnałów, stosuje się ogólną entropię warunkową:
Oznacza to entropię po stronie źródła; entropię po stronie odbiornika rozważa się w podobny sposób: zamiast wszędzie jest ona wskazana (sumując elementy linii można otrzymać P(A I) , a elementy ukośne oznaczają prawdopodobieństwo, że wysłany został dokładnie taki znak, jaki został odebrany, czyli prawdopodobieństwo poprawnej transmisji).
Wzajemna entropia
Wzajemna entropia, czyli entropia unijna, służy do obliczania entropii wzajemnie połączonych systemów (entropii wspólnego występowania komunikatów statystycznie zależnych) i jest oznaczany H(AB) , Gdzie A, jak zawsze, charakteryzuje nadajnik i B- odbiorca.
Zależność pomiędzy sygnałami nadawanymi i odbieranymi opisuje prawdopodobieństwa wspólnych zdarzeń P(A I B J) , i dla pełny opis charakterystyki kanału, wymagana jest tylko jedna matryca:
| P(A 1 B 1) | P(A 1 B 2) | … | P(A 1 B J) | … | P(A 1 B M) |
| P(A 2 B 1) | P(A 2 B 2) | … | P(A 2 B J) | … | P(A 2 B M) |
| … | … | … | … | … | … |
| P(A I B 1) | P(A I B 2) | … | P(A I B J) | … | P(A I B M) |
| … | … | … | … | … | … |
| P(A M B 1) | P(A M B 2) | … | P(A M B J) | … | P(A M B M) |
W bardziej ogólnym przypadku, gdy nie jest opisywany kanał, ale po prostu systemy oddziałujące na siebie, macierz nie musi być kwadratowa. Oczywiście suma wszystkich elementów kolumny z numerem J da P(B J) , suma numeru linii I Jest P(A I) , a suma wszystkich elementów macierzy jest równa 1. Prawdopodobieństwo łączne P(A I B J) wydarzenia A I I B J oblicza się jako iloczyn prawdopodobieństwa pierwotnego i warunkowego,
Prawdopodobieństwa warunkowe oblicza się za pomocą wzoru Bayesa. Zatem istnieją wszystkie dane do obliczenia entropii źródła i odbiornika:

Wzajemną entropię oblicza się, sumując po wierszach (lub kolumnach) wszystkie prawdopodobieństwa macierzy, pomnożone przez ich logarytm:
| H(AB) = − | ∑ | ∑ | P(A I B J)dziennik P(A I B J). |
| I | J |
Jednostką miary jest bit/dwa symbole, co tłumaczy się faktem, że wzajemna entropia opisuje niepewność na parę symboli - wysłanych i odebranych. Przez proste przekształcenia również otrzymujemy
Wzajemna entropia ma tę właściwość kompletność informacji- z niego można uzyskać wszystkie rozważane ilości.
Fabuła
Notatki
Zobacz też
Spinki do mankietów
- Claude’a E. Shannona. Matematyczna teoria komunikacji
- S. M. Korotaev.
„Informacja jest formą życia” – napisał Amerykański poeta i eseista John Perry Barlow. Rzeczywiście stale spotykamy się ze słowem „informacja” - jest ona odbierana, przesyłana i przechowywana. Dowiedz się o prognozę pogody, wynik meczu piłkarskiego, treść filmu czy książki, porozmawiaj przez telefon – zawsze wiadomo, z jakim rodzajem informacji mamy do czynienia. Jednak zazwyczaj nikt nie myśli o tym, czym jest sama informacja i, co najważniejsze, w jaki sposób można ją zmierzyć. Tymczasem informacja i sposoby jej przekazywania są ważną rzeczą, która w dużej mierze determinuje nasze życie, którego staliśmy się integralną częścią. technologia informacyjna. Redaktor naukowy publikacji Laba.Media Władimir Gubajłowski wyjaśnia, czym jest informacja, jak ją mierzyć i dlaczego najtrudniej jest przekazać informację bez zniekształceń.
Przestrzeń zdarzeń losowych
W 1946 roku amerykański statystyk John Tukey zaproponował nazwę BIT (BINary digiT - „liczba binarna” - „High-Tech”) - jedna z głównych koncepcji XX wieku. Tukey wybrał bit do oznaczenia jednej cyfry binarnej, która może przyjmować wartość 0 lub 1. Claude Shannon w swoim przełomowym artykule „Matematyczna teoria komunikacji” zaproponował mierzenie ilości informacji w bitach. Ale nie jest to jedyna koncepcja przedstawiona i zbadana przez Shannona w jego artykule.
Wyobraźmy sobie przestrzeń zdarzeń losowych polegającą na rzuceniu jednej fałszywej monety z orłami po obu stronach. Kiedy to przychodzi do głowy? Jasne, zawsze. Wiemy to z góry, bo tak jest skonstruowana nasza przestrzeń. Lądowanie orłów jest pewnym zdarzeniem, czyli jego prawdopodobieństwo wynosi 1. Ile informacji przekażemy, jeśli będziemy mówić o spadających głowach? NIE. Ilość informacji w takiej wiadomości uznamy za 0.
Rzućmy teraz właściwą monetą: zgodnie z oczekiwaniami ma orzeł po jednej stronie i reszkę po drugiej. Lądujące orły lub reszki będą dwoma różnymi zdarzeniami, które tworzą naszą przestrzeń zdarzeń losowych. Jeśli zgłosimy wynik jednego rzutu, to rzeczywiście tak będzie Nowa informacja. Jeśli wypadnie orzeł, zgłosimy 0, a jeśli reszka wyniesie 1. Aby zgłosić tę informację, potrzebujemy tylko 1 bitu.
Co się zmieniło? W naszej przestrzeni eventowej pojawiła się niepewność. Mamy co o tym powiedzieć komuś, kto sam nie rzuca monetą i nie widzi wyniku rzutu. Aby jednak właściwie zrozumieć nasz przekaz, musi dokładnie wiedzieć, co robimy, co oznaczają 0 i 1. Nasze przestrzenie zdarzeń muszą się zgadzać, a proces dekodowania musi jednoznacznie odtworzyć wynik rzutu. Jeżeli przestrzeń zdarzeń nadajnika i odbiornika nie pokrywa się lub nie ma możliwości jednoznacznego odkodowania komunikatu, informacja pozostanie jedynie szumem w kanale komunikacyjnym.
Jeśli rzucimy dwie monety niezależnie i jednocześnie, otrzymamy cztery różne, równie prawdopodobne wyniki: reszka-reszka, reszka-reszka, reszka-reszka i reszka-reszka. Do przesłania informacji potrzebne będą nam 2 bity, a nasze komunikaty będą następujące: 00, 01, 10 i 11. Informacji jest dwa razy więcej. Stało się tak, ponieważ wzrosła niepewność. Jeśli spróbujemy odgadnąć wynik takiego rzutu parami, mamy dwukrotnie większe ryzyko, że się mylimy.
Im większa niepewność przestrzeni zdarzeń, tym więcej informacji o jej stanie zawiera komunikat.
Skomplikujmy trochę naszą przestrzeń eventową. Jak dotąd wszystkie zdarzenia, które miały miejsce, były równie prawdopodobne. Ale w przestrzeniach rzeczywistych nie wszystkie zdarzenia mają równe prawdopodobieństwo. Załóżmy, że prawdopodobieństwo, że wrona, którą zobaczymy, będzie czarna, jest bliskie 1. Prawdopodobieństwo, że pierwszym przechodniem, którego spotkamy na ulicy, będzie mężczyzną, wynosi około 0,5. Ale spotkanie krokodyla na ulicach Moskwy jest prawie niemożliwe. Intuicyjnie rozumiemy, że relacja o spotkaniu z krokodylem ma znacznie większą wartość informacyjną niż o czarnej wronie. Im mniejsze prawdopodobieństwo wystąpienia zdarzenia, tym więcej informacji o takim zdarzeniu zawiera wiadomość.
Niech przestrzeń eventowa nie będzie aż tak egzotyczna. Po prostu stoimy przy oknie i patrzymy na przejeżdżające samochody. Musimy zgłosić, że obok przejeżdżają samochody w czterech różnych kolorach. W tym celu kodujemy kolory: czarny – 00, biały – 01, czerwony – 10, niebieski – 11. Aby zgłosić, który samochód przejechał, wystarczy przesłać 2 bity informacji.
Jednak obserwując samochody od dłuższego czasu, zauważamy, że kolor samochodów rozkłada się nierównomiernie: czarny – 50% (co sekundę), biały – 25% (co czwarta), czerwony i niebieski – po 12,5% (co każdą ósma). Następnie możesz zoptymalizować przesyłane informacje.
Większość samochodów jest czarna, więc oznaczmy czarny - 0 - najkrótszy kod, a kod całej reszty niech zacznie się od 1. Z pozostałej połowy biały - 10, a pozostałe kolory zaczynają się od 11. Podsumowując, oznaczmy czerwony - 110, a niebieski - 111.
Teraz, przesyłając informację o kolorze samochodów, możemy ją gęstiej zakodować.
Entropia Shannona
Niech nasza przestrzeń eventowa będzie składać się z n różnych wydarzeń. Przy rzucie monetą dwiema reszkami występuje dokładnie jedno takie zdarzenie, przy rzucie jedną prawidłową monetą – 2, przy rzucie dwiema monetami lub oglądaniu samochodów – 4. Każde zdarzenie ma odpowiednie prawdopodobieństwo wystąpienia. Przy rzucie monetą z dwiema reszkami mamy do czynienia z jednym zdarzeniem (wypadnięciem reszki) i jego prawdopodobieństwo wynosi p1 = 1. Przy rzucie uczciwą monetą mamy do czynienia z dwoma zdarzeniami, są one jednakowo prawdopodobne i prawdopodobieństwo każdego z nich wynosi 0,5: p1 = 0,5, p2 = 0,5. Przy rzucie dwiema uczciwymi monetami zachodzą cztery zdarzenia, wszystkie są jednakowo prawdopodobne, a prawdopodobieństwo każdego z nich wynosi 0,25: p1 = 0,25, p2 = 0,25, p3 = 0,25, p4 = 0,25. Obserwując samochody, mamy do czynienia z czterema zdarzeniami i mają one różne prawdopodobieństwa: czarne – 0,5, białe – 0,25, czerwone – 0,125, niebieskie – 0,125: p1 = 0,5, p2 = 0,25, p3 = 0,125, p4 = 0,125.

To nie jest przypadek. Shannon wybrał entropię (miarę niepewności w przestrzeni zdarzeń) tak, aby spełnione były trzy warunki:
- 1Entropia wiarygodne wydarzenie, którego prawdopodobieństwo wynosi 1, jest równe 0.
- Entropia dwóch niezależnych zdarzeń jest równa sumie entropii tych zdarzeń.
- Entropia jest maksymalna, jeśli wszystkie zdarzenia są jednakowo prawdopodobne.
Wszystkie te wymagania są w pełni zgodne z naszymi wyobrażeniami o niepewności przestrzeni eventowej. Jeśli istnieje tylko jedno zdarzenie (pierwszy przykład), nie ma niepewności. Jeżeli zdarzenia są niezależne – niepewność sumy jest równa sumie niepewności – po prostu się sumują (przykład rzutu dwiema monetami). I wreszcie, jeśli wszystkie zdarzenia są jednakowo prawdopodobne, wówczas stopień niepewności układu jest maksymalny. Podobnie jak w przypadku rzutu dwiema monetami, wszystkie cztery zdarzenia są jednakowo prawdopodobne, a entropia wynosi 2, jest większa niż w przypadku samochodów, gdzie również występują cztery zdarzenia, ale mają one inne prawdopodobieństwa - w tym przypadku entropia wynosi 1,75.
Wielkość H odgrywa kluczową rolę w teorii informacji jako miara informacji, wyboru i niepewności.

Claude'a Shannona
Claude'a Elwooda Shannona- Amerykański inżynier, kryptoanalityk i matematyk. Uważany za „ojca” wiek informacji" Twórca teorii informacji, która znalazła zastosowanie w nowoczesnych, zaawansowanych technologicznie systemach komunikacyjnych. Podane zostały podstawowe pojęcia, idee i ich matematyczne sformułowania, które obecnie stanowią podstawę nowoczesnych technologii komunikacyjnych.
W 1948 roku zaproponował użycie słowa „bit” do określenia najmniejszej jednostki informacji. Wykazał także, że wprowadzona przez niego entropia jest równoznaczna z miarą niepewności informacji zawartej w przesyłanym komunikacie. Artykuły Shannona „Matematyczna teoria komunikacji” i „Teoria komunikacji w tajne systemy„są uważane za fundamentalne dla teorii informacji i kryptografii.
Podczas II wojny światowej Shannon pracował w Bell Laboratories nad opracowaniem systemów kryptograficznych, które później pomogły mu odkryć metody kodowania korygujące błędy.
Shannon wniósł kluczowy wkład do teorii obwodów probabilistycznych, teorii gier, teorii automatów i teorii systemów sterowania – dziedzin nauki objętych pojęciem „cybernetyki”.
Kodowanie
Zarówno rzucanie monetami, jak i przejeżdżające samochody nie przypominają cyfr 0 i 1. Aby przekazać informacje o zdarzeniach zachodzących w przestrzeniach, trzeba wymyślić sposób na ich opisanie. Ten opis nazywa się kodowaniem.
Wiadomości można kodować na nieskończoną liczbę różnych sposobów. Shannon pokazał jednak, że najkrótszy kod nie może być mniejszy w bitach niż entropia.
Dlatego entropia wiadomości jest miarą informacji zawartej w wiadomości. Ponieważ we wszystkich rozpatrywanych przypadkach liczba bitów podczas kodowania jest równa entropii, oznacza to, że kodowanie było optymalne. Krótko mówiąc, nie ma już możliwości kodowania komunikatów o wydarzeniach w naszych przestrzeniach.
Dzięki optymalnemu kodowaniu żaden przesyłany bit w wiadomości nie może zostać utracony ani zniekształcony. Jeśli utracony zostanie choć jeden bit, informacja zostanie zniekształcona. Jednak nie wszystkie rzeczywiste kanały komunikacji dają 100-procentową pewność, że wszystkie fragmenty przekazu dotrą do odbiorcy w niezniekształconej formie.
Aby wyeliminować ten problem, konieczne jest, aby kod nie był optymalny, ale redundantny. Przykładowo, prześlij wraz z wiadomością jej sumę kontrolną – specjalnie obliczoną wartość uzyskaną podczas konwersji kodu wiadomości, którą można sprawdzić przeliczając w momencie otrzymania wiadomości. Jeśli przesłana suma kontrolna będzie zgodna z obliczoną, prawdopodobieństwo, że transmisja przebiegła bez błędów, będzie dość duże. A jeśli suma kontrolna nie jest zgodna, należy poprosić o retransmisję. Tak mniej więcej działa obecnie większość kanałów komunikacyjnych, na przykład podczas przesyłania pakietów informacji przez Internet.
Wiadomości w języku naturalnym
Rozważmy przestrzeń zdarzeń składającą się z komunikatów w języku naturalnym. To przypadek szczególny, ale jeden z najważniejszych. Do zdarzeń tutaj przesyłane będą znaki (litery ustalonego alfabetu). Symbole te występują w języku z różnym prawdopodobieństwem.
Najbardziej powszechnym znakiem (czyli tym, który występuje najczęściej we wszystkich tekstach pisanych w języku rosyjskim) jest spacja: na tysiąc znaków spacja występuje średnio 175 razy. Drugim najpopularniejszym symbolem jest „o” - 90, po którym następują inne samogłoski: „e” (lub „e” - nie będziemy ich rozróżniać) - 72, „a” - 62, „i” - 62 i tylko dalej pojawia się pierwsza spółgłoska „t” to 53. A najrzadsze „f” - ten symbol występuje tylko dwa razy na tysiąc znaków.
Będziemy posługiwać się 31-literowym alfabetem języka rosyjskiego (nie rozróżnia on „e” i „ё”, ani „ъ” i „ь”). Gdyby wszystkie litery występowały w języku z takim samym prawdopodobieństwem, to entropia na znak wyniosłaby H = 5 bitów, ale jeśli weźmiemy pod uwagę rzeczywiste częstotliwości występowania symboli, to entropia będzie mniejsza: H = 4,35 bitów. (To prawie dwa razy mniej niż w przypadku tradycyjnego kodowania, gdy znak przesyłany jest w postaci bajtu - 8 bitów).
Ale entropia symbolu w języku jest jeszcze niższa. Prawdopodobieństwo pojawienia się kolejnego znaku nie jest całkowicie określone przez średnią częstotliwość występowania znaku we wszystkich tekstach. To, który znak następuje, zależy od znaków już przesłanych. Na przykład we współczesnym języku rosyjskim po symbolu „ъ” nie może następować symbol spółgłoski. Po dwóch samogłoskach „e” z rzędu niezwykle rzadko pojawia się trzecia samogłoska „e”, z wyjątkiem słowa „długa szyja”. Oznacza to, że następny znak jest w pewnym stopniu z góry określony. Jeżeli uwzględnimy to ustalenie kolejnego symbolu, to niepewność (czyli informacja) kolejnego symbolu będzie nawet mniejsza niż 4,35. Według niektórych szacunków kolejny znak w języku rosyjskim jest z góry określony przez strukturę języka w ponad 50%, to znaczy przy optymalnym kodowaniu wszystkie informacje można przekazać poprzez usunięcie połowy liter z wiadomości.
Inna sprawa, że nie każdą literę da się przekreślić bezboleśnie. Na przykład „o” (i ogólnie samogłoski) o wysokiej częstotliwości można łatwo przekreślić, ale rzadkie „f” lub „e” są dość problematyczne.
Naturalny język, w którym się ze sobą porozumiewamy, jest wysoce redundantny, a co za tym idzie niezawodny – jeśli coś przesłyszeliśmy, nie ma problemu, informacja i tak zostanie przekazana.
Ale dopóki Shannon nie wprowadził miary informacji, nie mogliśmy zrozumieć, że język jest zbędny ani w jakim stopniu możemy kompresować wiadomości (ani dlaczego pliki tekstowe są tak dobrze kompresowane przez archiwizator).
Redundancja języka naturalnego
W artykule „O tym, jak piszemy tekst” (tytuł brzmi dokładnie tak!) wyjęto i poddano pewnemu przekształceniu fragment powieści Iwana Turgieniewa „Gniazdo szlachty”: 34% liter zostało usuniętych z tekstu fragment, ale nie przypadkowy. Pozostawiono pierwszą i ostatnią literę w wyrazie, przekreślono tylko samogłoski i nie wszystkie. Celem było nie tylko odzyskanie wszystkich informacji z przekonwertowanego tekstu, ale także zapewnienie, że osoba czytająca ten tekst nie będzie miała żadnych szczególnych trudności z powodu brakujących liter.

Dlaczego stosunkowo łatwo jest przeczytać ten uszkodzony tekst? W rzeczywistości zawiera informacje niezbędne do rekonstrukcji całych słów. Native speaker języka rosyjskiego ma określony zestaw zdarzeń (słów i całych zdań), których używa w celu rozpoznania. Ponadto mówiący ma do dyspozycji także standardowe struktury językowe, które pomagają mu odzyskać informacje. Na przykład, „Jest cholernie wrażliwa”- z dużym prawdopodobieństwem można odczytać jako „Była bardziej wrażliwa”. Ale brane osobno „Ona jest bla bla” raczej zostanie przywrócony jako „Była bielsza”. Ponieważ w codziennej komunikacji mamy do czynienia z kanałami, w których występuje szum i zakłócenia, całkiem nieźle radzimy sobie z odtwarzaniem informacji, ale tylko tych, które już znamy z góry. Na przykład zdanie „Diabeł nie lubił jej przyjemności, mimo że wybuchała płaczem i się rozpadała” czyta się dobrze, z wyjątkiem ostatniego słowa „zalany” - „zalany”. Tego słowa nie ma we współczesnym leksykonie. Podczas szybkiego czytania słowa „rozpryski” brzmi raczej jak „sklejeni razem”, a gdy jest powolny, po prostu wprawia w zakłopotanie.
Digitalizacja sygnału
Dźwięk lub wibracje akustyczne to sinusoida. Widać to chociażby na ekranie edytora dźwięku. Aby dokładnie przekazać dźwięk, będziesz potrzebować nieskończonej liczby wartości - całej fali sinusoidalnej. Jest to możliwe dzięki połączeniu analogowemu. Śpiewa – słuchasz, kontakt nie zostaje przerwany, dopóki piosenka trwa.
W komunikacji cyfrowej kanałem możemy przesyłać tylko skończoną liczbę wartości. Czy to oznacza, że dźwięku nie da się dokładnie odtworzyć? Okazuje się, że nie.
Różne dźwięki są różnie modulowaną falą sinusoidalną. Przesyłamy jedynie wartości dyskretne (częstotliwości i amplitudy) i nie ma potrzeby przesyłania samej sinusoidy – może ona zostać wygenerowana przez urządzenie odbiorcze. Generuje falę sinusoidalną, na którą nakładana jest modulacja, utworzona z wartości przesyłanych kanałem komunikacyjnym. Istnieją dokładne zasady, które muszą być przesyłane wartości dyskretne, aby dźwięk na wejściu do kanału komunikacyjnego pokrywał się z dźwiękiem na wyjściu, gdzie wartości te nakładają się na jakąś standardową sinusoidę (tak brzmi twierdzenie Kotelnikowa o).
Twierdzenie Kotelnikowa (w literaturze angielskiej - twierdzenie Nyquista-Shannona, twierdzenie o próbkowaniu)- fundamentalne stwierdzenie z zakresu cyfrowego przetwarzania sygnałów, odnoszące się do sygnałów ciągłych i dyskretnych oraz stwierdzające, że „dowolna funkcja F(t), składająca się z częstotliwości od 0 do f1, może być przekazywana w sposób ciągły z dowolną dokładnością za pomocą następujących po sobie liczb przez 1 /(2*f1) sekundy.
Kodowanie odporne na zakłócenia. Kody Hamminga
Jeśli prześlesz zakodowany tekst Iwana Turgieniewa niewiarygodnym kanałem, choć z pewną liczbą błędów, otrzymasz tekst całkowicie znaczący. Jeśli jednak będziemy musieli przesłać wszystko z dokładnością bitową, problem pozostanie nierozwiązany: nie wiemy, które bity są błędne, ponieważ błąd jest losowy. Nawet suma kontrolna nie zawsze pomaga.
Dlatego dzisiaj, przesyłając dane sieciami, dąży się nie tyle do optymalnego kodowania, w którym można wcisnąć do kanału maksymalną ilość informacji, ale raczej do takiego kodowania (oczywiście redundantnego), w którym można przywrócić błędy - mniej więcej w ten sam sposób, w jaki przywracaliśmy słowa, czytając fragment Iwana Turgieniewa.
Istnieją specjalne kody odporne na hałas, które pozwalają przywrócić informacje po awarii. Jednym z nich jest kod Hamminga. Załóżmy, że cały nasz język składa się z trzech słów: 111000, 001110, 100011. Zarówno źródło wiadomości, jak i odbiorca znają te słowa. A wiemy, że w kanale komunikacyjnym zdarzają się błędy, ale przy przesyłaniu jednego słowa zniekształca się nie więcej niż jeden bit informacji.
Załóżmy, że najpierw przesyłamy słowo 111000. W wyniku co najwyżej jednego błędu (błędy podkreśliliśmy) może ono zamienić się w jedno ze słów:
1) 111000, 0 11000, 10 1000, 110 000, 1111 00, 11101 0, 111001 .
Podając słowo 001110, można uzyskać dowolne ze słów:
2) 001110, 1 01110, 01 1110, 000 110, 0010 10, 00110 0, 001111 .
Wreszcie dla 100011 możemy otrzymać:
3) 100011, 0 00011, 11 0011, 101 011, 1001 11, 10000 1, 100010 .
Należy zauważyć, że wszystkie trzy listy są parami rozłączne. Innymi słowy, jeśli na drugim końcu kanału komunikacyjnego pojawi się jakiekolwiek słowo z listy 1, odbiorca wie na pewno, że przesłano do niego słowo 111000, a jeśli pojawi się jakiekolwiek słowo z listy 2 - słowo 001110, a z listy 3 - słowo 100011. W tym przypadku mówią, że nasz kod naprawił jeden błąd.
Korekta nastąpiła pod wpływem dwóch czynników. Po pierwsze, odbiorca zna cały „słownictwo”, czyli przestrzeń zdarzeń odbiorcy komunikatu pokrywa się z przestrzenią tego, który przekazał komunikat. Kiedy kod został przesłany z tylko jednym błędem, na wyjściu pojawiło się słowo, którego nie było w słowniku.
Po drugie, słowa w słowniku zostały wybrane w specjalny sposób. Nawet jeśli pojawił się błąd, odbiorca nie mógł pomylić jednego słowa z drugim. Przykładowo, jeśli słownik składa się ze słów „córka”, „kropka”, „guz”, a podczas transmisji wynikiem jest „woczka”, to odbiorca wiedząc, że takie słowo nie istnieje, nie będzie w stanie popraw błąd - dowolne z trzech słów może okazać się poprawne. Jeśli w słowniku występuje „kropka”, „dawka”, „gałąź” i wiemy, że dopuszczalny jest nie więcej niż jeden błąd, to „wochka” jest zdecydowanie „kropką”, a nie „dawką”. W kodach korygujących błędy słowa są dobierane precyzyjnie tak, aby były „rozpoznawalne” nawet po wystąpieniu błędu. Jedyna różnica polega na tym, że kod „alfabet” ma tylko dwie litery - zero i jedną.
Redundancja takiego kodowania jest bardzo duża, a liczba słów, które możemy w ten sposób przekazać, stosunkowo niewielka. W końcu musimy wykluczyć ze słownika każde słowo, które w przypadku pomyłki mogłoby pokrywać się z całą listą odpowiadającą przesyłanym słowom (na przykład słowa „córka” i „kropka” nie mogą znajdować się w słowniku). Jednak dokładne przesyłanie komunikatów jest tak ważne, że wiele wysiłku włożono w badania nad kodami odpornymi na błędy.
Uczucie
Pojęcia entropii (czyli niepewności i nieprzewidywalności) przekazu oraz redundancji (czyli determinalności i przewidywalności) w bardzo naturalny sposób odpowiadają naszym intuicjom co do ilości informacji. Im bardziej nieprzewidywalny jest komunikat (im większa jest jego entropia, bo mniejsze prawdopodobieństwo), tym więcej informacji niesie. Sensacja (na przykład spotkanie z krokodylem na Twerskiej) jest rzadkim wydarzeniem, jego przewidywalność jest bardzo niska, a zatem koszt informacji jest wysoki. Informacje często nazywane są newsami – komunikatami o wydarzeniach, które właśnie miały miejsce, o których wciąż nic nie wiemy. Ale jeśli opowiedzą nam o tym, co wydarzyło się drugi i trzeci raz, mniej więcej tymi samymi słowami, redundancja przekazu będzie duża, jego nieprzewidywalność spadnie do zera, a my po prostu nie będziemy słuchać, strząsając mówcę słowami „ Wiem wiem." Dlatego media tak bardzo starają się być pierwsze. To właśnie ta zgodność z intuicyjnym poczuciem nowości, rodząca naprawdę nieoczekiwane wieści, odegrała główną rolę w tym, że artykuł Shannon, który wcale nie był przeznaczony dla ogółu czytelnika, stał się sensacją, która została podjęta przez prasę, co zostało przyjęte jako uniwersalny klucz do poznania przyrody przez naukowców różnych specjalności – od językoznawców i krytyków literackich po biologów.
Ale Koncepcja informacji Shannona – ścisła teoria matematyczna , a jego zastosowanie poza teorią komunikacji jest bardzo zawodne. Jednak w samej teorii komunikacji odgrywa ona kluczową rolę.
Informacje semantyczne
Shannon, wprowadzając pojęcie entropii jako miary informacji, potrafił pracować z informacją – przede wszystkim ją mierzyć i oceniać cechy takie jak przepustowość kanału czy optymalne kodowanie. Jednak głównym założeniem, które pozwoliło Shannonowi skutecznie operować informacją, było założenie, że generowanie informacji jest procesem losowym, który z powodzeniem można opisać w kategoriach teorii prawdopodobieństwa. Jeśli proces jest nielosowy, to znaczy podlega prawom (i nie zawsze jasnym, jak to się dzieje w języku naturalnym), to rozumowanie Shannona nie ma do niego zastosowania. Nic, co mówi Shannon, nie ma nic wspólnego z znaczeniem informacji.
Kiedy mówimy o symbolach (lub literach alfabetu), z łatwością możemy myśleć w kategoriach zdarzeń losowych, ale gdy tylko przejdziemy do słów danego języka, sytuacja zmienia się diametralnie. Mowa jest procesem zorganizowanym w szczególny sposób i tutaj struktura przekazu jest nie mniej ważna niż symbole, za pomocą których jest on przekazywany.
Do niedawna wydawało się, że nic nie możemy zrobić, aby zbliżyć się do pomiaru sensowności tekstu, ale w ostatnie lata sytuacja zaczęła się zmieniać. A dzieje się tak przede wszystkim dzięki zastosowaniu sztucznych sieci neuronowych do zadań tłumaczenia maszynowego, automatycznego podsumowania tekstów, wydobywania informacji z tekstów i generowania raportów w języku naturalnym. Wszystkie te zadania obejmują przekształcanie, kodowanie i dekodowanie znaczących informacji zawartych w języku naturalnym. I stopniowo kształtuje się pojęcie o utracie informacji podczas takich transformacji, a co za tym idzie, o zakresie znaczącej informacji. Jednak dzisiaj jasność i dokładność, jaką posiada teoria informacji Shannona, nie jest jeszcze dostępna w przypadku tych trudnych problemów.