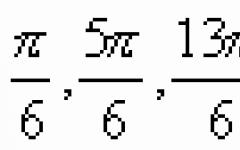A) Rozwiąż równanie 2(\sin x-\cos x)=tgx-1.
B) \left[ \frac(3\pi )2;\,3\pi \right].
Pokaż rozwiązanieRozwiązanie
A) Otwierając nawiasy i przesuwając wszystkie wyrazy na lewą stronę, otrzymujemy równanie 1+2 \sin x-2 \cos x-tg x=0. Biorąc pod uwagę, że \cos x \neq 0, wyraz 2 \sin x można zastąpić przez 2 tan x \cos x, otrzymujemy równanie 1+2 tg x \cos x-2 \cos x-tg x=0,
1) które poprzez grupowanie można sprowadzić do postaci (1-tg x)(1-2 \cos x)=0. 1-tgx=0, tan x=1,
2) x=\frac\pi 4+\pi n, n \in \mathbb Z; 1-2 \cos x=0, \cos x=\frac12,
B) x=\pm \frac\pi 3+2\pi n, n \in \mathbb Z. Używając okrąg liczbowy wybierz pierwiastki należące do przedziału
\left[ \frac(3\pi )2;\, 3\pi \right].
x_1=\frac\pi 4+2\pi =\frac(9\pi )4,
x_2=\frac\pi 3+2\pi =\frac(7\pi )3,
x_3=-\frac\pi 3+2\pi =\frac(5\pi )3.
A) Odpowiedź \frac\pi 4+\pi n,
B) \pm\frac\pi 3+2\pi n, n \in \mathbb Z; \frac(5\pi)3, \frac(7\pi)3,
\frac(9\pi)4.
A) Stan Rozwiąż równanie
B)(2\sin ^24x-3\cos 4x)\cdot \sqrt (tgx)=0. Wskaż pierwiastki tego równania należące do przedziału
Pokaż rozwiązanieRozwiązanie
A)\left(0;\,\frac(3\pi )2\right] ; OZ:
\begin(cases) tgx\geqslant 0\\x\neq \frac\pi 2+\pi k,k \in \mathbb Z. \end(cases)
Oryginalne równanie na ODZ jest równoważne zbiorowi równań
\left[\!\!\begin(array)(l) 2 \sin ^2 4x-3 \cos 4x=0,\\tg x=0. \end(tablica)\right. Rozwiążmy pierwsze równanie. W tym celu dokonamy wymiany \cos 4x=t, t \in [-1; 1].
Wtedy \sin^24x=1-t^2.
Otrzymujemy:
2(1-t^2)-3t=0, 2t^2+3t-2=0,
t_1=\frac12,
t_2=-2, t_2\notin [-1; 1].
\cos 4x=\frac12,
4x=\pm\frac\pi 3+2\pi n,
x=\pm \frac\pi (12)+\frac(\pi n)2, n \in \mathbb Z.
Rozwiążmy drugie równanie. tg x=0,\, x=\pi k, k \in \mathbb Z. Z pomocą

okrąg jednostkowy
Znajdźmy rozwiązania, które zadowolą ODZ. Znak „+” oznacza 1. i 3. ćwiartkę, w której tg x>0. Otrzymujemy: x=\pi k, k \in \mathbb Z;
B) x=\frac\pi (12)+\pi n, n \in \mathbb Z; x=\frac(5\pi )(12)+\pi m, m \in \mathbb Z.
.png)
Znajdźmy pierwiastki należące do przedziału \left(0;\,\frac(3\pi )2\right]. x=\frac\pi (12), x=\frac(5\pi )(12); x=\pi;
x_3=-\frac\pi 3+2\pi =\frac(5\pi )3.
A) x=\frac(13\pi )(12); x=\frac(17\pi )(12). \pi k, k \in \mathbb Z;
B) \frac\pi (12)+\pi n, n \in \mathbb Z; \frac(5\pi )(12)+\pi m, m \in \mathbb Z. \liczba pi; \frac\pi (12); \frac(5\pi )(12);
\frac(13\pi )(12); \frac(17\pi )(12)." wyd. F. F. Łysenko, S. Yu.
\frac(9\pi)4.
A) Rozwiąż równanie: \cos ^2x+\cos ^2\frac\pi 6=\cos ^22x+\sin ^2\frac\pi 3;
B) Wypisz wszystkie pierwiastki należące do przedziału \left(\frac(7\pi )2;\,\frac(9\pi )2\right].
Pokaż rozwiązanieRozwiązanie
A) Ponieważ \sin \frac\pi 3=\cos \frac\pi 6, To \sin ^2\frac\pi 3=\cos ^2\frac\pi 6, Oznacza, dane równanie jest równoważne równaniu \cos^2x=\cos ^22x, które z kolei jest równoważne równaniu \cos^2x-\cos ^2 2x=0.
Ale \cos ^2x-\cos ^22x= (\cos x-\cos 2x)\cdot (\cos x+\cos 2x) I
\cos 2x=2 \cos ^2 x-1, więc równanie przyjmie postać
(\cos x-(2 \cos ^2 x-1))\,\cdot(\cos x+(2 \cos ^2 x-1))=0,
(2 \cos ^2 x-\cos x-1)\,\cdot (2 \cos ^2 x+\cos x-1)=0.
Wtedy albo 2 \cos ^2 x-\cos x-1=0, albo 2 \cos ^2 x+\cos x-1=0.
Rozwiązanie pierwszego równania jako równanie kwadratowe względem \cos x otrzymujemy:
(\cos x)_(1,2)=\frac(1\pm\sqrt 9)4=\frac(1\pm3)4. Zatem albo \cos x=1 albo \cos x=-\frac12. Jeśli \cos x=1, to x=2k\pi , k \in \mathbb Z. If \cos x=-\frac12, To x=\pm \frac(2\pi )3+2s\pi , s \in \mathbb Z.
Podobnie, rozwiązując drugie równanie, otrzymujemy \cos x=-1 lub \cosx=\frac12. Jeśli \cos x=-1, to pierwiastki x=\pi +2m\pi , m \in \mathbb Z. Jeśli \cos x=\frac12, To x=\pm \frac\pi 3+2n\pi , n \in \mathbb Z.
Połączmy otrzymane rozwiązania:
x=m\pi , m \in \mathbb Z; x=\pm \frac\pi 3 +s\pi , s \in \mathbb Z.
B) Wybierzmy pierwiastki mieszczące się w danym przedziale za pomocą koła liczbowego.

Otrzymujemy: x_1 =\frac(11\pi)3, x_2=4\pi , x_3 =\frac(13\pi )3.
x_3=-\frac\pi 3+2\pi =\frac(5\pi )3.
A) m\pi, m\in \mathbb Z; \pm \frac\pi 3 +s\pi , s \in \mathbb Z;
B) \frac(11\pi)3, 4\pi, \frac(13\pi)3.
Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu.
\frac(9\pi)4.
A) Stan 10\cos ^2\frac x2=\frac(11+5ctg\left(\dfrac(3\pi )2-x\right) )(1+tgx).
B) Wskaż pierwiastki tego równania należące do przedziału \left(-2\pi ; -\frac(3\pi )2\right).
Pokaż rozwiązanieRozwiązanie
A) 1. Zgodnie ze wzorem redukcyjnym, ctg\lewo(\frac(3\pi )2-x\prawo) =tgx. Dziedziną definicji równania będą takie wartości x, że \cos x \neq 0 i tan x \neq -1. Przekształćmy równanie, korzystając ze wzoru na cosinus podwójnego kąta 2 \cos ^2 \frac x2=1+\cos x. Otrzymujemy równanie:
5(1+\cos x) =\frac(11+5tgx)(1+tgx). Zauważ to \frac(11+5tgx)(1+tgx)= \frac(5(1+tgx)+6)(1+tgx)= 5+\frac(6)(1+tgx), więc równanie staje się: 5+5 \cos x=5 +\frac(6)(1+tgx). Stąd \cos x =\frac(\dfrac65)(1+tgx),
\cos x+\sin x =\frac65. 2. Przekształć \sin x+\cos x korzystając ze wzoru na redukcję i wzoru na sumę cosinusów: \sin x=\cos \left(\frac\pi 2-x\right), \cos x+\cos \left(\frac\pi 2-x\right)= 2\cos \frac\pi 4\cos \lewo(x-\frac\pi 4\prawo)= \sqrt 2\cos \left(x-\frac\pi 4\right) = \frac65.
Stąd \cos \left(x-\frac\pi 4\right) =\frac(3\sqrt 2)5. Oznacza, x-\frac\pi 4= arc\cos \frac(3\sqrt 2)5+2\pi k, k \in \mathbb Z,
Lub x-\frac\pi 4= -arc\cos \frac(3\sqrt 2)5+2\pi t, t \in \mathbb Z.
Dlatego x=\frac\pi 4+arc\cos \frac(3\sqrt 2)5+2\pi k,k \in \mathbb Z,
Lub x =\frac\pi 4-arc\cos \frac(3\sqrt 2)5+2\pi t,t \in \mathbb Z.
Znalezione wartości x należą do dziedziny definicji.
B) Najpierw dowiedzmy się, gdzie pierwiastki równania znajdują się przy k=0 i t=0. Będą to odpowiednio liczby a=\frac\pi 4+arccos \frac(3\sqrt 2)5 I
b=\frac\pi 4-arccos \frac(3\sqrt 2)5.
1. Udowodnijmy nierówność pomocniczą:<\frac{3\sqrt 2}2<1.
\frac(\sqrt 2)(2) Naprawdę,<\frac{6\sqrt2}{10}=\frac{3\sqrt2}{5}.
\frac(\sqrt 2)(2)=\frac(5\sqrt 2)(10) Zauważ też, że<1^2=1, \left(\frac(3\sqrt 2)5\right) ^2=\frac(18)(25) Oznacza<1.
\frac(3\sqrt 2)5 (1) 2. Z nierówności
Z własności arc cosinus otrzymujemy: 0 Stąd Arcos 1<\frac\pi 4+arc\cos \frac{3\sqrt 2}5<\frac\pi 4+\frac\pi 4,
0<\frac\pi 4+arccos \frac{3\sqrt 2}5<\frac\pi 2,
0 \frac\pi 4+0 Podobnie, -\frac\pi 4<\frac\pi 4-arccos \frac{3\sqrt 2}5<
0 \frac\pi 4 Dla k=-1 i t=-1 otrzymujemy pierwiastki równania a-2\pi i b-2\pi. \Bigg(a-2\pi =-\frac74\pi +arccos \frac(3\sqrt 2)5,\, b-2\pi =-\frac74\pi -arccos \frac(3\sqrt 2)5\Bigg). Naraz -2\pi \left(-2\pi , -\frac(3\pi )2\right). Dla innych wartości k i t pierwiastki równania nie należą do danego przedziału. Rzeczywiście, jeśli k\geqslant 1 i t\geqslant 1, to pierwiastki są większe niż 2\pi. A) Jeśli k\leqslant -2 i t\leqslant -2, to pierwiastki są mniejsze B) -\frac(7\pi)2. Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu. A) Stan \frac\pi4\pm arccos\frac(3\sqrt2)5+2\pi k, k\in\mathbb Z; B)-\frac(7\pi)4\pm arccos\frac(3\sqrt2)5. A)\sin \left(\frac\pi 2+x\right) =\sin (-2x). Znajdź wszystkie pierwiastki tego równania należące do przedziału; Przekształćmy równanie: \cos x =-\sin 2x, \cos x+2 \sin x \cos x=0, \cos x(1+2 \sin x)=0, \cosx=0, x =\frac\pi 2+\pi n, n\in \mathbb Z; 1+2 \sinx=0, B)\sin x=-\frac12, x=(-1)^(k+1)\cdot \frac\pi 6+\pi k, k \in \mathbb Z. Pierwiastki należące do segmentu znajdujemy za pomocą okręgu jednostkowego. A) Wskazany przedział zawiera pojedynczą liczbę \frac\pi 2. B) Pierwiastki należące do segmentu znajdujemy za pomocą okręgu jednostkowego. Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu. (-1)^(k+1)\cdot \frac\pi 6+\pi k, k \in \mathbb Z; nie jest uwzględniony w DZ. Oznacza, \sin x \neq 1. Podziel obie strony równania przez współczynnik (\sin x-1), różny od zera. Otrzymujemy równanie \frac 1(1+\cos 2x)=\frac 1(1+\cos (\pi +x)), lub równanie 2 \cos ^2 x=1-\cos x. To równanie wynika z podstawienia \cos x=t, Gdzie -1 \leqslant t \leqslant 1 sprowadź do kwadratu: 2t^2+t-1=0, czyje korzenie t_1=-1 a=\frac\pi 4+arccos \frac(3\sqrt 2)5 t_2=\frac12. Wracając do zmiennej x, otrzymujemy \cos x = \frac12 Lub \cos x=-1, Gdzie x=\frac \pi 3+2\pi m, m \in \mathbb Z, x=-\frac \pi 3+2\pi n, n \in \mathbb Z, x=\pi +2\pi k, k \in \mathbb Z. B) Rozwiążmy nierówności 1) -\frac(3\pi )2 \leqslant \frac(\pi )3+2\pi m \leqslant -\frac \pi 2 , 2) -\frac(3\pi )2 \leqslant -\frac \pi 3+2\pi n \leqslant -\frac \pi (2,) 3) -\frac(3\pi )2 \leqslant \pi+2\pi k \leqslant -\frac \pi 2 , 1)
-\frac(3\pi )2 \leqslant \frac(\pi )3+2\pi m \leqslant -\frac \pi 2 , -\frac32\leqslant \frac13+2m \leqslant -\frac12 -\frac(11)6 \leqslant 2m\leqslant -\frac56 , -\frac(11)(12) \leqslant m \leqslant -\frac5(12). \left [-\frac(11)(12);-\frac5(12)\right]. 2)
-\frac (3\pi) 2 \leqslant -\frac(\pi )3+2\pi n \leqslant -\frac(\pi )(2), -\frac32 \leqslant -\frac13 +2n \leqslant -\frac12 , -\frac76 \leqslant 2n \leqslant -\frac1(6), -\frac7(12) \leqslant n \leqslant -\frac1(12). W zakresie nie ma liczb całkowitych \left[ -\frac7(12) ; -\frac1(12)\prawo]. 3)
-\frac(3\pi )2 \leqslant \pi +2\pi k\leqslant -\frac(\pi )2, -\frac32 \leqslant 1+2k\leqslant -\frac12, -\frac52 \leqslant 2k \leqslant -\frac32, -\frac54 \leqslant k \leqslant -\frac34. Nierówność tę spełnia k=-1, a następnie x=-\pi. A) \frac \pi 3+2\pi m; -\frac \pi 3+2\pi n; \pi +2\pi k, M, N, k \in \mathbb Z; B) -\pi . W tym artykule postaram się wyjaśnić 2 sposoby wybieranie pierwiastków w równaniu trygonometrycznym: wykorzystanie nierówności i wykorzystanie koła trygonometrycznego. Przejdźmy od razu do ilustrującego przykładu i dowiemy się, jak to działa. A) Rozwiąż równanie sqrt(2)cos^2x=sin(Pi/2+x) Rozwiążmy punkt a. Skorzystajmy ze wzoru redukcyjnego na sinus sin(Pi/2+x) = cos(x) Kwadrat(2)cos^2x = cosx Kwadrat(2)cos^2x - cosx = 0 Cosx(sqrt(2)cosx - 1) = 0 X1 = Pi/2 + Pin, n ∈ Z Kwadrat(2)cosx - 1 = 0 Cosx = 1/kwadrat(2) Cosx = sqrt(2)/2 X2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z X2 = Pi/4 + 2Pin, n ∈ Z Rozwiążmy punkt b. 1) Dobór pierwiastków za pomocą nierówności Tutaj wszystko jest zrobione po prostu, podstawiamy powstałe pierwiastki do podanego nam przedziału [-7Pi/2; -2Pi], znajdź wartości całkowite dla n. 7Pi/2 mniejsze lub równe Pi/2 + Pin mniejsze lub równe -2Pi Natychmiast dzielimy wszystko przez Pi 7/2 mniejsze lub równe 1/2 + n mniejsze lub równe -2 7/2 - 1/2 mniejsze lub równe n mniejsze lub równe -2 - 1/2 4 mniejsze lub równe n mniejsze lub równe -5/2 Liczby całkowite n w tym przedziale to -4 i -3. Oznacza to, że pierwiastki należące do tego przedziału będą wynosić Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2 Podobnie tworzymy jeszcze dwie nierówności 7Pi/2 mniejsze lub równe Pi/4 + 2Pin mniejsze lub równe -2Pi W tym przedziale nie ma całych n 7Pi/2 mniejsze lub równe -Pi/4 + 2Pin mniejsze lub równe -2Pi Jedna liczba całkowita n w tym przedziale to -1. Oznacza to, że wybrany pierwiastek w tym przedziale to -Pi/4 + 2Pi*(-1) = -9Pi/4. Zatem odpowiedź w punkcie b: -7Pi/2, -5Pi/2, -9Pi/4 2) Wybór pierwiastków za pomocą okręgu trygonometrycznego Aby skorzystać z tej metody, musisz zrozumieć, jak działa ten okrąg. Spróbuję wytłumaczyć prostym językiem jak to rozumiem. Myślę, że w szkołach, na lekcjach algebry, ten temat był wielokrotnie wyjaśniany mądrymi słowami nauczyciela, w podręcznikach pojawiały się skomplikowane sformułowania. Osobiście rozumiem to jako okrąg, który można obejść nieskończoną liczbę razy, tłumaczy się to tym, że funkcje sinus i cosinus są okresowe. Obejdźmy się w kierunku przeciwnym do ruchu wskazówek zegara Obejdźmy 2 razy w kierunku przeciwnym do ruchu wskazówek zegara Obejdźmy 1 raz zgodnie z ruchem wskazówek zegara (wartości będą ujemne) Wróćmy do naszego pytania, musimy wybrać pierwiastki z przedziału [-7Pi/2; -2Pi] Aby dostać się do liczb -7Pi/2 i -2Pi należy dwukrotnie okrążyć okrąg w kierunku przeciwnym do ruchu wskazówek zegara. Aby znaleźć pierwiastki równania na tym przedziale, należy oszacować i zastąpić. Rozważ x = Pi/2 + Pin. Jakie w przybliżeniu powinno być n, aby x znajdowało się gdzieś w tym zakresie? Podstawiamy, powiedzmy -2, otrzymujemy Pi/2 - 2Pi = -3Pi/2, oczywiście nie jest to uwzględnione w naszym przedziale, więc bierzemy mniej niż -3, Pi/2 - 3Pi = -5Pi/2, to jest odpowiednie, spróbujmy ponownie -4 , Pi/2 - 4Pi = -7Pi/2, również odpowiednie. Rozumując podobnie dla Pi/4 + 2Pin i -Pi/4 + 2Pin, znajdujemy kolejny pierwiastek -9Pi/4. Porównanie dwóch metod. Pierwsza metoda (wykorzystująca nierówności) jest znacznie bardziej niezawodna i znacznie łatwiejsza do zrozumienia, ale jeśli naprawdę poważnie podchodzisz do okręgu trygonometrycznego i drugiej metody selekcji, to wybieranie pierwiastków będzie znacznie szybsze, możesz zaoszczędzić około 15 minut na egzaminie . a) Rozwiąż równanie: . b) Znajdź wszystkie pierwiastki tego równania należące do odcinka. W tej lekcji omówiono przykład rozwiązania równania trygonometrycznego, które można wykorzystać jako przykład rozwiązywania problemów typu C1 podczas przygotowań do jednolitego egzaminu państwowego z matematyki. Przede wszystkim określa się zakres funkcji - wszystkie prawidłowe wartości argumentu. Następnie w trakcie rozwiązania funkcja sinus trygonometryczna jest konwertowana na cosinus za pomocą wzoru redukcyjnego. Następnie wszystkie wyrazy równania przenosi się na jego lewą stronę, gdzie wspólny czynnik jest usuwany z nawiasów. Każdy współczynnik jest równy zero, co pozwala nam wyznaczyć pierwiastki równania. Następnie metodą zwojów wyznaczane są pierwiastki należące do danego odcinka. W tym celu na skonstruowanym okręgu jednostkowym zaznacza się zakręt od lewej krawędzi danego odcinka w prawo. Następnie znalezione pierwiastki na okręgu jednostkowym łączymy odcinkami z jego środkiem i wyznaczamy punkty, w których te odcinki przecinają się z zakrętem. Te punkty przecięcia są pożądaną odpowiedzią na drugą część problemu. Możesz zamówić szczegółowe rozwiązanie swojego problemu!!! Równość zawierająca niewiadomą pod znakiem funkcji trygonometrycznej („sin x, cos x, tan x” lub „ctg x”) nazywa się równaniem trygonometrycznym i to właśnie ich wzory rozważymy dalej. Najprostsze równania nazywane są „sin x=a, cos x=a, tg x=a, ctg x=a”, gdzie „x” to kąt, który należy znaleźć, „a” to dowolna liczba. Zapiszmy podstawowe formuły dla każdego z nich. 1. Równanie „grzech x=a”. Dla `|a|>1` nie ma rozwiązań. Kiedy `|a| \równ. 1` ma nieskończoną liczbę rozwiązań. Wzór pierwiastkowy: `x=(-1)^n arcsin a + \pi n, n \in Z` 2. Równanie „cos x=a”. Dla `|a|>1` - podobnie jak w przypadku sinusa, nie ma ono rozwiązań wśród liczb rzeczywistych. Kiedy `|a| \równ. 1` ma nieskończoną liczbę rozwiązań. Wzór na pierwiastek: `x=\pm arccos a + 2\pi n, n \in Z` Specjalne przypadki sinusa i cosinusa na wykresach. 3. Równanie `tg x=a` Ma nieskończoną liczbę rozwiązań dla dowolnych wartości `a`. Wzór na pierwiastek: `x=arctg a + \pi n, n \in Z` 4. Równanie `ctg x=a` Ma również nieskończoną liczbę rozwiązań dla dowolnych wartości `a`. Wzór na pierwiastek: `x=arcctg a + \pi n, n \in Z` Dla sinusa: Rozwiązanie dowolnego równania trygonometrycznego składa się z dwóch etapów: Przyjrzyjmy się głównym metodom rozwiązań na przykładach. Metoda ta polega na zastąpieniu zmiennej i podstawieniu jej do równości. Przykład. Rozwiąż równanie: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0` `2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`, dokonaj zamiany: `cos(x+\frac \pi 6)=y`, następnie `2y^2-3y+1=0`, znajdujemy pierwiastki: `y_1=1, y_2=1/2`, z czego wynikają dwa przypadki: 1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`. 2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`. Odpowiedź: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`. Przykład. Rozwiąż równanie: `sin x+cos x=1`. Rozwiązanie. Przesuńmy wszystkie wyrazy równości w lewo: `sin x+cos x-1=0`. Używając , przekształcamy i rozkładamy na czynniki lewą stronę: `sin x — 2sin^2 x/2=0`, `2sin x/2 cos x/2-2sin^2 x/2=0`, `2sin x/2 (cos x/2-sin x/2)=0`, Odpowiedź: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`. Najpierw musisz zredukować to równanie trygonometryczne do jednej z dwóch postaci: `a sin x+b cos x=0` (jednorodne równanie pierwszego stopnia) lub `a sin^2 x + b sin x cos x +c cos^2 x=0` (jednorodne równanie drugiego stopnia). Następnie podziel obie części przez `cos x \ne 0` - w pierwszym przypadku i przez `cos^2 x \ne 0` - w drugim przypadku. Otrzymujemy równania dla `tg x`: `a tg x+b=0` i `a tg^2 x + b tg x +c =0`, które należy rozwiązać znanymi metodami. Przykład. Rozwiąż równanie: `2 sin^2 x+sin x cos x - cos^2 x=1`. Rozwiązanie. Zapiszmy prawą stronę jako `1=sin^2 x+cos^2 x`: `2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`, `2 grzech^2 x+sin x cos x — cos^2 x -` ` grzech^2 x — cos^2 x=0` `sin^2 x+sin x cos x — 2 cos^2 x=0`. Jest to jednorodne równanie trygonometryczne drugiego stopnia, dzielimy jego lewą i prawą stronę przez `cos^2 x \ne 0`, otrzymujemy: `\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0` `tg^2 x+tg x — 2=0`. Wprowadźmy zamianę `tg x=t`, w wyniku której otrzymamy `t^2 + t - 2=0`. Pierwiastkami tego równania są „t_1=-2” i „t_2=1”. Następnie: Odpowiedź. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`. Przykład. Rozwiąż równanie: `11 grzech x - 2 cos x = 10`. Rozwiązanie. Zastosujmy wzory na podwójny kąt i otrzymamy: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2` `4 tg^2 x/2 — 11 tg x/2 +6=0` Stosując opisaną powyżej metodę algebraiczną otrzymujemy: Odpowiedź. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`. W równaniu trygonometrycznym „a sin x + b cos x = c”, gdzie a, b, c to współczynniki, a x to zmienna, podziel obie strony przez „sqrt (a^2+b^2)”: `\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) ) +b^2))`. Współczynniki po lewej stronie mają właściwości sinusa i cosinusa, czyli suma ich kwadratów jest równa 1, a moduły nie większe niż 1. Oznaczmy je następująco: `\frac a(sqrt (a^2 +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, następnie: `cos \varphi sin x + sin \varphi cos x =C`. Przyjrzyjmy się bliżej następującemu przykładowi: Przykład. Rozwiąż równanie: `3 grzech x+4 cos x=2`. Rozwiązanie. Podziel obie strony równości przez „sqrt (3^2+4^2)”, otrzymamy: `\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))` `3/5 grzech x+4/5 cos x=2/5`. Oznaczmy `3/5 = cos \varphi` , `4/5=sin \varphi`. Ponieważ `sin \varphi>0`, `cos \varphi>0`, przyjmujemy `\varphi=arcsin 4/5` jako kąt pomocniczy. Następnie zapisujemy naszą równość w postaci: `cos \varphi sin x+sin \varphi cos x=2/5` Stosując wzór na sumę kątów dla sinusa, naszą równość zapisujemy w postaci: `grzech (x+\varphi)=2/5`, `x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`, `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`. Odpowiedź. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`. Są to równości z ułamkami, których liczniki i mianowniki zawierają funkcje trygonometryczne. Przykład. Rozwiąż równanie. `\frac (sin x)(1+cos x)=1-cos x`. Rozwiązanie. Pomnóż i podziel prawą stronę równości przez „(1+cos x)”. W rezultacie otrzymujemy: `\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)` `\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)` `\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)` `\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0` `\frac (sin x-sin^2 x)(1+cos x)=0` Biorąc pod uwagę, że mianownik nie może być równy zero, otrzymujemy `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`. Przyrównajmy licznik ułamka do zera: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Następnie `sin x=0` lub `1-sin x=0`. Biorąc pod uwagę, że ` x \ne \pi+2\pi n, n \in Z`, rozwiązaniami są `x=2\pi n, n \in Z` i `x=\pi /2+2\pi n` , `n \w Z`. Odpowiedź. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`. Trygonometria, a w szczególności równania trygonometryczne, są stosowane w prawie wszystkich obszarach geometrii, fizyki i inżynierii. Naukę rozpoczyna się w 10. klasie, zawsze są zadania na egzaminie Unified State Exam, więc postaraj się zapamiętać wszystkie wzory równań trygonometrycznych - na pewno ci się przydadzą! Jednak nie musisz ich nawet zapamiętywać, najważniejsze jest zrozumienie istoty i umiejętność jej wyciągnięcia. To nie jest tak trudne, jak się wydaje. Przekonaj się sam, oglądając wideo. Cel lekcji: A) wzmocnić umiejętność rozwiązywania prostych równań trygonometrycznych; B) uczyć, jak wybierać pierwiastki równań trygonometrycznych z zadanego przedziału a) Sprawdzenie pracy domowej: klasa otrzymuje zaawansowaną pracę domową - rozwiąż równanie i znajdź sposób na wybranie pierwiastków z zadanego przedziału. 1) ponieważ X= -0,5, gdzie xI [-]. Odpowiedź:. 2) grzech X= , gdzie xI . Odpowiedź: ; . 3) cos 2 X= -, gdzie xI. Odpowiedź: Uczniowie zapisują rozwiązanie na tablicy, niektórzy posługują się wykresem, inni metodą selekcji. W tym czasie zajęcia działa doustnie. Znajdź znaczenie wyrażenia: a) tg – grzech + cos + grzech. Odpowiedź: 1. b) 2 arccos 0 + 3 arccos 1. Odpowiedź: ? c) arcsin + arcsin. Odpowiedź:. d) 5 arctg (-) – arccos (-). Odpowiedź:-. – Sprawdźmy Twoją pracę domową, otwórz zeszyty z pracą domową. Część z Was znalazła rozwiązanie stosując metodę selekcji, a część korzystając z wykresu. 2. Wnioski dotyczące sposobów rozwiązania tych zadań oraz sformułowanie problemu, czyli przekazanie tematu i celu lekcji. – a) Trudno jest rozwiązać problem metodą selekcji, jeśli podany jest duży przedział. – b) Metoda graficzna nie daje dokładnych wyników, wymaga weryfikacji i zajmuje dużo czasu. – Zatem musi istnieć jeszcze co najmniej jedna metoda, najbardziej uniwersalna – spróbujmy ją znaleźć. Więc co będziemy dzisiaj robić na zajęciach? (Naucz się wybierać pierwiastki równania trygonometrycznego w danym przedziale.) – Przykład 1. (Uczeń podchodzi do tablicy) sałata X= -0,5, gdzie xI [-]. Pytanie: Co decyduje o odpowiedzi na to zadanie? (Z ogólnego rozwiązania równania. Zapiszmy rozwiązanie w postaci ogólnej). Rozwiązanie jest zapisane na tablicy x = + 2?k, gdzie k R. – Zapiszmy to rozwiązanie w postaci zbioru: – Jak myślisz, jaki jest najwygodniejszy zapis rozwiązania wyboru pierwiastków na przedziale? (z drugiego wpisu). Ale to znowu metoda selekcji. Co musimy wiedzieć, aby uzyskać właściwą odpowiedź? (Musisz znać wartości k). (Stwórzmy model matematyczny, aby znaleźć k). ponieważ kI Z, to k = 0, stąd X= = Z tej nierówności jasno wynika, że nie ma wartości całkowitych k. Wniosek: Aby wybrać pierwiastki z danego przedziału przy rozwiązywaniu równania trygonometrycznego, należy: Rozwiąż przykład nr 2 i nr 3 z pracy domowej, korzystając z otrzymanego algorytmu. Przy tablicy jednocześnie pracuje dwóch uczniów, po czym następuje sprawdzenie pracy.x_3=-\frac\pi 3+2\pi =\frac(5\pi )3.
\frac(9\pi)4.
Rozwiązanie

x_3=-\frac\pi 3+2\pi =\frac(5\pi )3.
\frac(9\pi)4.
\frac\pi 2+\pi n, n \in \mathbb Z; x_3=-\frac\pi 3+2\pi =\frac(5\pi )3.
b) Znajdź wszystkie pierwiastki tego równania należące do przedziału [-7Pi/2; -2Pi]
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
-15/8 mniejsze lub równe n mniejsze lub równe -9/8
-13/8 mniejsze lub równe n mniejsze lub równe -7/8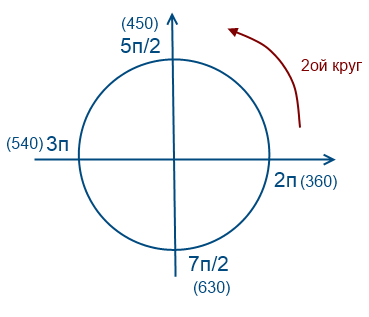


Rozwiązanie problemu





Wzory na pierwiastki równań trygonometrycznych w tabeli
 Dla cosinusa:
Dla cosinusa:  Dla stycznych i cotangensów:
Dla stycznych i cotangensów:  Wzory do rozwiązywania równań zawierających odwrotne funkcje trygonometryczne:
Wzory do rozwiązywania równań zawierających odwrotne funkcje trygonometryczne:
Metody rozwiązywania równań trygonometrycznych
Metoda algebraiczna.
Faktoryzacja.
Redukcja do równania jednorodnego
Przejście do połowy kąta
Wprowadzenie kąta pomocniczego
Ułamkowe racjonalne równania trygonometryczne
Postęp lekcji.
1. Aktualizowanie wiedzy.

3. Konsolidacja.