Rozwiązywanie równań w matematyce zajmuje szczególne miejsce. Proces ten poprzedzony jest wielogodzinną nauką teorii, podczas której student uczy się rozwiązywania równań, określania ich rodzaju oraz doprowadza umiejętność całkowitej automatyzacji. Jednak szukanie korzeni nie zawsze ma sens, gdyż mogą one po prostu nie istnieć. Istnieją specjalne techniki wyszukiwania korzeni. W tym artykule przeanalizujemy główne funkcje, ich dziedziny definicji, a także przypadki, w których brakuje ich pierwiastków.
Które równanie nie ma pierwiastków?
Równanie nie ma pierwiastków, jeśli nie ma rzeczywistych argumentów x, dla których równanie jest identycznie prawdziwe. Dla laika to sformułowanie, jak większość twierdzenia matematyczne i formuły, wyglądają bardzo niewyraźnie i abstrakcyjnie, ale tak jest w teorii. W praktyce wszystko staje się niezwykle proste. Na przykład: równanie 0 * x = -53 nie ma rozwiązania, ponieważ nie ma liczby x, której iloczyn z zerem dałby coś innego niż zero.
Teraz przyjrzymy się najbardziej podstawowe typy równania.
1. Równanie liniowe
Równanie nazywa się liniowym, jeśli jego prawa i lewa strona są przedstawione w postaci funkcje liniowe: ax + b = cx + d lub w formie uogólnionej kx + b = 0. Gdzie a, b, c, d są znanymi liczbami, a x jest nieznaną wielkością. Które równanie nie ma pierwiastków? Przykłady równań liniowych przedstawiono na poniższej ilustracji.
Zasadniczo równania liniowe rozwiązuje się po prostu przenosząc część liczbową do jednej części i zawartość x do drugiej. Wynikiem jest równanie w postaci mx = n, gdzie m i n są liczbami, a x jest niewiadomą. Aby znaleźć x, po prostu podziel obie strony przez m. Wtedy x = n/m. Większość równań liniowych ma tylko jeden pierwiastek, ale zdarzają się przypadki, gdy pierwiastków jest nieskończenie wiele lub nie ma ich wcale. Gdy m = 0 i n = 0, równanie przyjmuje postać 0 * x = 0. Rozwiązaniem takiego równania będzie absolutnie dowolna liczba.
Które równanie nie ma jednak pierwiastków?
Dla m = 0 i n = 0 równanie nie ma pierwiastków ze zbioru liczby rzeczywiste. 0 * x = -1; 0 * x = 200 - te równania nie mają pierwiastków.
2. Równanie kwadratowe
Równanie kwadratowe to równanie w postaci ax 2 + bx + c = 0 dla a = 0. Najczęstszym rozwiązaniem jest dyskryminator. Wzór na znalezienie dyskryminatora równanie kwadratowe: re = b 2 - 4 * a * do. Dalej są dwa pierwiastki x 1,2 = (-b ± √D) / 2 * a.
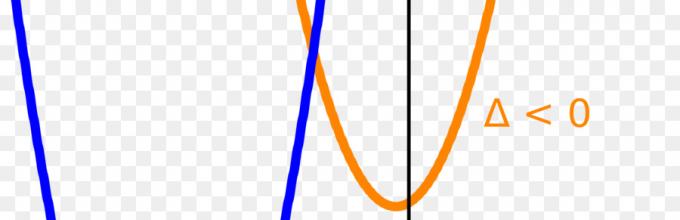
Dla D > 0 równanie ma dwa pierwiastki, dla D = 0 ma jeden pierwiastek. Ale które równanie kwadratowe nie ma pierwiastków? Najłatwiejszym sposobem zaobserwowania liczby pierwiastków równania kwadratowego jest wykreślenie funkcji, którą jest parabola. Dla a > 0 gałęzie są skierowane w górę, dla a< 0 ветви опущены вниз. Если дискриминант отрицателен, такое квадратное уравнение не имеет корней на множестве действительных чисел.

Możesz także wizualnie określić liczbę pierwiastków bez obliczania dyskryminatora. Aby to zrobić, musisz znaleźć wierzchołek paraboli i określić, w którym kierunku skierowane są gałęzie. Współrzędną x wierzchołka można wyznaczyć ze wzoru: x 0 = -b / 2a. W tym przypadku współrzędną y wierzchołka można znaleźć po prostu podstawiając wartość x 0 do pierwotnego równania.

Równanie kwadratowe x 2 - 8x + 72 = 0 nie ma pierwiastków, ponieważ ma ujemny dyskryminator D = (-8) 2 - 4 * 1 * 72 = -224. Oznacza to, że parabola nie dotyka osi x, a funkcja nigdy nie przyjmuje wartości 0, dlatego równanie nie ma pierwiastków rzeczywistych.
3. Równania trygonometryczne
Funkcje trygonometryczne są rozpatrywane na okręgu trygonometrycznym, ale można je również przedstawić w kartezjańskim układzie współrzędnych. W tym artykule przyjrzymy się dwóm głównym funkcje trygonometryczne i ich równania: sinx i cosx. Ponieważ tworzą się te funkcje okrąg trygonometryczny o promieniu 1, |sinx| i |cosx| nie może być większe niż 1. Które równanie sinx nie ma pierwiastków? Spójrzmy na wykres funkcje sinx, pokazany na poniższym obrazku.

Widzimy, że funkcja jest symetryczna i ma okres powtarzania 2pi. Na tej podstawie możemy powiedzieć, że maksymalna wartość tej funkcji może wynosić 1, a minimalna -1. Na przykład wyrażenie cosx = 5 nie będzie miało pierwiastków, ponieważ jego wartość bezwzględna jest większa niż jeden.
To najprostszy przykład równań trygonometrycznych. Tak naprawdę ich rozwiązanie może zająć wiele stron, na końcu zorientujesz się, że użyłeś niewłaściwego wzoru i musisz zacząć wszystko od nowa. Czasami, nawet jeśli poprawnie znajdziesz pierwiastki, możesz zapomnieć o uwzględnieniu ograniczeń OD, dlatego w odpowiedzi pojawia się dodatkowy pierwiastek lub interwał, a cała odpowiedź zamienia się w błąd. Dlatego ściśle przestrzegaj wszystkich ograniczeń, ponieważ nie wszystkie korzenie mieszczą się w zakresie zadania.
4. Układy równań
Układ równań to zbiór równań połączonych nawiasami klamrowymi lub kwadratowymi. Nawiasy klamrowe wskazują, że wszystkie równania są uruchamiane razem. Oznacza to, że jeśli przynajmniej jedno z równań nie ma pierwiastków lub jest sprzeczne z innym, cały układ nie ma rozwiązania. Nawiasy kwadratowe oznaczają słowo „lub”. Oznacza to, że jeśli przynajmniej jedno z równań układu ma rozwiązanie, to cały układ ma rozwiązanie.

Odpowiedzią układu c jest zbiór wszystkich pierwiastków poszczególnych równań. A systemy z nawiasami klamrowymi mają tylko wspólne korzenie. Układy równań mogą zawierać zupełnie różne funkcje, więc taka złożoność nie pozwala od razu stwierdzić, które równanie nie ma pierwiastków.
Znaleziono w książkach problemowych i podręcznikach różne rodzaje równania: te, które mają pierwiastki i te, które ich nie mają. Po pierwsze, jeśli nie możesz znaleźć korzeni, nie myśl, że ich w ogóle nie ma. Być może gdzieś popełniłeś błąd, musisz po prostu dokładnie sprawdzić swoją decyzję.
Przyjrzeliśmy się najbardziej podstawowym równaniom i ich typom. Teraz możesz stwierdzić, które równanie nie ma pierwiastków. W większości przypadków nie jest to trudne. Osiągnięcie sukcesu w rozwiązywaniu równań wymaga jedynie uwagi i koncentracji. Ćwicz więcej, pomoże Ci to znacznie lepiej i szybciej poruszać się po materiale.
Zatem równanie nie ma pierwiastków, jeśli:
- w równaniu liniowym mx = n wartość wynosi m = 0 i n = 0;
- w równaniu kwadratowym, jeśli dyskryminator jest mniejszy od zera;
- V równanie trygonometryczne postaci cosx = m / sinx = n, jeśli |m| > 0, |n| > 0;
- w układzie równań z nawiasami klamrowymi, jeśli choć jedno równanie nie ma pierwiastków, oraz z nawiasami kwadratowymi, jeśli wszystkie równania nie mają pierwiastków.
Samouczek wideo 2: Rozwiązywanie równań kwadratowych
Wykład: Równania kwadratowe
Równanie
Równanie- jest to rodzaj równości, w wyrażeniach których występuje zmienna.
Rozwiązać równanie- oznacza znalezienie liczby zamiast zmiennej, która doprowadzi ją do prawidłowej równości.
Równanie może mieć jedno rozwiązanie, kilka lub wcale.
Aby rozwiązać dowolne równanie należy je maksymalnie uprościć do postaci:
Liniowy: a*x = b;
Kwadrat: a*x 2 + b*x + do = 0.
Oznacza to, że przed rozwiązaniem wszelkie równania należy przekształcić do postaci standardowej.
Każde równanie można rozwiązać na dwa sposoby: analitycznie i graficznie.
Na wykresie za rozwiązanie równania uważa się punkty, w których wykres przecina oś OX.
Równania kwadratowe
Równanie można nazwać kwadratowym, jeśli po uproszczeniu ma postać:
a*x 2 + b*x + do = 0.
W której a, b, c są współczynnikami równania różniącymi się od zera. A "X"- pierwiastek równania. Uważa się, że równanie kwadratowe ma dwa pierwiastki lub może w ogóle nie mieć rozwiązania. Powstałe korzenie mogą być takie same.
"A"- współczynnik stojący przed pierwiastkiem kwadratowym.
"B"- stoi przed nieznanym w pierwszym stopniu.
"Z" - Wolny Członek równania
Jeśli na przykład mamy równanie postaci:
2x 2 -5x+3=0
W nim „2” jest współczynnikiem wiodącego składnika równania, „-5” jest drugim współczynnikiem, a „3” jest terminem wolnym.
Rozwiązywanie równania kwadratowego
Istnieje wiele różnych sposobów rozwiązywania równań kwadratowych. Jednak w kurs szkolny W matematyce rozwiązanie bada się za pomocą twierdzenia Viety, a także za pomocą dyskryminatora.
Rozwiązanie dyskryminacyjne:
Podczas rozwiązywania za pomocą Ta metoda należy obliczyć dyskryminator korzystając ze wzoru:
![]()
Jeśli podczas obliczeń okaże się, że dyskryminator jest mniejszy od zera, oznacza to, że to równanie nie ma rozwiązań.
Jeśli dyskryminator wynosi zero, równanie ma dwa identyczne rozwiązania. W takim przypadku wielomian można zwinąć za pomocą skróconego wzoru na mnożenie do kwadratu sumy lub różnicy. Następnie rozwiąż to tak równanie liniowe. Lub skorzystaj ze wzoru:
Jeśli dyskryminator jest większy od zera, należy zastosować następującą metodę:

Twierdzenie Viety
Jeśli podano równanie, to znaczy współczynnik składnika wiodącego jest równy jeden, można go użyć Twierdzenie Viety.
Załóżmy więc, że równanie wygląda następująco:
Pierwiastki równania znajdują się w następujący sposób:

Niekompletne równanie kwadratowe
Istnieje kilka opcji uzyskania niepełnego równania kwadratowego, którego forma zależy od obecności współczynników.
1. Jeśli drugi i trzeci współczynnik wynoszą zero (b = 0, do = 0), wówczas równanie kwadratowe będzie wyglądać następująco:
To równanie będzie miało jedyna decyzja. Równość będzie prawdziwa tylko wtedy, gdy rozwiązaniem równania będzie zero.
Niektóre problemy matematyczne wymagają umiejętności obliczenia wartości pierwiastka kwadratowego. Takie problemy obejmują rozwiązywanie równań drugiego rzędu. W tym artykule przedstawimy skuteczna metoda obliczenia pierwiastki kwadratowe i używaj go podczas pracy ze wzorami na pierwiastki równania kwadratowego.
Co to jest pierwiastek kwadratowy?
W matematyce pojęcie to odpowiada symbolowi √. Dane historyczne mówią, że po raz pierwszy zastosowano go około pierwszej połowy XVI wieku w Niemczech (pierwsza niemiecka praca z algebry autorstwa Christopha Rudolfa). Naukowcy uważają, że symbolem jest przekształcona łacińska litera r (radix oznacza po łacinie „rdzeń”).
Pierwiastek dowolnej liczby jest równy wartości, której kwadrat odpowiada wyrażeniu pierwiastkowemu. W języku matematyki definicja ta będzie wyglądać następująco: √x = y, jeśli y 2 = x.
Pierwiastek liczby dodatniej (x > 0) jest także liczbą dodatnią (y > 0), ale jeśli weźmiemy pierwiastek z liczby ujemnej (x< 0), то его результатом уже будет Liczba zespolona, łącznie z jednostką urojoną i.
Oto dwa proste przykłady:
√9 = 3, ponieważ 3 2 = 9; √(-9) = 3i, ponieważ i 2 = -1.
Iteracyjny wzór Herona na znajdowanie wartości pierwiastków kwadratowych
Powyższe przykłady są bardzo proste, a obliczenie w nich pierwiastków nie jest trudne. Trudności zaczynają się pojawiać przy znajdowaniu wartości pierwiastkowych dla dowolnej wartości, której nie można przedstawić w postaci kwadratu Liczba naturalna, na przykład √10, √11, √12, √13, nie mówiąc już o tym, że w praktyce konieczne jest znalezienie pierwiastków dla liczb niecałkowitych: na przykład √(12,15), √(8,5) i tak dalej.

We wszystkich powyższych przypadkach należy zastosować specjalną metodę obliczania pierwiastka kwadratowego. Obecnie znanych jest kilka takich metod: na przykład rozwinięcie szeregu Taylora, dzielenie kolumnowe i inne. Ze wszystkich znanych metod być może najprostszą i najskuteczniejszą jest zastosowanie iteracyjnego wzoru Herona, znanego również jako babilońska metoda wyznaczania pierwiastków kwadratowych (istnieją dowody, że starożytni Babilończycy używali jej w swoich praktycznych obliczeniach).
Niech będzie konieczne wyznaczenie wartości √x. Wzór na znalezienie pierwiastka kwadratowego jest następujący:
a n+1 = 1/2(a n +x/a n), gdzie lim n->∞ (a n) => x.
Rozszyfrujmy ten zapis matematyczny. Aby obliczyć √x, należy przyjąć pewną liczbę a 0 (może być dowolna, ale aby szybko uzyskać wynik, należy ją tak dobrać, aby (a 0) 2 była jak najbliżej x. Następnie podstawimy ją do wskazany wzór do obliczenia pierwiastka kwadratowego i uzyskaj nową liczbę 1, która będzie już bliższa pożądanej wartości. Następnie musisz podstawić 1 do wyrażenia i uzyskać 2. Procedurę tę należy powtarzać aż do wymaganej uzyskuje się dokładność.
Przykład zastosowania iteracyjnej formuły Herona
Opisany powyżej algorytm uzyskiwania pierwiastka kwadratowego z danej liczby może dla wielu wydawać się dość skomplikowany i mylący, ale w rzeczywistości wszystko okazuje się znacznie prostsze, ponieważ formuła ta zbiega się bardzo szybko (szczególnie jeśli zostanie wybrana pomyślna liczba 0) .
Podajmy prosty przykład: musisz obliczyć √11. Wybierzmy 0 = 3, ponieważ 3 2 = 9, czyli bliżej 11 niż 4 2 = 16. Podstawiając do wzoru otrzymujemy:
za 1 = 1/2(3 + 11/3) = 3,333333;
za 2 = 1/2(3,33333 + 11/3,33333) = 3,316668;
za 3 = 1/2(3,316668 + 11/3,316668) = 3,31662.
Nie ma sensu kontynuować obliczeń, ponieważ odkryliśmy, że 2 i 3 zaczynają się różnić dopiero na 5. miejscu po przecinku. Wystarczyło zatem zastosować wzór tylko 2 razy, aby obliczyć √11 z dokładnością do 0,0001.
Obecnie do obliczania pierwiastków powszechnie wykorzystuje się kalkulatory i komputery, warto jednak pamiętać o zaznaczonym wzorze, aby móc ręcznie obliczyć ich dokładną wartość.
Równania drugiego rzędu
Zrozumienie, czym jest pierwiastek kwadratowy i umiejętność jego obliczenia, wykorzystywane jest przy rozwiązywaniu równań kwadratowych. Równania te nazywane są równościami z jedną niewiadomą, których ogólną postać pokazano na poniższym rysunku.

Tutaj c, b i a reprezentują pewne liczby, a a nie może być równe zeru, a wartości c i b mogą być całkowicie dowolne, w tym równe zero.
Wszelkie wartości x, które spełniają równość wskazaną na rysunku, nazywane są jego pierwiastkami (nie należy mylić tego pojęcia z pierwiastkiem kwadratowym √). Ponieważ rozważane równanie jest drugiego rzędu (x 2), nie może być dla niego więcej niż dwóch pierwiastków. Przyjrzyjmy się dalej w artykule, jak znaleźć te korzenie.
Znajdowanie pierwiastków równania kwadratowego (wzór)
Ta metoda rozwiązywania rozważanego rodzaju równości nazywana jest również metodą uniwersalną lub metodą dyskryminacyjną. Można go używać do dowolnych równań kwadratowych. Wzór na dyskryminator i pierwiastki równania kwadratowego jest następujący:

Pokazuje, że pierwiastki zależą od wartości każdego z trzech współczynników równania. Co więcej, obliczenie x 1 różni się od obliczenia x 2 jedynie znakiem przed pierwiastkiem kwadratowym. Wyrażenie radykalne, które jest równe b 2 - 4ac, jest niczym innym jak wyróżnikiem omawianej równości. Dyskryminator we wzorze na pierwiastki równania kwadratowego odgrywa ważną rolę, ponieważ określa liczbę i rodzaj rozwiązań. Tak więc, jeśli jest równe zero, to będzie tylko jedno rozwiązanie, jeśli jest dodatnie, to równanie ma dwa rzeczywiste pierwiastki i ostatecznie ujemny dyskryminator prowadzi do dwóch zespolonych pierwiastków x 1 i x 2.
Twierdzenie Viety lub niektóre własności pierwiastków równań drugiego rzędu
Pod koniec XVI wieku jednemu z twórców współczesnej algebry, Francuzowi, badającemu równania drugiego rzędu, udało się uzyskać właściwości jej pierwiastków. Matematycznie można je zapisać w następujący sposób:
x 1 + x 2 = -b / a i x 1 * x 2 = c / a.
Obie równości każdy może łatwo otrzymać, wystarczy w tym celu wykonać odpowiednie działania matematyczne na pierwiastkach uzyskanych ze wzoru z dyskryminatorem.

Połączenie tych dwóch wyrażeń można słusznie nazwać drugim wzorem na pierwiastki równania kwadratowego, co pozwala odgadnąć jego rozwiązania bez użycia dyskryminatora. W tym miejscu należy zauważyć, że chociaż oba wyrażenia są zawsze poprawne, wygodnie jest ich używać do rozwiązywania równania tylko wtedy, gdy można je rozłożyć na czynniki.
Zadanie utrwalenia zdobytej wiedzy
Zdecydujmy problem matematyczny, w którym zademonstrujemy wszystkie techniki omówione w artykule. Warunki zadania są następujące: musisz znaleźć dwie liczby, których iloczyn wynosi -13, a suma wynosi 4.

Warunek ten od razu przypomina nam twierdzenie Viety, korzystając ze wzorów na sumę pierwiastków kwadratowych i ich iloczyn piszemy:
x 1 + x 2 = -b / a = 4;
x 1 * x 2 = c / a = -13.
Jeśli założymy, że a = 1, to b = -4 i c = -13. Współczynniki te pozwalają nam utworzyć równanie drugiego rzędu:
x 2 - 4x - 13 = 0.
Użyjmy wzoru z dyskryminatorem i uzyskajmy następujące pierwiastki:
x 1,2 = (4 ± √D)/2, D = 16 - 4 * 1 * (-13) = 68.
Oznacza to, że problem został zredukowany do znalezienia liczby √68. Zauważ, że 68 = 4 * 17, zatem korzystając z pierwiastka kwadratowego otrzymujemy: √68 = 2√17.
Skorzystajmy teraz z rozważanego wzoru na pierwiastek kwadratowy: a 0 = 4, wówczas:
za 1 = 1/2(4 + 17/4) = 4,125;
za 2 = 1/2(4,125 + 17/4,125) = 4,1231.
Nie ma potrzeby obliczania 3, ponieważ znalezione wartości różnią się tylko o 0,02. Zatem √68 = 8,246. Podstawiając to do wzoru na x 1,2, otrzymujemy:
x 1 = (4 + 8,246)/2 = 6,123 i x 2 = (4 - 8,246)/2 = -2,123.
Jak widać suma znalezionych liczb jest w rzeczywistości równa 4, ale jeśli znajdziemy ich iloczyn, to będzie on równy -12,999, co spełnia warunki zadania z dokładnością do 0,001.
Przypominamy, że pełne równanie kwadratowe to równanie postaci:
Rozwiązywanie pełnych równań kwadratowych jest trochę trudniejsze (tylko trochę) niż te.
Pamiętać, Każde równanie kwadratowe można rozwiązać za pomocą dyskryminatora!
Nawet niekompletny.
Inne metody pomogą ci to zrobić szybciej, ale jeśli masz problemy z równaniami kwadratowymi, najpierw opanuj rozwiązanie za pomocą dyskryminatora.
1. Rozwiązywanie równań kwadratowych z wykorzystaniem dyskryminatora.
Rozwiązywanie równań kwadratowych za pomocą tej metody jest bardzo proste, najważniejsze jest zapamiętanie sekwencji działań i kilku wzorów.
Jeśli, to równanie ma 2 pierwiastki. Szczególną uwagę należy zwrócić na krok 2.
Dyskryminator D informuje nas o liczbie pierwiastków równania.
- Jeśli, wówczas formuła w tym kroku zostanie zredukowana do. Zatem równanie będzie miało tylko pierwiastek.
- Jeśli, to nie będziemy w stanie wyodrębnić pierwiastka dyskryminatora na tym etapie. Oznacza to, że równanie nie ma pierwiastków.
Przejdźmy do zmysł geometryczny równanie kwadratowe.
Wykresem funkcji jest parabola:
Wróćmy do naszych równań i spójrzmy na kilka przykładów.
Przykład 9
Rozwiązać równanie
Krok 1 pomijamy.
Krok 2.
Znajdujemy wyróżnik:
Oznacza to, że równanie ma dwa pierwiastki.
Krok 3.
Odpowiedź:
Przykład 10
Rozwiązać równanie
Równanie przedstawiono w postaci standardowej, tj Krok 1 pomijamy.
Krok 2.
Znajdujemy wyróżnik:
Oznacza to, że równanie ma jeden pierwiastek.
Odpowiedź:
Przykład 11
Rozwiązać równanie
Równanie przedstawiono w postaci standardowej, tj Krok 1 pomijamy.
Krok 2.
Znajdujemy wyróżnik:
Oznacza to, że nie będziemy w stanie wyodrębnić pierwiastka dyskryminatora. Równanie nie ma pierwiastków.
Teraz wiemy, jak poprawnie zapisać takie odpowiedzi.
Odpowiedź:żadnych korzeni
2. Rozwiązywanie równań kwadratowych z wykorzystaniem twierdzenia Viety
Jeśli pamiętasz, istnieje rodzaj równania, który nazywa się zredukowanym (gdy współczynnik a jest równy):
Równania takie bardzo łatwo rozwiązać korzystając z twierdzenia Viety:
Suma pierwiastków dany równanie kwadratowe jest równe i iloczyn pierwiastków jest równy.
Wystarczy wybrać parę liczb, których iloczyn jest równy wolnemu członowi równania, a suma jest równa drugiemu współczynnikowi, wziętemu z przeciwnym znakiem.
Przykład 12
Rozwiązać równanie
Równanie to można rozwiązać za pomocą twierdzenia Viety, ponieważ .
Suma pierwiastków równania jest równa, tj. otrzymujemy pierwsze równanie:
A iloczyn jest równy:
Skomponujmy i rozwiążmy system:
- I. Kwota jest równa;
- I. Kwota jest równa;
- I. Kwota jest równa.
i są rozwiązaniem układu:
Odpowiedź: ; .
Przykład 13
Rozwiązać równanie
Odpowiedź:
Przykład 14
Rozwiązać równanie
Podane jest równanie, które oznacza:
Odpowiedź:
RÓWNANIA KWADRATOWE. ŚREDNI POZIOM
Co to jest równanie kwadratowe?
Innymi słowy, równanie kwadratowe jest równaniem postaci, gdzie - niewiadoma, - niektóre liczby i.
Liczba nazywana jest najwyższą lub pierwszy współczynnik równanie kwadratowe, - drugi współczynnik, A - Wolny Członek.
Ponieważ jeśli równanie natychmiast stanie się liniowe, ponieważ zniknie.
W tym przypadku i może być równe zeru. W tym równaniu krzesła nazywa się niekompletny.
Jeśli wszystkie warunki są spełnione, to znaczy, że równanie jest kompletny.
Metody rozwiązywania niepełnych równań kwadratowych
Najpierw przyjrzyjmy się metodom rozwiązywania niepełnych równań kwadratowych - są prostsze.
Wyróżniamy następujące typy równań:
I. w tym równaniu współczynnik i wolny wyraz są równe.
II. , w tym równaniu współczynnik jest równy.
III. , w tym równaniu wolny termin jest równy.
Przyjrzyjmy się teraz rozwiązaniu dla każdego z tych podtypów.
Oczywiście to równanie ma zawsze tylko jeden pierwiastek:
Liczba podniesiona do kwadratu nie może być liczbą ujemną, ponieważ po pomnożeniu dwóch liczb ujemnych lub dwóch dodatnich wynik zawsze będzie liczbą dodatnią. Dlatego:
jeśli, to równanie nie ma rozwiązań;
jeśli mamy dwa korzenie
Nie ma potrzeby zapamiętywania tych formuł. Najważniejszą rzeczą do zapamiętania jest to, że nie może być mniejsza.
Przykłady rozwiązywania równań kwadratowych
Przykład 15
Odpowiedź:
Nigdy nie zapominaj o korzeniach ze znakiem ujemnym!
Przykład 16
Kwadrat liczby nie może być ujemny, co oznacza, że równanie
żadnych korzeni.
Aby krótko zapisać, że problem nie ma rozwiązań, używamy ikony pustego zestawu.
Odpowiedź:
Przykład 17
Zatem to równanie ma dwa pierwiastki: i.
Odpowiedź:
Wyjmijmy wspólny czynnik z nawiasów:
Iloczyn jest równy zero, jeśli przynajmniej jeden z czynników jest równy zero. Oznacza to, że równanie ma rozwiązanie, gdy:
Zatem to równanie kwadratowe ma dwa pierwiastki: i.
Przykład:
Rozwiązać równanie.
Rozwiązanie:
Rozważmy lewą stronę równania i znajdźmy pierwiastki:
Odpowiedź:
Metody rozwiązywania pełnych równań kwadratowych
1. Dyskryminujący
Rozwiązywanie równań kwadratowych w ten sposób jest łatwe, najważniejsze jest zapamiętanie sekwencji działań i kilku wzorów. Pamiętaj, że każde równanie kwadratowe można rozwiązać za pomocą dyskryminatora! Nawet niekompletny.
Czy zauważyłeś pierwiastek z wyróżnika we wzorze na pierwiastki?
Ale dyskryminator może być ujemny.
Co robić?
Musimy zwrócić szczególną uwagę na krok 2. Dyskryminator informuje nas o liczbie pierwiastków równania.
- Jeśli, to równanie ma pierwiastki:
- Jeśli to równanie ma te same pierwiastki, a właściwie jeden pierwiastek:
Takie korzenie nazywane są podwójnymi korzeniami.
- Jeśli, to pierwiastek dyskryminatora nie jest wyodrębniany. Oznacza to, że równanie nie ma pierwiastków.
Dlaczego to możliwe różne ilości korzenie?
Przejdźmy do geometrycznego znaczenia równania kwadratowego. Wykresem funkcji jest parabola:

W szczególnym przypadku, którym jest równanie kwadratowe, .
Oznacza to, że pierwiastkami równania kwadratowego są punkty przecięcia z osią (osią) odciętej.
Parabola może w ogóle nie przecinać osi lub może przecinać ją w jednym (gdy wierzchołek paraboli leży na osi) lub w dwóch punktach.
Ponadto współczynnik odpowiada za kierunek gałęzi paraboli. Jeśli, to gałęzie paraboli są skierowane w górę, a jeśli, to w dół.
4 przykłady rozwiązywania równań kwadratowych
Przykład 18
Odpowiedź:
Przykład 19
Odpowiedź: .
Przykład 20
Odpowiedź:
Przykład 21
Oznacza to, że nie ma rozwiązań.
Odpowiedź: .
2. Twierdzenie Viety
Korzystanie z twierdzenia Viety jest bardzo łatwe.
Wszystko czego potrzebujesz to ulec poprawie taka para liczb, której iloczyn jest równy wolnemu członowi równania, a suma jest równa drugiemu współczynnikowi, wziętemu z przeciwnym znakiem.
Należy pamiętać, że twierdzenie Viety można zastosować jedynie w zredukowane równania kwadratowe ().
Spójrzmy na kilka przykładów:
Przykład 22
Rozwiązać równanie.
Rozwiązanie:
Równanie to można rozwiązać za pomocą twierdzenia Viety, ponieważ . Inne współczynniki: ; .
Suma pierwiastków równania wynosi:
A iloczyn jest równy:
Wybierzmy pary liczb, których iloczyn jest równy i sprawdźmy, czy ich suma jest równa:
- I. Kwota jest równa;
- I. Kwota jest równa;
- I. Kwota jest równa.
i są rozwiązaniem układu:
Zatem i są pierwiastkami naszego równania.
Odpowiedź: ; .
Przykład 23
Rozwiązanie:
Wybierzmy pary liczb, które dają iloczyn, a następnie sprawdźmy, czy ich suma jest równa:
i: dają w sumie.
i: dają w sumie. Aby uzyskać, wystarczy po prostu zmienić znaki rzekomych korzeni: a przecież i produkt.
Odpowiedź:
Przykład 24
Rozwiązanie:
Wolny wyraz równania jest ujemny, a zatem iloczyn pierwiastków jest liczba ujemna. Jest to możliwe tylko wtedy, gdy jeden z pierwiastków jest ujemny, a drugi dodatni. Zatem suma pierwiastków jest równa różnice w ich modułach.
Wybierzmy pary liczb, które dają iloczyn, a których różnica jest równa:
i: ich różnica jest równa - nie pasuje;
oraz: - nie nadaje się;
oraz: - nie nadaje się;
oraz: - odpowiedni. Pozostaje tylko pamiętać, że jeden z pierwiastków jest ujemny. Ponieważ ich suma musi być równa, pierwiastek o mniejszym module musi być ujemny: . Sprawdzamy:
Odpowiedź:
Przykład 25
Rozwiązać równanie.
Rozwiązanie:
Podane jest równanie, które oznacza:
Wolny termin jest ujemny, a zatem iloczyn pierwiastków jest ujemny. Jest to możliwe tylko wtedy, gdy jeden pierwiastek równania jest ujemny, a drugi dodatni.
Wybierzmy pary liczb, których iloczyn jest równy, a następnie określmy, które pierwiastki powinny mieć znak ujemny:
Oczywiście tylko korzenie i nadają się do pierwszego warunku:
Odpowiedź:
Przykład 26
Rozwiązać równanie.
Rozwiązanie:
Podane jest równanie, które oznacza:
Suma pierwiastków jest ujemna, co oznacza, że przynajmniej jeden z pierwiastków jest ujemny. Ale ponieważ ich iloczyn jest dodatni, oznacza to, że oba pierwiastki mają znak minus.
Wybierzmy pary liczb, których iloczyn jest równy:
Oczywiście pierwiastkami są liczby i.
Odpowiedź:
Zgadzam się, bardzo wygodnie jest wymyślić korzenie ustnie, zamiast liczyć ten paskudny dyskryminator.
Staraj się korzystać z twierdzenia Viety tak często, jak to możliwe!
Ale twierdzenie Viety jest potrzebne, aby ułatwić i przyspieszyć znalezienie pierwiastków.
Aby móc z niego skorzystać, należy doprowadzić działania do automatyzmu. I w tym celu rozwiąż pięć kolejnych przykładów.
Ale nie oszukuj: nie możesz używać dyskryminatora! Tylko twierdzenie Viety!
5 przykładów twierdzenia Viety na pracę niezależną
Przykład 27
Zadanie 1. ((x)^(2))-8x+12=0
Zgodnie z twierdzeniem Viety:
Tradycyjnie selekcję zaczynamy od utworu:
Nie nadaje się ze względu na ilość;
: ilość jest dokładnie taka, jakiej potrzebujesz.
Odpowiedź: ; .
Przykład 28
Zadanie 2.
I znowu nasze ulubione twierdzenie Viety: suma musi być równa i iloczyn musi być równy.
Ale ponieważ tak nie musi być, ale zmieniamy znaki pierwiastków: i (w sumie).
Odpowiedź: ; .
Przykład 29
Zadanie 3.
Hmm... Gdzie to jest?
Musisz przenieść wszystkie terminy do jednej części:
Suma pierwiastków jest równa iloczynowi.
OK, przestań! Równanie nie jest podane.
Ale twierdzenie Viety ma zastosowanie tylko w danych równaniach.
Najpierw musisz podać równanie.
Jeśli nie potrafisz przewodzić, porzuć ten pomysł i rozwiąż go w inny sposób (na przykład poprzez dyskryminację).
Przypomnę, że podanie równania kwadratowego oznacza zrównanie współczynnika wiodącego:
Wtedy suma pierwiastków jest równa i iloczynowi.
Tutaj wybór jest tak prosty, jak obieranie gruszek: w końcu jest to liczba pierwsza (przepraszam za tautologię).
Odpowiedź: ; .
Przykład 30
Zadanie 4.
Wolny członek jest ujemny.
Co jest w tym specjalnego?
Faktem jest, że korzenie będą miały różne znaki.
A teraz podczas selekcji sprawdzamy nie sumę pierwiastków, ale różnicę w ich modułach: ta różnica jest równa, ale iloczyn.
Zatem pierwiastki są równe i, ale jeden z nich to minus.
Twierdzenie Viety mówi nam, że suma pierwiastków jest równa drugiemu współczynnikowi o przeciwnym znaku, to znaczy.
Oznacza to, że mniejszy pierwiastek będzie miał minus: i, ponieważ.
Odpowiedź: ; .
Przykład 31
Zadanie 5.
Co powinieneś zrobić najpierw?
Zgadza się, podaj równanie:
Ponownie: wybieramy współczynniki liczby, a ich różnica powinna być równa:
Pierwiastki są równe i, ale jeden z nich to minus. Który? Ich suma powinna być równa, co oznacza, że minus będzie miał większy pierwiastek.
Odpowiedź: ; .
Podsumować
- Twierdzenie Viety jest używane tylko w podanych równaniach kwadratowych.
- Korzystając z twierdzenia Viety, możesz znaleźć pierwiastki poprzez selekcję, ustnie.
- Jeśli równanie nie zostanie podane lub nie zostanie znaleziona odpowiednia para czynników terminu wolnego, wówczas nie ma pełnych pierwiastków i należy je rozwiązać w inny sposób (na przykład poprzez dyskryminator).
3. Metoda wyboru całego kwadratu
Jeśli wszystkie wyrazy zawierające niewiadomą przedstawimy w postaci wyrazów ze skróconych wzorów na mnożenie – kwadratu sumy lub różnicy – to po zastąpieniu zmiennych równanie można przedstawić w postaci niepełnego równania kwadratowego typu.
Na przykład:
Przykład 32
Rozwiązać równanie: .
Rozwiązanie:
Odpowiedź:
Przykład 33
Rozwiązać równanie: .
Rozwiązanie:
Odpowiedź:
Ogólnie transformacja będzie wyglądać następująco:
Oznacza to: .
Nic Ci nie przypomina?
To dyskryminacja! Dokładnie w ten sposób otrzymaliśmy wzór na dyskryminację.
RÓWNANIA KWADRATOWE. KRÓTKO O NAJWAŻNIEJSZYCH RZECZACH
Równanie kwadratowe- jest to równanie postaci, w której - niewiadoma, - współczynniki równania kwadratowego, - człon wolny.
Pełne równanie kwadratowe- równanie, w którym współczynniki nie są równe zeru.
Zredukowane równanie kwadratowe- równanie, w którym współczynnik, czyli: .
Niekompletne równanie kwadratowe- równanie, w którym współczynnik i/lub człon wolny c są równe zeru:
- jeśli współczynnik, równanie wygląda następująco: ,
- jeżeli istnieje wyraz wolny, równanie ma postać: ,
- jeśli i, równanie wygląda następująco: .
1. Algorytm rozwiązywania niepełnych równań kwadratowych
1.1. Niepełne równanie kwadratowe postaci, gdzie:
1) Wyraźmy niewiadomą: ,
2) Sprawdź znak wyrażenia:
- jeżeli, to równanie nie ma rozwiązań,
- jeśli, to równanie ma dwa pierwiastki.
1.2. Niepełne równanie kwadratowe postaci, gdzie:
1) Wyjmijmy wspólny czynnik z nawiasów: ,
2) Iloczyn jest równy zero, jeżeli przynajmniej jeden z czynników jest równy zero. Zatem równanie ma dwa pierwiastki:
1.3. Niepełne równanie kwadratowe postaci, gdzie:
To równanie ma zawsze tylko jeden pierwiastek: .
2. Algorytm rozwiązywania pełnych równań kwadratowych w postaci gdzie
2.1. Rozwiązanie wykorzystujące dyskryminator
1) Sprowadźmy równanie do postaci standardowej: ,
2) Obliczmy dyskryminator korzystając ze wzoru: , który wskazuje liczbę pierwiastków równania:
3) Znajdź pierwiastki równania:
- jeśli, to równanie ma pierwiastki, które można znaleźć według wzoru:
- jeśli, to równanie ma pierwiastek, który można znaleźć za pomocą wzoru:
- jeśli, to równanie nie ma pierwiastków.
2.2. Rozwiązanie wykorzystujące twierdzenie Viety
Suma pierwiastków zredukowanego równania kwadratowego (równanie postaci gdzie) jest równa, a iloczyn pierwiastków jest równy, tj. , A.
2.3. Rozwiązanie metodą wyboru pełnego kwadratu
Równanie kwadratowe lub równanie drugiego stopnia z jedną niewiadomą to równanie, które po przekształceniach można sprowadzić do postaci:
topór 2 + bx + C = 0 - równanie kwadratowe
Gdzie X- to niewiadoma, ale A, B I C- współczynniki równania. W równaniach kwadratowych A zwany pierwszym współczynnikiem ( A ≠ 0), B nazywa się drugim współczynnikiem i C zwany znanym lub wolnym członkiem.
Równanie:
topór 2 + bx + C = 0
zwany kompletny równanie kwadratowe. Jeżeli jeden ze współczynników B Lub C jest równa zero lub oba te współczynniki są równe zero, wówczas równanie przedstawia się w postaci niepełnego równania kwadratowego.
Zredukowane równanie kwadratowe
Pełne równanie kwadratowe można sprowadzić do wygodniejszej postaci, dzieląc wszystkie jego wyrazy przez A, czyli dla pierwszego współczynnika:
Równanie X 2 + pikseli + Q= 0 nazywa się zredukowanym równaniem kwadratowym. Dlatego każde równanie kwadratowe, w którym pierwszy współczynnik jest równy 1, można nazwać zredukowanym.
Na przykład równanie:
X 2 + 10X - 5 = 0
jest zmniejszona, a równanie:
3X 2 + 9X - 12 = 0
można zastąpić powyższym równaniem, dzieląc wszystkie jego wyrazy przez -3:
X 2 - 3X + 4 = 0
Rozwiązywanie równań kwadratowych
Aby rozwiązać równanie kwadratowe, należy je sprowadzić do jednej z następujących postaci:
topór 2 + bx + C = 0
topór 2 + 2kx + C = 0
X 2 + pikseli + Q = 0
Dla każdego rodzaju równania istnieje własny wzór na znalezienie pierwiastków:
Zwróć uwagę na równanie:
topór 2 + 2kx + C = 0
to jest przekształcone równanie topór 2 + bx + C= 0, w którym współczynnik B- parzysty, co pozwala na zastąpienie go typem 2 k. Dlatego wzór na znalezienie pierwiastków tego równania można uprościć, podstawiając do niego 2 k zamiast B:

Przykład 1. Rozwiązać równanie:
3X 2 + 7X + 2 = 0
Ponieważ drugi współczynnik w równaniu nie jest liczbą parzystą, a pierwszy współczynnik nie jest równy jedności, pierwiastków będziemy szukać korzystając z pierwszego wzoru, zwanego ogólnym wzorem na pierwiastki równania kwadratowego. Najpierw
A = 3, B = 7, C = 2
Teraz, aby znaleźć pierwiastki równania, po prostu podstawiamy wartości współczynników do wzoru:

| X 1 = | -2 | = - | 1 | , X 2 = | -12 | = -2 |
| 6 | 3 | 6 |
| Odpowiedź: - | 1 | , -2. |
| 3 |
Przykład 2:
X 2 - 4X - 60 = 0
Ustalmy, jakie są współczynniki:
A = 1, B = -4, C = -60
Ponieważ w równaniu jest drugi współczynnik Liczba parzysta, wówczas skorzystamy ze wzoru na równania kwadratowe z parzystym drugim współczynnikiem:
X 1 = 2 + 8 = 10, X 2 = 2 - 8 = -6
Odpowiedź: 10, -6.
Przykład 3.
y 2 + 11y = y - 25
Sprowadźmy równanie do Ogólny wygląd:
y 2 + 11y = y - 25
y 2 + 11y - y + 25 = 0
y 2 + 10y + 25 = 0
Ustalmy, jakie są współczynniki:
A = 1, P = 10, Q = 25
Ponieważ pierwszy współczynnik jest równy 1, pierwiastków będziemy szukać korzystając ze wzoru na powyższe równania z parzystym drugim współczynnikiem:
Odpowiedź: -5.
Przykład 4.
X 2 - 7X + 6 = 0
Ustalmy, jakie są współczynniki:
A = 1, P = -7, Q = 6
Ponieważ pierwszy współczynnik jest równy 1, pierwiastków będziemy szukać korzystając ze wzoru na powyższe równania z drugim nieparzystym współczynnikiem:
X 1 = (7 + 5) : 2 = 6, X 2 = (7 - 5) : 2 = 1