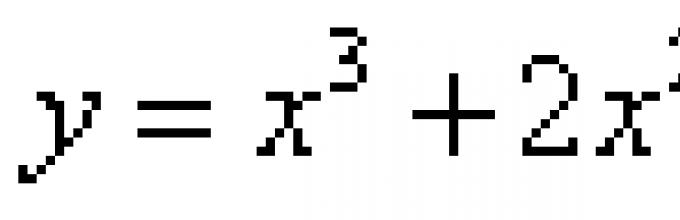Styczna jest linią prostą , który dotyka wykresu funkcji w jednym punkcie i którego wszystkie punkty znajdują się w najmniejszej odległości od wykresu funkcji. Dlatego styczna przechodzi styczną do wykresu funkcji pod pewnym kątem, a kilka stycznych pod różnymi kątami nie może przejść przez punkt styczności. Równania styczne i równania normalne do wykresu funkcji konstruuje się za pomocą pochodnej.
Równanie styczne wyprowadza się z równania linii .
Wyprowadźmy równanie stycznej, a następnie równanie normalnej do wykresu funkcji.
y = kx + B .
W nim k- współczynnik kątowy.
Stąd otrzymujemy następujący wpis:
y - y 0 = k(X - X 0 ) .
Wartość pochodna F "(X 0 ) Funkcje y = F(X) w tym punkcie X0 równy nachyleniu k= tg φ styczna do wykresu funkcji poprowadzonej przez punkt M0 (X 0 , y 0 ) , Gdzie y0 = F(X 0 ) . To jest znaczenie geometryczne pochodna .
W ten sposób możemy wymienić k NA F "(X 0 ) i uzyskaj następujące informacje równanie stycznej do wykresu funkcji :
y - y 0 = F "(X 0 )(X - X 0 ) .
W zadaniach polegających na ułożeniu równania stycznej na wykresie funkcji (i do nich wkrótce przejdziemy) konieczne jest sprowadzenie równania otrzymanego z powyższego wzoru do postaci równanie prostej w postaci ogólnej. Aby to zrobić, musisz przenieść wszystkie litery i cyfry na lewą stronę równania, a zero pozostawić po prawej stronie.
Teraz o równaniu normalnym. Normalna - jest to prosta przechodząca przez punkt styczności z wykresem funkcji prostopadłej do stycznej. Normalne równanie :
(X - X 0 ) + F "(X 0 )(y - y 0 ) = 0
Na rozgrzewkę prosimy o samodzielne rozwiązanie pierwszego przykładu, a następnie spojrzenie na rozwiązanie. Można mieć nadzieję, że to zadanie nie będzie dla naszych czytelników „zimnym prysznicem”.
Przykład 0. Utwórz równanie styczne i równanie normalne dla wykresu funkcji w punkcie M (1, 1) .
Przykład 1. Zapisz równanie styczne i równanie normalne dla wykresu funkcji ![]() , jeśli odcięta jest styczna .
, jeśli odcięta jest styczna .
Znajdźmy pochodną funkcji:
Teraz mamy wszystko, co należy podstawić do wpisu podanego w pomocy teoretycznej, aby otrzymać równanie styczne. Dostajemy
![]()
W tym przykładzie mieliśmy szczęście: współczynnik nachylenia okazał się zerowy, więc nie było potrzeby osobnego doprowadzania równania do jego ogólnej postaci. Teraz możemy utworzyć równanie normalne:
![]()
Na rysunku poniżej: wykres funkcji w kolorze bordowym, tangens Zielony kolor, pomarańczowy normalny.

Następny przykład również nie jest skomplikowany: funkcja, podobnie jak w poprzednim, również jest wielomianem, ale nachylenie nie będzie równe zero, dlatego zostanie dodany jeszcze jeden krok - doprowadzenie równania do postaci ogólnej.
Przykład 2.
Rozwiązanie. Znajdźmy współrzędną punktu stycznego:
Znajdźmy pochodną funkcji:
![]() .
.
Znajdźmy wartość pochodnej w punkcie styczności, czyli nachyleniu stycznej:
Podstawiamy wszystkie uzyskane dane do „pustego wzoru” i otrzymujemy równanie styczne:
![]()
Doprowadzamy równanie do jego ogólnej postaci (zbieramy wszystkie litery i cyfry inne niż zero po lewej stronie, a zero zostawiamy po prawej stronie):
Tworzymy równanie normalne:

Przykład 3. Zapisz równanie stycznej i równanie normalnej do wykresu funkcji, jeśli odcięta jest punktem styczności.
Rozwiązanie. Znajdźmy współrzędną punktu stycznego:
Znajdźmy pochodną funkcji:
![]() .
.
Znajdźmy wartość pochodnej w punkcie styczności, czyli nachyleniu stycznej:
![]() .
.
Znajdujemy równanie styczne:

Zanim doprowadzisz równanie do jego ogólnej postaci, musisz je trochę „przeczesać”: pomnóż wyraz po wyrazie przez 4. Robimy to i doprowadzamy równanie do jego ogólnej postaci:
Tworzymy równanie normalne:

Przykład 4. Zapisz równanie stycznej i równanie normalnej do wykresu funkcji, jeśli odcięta jest punktem styczności.
Rozwiązanie. Znajdźmy współrzędną punktu stycznego:
![]() .
.
Znajdźmy pochodną funkcji:
Znajdźmy wartość pochodnej w punkcie styczności, czyli nachyleniu stycznej:
![]() .
.
Otrzymujemy równanie styczne:
Doprowadzamy równanie do jego ogólnej postaci:
Tworzymy równanie normalne:
![]()
Częstym błędem przy pisaniu równań stycznych i normalnych jest niezauważenie, że podana w przykładzie funkcja jest złożona i obliczenie jej pochodnej jako pochodnej funkcji prostej. Poniższe przykłady pochodzą już z złożone funkcje(odpowiednia lekcja otworzy się w nowym oknie).
Przykład 5. Zapisz równanie stycznej i równanie normalnej do wykresu funkcji, jeśli odcięta jest punktem styczności.
Rozwiązanie. Znajdźmy współrzędną punktu stycznego:
Uwaga! Funkcja ta jest złożona, ponieważ argument tangens (2 X) sama w sobie jest funkcją. Dlatego pochodną funkcji znajdujemy jako pochodną funkcji zespolonej.
Definicja: normalna do krzywej y = ¦(x) w punkcie M 0 jest prostą przechodzącą przez punkt M 0 i prostopadłą do stycznej w punkcie M 0 do tej krzywej.
Napiszmy równanie stycznej i normalnej, znając równanie krzywej i współrzędne punktu M 0. Styczna ma współczynnik kątowy k = t g = ¦, (x 0). Z geometrii analitycznej wiadomo, że prosta ma równanie y-y 0 = k(x – x 0).
Dlatego równanie styczne ma postać: y - y 0 = ¦, (x 0)(x – x 0); (1)
Współczynnik kątowy normalnej wynosi Kn = (ponieważ są prostopadłe), ale równanie normalnej wygląda następująco:
y-y 0 =(-1/ ¦, (x 0)(x – x 0); (2)
Jeżeli w danym punkcie nie ma pochodnej, to w tym punkcie nie istnieje również styczna.
Na przykład funkcja ¦(x)=|x| w punkcie x=0 nie ma pochodnej.
lim D x ®0 (D y/ D x)= lim D x ®0 (| D x|/ D x)=
Istnieją jednostronne granice, ale nie istnieje lim D x ®0 (D y/D x).
Styczna też.
Punkt ten nazywany jest punktem narożnym wykresu.
§4. Związek między ciągłością a różniczkowalnością funkcji.
Prawidłowe jest następujące twierdzenie o funkcji różniczkowalnej.
Twierdzenie: jeśli funkcja y = ¦(x) ma skończoną pochodną w punkcie x 0, to jest w tym punkcie ciągła.
Dowód:
Ponieważ w punkcie x 0 występuje pochodna ¦, (x 0), tj. istnieje granica
lim D x ®0 (D y/ D x)= ¦, (x 0), następnie D y/ D x= ¦, (x 0)+, gdzie
B.m.v., w zależności od D x. Gdy D x®0, ®0, ponieważ = (D y/ D x) - ¦, (x 0) ®0 przy D x®0
Stąd mamy: D y= ¦, (x 0) D x + D x.
Ale wtedy
Nieskończenie mały przyrost argumentu odpowiada nieskończenie małemu przyrostowi funkcji, zatem ¦(x) jest ciągłe w punkcie x 0 .
Ważne jest, aby to zrozumieć twierdzenie odwrotne nie prawda!
Nie każdy funkcja ciągła jest różniczkowalna.
Zatem ¦(x) =|x| jest ciągła w punkcie x 0 =0, wykres jest linią ciągłą, ale ¦, (0) nie istnieje.
§5. Pochodne funkcji stałych, sinusowych, cosinusowych i potęgowych.
1. y= ¦(x) =c; y, = (c), = 0; (1)
Dowód:
a) w dowolnym punkcie x ¦(x) = c
b) podaj x przyrost D x, x + D x, wartość funkcji ¦ (x + D x) = c;
c) ¦ (x + re x)- ¦ (x)= с- с= 0;
d) D y/ re x = 0/ re x = 0
e) lim D x ®0 (D y/ D x)= lim D x ®0 0 = 0
2. y= grzech x; y, = (sin x), = cos x; (2)
Dowód:
a) w dowolnym punkcie x ¦(x) = grzech x;
b) podaj x przyrost D x, x + D x, wartość funkcji
Temat : Pojęcia stycznej i normalnej.
Równania styczne i normalne.
Cele:
Temat: zapoznanie uczniów z pojęciami: styczna i normalna do krzywej; konsolidować te koncepcje podczas rozwiązywania problemów związanych z układaniem równań stycznych i normalnych; dowiedz się, jakie właściwości mają współczynniki kątowe stycznej i normalnej.
Rozmowny: argumentuj swój punkt widzenia, argumentuj i broń swojego stanowiska w sposób niewrogi wobec przeciwników; móc się słuchać i słyszeć siebie nawzajem.
Kognitywny : ustalić związki przyczynowo-skutkowe; wyrazić znaczenie sytuacji za pomocą różnych środków (rysunki, symbole, diagramy, znaki).
Przepisy: zaakceptować cel poznawczy, zachowują go podczas wykonywania działań edukacyjnych, regulują cały proces ich realizacji i wyraźnie spełniają wymagania zadania poznawczego.
Osobisty: kształtowanie zainteresowania poznawczego uczeniem się nowych rzeczy, motywacja do samodzielnej i zbiorowej działalności badawczej.
Podczas zajęć:
1. Aktualizacja wiedza podstawowa studenci:
(Wprowadzenie pojęć stycznej i normalnej do krzywej)
Znamy analityczne i fizyczne znaczenie pochodnej: (odpowiedzi uczniów :
znaczenie analityczne to znaczenie fizyczne, to szybkość procesu określona przez funkcję).
Odkryjmy geometryczne znaczenie pochodnej.
W tym celu wprowadzamy pojęcie stycznej do krzywej w danym punkcie.
Z kurs szkolny geometrii, znasz pojęcie stycznej do okręgu. (odpowiedzi uczniów : styczną do okręgu definiuje się jako linię prostą leżącą w tej samej płaszczyźnie co okrąg i mającą z nią jeden wspólny punkt).
Ale taka definicja stycznej nie ma zastosowania w przypadku dowolnej krzywej. Na przykład w przypadku paraboli każda oś ma po jednej wspólny punkt z parabolą. Jednakże oś jest styczna do paraboli, ale oś nie. Dajmy ogólna definicja styczna do krzywa w danym punkcie.
Niech niektóre punkty dowolnej krzywej będą sieczną krzywej. Gdy punkt zbliża się do krzywej, sieczna będzie się obracać wokół tego punktu
Definicja. Nazywa się położenie graniczne siecznej dla nieograniczonego zbliżania się do punktu po krzywejtangens do krzywej w tym punkcie
Definicja . Normalna do krzywej w punkcie jest linią prostą przechodzącą przez punkt prostopadły do stycznej do krzywej w tym punkcie.
Jeśli jest styczną do krzywej w punkcie,
wówczas prostopadła będzie normalną do krzywej w tym punkcie
Wyjaśnienie nowego materiału:
(Dowiedzmy się, jakie jest geometryczne znaczenie pochodnej , jakie właściwości mają współczynniki kątowe stycznej i normalnej?
Niech krzywa będzie wykresem funkcji. Zwrotnica
leżą na wykresie funkcji. Linia prosta jest styczna do krzywej.
Kąt styczny
Pochodna funkcji w punkcie jest równa tangensowi kąta nachylenia stycznej narysowanej w punkcie lub nachyleniu stycznej do wykresu funkcji w tym punkcie .
Równanie styczne do krzywej w punkcie ma postać
Normalne równanie do krzywej w punkcie ma postać
(3)
Problematyczne kwestie : spójrz na równania styczne i normalne, jakie są ich różnice i podobieństwa?
Czemu równa się produkt? Dlaczego to się dzieje?
(Uczniowie muszą udzielić następujących odpowiedzi na pytania: -1, ponieważ styczna i normalna są wzajemnie prostopadłe)
Utrwalenie materiału teoretycznego w praktyce:
( Rozwiązywanie problemów w klasie)
Przykład 1. Oblicz współczynniki kątowe stycznych do paraboli w punktach.
Rozwiązanie. Z geometrycznego znaczenia pochodnej (wzór 1) nachylenie stycznej.
Znajdźmy pochodną funkcji: .
. Stąd, .
Znajdźmy wartość pochodnej w tym punkcie
Stąd, .
Przykład 2. Narysuj styczne paraboli w punktach. Znajdź kąty nachylenia stycznych do osi Wołu.
Rozwiązanie. Według wzoru (1)
Znajdźmy to. .
Obliczmy wartość pochodnej w punkcie: .
Dlatego i.
Podobnie w tym punkcie.
Dlatego i
Przykład 3. W którym punkcie styczna do krzywej jest nachylona do osi Wołu?
pod kątem
Rozwiązanie. Według wzoru (1)
; . Dlatego i
Podstawiając do funkcji, otrzymujemy. Rozumiemy, o co chodzi.
Przykład 4. Napisz równanie stycznej i normalnej do paraboli w punkcie
Rozwiązanie. Równanie stycznej do krzywej wygląda następująco:
Od warunków problemowych. Znajdźmy pochodną.
; .
Podstawiając wszystkie wartości do równania otrzymujemy równanie styczne
Lub.
Utwórzmy równanie normalne, korzystając ze wzoru:
Lub
Zadania dla niezależna decyzja:
1. Znajdź współczynnik kątowy stycznej poprowadzonej do krzywej w tym punkcie.
2. Krzywą podaje równanie. Wyznacz kąty nachylenia stycznych do dodatniego kierunku osi narysowanej do krzywej w punktach w punktach z odciętymi.
3. Znajdź punkt na krzywej, w którym styczna jest równoległa do prostej.
4. W którym punkcie styczna do krzywej jest: a) równoległa do osi; b) tworzy z osią kąt 45°?
5. Znajdź odciętą punktu paraboli, w którym styczna jest równoległa do osi odciętych.
6. Znajdź współczynnik kątowy stycznej poprowadzonej do krzywej w tym punkcie.
7. W którym punkcie styczna do krzywej tworzy z osią kąt 30°?
8. W którym punkcie styczna do wykresu funkcji tworzy kąt 135?
z osią?
9. W którym punkcie styczna do wykresu funkcji jest równoległa do osi x?
10. W jakich punktach współczynnik kątowy stycznej do paraboli sześciennej jest równy 3?
11. Znajdź kąt nachylenia stycznej do krzywej w punkcie, którego odcięta jest równa 2.
12.Ułóż równanie stycznej do paraboli w punkcie z odciętą
13.Ułóż równanie stycznej do hiperboli w punkcie
14.Ułóż równanie stycznej do krzywej w punkcie.
15.Znajdź styczną do krzywej w punkcie z odciętą.
Odpowiedzi : 1) .12 2). 45°,arctg 5 3) .(1;1) 4) .(0;-1) (0,5;-0,75) 5) .1/2 6) .1 7) .(/6;61/12) 8) .(0:-1) (4;3) 9) .(0;4) (1;-5) 10) .(1;1) (-1;-1) 11) . 45°12) .y = -2x-113) .y = -x+214) .y=4x+615) .y = 4x-2.
Kryterium oceny : „5”- 15 zadań
„4”- 11-14 zadań
„3”- 8 zadań
4. Podsumowanie lekcji : cieniowanie; + i – lekcja dla ucznia (co zrozumiałeś, a co jeszcze musisz zrozumieć?)
5. Praca domowa: przygotuj odpowiedzi na pytania:
Zdefiniuj styczną do krzywej.
Jaka jest normalna do krzywej?
Jakie jest geometryczne znaczenie pochodnej? Zapisz formułę.
Zapisz równanie stycznej do krzywej w tym punkcie.
Zapisz w tym punkcie równanie normalnej do krzywej.
Rozwiąż zadania 1-15 dotyczące wyboru kryterium oceny;dodatkowo na zamówienie : utwórz i rozwiąż kartę na ten temat.
Równanie normalne w postaci ogólnej zapisuje się jako:
Jeśli funkcja jest określona w postać parametryczna x(t) , y(t) , wówczas równanie normalne wyznacza się ze wzoru:
(x–x 0)x’+(y-y 0)y’=0
Cel usługi. Ta usługa ma na celu znalezienie równania normalnej do krzywej. Rozwiązanie jest sporządzone w formacie Word. Aby otrzymać równanie należy wybrać typ danej funkcji.
Algorytm komponowania równania normalnej do wykresu funkcji
- Obliczenie wartości funkcji y 0 w punkcie x 0: y 0 = f(x 0). Jeśli określono wartość początkową y 0, przejdź do kroku 2.
- Znajdowanie pochodnej y”(x).
- Obliczanie wartości pochodnej przy x 0.
- Zapisanie równania normalnej do krzywej w postaci: y k = y 0 - 1/y"(y 0)(x - x 0)
Przykład Zadanie nr 1
Znajdź równanie normalnej do paraboli y = 1/2*x 2 w punkcie (-2;2).
Rozwiązanie znaleźć za pomocą kalkulatora.
Zapiszmy równania normalne w postaci ogólnej: ![]()
Zgodnie z warunkami zadania x 0 = -2, następnie y 0 = 2
Teraz znajdźmy pochodną:
y" = (1/2 x 2)" = x
stąd:
f"(-2) = -2 = -2
W rezultacie mamy: ![]()
Lub
y k = 1/2 x+3
Zadanie nr 2
Zapisz równania normalnej do krzywej y 2 -1/2*x 3 -8 w punkcie M 0 (0;2).
Rozwiązanie.
Ponieważ funkcja jest określona w sposób dorozumiany, szukamy pochodnej korzystając ze wzoru: 
Dla naszej funkcji: ![]()
Następnie: 
Lub
stąd:
F x "(0;2) = 3 / 4 0 2 /2 = 0
W rezultacie mamy: ![]()
Lub
x = 0
Zadanie nr 3
Zapisz równania normalnej do elipsy podanej w postaci parametrycznej: x = 5*sqrt(2)*cos(t);y = 3*sqrt(2)*sin(t) w punkcie M 0 (-5;3 ).
Rozwiązanie.
Zapiszmy równania normalne dla funkcji określonej w postaci parametrycznej:
(x - x 0)x" + (y - y 0)y" = 0
Ten punkt M 0 (-5;3) odpowiada wartości t = 3 / 4 π
Dla naszej funkcji: ![]()
![]()
stąd:
W rezultacie mamy:
(x +5)-5 + (y - 3)-3 = 0
Lub
y k = -5x-3y-16
Jak znaleźć równanie normalnej do wykresu funkcji w dany punkt?
Na tej lekcji nauczymy się, jak znaleźć równanie normalnej do wykres funkcji w pewnym momencie i przyjrzyj się licznym przykładom odnoszącym się do tego problemu. Aby właściwie przyswoić materiał, trzeba zrozumieć geometryczne znaczenie pochodnej i móc je znaleźć przynajmniej na poziomie następujących artykułów:
Jak znaleźć pochodną? Pochodna funkcji zespolonej I .
Wymienione lekcje pozwolą „manekinom” szybko poruszać się po temacie i doskonalić umiejętności różnicowania niemal od zera. całkowite zero. Zasadniczo poniżej znajduje się szczegółowa kontynuacja akapitu dot równanie styczne Trzeci artykuł z powyższej listy. Dlaczego kontynuacja? Równanie normalne jest ściśle powiązane z równaniem stycznym. Rozważę między innymi problemy dotyczące konstrukcji równań tych prostych w sytuacjach, w których występuje funkcja jest określone pośrednio Lub parametrycznie .
Ale najpierw odświeżmy nasze wspomnienia: jeśli funkcja różniczkowalne w pewnym momencie (tj. jeśli istnieje finał pochodna), to równanie stycznej do wykresu funkcji w punkcie można znaleźć korzystając ze wzoru:
Jest to najczęstszy przypadek, z jakim spotkaliśmy się już na lekcji. Najprostsze problemy z instrumentami pochodnymi . Jednak sprawa nie ogranicza się do tego: jeśli w punkcie istnieje nieskończona pochodna: , to styczna będzie równoległa do osi i jej równanie będzie miało postać . Standardowy przykład: funkcja z pochodną zmierzającą do nieskończoności punkt krytyczny . Odpowiednia tangens zostanie wyrażona równaniem: (oś rzędnych).
Jeżeli pochodna nie istnieje (na przykład pochodna w punkcie), to oczywiście nie istnieje i wspólna tangens .
O tym, jak rozróżnić dwa ostatnie przypadki, opowiem nieco później, ale na razie wróćmy do głównego wątku dzisiejszej lekcji:
Co jest normalne? Normalna do wykresu funkcji w punkcie prosty , przechodząc przez dany punkt prostopadle do stycznej do wykresu funkcji w tym punkcie (jest oczywiste, że tangens musi istnieć). Krótko mówiąc, normalna to linia prostopadła do stycznej i przechodząca przez punkt styczności.
Jak znaleźć równanie normalne? Z kurs geometrii analitycznej sugeruje się bardzo prosty algorytm: znajdujemy równanie styczne i przedstawić go ogólna perspektywa . Następnie „usuwamy” wektor normalny i utwórz równanie normalnej w punkcie i wektora kierunku.
Można zastosować tę metodę, ale w analizie matematycznej zwykle stosuje się gotowy wzór oparty na zależności pomiędzy współczynnikami kątowymi prostych prostopadłych
. Jeśli istnieje finał I niezerowy pochodną, wówczas równanie normalnej do wykresu funkcji w punkcie wyraża się równaniem: ![]()
Na pewno rozważymy przypadki szczególne, gdy jest ono równe zero lub nieskończoności, ale najpierw „zwykłe” przykłady:
Przykład 1
Zapisz równania stycznej i normalnej do wykresu krzywej ![]() w punkcie, którego odcięta jest równa .
w punkcie, którego odcięta jest równa .
W zadaniach praktycznych często trzeba znaleźć również linię styczną. Dotyczy to jednak tylko ręki - lepiej byłoby mieć „pełną rękę” =)
Rozwiązanie: Pierwsza część zadania jest dobrze znana, ułóżmy równanie styczne korzystając ze wzoru:
W tym przypadku: 
Znajdźmy pochodna
:
 Tutaj na pierwszym etapie przesunął stałą poza znak pochodnej
, na drugim – używany reguła różniczkowania funkcji zespolonej
.
Tutaj na pierwszym etapie przesunął stałą poza znak pochodnej
, na drugim – używany reguła różniczkowania funkcji zespolonej
.
Teraz obliczmy pochodna w punkcie :
Otrzymane ostateczny numer i to się podoba. Podstawiamy to do wzoru:
![]()
Przesuńmy to na górę lewej strony, otwórzmy nawiasy i przedstawmy równanie styczne ogólna perspektywa
:
 Druga część zadania nie jest już trudniejsza. Ułóżmy równanie normalne, korzystając ze wzoru:
Druga część zadania nie jest już trudniejsza. Ułóżmy równanie normalne, korzystając ze wzoru:  Pozbywając się frakcja trzypiętrowa
i przypomnij sobie równanie:
Pozbywając się frakcja trzypiętrowa
i przypomnij sobie równanie: ![]() – wymagane równanie.
– wymagane równanie.
Odpowiedź:
Tutaj możesz przeprowadzić częściową kontrolę. Po pierwsze, współrzędne punktu muszą spełniać każde równanie:
![]() - prawdziwa równość.
- prawdziwa równość.
![]() - prawdziwa równość.
- prawdziwa równość.
I po drugie, wektory normalne musi być ortogonalny. Można to łatwo sprawdzić za pomocą produkt kropkowy : , co należało sprawdzić.
Alternatywnie zamiast normalnych wektorów możesz użyć wektory kierunkowe linii prostych .
! Sprawdzenie to okazuje się bezużyteczne, jeśli pochodna i/lub pochodna w danym punkcie zostaną znalezione niepoprawnie. To „słabe ogniwo” zadania – bądź bardzo ostrożny!
Rysunek nie był wymagany, ale dla kompletności:  To zabawne, ale w rzeczywistości uzyskano pełną kontrolę, ponieważ rysunek został wykonany dość dokładnie =) Nawiasem mówiąc, funkcja
To zabawne, ale w rzeczywistości uzyskano pełną kontrolę, ponieważ rysunek został wykonany dość dokładnie =) Nawiasem mówiąc, funkcja ![]() ustawia górny łuk elipsa
.
ustawia górny łuk elipsa
.
Poniższe zadanie należy rozwiązać samodzielnie:
Przykład 2
Zapisz równania stycznej i normalnej do wykresu funkcji w punkcie .
Przybliżona próbka końcowego zadania na końcu lekcji.
Przyjrzyjmy się teraz dwóm szczególnym przypadkom:
1) Jeżeli pochodna w punkcie jest równa zeru: , to równanie styczne zostanie uproszczone:  Oznacza to, że styczna będzie równoległa do osi.
Oznacza to, że styczna będzie równoległa do osi.
W związku z tym normalna przejdzie przez punkt równoległy do osi, co oznacza, że jej równanie przyjmie postać .
2) Jeżeli pochodna w punkcie istnieje, ale jest nieskończona: , to jak zauważono na samym początku artykułu, styczna stanie się pionowa: . A ponieważ normalna przechodzi przez punkt równoległy do osi, jej równanie zostanie wyrażone w sposób „lustrzany”:
To proste:
Przykład 3
Zapisz równania stycznej i normalnej do paraboli ![]() W punkcie . Narysuj coś.
W punkcie . Narysuj coś.
Nie dodałem wymogu ukończenia rysunku – tak zadanie zostało sformułowane w oryginale. Chociaż jest to rzadkie.
Rozwiązanie: utwórzmy równanie tangensa. W tym przypadku
Wydawałoby się, że obliczenia są trywialne, ale pomylenie znaków jest więcej niż możliwe: 
Zatem: ![]()
Ponieważ styczna jest równoległa do osi (Przypadek nr 1), to normalna przechodząca przez ten sam punkt będzie równoległa do osi rzędnych:
Rysunek to oczywiście dodatkowy kłopot, ale stanowi dobrą kontrolę rozwiązania analitycznego: 
Odpowiedź: ,
Na szkolnych kursach matematyki powszechna jest uproszczona definicja stycznej, która jest sformułowana mniej więcej tak: „Styczna do wykresu funkcji to prosta, która ma jeden punkt wspólny z danym wykresem”. Jak widać, w ogólnym przypadku stwierdzenie to jest błędne. Według geometryczne znaczenie pochodnej , styczna jest linią zieloną, a nie niebieską.
Poniższy przykład poświęcony jest tej samej sprawie nr 1, gdy:
Przykład 4
Zapisz równanie stycznej i normalnej do krzywej w tym punkcie.
Krótkie rozwiązanie i odpowiedź na końcu lekcji
Przypadek nr 2, który w praktyce rzadko się zdarza, dlatego początkujący nie powinni się zbytnio przejmować i z lekkim sercem pominąć piąty przykład. Informacje zapisane kursywą przeznaczone są dla zaawansowanych czytelników, którzy dobrze rozumieją definicje pochodnej i tangensa a także mieć doświadczenie znalezienie pochodnej z definicji :
Przykład 5
Znajdź równania stycznej i normalnej do wykresu funkcji w punkcie
Rozwiązanie
: Vpunkt krytyczny
mianownik pochodnej ![]() znika, dlatego tutaj należy obliczyć jednostronne pochodne korzystając z definicji pochodnej (patrz koniec artykułuPochodna z definicji
):
znika, dlatego tutaj należy obliczyć jednostronne pochodne korzystając z definicji pochodnej (patrz koniec artykułuPochodna z definicji
):
 Obie pochodne są nieskończone, dlatego w tym punkcie istnieje wspólna styczna pionowa:
Cóż, jest oczywiste, że oś x jest normalna. Formalnie według wzoru:
Dla lepszego zrozumienia problemu załączam rysunek:
Obie pochodne są nieskończone, dlatego w tym punkcie istnieje wspólna styczna pionowa:
Cóż, jest oczywiste, że oś x jest normalna. Formalnie według wzoru:
Dla lepszego zrozumienia problemu załączam rysunek:
 Odpowiedź
:
Odpowiedź
:
Cieszę się, że nie surfowałeś po Internecie, bo cała zabawa dopiero się zaczyna! Aby opanować materiał z następnego akapitu, musisz umieć znaleźć pochodna funkcji ukrytej :
Jak znaleźć równanie styczne i równanie normalne, jeśli funkcja jest określona pośrednio?
Wzory styczne i normalne pozostają takie same, ale zmienia się technika rozwiązywania:
Przykład 6
Znajdź równania stycznej i normalnej do krzywej w tym punkcie.
Rozwiązanie: sądząc po równaniu, jest to pewnego rodzaju Trzecia linia zamówienia , który akurat nas teraz w ogóle nie interesuje.
W równaniu znajduje się złośliwe oprogramowanie, więc perspektywa wyrażenia funkcji w wyraźnie wygląda dość mgliście.
Ale to nie jest wymagane! Istnieje o wiele bardziej pomysłowe rozwiązanie. Utwórzmy równanie styczne, korzystając z tego samego wzoru.
Wartości są znane z warunku, przy okazji nie zaszkodzi upewnić się, że rzeczywiście spełniają zaproponowane równanie:  Otrzymuje się poprawną równość, co oznacza, że wszystko jest w porządku z punktem.
Otrzymuje się poprawną równość, co oznacza, że wszystko jest w porządku z punktem.
Pozostaje tylko obliczyć. Najpierw, korzystając ze standardowego schematu, znajdujemy pochodna funkcji określonej domyślnie
:

Zapiszmy wynik w notacji bardziej odpowiedniej dla naszego zadania: ![]()
W drugim kroku podstawiamy : do znalezionego wyrażenia pochodnego:
Otóż to!
Pozostaje dokładnie zrozumieć równanie: 
Utwórzmy równanie normalne: 
Odpowiedź:
Gotowy! I na początku wszystko wydawało się trudne. Chociaż pochodna tutaj jest oczywiście miejscem wrażliwym. Miniaturka do samodzielnego rozwiązania:
Przykład 7
Znajdź równanie normalnej do prostej w punkcie
Dość już stycznej =)
W tym przypadku łatwo jest dowiedzieć się, co to jest koło
wyśrodkować w punkcie promienia, a nawet wyrazić żądaną funkcję ![]() . Ale dlaczego?! W końcu znajdź pochodną funkcja ukryta
dużo łatwiej! Jest tutaj prawie najbardziej prymitywna.
. Ale dlaczego?! W końcu znajdź pochodną funkcja ukryta
dużo łatwiej! Jest tutaj prawie najbardziej prymitywna.
Krótkie rozwiązanie i odpowiedź na końcu lekcji.
Jak znaleźć równanie styczne i równanie normalne, jeśli funkcja jest określona parametrycznie?
Jeszcze łatwiej. Ale w tym celu musisz poćwiczyć znajdowanie pochodna funkcji parametrycznie zdefiniowanej . A to prawie gratis:
Przykład 8
Narysuj równania stycznej i normalnej do cykloidy narysowane w punkcie, dla którego .
Rysunek cykloidy można znaleźć na stronie S i V, jeśli linia jest określona parametrycznie (tak się składa, że ten artykuł powstał wcześniej). Pokazuje nawet punkt styku.
Rozwiązanie: Odcięta i rzędna punktu stycznego są obliczane bezpośrednio z równań parametrycznych krzywej: 
Znajdźmy Pierwsza pochodna funkcji parametrycznie określonej :
I obliczmy jego wartość przy: 
Ułóżmy równanie styczne, korzystając ze zwykłego wzoru, dostosowanego do nieco innych zapisów: 
Równanie normalne: 
Odpowiedź:
Podsumowując, sugeruję zapoznanie się z inną interesującą linią:
Przykład 9
Napisz równanie paraboli normalnej do półsześciennej narysowane w punkcie, dla którego .
To jest przykład, który możesz rozwiązać samodzielnie. Przypomnę, że wykresy funkcji parametrycznie określonych można zbudować np. korzystając z my zaprojektuj układ geometryczny .
No cóż, nasza lekcja dobiegła końca i mam nadzieję, że przedstawiony materiał nie był dla Was styczny, ale normalny =)
Dziękuję za uwagę i życzę powodzenia!
Rozwiązania i odpowiedzi:
Przykład 2:Rozwiązanie
W tym przypadku:
 Zatem:
Zatem:
 Ułóżmy równanie normalne za pomocą wzoru
Ułóżmy równanie normalne za pomocą wzoru ![]() :
:
 Odpowiedź
:
Odpowiedź
:
Przykład 4:Rozwiązanie
: ułóżmy równanie styczne korzystając ze wzoru:
W tym zadaniu:
 Zatem:
Zatem:
 W pewnym punkcie styczna jest równoległa do osi, więc odpowiadające jej równanie normalne wygląda następująco:
Odpowiedź
:
W pewnym punkcie styczna jest równoległa do osi, więc odpowiadające jej równanie normalne wygląda następująco:
Odpowiedź
:
Przykład 7:Rozwiązanie
: w tym problemie: .
Znajdźmy pochodną:
 Lub:
Podstawiamy pochodną do wyrażenia:
Lub:
Podstawiamy pochodną do wyrażenia:
![]() Wymagane równanie normalne:
Wymagane równanie normalne:
 Odpowiedź
:
Odpowiedź
:
Przykład 9:Rozwiązanie
: w tym przypadku:
![]() Znajdźmy pochodną i obliczmy jej wartość przy:
Znajdźmy pochodną i obliczmy jej wartość przy:
 Równanie normalne:
Równanie normalne:
 Odpowiedź
:
Odpowiedź
:
Zaczerpnięto ze strony http://www.mathprofi.ru