Konwersja postaci zespolonej do postaci trygonometrycznej. Postacie trygonometryczne i wykładnicze liczb zespolonych. Liczby zespolone xi

W tej sekcji porozmawiamy więcej o postaci trygonometrycznej liczby zespolonej. Forma demonstracyjna jest znacznie mniej powszechna w zadaniach praktycznych. Jeśli to możliwe, zalecam pobranie i wydrukowanie. tablice trygonometryczne, materiał metodyczny znajduje się na stronie Wzory i tablice matematyczne. Bez stolików nie zajedziesz daleko.

Dowolną liczbę zespoloną (z wyjątkiem zera) można zapisać w formie trygonometrycznej:

Gdzie to jest moduł liczby zespolonej, A - argument liczbowy zespolony.

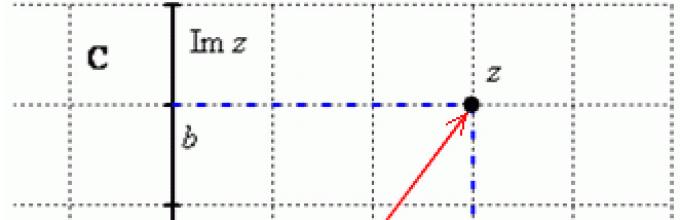
Przedstawmy liczbę na płaszczyźnie zespolonej. Dla pewności i prostoty wyjaśnienia umieścimy go w pierwszej ćwiartce współrzędnych, tj. Wierzymy, że:

Moduł liczby zespolonej jest odległością od początku do odpowiedniego punktu na płaszczyźnie zespolonej. Mówiąc najprościej, moduł to długość wektor promienia, który na rysunku jest zaznaczony na czerwono.

Moduł liczby zespolonej jest zwykle oznaczany przez: lub

Korzystając z twierdzenia Pitagorasa, łatwo jest wyprowadzić wzór na znalezienie modułu liczby zespolonej: . Ta formuła jest poprawna dla każdego oznacza „a” i „być”.

Notatka : Moduł liczby zespolonej jest uogólnieniem pojęcia moduł liczby rzeczywistej, jako odległość od punktu do początku.

Argument liczby zespolonej zwany narożnik między dodatnia półoś rzeczywista oś i wektor promienia narysowany od początku do odpowiedniego punktu. Argument nie jest zdefiniowany dla liczby pojedynczej:.

Rozważana zasada jest w rzeczywistości podobna do współrzędnych biegunowych, gdzie promień biegunowy i kąt biegunowy jednoznacznie definiują punkt.

Argument liczby zespolonej jest standardowo oznaczany: lub

Z rozważań geometrycznych otrzymujemy następujący wzór na znalezienie argumentu:

. Uwaga! Ta formuła działa tylko w prawej półpłaszczyźnie! Jeśli liczba zespolona nie znajduje się w 1. lub 4. ćwiartce współrzędnych, wówczas wzór będzie nieco inny. Przeanalizujemy również te przypadki.

Ale najpierw spójrzmy na najprostsze przykłady, kiedy Liczby zespolone znajdują się na osiach współrzędnych.

Przykład 7

Przedstaw liczby zespolone w formie trygonometrycznej: ,,,. Zróbmy rysunek:

W rzeczywistości zadanie ma charakter ustny. Dla jasności przepiszę postać trygonometryczną liczby zespolonej:

Pamiętajmy mocno, moduł – długość(co jest zawsze nieujemne), argument - narożnik

1) Przedstawmy liczbę w formie trygonometrycznej. Znajdźmy jego moduł i argument. To oczywiste. Formalne obliczenia przy użyciu wzoru:. Jest to oczywiste (liczba leży bezpośrednio na rzeczywistej półosi dodatniej). Zatem liczba w formie trygonometrycznej:.

Działanie odwrotnej kontroli jest jasne jak słońce:

2) Przedstawmy liczbę w formie trygonometrycznej. Znajdźmy jego moduł i argument. To oczywiste. Formalne obliczenia przy użyciu wzoru:. Oczywiście (lub 90 stopni). Na rysunku narożnik jest oznaczony kolorem czerwonym. Zatem liczba w formie trygonometrycznej to: .

Za pomocą , łatwo jest odzyskać postać algebraiczną liczby (jednocześnie sprawdzając):

3) Przedstawmy liczbę w formie trygonometrycznej. Znajdźmy jego moduł i

argument. To oczywiste. Formalne obliczenia przy użyciu wzoru:

Oczywiście (lub 180 stopni). Na rysunku narożnik zaznaczony jest na niebiesko. Zatem liczba w formie trygonometrycznej:.

Badanie:

4) I czwarty ciekawy przypadek. To oczywiste. Formalne obliczenia przy użyciu wzoru:.

Argument można zapisać na dwa sposoby: Pierwszy sposób: (270 stopni) i odpowiednio: . Badanie:

Jednak następująca zasada jest bardziej standardowa: Jeśli kąt jest większy niż 180 stopni, wówczas jest on zapisywany ze znakiem minus i przeciwną orientacją („przewijaniem”) kąta: (minus 90 stopni), na rysunku kąt jest zaznaczony na zielono. Łatwo to zauważyć

czyli ten sam kąt.

Zatem wpis ma postać:

Uwaga! W żadnym wypadku nie należy używać parzystości cosinusa, nieparzystości sinusa i dalej „upraszczać” zapis:

Swoją drogą, warto o tym pamiętać wygląd oraz właściwości trygonometryczne i odwrotne funkcje trygonometryczne, materiały referencyjne znajdują się w ostatnich akapitach strony Wykresy i właściwości podstawowych funkcji elementarnych. A liczb zespolonych nauczysz się znacznie łatwiej!

Projektując najprostsze przykłady, należy to zapisać w następujący sposób: : „jest oczywiste, że moduł jest… jest oczywiste, że argumentem jest…”. Jest to naprawdę oczywiste i łatwe do rozwiązania werbalnie.

Przejdźmy do rozważenia bardziej powszechnych przypadków. Z modułem nie ma żadnych problemów, należy zawsze stosować formułę. Ale wzory na znalezienie argumentu będą różne, zależy to od tego, w której ćwiartce współrzędnych leży liczba. W takim przypadku możliwe są trzy opcje (przydaje się je przepisać):

1) Jeśli (pierwsza i czwarta ćwiartka współrzędnych lub prawa półpłaszczyzna), to argument należy znaleźć za pomocą wzoru.

2) Jeśli (2. ćwiartka współrzędnych), to argument należy znaleźć za pomocą wzoru .

3) Jeżeli (3. ćwiartka współrzędnych), to argument należy znaleźć korzystając ze wzoru .

Przykład 8

Przedstaw liczby zespolone w formie trygonometrycznej: ,,,.

Ponieważ istnieją gotowe formuły, nie jest konieczne uzupełnianie rysunku. Ale jest jeden punkt: wtedy, gdy zostaniesz poproszony o przedstawienie liczby w formie trygonometrycznej Tak czy inaczej lepiej zrobić rysunek. Faktem jest, że rozwiązanie bez rysunku jest często odrzucane przez nauczycieli, brak rysunku jest poważnym powodem minusów i niepowodzeń.

Liczby przedstawiamy w postaci zespolonej, a liczba pierwsza i trzecia będą do samodzielnego rozwiązania.

Przedstawmy liczbę w formie trygonometrycznej. Znajdźmy jego moduł i argument.

Ponieważ (przypadek 2) zatem

– w tym miejscu należy wykorzystać osobliwość arcustangens. Niestety w tabeli nie ma wartości , dlatego w takich przypadkach argument należy pozostawić w kłopotliwej formie: – liczby w postaci trygonometrycznej.

Przedstawmy liczbę w formie trygonometrycznej. Znajdźmy jego moduł i argument.

Ponieważ (przypadek 1), to (minus 60 stopni).

Zatem:

– liczba w formie trygonometrycznej.

Ale tutaj, jak już wspomniano, są wady nie dotykaj.

Oprócz zabawnej metody weryfikacji graficznej istnieje również weryfikacja analityczna, która została przeprowadzona już w przykładzie 7. Używamy tabela wartości funkcji trygonometrycznych, biorąc pod uwagę, że kąt jest dokładnie kątem stołowym (lub 300 stopni): – liczby w pierwotnej postaci algebraicznej.

Przedstaw liczby samodzielnie w formie trygonometrycznej. Krótkie rozwiązanie i odpowiedź na końcu lekcji.

Na koniec części krótko o wykładniczej postaci liczby zespolonej.

Dowolną liczbę zespoloną (z wyjątkiem zera) można zapisać w postaci wykładniczej:

Gdzie jest modułem liczby zespolonej i jest argumentem liczby zespolonej.

Co musisz zrobić, aby przedstawić liczbę zespoloną w postaci wykładniczej? Prawie to samo: wykonaj rysunek, znajdź moduł i argument. I wpisz numer w formularzu.

Przykładowo dla liczby z poprzedniego przykładu znaleźliśmy moduł i argument:,. Następnie podany numer w formie wykładniczej zostanie to zapisane w następujący sposób:

Liczba w postaci wykładniczej będzie wyglądać następująco:

Numer - Więc:

Jedyna rada jest taka nie dotykaj wskaźnika wykładników, nie ma potrzeby zmiany układu czynników, otwierania nawiasów itp. Liczbę zespoloną zapisuje się w postaci wykładniczej rygorystycznie zgodnie z formą.

3.1. Współrzędne biegunowe

Często używany w samolocie biegunowy układ współrzędnych . Definiuje się go, jeśli dany jest punkt O, tzw Polak i promień wychodzący z bieguna (dla nas jest to oś Wół) – oś biegunowa. Położenie punktu M wyznaczają dwie liczby: promień (lub wektor promienia) i kąt φ pomiędzy osią biegunową a wektorem. Nazywa się kąt φ kąt biegunowy; mierzona w radianach i liczona przeciwnie do ruchu wskazówek zegara od osi biegunowej.

Położenie punktu w układzie współrzędnych biegunowych określa się za pomocą uporządkowanej pary liczb (r; φ). Na Polu r = 0, oraz φ nie jest zdefiniowane. Dla wszystkich pozostałych punktów r > 0, a φ definiuje się aż do składnika będącego wielokrotnością 2π. W tym przypadku pary liczb (r; φ) i (r 1 ; φ 1) są powiązane z tym samym punktem, jeśli .

Dla prostokątnego układu współrzędnych xOj Współrzędne kartezjańskie punktu można łatwo wyrazić w postaci jego współrzędnych biegunowych w następujący sposób:

3.2. Interpretacja geometryczna liczby zespolonej

Rozważmy kartezjański prostokątny układ współrzędnych na płaszczyźnie xOj.

Dowolna liczba zespolona z=(a, b) jest powiązana z punktem na płaszczyźnie o współrzędnych ( x, y), Gdzie współrzędna x = a, tj. część rzeczywista liczby zespolonej, a współrzędna y = bi jest częścią urojoną.

Płaszczyzna, której punkty są liczbami zespolonymi, jest płaszczyzną zespoloną.

Na rysunku liczba zespolona z = (a, b) odpowiada punktowi M(x, y).

Ćwiczenia.Naciągnąć płaszczyzna współrzędnych Liczby zespolone:

3.3. Postać trygonometryczna liczby zespolonej

Liczba zespolona na płaszczyźnie ma współrzędne punktu M(x;y). W której:

Zapisywanie liczby zespolonej - postać trygonometryczna liczby zespolonej.

Nazywa się liczbę r moduł Liczba zespolona z i jest wyznaczony. Moduł jest nieujemną liczbą rzeczywistą. Dla .

Moduł wynosi zero wtedy i tylko wtedy, gdy z = 0, tj. a = b = 0.

Nazywa się liczbę φ argument z i jest wyznaczony. Argument z jest zdefiniowany niejednoznacznie, podobnie jak kąt biegunowy w biegunowym układzie współrzędnych, czyli aż do wyrazu będącego wielokrotnością 2π.

Następnie przyjmujemy: , gdzie φ jest najmniejszą wartością argumentu. To oczywiste

Przy głębszym badaniu tematu wprowadza się argument pomocniczy φ*, taki że

Przykład 1. Znajdź postać trygonometryczną liczby zespolonej.

Rozwiązanie. 1) rozważ moduł: ;

2) szukam φ: ;

3) forma trygonometryczna:

Przykład 2. Znajdź postać algebraiczną liczby zespolonej .

Tutaj wystarczy zastąpić wartości funkcji trygonometrycznych i przekształcić wyrażenie:

Przykład 3. Znajdź moduł i argument liczby zespolonej;

1) ;

2) ; φ – w 4 kwartałach:

3.4. Działania na liczbach zespolonych w postaci trygonometrycznej

· Dodawanie i odejmowanie Wygodniej jest operować liczbami zespolonymi w formie algebraicznej:

· Mnożenie- za pomocą prostego przekształcenia trygonometryczne można to wykazać Podczas mnożenia mnożone są moduły liczb i dodawane są argumenty: ;

Działania na liczbach zespolonych zapisanych w postaci algebraicznej

Postać algebraiczna liczby zespolonej z =(A,B).nazywa się wyrażeniem algebraicznym postaci

z = A + bi.

Działania arytmetyczne na liczbach zespolonych z 1 = za 1 +b 1 I I z 2 = za 2 +b 2 I, zapisane w formie algebraicznej, przeprowadza się w następujący sposób.

1. Suma (różnica) liczb zespolonych

z 1 ±z 2 = (A 1 ± a 2) + (B 1 ±b 2)∙i,

te. dodawanie (odejmowanie) odbywa się zgodnie z zasadą dodawania wielomianów z redukcją wyrazów podobnych.

2. Iloczyn liczb zespolonych

z 1 ∙z 2 = (A 1 ∙a 2 - B 1 ∙b 2) + (A 1 ∙b 2 +a 2 ∙b 1)∙i,

te. mnożenie przeprowadza się zgodnie ze zwykłą zasadą mnożenia wielomianów, biorąc pod uwagę fakt, że I 2 = 1.

3. Podział dwóch liczb zespolonych przeprowadza się wg następna zasada:

, (z 2 ≠ 0),

te. dzielenie przeprowadza się poprzez pomnożenie dzielnej i dzielnika przez liczbę sprzężoną dzielnika.

Potęgowanie liczb zespolonych definiuje się w następujący sposób:

Łatwo to pokazać

Przykłady.

1. Znajdź sumę liczb zespolonych z 1 = 2 – I I z 2 = – 4 + 3I.

z 1 + z 2 = (2 + (–1)∙i)+ (–4 + 3I) = (2 + (–4)) + ((–1) + 3) I = –2+2I.

2. Znajdź iloczyn liczb zespolonych z 1 = 2 – 3I I z 2 = –4 + 5I.

= (2 – 3I) ∙ (–4 + 5I) = 2 ∙(–4) + (-4) ∙(–3I)+ 2∙5I– 3ja∙ 5ja = 7+22I.

3. Znajdź iloraz z z podziału z 1 = 3 – 2na z 2 = 3 – I.

z = .

4. Rozwiąż równanie: , X I y Î R.

(2x+y) + (x+y)ja = 2 + 3I.

Z równości liczb zespolonych mamy:

Gdzie x =–1 , y= 4.

5. Oblicz: I 2 ,I 3 ,I 4 ,I 5 ,I 6 ,I -1 ,I -2 .

6. Oblicz, czy .

7. Oblicz liczbę odwrotność liczby z=3-I.

Liczby zespolone w postaci trygonometrycznej

Złożona płaszczyzna nazywana płaszczyzną o współrzędnych kartezjańskich ( x, y), jeśli każdy punkt o współrzędnych ( a, b) jest powiązany z liczbą zespoloną z = a + bi. W tym przypadku wywoływana jest oś odciętych prawdziwa oś, a oś rzędnych to wyimaginowany. Następnie każda liczba zespolona a+bi geometrycznie przedstawiony na płaszczyźnie jako punkt A (a, b) lub wektor.

Dlatego położenie punktu A(a zatem liczba zespolona z) można określić za pomocą długości wektora | | = R i kąt J, utworzony przez wektor | | z dodatnim kierunkiem osi rzeczywistej. Nazywa się długość wektora moduł liczby zespolonej i jest oznaczony przez | z |=r i kąt J zwany argument liczbowy zespolony i jest wyznaczony j = argument z.

Jasne jest, że | z| ³ 0 i | z | = 0 Û z = 0.

Z ryc. 2 jest rzeczą oczywistą.

Argument liczby zespolonej jest określany niejednoznacznie, ale z dokładnością do 2 pk, kÎ Z.

Z ryc. 2 jasne jest również, że jeśli z=a+bi I j=arg z, To

sałata j =,grzech j =, tg j = .

Jeśli zÎR I z> 0, zatem argument z = 0 +2pk;

Jeśli z ОR I z< 0, zatem argument z = p + 2pk;

Jeśli z = 0,argument z nieokreślony.

Wartość główna argumentu jest wyznaczana w przedziale 0 £ arg z 2 funty P,

Lub -P£ arg z £ str.

Przykłady:

1. Znajdź moduł liczb zespolonych z 1 = 4 – 3I I z 2 = –2–2I.

2. Zdefiniuj obszary na płaszczyźnie zespolonej określone warunkami:

1) | z | = 5; 2) | z| 6 funtów; 3) | z – (2+I) | 3 funty; 4) 6 funtów | z – I| 7 funtów.

Rozwiązania i odpowiedzi:

1) | z| = 5 Û Û - równanie okręgu o promieniu 5 i środku w początku.

2) Okrąg o promieniu 6 ze środkiem w początku.

3) Okrąg o promieniu 3 ze środkiem w punkcie z 0 = 2 + I.

4) Pierścień ograniczony okręgami o promieniach 6 i 7 ze środkiem w punkcie z 0 = I.

3. Znajdź moduł i argument liczb: 1) ; 2) .

1) ; A = 1, B = Þ ,

Þ jot 1 = .

2) z 2 = –2 – 2I; a =–2, b =-2 Þ ,

Wskazówka: Przy ustalaniu głównego argumentu korzystaj z płaszczyzny zespolonej.

Zatem: z 1 = .

2) , R 2 = 1, jot 2 = , .

3) , R 3 = 1, jot 3 = , .

4) , R 4 = 1, jot 4 = , .

LICZBY ZŁOŻONE XI

§ 256. Postać trygonometryczna liczb zespolonych

Niech liczba zespolona a + bi odpowiada wektorowi O.A.> ze współrzędnymi ( a, b ) (patrz ryc. 332).

Oznaczmy długość tego wektora przez R i kąt, jaki tworzy z osią X , Poprzez φ . Z definicji sinusa i cosinusa:

A / R =co φ , B / R = grzech φ .

Dlatego A = R sałata φ , B = R grzech φ . Ale w tym przypadku liczba zespolona a + bi można zapisać jako:

a + bi = R sałata φ + ir grzech φ = R (sałata φ + I grzech φ ).

Jak wiadomo, kwadrat długości dowolnego wektora jest równy sumie kwadratów jego współrzędnych. Dlatego R 2 = A 2 + B 2, skąd R = √a 2 + B 2

Więc, dowolna liczba zespolona a + bi można przedstawić w postaci :

a + bi = R (sałata φ + I grzech φ ), (1)

gdzie r = √a 2 + B 2 i kąt φ wyznacza się z warunku:

Ta forma zapisywania liczb zespolonych nazywa się trygonometryczny.

Numer R we wzorze (1) nazywa się moduł i kąt φ - argument, Liczba zespolona a + bi .

Jeśli liczba zespolona a + bi nie jest równy zero, to jego moduł jest dodatni; Jeśli a + bi = 0, zatem a = b = 0 i wtedy R = 0.

Moduł dowolnej liczby zespolonej jest określony jednoznacznie.

Jeśli liczba zespolona a + bi nie jest równy zero, wówczas jego argument wyznaczają wzory (2) zdecydowanie z dokładnością do kąta podzielnego przez 2 π . Jeśli a + bi = 0, zatem a = b = 0. W tym przypadku R = 0. Ze wzoru (1) łatwo zrozumieć, że jest to argument φ w tym przypadku możesz wybrać dowolny kąt: w końcu dla dowolnego φ

0 (kos φ + I grzech φ ) = 0.

Dlatego argument zerowy jest niezdefiniowany.

Moduł liczby zespolonej R czasami oznaczane | z | i argument arg z . Przyjrzyjmy się kilku przykładom przedstawiania liczb zespolonych w formie trygonometrycznej.

Przykład. 1. 1 + I .

Znajdźmy moduł R i argumentacja φ ten numer.

R = √ 1 2 + 1 2 = √ 2 .

Dlatego grzech φ = 1 / √ 2, sałata φ = 1 / √ 2, skąd φ = π / 4 + 2Nπ .

Zatem,

1 + I = √ 2 ,

Gdzie P - dowolna liczba całkowita. Zwykle z nieskończonego zbioru wartości argumentu liczby zespolonej wybiera się tę z zakresu od 0 do 2 π . W tym przypadku jest to wartość π / 4. Dlatego

1 + I = √ 2 (kos π / 4 + I grzech π / 4)

Przykład 2. Zapisz liczbę zespoloną w postaci trygonometrycznej √ 3 - I . Mamy:

R = √ 3+1 = 2, sałata φ = √ 3 / 2, grzech φ = - 1 / 2

Dlatego aż do kąta podzielnego przez 2 π , φ = 11 / 6 π ; stąd,

√ 3 - I = 2(cos 11 / 6 π + I grzech 11/6 π ).

Przykład 3 Zapisz liczbę zespoloną w postaci trygonometrycznej I.

Liczba zespolona I odpowiada wektorowi O.A.> , kończący się w punkcie A osi Na o rzędnej 1 (ryc. 333). Długość takiego wektora wynosi 1, a kąt, jaki tworzy z osią x, jest równy π / 2. Dlatego

I =co π / 2 + I grzech π / 2 .

Przykład 4. Zapisz liczbę zespoloną 3 w formie trygonometrycznej.

Liczba zespolona 3 odpowiada wektorowi O.A. > X odcięta 3 (ryc. 334).

Długość takiego wektora wynosi 3, a kąt, jaki tworzy z osią x, wynosi 0. Zatem

3 = 3 (cos 0 + I grzech 0),

Przykład 5. Zapisz liczbę zespoloną -5 w formie trygonometrycznej.

Liczba zespolona -5 odpowiada wektorowi O.A.> kończący się w punkcie osi X z odciętą -5 (ryc. 335). Długość takiego wektora wynosi 5, a kąt, jaki tworzy z osią x, jest równy π . Dlatego

5 = 5 (kos π + I grzech π ).

Ćwiczenia

2047. Zapisz te liczby zespolone w formie trygonometrycznej, określając ich moduły i argumenty:

1) 2 + 2√3 I , 4) 12I - 5; 7).3I ;

2) √3 + I ; 5) 25; 8) -2I ;

3) 6 - 6I ; 6) - 4; 9) 3I - 4.

2048. Wskaż na płaszczyźnie zbiór punktów reprezentujących liczby zespolone, których moduły r i argumenty φ spełniają warunki:

1) R = 1, φ = π / 4 ; 4) R < 3; 7) 0 < φ < π / 6 ;

2) R =2; 5) 2 < R <3; 8) 0 < φ < я;

3) R < 3; 6) φ = π / 3 ; 9) 1 < R < 2,

10) 0 < φ < π / 2 .

2049. Czy liczby mogą być jednocześnie modułem liczby zespolonej? R I - R ?