Funkcje trygonometryczne argumentów liczbowych i kątowych. Formuły redukcyjne Obliczanie wyrażenia trygonalnego argumentu numerycznego

Funkcje trygonometryczne argumentu numerycznego.

Funkcje trygonometryczne argumentu numerycznegoT są funkcjami formy y= koszt t,
y= grzech t, y= tg t, y= ctg t.

Korzystając z tych wzorów, poprzez znaną wartość jednej funkcji trygonometrycznej, można znaleźć nieznane wartości innych funkcji trygonometrycznych.

Wyjaśnienia.

1) Weźmy wzór cos 2 t + sin 2 t = 1 i wyprowadźmy z niego nowy wzór.

Aby to zrobić, podziel obie strony wzoru przez cos 2 t (dla t ≠ 0, czyli t ≠ π/2 + π k). Więc:

cos 2 t grzech 2 t 1
--- + --- = ---
cos 2 t cos 2 t cos 2 t

Pierwszy wyraz jest równy 1. Wiemy, że stosunek sinusa do conis jest styczny, co oznacza, że ​​drugi wyraz jest równy tg 2 t. W rezultacie otrzymujemy nową (i już znaną Wam) formułę:

2) Teraz podziel cos 2 t + sin 2 t = 1 przez sin 2 t (dla t ≠ π k):

cos 2 t grzech 2 t 1
--- + --- = ---, gdzie t ≠ π k + π k, k– liczba całkowita
grzech 2 t grzech 2 t grzech 2 t

Stosunek cosinusa do sinusa to kotangens. Oznacza:

Znając podstawowe zasady matematyki i poznawszy podstawowe wzory trygonometrii, większość pozostałych tożsamości trygonometrycznych można łatwo wyprowadzić samodzielnie. Jest to nawet lepsze niż samo zapamiętywanie: to, czego nauczysz się na pamięć, szybko zostaje zapomniane, ale to, co rozumiesz, zostaje zapamiętane na długo, jeśli nie na zawsze. Na przykład nie trzeba zapamiętywać, ile wynosi suma jedności i kwadratu stycznej. Jeśli zapomniałeś, możesz łatwo zapamiętać, jeśli znasz najprostszą rzecz: tangens to stosunek sinusa do cosinusa. Dodatkowo zastosuj prostą zasadę dodawania ułamków za pomocą różne mianowniki– i uzyskaj wynik:

grzech 2 t 1 grzech 2 t cos 2 t + grzech 2 t 1
1 + tg 2 t = 1 + --- = - + --- = ------ = ---
cos 2 t 1 cos 2 t cos 2 t cos 2 t

W ten sam sposób możesz łatwo znaleźć sumę jedności i kwadrat cotangensu, a także wiele innych tożsamości.

Funkcje trygonometryczne argumentu kątowego.

W funkcjachNa = sałataT, Na = grzechT, Na = tgT, Na = ctgT zmiennyt może być czymś więcej niż tylko argumentem numerycznym. Można to również uznać za miarę kąta - czyli argument kątowy.

Używając okrąg liczbowy i układy współrzędnych, możesz łatwo znaleźć sinus, cosinus, tangens i cotangens dowolnego kąta. Aby to zrobić, muszą zostać spełnione dwie rzeczy ważne warunki:
1) wierzchołek kąta musi znajdować się w środku okręgu, który jest jednocześnie środkiem osi współrzędnych;

2) jeden z boków kątownika musi być belką o osi dodatniej X.

W tym przypadku rzędna punktu, w którym przecinają się okrąg i drugi bok kąta, jest sinusem tego kąta, a odcięta tego punktu jest cosinusem tego kąta.

Wyjaśnienie. Narysujmy kąt, którego jedna strona jest promieniem dodatnim osi X, a drugi bok wychodzi z początku osi współrzędnych (i ze środka okręgu) pod kątem 30° (patrz rysunek). Wtedy punkt przecięcia drugiego boku z okręgiem odpowiada π/6. Znamy rzędną i odciętą tego punktu. Są one także cosinusem i sinusem naszego kąta:

√3 1
--; --
2 2

A znając sinus i cosinus kąta, możesz łatwo znaleźć jego tangens i cotangens.

Zatem okrąg liczbowy umieszczony w układzie współrzędnych jest wygodnym sposobem znalezienia sinusa, cosinusa, stycznej lub cotangensu kąta.

Ale jest łatwiejszy sposób. Nie musisz rysować okręgu i układu współrzędnych. Możesz użyć prostych i wygodnych formuł:

Przykład: znajdź sinus i cosinus kąta równego 60°.

Rozwiązanie :

π 60 π √3
grzech 60° = grzech --- = grzech -- = --
180 3 2

π 1
cos 60° = cos -- = -
3 2

Wyjaśnienie: odkryliśmy, że sinus i cosinus kąta 60° odpowiadają wartościom punktu na okręgu π/3. Następnie po prostu znajdujemy wartości tego punktu w tabeli - i w ten sposób rozwiązujemy nasz przykład. Tabela sinusów i cosinusów głównych punktów koła liczbowego znajduje się w poprzedniej sekcji oraz na stronie „Tabele”.

W tym rozdziale przedstawimy funkcje trygonometryczne argumentu liczbowego. Wiele pytań z matematyki, mechaniki, fizyki i innych nauk prowadzi do funkcji trygonometrycznych nie tylko kąta (łuku), ale także argumentów o zupełnie innym charakterze (długość, czas, temperatura itp.). Do tej pory argument funkcji trygonometrycznej był rozumiany jako kąt mierzony w stopniach lub radianach. Uogólnimy teraz pojęcia sinus, cosinus, tangens, cotangens, sieczna i cosekans, wprowadzając je jako funkcje argumentu liczbowego.

Definicja. Funkcje trygonometryczne argumentu liczbowego to funkcje trygonometryczne kąta równego radianom, o tej samej nazwie.

Wyjaśnijmy tę definicję na konkretnych przykładach.

Przykład 1. Obliczmy wartość. Mamy tu na myśli abstrakcję Liczba niewymierna. Zgodnie z definicją. Więc, .

Przykład 2. Obliczmy wartość. Tutaj przez 1,5 mamy na myśli liczbę abstrakcyjną. Zgodnie z definicją (patrz dodatek II).

Przykład 3. Oblicz wartość. Otrzymujemy to samo, co powyżej (patrz załącznik II).

Tak więc w przyszłości przez argument funkcji trygonometrycznych będziemy rozumieć kąt (łuk) lub po prostu liczbę, w zależności od problemu, który rozwiązujemy. W niektórych przypadkach argumentem może być wielkość, która ma inny wymiar, na przykład czas itp. Nazywając argument kątem (łukiem), możemy przez to rozumieć liczbę, za pomocą której jest on mierzony w radianach.

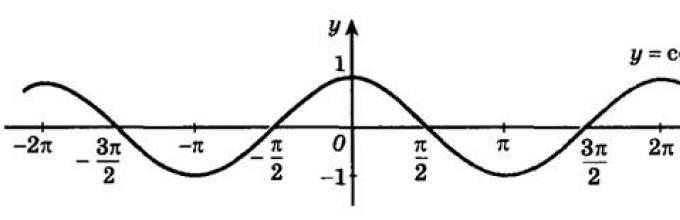
Definicja 1: Funkcja numeryczna, podane przez wzór y=sin x nazywa się sinusem.

Ta krzywa nazywa się - sinusoida.

Własności funkcji y=sin x

2. Zakres wartości funkcji: E(y)=[-1; 1]

3. Funkcja parzystości:

y=sin x – nieparzyste,.

4. Okresowość: sin(x+2πn)=sin x, gdzie n jest liczbą całkowitą.

Funkcja ta przyjmuje te same wartości po pewnym czasie. Ta właściwość funkcji nazywa się częstotliwość. Przedział to okres funkcji.

Dla funkcji y=sin x okres wynosi 2π.

Funkcja y=sin x jest okresowa, z okresem Т=2πn, n jest liczbą całkowitą.

Najmniejszy okres dodatni to T=2π.

Matematycznie można to zapisać w następujący sposób: sin(x+2πn)=sin x, gdzie n jest liczbą całkowitą.

Definicja2: Funkcja numeryczna określona wzorem y=cosx nazywana jest cosinusem.

Własności funkcji y=cos x

1. Dziedzina funkcji: D(y)=R

2. Obszar wartości funkcji: E(y)=[-1;1]

3. Funkcja parzystości:

y=cos x – parzysty.

4. Okresowość: cos(x+2πn)=cos x, gdzie n jest liczbą całkowitą.

Funkcja y=cos x jest okresowa z okresem Т=2π.

Definicja 3: Funkcja numeryczna określona wzorem y=tg x nazywana jest tangensem.

Własności funkcji y=tg x

1. Dziedzina funkcji: D(y) - wszystkie liczby rzeczywiste, z wyjątkiem π/2+πk, k jest liczbą całkowitą. Ponieważ w tych punktach styczna nie jest zdefiniowana.

3. Funkcja parzystości:

y=tg x – nieparzyste.

4. Okresowość: tg(x+πk)=tg x, gdzie k jest liczbą całkowitą.

Funkcja y=tg x jest okresowa z okresem π.

Definicja 4: Funkcja liczbowa określona wzorem y=ctg x nazywana jest cotangensem.

Własności funkcji y=ctg x

1. Dziedzina definicji funkcji: D(y) - wszystkie liczby rzeczywiste z wyjątkiem πk, k jest liczbą całkowitą. Ponieważ w tych punktach cotangens nie jest zdefiniowany.

2. Zakres funkcji: E(y)=R.

Powrót do przodu

Uwaga! Podglądy slajdów służą wyłącznie celom informacyjnym i mogą nie odzwierciedlać wszystkich funkcji prezentacji. Jeśli jesteś zainteresowany tą pracą, pobierz pełną wersję.

Cele Lekcji:

1. Rozwój umiejętności i umiejętności stosowania wzory trygonometryczne uprościć wyrażenia trygonometryczne.
2. Wdrażanie zasady podejścia aktywistycznego w nauczaniu uczniów, rozwijanie u uczniów umiejętności komunikacyjnych i tolerancji, umiejętności słuchania i słyszenia innych oraz wyrażania swojej opinii.
3. Zwiększanie zainteresowania uczniów matematyką.

Typ lekcji: szkolenie.

Typ lekcji: lekcja umiejętności i zdolności.

Forma studiów: Grupa.

Typ grup: grupa siedzi razem. Studenci o różnym poziomie wykształcenia, świadomości danego przedmiotu, zgodni uczniowie, co pozwala im się uzupełniać i wzbogacać.

Sprzęt: tablica; kreda; tabela „Trygonometr”; arkusze tras; karty z literami (A, B, C.) umożliwiające wykonanie testu; tablice z nazwiskami załogi; arkusze wyników; tablice z nazwami etapów podróży; magnesy, kompleks multimedialny.

Podczas zajęć

Uczniowie siedzą w grupach: 4 grupy po 5-6 osób. Każda grupa to załoga samochodu o nazwach odpowiadających nazwom funkcji trygonometrycznych, prowadzona przez kierownicę. Każda załoga otrzymuje kartę trasy i wyznacza sobie cel: pokonać daną trasę pomyślnie, bez błędów. Lekcji towarzyszy prezentacja.

I. Moment organizacyjny.

Prowadzący informuje o temacie lekcji, celu lekcji, przebiegu lekcji, planie pracy grup, roli sterników.

Uwagi wstępne nauczyciela:

– Chłopaki! Zapisz numer i temat lekcji: „Funkcje trygonometryczne argumentu liczbowego”.

Dziś na zajęciach dowiemy się:

1. Oblicz wartości funkcji trygonometrycznych;
2. Uproszczać wyrażenia trygonometryczne.

Aby to zrobić, musisz wiedzieć:

1. Definicje funkcji trygonometrycznych
2. Relacje trygonometryczne (wzory).

Od dawna wiadomo, że jedna głowa jest dobra, ale dwie są lepsze, dlatego dziś pracuje się w grupach. Wiadomo też, że ten, kto idzie, opanuje drogę. Ale żyjemy w epoce prędkości, a czas jest cenny, dlatego możemy powiedzieć tak: „Drogę opanują ci, którzy prowadzą”, dlatego dzisiaj nasza lekcja odbędzie się w formie gry „Rajd matematyczny”. Każda grupa to załoga pojazdu, na której czele stoi kierownica.

Cel gry:

• pomyślnie ukończyć trasę dla każdej załogi;
• wyłonić rajdowych mistrzów.

Nazwiska załóg odpowiadają marce samochodu, którym jeździsz.

Załogi i ich sternicy zostają przedstawieni:

• Załoga – „sinus”
• Załoga – „cosinus”
• Załoga - „styczna”
• Załoga – „cotangens”

Motto wyścigu: „Śpiesz się powoli!”

Trzeba przebiec przez „teren matematyczny” z wieloma przeszkodami.

Każdej załodze wydano karty tras. Załogi znające definicje i wzory trygonometryczne będą w stanie pokonać przeszkody.

Podczas rejsu każdy sternik kieruje załogą, pomagając i oceniając wkład każdego członka załogi w pokonanie trasy w formie „za” i „przeciw” na karcie punktacji. Za każdą poprawną odpowiedź grupa otrzymuje „+”, a błędną odpowiedź „-”.

Musisz pokonać następujące etapy podróży:

Etap I. SDA (przepisy ruchu drogowego).
Etap II. Inspekcja techniczna.
Etap III. Bieg przełajowy.
Etap IV. Nagłe zatrzymanie to wypadek.
Etap V. Postój.
Etap VI. Skończyć.
Etap VII. Wyniki.

I tak jedziemy!

Etap I. SDA (przepisy ruchu drogowego).

1) W każdej załodze sternicy rozdają każdemu członkowi załogi bilety z pytaniami teoretycznymi:

1. Wyjaśnij definicję sinusa t i jego znaków w ćwiartkach.
2. Wyjaśnij definicję cosinusa liczby t i jej znaków w ćwiartkach.
3. Nazwij najmniejszy i najwyższa wartość grzech t i koszt t.
4. Wyjaśnij definicję tangensa liczby t i jej znaków w ćwiartkach.
5. Wyjaśnij definicję kotangensu liczby t i jej znaków w ćwiartkach.
6. Powiedz nam, jak znaleźć wartość funkcji sin t ze znanej liczby t.

2) Zbierz „rozproszone” formuły. Na sekretnej tablicy znajduje się stół (patrz poniżej). Załogi muszą ujednolicić formuły. Każdy zespół zapisuje odpowiedź na tablicy w formie rzędu odpowiednich liter (w parach).

A	tg 2 t + 1	mi	1
V	tg t	I	cos t / sin t, t ≠ k, kZ.
D	grzech 2 t + sałata 2 t	I	1/ sin 2 t, t ≠ k, kZ.
mi	ctg t	Do	1,t ≠ k / 2, kZ.
H	1 + ctg 2 t	G	sin t /cos t, t ≠ /2 + k, kZ.
t	tg t ∙ctg t	B	1/ cos 2 t, t ≠ /2 + k, kZ.

Odpowiedź: ab, vg, de, jeż, zi, yk.

Etap II. Inspekcja techniczna.

Praca ustna: test.

Na tajnej tablicy jest napisane: zadanie: uprościć wyrażenie.

Opcje odpowiedzi są zapisane obok nich. Załogi ustalają prawidłowe odpowiedzi w ciągu 1 minuty. i podnieś odpowiedni zestaw liter.

№	Wyrażenie	Opcje odpowiedzi
		A	W	Z
1.	1 – cos 2 t	cos 2 t	- grzech 2 t	grzech 2 t
2.	grzech 2 t – 1	cos 2 t	- cos 2 t	2 razy 2 t
3.	(koszt t – 1)(1+ koszt t)	-grzech 2 t	(1+ koszt t) 2	(koszt t – 1) 2

Odpowiedź: CVA.

Etap III. Bieg przełajowy.

Załogi mają 3 minuty na spotkanie w celu ustalenia zadania, a następnie przedstawiciele załogi zapisują decyzję na tablicy. Kiedy przedstawiciele ekipy zakończą zapisywanie rozwiązania pierwszego zadania, wszyscy uczniowie (wraz z nauczycielem) sprawdzają poprawność i racjonalność rozwiązań i zapisują je w zeszycie. Sternicy oceniają wkład każdego członka załogi, posługując się znakami „+” i „–” na arkuszach oceny.

Zadania z podręcznika:

• Załoga – „sinus”: nr 118 g;
• Załoga – „cosinus”: nr 122 a;
• Załoga – „styczna”: nr 123 g;
• Załoga – „cotangent”: nr 125

Etap IV. Nagłe zatrzymanie to wypadek.

– Twój samochód się zepsuł. Twój samochód wymaga naprawy.

Oświadczenia podane są dla każdej załogi, ale są w nich błędy. Znajdź te błędy i wyjaśnij, dlaczego zostały popełnione. W zeznaniach wykorzystywane są funkcje trygonometryczne odpowiadające marce Twojego samochodu.

Etap V. Postój.

Jesteś zmęczony i potrzebujesz odpoczynku. W czasie odpoczynku załogi sternicy podsumowują wstępne wyniki: liczą „za” i „przeciw” członków załogi i całej załogi.

Dla uczniów:

3 lub więcej „+” – ocena „5”;
2 „+” – ocena „4”;
1 „+” – ocena „3”.

Dla załóg:„+” i „-” znoszą się nawzajem. Liczone są tylko pozostałe znaki.

Zgadnij farsę.

Z liczb bierzesz moją pierwszą sylabę,
Drugie pochodzi od słowa „dumny”.
A trzecie konie poprowadzisz,
Czwartym będzie beczenie owcy.
Moja piąta sylaba jest taka sama jak pierwsza
Ostatnia litera alfabetu jest szóstą,
A jeśli odgadniesz wszystko poprawnie,
Następnie w matematyce otrzymasz sekcję taką jak ta.
(Trygonometria)

Słowo „trygonometria” (od greckich słów „trigonon” – trójkąt i „metreo” – miara) oznacza „pomiar trójkątów”. Pojawienie się trygonometrii wiąże się z rozwojem geografii i astronomii – nauki o ruchu ciała niebieskie, o budowie i rozwoju Wszechświata.

W wyniku przeprowadzonych obserwacji astronomicznych powstała potrzeba określenia położenia opraw, obliczenia odległości i kątów. Ponieważ niektórych odległości, na przykład z Ziemi do innych planet, nie można było zmierzyć bezpośrednio, naukowcy zaczęli opracowywać techniki znajdowania relacji między bokami i kątami trójkąta, w którym dwa wierzchołki znajdują się na Ziemi, a trzeci jest planetą lub gwiazdą. Takie zależności można wyprowadzić badając różne trójkąty i ich właściwości. Dlatego obliczenia astronomiczne doprowadziły do ​​rozwiązania (tj. znalezienia elementów) trójkąta. To właśnie robi trygonometria.

Początki trygonometrii odkryto w starożytnym Babilonie. Babilońscy naukowcy byli w stanie przewidzieć energię słoneczną i zaćmienia Księżyca. Niektóre informacje o charakterze trygonometrycznym można znaleźć w starożytnych pomnikach innych starożytnych ludów.

Etap VI. Skończyć.

Aby pomyślnie przekroczyć linię mety, wystarczy się wysilić i wykonać „sprint”. W trygonometrii bardzo ważne jest, aby móc szybko określić wartości sin t, koszt, tgt, ctg t, gdzie 0 ≤ t ≤ . Zamknij podręczniki.

Załogi na zmianę podają wartości. funkcjonuje grzech t, koszt, tgt, ctg t jeśli:

Etap VII. Wyniki.

Wyniki gry.

Sternicy przekazują arkusze ocen. Zdeterminowano załogę, która została mistrzem „Raju Matematycznego”, scharakteryzowano pracę pozostałych grup. Dalej znajdują się nazwiska osób, które otrzymały oceny „5” i „4”.

Podsumowanie lekcji.

- Chłopaki! Czego nauczyłeś się dzisiaj na zajęciach? (uprość wyrażenia trygonometryczne; znajdź wartości funkcji trygonometrycznych). Co musisz w tym celu wiedzieć?

• definicje i właściwości grzechu t, koszt t, tg t, ctg t;
• relacje łączące wartości różnych funkcji trygonometrycznych;
• znaki funkcji trygonometrycznych na ćwiartkach koła liczbowego.
• wartości funkcji trygonometrycznych pierwszej ćwiartki koła liczbowego.

– Myślę, że rozumiesz, że trzeba dobrze znać formuły, żeby je poprawnie zastosować. Uświadomiłeś sobie również, że trygonometria jest bardzo ważną częścią matematyki, ponieważ jest wykorzystywana w innych naukach: astronomii, geografii, fizyce itp.

Praca domowa:

• dla uczniów, którzy otrzymali „5” i „4”: §6, nr 128a, 130a, 134a.
• dla pozostałych uczniów: §6, nr 119g, nr 120g, nr 121g.

Lekcja wideo „Funkcje trygonometryczne argumentu liczbowego” zawiera materiał wizualny zapewniający przejrzystość podczas wyjaśniania tematu na zajęciach. Podczas demonstracji rozważana jest zasada tworzenia wartości funkcji trygonometrycznych z liczby, opisano szereg przykładów, które uczą, jak obliczać wartości funkcji trygonometrycznych z liczby. Za pomocą tego podręcznika łatwiej jest rozwinąć umiejętności rozwiązywania odpowiednich problemów i osiągnąć zapamiętanie materiału. Korzystanie z podręcznika zwiększa efektywność lekcji i pozwala szybko osiągnąć cele nauczania.

Na początku lekcji wyświetlany jest tytuł tematu. Następnie zadaniem jest znalezienie odpowiedniego cosinusa dla jakiegoś argumentu numerycznego. Zaznacza się, że to zadanie Rozwiązanie jest proste i można je jasno wykazać. Na ekranie wyświetlany jest okrąg jednostkowy ze środkiem w początku. Należy zauważyć, że punkt przecięcia okręgu z dodatnią półosią osi odciętych znajduje się w punkcie A(1;0). Podano przykład punktu M, który reprezentuje argument t=π/3. Ten punkt jest zaznaczony okrąg jednostkowy, a od niego prostopadła schodzi do osi odciętej. Znaleziona odcięta punktu jest cosinusem kosztu t. W tym przypadku odcięta punktu będzie wynosić x=1/2. Zatem cos t=1/2.

Podsumowując rozważone fakty, należy zauważyć, że warto mówić o funkcji s=cos t. Należy zauważyć, że studenci mają już pewną wiedzę na temat tej funkcji. Obliczane są niektóre wartości cosinus: cos 0=1, cos π/2=0, cos π/3=1/2. Z tą funkcją powiązane są także funkcje s=sin t, s=tg t, s=ctg t. Należy zauważyć, że mają one wspólną nazwę dla wszystkich - funkcje trygonometryczne.

Ważne relacje wykorzystywane przy rozwiązywaniu problemów funkcje trygonometryczne: tożsamość główna sin 2 t+ cos 2 t=1, wyrażenie tangensa i cotangensa poprzez sinus i cosinus tg t=sin t/cos t, gdzie t≠π/2+πk dla kϵZ, ctg t= cos t/sin t, gdzie t≠πk dla kϵZ, a także stosunek stycznej do cotangens tg t·ctg t=1 gdzie t≠πk/2 dla kϵZ.

Następnie proponujemy rozważyć dowód relacji 1+ tg 2 t=1/ cos 2 t, gdzie t≠π/2+πk dla kϵZ. Aby udowodnić identyczność, należy przedstawić tg 2 t w postaci stosunku sinusa i cosinusa, a następnie sprowadzić wyrazy po lewej stronie do wspólnego mianownika 1+ tg 2 t=1+sin 2 t/cos 2 t = (sin 2 t + cos 2 t )/ cos 2 t. Korzystając z podstawowej tożsamości trygonometrycznej, otrzymujemy 1 w liczniku, czyli końcowe wyrażenie 1/ cos 2 t. co było do okazania

Tożsamość 1+ cot 2 t=1/ sin 2 t dowodzimy w podobny sposób dla t≠πk dla kϵZ. Podobnie jak w poprzednim dowodzie, cotangens zastępuje się odpowiednim stosunkiem cosinusa i sinusa, a oba wyrazy po lewej stronie sprowadza się do wspólnego mianownika 1+ cot 2 t=1+ cos 2 t/sin 2 t= ( grzech 2 t+cos 2 t)/sin 2 t. Po zastosowaniu głównego tożsamość trygonometryczna do licznika otrzymujemy 1/ sin 2 t. To jest wyrażenie, którego szukamy.

Rozważane jest rozwiązanie przykładów wykorzystania zdobytej wiedzy. W pierwszym zadaniu należy znaleźć wartości kosztu, tgt, ctgt, jeśli znany jest sinus liczby sint=4/5, a t należy do przedziału π/2< t<π. Для нахождения косинуса в данном примере рекомендуется использовать тождество sin 2 t+ cos 2 t=1, из которого следует cos 2 t=1-sin 2 t. Зная значение синуса, можно найти косинус cos 2 t=1-(4/5) 2 =9/25. То есть значение косинуса cost=3/5 и cost=-3/5. В условии указано, что аргумент принадлежит второй четверти координатной плоскости. В этой четверти значение косинуса отрицательное. С учетом данного ограничения находим cost=-3/5. Для нахождения тангенса числа пользуемся его определением tgt= sint/cost. Подставив известные значения синуса и косинуса, получаем tgt=4/5:(-3/5)=-4/3. Чтобы найти значение котангенса, также используется определение котангенса ctgt= cost/sint. Подставив известные значения синуса и косинуса в отношение, получаем ctgt=(-3/5):4/5=-3/4.

Następnie rozważamy rozwiązanie podobnego problemu, w którym znana jest tangens tgt = -8/15, a argument ogranicza się do wartości 3π/2

Aby znaleźć wartość sinusa, używamy definicji tangensa tgt= sint/koszt. Z tego wynika, że ​​sint= tgt·cost=(-8/15)·(15/17)=-8/17. Wiedząc, że cotangens jest funkcją odwrotną tangensa, znajdujemy ctgt=1/(-8/15)=-15/8.

Lekcja wideo „Funkcje trygonometryczne argumentu liczbowego” służy zwiększeniu efektywności lekcji matematyki w szkole. Podczas nauczania na odległość materiał ten może służyć jako pomoc wizualna w rozwijaniu umiejętności rozwiązywania problemów związanych z funkcjami trygonometrycznymi liczb. Aby nabyć te umiejętności, uczniowi można zalecić samodzielne zapoznanie się z materiałem wizualnym.

DEKODOWANIE TEKSTU:

Temat lekcji to „Funkcje trygonometryczne argumentu liczbowego”.

Dowolną liczbę rzeczywistą t można powiązać z jednoznacznie zdefiniowanym kosztem t. Aby to zrobić, musisz wykonać następujące czynności:

1) ustawić okrąg liczbowy na płaszczyźnie współrzędnych tak, aby środek okręgu pokrywał się z początkiem współrzędnych, a punkt początkowy A okręgu przypadał na punkt (1;0);

2) znajdź punkt na okręgu odpowiadający liczbie t;

3) znajdź odciętą tego punktu. To jest koszt t.

Dlatego porozmawiamy o funkcji s = koszt t (es równa się cosinus te), gdzie t jest dowolną liczbą rzeczywistą. Mamy już pewne pojęcie o tej funkcji:

• nauczyłem się obliczać pewne wartości, na przykład cos 0=1, cos = 0, cos = itd. (cosinus zera jest równy jeden, cosinus pi przez dwa jest równy zero, cosinus pi przez trzy to równy połowie itd.).
• a ponieważ wartości sinusa, cosinusa, tangensa i cotangens są ze sobą powiązane, mamy pewne pojęcie o trzech kolejnych funkcjach: s = sint; s= tgt; s = ctgt. (es równa się sinus te, es równa się tangens te, es równa się cotangens te)

Wszystkie te funkcje nazywane są funkcjami trygonometrycznymi argumentu numerycznego t.

Z definicji sinusa, cosinusa, tangensa i cotangens wynikają niektóre zależności:

1) sin 2 t + cos 2 t = 1 (sinus kwadrat te plus cosinus kwadrat te równa się jeden)

2)tgt = dla t ≠ + πk, kϵZ (styczna te jest równa stosunkowi sinusa te do cosinusa te przy czym te nie jest równe pi przez dwa plus pi ka, ka należy do zet)

3) ctgt = dla t ≠ πk, kϵZ (cotangens te jest równy stosunkowi cosinusa te do sinusa te, gdy te nie jest równe pi ka, ka należy do zet).

4) tgt ∙ ctgt = 1 dla t ≠ , kϵZ (iloczyn stycznej te przez cotangens te jest równy jeden, gdy te nie jest równe pikowi ka, podzielone przez dwa, ka należy do zet)

Udowodnijmy jeszcze dwa ważne wzory:

Jeden plus tangens do kwadratu te jest równy stosunkowi jeden do cosinus kwadrat te, gdy te nie jest równe pi przez dwa plus pi ka.

Dowód. Sprowadźmy wyrażenie jeden plus tangens kwadrat te do wspólnego mianownika cosinus kwadrat te. W liczniku otrzymujemy sumę kwadratów cosinus te i sinus te, która jest równa jeden. A mianownikiem pozostaje kwadrat cosinusa te.

Suma jedności i kwadratu cotangens te jest równa stosunkowi jedności do kwadratu sinusa te, gdy te nie jest równe pi ka.

Dowód. Wyrażenie jeden plus cotangens do kwadratu te podobnie sprowadzamy do wspólnego mianownika i stosujemy pierwszą relację.

Spójrzmy na przykłady.

PRZYKŁAD 1. Znajdź koszt, tgt, ctgt jeśli sint = i< t < π.(если синус тэ равен четырем пятым и тэ из промежутка от пи на два до пи)

Rozwiązanie. Z pierwszej zależności wynika, że ​​cosinus kwadrat te jest równy jeden minus sinus kwadrat te: cos 2 t = 1 - sin 2 t.

Oznacza to, że cos 2 t = 1 -() 2 = (cosinus kwadrat te jest równy dziewięciu dwudziestym piątym), czyli koszt = (cosinus te jest równy trzem piątym) lub koszt = - (cosinus te jest równy minus trzy piąte). Pod warunkiem, argument t należy do drugiego kwartału i w nim kosztuje t< 0 (косинус тэ отрицательный).

Oznacza to, że cosinus te jest równy minus trzy piąte, koszt = - .

Obliczmy tangens te:

tgt = = ׃ (-)= - ;(styczna te jest równa stosunkowi sinus te do cosinus te, a zatem cztery piąte do minus trzy piąte i równe minus cztery trzecie)

W związku z tym obliczamy (cotangens liczby te. ponieważ cotangens te jest równy stosunkowi cosinusa te do sinusa te) ctgt = = - .

(cotangens te jest równy minus trzy czwarte).

Odpowiedź: koszt = -, tgt= -; ctgt = - . (wypełniamy odpowiedź w miarę jej rozwiązywania)

PRZYKŁAD 2. Wiadomo, że tgt = - i< t < 2π(тангенс тэ равен минус восемь пятнадцатых и тэ принадлежит промежутку от трех пи на два до двух пи). Найти значения cost, sint, ctgt.

Rozwiązanie. Skorzystajmy z tej zależności i podstawmy wartość do tego wzoru, aby otrzymać:

1 + (-) 2 = (jeden na cosinus kwadrat te jest równy sumie jeden i kwadratu minus osiem piętnastych). Stąd znajdziemy cos 2 t =

(cosinus kwadrat te jest równy dwieście dwadzieścia pięć dwieście osiemdziesiąt dziewięć). Oznacza to koszt = (cosinus te wynosi piętnaście siedemnastych) lub

koszt = . Warunek: argument t należy do czwartego kwartału, gdzie koszt > 0. Zatem koszt = .(cosenus te wynosi piętnaście siedemnastych)

Znajdźmy wartość argumentu sine te. Ponieważ z zależności (pokaż relację tgt = dla t ≠ + πk, kϵZ) sinus te jest równy iloczynowi tangensu te przez cosinus te, to podstawiając wartość argumentu te..tangens te równa się minus osiem piętnastych .. według warunku i cosinus te jest równy rozwiązanemu wcześniej, otrzymujemy

sint = tgt ∙ koszt = (-) ∙ = - , (sinus te jest równy minus osiem siedemnastych)

ctgt = = - . (ponieważ cotangens te jest odwrotnością tangensu, co oznacza, że ​​cotangens te jest równy minus piętnaście osiemnastych)