Rozwiązywanie problemów dotyczących równowagi zbieżnych sił poprzez konstruowanie wielokątów sił zamkniętych wymaga uciążliwych konstrukcji. Uniwersalną metodą rozwiązania tego typu problemów jest przejście do wyznaczania rzutów danych sił na osie współrzędnych i operowanie tymi rzutami. Oś to linia prosta, której przypisano określony kierunek.
Rzut wektora na oś jest wielkością skalarną, którą wyznacza odcinek osi odcięty przez prostopadłe narzucone na nią z początku i końca wektora.
Rzut wektorowy uważa się za dodatni, jeśli kierunek od początku rzutu do jego końca pokrywa się z dodatnim kierunkiem osi. Rzut wektorowy uważa się za ujemny, jeśli kierunek od początku rzutu do jego końca jest przeciwny do dodatniego kierunku osi.
Zatem rzut siły na oś współrzędnych jest równy iloczynowi modułu siły i cosinusa kąta między wektorem siły a dodatnim kierunkiem osi.
Rozważmy kilka przypadków rzutowania sił na oś:
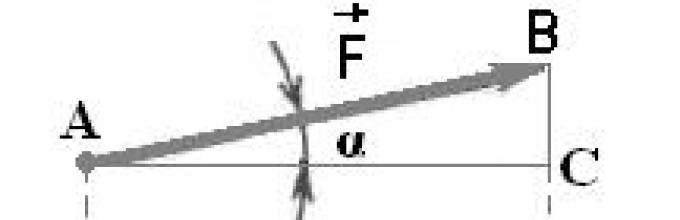
Wektor siły F(Rys. 15) tworzy kąt ostry z dodatnim kierunkiem osi x.

Aby znaleźć rzut, od początku i końca wektora siły obniżamy prostopadłe do osi Oh; dostajemy
1. Fx = F ponieważ α
Rzut wektora w tym przypadku jest dodatni
Siła F(Rys. 16) jest z dodatnim kierunkiem osi X kąt rozwarty α.

Następnie F x = F cos α, ale ponieważ α = 180 0 - φ,
F x = F sałata α = F cos180 0 - φ =- F cos φ.
Projekcja siły F na oś Oh w tym przypadku jest negatywny.
Siła F(Rys. 17) prostopadle do osi Oh.

Rzut siły F na oś X równy zeru
F x = F cos 90° = 0.
Siła zlokalizowana na płaszczyźnie jak(Rys. 18), można rzutować na dwie osie współrzędnych Oh I Jednostka organizacyjna.

Wytrzymałość F można podzielić na elementy: F x i F y. Moduł wektorowy F x jest równe rzutowi wektora F na oś wół i moduł wektorowy F y jest równe rzutowi wektora F na oś Oh.
Od Δ OAV: F x = F cos α, F x = F grzech α.
Od Δ OAS: F x = F cos φ, F x = F grzech φ.
Wielkość siły można wyznaczyć korzystając z twierdzenia Pitagorasa:
![]()
Rzut sumy wektorów lub wypadkowej na dowolną oś jest równy sumie algebraicznej rzutów sum wektorów na tę samą oś.
Rozważ zbieżne siły F 1 , F 2 , F 3 i F 4, (ryc. 19, a). Suma geometryczna lub wypadkowa tych sił F określona przez zamykającą stronę wielokąta sił


Spuśćmy się z wierzchołków wielokąta sił na oś X prostopadłe.
Uwzględniając otrzymane rzuty sił bezpośrednio z ukończonej konstrukcji, mamy
F= F 1x+ F 2x+ F 3x+ F 4x
gdzie n jest liczbą terminów wektorowych. Ich rzuty wchodzą do powyższego równania z odpowiednim znakiem.
Na płaszczyźnie geometryczną sumę sił można rzutować na dwie osie współrzędnych, a w przestrzeni odpowiednio na trzy.
Najpierw przypomnijmy sobie, co to jest oś współrzędnych, rzut punktu na oś I współrzędne punktu na osi.
Oś współrzędnych- To jest linia prosta, która ma określony kierunek. Można o tym myśleć jak o wektorze o nieskończenie dużym module.
Oś współrzędnych oznaczone literą: X, Y, Z, s, t... Zwykle wybiera się (dowolnie) punkt na osi, który nazywa się początkiem i z reguły oznacza się literą O. Z tego punktu mierzone są odległości do innych interesujących nas miejsc.
Rzut punktu na oś- jest to podstawa prostopadłej obniżonej z tego punktu do tej osi (ryc. 8). Oznacza to, że rzut punktu na oś jest punktem.
Współrzędna punktu na osi- jest to liczba, której wartość bezwzględna jest równa długości odcinka osi (w wybranej skali) zawartego pomiędzy początkiem osi a rzutem punktu na tę oś. Liczbę tę przyjmuje się ze znakiem plus, jeśli rzut punktu znajduje się w kierunku osi od jego początku, i ze znakiem minus, jeśli w kierunku przeciwnym.
Rzut skalarny wektora na oś- Ten numer, którego wartość bezwzględna jest równa długości odcinka osi (w wybranej skali) zawartego pomiędzy rzutami punktu początkowego i punktu końcowego wektora. Ważny! Zwykle zamiast wyrażenia Rzut skalarny wektora na oś po prostu mówią - rzut wektora na oś, czyli słowo skalarny obniżony. Projekcja wektorowa jest oznaczony tą samą literą co rzutowany wektor (normalnym, niepogrubionym pismem), z niższym (z reguły) indeksem nazwy osi, na którą rzutowany jest ten wektor. Na przykład, jeśli wektor jest rzutowany na oś X A, wówczas jego rzut jest oznaczony przez x. Podczas rzutowania tego samego wektora na inną oś, powiedzmy, oś Y, jego rzut zostanie oznaczony jako y (ryc. 9).

Liczyć rzut wektora na oś(na przykład oś X), należy odjąć współrzędną punktu początkowego od współrzędnej jego punktu końcowego, czyli
za x = x k - x n.
Musimy pamiętać: rzut skalarny wektora na oś (lub po prostu rzut wektora na oś) jest liczbą (nie wektorem)! Ponadto rzut może być dodatni, jeśli wartość x k jest większa od wartości x n, ujemny, jeśli wartość x k jest mniejsza od wartości x n i równa zeru, jeśli x k jest równa x n (ryc. 10).

Rzut wektora na oś można również znaleźć, znając moduł wektora i kąt, jaki tworzy z tą osią.
Z rysunku 11 jasno wynika, że a x = a Cos α
Oznacza to, że rzut wektora na oś jest równy iloczynowi modułu wektora i cosinusa kąta pomiędzy kierunkiem osi a kierunkiem wektora. Jeśli kąt jest ostry, to Cos α > 0 i a x > 0, a jeśli jest rozwarty, to cosinus kąta rozwartego jest ujemny i rzut wektora na oś również będzie ujemny.

Kąty mierzone od osi przeciwnie do ruchu wskazówek zegara uważa się za dodatnie, a kąty mierzone wzdłuż osi za ujemne. Ponieważ jednak cosinus jest funkcją parzystą, to znaczy Cos α = Cos (− α), przy obliczaniu rzutów kąty można liczyć zarówno zgodnie z ruchem wskazówek zegara, jak i przeciwnie do ruchu wskazówek zegara.
Przy rozwiązywaniu problemów często wykorzystywane będą następujące właściwości rzutów: jeśli
A = B + C +…+ D, wtedy a x = b x + c x +…+ d x (podobnie jak inne osie),
A= m B, to a x = mb x (podobnie dla pozostałych osi).
Wzór a x = a Cos α będzie wynosił Często pojawiają się podczas rozwiązywania problemów, więc zdecydowanie musisz to wiedzieć. Musisz znać zasadę wyznaczania projekcji na pamięć!
Pamiętać!
Aby znaleźć rzut wektora na oś, moduł tego wektora należy pomnożyć przez cosinus kąta między kierunkiem osi a kierunkiem wektora.
Jeszcze raz - na pamięć!
Występ wektor na oś to wektor otrzymywany przez pomnożenie rzutu skalarnego wektora na tę oś przez wektor jednostkowy tej osi. Na przykład, jeśli x – projekcja skalarna wektor A do osi X, a następnie x I- jego rzut wektorowy na tę oś.
Oznaczmy projekcja wektorowa taki sam jak sam wektor, ale z indeksem osi, na którą wektor jest rzutowany. Zatem rzut wektorowy wektora A na osi X, którą oznaczamy A X( tłuszcz litera oznaczająca wektor i indeks dolny nazwy osi) lub (niepogrubiona litera oznaczająca wektor, ale ze strzałką u góry (!) i indeksem dolnym nazwy osi).
Projekcja skalarna wektor na oś nazywa się numer, którego wartość bezwzględna jest równa długości odcinka osi (w wybranej skali) zawartego pomiędzy rzutami punktu początkowego i punktu końcowego wektora. Zwykle zamiast wyrażenia projekcja skalarna po prostu mówią - występ. Rzut jest oznaczony tą samą literą, co wektor rzutowany (normalnym, niepogrubionym pismem), z niższym indeksem (zwykle) nazwy osi, na którą rzutowany jest ten wektor. Na przykład, jeśli wektor jest rzutowany na oś X A, wówczas jego rzut jest oznaczony przez x. Podczas rzutowania tego samego wektora na inną oś, jeśli osią jest Y, jego rzut zostanie oznaczony jako y.
Aby obliczyć projekcję wektor na osi (na przykład osi X) należy odjąć współrzędną punktu początkowego od współrzędnej jego punktu końcowego, czyli
za x = x k - x n.
Rzut wektora na oś jest liczbą. Co więcej, rzut może być dodatni, jeżeli wartość x k jest większa od wartości x n,
ujemna, jeśli wartość x k jest mniejsza niż wartość x n
i równe zeru, jeśli x k równa się x n.
Rzut wektora na oś można również znaleźć, znając moduł wektora i kąt, jaki tworzy z tą osią.
Z rysunku jasno wynika, że a x = a Cos α
oznacza to, że rzut wektora na oś jest równy iloczynowi modułu wektora i cosinusowi kąta między kierunkiem osi i kierunek wektora. Jeśli kąt jest ostry, to
Cos α > 0 i a x > 0, a jeśli jest rozwarty, to cosinus kąta rozwartego jest ujemny i rzut wektora na oś również będzie ujemny.
Kąty mierzone od osi przeciwnie do ruchu wskazówek zegara uważa się za dodatnie, a kąty mierzone wzdłuż osi za ujemne. Ponieważ jednak cosinus jest funkcją parzystą, to znaczy Cos α = Cos (− α), przy obliczaniu rzutów kąty można liczyć zarówno zgodnie z ruchem wskazówek zegara, jak i przeciwnie do ruchu wskazówek zegara.
Aby znaleźć rzut wektora na oś, moduł tego wektora należy pomnożyć przez cosinus kąta między kierunkiem osi a kierunkiem wektora.
Współrzędne wektora— współczynniki jedynej możliwej kombinacji liniowej wektorów bazowych w wybranym układzie współrzędnych, równe danemu wektorowi.
gdzie są współrzędne wektora.
Iloczyn skalarny wektorów
Iloczyn skalarny wektorów[- w skończonych wymiarach Przestrzeń wektorowa definiuje się jako sumę iloczynów identycznych składników wektory.
Na przykład spółka S.p.v. A = (A 1 , ..., jakiś) I B = (B 1 , ..., b n):
(A , B ) = A 1 B 1 + A 2 B 2 + ... + an b n
Z fizyki dla klasy 9 (I.K.Kikoin, A.K.Kikoin, 1999),
zadanie №5
do rozdziału” ROZDZIAŁ 1. OGÓLNE INFORMACJE O RUCHU».
1. Jak nazywa się rzut wektora na oś współrzędnych?
1. Rzut wektora a na oś współrzędnych to długość odcinka pomiędzy rzutami początku i końca wektora a (prostopadłymi wyrzuconymi z tych punktów na oś) na tę oś współrzędnych.
2. Jak wektor przemieszczenia ciała jest powiązany z jego współrzędnymi?
2. Rzuty wektora przemieszczenia s na osie współrzędnych są równe zmianie odpowiednich współrzędnych ciała.
3. Jeżeli współrzędna punktu rośnie w czasie, to jaki znak ma rzut wektora przemieszczenia na oś współrzędnych? A co jeśli się zmniejszy?
3. Jeżeli współrzędna punktu rośnie w czasie, to rzut wektora przemieszczenia na oś współrzędnych będzie dodatni, ponieważ w tym przypadku przejdziemy od rzutu początku do rzutu końca wektora w kierunku samej osi.
Jeśli współrzędna punktu zmniejsza się w czasie, wówczas rzut wektora przemieszczenia na oś współrzędnych będzie ujemny, ponieważ w tym przypadku przejdziemy od rzutu początku do rzutu końca wektora na prowadnicę samej osi.
4. Jeżeli wektor przemieszczenia jest równoległy do osi X, to jaki jest moduł rzutu wektora na tę oś? A co z modułem rzutu tego samego wektora na oś Y?
4. Jeżeli wektor przemieszczenia jest równoległy do osi X, to moduł rzutu wektora na tę oś jest równy modułowi samego wektora, a jego rzut na oś Y wynosi zero.
5. Wyznacz znaki rzutów na oś X wektorów przemieszczeń pokazanych na rysunku 22. Jak zmieniają się współrzędne ciała podczas tych przemieszczeń?
5. We wszystkich poniższych przypadkach współrzędna Y ciała nie zmienia się, a współrzędna X ciała zmienia się w następujący sposób:
a) s 1;
rzut wektora s 1 na oś X jest ujemny i jest w wartości bezwzględnej równy długości wektora s 1 . Przy takim ruchu współrzędna X ciała zmniejszy się o długość wektora s 1.
b) s 2;
rzut wektora s 2 na oś X jest dodatni i ma wielkość równą długości wektora s 1 . Przy takim ruchu współrzędna X ciała wzrośnie o długość wektora s 2.
c) s 3;
rzut wektora s 3 na oś X jest ujemny i równy długości wektora s 3 . Przy takim ruchu współrzędna X ciała zmniejszy się o długość wektora s 3.
d) s 4;
rzut wektora s 4 na oś X jest dodatni i ma wielkość równą długości wektora s 4 . Przy takim ruchu współrzędna X ciała wzrośnie o długość wektora s 4.
e) s 5;
rzut wektora s 5 na oś X jest ujemny i równy co do długości wektorowi s 5 . Przy takim ruchu współrzędna X ciała zmniejszy się o długość wektora s 5.
6. Jeżeli wartość przebytej drogi jest duża, to czy moduł przemieszczenia może być mały?
6. Może. Wynika to z faktu, że przemieszczenie (wektor przemieszczenia) jest wielkością wektorową, tj. jest skierowanym odcinkiem linii prostej łączącym początkowe położenie ciała z jego kolejnymi położeniami. A ostateczna pozycja ciała (niezależnie od przebytej odległości) może być jak najbardziej zbliżona do początkowej pozycji ciała. Jeżeli położenie końcowe i początkowe ciała pokrywają się, moduł przemieszczenia będzie równy zeru.
7. Dlaczego w mechanice wektor ruchu ciała jest ważniejszy niż droga, jaką ono przebyło?
7. Głównym zadaniem mechaniki jest określenie w dowolnym momencie położenia ciała. Znając wektor ruchu ciała, możemy wyznaczyć współrzędne ciała, tj. położenia ciała w dowolnym momencie, a znając jedynie przebytą drogę, nie jesteśmy w stanie określić współrzędnych ciała, gdyż nie mamy informacji o kierunku ruchu, możemy jedynie ocenić długość przebytej drogi w danym momencie.
Oś jest kierunkiem. Oznacza to, że rzut na oś lub na linię skierowaną jest uważany za taki sam. Rzutowanie może być algebraiczne lub geometryczne. W ujęciu geometrycznym rzut wektora na oś rozumiany jest jako wektor, a w ujęciu algebraicznym jako liczba. Oznacza to, że stosuje się koncepcje rzutowania wektora na oś i numerycznego rzutowania wektora na oś.
Jeśli mamy oś L i niezerowy wektor A B →, to możemy skonstruować wektor A 1 B 1 ⇀, oznaczający rzuty jego punktów A 1 i B 1.
A 1 B → 1 będzie rzutem wektora A B → na L.
Definicja 1
Rzut wektora na oś jest wektorem, którego początek i koniec są rzutami początku i końca danego wektora. n p L A B → → zwyczajowo oznacza się rzut A B → na L. Aby skonstruować rzut na L, prostopadłe są upuszczane na L.
Przykład 1
Przykład rzutu wektorowego na oś.
Na płaszczyźnie współrzędnych O x y określony jest punkt M 1 (x 1, y 1). Aby zobrazować wektor promienia punktu M 1, należy skonstruować rzuty na O x i O y. Otrzymujemy współrzędne wektorów (x 1, 0) i (0, y 1).

Jeśli mówimy o rzucie a → na niezerowe b → lub rzucie a → na kierunek b → , to mamy na myśli rzut a → na oś, z którą kierunek b → pokrywa się. Rzut a → na linię określoną przez b → oznaczono n p b → a → → . Wiadomo, że gdy kąt pomiędzy a → i b → , n p b → a → → i b → można uznać za współkierunkowy. W przypadku, gdy kąt jest rozwarty, n p b → a → → i b → są w przeciwnych kierunkach. W sytuacji prostopadłości a → i b → oraz a → wynosi zero, rzut a → w kierunku b → jest wektorem zerowym.
Numeryczną charakterystyką rzutowania wektora na oś jest numeryczny rzut wektora na daną oś.
Definicja 2
Numeryczne odwzorowanie wektora na oś to liczba równa iloczynowi długości danego wektora i cosinusa kąta między danym wektorem a wektorem wyznaczającym kierunek osi.
Rzut numeryczny A B → na L oznaczamy n p L A B → , a a → na b → - n p b → a → .
Na podstawie wzoru otrzymujemy n p b → a → = a → · cos a → , b → ^ , skąd a → jest długością wektora a → , a ⇀ , b → ^ jest kątem pomiędzy wektorami a → i b → .
Otrzymujemy wzór na obliczenie rzutu numerycznego: n p b → a → = a → · cos a → , b → ^ . Ma to zastosowanie dla znanych długości a → i b → oraz kąta między nimi. Wzór ma zastosowanie dla znanych współrzędnych a → i b →, ale istnieje uproszczona forma.
Przykład 2
Znajdź rzut numeryczny a → na linię prostą w kierunku b → o długości a → równej 8 i kącie między nimi 60 stopni. Według warunku mamy a ⇀ = 8, a ⇀, b → ^ = 60 °. Oznacza to, że podstawiamy wartości liczbowe do wzoru n p b ⇀ a → = a → · cos a → , b → ^ = 8 · cos 60 ° = 8 · 1 2 = 4 .
Odpowiedź: 4.
Przy znanym cos (a → , b → ^) = a ⇀ , b → a → · b → , mamy a → , b → jako iloczyn skalarny a → i b → . Korzystając ze wzoru n p b → a → = a → · cos a ⇀ , b → ^ , możemy znaleźć rzut liczbowy a → skierowany wzdłuż wektora b → i otrzymać n p b → a → = a → , b → b → . Wzór jest równoważny definicji podanej na początku akapitu.
Definicja 3
Rzut numeryczny wektora a → na oś pokrywającą się w kierunku z b → jest stosunkiem iloczynu skalarnego wektorów a → i b → do długości b → . Wzór n p b → a → = a → , b → b → można zastosować do znalezienia rzutu numerycznego a → na linię zbieżną w kierunku z b → , o znanych współrzędnych a → i b →.
Przykład 3
Biorąc pod uwagę b → = (- 3 , 4) . Znajdź projekcję numeryczną a → = (1, 7) na L.
Rozwiązanie
Na płaszczyźnie współrzędnych n p b → a → = a → , b → b → ma postać n p b → a → = a → , b → b → = a x b x + a y b y b x 2 + b y 2 , gdzie a → = (a x , a y ) i b → = b x , b y . Aby znaleźć rzut numeryczny wektora a → na oś L, potrzebujemy: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · (- 3) + 7 · 4 (- 3) 2 + 4 2 = 5.
Odpowiedź: 5.
Przykład 4
Znajdź rzut a → na L, pokrywający się z kierunkiem b →, gdzie znajduje się a → = - 2, 3, 1 i b → = (3, - 2, 6). Określona jest przestrzeń trójwymiarowa.
Rozwiązanie
Mając dane a → = a x , a y , a z i b → = b x , b y , b z , obliczamy iloczyn skalarny: a ⇀ , b → = a x · b x + a y · b y + a z · b z . Długość b → oblicza się ze wzoru b → = b x 2 + b y 2 + b z 2 . Wynika z tego, że wzór na określenie rzutu numerycznego a → będzie następujący: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .
Zastąp wartości liczbowe: n p L a → = n p b → a → = (- 2) 3 + 3 (- 2) + 1 6 3 2 + (- 2) 2 + 6 2 = - 6 49 = - 6 7 .
Odpowiedź: - 6 7.
Przyjrzyjmy się powiązaniu pomiędzy a → na L i długością rzutu a → na L. Narysujmy oś L, dodając a → i b → z punktu na L, po czym rysujemy linię prostopadłą od końca a → do L i rysujemy rzut na L. Istnieje 5 odmian obrazu:

Pierwszy przypadek z a → = n p b → a → → oznacza a → = n p b → a → → , stąd n p b → a → = a → · cos (a , → b → ^) = a → · cos 0 ° = a → = n p b → za → → .
Drugi przypadek implikuje użycie n p b → a → ⇀ = a → · cos a → , b → , co oznacza n p b → a → = a → · cos (a → , b →) ^ = n p b → a → → .
Trzeci przypadek wyjaśnia, że gdy n p b → a → → = 0 → otrzymujemy n p b ⇀ a → = a → · cos (a → , b → ^) = a → · cos 90 ° = 0 , wtedy n p b → a → → = 0 i n p b → za → = 0 = n p b → za → → .
Czwarty przypadek pokazuje n p b → a → → = a → · cos (180 ° - a → , b → ^) = - a → · cos (a → , b → ^) , następuje n p b → a → = a → · cos ( a → , b → ^) = - n p b → a → → .
Piąty przypadek pokazuje a → = n p b → a → → , co oznacza a → = n p b → a → → , stąd mamy n p b → a → = a → · cos a → , b → ^ = a → · cos 180° = - za → = - n p b → za → .
Definicja 4
Numeryczny rzut wektora a → na oś L, która jest skierowana tak samo jak b →, ma następującą wartość:
- długość rzutu wektora a → na L, pod warunkiem, że kąt pomiędzy a → i b → jest mniejszy niż 90 stopni lub równy 0: n p b → a → = n p b → a → → z warunkiem 0 ≤ (a → , b →) ^< 90 ° ;
- zero pod warunkiem, że a → i b → są prostopadłe: n p b → a → = 0, gdy (a → , b → ^) = 90 °;
- długość rzutu a → na L, pomnożona przez -1, gdy wektory a → i b → mają kąt rozwarty lub prosty: n p b → a → = - n p b → a → → z warunkiem 90 °< a → , b → ^ ≤ 180 ° .
Przykład 5
Biorąc pod uwagę długość rzutu a → na L, równą 2. Znajdź rzut liczbowy a → pod warunkiem, że kąt wynosi 5 π 6 radianów.
Rozwiązanie
Z warunku jasno wynika, że kąt ten jest rozwarty: π 2< 5 π 6 < π . Тогда можем найти числовую проекцию a → на L: n p L a → = - n p L a → → = - 2 .
Odpowiedź: - 2.
Przykład 6
Biorąc pod uwagę płaszczyznę O x y z o długości wektora a → równej 6 3, b → (- 2, 1, 2) o kącie 30 stopni. Znajdź współrzędne rzutu a → na oś L.
Rozwiązanie
Najpierw obliczamy odwzorowanie numeryczne wektora a →: n p L a → = n p b → a → = a → · cos (a → , b →) ^ = 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .
Pod warunkiem, że kąt jest ostry, wówczas rzut numeryczny a → = długość rzutu wektora a →: n p L a → = n p L a → → = 9. Ten przypadek pokazuje, że wektory n p L a → → i b → są współkierunkowe, co oznacza, że istnieje liczba t, dla której zachodzi równość: n p L a → → = t · b → . Widzimy stąd, że n p L a → → = t · b → , co oznacza, że możemy znaleźć wartość parametru t: t = n p L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 9 9 = 3 .
Następnie n p L a → → = 3 · b → ze współrzędnymi rzutu wektora a → na oś L równymi b → = (- 2 , 1 , 2) , gdzie należy pomnożyć wartości przez 3. Mamy n p L a → → = (- 6 , 3 , 6) . Odpowiedź: (- 6, 3, 6).
Należy powtórzyć poznane wcześniej informacje o warunku kolinearności wektorów.
Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter