Projekt algebraiczny „Rozwiązywanie nierówności trygonometrycznych” Ukończony przez uczennicę klasy 10 „B” Kazachkovą Julię Opiekun: nauczyciel matematyki Kochakova N.N.
Cel Utrwalić materiał na temat „Rozwiązywanie nierówności trygonometrycznych” i stworzyć przypomnienie dla uczniów o przygotowaniu się do nadchodzącego egzaminu.
Cele: Podsumowanie materiału na ten temat. Usystematyzuj otrzymane informacje. Rozważać ten temat w jednolitym egzaminie państwowym.
Trafność Znaczenie wybranego przeze mnie tematu polega na tym, że zadania na temat „Rozwiązywanie nierówności trygonometrycznych” są zawarte w zadaniach Unified State Exam.
Nierówności trygonometryczne Nierówność to relacja łącząca dwie liczby lub wyrażenia poprzez jeden ze znaków: (większy niż); ≥ (większy lub równy). Nierówność trygonometryczna to nierówność obejmująca funkcje trygonometryczne.
Nierówności trygonometryczne Rozwiązanie nierówności zawierających funkcje trygonometryczne sprowadza się z reguły do rozwiązania najprostszych nierówności postaci: sin x>a, sin x a, cos x a, tg x a,ctg x
Algorytm rozwiązywania nierówności trygonometrycznych Na osi odpowiadającej danej funkcji trygonometrycznej zaznacz podaną wartość liczbową tej funkcji. Narysuj linię przechodzącą przez zaznaczony punkt przecinający okrąg jednostkowy. Wybierz punkty przecięcia prostej i okręgu, biorąc pod uwagę znak nierówności ścisłej lub nieścisłej. Wybierz łuk okręgu, na którym znajdują się rozwiązania nierówności. Określ wartości kątów w punktach początkowym i końcowym łuku kołowego. Zapisz rozwiązanie nierówności uwzględniając okresowość danej funkcji trygonometrycznej.
Wzory na rozwiązanie nierówności trygonometrycznych sinx >a; x (arcsin a + 2πn; π- arcsin a + 2πn). grzech A; x (- arccos a + 2πn; arccos a + 2πn). cosxA; x (arctg a + πn ; + πn). tgx A; x (πn ; arctan + πn). ctgx
Rozwiązanie graficzne podstawowe nierówności trygonometryczne sinx >a
Graficzne rozwiązanie podstawowych nierówności trygonometrycznych sinx Graficzne rozwiązanie podstawowych nierówności trygonometrycznych cosx >a Graficzne rozwiązanie podstawowych nierówności trygonometrycznych cosx Graficzne rozwiązanie podstawowych nierówności trygonometrycznych tgx >a Graficzne rozwiązanie podstawowych nierówności trygonometrycznych tgx Graficzne rozwiązanie podstawowych nierówności trygonometrycznych ctgx >a
Nierówności to relacje postaci a·b, gdzie aib są wyrażeniami zawierającymi co najmniej jedną zmienną. Nierówności mogą być ostre - ‹, › i nierygorystyczne - ≥, ≤.
Nierówności trygonometryczne są wyrażeniami postaci: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, gdzie F(x) jest reprezentowane przez jedną lub więcej funkcji trygonometrycznych .
Przykładem najprostszej nierówności trygonometrycznej jest: sin x ‹ 1/2. Zwyczajowo rozwiązuje się takie problemy graficznie, w tym celu opracowano dwie metody.
Metoda 1 - Rozwiązywanie nierówności poprzez wykreślenie funkcji
Aby znaleźć przedział spełniający warunki nierówności sin x ‹ 1/2 należy wykonać następujące kroki:
- NA oś współrzędnych skonstruuj sinusoidę y = sin x.
- Narysuj wykres na tej samej osi argument numeryczny nierówności, czyli prostą przechodzącą przez punkt ½ rzędnej OY.
- Zaznacz punkty przecięcia dwóch wykresów.
- Zacień segment będący rozwiązaniem przykładu.
Jeśli w wyrażeniu występują znaki ścisłe, punkty przecięcia nie są rozwiązaniami. Ponieważ najmniejszy dodatni okres sinusoidy wynosi 2π, odpowiedź zapisujemy w następujący sposób:
![]()
Jeżeli znaki wyrażenia nie są ścisłe, wówczas przedział rozwiązania należy ująć w nawiasy kwadratowe - . Odpowiedź na zadanie można również zapisać w postaci następującej nierówności: ![]()
Metoda 2 - Rozwiązywanie nierówności trygonometrycznych za pomocą okręgu jednostkowego
Takie problemy można łatwo rozwiązać za pomocą okrąg trygonometryczny. Algorytm wyszukiwania odpowiedzi jest bardzo prosty:
- Najpierw musisz narysować okrąg jednostkowy.
- Następnie należy zanotować wartość funkcji łuku argumentu prawej strony nierówności na łuku koła.
- Należy poprowadzić linię prostą przechodzącą przez wartość funkcji łuku równolegle do osi odciętej (OX).
- Następnie pozostaje tylko wybrać łuk koła, który jest zbiorem rozwiązań nierówności trygonometrycznej.
- Zapisz odpowiedź w wymaganej formie.
Przeanalizujmy etapy rozwiązania na przykładzie nierówności sin x › 1/2. Na okręgu zaznaczono punkty α i β – wartości
![]()
Punkty łuku znajdujące się nad α i β stanowią przedział rozwiązania danej nierówności.

Jeśli chcesz rozwiązać przykład dla cos, wówczas łuk odpowiedzi będzie zlokalizowany symetrycznie do osi OX, a nie OY. Możesz rozważyć różnicę między przedziałami rozwiązań dla sin i cos na poniższych diagramach w tekście.

Graficzne rozwiązania nierówności stycznych i cotangensów będą się różnić od sinusa i cosinusa. Wynika to z właściwości funkcji.

Arcus tangens i arccotangens są stycznymi do okręgu trygonometrycznego, a minimalny okres dodatni dla obu funkcji wynosi π. Aby szybko i poprawnie zastosować drugą metodę, należy pamiętać, na której osi wykreślone są wartości sin, cos, tg i ctg.
Styczna styczna biegnie równolegle do osi OY. Jeśli na okręgu jednostkowym naniesiemy wartość arctanu a, to drugi wymagany punkt będzie znajdował się w ćwiartce przekątnej. Kąty
Są to punkty przerwania funkcji, ponieważ wykres dąży do nich, ale nigdy ich nie osiąga.

W przypadku cotangensa styczna przebiega równolegle do osi OX, a funkcja jest przerywana w punktach π i 2π.

Złożone nierówności trygonometryczne
Jeśli argument funkcji nierówności jest reprezentowany nie tylko przez zmienną, ale przez całe wyrażenie zawierające niewiadomą, to mówimy już o złożona nierówność. Proces i procedura jego rozwiązania różnią się nieco od metod opisanych powyżej. Załóżmy, że musimy znaleźć rozwiązanie następującej nierówności:

Rozwiązanie graficzne polega na skonstruowaniu zwykłej sinusoidy y = sin x przy użyciu dowolnie wybranych wartości x. Obliczmy tabelę ze współrzędnymi punktów kontrolnych wykresu:

Rezultatem powinna być piękna krzywa.
Aby ułatwić znalezienie rozwiązania, zamieńmy argument funkcji zespolonej

Przecięcie dwóch wykresów pozwala nam wyznaczyć obszar pożądanych wartości, przy którym spełniony jest warunek nierówności.

Znaleziony segment jest rozwiązaniem dla zmiennej t:

Celem zadania jest jednak znalezienie wszystkiego możliwe opcje nieznany x:

Rozwiązanie podwójnej nierówności jest dość proste, należy przesunąć π/3 do skrajnych części równania i wykonać wymagane obliczenia:

Odpowiedź na zadanie będzie wyglądać jak przedział dla ścisłej nierówności:

Takie problemy będą wymagały od uczniów doświadczenia i zręczności w posługiwaniu się funkcjami trygonometrycznymi. Więcej zadania szkoleniowe zostanie ustalone w procesie przygotowawczym, im łatwiej i szybciej uczeń znajdzie odpowiedź Pytanie z egzaminu jednolitego stanu test.
DEFINICJA
Nierówności trygonometryczne to nierówności, które zawierają zmienną pod znakiem funkcji trygonometrycznej.
Rozwiązywanie nierówności trygonometrycznych
Rozwiązywanie nierówności trygonometrycznych często sprowadza się do rozwiązania najprostszych nierówności trygonometrycznych w postaci: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname(tg) x > a \), \(\ \ nazwa operatora(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \nazwa operatora(tg) x \leq a \), \ (\ \nazwa operatora(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \nazwa operatora(tg) x \geq a \ ), \(\ \nazwa operatora(tg) x \geq a \)
Najprostsze nierówności trygonometryczne rozwiązuje się graficznie lub za pomocą jednostkowego okręgu trygonometrycznego.
Z definicji sinus kąta \(\\alpha \) jest rzędną punktu \(\P_(\alpha)(x, y)\) okręgu jednostkowego (ryc. 1), a cosinus to odcięta tego punktu. Fakt ten wykorzystuje się do rozwiązywania prostych nierówności trygonometrycznych z cosinusem i sinusem za pomocą koła jednostkowego.
Przykłady rozwiązywania nierówności trygonometrycznych
Rozwiąż nierówność \(\ \sin x \leq \frac(\sqrt(3))(2) \)
Ponieważ \(\ \left|\frac(\sqrt(3))(2)\right| , to ta nierówność ma rozwiązanie i można je rozwiązać na dwa sposoby
Pierwszy sposób. Rozwiążmy tę nierówność graficznie. Aby to zrobić, zbudujmy wykres sinusa \(\ y=\sin x \) (ryc. 2) i linii prostej \(\ y=\frac(\sqrt(3))(2) \) w jeden układ współrzędnych
Zaznaczmy odstępy, w jakich sinusoida znajduje się pod wykresem prostej \(\ y=\frac(\sqrt(3))(2) \) . Znajdźmy odcięte \(\ x_(1) \) i \(\ x_(2) \) punktów przecięcia tych wykresów: \(\ x_(1)=\pi-\arcsin \frac(\sqrt( 3))(2 )=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+ 2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Otrzymaliśmy przedział \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \), ale ponieważ funkcja \(\ y=\sin x \) jest okresowy i ma okres \(\ 2 \pi \) , wówczas odpowiedzią będzie suma przedziałów: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac( 7 \pi)(3)+ 2 \pi k\right] \), \(\ k \in Z \)
Drugi sposób. Skonstruujmy okrąg jednostkowy i prostą \(\ y=\frac(\sqrt(3))(2) \), punkty ich przecięcia oznaczamy \(\ P_(x_(1)) \) i \ (\ P_(x_(2 )) \) (ryc. 3). Rozwiązaniem pierwotnej nierówności będzie zbiór punktów o współrzędnych mniejszych niż \(\ \frac(\sqrt(3))(2) \) . Znajdźmy wartość \(\ \boldsymbol(I)_(1) \) i \(\ \boldsymbol(I)_(2) \) obracając się w kierunku przeciwnym do ruchu wskazówek zegara, \(\ x_(1) Rys. 3
\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Biorąc pod uwagę okresowość funkcji sinus, ostatecznie otrzymujemy przedziały \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ pi\right] \), \(\k\in Z\)
Rozwiąż nierówność \(\ \sin x>2\)
Sinus jest funkcją ograniczoną: \(\ |\sin x| \leq 1 \) , a prawa strona tej nierówności jest większa niż jeden, więc nie ma rozwiązań.
Rozwiąż nierówność \(\ \cos x>\frac(1)(2) \)
Nierówność tę można rozwiązać na dwa sposoby: graficznie i za pomocą okręgu jednostkowego. Rozważmy każdą z metod.
Pierwszy sposób. Przedstawmy w jednym układzie współrzędnych funkcje opisujące lewą i prawą stronę nierówności, czyli \(\ y=\cos x \) i \(\ y=\frac(1)(2) \) . Zaznaczmy przedziały, w których wykres funkcji cosinus \(\ y=\cos x \) znajduje się nad wykresem prostej \(\ y=\frac(1)(2) \) (ryc. 4 ).
Znajdźmy odcięte punktów \(\ \boldsymbol(x)_(1) \) i \(\ x_(2) \) – punkty przecięcia wykresów funkcji \(\ y=\cos x \) i \(\ y=\frac (1)(2) \) , które są końcami jednego z przedziałów, w których zachodzi wskazana nierówność. \(\x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3)\); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)
Biorąc pod uwagę, że cosinus jest funkcją okresową, z kropką \(\ 2 \pi \) odpowiedzią będą wartości \(\ x \) z przedziałów \(\ \left(-\frac(\pi) (3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \in Z \)
Drugi sposób. Skonstruujmy okrąg jednostkowy i prostą \(\x=\frac(1)(2)\) (ponieważ okrąg jednostkowy Oś odciętych odpowiada cosinusom). Oznaczmy \(\ P_(x_(1)) \) i \(\ P_(x_(2)) \) (rys. 5) – punkty przecięcia prostej i okręgu jednostkowego. Rozwiązaniem pierwotnego równania będzie zbiór punktów odciętych, które są mniejsze niż \(\ \frac(1)(2) \) . Znajdźmy wartość \(\ x_(1) \) i \(\ 2 \) obracając się w kierunku przeciwnym do ruchu wskazówek zegara, tak że \(\ x_(1) Biorąc pod uwagę okresowość cosinusa, w końcu otrzymamy przedziały \( \ \left(-\frac (\pi)(3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \),\(\k \in Z\)
Rozwiąż nierówność \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)
Skonstruujmy wykresy funkcji \(\ y=\operatorname(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) w jednym układzie współrzędnych
Zaznaczmy przedziały, w których wykres funkcji \(\ y=\operatorname(ctg) x \) znajduje się nie wyżej niż wykres linii prostej \(\ y=-\frac(\sqrt(3) )(3) \) (ryc. 6) .
Znajdźmy odciętą punktu \(\ x_(0) \) , będącego końcem jednego z przedziałów, w którym występuje nierówność \(\ x_(0)=\operatorname(arcctg)\left(-\frac( \sqrt(3))( 3)\right)=\pi-\nazwaoperatora(arcctg)\left(\frac(\sqrt(3))(3)\right)=\pi-\frac(\pi)( 3)=\frac(2\pi)(3)\)
Drugim końcem tego przedziału jest punkt \(\ \pi \) , a funkcja \(\ y=\operatorname(ctg) x \) w tym punkcie jest niezdefiniowana. Zatem jednym z rozwiązań tej nierówności jest przedział \(\ \frac(2 \pi)(3) \leq x
Nierówności trygonometryczne z złożona argumentacja
Nierówności trygonometryczne ze złożonymi argumentami można zredukować do prostych nierówności trygonometrycznych za pomocą podstawienia. Po rozwiązaniu dokonuje się odwrotnego podstawienia i wyraża się pierwotną niewiadomą.
Rozwiąż nierówność \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)
Wyraźmy cosinus po prawej stronie nierówności: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)
Dokonujemy zamiany \(\ t=2 x+100^(\circ) \) , po czym nierówność ta zostaje przekształcona w najprostszą nierówność \(\ \cos t \leq-\frac(1)(2) \)
Rozwiążmy to za pomocą koła jednostkowego. Skonstruujmy okrąg jednostkowy i linię prostą \(\ x=-\frac(1)(2) \) . Oznaczmy \(\P_(1)\) i \(\P_(2)\) – punkty przecięcia prostej i okręgu jednostkowego (rys. 7).
Rozwiązaniem pierwotnej nierówności będzie zbiór punktów odciętych, których jest nie więcej niż \(\ -\frac(1)(2)\). Punkt \(\ P_(1) \) odpowiada kątowi \(\ 120^(\circ) \) , a punkt \(\ P_(2) \) . Zatem biorąc pod uwagę okres cosinusa, otrzymujemy \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \) ,\(\n\w Z\)
Zróbmy odwrotną zamianę \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n\), \(\n \in Z\)
Wyraźmy \(\ \mathbf(x) \), aby najpierw odjąć \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot n \ leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \n\ w Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)
a następnie podziel przez 2 \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^ (\circ)+360^(\circ) \cdot n)(2) \), \(\n \in Z\); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\n \in Z \)
Podwójne nierówności trygonometryczne
Rozwiąż podwójną nierówność trygonometryczną \(\ \frac(1)(2)
Wprowadźmy zamianę \(\ t=\frac(x)(2) \) , wówczas pierwotna nierówność przyjmie postać \(\ \frac(1)(2)
Rozwiążmy to za pomocą koła jednostkowego. Ponieważ oś rzędnych na okręgu jednostkowym odpowiada sinusowi, wybieramy na nim zbiór rzędnych, których rzędne są większe niż \(\ x=\frac(1)(2) \) i mniejsze lub równe \(\ \frac(\sqrt(2))(2 ) \) . Na rysunku 8 punkty te będą zlokalizowane na łukach \(\P_(t_(1))\), \(\P_(t_(2))\) i \(\P_(t_(3))\) , \(\P_(t_(4))\) . Znajdźmy wartość \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \), obracając się w kierunku przeciwnym do ruchu wskazówek zegara, i \ (\t_(1)\(\t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3\ pi)(4) \);\(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi) (6)\)
Otrzymujemy w ten sposób dwa przedziały, które biorąc pod uwagę okresowość funkcji sinus, można zapisać następująco \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k Dokonajmy odwrotnej zamiany \(\ t=\frac(x)(2) \frac(\pi)( 6)+2 \pi k \ leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \), \(\ \frac(3 \pi)(4)+2 \ pi k Wyraźmy \(\ \mathbf( x) \), aby to zrobić, pomnóż wszystkie strony obu nierówności przez 2, otrzymamy \(\ \frac(\pi)(3)+4 \pi k \leq X
Podczas lekcji praktycznej powtórzymy główne typy zadań z tematu „Trygonometria”, dodatkowo przeanalizujemy problemy o zwiększonej złożoności i rozważymy przykłady rozwiązywania różnych nierówności trygonometrycznych i ich układów.
Ta lekcja pomoże Ci przygotować się do jednego z typów zadań B5, B7, C1 i C3.
Zacznijmy od przejrzenia głównych typów zadań, które omówiliśmy w temacie „Trygonometria” i rozwiążmy kilka niestandardowych problemów.
Zadanie nr 1. Konwersja kątów na radiany i stopnie: a) ; B) .
a) Skorzystajmy ze wzoru na przeliczenie stopni na radiany
![]()
Podstawmy do niego określoną wartość.
b) Zastosuj wzór na przeliczenie radianów na stopnie
![]()
Dokonajmy podstawienia ![]() .
.
Odpowiedź. A) ; B) .
Zadanie nr 2. Oblicz: a) ; B) .
a) Ponieważ kąt wykracza daleko poza tabelę, zmniejszymy go, odejmując okres sinusoidalny. Ponieważ Kąt jest podawany w radianach, wówczas okres będziemy rozpatrywać jako .
b) W tym przypadku sytuacja jest podobna. Ponieważ kąt jest podawany w stopniach, okres stycznej będziemy rozważać jako .
Powstały kąt, choć mniejszy od kropki, jest większy, co oznacza, że nie odnosi się już do głównej, ale do przedłużonej części stołu. Aby po raz kolejny nie ćwiczyć pamięci zapamiętywaniem rozszerzonej tabeli wartości funkcji trygony, odejmiemy jeszcze raz okres styczny:
Wykorzystaliśmy dziwność funkcji stycznej.
Odpowiedź. a) 1; B) .
Zadanie nr 3. Oblicz ![]() , Jeśli .
, Jeśli .
Sprowadźmy całe wyrażenie do tangensów, dzieląc licznik i mianownik ułamka przez . Jednocześnie nie możemy się tego bać, bo w tym przypadku wartość tangensa nie istniałaby.
Zadanie nr 4. Uprość wyrażenie.
Określone wyrażenia są konwertowane przy użyciu formuł redukcyjnych. Są po prostu niezwykle napisane przy użyciu stopni. Pierwsze wyrażenie zazwyczaj reprezentuje liczbę. Uprośćmy wszystkie funkcje trygologiczne jeden po drugim:
Ponieważ , wówczas funkcja zmienia się na kofunkcję, tj. do cotangensu, a kąt przypada na drugą ćwiartkę, w której pierwotna styczna ma znak ujemny.

Z tych samych powodów, co w poprzednim wyrażeniu, funkcja zmienia się na kofunkcję, tj. do cotangensu, a kąt przypada na pierwszą ćwiartkę, w której pierwotna styczna ma znak dodatni.
Zastąpmy wszystko uproszczonym wyrażeniem:
Problem nr 5. Uprość wyrażenie.
Zapiszmy tangens kąta podwójnego, korzystając z odpowiedniego wzoru i uprośćmy wyrażenie:
Ostatnia tożsamość jest jednym z uniwersalnych wzorów zastępczych dla cosinusa.
Problem nr 6. Oblicz.
Najważniejsze, aby nie popełnić standardowego błędu i nie udzielić odpowiedzi, że wyrażenie jest równe . Nie możesz użyć podstawowej właściwości arcus tangens, jeśli obok niego znajduje się czynnik w postaci dwójki. Aby się tego pozbyć napiszemy wyrażenie według wzoru na tangens kąta podwójnego, traktując , jako zwykły argument.
![]()
Teraz możemy zastosować podstawową właściwość arcustangens; pamiętajmy, że nie ma żadnych ograniczeń co do jego wyniku numerycznego.
Problem nr 7. Rozwiązać równanie.
Decydując równanie ułamkowe, który jest równy zero, zawsze wskazuje się, że licznik jest równy zero, ale mianownik nie jest, ponieważ Nie można dzielić przez zero.

Pierwsze równanie to szczególny przypadek najprostsze równanie, które można rozwiązać za pomocą koła trygonometrycznego. Zapamiętaj sobie to rozwiązanie. Drugą nierówność rozwiązuje się najprościej, korzystając ze wzoru ogólnego na pierwiastki stycznej, ale tylko ze znakiem nierównym.

Jak widzimy, jedna rodzina pierwiastków wyklucza inną rodzinę dokładnie tego samego typu pierwiastków, która nie spełnia równania. Te. nie ma korzeni.
Odpowiedź. Nie ma korzeni.
Problem nr 8. Rozwiązać równanie.
Od razu zauważmy, że możemy wyjąć wspólny czynnik i zróbmy to:
Równanie zostało sprowadzone do jednej ze standardowych postaci, gdzie iloczyn kilku czynników wynosi zero. Wiemy już, że w tym przypadku albo jedna z nich jest równa zeru, albo druga, albo trzecia. Zapiszmy to w postaci układu równań:

Pierwsze dwa równania są szczególnymi przypadkami najprostszych, z podobnymi równaniami spotykaliśmy się już wielokrotnie, dlatego od razu wskażemy ich rozwiązania. Trzecie równanie redukujemy do jednej funkcji, korzystając ze wzoru na sinus podwójnego kąta.

Rozwiążmy ostatnie równanie osobno:
![]()
To równanie nie ma pierwiastków, ponieważ wartość sinusoidalna nie może przekroczyć ![]() .
.
Zatem rozwiązaniem są tylko dwie pierwsze rodziny pierwiastków, można je połączyć w jedną, co łatwo pokazać na okręgu trygonometrycznym:
 |
Jest to rodzina wszystkich połówek, tj.
Przejdźmy do rozwiązywania nierówności trygonometrycznych. Najpierw przyjrzyjmy się podejściu do rozwiązania przykładu bez użycia formuł rozwiązania ogólne, ale używając koła trygonometrycznego.
Problem nr 9. Rozwiąż nierówność.
Narysujmy na okręgu trygonometrycznym linię pomocniczą odpowiadającą wartości sinusoidalnej równej , i pokażmy zakres kątów spełniających nierówność.
 |
Bardzo ważne jest, aby dokładnie zrozumieć, jak wskazać wynikowy odstęp kątów, tj. jaki jest jego początek i jaki jest jego koniec. Początkiem interwału będzie kąt odpowiadający punktowi, w który wejdziemy na samym początku interwału, jeśli będziemy poruszać się w kierunku przeciwnym do ruchu wskazówek zegara. W naszym przypadku jest to punkt po lewej stronie, ponieważ poruszając się w kierunku przeciwnym do ruchu wskazówek zegara i mijając właściwy punkt, wręcz przeciwnie, pozostawiamy wymagany zakres kątów. Właściwy punkt będzie zatem odpowiadał końcowi luki.
Teraz musimy zrozumieć kąty początku i końca naszego przedziału rozwiązań nierówności. Częsty błąd- ma to na celu od razu wskazać, że prawy punkt odpowiada kątowi, lewy i podać odpowiedź. To nie jest prawda! Proszę zwrócić uwagę, że właśnie wskazaliśmy przedział odpowiadający górnej części okręgu, chociaż interesuje nas dolna część, innymi słowy, pomyliliśmy początek i koniec potrzebnego nam przedziału rozwiązania.
Aby odstęp zaczynał się od narożnika prawego punktu i kończył się narożnikiem lewego punktu, konieczne jest, aby pierwszy określony kąt był mniejszy od drugiego. Aby to zrobić, będziemy musieli zmierzyć kąt prawego punktu w ujemnym kierunku odniesienia, tj. zgodnie z ruchem wskazówek zegara i będzie równa . Następnie zaczynając od niego poruszać się w kierunku dodatnim zgodnie z ruchem wskazówek zegara, dotrzemy do prawego punktu po lewym punkcie i otrzymamy dla niego wartość kąta. Teraz początek przedziału kątów jest mniejszy niż koniec i możemy zapisać przedział rozwiązań bez uwzględnienia okresu:
Biorąc pod uwagę, że takie interwały będą się powtarzać nieskończona liczba razy po dowolnej liczbie całkowitej obrotów otrzymujemy rozwiązanie ogólne uwzględniające okres sinusoidalny:
Umieszczamy nawiasy, ponieważ nierówność jest ścisła i wybieramy punkty na okręgu, które odpowiadają końcom przedziału.
Porównaj otrzymaną odpowiedź ze wzorem na rozwiązanie ogólne, który podaliśmy na wykładzie.
Odpowiedź. ![]() .
.
Metoda ta jest dobra do zrozumienia, skąd pochodzą wzory na ogólne rozwiązania najprostszych nierówności trygonalnych. Ponadto jest to przydatne dla tych, którzy są zbyt leniwi, aby nauczyć się tych wszystkich uciążliwych formuł. Jednak sama metoda również nie jest łatwa, wybierz takie podejście do rozwiązania, które jest dla Ciebie najwygodniejsze.
Do rozwiązywania nierówności trygonometrycznych można także wykorzystać wykresy funkcji, na których zbudowana jest linia pomocnicza, podobnie jak w przypadku metody pokazanej przy użyciu okręgu jednostkowego. Jeśli jesteś zainteresowany, spróbuj sam znaleźć takie podejście do rozwiązania. W dalszej części będziemy używać ogólnych wzorów do rozwiązywania prostych nierówności trygonometrycznych.
Problem nr 10. Rozwiąż nierówność.
Skorzystajmy ze wzoru na rozwiązanie ogólne, biorąc pod uwagę fakt, że nierówność nie jest ścisła:
W naszym przypadku otrzymujemy:
Odpowiedź. ![]()
Zadanie nr 11. Rozwiąż nierówność.
Skorzystajmy ze wzoru ogólnego na rozwiązanie odpowiadającej mu ściśle nierówności:
Odpowiedź. ![]() .
.
Zadanie nr 12. Rozwiązuj nierówności: a) ; B) .
W tych nierównościach nie ma potrzeby spieszyć się ze stosowaniem wzorów na rozwiązania ogólne lub okrąg trygonometryczny, wystarczy po prostu zapamiętać zakres wartości sinusa i cosinusa.
a) Od ![]() , to nierówność nie ma sensu. Dlatego nie ma rozwiązań.
, to nierówność nie ma sensu. Dlatego nie ma rozwiązań.
b) Ponieważ podobnie sinus dowolnego argumentu zawsze spełnia nierówność określoną w warunku. Dlatego wszystkie rzeczywiste wartości argumentu spełniają nierówność.
Odpowiedź. a) nie ma rozwiązań; B) .
Problem 13. Rozwiąż nierówność ![]() .
.
Rozwiązywanie prostych równań trygonometrycznych
Na początek pamiętajmy o wzorach rozwiązywania najprostszych równań trygonometrycznych.
- $sinx=a$
- $cosx=a$
- $tgx=a$
- $ctgx=a$
Rozwiązywanie prostych nierówności trygonometrycznych.
Aby rozwiązać najprostsze nierówności trygonometryczne, musimy najpierw rozwiązać odpowiednie równanie, a następnie za pomocą koła trygonometrycznego znaleźć rozwiązanie nierówności. Rozważmy rozwiązania najprostszych nierówności trygonometrycznych na przykładach.
Przykład 1
$sinx\ge \frac(1)(2)$
Znajdźmy rozwiązanie nierówności trygonometrycznej $sinx=\frac(1)(2)$
\ \
Rysunek 1. Rozwiązanie nierówności $sinx\ge \frac(1)(2)$.
Ponieważ nierówność ma znak „większy lub równy”, rozwiązanie leży na górnym łuku okręgu (w stosunku do rozwiązania równania).
Odpowiedź: $\lewy[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\prawy]$.
Przykład 2
Znajdźmy rozwiązanie nierówności trygonometrycznej $cosx=\frac(\sqrt(3))(2)$
\ \
Zaznaczmy rozwiązanie na okręgu trygonometrycznym
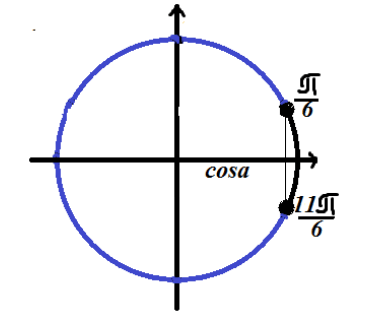
Ponieważ nierówność ma znak „mniejszy niż”, rozwiązanie leży na łuku koła znajdującego się po lewej stronie (w stosunku do rozwiązania równania).
Odpowiedź: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.
Przykład 3
$tgx\le \frac(\sqrt(3))(3)$
Znajdźmy rozwiązanie nierówności trygonometrycznej $tgx=\frac(\sqrt(3))(3)$
\ \
Tutaj również potrzebujemy dziedziny definicji. Jak pamiętamy, funkcja tangensa $x\ne \frac(\pi )(2)+\pi n,n\in Z$
Zaznaczmy rozwiązanie na okręgu trygonometrycznym
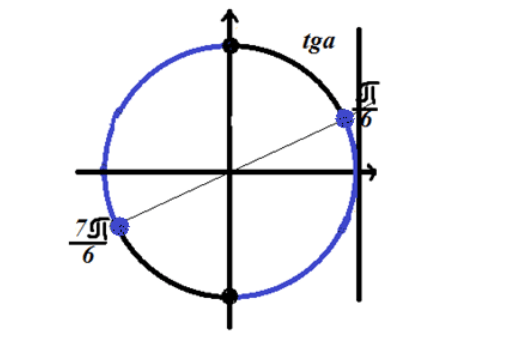
Rysunek 3. Rozwiązanie nierówności $tgx\le \frac(\sqrt(3))(3)$.
Ponieważ nierówność ma znak „mniejszy lub równy”, rozwiązaniem są łuki zaznaczone na niebiesko na rysunku 3.
Odpowiedź:$\ \left(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\cup \left (\frac(\pi )(2)+2\pi n,\right.\left.\frac(7\pi )(6)+2\pi n\right]$
Przykład 4
Znajdźmy rozwiązanie nierówności trygonometrycznej $ctgx=\sqrt(3)$
\ \
Tutaj również potrzebujemy dziedziny definicji. Jak pamiętamy, funkcja tangensowa $x\ne \pi n,n\in Z$
Zaznaczmy rozwiązanie na okręgu trygonometrycznym

Rysunek 4. Rozwiązanie nierówności $ctgx\le \sqrt(3)$.
Ponieważ nierówność ma znak „większy niż”, rozwiązaniem są łuki zaznaczone na niebiesko na rysunku 4.
Odpowiedź:$\ \left(2\pi n,\frac(\pi )(6)+2\pi n\right)\cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\prawo)$








