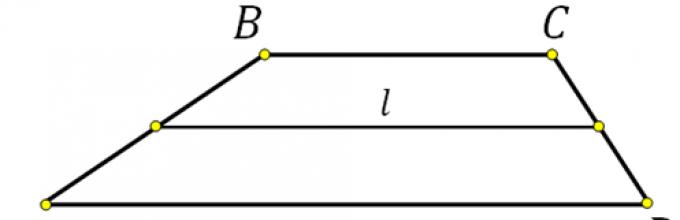
Linia środkowa figury w planimetrii - odcinek łączący środki dwóch boków danej figury. Pojęcie to stosuje się do figur: trójkąta, czworoboku, trapezu.
Środkowa linia trójkąta
Właściwości
- środkowa linia trójkąta jest równoległa do podstawy i równa jej połowie.
- linia środkowa odcina trójkąt podobny i homotetyczny do pierwotnego o współczynniku 1/2; jego powierzchnia jest równa jednej czwartej powierzchni pierwotnego trójkąta.
- trzy środkowe linie dzielą pierwotny trójkąt na cztery równe trójkąty. Środek tych trójkątów nazywany jest trójkątem dopełniającym lub środkowym.
Znaki
- Jeśli odcinek trójkąta przechodzi przez środek jednego z jego boków, przecina drugi i jest równoległy do trzeciego, to ten odcinek jest linią środkową.
- Pole i odpowiednio objętość trójkąta odciętego linią środkową jest równa 1/4 pola i odpowiednio objętości całego danego trójkąta.
Linia środkowa czworokąta
Linia środkowa czworokąta- odcinek łączący środki przeciwległych boków czworoboku.
Właściwości
Pierwsza linia łączy 2 przeciwne strony. Drugi łączy pozostałe 2 przeciwne strony. Trzeci łączy środki dwóch przekątnych (nie we wszystkich czworokątach przekątne są podzielone na pół w miejscu przecięcia).
- Jeśli w czworokącie wypukłym linia środkowa tworzy kąty równe z przekątnymi czworoboku, to przekątne są równe.
- Długość linii środkowej czworokąta jest mniejsza od połowy sumy dwóch pozostałych boków lub jej równa, jeśli te boki są równoległe, i tylko w tym przypadku.
- Środki boków dowolnego czworokąta są wierzchołkami równoległoboku. Jego powierzchnia jest równa połowie powierzchni czworoboku, a jego środek leży w punkcie przecięcia linii środkowych. Ten równoległobok nazywany jest równoległobokiem Varignona;
- Ostatni punkt oznacza, co następuje: W wypukłym czworokącie możesz narysować cztery linie środkowe drugiego rodzaju. Linie środkowe drugiego rodzaju- cztery odcinki wewnątrz czworoboku przechodzące przez środki sąsiednich boków równoległych do przekątnych. Cztery linie środkowe drugiego rodzaju wypukłego czworoboku przetnij go na cztery trójkąty i jeden środkowy czworobok. Ten centralny czworobok jest równoległobokiem Varignona.
- Punkt przecięcia linii środkowych czworokąta jest ich wspólnym punktem środkowym i przecina odcinek łączący środki przekątnych na pół. Ponadto jest to środek ciężkości wierzchołków czworoboku.
- W dowolnym czworokącie wektor linii środkowej jest równy połowie sumy wektorów podstaw.
Linia środkowa trapezu
Linia środkowa trapezu
Linia środkowa trapezu- odcinek łączący środki boków tego trapezu. Odcinek łączący środki podstaw trapezu nazywa się drugą linią środkową trapezu.
Oblicza się go za pomocą wzoru: mi fa = ZA re + b do 2 (\ displaystyle EF = (\ frac (AD + BC) (2))), Gdzie OGŁOSZENIE I przed Chrystusem- podstawa trapezu.
W tym artykule przygotowaliśmy dla Ciebie kolejny wybór problemów z trapezem. Warunki są w jakiś sposób powiązane z jego linią środkową. Typy zadań pochodzą z otwartego banku typowych zadań. Jeśli chcesz, możesz odświeżyć swoją wiedzę teoretyczną. Na blogu omawialiśmy już zadania, których warunki są związane, a także. Krótko o środkowej linii:

Linia środkowa trapezu łączy środki boków bocznych. Jest równoległy do podstaw i równy ich połowie sumy.
Przed rozwiązaniem problemów spójrzmy na teoretyczny przykład.
Biorąc pod uwagę trapez ABCD. Przekątna AC przecinająca się z linią środkową tworzy punkt K, przekątna BD punkty L. Udowodnij, że odcinek KL jest równy połowie różnicy podstaw.

Najpierw zauważmy, że linia środkowa trapezu przecina na pół każdy odcinek, którego końce leżą na jego podstawach. Wniosek ten nasuwa się sam. Wyobraź sobie odcinek łączący dwa punkty podstaw; podzieli on ten trapez na dwa inne. Okazuje się, że odcinek równoległy do podstaw trapezu i przechodzący przez środek boku przejdzie przez środek drugiego boku.
Opiera się to również na twierdzeniu Talesa:
Jeśli na jednej z dwóch linii ułoży się kolejno kilka równych odcinków, a przez ich końce przecinające się z drugą linią przeciągnie się równoległe linie, wówczas na drugiej linii odetną one równe odcinki.
Oznacza to, że w tym przypadku K jest środkiem AC, a L jest środkiem BD. Zatem EK jest linią środkową trójkąta ABC, LF jest linią środkową trójkąta DCB. Zgodnie z właściwością linii środkowej trójkąta:

Możemy teraz wyrazić odcinek KL za pomocą podstaw:
Udowodniony!
Ten przykład podano nie bez powodu. W zadaniach do samodzielnego rozwiązania jest właśnie takie zadanie. Tyle że nie jest tam napisane, że odcinek łączący środki przekątnych leży na linii środkowej. Rozważmy zadania:
27819. Znajdź linię środkową trapezu, jeśli jego podstawy wynoszą 30 i 16.

Obliczamy korzystając ze wzoru:

27820. Linia środkowa trapezu wynosi 28, a mniejsza podstawa wynosi 18. Znajdź większą podstawę trapezu.

Wyraźmy większą podstawę:
Zatem:
27836. Prostopadła rzucona z wierzchołka kąta rozwartego na większą podstawę trapezu równoramiennego dzieli go na części o długościach 10 i 4. Znajdź linię środkową tego trapezu.

Aby znaleźć linię środkową, musisz znać podstawy. Podstawę AB łatwo znaleźć: 10+4=14. Znajdźmy DC.
Skonstruujmy drugą prostopadłą DF:

Segmenty AF, FE i EB będą równe odpowiednio 4, 6 i 4. Dlaczego?
W trapezie równoramiennym prostopadłe obniżone do większej podstawy dzielą go na trzy odcinki. Dwa z nich, będące ramionami odciętych trójkątów prostokątnych, są sobie równe. Trzeci segment jest równy mniejszej podstawie, ponieważ podczas konstruowania wskazanych wysokości powstaje prostokąt, a w prostokącie przeciwne boki są równe. W tym zadaniu:

Zatem DC=6. Obliczamy:

27839. Podstawy trapezu mają stosunek 2:3, a linia środkowa wynosi 5. Znajdź mniejszą podstawę.

Wprowadźmy współczynnik proporcjonalności x. Wtedy AB=3x, DC=2x. Możemy napisać:
Zatem mniejsza podstawa to 2∙2=4.
27840. Obwód trapezu równoramiennego wynosi 80, jego linia środkowa jest równa boku bocznemu. Znajdź bok trapezu.

Na podstawie warunku możemy napisać:
Jeśli oznaczymy linię środkową przechodzącą przez wartość x, otrzymamy:

Drugie równanie można już zapisać jako:

27841. Linia środkowa trapezu wynosi 7, a jedna z jego podstaw jest o 4 większa od drugiej. Znajdź większą podstawę trapezu.

Oznaczmy mniejszą podstawę (DC) jako x, wówczas większa (AB) będzie równa x+4. Możemy to zapisać
Odkryliśmy, że mniejsza podstawa to wczesna piątka, co oznacza, że większa jest równa 9.
27842. Linia środkowa trapezu wynosi 12. Jedna z przekątnych dzieli go na dwie części, których różnica wynosi 2. Znajdź większą podstawę trapezu.

Większą podstawę trapezu łatwo znajdziemy obliczając odcinek EO. Jest to linia środkowa trójkąta ADB i AB=2∙EO.
Co mamy? Mówi się, że linia środkowa wynosi 12, a różnica między odcinkami EO i ОF wynosi 2. Możemy zapisać dwa równania i rozwiązać układ:
![]()
Oczywiste jest, że w tym przypadku możesz wybrać parę liczb bez obliczeń, są to 5 i 7. Niemniej jednak rozwiążmy system:

Zatem EO=12–5=7. Zatem większa podstawa jest równa AB=2∙EO=14.
27844. W trapezie równoramiennym przekątne są prostopadłe. Wysokość trapezu wynosi 12. Znajdź jego linię środkową.

Zauważmy od razu, że wysokość narysowana przez punkt przecięcia przekątnych w trapezie równoramiennym leży na osi symetrii i dzieli trapez na dwa równe trapezy prostokątne, czyli podstawy tej wysokości są podzielone na pół.
Wydawać by się mogło, że aby obliczyć linię środkową, trzeba znaleźć powody. Tutaj pojawia się mały ślepy zaułek... Jak, znając wysokość, w tym przypadku obliczyć podstawy? Nie ma mowy! Takich trapezów o stałej wysokości i przekątnych przecinających się pod kątem 90 stopni jest wiele. Co powinienem zrobić?
Spójrz na wzór na linię środkową trapezu. Przecież nie musimy znać samych przyczyn, wystarczy znać ich sumę (lub połowę). Możemy to zrobić.
Ponieważ przekątne przecinają się pod kątem prostym, powstają trójkąty prostokątne równoramienne o wysokości EF:
Z powyższego wynika, że FO=DF=FC i OE=AE=EB. Zapiszmy teraz, jaka jest wysokość wyrażona poprzez odcinki DF i AE:

Zatem środkowa linia to 12.
* Ogólnie rzecz biorąc, jest to problem, jak rozumiesz, związany z kalkulacją mentalną. Jestem jednak pewien, że przedstawione szczegółowe wyjaśnienia są konieczne. I tak... Jeśli spojrzysz na rysunek (pod warunkiem, że podczas budowy zachowany zostanie kąt między przekątnymi), od razu rzuca się w oczy równość FO=DF=FC i OE=AE=EB.
W prototypach znajdują się także rodzaje zadań z trapezami. Jest zbudowany na kartce papieru w klatce i trzeba znaleźć środkową linię; bok klatki jest zwykle równy 1, ale może to być inna wartość.
27848. Znajdź linię środkową trapezu ABCD, jeśli boki komórek kwadratowych są równe 1.

To proste, obliczamy podstawy według komórek i korzystamy ze wzoru: (2+4)/2=3
Jeśli podstawy są zbudowane pod kątem do siatki komórek, istnieją dwa sposoby. Na przykład!
Nazywa się czworokąt, w którym tylko dwa boki są równoległe trapez.
Nazywa się je równoległymi bokami trapezu powodów, a te boki, które nie są równoległe, nazywane są strony. Jeśli boki są równe, to taki trapez jest równoramienny. Odległość między podstawami nazywa się wysokością trapezu.
Trapez linii środkowej
Linia środkowa to odcinek łączący środki boków trapezu. Linia środkowa trapezu jest równoległa do jego podstaw.
Twierdzenie:
Jeżeli prosta przechodząca przez środek jednego boku jest równoległa do podstaw trapezu, to przecina drugi bok trapezu na pół.
Twierdzenie:
Długość linii środkowej jest równa średniej arytmetycznej długości jej podstaw
MN || AB || DCAM = MD; BN=NC
Linia środkowa MN, AB i CD - podstawy, AD i BC - boki
MN = (AB + DC)/2
Twierdzenie:
Długość linii środkowej trapezu jest równa średniej arytmetycznej długości jego podstaw.
Główne zadanie: Udowodnić, że linia środkowa trapezu przecina odcinek, którego końce leżą pośrodku podstaw trapezu.
Środkowa linia trójkąta
Odcinek łączący środki dwóch boków trójkąta nazywa się linią środkową trójkąta. Jest równoległy do trzeciego boku i jego długość jest równa połowie długości trzeciego boku.
Twierdzenie: Jeśli linia przecinająca środek jednego boku trójkąta jest równoległa do drugiego boku trójkąta, to przecina trzeci bok na pół.

AM = MC i BN = NC =>
Stosowanie właściwości linii środkowej trójkąta i trapezu
Dzielenie odcinka na określoną liczbę równych części.
Zadanie: Podziel odcinek AB na 5 równych części.
Rozwiązanie:
Niech p będzie półprostą losową, której początek znajduje się w punkcie A i który nie leży na prostej AB. Kolejno odkładamy 5 równych segmentów na p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Łączymy A 5 z B i rysujemy takie linie przez A 4, A 3, A 2 i A 1, które są równoległe do A 5 B. Przecinają one AB odpowiednio w punktach B 4, B 3, B 2 i B 1. Punkty te dzielą odcinek AB na 5 równych części. Rzeczywiście z trapezu BB 3 A 3 A 5 widzimy, że BB 4 = B 4 B 3. W ten sam sposób z trapezu B 4 B 2 A 2 A 4 otrzymujemy B 4 B 3 = B 3 B 2

Natomiast z trapezu B 3 B 1 A 1 A 3, B 3 B 2 = B 2 B 1.
Następnie z B 2 AA 2 wynika, że B 2 B 1 = B 1 A. Podsumowując, otrzymujemy:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Oczywiste jest, że aby podzielić odcinek AB na inną liczbę równych części, musimy rzutować tę samą liczbę równych odcinków na półprostą p. A następnie kontynuuj w sposób opisany powyżej.
Pojęcie linii środkowej trapezu
Najpierw pamiętajmy, jaki rodzaj figury nazywa się trapezem.
Definicja 1
Trapez to czworokąt, w którym dwa boki są równoległe, a pozostałe dwa nie są równoległe.
W tym przypadku boki równoległe nazywane są podstawami trapezu, a boki nierównoległe nazywane są bocznymi bokami trapezu.
Definicja 2
Linia środkowa trapezu to odcinek łączący środki boków trapezu.
Twierdzenie o linii środkowej trapezu
Teraz wprowadzimy twierdzenie o linii środkowej trapezu i udowodnimy je metodą wektorową.
Twierdzenie 1
Linia środkowa trapezu jest równoległa do podstaw i równa ich połowie.
Dowód.
Weźmy trapez $ABCD$ o podstawach $AD\ i\ BC$. I niech $MN$ będzie linią środkową tego trapezu (ryc. 1).
Rysunek 1. Linia środkowa trapezu
Udowodnimy, że $MN||AD\ i\ MN=\frac(AD+BC)(2)$.
Rozważmy wektor $\overrightarrow(MN)$. Następnie używamy reguły wielokąta, aby dodać wektory. Z jednej strony to rozumiemy
Po drugiej stronie
Dodajmy dwie ostatnie równości i otrzymamy
Ponieważ $M$ i $N$ są środkami bocznych boków trapezu, będziemy mieli
Otrzymujemy:
Stąd
Z tej samej równości (ponieważ $\overrightarrow(BC)$ i $\overrightarrow(AD)$ są współkierunkowe, a zatem współliniowe) otrzymujemy $MN||AD$.
Twierdzenie zostało udowodnione.
Przykłady problemów z pojęciem linii środkowej trapezu
Przykład 1
Boki boczne trapezu wynoszą odpowiednio 15 $ cm $ i 17 $ cm $. Obwód trapezu wynosi 52 $\cm$. Znajdź długość linii środkowej trapezu.
Rozwiązanie.
Oznaczmy linię środkową trapezu przez $n$.
Suma boków jest równa
Zatem, ponieważ obwód wynosi 52 $ cm $, suma podstaw jest równa
Zatem z Twierdzenia 1 otrzymujemy
Odpowiedź: 10 $\cm$.
Przykład 2
Końce średnicy okręgu są oddalone odpowiednio o 9$ cm i 5$ cm od jego stycznej. Znajdź średnicę tego okręgu.
Rozwiązanie.
Otrzymamy okrąg o środku w punkcie $O$ i średnicy $AB$. Narysujmy tangens $l$ i skonstruujmy odległości $AD=9\ cm$ i $BC=5\ cm$. Narysujmy promień $OH$ (ryc. 2).

Rysunek 2.
Ponieważ $AD$ i $BC$ to odległości do stycznej, to $AD\bot l$ i $BC\bot l$, a ponieważ $OH$ to promień, to $OH\bot l$, zatem $OH |\lewy|AD\prawy||BC$. Z tego wszystkiego wynika, że $ABCD$ jest trapezem, a $OH$ jest jego linią środkową. Z twierdzenia 1 otrzymujemy
W tym artykule postaramy się jak najpełniej odzwierciedlić właściwości trapezu. W szczególności omówimy ogólne cechy i właściwości trapezu, a także właściwości trapezu wpisanego i okręgu wpisanego w trapez. Dotkniemy także właściwości trapezu równoramiennego i prostokątnego.
Przykład rozwiązania problemu z wykorzystaniem omawianych właściwości pomoże Ci uporządkować go w miejsca w głowie i lepiej zapamiętać materiał.
Trapez i wszystko-wszystko
Na początek przypomnijmy sobie krótko, czym jest trapez i jakie inne pojęcia są z nim związane.
Zatem trapez jest figurą czworoboczną, której dwa boki są do siebie równoległe (są to podstawy). I te dwa nie są równoległe - to są boki.
W trapezie wysokość można obniżyć - prostopadle do podstaw. Rysowana jest linia środkowa i przekątne. Możliwe jest również narysowanie dwusiecznej z dowolnego kąta trapezu.
Porozmawiamy teraz o różnych właściwościach związanych ze wszystkimi tymi elementami i ich kombinacjami.
Własności przekątnych trapezowych
Aby było to jaśniejsze, podczas czytania naszkicuj trapez ACME na kartce papieru i narysuj w nim przekątne.
- Jeśli znajdziesz środki każdej z przekątnych (nazwijmy te punkty X i T) i połącz je, otrzymasz odcinek. Jedną z właściwości przekątnych trapezu jest to, że odcinek HT leży na linii środkowej. A jego długość można uzyskać, dzieląc różnicę podstaw przez dwa: ХТ = (a – b)/2.
- Przed nami ten sam trapez ACME. Przekątne przecinają się w punkcie O. Przyjrzyjmy się trójkątom AOE i MOK utworzonym z odcinków przekątnych wraz z podstawami trapezu. Te trójkąty są podobne. Współczynnik podobieństwa k trójkątów wyraża się stosunkiem podstaw trapezu: k = AE/KM.
Stosunek pól trójkątów AOE i MOK opisuje współczynnik k 2 . - Ten sam trapez, te same przekątne przecinające się w punkcie O. Tylko tym razem rozważymy trójkąty, które utworzyły odcinki przekątnych razem z bokami trapezu. Pola trójkątów AKO i EMO są równej wielkości - ich pola są takie same.
- Inną właściwością trapezu jest konstrukcja przekątnych. Tak więc, jeśli będziesz kontynuować boki AK i ME w kierunku mniejszej podstawy, to prędzej czy później przetną się w pewnym punkcie. Następnie narysuj linię prostą przez środek podstaw trapezu. Przecina podstawy w punktach X i T.
Jeśli teraz przedłużymy linię XT, to połączy ona ze sobą punkt przecięcia przekątnych trapezu O, punkt, w którym przecinają się przedłużenia boków i środki podstaw X i T. - Przez punkt przecięcia przekątnych narysujemy odcinek, który połączy podstawy trapezu (T leży na mniejszej podstawie KM, X na większej AE). Punkt przecięcia przekątnych dzieli ten odcinek w następującym stosunku: TO/OX = KM/AE.
- Teraz przez punkt przecięcia przekątnych narysujemy odcinek równoległy do podstaw trapezu (a i b). Punkt przecięcia podzieli go na dwie równe części. Długość odcinka można znaleźć za pomocą wzoru 2ab/(a + b).
Właściwości linii środkowej trapezu
Narysuj środkową linię trapezu równolegle do jego podstaw.
- Długość linii środkowej trapezu można obliczyć, dodając długości podstaw i dzieląc je na pół: m = (a + b)/2.
- Jeśli przeciągniesz dowolny odcinek (na przykład wysokość) przez obie podstawy trapezu, środkowa linia podzieli go na dwie równe części.
Własność dwusiecznej trapezu
Wybierz dowolny róg trapezu i narysuj dwusieczną. Weźmy na przykład kąt KAE naszego trapezu ACME. Po samodzielnym wykonaniu konstrukcji łatwo sprawdzić, czy dwusieczna odcina od podstawy (lub jej kontynuacji na linii prostej poza samą figurą) odcinek o tej samej długości co bok.
Właściwości kątów trapezowych
- Niezależnie od tego, którą z dwóch par kątów przylegających do boku wybierzesz, suma kątów w parze wynosi zawsze 180 0: α + β = 180 0 i γ + δ = 180 0.
- Połączmy środki podstaw trapezu z odcinkiem TX. Przyjrzyjmy się teraz kątom u podstaw trapezu. Jeżeli suma kątów któregokolwiek z nich wynosi 90 0, długość odcinka TX można łatwo obliczyć na podstawie różnicy długości podstaw podzielonej na pół: TX = (AE – KM)/2.
- Jeśli przez boki kąta trapezowego poprowadzono równoległe linie, podzielą one boki kąta na proporcjonalne odcinki.
Właściwości trapezu równobocznego
- W trapezie równoramiennym kąty przy każdej podstawie są równe.
- Teraz zbuduj ponownie trapez, aby łatwiej było sobie wyobrazić, o czym mówimy. Przyjrzyj się uważnie bazie AE - wierzchołek przeciwnej podstawy M jest rzutowany do pewnego punktu na linii zawierającej AE. Odległość wierzchołka A od punktu rzutu wierzchołka M i linii środkowej trapezu równoramiennego są równe.
- Kilka słów o własności przekątnych trapezu równoramiennego - ich długości są równe. A także kąty nachylenia tych przekątnych do podstawy trapezu są takie same.
- Okrąg można opisać tylko wokół trapezu równoramiennego, ponieważ suma przeciwnych kątów czworoboku wynosi 180 0 - jest to warunek wstępny.
- Właściwość trapezu równoramiennego wynika z poprzedniego akapitu - jeśli w pobliżu trapezu można opisać okrąg, jest to równoramienny.
- Z cech trapezu równoramiennego wynika właściwość wysokości trapezu: jeśli jego przekątne przecinają się pod kątem prostym, wówczas długość wysokości jest równa połowie sumy podstaw: h = (a + b)/2.
- Ponownie narysuj odcinek TX przez środki podstaw trapezu - w trapezie równoramiennym jest on prostopadły do podstaw. Jednocześnie TX jest osią symetrii trapezu równoramiennego.
- Tym razem obniż wysokość z przeciwnego wierzchołka trapezu na większą podstawę (nazwijmy to a). Otrzymasz dwa segmenty. Długość jednego można obliczyć, dodając długości podstaw i dzieląc je na pół: (a + b)/2. Drugą otrzymamy, gdy od większej podstawy odejmiemy mniejszą i uzyskaną różnicę podzielimy przez dwa: (a – b)/2.
Właściwości trapezu wpisanego w okrąg
Ponieważ mówimy już o trapezie wpisanym w okrąg, zastanówmy się nad tym zagadnieniem bardziej szczegółowo. W szczególności, gdy środek okręgu znajduje się w stosunku do trapezu. Tutaj również zaleca się poświęcenie czasu na chwycenie ołówka i narysowanie tego, co zostanie omówione poniżej. W ten sposób szybciej zrozumiesz i lepiej zapamiętasz.
- Położenie środka okręgu wyznacza kąt nachylenia przekątnej trapezu na jego bok. Na przykład przekątna może rozciągać się od góry trapezu pod kątem prostym do boku. W tym przypadku większa podstawa przecina środek okręgu opisanego dokładnie w środku (R = ½AE).
- Przekątna i bok mogą również spotykać się pod kątem ostrym - wtedy środek okręgu znajduje się wewnątrz trapezu.
- Środek okręgu opisanego może znajdować się na zewnątrz trapezu, poza jego większą podstawą, jeśli między przekątną trapezu a jego bokiem istnieje kąt rozwarty.
- Kąt utworzony przez przekątną i dużą podstawę trapezu ACME (kąt wpisany) jest połową odpowiadającego mu kąta środkowego: MAE = ½MOE.
- Krótko o dwóch sposobach wyznaczania promienia opisanego okręgu. Metoda pierwsza: przyjrzyj się uważnie swojemu rysunkowi – co widzisz? Łatwo zauważyć, że przekątna dzieli trapez na dwa trójkąty. Promień można obliczyć ze stosunku boku trójkąta do sinusa przeciwnego kąta pomnożonego przez dwa. Na przykład, R = AE/2*sinAME. Wzór można zapisać w podobny sposób dla dowolnego boku obu trójkątów.
- Metoda druga: znajdź promień opisanego koła przez obszar trójkąta utworzonego przez przekątną, bok i podstawę trapezu: R = AM*ME*AE/4*S AME.
Właściwości trapezu opisanego na okręgu
Można zmieścić okrąg w trapezie, jeśli spełniony jest jeden warunek. Przeczytaj więcej na ten temat poniżej. Razem ta kombinacja liczb ma wiele interesujących właściwości.
- Jeśli w trapez wpisano okrąg, długość jego linii środkowej można łatwo obliczyć, dodając długości boków i dzieląc otrzymaną sumę na pół: m = (c + d)/2.
- Dla trapezu ACME opisanego na okręgu suma długości podstaw jest równa sumie długości boków: AK + ME = KM + AE.
- Z tej właściwości podstaw trapezu wynika stwierdzenie odwrotne: w trapezoid, którego suma podstaw jest równa sumie jego boków, można wpisać okrąg.
- Punkt styczny okręgu o promieniu r wpisanego w trapez dzieli bok na dwa odcinki, nazwijmy je a i b. Promień okręgu można obliczyć ze wzoru: r = √ab.
- I jeszcze jedna nieruchomość. Aby uniknąć nieporozumień, sam również narysuj ten przykład. Mamy stary, dobry trapez ACME opisany wokół okręgu. Zawiera przekątne przecinające się w punkcie O. Trójkąty AOK i EOM utworzone przez odcinki przekątnych i boki boczne są prostokątne.
Wysokości tych trójkątów, obniżone do przeciwprostokątnych (tj. bocznych boków trapezu), pokrywają się z promieniami okręgu wpisanego. A wysokość trapezu pokrywa się ze średnicą wpisanego koła.
Właściwości trapezu prostokątnego
Trapez nazywa się prostokątnym, jeśli jeden z jego kątów jest prosty. I z tej okoliczności wynikają jego właściwości.
- Trapez prostokątny ma jeden bok prostopadły do podstawy.
- Wysokość i bok trapezu sąsiadującego z kątem prostym są równe. Pozwala to obliczyć pole prostokątnego trapezu (wzór ogólny S = (a + b) * godz/2) nie tylko przez wysokość, ale także przez bok przylegający do kąta prostego.
- W przypadku trapezu prostokątnego istotne są ogólne właściwości przekątnych trapezu opisane już powyżej.
Dowody na niektóre właściwości trapezu
Równość kątów u podstawy trapezu równoramiennego:
- Prawdopodobnie już zgadłeś, że tutaj znów będziemy potrzebować trapezu AKME - narysuj trapez równoramienny. Narysuj linię prostą MT z wierzchołka M, równoległą do boku AK (MT || AK).
Powstały czworobok AKMT jest równoległobokiem (AK || MT, KM || AT). Ponieważ ME = KA = MT, ∆ MTE jest równoramienne, a MET = MTE.
AK || MT, zatem MTE = KAE, MET = MTE = KAE.
Gdzie AKM = 180 0 - MET = 180 0 - KAE = KME.
co było do okazania
Teraz, bazując na własności trapezu równoramiennego (równość przekątnych), udowodnimy to trapez ACME jest równoramienny:
- Najpierw narysujmy linię prostą MX – MX || KE. Otrzymujemy równoległobok KMHE (podstawa – MX || KE i KM || EX).
∆AMX jest równoramienne, ponieważ AM = KE = MX i MAX = MEA.
MH || KE, KEA = MXE, zatem MAE = MXE.
Okazało się, że trójkąty AKE i EMA są sobie równe, ponieważ AM = KE i AE są wspólnymi bokami obu trójkątów. A także MAE = MXE. Możemy stwierdzić, że AK = ME i z tego wynika, że trapez AKME jest równoramienny.

Przejrzyj zadanie
Podstawy trapezu ACME mają długości 9 cm i 21 cm, bok KA równy 8 cm tworzy z mniejszą podstawą kąt 150 0. Musisz znaleźć obszar trapezu.
Rozwiązanie: Z wierzchołka K obniżamy wysokość do większej podstawy trapezu. Zacznijmy patrzeć na kąty trapezu.
Kąty AEM i KAN są jednostronne. Oznacza to, że w sumie dają 180 0. Zatem KAN = 30 0 (na podstawie właściwości kątów trapezowych).
Rozważmy teraz prostokątną ∆ANC (uważam, że ten punkt jest oczywisty dla czytelników bez dodatkowych dowodów). Z niego znajdziemy wysokość trapezu KH - w trójkącie jest to noga leżąca naprzeciwko kąta 30 0. Zatem KH = ½AB = 4 cm.
Pole trapezu obliczamy ze wzoru: S ACME = (KM + AE) * KN/2 = (9 + 21) * 4/2 = 60 cm 2.
Posłowie
Jeśli dokładnie i starannie przestudiowałeś ten artykuł, nie byłeś zbyt leniwy, aby narysować trapezy dla wszystkich podanych właściwości ołówkiem w dłoniach i przeanalizować je w praktyce, powinieneś dobrze opanować materiał.
Oczywiście jest tu mnóstwo informacji, różnorodnych, a czasem nawet zagmatwanych: nie tak trudno pomylić właściwości opisywanego trapezu z właściwościami wpisanego. Ale sam widziałeś, że różnica jest ogromna.
Teraz masz szczegółowy zarys wszystkich ogólnych właściwości trapezu. A także specyficzne właściwości i cechy trapezów równoramiennych i prostokątnych. Jest bardzo wygodny w użyciu w celu przygotowania się do sprawdzianów i egzaminów. Wypróbuj sam i udostępnij link swoim znajomym!
blog.site, przy kopiowaniu materiału w całości lub w części wymagany jest link do oryginalnego źródła.