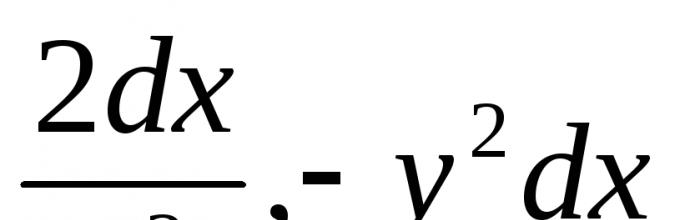Uogólnione równanie jednorodne. Funkcje uogólnione odpowiadające formom kwadratowym o współczynnikach zespolonych. Równania różniczkowe w funkcjach uogólnionych

Równanie M(X, y) dx+ N(X, y) dy=0 nazywa się uogólnioną jednorodną, jeśli można wybrać taką liczbę k, że lewa strona tego równania staje się w pewnym stopniu funkcją jednorodną M stosunkowo X, y, dx I dy pod warunkiem że X uważa się za wartość pierwszego wymiaru, y – k‑ pomiary , dx I dy – odpowiednio zero i (k-1) pomiary. Na przykład byłoby to równanie. (6.1)

Obowiązuje przy założeniach dotyczących pomiarów

X, y, dx I dy członkowie lewicy
I dy będą miały odpowiednio wymiary -2, 2 k I k-1. Przyrównując je otrzymujemy warunek, który musi spełniać wymagana liczba k: -2 = 2k = k-1. Warunek ten jest spełniony, gdy k = -1 (z tym k wszystkie wyrazy po lewej stronie rozważanego równania będą miały wymiar -2). W konsekwencji równanie (6.1) jest uogólnione jako jednorodne.

Uogólnione równanie jednorodne sprowadza się do równania z rozłącznymi zmiennymi za pomocą podstawienia
, Gdzie z– nowa nieznana funkcja. Całkujmy równanie (6.1) wskazaną metodą. Ponieważ k = -1, zatem
, po czym otrzymujemy równanie.

Integrując to, znajdujemy
, Gdzie
. Jest to ogólne rozwiązanie równania (6.1).

§ 7. Liniowe równania różniczkowe I rzędu.

Równanie liniowe pierwszego rzędu to równanie liniowe względem żądanej funkcji i jej pochodnej. To wygląda jak:

, (7.1)

Gdzie P(X) I Q(X) – dane funkcje ciągłe X. Jeśli funkcja
, wówczas równanie (7.1) ma postać:
(7.2)

i w przeciwnym razie nazywa się liniowym równaniem jednorodnym
nazywa się to liniowym równaniem niejednorodnym.

Liniowe jednorodne równanie różniczkowe (7.2) jest równaniem z rozłącznymi zmiennymi:

(7.3)

Wyrażenie (7.3) jest ogólnym rozwiązaniem równania (7.2). Aby znaleźć ogólne rozwiązanie równania (7.1), w którym funkcja P(X) oznacza tę samą funkcję co w równaniu (7.2), stosujemy technikę zwaną metodą wariacji dowolnej stałej i polega na tym, co następuje: spróbujemy wybrać funkcję C=C(X) tak że ogólne rozwiązanie liniowego równania jednorodnego (7.2) byłoby rozwiązaniem niejednorodnego równania liniowego (7.1). Następnie dla pochodnej funkcji (7.3) otrzymujemy:

Podstawiając znalezioną pochodną do równania (7.1), otrzymamy:

Lub
.

Gdzie
, Gdzie - dowolna stała. W rezultacie ogólnym rozwiązaniem niejednorodnego równania liniowego (7.1) będzie (7.4)

Pierwszy wyraz tego wzoru reprezentuje rozwiązanie ogólne (7.3) liniowego równania różniczkowego jednorodnego (7.2), a drugi wyraz wzoru (7.4) jest rozwiązaniem szczególnym liniowego równania niejednorodnego (7.1), otrzymanym z ogólnego ( 7.4) z
. Podkreślamy ten ważny wniosek w formie twierdzenia.

Twierdzenie. Jeśli znane jest jedno szczególne rozwiązanie liniowego niejednorodnego równania różniczkowego
, to wszystkie inne rozwiązania mają postać
, Gdzie
- ogólne rozwiązanie odpowiedniego liniowego jednorodnego równania różniczkowego.

Należy jednak zauważyć, że do rozwiązania liniowego niejednorodnego równania różniczkowego pierwszego rzędu (7.1) częściej stosuje się inną metodę, czasami nazywaną metodą Bernoulliego. Będziemy szukać rozwiązania równania (7.1) w postaci
. Następnie
. Podstawmy znalezioną pochodną do pierwotnego równania:
.

Połączmy na przykład drugi i trzeci wyraz ostatniego wyrażenia i wyodrębnijmy funkcję ty(X) za nawiasem:
(7.5)

Wymagamy, aby nawias został unieważniony:
.

Rozwiążmy to równanie, ustalając dowolną stałą C równe zeru:
. Ze znalezioną funkcją w(X) Wróćmy do równania (7.5):
.

Rozwiązując to otrzymujemy:
.

W związku z tym ogólne rozwiązanie równania (7.1) ma postać.

.
Równania różniczkowe.

§ 1. Podstawowe pojęcia dotyczące równań różniczkowych zwyczajnych.

Definicja 1. Równanie różniczkowe zwyczajne N– rząd funkcji y argument X nazywa się relacją formy

Gdzie F– dana funkcja jego argumentów. W nazwie tej klasy równań matematycznych termin „różniczkowy” podkreśla, że obejmują one pochodne
(funkcje powstałe w wyniku różniczkowania); termin „zwykły” wskazuje, że żądana funkcja zależy tylko od jednego rzeczywistego argumentu.

Zwykłe równanie różniczkowe nie może zawierać wyraźnego argumentu X, wymaganą funkcję
i dowolna z jego pochodnych, ale najwyższa pochodna
należy uwzględnić w równaniu N- zamówienie. Na przykład

A)
– równanie pierwszego rzędu;

B)
– równanie trzeciego rzędu.

Pisząc zwykłe równania różniczkowe, często stosuje się zapis pochodnych w kategoriach różniczkowych:

V)
– równanie drugiego rzędu;

G)
– równanie pierwszego rzędu,

generator po podzieleniu przez dx równoważna forma określenia równania:
.

Funkcjonować
nazywa się rozwiązaniem zwykłego równania różniczkowego, jeśli po podstawieniu do niego zamienia się w tożsamość.

Na przykład równanie trzeciego rzędu

Ma rozwiązanie
.

Znalezienie tą czy inną metodą, na przykład selekcją, jednej funkcji spełniającej równanie, nie oznacza jej rozwiązania. Rozwiązanie zwykłego równania różniczkowego oznacza znalezienie Wszystko funkcje, które po podstawieniu do równania tworzą tożsamość. W przypadku równania (1.1) rodzina takich funkcji jest tworzona przy użyciu dowolnych stałych i nazywana jest ogólnym rozwiązaniem równania różniczkowego zwyczajnego N-tego rzędu, a liczba stałych pokrywa się z rzędem równania: Ogólne rozwiązanie może być, ale nie jest jednoznacznie rozwiązane w odniesieniu do y(X) : W tym przypadku rozwiązanie nazywa się zwykle całką ogólną równania (1.1).

Na przykład ogólne rozwiązanie równania różniczkowego
jest następującym wyrażeniem: , a drugi termin można również zapisać jako
, ponieważ jest to dowolna stała , podzielone przez 2, można zastąpić nową dowolną stałą .

Przypisując pewne dopuszczalne wartości wszystkim dowolnym stałym w rozwiązaniu ogólnym lub całce ogólnej, otrzymujemy pewną funkcję, która nie zawiera już dowolnych stałych. Funkcja ta nazywana jest rozwiązaniem częściowym lub całką cząstkową równania (1.1). Aby znaleźć wartości dowolnych stałych, a tym samym konkretne rozwiązanie, stosuje się różne dodatkowe warunki do równania (1.1). Na przykład tak zwane warunki początkowe można określić w (1.2)

Po prawej stronie warunków początkowych (1.2) podano wartości liczbowe funkcji i pochodnych, a całkowita liczba warunków początkowych jest równa liczbie zdefiniowanych dowolnych stałych.

Problem znalezienia konkretnego rozwiązania równania (1.1) w oparciu o warunki początkowe nazywa się problemem Cauchy'ego.

§ 2. Równania różniczkowe zwyczajne I rzędu - podstawowe pojęcia.

Równanie różniczkowe zwyczajne pierwszego rzędu ( N=1) ma postać:
lub, jeżeli można to rozwiązać w odniesieniu do instrumentu pochodnego:
. Wspólna decyzja y= y(X,Z) lub całka ogólna
Równania pierwszego rzędu zawierają jedną dowolną stałą. Jedyny warunek początkowy równania pierwszego rzędu
pozwala wyznaczyć wartość stałej z rozwiązania ogólnego lub z całki ogólnej. W ten sposób zostanie znalezione konkretne rozwiązanie lub, co oznacza, problem Cauchy'ego zostanie rozwiązany. Zagadnienie istnienia i jednoznaczności rozwiązania problemu Cauchy'ego jest jednym z centralnych w ogólnej teorii równań różniczkowych zwyczajnych. W szczególności dla równania pierwszego rzędu twierdzenie jest ważne, co zostało tutaj przyjęte bez dowodu.

Twierdzenie 2.1. Jeśli w równaniu jest funkcja
i jego pochodna cząstkowa
ciągły w jakimś regionie D samolot XOY, i w tym obszarze jest określony punkt
, wówczas istnieje unikalne rozwiązanie, które spełnia zarówno równanie, jak i warunek początkowy
.

Z geometrycznego punktu widzenia ogólnym rozwiązaniem równania pierwszego rzędu jest rodzina krzywych na płaszczyźnie XOY, nie mające punktów wspólnych i różniące się między sobą jednym parametrem - wartością stałej C. Krzywe te nazywane są krzywymi całkowymi dla danego równania. Krzywe równań całkowych mają oczywistą właściwość geometryczną: w każdym punkcie tangens stycznej do krzywej jest równy wartości prawej strony równania w tym punkcie:
. Innymi słowy, równanie jest dane na płaszczyźnie XOY pole kierunków stycznych do krzywych całkowych. Komentarz: Należy zauważyć, że do równania.
równanie i tzw. równanie podane są w postaci symetrycznej
.

§ 3. Równania różniczkowe I rzędu ze zmiennymi rozłącznymi.

Definicja. Równanie różniczkowe ze zmiennymi rozłącznymi jest równaniem postaci
(3.1)

lub równanie postaci (3.2)

Aby rozdzielić zmienne w równaniu (3.1), tj. zredukuj to równanie do tak zwanego równania zmiennej rozdzielonej, wykonaj następujące czynności:

;

Teraz musimy rozwiązać równanie G(y)= 0 . Jeśli ma realne rozwiązanie y= A, To y= A będzie również rozwiązaniem równania (3.1).

Równanie (3.2) sprowadza się do oddzielnego równania zmiennej poprzez podzielenie przez iloczyn
:

, co pozwala nam otrzymać całkę ogólną z równania (3.2):
. (3.3)

Krzywe całkowe (3.3) zostaną uzupełnione rozwiązaniami
jeśli takie rozwiązania istnieją.

Rozwiązać równanie: .

Rozdzielamy zmienne:

Całkując, otrzymujemy

Dalej od równań
I
znaleźliśmy X=1, y=-1. Rozwiązania te są rozwiązaniami prywatnymi.

§ 4. Równania różniczkowe jednorodne I rzędu.

Definicja 1. Równanie pierwszego rzędu nazywa się jednorodnym, jeśli ma swoją prawą stronę dla dowolnego
stosunek jest ważny
, zwany warunkiem jednorodności funkcji dwóch zmiennych o wymiarze zerowym.

Przykład 1. Pokaż tę funkcję
- jednorodny wymiar zerowy.

Rozwiązanie.

co było do okazania

Twierdzenie. Dowolna funkcja
- jednorodna i odwrotnie, dowolna funkcja jednorodna
wymiar zerowy zostaje zredukowany do postaci
.

Dowód.

Pierwsze stwierdzenie twierdzenia jest oczywiste, ponieważ
. Udowodnijmy drugie twierdzenie. Włóżmy
, a następnie dla funkcji jednorodnej
, co należało udowodnić.

Definicja 2. Równanie (4.1)

w którym M I N– funkcje jednorodne tego samego stopnia, tj. mieć własność dla wszystkich , nazywa się jednorodnym.

Oczywiście równanie to zawsze można sprowadzić do postaci
(4.2), chociaż aby go rozwiązać, nie musisz tego robić.

Równanie jednorodne sprowadza się do równania z rozłącznymi zmiennymi poprzez zastąpienie żądanej funkcji y według formuły y= zx, Gdzie z(X) – nowa wymagana funkcja. Po wykonaniu podstawienia w równaniu (4.2) otrzymujemy:
Lub
Lub
.

Całkując otrzymujemy całkę ogólną równania po funkcji z(X)
, które po wielokrotnej wymianie
daje całkę ogólną pierwotnego równania. Co więcej, jeśli - pierwiastki równania
, a następnie funkcje
- rozwiązanie jednorodnego zadanego równania. Jeśli
, wówczas równanie (4.2) przyjmuje postać

i staje się równaniem z rozdzielnymi zmiennymi. Jego rozwiązania są półbezpośrednie:
.

Komentarz. Czasami wskazane jest użycie podstawienia zamiast powyższego podstawienia X= zy.

§ 5. Równania różniczkowe zredukowane do jednorodnych.

Rozważmy równanie postaci
. (5.1)

Jeśli
, to jest to równanie wykorzystujące podstawienie, gdzie I - nowe zmienne oraz - pewne liczby stałe wyznaczane z systemu

Sprowadzone do równania jednorodnego

Jeśli
, wówczas równanie (5.1) przyjmuje postać

Wierzyć z= topór+ przez, dochodzimy do równania, które nie zawiera zmiennej niezależnej.

Spójrzmy na przykłady.

Przykład 1.

Całkuj równanie

i zaznacz krzywą całkową przechodzącą przez punkty: a) (2;2); b) (1;-1).

Rozwiązanie.

Włóżmy y= zx. Następnie dy= xdz+ zdx I

Skróćmy to i zbieraj członków o godz dx I dz:

Oddzielmy zmienne:

.

Całkując otrzymujemy ;

Lub
,
.

Zamieniam tutaj z NA , otrzymujemy całkę ogólną danego równania w postaci (5.2)
Lub

.

To jest rodzina kręgów
, których środki leżą na linii prostej y = X i które w początku są styczne do prostej y + X = 0. Ta liniay = - X z kolei szczególne rozwiązanie równania.

Teraz tryb problemu Cauchy'ego:

A) wstawienie całki ogólnej X=2, y=2, znaleźliśmy C=2, dlatego wymagane będzie rozwiązanie
.

B) żaden z okręgów (5.2) nie przechodzi przez punkt (1;-1). Ale jest półprosty y = - X,
przechodzi przez punkt i daje wymagane rozwiązanie.

Przykład 2. Rozwiązać równanie: .

Rozwiązanie.

Równanie jest szczególnym przypadkiem równania (5.1).

Wyznacznik
w tym przykładzie
, więc musimy rozwiązać następujący układ

Rozwiązujemy to
. Dokonując podstawienia w danym równaniu
, otrzymujemy równanie jednorodne. Całkowanie za pomocą podstawienia
, znaleźliśmy
.

Wracając do starych zmiennych X I y według formuł
, mamy .

§ 6. Uogólnione równanie jednorodne.

Równanie M(X, y) dx+ N(X, y) dy=0 nazywa się uogólnioną jednorodnością, jeśli można wybrać taką liczbę k, że lewa strona tego równania staje się w pewnym stopniu funkcją jednorodną M stosunkowo X, y, dx I dy pod warunkiem że X uważa się za wartość pierwszego wymiaru, y – k pomiary , dx I dy – odpowiednio zero i (k-1) pomiary. Na przykład byłoby to równanie
. (6.1)

Obowiązuje przy założeniach dotyczących pomiarów

X, y, dx I dy członkowie lewicy
I dy będą miały odpowiednio wymiary -2, 2 k I k-1. Przyrównując je otrzymujemy warunek, który musi spełniać wymagana liczba k: -2 = 2k=k-1. Warunek ten jest spełniony, gdy k= -1 (z tym k wszystkie wyrazy po lewej stronie rozważanego równania będą miały wymiar -2). W konsekwencji równanie (6.1) jest uogólnione jako jednorodne.

Integrując to, znajdujemy
, Gdzie
. Jest to ogólne rozwiązanie równania (6.1).

§ 7. Liniowe równania różniczkowe I rzędu.

Równanie liniowe pierwszego rzędu to równanie liniowe względem żądanej funkcji i jej pochodnej. To wygląda jak:

, (7.1)

Gdzie P(X) I Q(X) – dane funkcje ciągłe X. Jeśli funkcja
, wówczas równanie (7.1) ma postać:
(7.2)

i w przeciwnym razie nazywa się liniowym równaniem jednorodnym
nazywa się to liniowym równaniem niejednorodnym.

Liniowe jednorodne równanie różniczkowe (7.2) jest równaniem z rozłącznymi zmiennymi:

(7.3)

Podstawiając znalezioną pochodną do równania (7.1), otrzymamy:

Lub
.

Gdzie
, gdzie jest dowolną stałą. W rezultacie ogólnym rozwiązaniem niejednorodnego równania liniowego (7.1) będzie (7.4)

Połączmy na przykład drugi i trzeci wyraz ostatniego wyrażenia i wyodrębnijmy funkcję ty(X) za nawiasem:
(7.5)

Wymagamy, aby nawias został unieważniony:
.

Rozwiążmy to równanie, ustalając dowolną stałą C równe zeru:
. Ze znalezioną funkcją w(X) Wróćmy do równania (7.5):
.

Rozwiązując to otrzymujemy:
.

Dlatego ogólne rozwiązanie równania (7.1) ma postać:

§ 8. Równanie Bernoulliego.

Definicja.

Równanie różniczkowe postaci
, Gdzie
, nazywa się równaniem Bernoulliego.

Przy założeniu, że
, podziel obie strony równania Bernoulliego przez . W rezultacie otrzymujemy:
(8.1)

Wprowadźmy nową funkcję
. Następnie
. Pomnóżmy równanie (8.1) przez
i przejdźmy do funkcji z(X) :
, tj. dla funkcji z(X) otrzymaliśmy liniowe niejednorodne równanie pierwszego rzędu. Równanie to rozwiązuje się metodami omówionymi w poprzednim akapicie. Zamiast tego podstawmy do jego rozwiązania ogólnego z(X) wyrażenie
, otrzymujemy całkę ogólną równania Bernoulliego, którą można łatwo rozwiązać w odniesieniu do y. Na
rozwiązanie jest dodawane y(X)=0 . Równanie Bernoulliego można również rozwiązać bez przechodzenia do równania liniowego przez podstawienie
, oraz przy użyciu metody Bernoulliego, szczegółowo omówionej w § 7. Rozważmy zastosowanie tej metody do rozwiązania równania Bernoulliego na konkretnym przykładzie.

Przykład. Znajdź ogólne rozwiązanie równania:
(8.2)

Rozwiązanie.

Zatem ogólne rozwiązanie tego równania ma postać:
, y(X)=0.

§ 9. Równania różniczkowe w różniczkach całkowitych.

Definicja. Jeśli w równaniu M(X, y) dx+ N(X, y) dy=0 (9.1) lewa strona to całkowita różniczka jakiejś funkcji U(X, y) , nazywa się to całkowitym równaniem różniczkowym. Równanie to można przepisać jako du(X, y)=0 , zatem jego całka ogólna wynosi ty(X, y)= C.

Na przykład równanie xdy+ ydx=0 w różnicach całkowitych istnieje równanie, ponieważ można je przepisać w postaci D(xy)=0. Całka ogólna będzie xy= C- dowolna funkcja różniczkowalna. Rozróżnijmy (9.3) ze względu na u
§ 10. Czynnik całkujący.

Jeśli równanie M(X, y) dx + N(X, y) dy = 0 nie jest całkowitym równaniem różniczkowym i istnieje funkcja µ = µ(X, y) , tak że po pomnożeniu przez nią obu stron równania otrzymamy równanie

µ(Mdx + Ndy) = 0 w sumie różnic, tj. µ(Mdx + Ndy)du, a następnie funkcja µ(X, y) nazywa się czynnikiem całkującym równania. W przypadku, gdy równanie jest już równaniem różnic całkowitych, zakładamy μ = 1.

Jeśli zostanie znaleziony czynnik całkujący µ , wówczas całkowanie tego równania sprowadza się do pomnożenia obu jego stron przez µ i znalezienie całki ogólnej otrzymanego równania w całkowitych różnicach.

Jeśli µ jest funkcją ciągle różniczkowalną X I y, To
.

Wynika z tego, że czynnik całkujący µ spełnia następujące równanie różniczkowe cząstkowe pierwszego rzędu:

(10.1).

Jeśli wiadomo to z góry µ= µ(ω) , Gdzie ω – dana funkcja z X I y, wówczas równanie (10.1) sprowadza się do zwykłego (i w dodatku liniowego) równania o nieznanej funkcji µ na zmiennej niezależnej ω :

(10.2),

Gdzie
, tj. ułamek jest funkcją tylko ω .

Rozwiązując równanie (10.2), znajdujemy czynnik całkujący

, Z = 1.

W szczególności równanie M(X, y) dx + N(X, y) dy = 0 ma czynnik całkujący, który zależy tylko od X(ω = X) lub tylko z y(ω = y), jeżeli spełnione zostaną odpowiednio następujące warunki:

,
.

Pokazano, jak rozpoznać uogólnione jednorodne równanie różniczkowe. Rozważano metodę rozwiązywania uogólnionego jednorodnego równania różniczkowego pierwszego rzędu. Podano przykład szczegółowego rozwiązania takiego równania.

Treść

Definicja

Uogólnione jednorodne równanie różniczkowe pierwszego rzędu jest równaniem postaci:
, gdzie α ≠ 0 , α ≠ 1 , f - funkcja.

Jak ustalić, czy równanie różniczkowe jest uogólnione jednorodne

Aby ustalić, czy równanie różniczkowe jest uogólnione jednorodnie, należy wprowadzić stałą t i dokonać podstawienia:
y → t α · y, x → t · x.
Jeśli można wybrać wartość α, przy której stała t maleje, to jest to - uogólnione jednorodne równanie różniczkowe. Zmiana pochodnej y′ przy tym podstawieniu ma postać:
.

Przykład

Określ, czy dane równanie jest uogólnione jednorodne:
.

Dokonujemy zamiany y → t α y, x → t x, y′ → t α- 1 y′:
;
.
Podziel przez t α+ 5 :
;
.
Równanie nie będzie zawierać t jeśli
4 α - 6 = 0, α = 3/2 .
Od kiedy α = 3/2 , t spadło jest to uogólnione równanie jednorodne.

Metoda rozwiązania

Rozważ uogólnione jednorodne równanie różniczkowe pierwszego rzędu:
(1) .
Pokażmy, że sprowadza się to do równania jednorodnego za pomocą podstawienia:
t = x α .
Naprawdę,
.
Stąd
; .
(1) :
;
.

Jest to równanie jednorodne. Można to rozwiązać przez podstawienie:
y = z t,
gdzie z jest funkcją t.
Rozwiązując problemy, łatwiej jest od razu zastosować podstawienie:
y = z x α,
gdzie z jest funkcją x.

Przykład rozwiązania uogólnionego jednorodnego równania różniczkowego pierwszego rzędu

Rozwiązać równanie różniczkowe
(P.1) .

Sprawdźmy, czy to równanie jest uogólnione jednorodnie. Aby to zrobić w (P.1) dokonać zamiany:
y → t α y , x → t x , y′ → t α- 1 y′.
.
Podziel przez t α:
.
t zostanie anulowane, jeśli ustawimy α = - 1 . Oznacza to, że jest to uogólnione równanie jednorodne.

Dokonajmy podstawienia:
y = z x α = z x - 1 ,
gdzie z jest funkcją x.
.
Podstaw do pierwotnego równania (P.1):
(P.1) ;
;
.
Pomnóż przez x i otwórz nawiasy:
;
;
.
Rozdzielamy zmienne - mnożymy przez dx i dzielimy przez x z 2 . Kiedy z ≠ 0 mamy:
.
Całkujemy korzystając z tablicy całek:
;
;
;
.
Wzmocnijmy:
.
Zastąpmy stałą e C → C i usuńmy znak modułu, ponieważ o wyborze pożądanego znaku decyduje wybór znaku stałej C:
.

Wróćmy do zmiennej y. Zastąp z = xy:
.
Podziel przez x:
(str. 2) .

Kiedy dzieliliśmy przez z 2 , założyliśmy, że z ≠ 0 . Rozważmy teraz rozwiązanie z = xy = 0 lub y = 0 .
Od kiedy y = 0 , lewa strona wyrażenia (str. 2) nie jest zdefiniowany, to do powstałej całki ogólnej dodajemy rozwiązanie y = 0 .

;
.

Bibliografia:
N.M. Gunther, RO Kuźmin, Zbiór problemów matematyki wyższej, „Lan”, 2003.

Równania różniczkowe pierwszego rzędu ze zmiennymi rozłącznymi.

Definicja. Równanie różniczkowe ze zmiennymi rozłącznymi jest równaniem postaci (3.1) lub równaniem postaci (3.2)

Aby rozdzielić zmienne w równaniu (3.1), tj. zredukuj to równanie do tak zwanego równania zmiennej rozdzielonej, wykonaj następujące czynności: ;

Teraz musimy rozwiązać równanie g(y)= 0. Jeśli ma realne rozwiązanie y=a, To y=a będzie również rozwiązaniem równania (3.1).

Równanie (3.2) sprowadza się do oddzielnego równania poprzez podzielenie przez iloczyn:

, co pozwala nam otrzymać całkę ogólną z równania (3.2): . (3.3)

Krzywe całkowe (3.3) zostaną uzupełnione rozwiązaniami jeśli takie rozwiązania istnieją.

Równania różniczkowe jednorodne pierwszego rzędu.

Definicja 1. Równanie pierwszego rzędu nazywa się jednorodnym, jeżeli jego prawa strona spełnia tę zależność , zwany warunkiem jednorodności funkcji dwóch zmiennych o wymiarze zerowym.

Przykład 1. Pokaż, że funkcja jest jednorodna o wymiarze zerowym.

Rozwiązanie. ,

co było do okazania

Twierdzenie. Każda funkcja jest jednorodna i odwrotnie, każda jednorodna funkcja o wymiarze zerowym sprowadza się do postaci .

Dowód. Pierwsze stwierdzenie twierdzenia jest oczywiste, ponieważ . Udowodnijmy drugie twierdzenie. Postawmy więc na funkcję jednorodną , co należało udowodnić.

Definicja 2. Równanie (4.1), w którym M I N– funkcje jednorodne tego samego stopnia, tj. mają właściwość dla wszystkich, zwaną jednorodną. Oczywiście równanie to można zawsze sprowadzić do postaci (4.2), chociaż może nie być to konieczne do jego rozwiązania. Równanie jednorodne sprowadza się do równania z rozłącznymi zmiennymi poprzez zastąpienie żądanej funkcji y według formuły y=zx, Gdzie z(x)– nowa wymagana funkcja. Po dokonaniu podstawienia w równaniu (4.2) otrzymujemy: lub lub .

Całkując otrzymujemy całkę ogólną równania po funkcji z(x) , co po wielokrotnym zastąpieniu daje całkę ogólną pierwotnego równania. Ponadto, jeśli są pierwiastkami równania, to funkcje są rozwiązaniami danego równania jednorodnego. Jeżeli , to równanie (4.2) przyjmuje postać

I staje się równaniem z rozdzielnymi zmiennymi. Jego rozwiązania są półbezpośrednie: .

Komentarz. Czasami wskazane jest użycie podstawienia zamiast powyższego podstawienia x=zy.

Uogólnione równanie jednorodne.

Równanie M(x,y)dx+N(x,y)dy=0 nazywa się uogólnioną jednorodną, jeśli można wybrać taką liczbę k, że lewa strona tego równania staje się w pewnym stopniu funkcją jednorodną M stosunkowo x, y, dx I dy pod warunkiem że X uważa się za wartość pierwszego wymiaru, y – k- pomiary ,dx I dy – odpowiednio zero i (k-1) pomiary. Na przykład byłoby to równanie . (6.1) Obowiązuje przy założeniach dotyczących pomiarów x, y, dx I dy członkowie lewicy i dy będą miały odpowiednio wymiary -2, 2 k I k-1. Przyrównując je otrzymujemy warunek, który musi spełniać wymagana liczba k: -2 = 2k=k-1. Warunek ten jest spełniony, gdy k= -1 (z tym k wszystkie wyrazy po lewej stronie rozważanego równania będą miały wymiar -2). W konsekwencji równanie (6.1) jest uogólnione jako jednorodne.