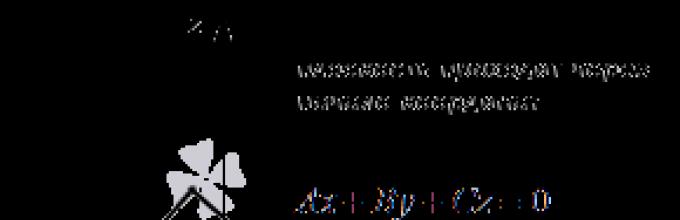
Jeżeli wszystkie liczby A, B, C i D są różne od zera, wówczas nazywa się ogólne równanie płaszczyzny kompletny. W przeciwnym razie wywoływane jest ogólne równanie płaszczyzny niekompletny.

Rozważmy wszystkie możliwe wspólne niekompletne równania płaszczyzna w prostokątnym układzie współrzędnych Oxyz w przestrzeni trójwymiarowej.

Niech D = 0, wówczas mamy ogólne niepełne równanie płaskie w postaci . Ta płaszczyzna w prostokątnym układzie współrzędnych Oxyz przechodzi przez początek układu współrzędnych. Rzeczywiście, podstawiając współrzędne punktu do powstałego niepełnego równania płaszczyzny, dochodzimy do tożsamości .


Dla , lub , lub mamy ogólne niepełne równania płaszczyzn , lub , lub , Odpowiednio. Równania te definiują płaszczyzny równoległe do płaszczyzn współrzędnych odpowiednio Oxy, Oxz i Oyz (warunek płaszczyzn równoległych patrz artykuł) i przechodzące przez punkty i odpowiednio. Na. Od tego momentu należy do płaszczyzny pod warunkiem, wówczas współrzędne tego punktu muszą spełniać równanie płaszczyzny, czyli równość musi być prawdziwa. Stąd znajdziemy. Zatem wymagane równanie ma postać .

Przedstawmy drugi sposób rozwiązania tego problemu.

Ponieważ płaszczyzna, której ogólne równanie musimy ułożyć, jest równoległa do płaszczyzny Oyz, to jako jej wektor normalny możemy przyjąć wektor normalny płaszczyzny Oyz. Normalny wektor płaszczyzna współrzędnych Oyz jest wektorem współrzędnych. Teraz znamy wektor normalny płaszczyzny i punkt płaszczyzny, dlatego możemy zapisać jego ogólne równanie (podobny problem rozwiązaliśmy w poprzednim akapicie tego artykułu):
, to jego współrzędne muszą spełniać równanie płaszczyzny. Zatem równość jest prawdziwa skąd to znajdziemy. Teraz możemy napisać pożądane ogólne równanie płaszczyzny, ma ono postać .

Odpowiedź:

Bibliografia.

  • Bugrov Ya.S., Nikolsky S.M. Wyższa matematyka. Tom pierwszy: Elementy algebra liniowa i geometrii analitycznej.
  • Ilyin V.A., Poznyak E.G. Geometria analityczna.

Można określić na różne sposoby (jeden punkt i wektor, dwa punkty i wektor, trzy punkty itp.). Mając to na uwadze, równanie płaszczyzny może mieć różne postacie. Ponadto, pod pewnymi warunkami, płaszczyzny mogą być równoległe, prostopadłe, przecinające się itp. Porozmawiamy o tym w tym artykule. Dowiemy się jak utworzyć ogólne równanie płaszczyzny i nie tylko.

Normalna postać równania

Powiedzmy, że istnieje przestrzeń R 3, która ma prostokątny układ współrzędnych XYZ. Zdefiniujmy wektor α, który zostanie uwolniony z punktu początkowego O. Przez koniec wektora α rysujemy płaszczyznę P, która będzie do niego prostopadła.

Oznaczmy dowolny punkt na P jako Q = (x, y, z). Oznaczmy wektor promienia punktu Q literą p. W tym przypadku długość wektora α jest równa р=IαI i Ʋ=(cosα,cosβ,cosγ).

Jest to wektor jednostkowy skierowany w bok, podobnie jak wektor α. α, β i γ to kąty utworzone pomiędzy wektorem Ʋ a dodatnimi kierunkami osi przestrzennych, odpowiednio x, y, z. Rzut dowolnego punktu QϵП na wektor Ʋ jest wartością stałą równą p: (p,Ʋ) = p(p≥0).

Powyższe równanie ma sens, gdy p=0. Tyle, że płaszczyzna P w tym przypadku przetnie punkt O (α=0), będący początkiem współrzędnych, a wersor Ʋ wypuszczony z punktu O będzie prostopadły do ​​P, pomimo jego kierunku, który oznacza, że ​​wektor Ʋ jest wyznaczany z dokładnością do znaku. Poprzednie równanie jest równaniem naszej płaszczyzny P, wyrażonym w postaci wektorowej. Ale we współrzędnych będzie to wyglądać tak:

P jest tutaj większe lub równe 0. Znaleźliśmy równanie płaszczyzny w przestrzeni w postaci normalnej.

Równanie ogólne

Jeśli pomnożymy równanie we współrzędnych przez dowolną liczbę różną od zera, otrzymamy równanie równoważne temu, określające właśnie tę płaszczyznę. Będzie to wyglądać tak:

Tutaj A, B, C są liczbami jednocześnie różnymi od zera. Równanie to nazywa się ogólnym równaniem płaszczyzny.

Równania płaszczyzn. Specjalne przypadki

Równanie w postaci ogólnej można zmodyfikować, jeśli istnieje dodatkowe warunki. Przyjrzyjmy się niektórym z nich.

Załóżmy, że współczynnik A wynosi 0. Oznacza to, że płaszczyzna ta jest równoległa do zadanej osi Ox. W tym przypadku zmieni się postać równania: Ву+Cz+D=0.

Podobnie postać równania zmieni się w następujących warunkach:

  • Po pierwsze, jeśli B = 0, to równanie zmieni się na Ax + Cz + D = 0, co będzie wskazywało równoległość do osi Oy.
  • Po drugie, jeśli C=0, to równanie zostanie przekształcone na Ax+By+D=0, co będzie wskazywało równoległość do zadanej osi Oz.
  • Po trzecie, jeśli D=0, równanie będzie wyglądać jak Ax+By+Cz=0, co będzie oznaczać, że płaszczyzna przecina O (początek układu współrzędnych).
  • Po czwarte, jeśli A=B=0, to równanie zmieni się na Cz+D=0, co okaże się równoległe do Oxy.
  • Po piąte, jeśli B=C=0, to równanie przyjmuje postać Ax+D=0, co oznacza, że ​​płaszczyzna do Oyz jest równoległa.
  • Po szóste, jeśli A=C=0, wówczas równanie przyjmie postać Ву+D=0, to znaczy będzie zgłaszać równoległość do Oxz.

Rodzaj równania w odcinkach

W przypadku, gdy liczby A, B, C, D są różne od zera, równanie (0) może mieć następującą postać:

x/a + y/b + z/c = 1,

w którym a = -D/A, b = -D/B, c = -D/C.

Otrzymamy w rezultacie Warto zauważyć, że płaszczyzna ta przetnie oś Ox w punkcie o współrzędnych (a,0,0), Oy - (0,b,0) i Oz - (0,0,c ).

Biorąc pod uwagę równanie x/a + y/b + z/c = 1, nietrudno wizualnie wyobrazić sobie położenie płaszczyzny względem zadanego układu współrzędnych.

Normalne współrzędne wektora

Wektor normalny n do płaszczyzny P ma współrzędne będące współczynnikami równanie ogólne danej płaszczyzny, czyli n (A, B, C).

Aby wyznaczyć współrzędne normalnej n, wystarczy znać ogólne równanie danej płaszczyzny.

Stosując równanie na odcinkach, które ma postać x/a + y/b + z/c = 1, a także stosując równanie ogólne, można zapisać współrzędne dowolnego wektora normalnego danej płaszczyzny: (1 /a + 1/b + 1/ Z).

Warto zauważyć, że wektor normalny pomaga rozwiązać wiele problemów. Do najpowszechniejszych zalicza się zadania polegające na wykazaniu prostopadłości lub równoległości płaszczyzn, problemy ze znalezieniem kątów pomiędzy płaszczyznami lub kątów pomiędzy płaszczyznami i prostymi.

Rodzaj równania płaszczyzny ze względu na współrzędne punktu i wektora normalnego

Niezerowy wektor n prostopadły do ​​danej płaszczyzny nazywa się normalnym dla danej płaszczyzny.

Załóżmy, że w przestrzeń współrzędnych(prostokątny układ współrzędnych) Oxyz otrzymują:

  • punkt Mₒ o współrzędnych (xₒ,yₒ,zₒ);
  • wektor zerowy n=A*i+B*j+C*k.

Należy utworzyć równanie płaszczyzny, która przejdzie przez punkt Mₒ prostopadły do ​​normalnej n.

Wybieramy dowolny punkt w przestrzeni i oznaczamy go M (x y, z). Niech wektor promienia dowolnego punktu M (x,y,z) będzie wynosić r=x*i+y*j+z*k, a wektor promienia punktu Mₒ (xₒ,yₒ,zₒ) - rₒ=xₒ* i+yₒ *j+zₒ*k. Punkt M będzie należeć do danej płaszczyzny, jeśli wektor MₒM jest prostopadły do ​​wektora n. Zapiszmy warunek ortogonalności za pomocą iloczynu skalarnego:

[MₒM, n] = 0.

Ponieważ MₒM = r-rₒ, równanie wektorowe płaszczyzny będzie wyglądać następująco:

Równanie to może mieć inną postać. W tym celu wykorzystuje się właściwości iloczynu skalarnego i przekształca się lewą stronę równania. = - . Jeśli oznaczymy to jako c, otrzymamy równanie: - c = 0 lub = c, które wyraża stałość rzutów na wektor normalny wektorów promieni danych punktów należących do płaszczyzny.

Teraz możesz uzyskać widok współrzędnych rekordu równanie wektorowe nasza płaszczyzna = 0. Ponieważ r-rₒ = (x-xₒ)*i + (y-yₒ)*j + (z-zₒ)*k, oraz n = A*i+B*j+C*k, to mamy:

Okazuje się, że mamy równanie dla płaszczyzny przechodzącej przez punkt prostopadły do ​​normalnej n:

A*(x- xₒ)+B*(y- yₒ)C*(z-zₒ)=0.

Rodzaj równania płaszczyzny według współrzędnych dwóch punktów i wektora współliniowego z płaszczyzną

Określmy dwa dowolne punkty M′ (x′,y′,z′) i M″ (x″,y″,z″) oraz wektor a (a′,a″,a‴).

Teraz możemy utworzyć równanie dla danej płaszczyzny, która będzie przechodzić przez istniejące punkty M′ i M″ oraz dowolny punkt M o współrzędnych (x, y, z) równoległych do zadanego wektora a.

W tym przypadku wektory M′M=(x-x′;y-y′;z-z′) i M″M=(x″-x′;y″-y′;z″-z′) muszą być współpłaszczyznowe z wektorem a=(a′,a″,a‴), co oznacza, że ​​(M′M, M″M, a)=0.

Zatem nasze równanie płaszczyzny w przestrzeni będzie wyglądać następująco:

Rodzaj równania płaszczyzny przecinającej trzy punkty

Załóżmy, że mamy trzy punkty: (x′,y′,z′), (x″,y″,z″), (x‴,y‴,z‴), które nie należą do tej samej prostej. Należy napisać równanie płaszczyzny przechodzącej przez dane trzy punkty. Teoria geometrii twierdzi, że taki rodzaj płaszczyzny istnieje naprawdę, jest jednak jedyny i niepowtarzalny. Ponieważ płaszczyzna ta przecina punkt (x′,y′,z′), jej równanie będzie miało następującą postać:

Tutaj A, B, C są jednocześnie różne od zera. Ponadto dana płaszczyzna przecina jeszcze dwa punkty: (x″,y″,z″) i (x‴,y‴,z‴). W tym zakresie muszą zostać spełnione następujące warunki:

Teraz możemy stworzyć jednorodny układ z niewiadomymi u, v, w:

W naszym przypadek x, y lub z pełni rolę dowolnego punktu spełniającego równanie (1). Mając dane równanie (1) oraz układ równań (2) i (3), układ równań pokazany na powyższym rysunku jest spełniony przez wektor N (A,B,C), który jest nietrywialny. Dlatego wyznacznik tego układu jest równy zeru.

Równanie (1), które otrzymaliśmy, jest równaniem płaszczyzny. Przechodzi dokładnie przez 3 punkty i łatwo to sprawdzić. Aby to zrobić, musimy rozszerzyć nasz wyznacznik na elementy pierwszego rzędu. Z istniejących własności wyznacznika wynika, że ​​nasza płaszczyzna przecina jednocześnie trzy początkowo dane punkty (x′,y′,z′), (x″,y″,z″), (x‴,y‴,z‴) . Oznacza to, że rozwiązaliśmy powierzone nam zadanie.

Kąt dwuścienny pomiędzy płaszczyznami

Kąt dwuścienny reprezentuje przestrzeń figura geometryczna, utworzony przez dwie półpłaszczyzny, które wychodzą z jednej linii prostej. Innymi słowy, jest to część przestrzeni ograniczona tymi półpłaszczyznami.

Załóżmy, że mamy dwie płaszczyzny z następującymi równaniami:

Wiemy, że wektory N=(A,B,C) i N¹=(A¹,B¹,C¹) są prostopadłe zgodnie z dane samoloty. Pod tym względem kąt φ między wektorami N i N¹ jest równy kątowi (dwuściennemu) znajdującemu się między tymi płaszczyznami. Iloczyn skalarny ma postać:

NN¹=|N||N¹|cos φ,

właśnie dlatego

cosφ= NN¹/|N||N¹|=(AA1+BB¹+CC¹)/((√(A²+B²+C²))*(√(A¹)²+(B¹)²+(C¹)²)).

Wystarczy wziąć pod uwagę, że 0≤φ≤π.

W rzeczywistości dwie przecinające się płaszczyzny tworzą dwa kąty (dwuścienne): φ 1 i φ 2. Ich suma jest równa π (φ 1 + φ 2 = π). Jeśli chodzi o ich cosinusy, ich wartości bezwzględne są równe, ale różnią się znakiem, to znaczy cos φ 1 = -cos φ 2. Jeśli w równaniu (0) zastąpimy A, B i C liczbami odpowiednio -A, -B i -C, to otrzymane równanie będzie wyznaczało tę samą płaszczyznę, jedyną, kąt φ w równaniu cos φ= NN 1 /| N||N 1 | zostanie zastąpione przez π-φ.

Równanie płaszczyzny prostopadłej

Płaszczyzny, pomiędzy którymi kąt wynosi 90 stopni, nazywane są prostopadłymi. Korzystając z materiału przedstawionego powyżej, możemy znaleźć równanie płaszczyzny prostopadłej do drugiej. Załóżmy, że mamy dwie płaszczyzny: Ax+By+Cz+D=0 i A¹x+B¹y+C¹z+D=0. Można powiedzieć, że będą one prostopadłe, jeśli cosφ=0. Oznacza to, że NN¹=AA¹+BB¹+CC¹=0.

Równanie płaszczyzny równoległej

Dwie płaszczyzny, które nie zawierają punktów wspólnych, nazywane są równoległymi.

Warunek (ich równania są takie same jak w poprzednim akapicie) jest taki, że wektory N i N¹, które są do nich prostopadłe, są współliniowe. Oznacza to, że spełnione są następujące warunki proporcjonalności:

A/A¹=B/B¹=C/C¹.

Jeśli rozszerzymy warunki proporcjonalności - A/A¹=B/B¹=C/C¹=DD¹,

oznacza to, że płaszczyzny te pokrywają się. Oznacza to, że równania Ax+By+Cz+D=0 i A¹x+B¹y+C¹z+D¹=0 opisują jedną płaszczyznę.

Odległość do płaszczyzny od punktu

Załóżmy, że mamy płaszczyznę P, która jest dana równaniem (0). Należy znaleźć odległość do niego od punktu o współrzędnych (xₒ,yₒ,zₒ)=Qₒ. Aby to zrobić, musisz doprowadzić równanie płaszczyzny P do postaci normalnej:

(ρ,v)=р (р≥0).

W tym przypadku ρ (x,y,z) jest wektorem promienia naszego punktu Q znajdującego się na P, p jest długością prostopadłej P, która została uwolniona z punktu zerowego, v jest wektorem jednostkowym, który znajduje się w kierunek A.

Różnica wektora promienia ρ-ρº pewnego punktu Q = (x, y, z), należącego do P, jak również wektor promienia danego punktu Q 0 = (xₒ, yₒ, zₒ) jest takim wektorem, całkowita wartość którego rzut na v jest równy odległości d, którą należy znaleźć od Q 0 = (xₒ,уₒ,zₒ) do P:

D=|(ρ-ρ 0 ,v)|, ale

(ρ-ρ 0,v)= (ρ,v)-(ρ 0,v) =р-(ρ 0,v).

Okazuje się, że

d=|(ρ 0,v)-р|.

W ten sposób znajdziemy wartość bezwzględną wynikowego wyrażenia, czyli pożądane d.

Używając języka parametrów, otrzymujemy oczywistość:

d=|Ахₒ+Вуₒ+Czₒ|/√(А²+В²+С²).

Jeśli punkt zadany Q 0 znajduje się po drugiej stronie płaszczyzny P, podobnie jak początek współrzędnych, wówczas pomiędzy wektorem ρ-ρ 0 i v znajduje się zatem:

d=-(ρ-ρ 0 ,v)=(ρ 0 ,v)-р>0.

W przypadku, gdy punkt Q 0 wraz z początkiem współrzędnych leży po tej samej stronie P, wówczas powstały kąt jest ostry, czyli:

d=(ρ-ρ 0 ,v)=р - (ρ 0 , v)>0.

W rezultacie okazuje się, że w pierwszym przypadku (ρ 0 ,v)>р, w drugim (ρ 0 ,v)<р.

Płaszczyzna styczna i jej równanie

Płaszczyzna styczna do powierzchni w punkcie styku M° jest płaszczyzną zawierającą wszystkie możliwe styczne do krzywych przechodzących przez ten punkt na powierzchni.

Przy tego typu równaniu powierzchni F(x,y,z)=0 równanie płaszczyzny stycznej w punkcie stycznym M°(x°,y°,z°) będzie wyglądać następująco:

F x (xş,yş,zş)(x- xş)+ F x (xş, yş, zş)(y- yş)+ F x (xş, yş,zş)(z-zş)=0.

Jeśli określisz powierzchnię w jawnej postaci z=f (x,y), to płaszczyzna styczna będzie opisana równaniem:

z-zş =f(xş, yş)(x- xş)+f(xş, yş)(y- yş).

Przecięcie dwóch płaszczyzn

W układzie współrzędnych (prostokątnym) znajduje się Oxyz, dane są dwie płaszczyzny П′ i П″, które przecinają się i nie pokrywają. Ponieważ dowolną płaszczyznę umieszczoną w prostokątnym układzie współrzędnych wyznacza równanie ogólne, założymy, że P′ i P″ są dane równaniami A′x+B′y+C′z+D′=0 i A″x +B″y+ С″z+D″=0. W tym przypadku mamy normalne n′ (A′,B′,C′) płaszczyzny P′ i normalne n″ (A″,B″,C″) płaszczyzny P″. Ponieważ nasze płaszczyzny nie są równoległe i nie pokrywają się, wektory te nie są współliniowe. Używając języka matematyki, możemy zapisać ten warunek w następujący sposób: n′≠ n″ ↔ (A′,B′,C′) ≠ (λ*A″,λ*B″,λ*C″), λϵR. Niech prostą leżącą na przecięciu P′ i P″ oznaczymy literą a, w tym przypadku a = P′ ∩ P″.

a jest linią prostą składającą się ze zbioru wszystkich punktów (wspólnych) płaszczyzn P′ i P″. Oznacza to, że współrzędne dowolnego punktu należącego do prostej a muszą jednocześnie spełniać równania A′x+B′y+C′z+D′=0 i A″x+B″y+C″z+D″=0 . Oznacza to, że współrzędne punktu będą częściowym rozwiązaniem następującego układu równań:

W rezultacie okazuje się, że (ogólne) rozwiązanie tego układu równań wyznaczy współrzędne każdego z punktów prostej, która będzie punktem przecięcia P′ i P″ oraz wyznaczy prostą a w (prostokątnym) układzie współrzędnych Oxyz w przestrzeni.

Własności prostej w geometrii euklidesowej.

Przez dowolny punkt można poprowadzić nieskończoną liczbę linii prostych.

Przez dowolne dwa nie pokrywające się punkty można poprowadzić pojedynczą linię prostą.

Dwie rozbieżne linie na płaszczyźnie albo przecinają się w jednym punkcie, albo są

równolegle (wynika z poprzedniego).

W przestrzeni trójwymiarowej istnieją trzy opcje względnego położenia dwóch linii:

  • linie przecinają się;
  • linie są równoległe;
  • linie proste przecinają się.

Prosty linia— krzywa algebraiczna pierwszego rzędu: linia prosta w kartezjańskim układzie współrzędnych

jest dana na płaszczyźnie równaniem pierwszego stopnia (równaniem liniowym).

Ogólne równanie prostej.

Definicja. Dowolną linię prostą na płaszczyźnie można określić za pomocą równania pierwszego rzędu

Topór + Wu + C = 0,

i stałe A, B nie są jednocześnie równe zeru. To równanie pierwszego rzędu nazywa się ogólny

równanie prostej. W zależności od wartości stałych A, B I Z Możliwe są następujące szczególne przypadki:

. C = 0, A ≠ 0, B ≠ 0- linia prosta przechodzi przez początek

. A = 0, B ≠0, C ≠0 (By + C = 0)- linia prosta równoległa do osi Oh

. B = 0, A ≠0, C ≠ 0 (Topór + C = 0)- linia prosta równoległa do osi Jednostka organizacyjna

. B = C = 0, A ≠0- linia prosta pokrywa się z osią Jednostka organizacyjna

. A = C = 0, B ≠0- linia prosta pokrywa się z osią Oh

Równanie prostej można przedstawić w różnych postaciach w zależności od danego

warunki początkowe.

Równanie prostej z punktu i wektora normalnego.

Definicja. W prostokątnym układzie współrzędnych kartezjańskich wektor ze składowymi (A, B)

prostopadle do prostej określonej równaniem

Topór + Wu + C = 0.

Przykład. Znajdź równanie prostej przechodzącej przez punkt A(1, 2) prostopadle do wektora (3, -1).

Rozwiązanie. Mając A = 3 i B = -1, ułóżmy równanie prostej: 3x - y + C = 0. Aby znaleźć współczynnik C

Do powstałego wyrażenia podstawiamy współrzędne danego punktu A. Otrzymujemy zatem: 3 - 2 + C = 0

C = -1. Razem: wymagane równanie: 3x - y - 1 = 0.

Równanie prostej przechodzącej przez dwa punkty.

Niech w przestrzeni będą dane dwa punkty M 1 (x 1 , y 1 , z 1) I M2 (x 2, y 2, z 2), Następnie równanie linii,

przechodząc przez te punkty:

Jeżeli którykolwiek z mianowników jest równy zero, odpowiadający mu licznik należy ustawić na zero. NA

płaszczyźnie, równanie prostej zapisane powyżej jest uproszczone:

Jeśli x 1 ≠ x 2 I x = x 1, Jeśli x 1 = x 2 .

Frakcja = k zwany nachylenie prosty.

Przykład. Znajdź równanie prostej przechodzącej przez punkty A(1, 2) i B(3, 4).

Rozwiązanie. Stosując napisany powyżej wzór otrzymujemy:

Równanie prostej za pomocą punktu i nachylenia.

Jeśli ogólne równanie linii Topór + Wu + C = 0 prowadzić do:

i wyznaczyć , to wynikowe równanie nazywa się

równanie prostej o nachyleniu k.

Równanie prostej z punktu i wektora kierunkowego.

Analogicznie do punktu uwzględniającego równanie prostej przechodzącej przez wektor normalny, możesz wprowadzić zadanie

linia prosta przechodząca przez punkt i wektor kierunkowy linii prostej.

Definicja. Każdy niezerowy wektor (α 1, α 2), których elementy spełniają warunek

Aα 1 + Ba 2 = 0 zwany wektor kierujący linii prostej.

Topór + Wu + C = 0.

Przykład. Znajdź równanie prostej z wektorem kierunku (1, -1) i przechodzącej przez punkt A(1, 2).

Rozwiązanie. Równania żądanej linii będziemy szukać w postaci: Topór + By + C = 0. Zgodnie z definicją,

współczynniki muszą spełniać następujące warunki:

1 * A + (-1) * B = 0, tj. A = B.

Wtedy równanie prostej ma postać: Topór + Ay + C = 0, Lub x + y + C / A = 0.

Na x = 1, y = 2 dostajemy C/A = -3, tj. wymagane równanie:

x + y - 3 = 0

Równanie prostej w odcinkach.

Jeśli w ogólnym równaniu linii prostej Ах + Ву + С = 0 С≠0, to dzieląc przez -С, otrzymujemy:

czy gdzie

Geometryczne znaczenie współczynników jest takie, że współczynnik a jest współrzędną punktu przecięcia

proste z osią Oh, A B- współrzędna punktu przecięcia linii z osią Jednostka organizacyjna.

Przykład. Podano ogólne równanie prostej x - y + 1 = 0. Znajdź równanie tej prostej w odcinkach.

C = 1, , a = -1, b = 1.

Równanie normalne linii.

Jeśli obie strony równania Topór + Wu + C = 0 podzielić przez liczbę który jest nazywany

czynnik normalizujący, wtedy otrzymamy

xcosφ + ysinφ - p = 0 -normalne równanie linii.

Znak ± współczynnika normalizującego należy tak dobrać, aby: µ*C< 0.

R- długość prostopadłej opuszczonej od początku do prostej,

A φ - kąt utworzony przez tę prostopadłą z dodatnim kierunkiem osi Oh.

Przykład. Podano ogólne równanie prostej 12x - 5 lat - 65 = 0. Wymagane do pisania różnych typów równań

tę linię prostą.

Równanie tej prostej w odcinkach:

Równanie tej prostej z nachyleniem: (podziel przez 5)

Równanie prostej:

cos φ = 12/13; grzech φ= -5/13; p = 5.

Należy zauważyć, że nie każdą linię prostą można przedstawić za pomocą równania w postaci odcinków, np. linie proste,

równolegle do osi lub przechodząc przez początek układu współrzędnych.

Kąt między prostymi na płaszczyźnie.

Definicja. Jeśli podano dwie linie y = k 1 x + b 1 , y = k 2 x + b 2, a następnie kąt ostry między tymi liniami

zostanie zdefiniowany jako

Dwie linie są równoległe jeśli k 1 = k 2. Dwie linie są prostopadłe

Jeśli k 1 = -1/ k 2 .

Twierdzenie.

Bezpośredni Topór + Wu + C = 0 I ZA 1 x + B 1 y + C 1 = 0 równoległe, gdy współczynniki są proporcjonalne

ZA 1 = λA, B 1 = λB. Jeśli także С 1 = λС, to linie się pokrywają. Współrzędne punktu przecięcia dwóch linii

znajdują się jako rozwiązanie układu równań tych prostych.

Równanie prostej przechodzącej przez dany punkt prostopadle do danej prostej.

Definicja. Linia przechodząca przez punkt M 1 (x 1, y 1) i prostopadle do linii y = kx + b

reprezentowane przez równanie:

Odległość punktu od linii.

Twierdzenie. Jeśli zostanie przyznany punkt M(x 0, y 0), następnie odległość do linii prostej Topór + Wu + C = 0 zdefiniowana jako:

Dowód. Niech chodzi M 1 (x 1, y 1)- podstawa prostopadłej rzucona z punktu M dla danego

bezpośredni. Następnie odległość między punktami M I M 1:

(1)

Współrzędne x 1 I o 1 można znaleźć jako rozwiązanie układu równań:

Drugie równanie układu jest równaniem prostej przechodzącej przez dany punkt M 0 prostopadle

dana linia prosta. Jeśli przekształcimy pierwsze równanie układu do postaci:

A(x - x 0) + B(y - y 0) + Ax 0 + O 0 + C = 0,

następnie rozwiązując otrzymujemy:

Podstawiając te wyrażenia do równania (1), otrzymujemy:

Twierdzenie zostało udowodnione.

Aby można było poprowadzić pojedynczą płaszczyznę przez dowolne trzy punkty w przestrzeni, konieczne jest, aby punkty te nie leżały na tej samej linii prostej.

Rozważ punkty M 1 (x 1, y 1, z 1), M 2 (x 2, y 2, z 2), M 3 (x 3, y 3, z 3) w ogólnym kartezjańskim układzie współrzędnych.

Aby dowolny punkt M(x, y, z) leżał w tej samej płaszczyźnie z punktami M 1, M 2, M 3, konieczne jest, aby wektory były współpłaszczyznowe.

(
) = 0

Zatem,

Równanie płaszczyzny przechodzącej przez trzy punkty:

Równanie płaszczyzny, mając dane dwa punkty i wektor współliniowy z płaszczyzną.

Niech będą dane punkty M 1 (x 1,y 1,z 1),M 2 (x 2,y 2,z 2) i wektor
.

Utwórzmy równanie dla płaszczyzny przechodzącej przez dane punkty M 1 i M 2 oraz dowolny punkt M (x, y, z) równoległy do ​​wektora .

Wektory
i wektor
muszą być współpłaszczyznowe, tj.

(
) = 0

Równanie płaszczyzny:

Równanie płaszczyzny za pomocą jednego punktu i dwóch wektorów,

współliniowy do płaszczyzny.

Niech zostaną dane dwa wektory
I
, płaszczyzny współliniowe. Następnie dla dowolnego punktu M(x, y, z) należącego do płaszczyzny wektory
muszą być współpłaszczyznowe.

Równanie płaszczyzny:

Równanie płaszczyzny przez punkt i wektor normalny .

Twierdzenie. Jeżeli punkt M jest dany w przestrzeni 0 (X 0 , j 0 , z 0 ), to równanie płaszczyzny przechodzącej przez punkt M 0 prostopadle do wektora normalnego (A, B, C) ma postać:

A(X – X 0 ) + B(y – y 0 ) + C(z – z 0 ) = 0.

Dowód. Dla dowolnego punktu M(x, y, z) należącego do płaszczyzny tworzymy wektor. Ponieważ wektor jest wektorem normalnym, to jest prostopadły do ​​płaszczyzny, a zatem prostopadły do ​​wektora
. Następnie iloczyn skalarny

= 0

W ten sposób otrzymujemy równanie płaszczyzny

Twierdzenie zostało udowodnione.

Równanie płaszczyzny w odcinkach.

Jeżeli w równaniu ogólnym Ax + Bi + Cz + D = 0 dzielimy obie strony przez (-D)

,

wymiana
, otrzymujemy równanie płaszczyzny w odcinkach:

Liczby a, b, c to punkty przecięcia płaszczyzny odpowiednio z osiami x, y, z.

Równanie płaszczyzny w postaci wektorowej.

Gdzie

- wektor promienia aktualnego punktu M(x, y, z),

Wektor jednostkowy mający kierunek prostopadły upuszczony na płaszczyznę z początku układu współrzędnych.

,  i  to kąty utworzone przez ten wektor z osiami x, y, z.

p jest długością tej prostopadłej.

We współrzędnych równanie to wygląda następująco:

xcos + ycos + zcos - p = 0.

Odległość punktu od płaszczyzny.

Odległość dowolnego punktu M 0 (x 0, y 0, z 0) od płaszczyzny Ax+By+Cz+D=0 wynosi:

Przykład. Znajdź równanie płaszczyzny, wiedząc, że punkt P(4; -3; 12) jest podstawą prostopadłej spuszczonej z początku układu współrzędnych na tę płaszczyznę.

Zatem A = 4/13; B = -3/13; C = 12/13, korzystamy ze wzoru:

A(x – x 0 ) + B(y – y 0 ) + C(z – z 0 ) = 0.

Przykład. Znajdź równanie płaszczyzny przechodzącej przez dwa punkty P(2; 0; -1) i

Q(1; -1; 3) prostopadle do płaszczyzny 3x + 2y – z + 5 = 0.

Wektor normalny do płaszczyzny 3x + 2y – z + 5 = 0
równolegle do żądanej płaszczyzny.

Otrzymujemy:

Przykład. Znajdź równanie płaszczyzny przechodzącej przez punkty A(2, -1, 4) i

B(3, 2, -1) prostopadle do płaszczyzny X + Na + 2z – 3 = 0.

Wymagane równanie płaszczyzny ma postać: A X+B y+C z+ D = 0, wektor normalny do tej płaszczyzny (A, B, C). Wektor
(1, 3, -5) należy do płaszczyzny. Podana nam płaszczyzna, prostopadła do pożądanej, ma wektor normalny (1, 1, 2). Ponieważ punkty A i B należą do obu płaszczyzn, a zatem płaszczyzny są do siebie prostopadłe

Zatem wektor normalny (11, -7, -2). Ponieważ punkt A należy do żądanej płaszczyzny, to jego współrzędne muszą spełniać równanie tej płaszczyzny, tj. 112 + 71 - 24 +D= 0;D= -21.

W sumie otrzymujemy równanie płaszczyzny: 11 X - 7y – 2z – 21 = 0.

Przykład. Znajdź równanie płaszczyzny, wiedząc, że punkt P(4, -3, 12) jest podstawą prostopadłej spuszczonej z początku na tę płaszczyznę.

Znajdowanie współrzędnych wektora normalnego
= (4, -3, 12). Wymagane równanie płaszczyzny ma postać: 4 X – 3y + 12z+ D = 0. Aby znaleźć współczynnik D, podstawiamy współrzędne punktu P do równania:

16 + 9 + 144 + D = 0

W sumie otrzymujemy wymagane równanie: 4 X – 3y + 12z – 169 = 0

Przykład. Podane są współrzędne wierzchołków piramidy A 1 (1; 0; 3), A 2 (2; -1; 3), A 3 (2; 1; 1),

    Znajdź długość krawędzi A 1 A 2.

    Znajdź kąt pomiędzy krawędziami A 1 A 2 i A 1 A 4.

    Znajdź kąt pomiędzy krawędzią A 1 A 4 i ścianą A 1 A 2 A 3.

Najpierw znajdujemy wektor normalny do ściany A 1 A 2 A 3 jako iloczyn wektorów
I
.

= (2-1; 1-0; 1-3) = (1; 1; -2);

Znajdźmy kąt między wektorem normalnym a wektorem
.

-4 – 4 = -8.

Pożądany kąt  między wektorem a płaszczyzną będzie równy  = 90 0 - .

    Znajdź obszar twarzy A 1 A 2 A 3.

    Znajdź objętość piramidy.

    Znajdź równanie płaszczyzny A 1 A 2 A 3.

Skorzystajmy ze wzoru na równanie płaszczyzny przechodzącej przez trzy punkty.

2x + 2y + 2z – 8 = 0

x + y + z – 4 = 0;

W przypadku korzystania z wersji komputerowej „ Wyższy kurs matematyki” możesz uruchomić program, który rozwiąże powyższy przykład dla dowolnych współrzędnych wierzchołków piramidy.

Aby uruchomić program, kliknij dwukrotnie ikonę:

W otwartym oknie programu wprowadź współrzędne wierzchołków piramidy i naciśnij Enter. W ten sposób można po kolei zdobyć wszystkie punkty decyzyjne.

Uwaga: Aby uruchomić program, na komputerze musi być zainstalowany program Maple ( Waterloo Maple Inc.) w dowolnej wersji, począwszy od MapleV Release 4.