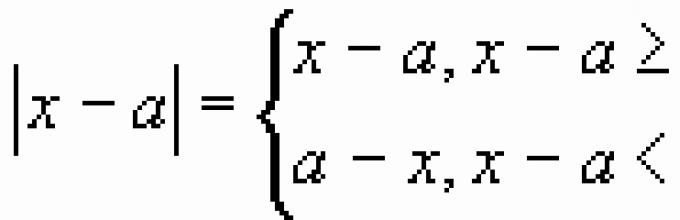W ostatnie lata NA egzaminy wstępne, podczas końcowych testów w Formularz jednolitego egzaminu państwowego oferowane są zadania z parametrami. Zadania te pozwalają zdiagnozować poziom wiedzy matematycznej i co najważniejsze, logiczne myślenie kandydatów, umiejętność prowadzenia działalności badawczej, a także po prostu znajomość głównych sekcji szkolnego kursu matematyki.
Pogląd parametru jako zmiennej równej znajduje odzwierciedlenie w metodach graficznych. W rzeczywistości, ponieważ parametr jest „równy pod względem praw” zmiennej, to oczywiście można go „przypisać” do własnej oś współrzędnych. W ten sposób powstaje płaszczyzna współrzędnych. Odmowa tradycyjnego wyboru liter do oznaczania osi określa jedną z najskuteczniejszych metod rozwiązywania problemów z parametrami - „metoda obszarowa”. Oprócz innych metod stosowanych przy rozwiązywaniu problemów z parametrami zapoznaję moich uczniów z technikami graficznymi, zwracając uwagę na to, jak rozpoznać „takie” problemy i jak wygląda proces rozwiązywania problemu.
Najbardziej znaki ogólne, które pomogą Ci rozpoznać zadania odpowiednie dla rozważanej metody:
Problem 1. „Dla jakich wartości parametru obowiązuje nierówność dla wszystkich?”
Rozwiązanie. 1).
Rozbudujmy moduły biorąc pod uwagę znak wyrażenia submodularnego: 
2). Zapiszmy wszystkie układy wynikowych nierówności:
A) 
B) 
V) 
G) 
3). Pokażmy zbiór punktów spełniających każdy układ nierówności (ryc. 1a).
4). Łącząc wszystkie obszary pokazane na rysunku z cieniowaniem widać, że nierówność nie jest spełniona przez punkty leżące wewnątrz paraboli.
Z rysunku wynika, że dla dowolnej wartości parametru można znaleźć obszar, w którym znajdują się punkty, których współrzędne spełniają pierwotną nierówność. Nierówność zachodzi dla wszystkich, jeśli . Odpowiedź: o godz.
Rozważany przykład to „problem otwarty” - można rozważyć rozwiązanie całej klasy problemów bez zmiany wyrażeń rozważanych w przykładzie 
, w którym przezwyciężono już trudności techniczne związane z sporządzaniem wykresów.
Zadanie. Dla jakich wartości parametru równanie nie ma rozwiązań? Odpowiedź: o godz.
Zadanie. Dla jakich wartości parametru równanie ma dwa rozwiązania? Zapisz oba znalezione rozwiązania.
Odpowiedź: wtedy 
, 
;
Następnie 
; , Następnie 
, .
Zadanie. Dla jakich wartości parametru równanie ma jeden pierwiastek? Znajdź ten korzeń. Odpowiedź: kiedy kiedy.
Zadanie. Rozwiąż nierówność.
(„Punkty leżące wewnątrz paraboli działają”).
,; , brak rozwiązań;
Zadanie 2. Znajdź wszystkie wartości parametru A, dla każdego z nich układ nierówności 
tworzy odcinek o długości 1 na osi liczbowej.
Rozwiązanie. Przepiszmy oryginalny system w tej formie 
Wszystkie rozwiązania tego układu (pary postaci ) tworzą pewien obszar ograniczony parabolami 
I 
(Rysunek 1).
Oczywiście rozwiązaniem układu nierówności będzie odcinek o długości 1 w i w . Odpowiedź: ; .
Zadanie 3. Znajdź wszystkie wartości parametru, dla którego zbiór rozwiązań nierówności 
zawiera liczbę , a także zawiera dwa odcinki długości , które nie mają wspólnych punktów.
Rozwiązanie. Zgodnie ze znaczeniem nierówności; Przepiszmy nierówność, mnożąc obie strony przez (), otrzymujemy nierówność:
, ,
(1)
Nierówność (1) jest równoważna połączeniu dwóch systemów:
(ryc. 2).
Oczywiście przedział nie może zawierać odcinka o długości . Oznacza to, że w przedziale znajdują się dwa nieprzecinające się odcinki długości.Jest to możliwe dla , tj. Na . Odpowiedź: .
Zadanie 4. Znajdź wszystkie wartości parametru, dla których istnieje wiele rozwiązań nierówności 
zawiera odcinek o długości 4 i jest zawarty w pewnym segmencie o długości 7.
Rozwiązanie. Przeprowadźmy równoważne przekształcenia, biorąc pod uwagę, że i .
, ,
; ostatnia nierówność jest równoważna kombinacji dwóch systemów:
Pokażmy obszary, które odpowiadają tym systemom (ryc. 3).
1) Gdy zbiór rozwiązań jest przedziałem o długości mniejszej niż 4. Gdy zbiór rozwiązań jest sumą dwóch przedziałów Tylko przedział może zawierać odcinek o długości 4. Ale wtedy , i suma nie jest już zawarta w żadnym odcinku o długości 7. Oznacza to, że nie spełniają one warunku.
2) zbiór rozwiązań jest przedziałem. Zawiera odcinek o długości 4 tylko wtedy, gdy jego długość jest większa niż 4, tj. Na . Zawarty jest w odcinku o długości 7 tylko wtedy, gdy jego długość jest nie większa niż 7, czyli dla , a następnie . Odpowiedź: .
Zadanie 5. Znajdź wszystkie wartości parametru, dla którego zbiór rozwiązań nierówności 
zawiera liczbę 4, a także zawiera dwa rozłączne segmenty o długości 4 każdy.
Rozwiązanie. Zgodnie z warunkami. Pomnóżmy obie strony nierówności przez (). Otrzymujemy równoważną nierówność, w której grupujemy wszystkie wyrazy po lewej stronie i przekształcamy je w iloczyn:
, ,
, 
.
Z ostatniej nierówności wynika:
1) 
2)
Pokażmy obszary, które odpowiadają tym systemom (ryc. 4).
a) W otrzymujemy przedział, który nie zawiera liczby 4. W otrzymujemy przedział, który również nie zawiera liczby 4.
b) W otrzymujemy sumę dwóch przedziałów. Nieprzecinające się odcinki o długości 4 można znaleźć tylko w przedziale . Jest to możliwe tylko wtedy, gdy długość interwału jest większa niż 8, tj. jeśli . W ich przypadku spełniony jest także inny warunek: . Odpowiedź: .
Zadanie 6. Znajdź wszystkie wartości parametru, dla którego zbiór rozwiązań nierówności 
zawiera pewien segment o długości 2, ale nie zawiera
brak odcinka długości 3.
Rozwiązanie. Zgodnie ze znaczeniem zadania mnożymy obie strony nierówności przez , grupujemy wszystkie wyrazy po lewej stronie nierówności i przekształcamy je w iloczyn:
, 
. Z ostatniej nierówności wynika:
1) 
2) 
Pokażmy obszar odpowiadający pierwszemu systemowi (ryc. 5).
Oczywiście warunek problemu jest spełniony, jeśli 
. Odpowiedź: .
Zadanie 7. Znajdź wszystkie wartości parametru, dla których zbiór rozwiązań nierówności 1+ 
zawiera się w pewnym odcinku o długości 1 i jednocześnie zawiera pewien odcinek o długości 0,5.
Rozwiązanie. 1). Wskażmy ODZ zmiennej i parametru: 
2). Zapiszmy nierówność w postaci
, 
,
(1). Nierówność (1) jest równoważna połączeniu dwóch systemów:
1) 
2) 
Biorąc pod uwagę ODZ, rozwiązania systemowe wyglądają następująco:
A) 
B) 
(ryc. 6).
A) 
B)
Pokażmy obszar odpowiadający systemowi a) (ryc. 7). Odpowiedź: .
Zadanie 8. Sześć liczb tworzy rosnący ciąg arytmetyczny. Pierwszy, drugi i czwarty wyraz tego ciągu są rozwiązaniami nierówności 
, i reszta
nie są rozwiązań tej nierówności. Znajdź zbiór wszystkich możliwych wartości pierwszego wyrazu takich progresji.
Rozwiązanie. I. Znajdź wszystkie rozwiązania nierówności
A). OZ: 
, tj.
(w rozwiązaniu uwzględniliśmy, że funkcja wzrasta o ).
B). Nierówności w zdrowiu dzieci 
równoznaczne z nierównością 
, tj. 
, co daje:
1). 
2). 
Oczywiście rozwiązanie nierówności ma wiele znaczeń 
.
II. Zilustrujmy drugą część problemu dotyczącą wyrazów rosnącego postępu arytmetycznego z figurą ( Ryż. 8 , gdzie jest pierwszym wyrazem, jest drugim itd.). Zauważ, że:
Albo mamy układ nierówności liniowych:
rozwiążmy to graficznie. Budujemy linie proste i , a także linie proste
Zatem... Pierwszy, drugi i szósty wyraz tego ciągu są rozwiązaniami nierówności 
, a pozostałe nie są rozwiązaniami tej nierówności. Znajdź zbiór wszystkich możliwych wartości różnicy tego postępu.
Równanie postaci F(X; A) = 0 równanie ze zmienną X i parametr A.
Rozwiąż równanie z parametrem A– oznacza to dla każdej wartości A znaleźć wartości X, spełniając to równanie.
Przykład 1. Oh= 0
Przykład 2. Oh = A
Przykład 3.
x + 2 = aha
x – ah = -2
x(1 – a) = -2
Jeśli 1 – A= 0, tj. A= 1, zatem X 0 = -2 bez pierwiastków
Jeśli 1 – A 0, tj. A 1, zatem X =
Przykład 4.
(A 2 – 1) X = 2A 2 + A – 3
(A – 1)(A + 1)X = 2(A – 1)(A – 1,5)
(A – 1)(A + 1)X = (1A – 3)(A – 1)
Jeśli A= 1, następnie 0 X = 0
X- każdy prawdziwy numer
Jeśli A= -1, następnie 0 X = -2
żadnych korzeni
Jeśli A 1, A-1, zatem X = (jedyna decyzja).
Oznacza to, że dla każdej prawidłowej wartości A pasuje do jednej wartości X.
Na przykład:
Jeśli A= 5, zatem X = = ;
Jeśli A= 0, zatem X= 3 itd.
Materiał dydaktyczny
1. Oh = X + 3
2. 4 + Oh = 3X – 1
3. A = +
Na A= 1 bez korzeni.
Na A= 3 bez pierwiastków.
Na A = 1 X– dowolna liczba rzeczywista z wyjątkiem X = 1
Na A = -1, A= 0 brak rozwiązań.
Na A = 0, A= 2 brak rozwiązań.
Na A = -3, A = 0, 5, A= -2 brak rozwiązań
Na A = -Z, Z= 0 brak rozwiązań.
Równania kwadratowe z parametrem
Przykład 1. Rozwiązać równanie
(A – 1)X 2 = 2(2A + 1)X + 4A + 3 = 0
Na A = 1 6X + 7 = 0
Gdy A 1, podkreślamy te wartości parametrów, przy których D idzie do zera.
D = (2(2 A + 1)) 2 – 4(A – 1)(4A + 30 = 16A 2 + 16A + 4 – 4(4A 2 + 3A – 4A – 3) = 16A 2 + 16A + 4 – 16A 2 + 4A + 12 = 20A + 16
20A + 16 = 0
20A = -16
Jeśli A < -4/5, то D < 0, уравнение имеет действительный корень.
Jeśli A> -4/5 i A 1, zatem D > 0,
X = 
Jeśli A= 4/5, zatem D = 0,
Przykład 2. Przy jakich wartościach parametru a wykonuje się równanie
x 2 + 2( A + 1)X + 9A– 5 = 0 ma 2 różne pierwiastki ujemne?
re = 4( A + 1) 2 – 4(9A – 5) = 4A 2 – 28A + 24 = 4(A – 1)(A – 6)
4(A – 1)(A – 6) > 0
przez t. Vieta: X 1 + X 2 = -2(A + 1)
X 1 X 2 = 9A – 5
Według warunku X 1 < 0, X 2 < 0 то –2(A + 1) < 0 и 9A – 5 > 0
| W końcu | 4(A – 1)(A – 6) > 0 - 2(A + 1) < 0 9A – 5 > 0 |
A < 1: а > 6 A > - 1 A > 5/9 |
 (Ryż. 1) < A < 1, либо A > 6 |
Przykład 3. Znajdź wartości A, dla którego to równanie ma rozwiązanie.
x 2 – 2( A – 1)X + 2A + 1 = 0
re = 4( A – 1) 2 – 4(2A + 10 = 4A 2 – 8A + 4 – 8A – 4 = 4A 2 – 16A
4A 2 – 16 0
4A(A – 4) 0
A( A – 4)) 0
A( A – 4) = 0
a = 0 lub A – 4 = 0
A = 4
(Ryż. 2)
Odpowiedź: A 0 i A 4
Materiał dydaktyczny
1. Przy jakiej wartości A równanie Oh 2 – (A + 1) X + 2A– 1 = 0 ma jeden pierwiastek?
2. Przy jakiej wartości A równanie ( A + 2) X 2 + 2(A + 2)X+ 2 = 0 ma jeden pierwiastek?
3. Dla jakich wartości a jest równanie ( A 2 – 6A + 8) X 2 + (A 2 – 4) X + (10 – 3A – A 2) = 0 ma więcej niż dwa pierwiastki?
4. Dla jakich wartości a równanie 2 X 2 + X – A= 0 ma co najmniej jeden wspólny pierwiastek z równaniem 2 X 2 – 7X + 6 = 0?
5. Dla jakich wartości równania X 2 +Oh+ 1 = 0 i X 2 + X + A= 0 ma co najmniej jeden wspólny pierwiastek?
1. Kiedy A = - 1/7, A = 0, A = 1
2. Kiedy A = 0
3. Kiedy A = 2
4. Kiedy A = 10
5. Kiedy A = - 2
Równania wykładnicze z parametrem
Przykład 1.Znajdź wszystkie wartości A, dla którego równanie
9 x – ( A+ 2)*3 x-1/x +2 A*3 -2/x = 0 (1) ma dokładnie dwa pierwiastki.
Rozwiązanie. Mnożąc obie strony równania (1) przez 3 2/x, otrzymujemy równanie równoważne
3 2(x+1/x) – ( A+ 2)*3 x+1/x + 2 A = 0 (2)
Niech 3 x+1/x = Na, wówczas równanie (2) przyjmie postać Na 2 – (A + 2)Na + 2A= 0 lub
(Na – 2)(Na – A) = 0, skąd Na 1 =2, Na 2 = A.
Jeśli Na= 2, tj. Zatem 3 x+1/x = 2 X + 1/X= log 3 2 lub X 2 – X log 3 2 + 1 = 0.
To równanie nie ma rzeczywistych pierwiastków, ponieważ D= log 2 3 2 – 4< 0.
Jeśli Na = A, tj. 3x+1/x = A To X + 1/X= log 3 A, Lub X 2 –X log 3 a + 1 = 0. (3)
Równanie (3) ma dokładnie dwa pierwiastki wtedy i tylko wtedy, gdy
D = log 2 3 2 – 4 > 0, lub |log 3 a| > 2.
Jeśli log 3 a > 2, to A> 9, a jeśli log 3 a< -2, то 0 < A < 1/9.
Odpowiedź: 0< A < 1/9, A > 9.
Przykład 2. Przy jakich wartościach a jest równanie 2 2х – ( A - 3) 2x – 3 A= 0 ma rozwiązania?
W celu dane równanie ma rozwiązania, konieczne i wystarczające jest równanie T 2 – (A - 3) T – 3A= 0 miało co najmniej jeden pierwiastek dodatni. Znajdźmy pierwiastki, korzystając z twierdzenia Viety: X 1 = -3, X 2 = A = >
a jest liczbą dodatnią.
Odpowiedź: kiedy A > 0
Materiał dydaktyczny
1. Znajdź wszystkie wartości a, dla których równanie
25x – (2 A+ 5)*5 x-1/x + 10 A* 5 -2/x = 0 ma dokładnie 2 rozwiązania.
2. Dla jakich wartości a jest równanie
2 (a-1)x?+2(a+3)x+a = 1/4 ma pojedynczy pierwiastek?
3. Przy jakich wartościach parametru a wykonuje się równanie
4x - (5 A-3)2 x +4 A 2 – 3A= 0 ma unikalne rozwiązanie?
Równania logarytmiczne z parametrem
Przykład 1. Znajdź wszystkie wartości A, dla którego równanie
log 4x (1 + Oh) = 1/2 (1)
ma unikalne rozwiązanie.
Rozwiązanie. Równanie (1) jest równoważne równaniu
1 + Oh = 2X Na X > 0, X 1/4 (3)
X = Na
aj 2 – Na + 1 = 0 (4)
Warunek (2) z (3) nie jest spełniony.
Pozwalać A 0, zatem UA 2 – 2Na+ 1 = 0 ma pierwiastki rzeczywiste wtedy i tylko wtedy D = 4 – 4A 0, tj. Na A 1. Aby rozwiązać nierówność (3), wykreślmy funkcje Galitsky M.L., Moshkovich M.M., Shvartsburd S.I. Pogłębione studium przebiegu algebry i analizy matematycznej. – M.: Edukacja, 1990
1. Systemy równania liniowe z parametrem
Układy równań liniowych z parametrem rozwiązuje się tymi samymi podstawowymi metodami, co zwykłe układy równań: metodą podstawienia, metodą dodawania równań i metodą graficzną. Znajomość interpretacji graficznej systemy liniowe ułatwia odpowiedź na pytanie o liczbę korzeni i ich istnienie.
Przykład 1.
Znajdź wszystkie wartości parametru a, dla których układ równań nie ma rozwiązań.
(x + (a 2 – 3) y = a,
(x + y = 2.
Rozwiązanie.
Spójrzmy na kilka sposobów rozwiązania tego zadania.
1 sposób. Korzystamy z własności: układ nie ma rozwiązań, jeśli stosunek współczynników przed x jest równy stosunkowi współczynników przed y, ale nie jest równy stosunkowi wolni członkowie(a/a 1 = b/b 1 ≠ c/c 1). Następnie mamy:
1/1 = (a 2 – 3)/1 ≠ a/2 lub system
(i 2 – 3 = 1,
(a ≠ 2.
Z pierwszego równania a 2 = 4 zatem, biorąc pod uwagę warunek, że a ≠ 2, otrzymujemy odpowiedź.
Odpowiedź: a = -2.
Metoda 2. Rozwiązujemy metodą podstawieniową.
(2 – y + (a 2 – 3) y = a,
(x = 2 – y,
((a 2 – 3)y – y = a – 2,
(x = 2 – y.
Po usunięciu wspólnego czynnika y z nawiasów w pierwszym równaniu otrzymujemy:
((a 2 – 4)y = a – 2,
(x = 2 – y.
Układ nie ma rozwiązań, jeśli pierwsze równanie nie ma rozwiązań, tzn
(i 2 – 4 = 0,
(a – 2 ≠ 0.
Oczywiście a = ±2, ale biorąc pod uwagę drugi warunek, odpowiedź daje tylko odpowiedź ujemną.
Odpowiedź: a = -2.
Przykład 2.
Znajdź wszystkie wartości parametru a, dla których układ równań ma nieskończoną liczbę rozwiązań.
(8x + ay = 2,
(topór + 2 lata = 1.
Rozwiązanie.
Zgodnie z własnością, jeśli stosunek współczynników x i y jest taki sam i równy stosunkowi wolnych członków układu, to ma on nieskończoną liczbę rozwiązań (tj. a/a 1 = b/ b 1 = do/do 1). Dlatego 8/a = a/2 = 2/1. Rozwiązując każde z otrzymanych równań, okazuje się, że w tym przykładzie odpowiedzią jest a = 4.
Odpowiedź: a = 4.
2. Systemy równania racjonalne z parametrem
Przykład 3.
(3|x| + y = 2,
(|x| + 2y = a.
Rozwiązanie.
Pomnóżmy pierwsze równanie układu przez 2:
(6|x| + 2y = 4,
(|x| + 2y = a.
Odejmując drugie równanie od pierwszego, otrzymujemy 5|x| = 4 – a. To równanie będzie miało unikalne rozwiązanie dla a = 4. W pozostałych przypadkach równanie to będzie miało dwa rozwiązania (dla a< 4) или ни одного (при а > 4).
Odpowiedź: a = 4.
Przykład 4.
Znajdź wszystkie wartości parametru a, dla których układ równań ma jednoznaczne rozwiązanie.
(x + y = a,
(y – x 2 = 1.
Rozwiązanie.
Układ ten rozwiążemy metodą graficzną. Zatem wykres drugiego równania układu jest parabolą podniesioną wzdłuż osi Oy w górę o jeden odcinek jednostkowy. Pierwsze równanie określa zbiór prostych równoległych do prostej y = -x (obrazek 1). Z rysunku widać wyraźnie, że układ ma rozwiązanie, jeśli prosta y = -x + a jest styczna do paraboli w punkcie o współrzędnych (-0,5, 1,25). Podstawiając te współrzędne do równania linii prostej zamiast x i y, znajdujemy wartość parametru a: 
1,25 = 0,5 + a;
Odpowiedź: a = 0,75.
Przykład 5.
Korzystając z metody podstawiania, dowiedz się, przy jakiej wartości parametru a układ ma rozwiązanie jednoznaczne.
(ax – y = a + 1,
(ax + (a + 2)y = 2.
Rozwiązanie.
Z pierwszego równania wyrażamy y i podstawiamy je do drugiego:
(y = topór – a – 1,
(topór + (a + 2)(topór – a – 1) = 2.
Sprowadźmy drugie równanie do postaci kx = b, która będzie miała jednoznaczne rozwiązanie dla k ≠ 0. Mamy:
topór + a 2 x – a 2 – a + 2ax – 2a – 2 = 2;
za 2 x + 3ax = 2 + za 2 + 3a + 2.
Trójmian kwadratowy a 2 + 3a + 2 reprezentujemy jako iloczyn nawiasów
(a + 2)(a + 1), a po lewej stronie wyciągamy x z nawiasów:
(a 2 + 3a)x = 2 + (a + 2)(a + 1).
Oczywiście a 2 + 3a nie powinno być równe zero, zatem
a 2 + 3a ≠ 0, a(a + 3) ≠ 0, co oznacza a ≠ 0 i ≠ -3.
Odpowiedź: a ≠ 0; ≠ -3.
Przykład 6.
Korzystając z metody rozwiązania graficznego, określ, przy jakiej wartości parametru a układ ma rozwiązanie jednoznaczne.
(x 2 + y 2 = 9,
(y – |x| = a.
Rozwiązanie.
Na podstawie warunku konstruujemy okrąg o środku w początku układu i promieniu 3 jednostkowych odcinków, co określa pierwsze równanie układu
x 2 + y 2 = 9. Drugie równanie układu (y = |x| + a) jest linią łamaną. Używając Rysunek 2 Rozważamy wszystkie możliwe przypadki jego położenia względem okręgu. Łatwo zauważyć, że a = 3. 
Odpowiedź: a = 3.
Nadal masz pytania? Nie wiesz jak rozwiązywać układy równań?
Aby uzyskać pomoc korepetytora zarejestruj się.
Pierwsza lekcja jest darmowa!
stronie internetowej, przy kopiowaniu materiału w całości lub w części wymagany jest link do źródła.
