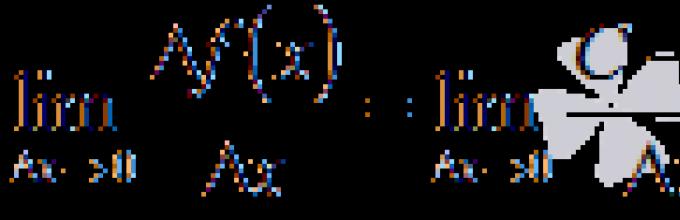Wyprowadzając pierwszy wzór tabeli, zaczniemy od definicji funkcji pochodnej w punkcie. Weźmy gdzie X- każdy prawdziwy numer, to jest, X– dowolna liczba z dziedziny definicji funkcji. Zapiszmy granicę stosunku przyrostu funkcji do przyrostu argumentu w punkcie: ![]()
Należy zauważyć, że pod znakiem granicznym uzyskuje się wyrażenie, które nie jest niepewnością zera podzieloną przez zero, ponieważ licznik nie zawiera wartości nieskończenie małej, ale dokładnie zero. Innymi słowy, przyrost funkcji stałej wynosi zawsze zero.
Zatem, pochodna funkcji stałejjest równa zeru w całym obszarze definicji.
Pochodna funkcji potęgowej.
Wzór na pochodną funkcji potęgowej ma postać ![]() , gdzie wykładnik P– dowolna liczba rzeczywista.
, gdzie wykładnik P– dowolna liczba rzeczywista.
Najpierw udowodnijmy wzór na wykładnik naturalny, czyli na p = 1, 2, 3, …
Będziemy korzystać z definicji pochodnej. Zapiszmy granicę stosunku przyrostu funkcji potęgowej do przyrostu argumentu: 
Aby uprościć wyrażenie w liczniku, zwracamy się do wzoru dwumianu Newtona: 
Stąd, 
Dowodzi to wzoru na pochodną funkcji potęgowej dla wykładnika naturalnego.
Pochodna funkcji wykładniczej.
Przedstawiamy wyprowadzenie wzoru na pochodną w oparciu o definicję:
Dotarliśmy do niepewności. Aby ją rozwinąć, wprowadzamy nową zmienną, a na . Następnie . W ostatnim przejściu wykorzystaliśmy wzór na przejście do nowej podstawy logarytmicznej.
Podstawmy do pierwotnej granicy: 
Jeśli przypomnimy sobie drugą niezwykłą granicę, dochodzimy do wzoru na pochodną funkcji wykładniczej: 
Pochodna funkcji logarytmicznej.
Udowodnijmy wzór na pochodną funkcji logarytmicznej dla wszystkich X z dziedziny definicji i wszystkich ważnych wartości podstawy A logarytm Z definicji pochodnej mamy: 
Jak zauważyłeś, w trakcie dowodu przekształcenia przeprowadzono wykorzystując własności logarytmu. Równość  jest prawdziwe ze względu na drugą niezwykłą granicę.
jest prawdziwe ze względu na drugą niezwykłą granicę.
Pochodne funkcji trygonometrycznych.
Aby wyprowadzić wzory na pochodne funkcji trygonometrycznych, będziemy musieli przypomnieć sobie niektóre wzory trygonometryczne, a także pierwszą niezwykłą granicę.
Z definicji pochodnej funkcji sinus mamy ![]() .
.
Skorzystajmy ze wzoru na różnicę sinusów: 
Pozostaje przejść do pierwszego niezwykłego ograniczenia: 
Zatem pochodna funkcji grzech x Jest bo x.
Wzór na pochodną cosinusa dowodzi się dokładnie w ten sam sposób. 
Zatem pochodna funkcji bo x Jest –grzech x.
Wzory na tablicę pochodnych na tangens i cotangens wyprowadzimy korzystając ze sprawdzonych zasad różniczkowania (pochodna ułamka). 
Pochodne funkcji hiperbolicznych.
Reguły różniczkowania oraz wzór na pochodną funkcji wykładniczej z tabeli pochodnych pozwalają nam wyprowadzić wzory na pochodne sinusa, cosinusa hiperbolicznego, tangensa i kotangensa. 
Pochodna funkcji odwrotnej.
Aby uniknąć zamieszania podczas prezentacji, oznaczmy w indeksie dolnym argument funkcji, za pomocą której dokonuje się różniczkowania, czyli jest to pochodna funkcji k(x) Przez X.
Teraz sformułujmy zasada znajdowania pochodnej funkcji odwrotnej.
Niech funkcje y = f(x) I x = g(y) wzajemnie odwrotne, określone odpowiednio na przedziałach i. Jeśli w punkcie istnieje skończona niezerowa pochodna funkcji k(x), to w tym punkcie istnieje skończona pochodna funkcji odwrotnej g(y), I ![]() . W innym poście
. W innym poście ![]() .
.
Zasadę tę można przeformułować dla dowolnego X z przedziału , to otrzymujemy  .
.
Sprawdźmy zasadność tych formuł.
Znajdźmy funkcję odwrotną logarytmu naturalnego ![]() (Tutaj y jest funkcją oraz X- argument). Po rozwiązaniu tego równania dla X, otrzymujemy (tutaj X jest funkcją oraz y– jej argumentacja). To jest,
(Tutaj y jest funkcją oraz X- argument). Po rozwiązaniu tego równania dla X, otrzymujemy (tutaj X jest funkcją oraz y– jej argumentacja). To jest, ![]() i funkcje wzajemnie odwrotne.
i funkcje wzajemnie odwrotne.
Widzimy to z tabeli instrumentów pochodnych ![]() I
I ![]() .
.
Upewnijmy się, że wzory na znalezienie pochodnych funkcji odwrotnej prowadzą nas do tych samych wyników: 
Lekcja i prezentacja na temat: „Liczba e. Funkcja. Wykres. Właściwości”
Dodatkowe materiały
Drodzy użytkownicy, nie zapomnijcie zostawić swoich komentarzy, recenzji i życzeń! Wszystkie materiały zostały sprawdzone programem antywirusowym.
Pomoce dydaktyczne i symulatory w sklepie internetowym Integral dla klasy 11
Podręcznik interaktywny dla klas 9–11 „Trygonometria”
Podręcznik interaktywny dla klas 10–11 „Logarity”
Chłopaki, dzisiaj przestudiujemy specjalną liczbę. Zajmuje osobne miejsce w matematyce „dla dorosłych” i ma wiele niezwykłych właściwości, z których niektóre rozważymy.
Wróćmy do funkcji wykładniczych $y=a^x$, gdzie $a>1$. Możemy wykreślić wiele różnych wykresów funkcji dla różnych baz.
Ale należy zauważyć, że:
- wszystkie funkcje przechodzą przez punkt (0;1),
- dla $x→-∞$ wykres ma asymptotę poziomą $y=0$,
- wszystkie funkcje rosną i są wypukłe w dół,
- a także ciągłe, co z kolei oznacza, że są one różniczkowalne.
Rozważmy funkcję $y=2^x$ i skonstruujmy do niej styczną.
Po dokładnym narysowaniu naszych wykresów widać, że kąt nachylenia stycznej wynosi 35°.
Teraz narysujmy funkcję $y=3^x$ i wykreślmy także linię styczną: 
Tym razem kąt styczny wynosi około 48°. Ogólnie rzecz biorąc, warto zauważyć: im większa podstawa funkcja wykładnicza, tym większy kąt nachylenia.
Szczególnie interesująca jest styczna o kącie nachylenia równym 45°. Do wykresu jakiej funkcji wykładniczej można poprowadzić taką styczną w punkcie (0;1)?
Podstawa funkcji wykładniczej musi być większa niż 2, ale mniejsza niż 3, ponieważ wymagany kąt styczny osiąga się gdzieś pomiędzy funkcjami $y=2^x$ i $y=3^x$. Znaleziono taką liczbę i okazała się ona dość unikalna.
Funkcję wykładniczą, w której styczna przechodząca przez punkt (0;1) ma kąt nachylenia równy 45°, zwykle oznaczamy przez: $y=e^x$ .
Podstawą naszej funkcji jest Liczba niewymierna. Matematycy obliczyli przybliżoną wartość tej liczby $e=2,7182818284590…$.
Na szkolnych lekcjach matematyki zwyczajowo zaokrągla się liczbę do najbliższej części dziesiątej, czyli $e=2,7$.
Zbudujmy wykres funkcji $y=e^x$ i styczną do tego wykresu. 
Nasza funkcja jest zwykle nazywana wykładniczą.
Własności funkcji $y=e^x$.
1. $D(f)=(-∞;+∞)$.
2. Nie jest ani parzysty, ani nieparzysty.
3. Przyrosty w całym zakresie definicji.
4. Nieograniczony z góry, ograniczony z dołu.
5. Największa wartość NIE, najniższa wartość NIE.
6. Ciągłe.
7. $E(f)=(0; +∞)$.
8. Wypukły w dół.
W matematyce wyższej udowodniono, że funkcja wykładnicza jest różniczkowalna wszędzie, a jej pochodna jest równa samej funkcji: $(e^x)"=e^x$.
Nasza funkcja jest szeroko stosowana w wielu obszarach matematyki (w analizie matematycznej, w teorii prawdopodobieństwa, w programowaniu) i wiele obiektów rzeczywistych jest powiązanych z tą liczbą.
Przykład.
Znajdź styczną do wykresu funkcji $y=e^x$ w punkcie $x=2$.
Rozwiązanie.
Równanie styczne opisuje wzór: $y=f(a)+f"(a)(x-a)$.
Kolejno znajdujemy wymagane wartości:
1. $f(a)=f(2)=e^2$.
2. $f"(a)=e^a$.
3. $f"(2)=e^2$.
4. $y=f(a)+f"(a)(x-a)=e^2+e^2(x-2)=e^2*x-e^2$.
Odpowiedź: $y=e^2*x-e^2$
Przykład.
Znajdź wartość pochodnej funkcji $y=e^(3x-15)$ w punkcie $x=5$.
Rozwiązanie.
Przypomnijmy sobie zasadę różniczkowania funkcji w postaci $y=f(kx+m)$.
$y"=k*f"(kx+m)$.
W naszym przypadku $f(kx+m)=e^(3x-15)$.
Znajdźmy pochodną:
$y"=(e^(3x-15))"=3*e^(3x-15)$.
$y"(5)=3*e^(15-15)=3*e^0=3$.
Odpowiedź: 3.
Przykład.
Sprawdź funkcję $y=x^3*e^x$ pod kątem ekstremów.
Rozwiązanie.
Znajdźmy pochodną naszej funkcji $y"=(x^3*e^x)"=(x^3)"*e^x+x^3(e^x)"=3x^2*e^x +x^ 3*e^x=x^2*e^x(x+3)$.
Funkcja nie ma punktów krytycznych, ponieważ pochodna istnieje dla dowolnego x.
Przyrównując pochodną do 0, otrzymujemy dwa pierwiastki: $x_1=0$ i $x_2=-3$.
Zaznaczmy nasze punkty na osi liczbowej: 
Problemy do samodzielnego rozwiązania
1. Znajdź styczną do wykresu funkcji $y=e^(2x)$ w punkcie $x=2$.2. Znajdź wartość pochodnej funkcji $y=e^(4x-36)$ w punkcie $x=9$.
3. Zbadaj ekstrema w funkcji $y=x^4*e^(2x)$.
Aby skorzystać z podglądu prezentacji utwórz konto Google i zaloguj się na nie: https://accounts.google.com
Podpisy slajdów:
POCHODNA FUNKCJI WYKŁADNICZEJ Liczba e Stopień 11
POWTARZANIE jest matką nauki!
Definicja funkcji wykładniczej Funkcja, podane przez wzór y = a x (gdzie a > 0, a ≠ 1) nazywa się funkcją wykładniczą o podstawie a.
Własności funkcji wykładniczej y = a x a>1 0
Wyznaczanie pochodnej funkcji w punkcie x 0. jako Δ → 0. Pochodna funkcji f w punkcie x 0 jest liczbą, do której stosunek różnicy zmierza jako Δx → 0.
Znaczenie geometryczne pochodnej x ₀ α A y = f(x) 0 x y к = tan α = f "(x ₀) Współczynnik kąta do stycznej do wykresu funkcji f (x) w punkcie (x 0 ; f (x 0) jest równe funkcjom pochodnym f "(x ₀). f(x 0)
Gra: „Znajdź pary” (u + v)” cos x e (u v)” n xⁿ ⁻” p (u / v)” - 1 /(sin² x) a (x ⁿ)” - sin x n C „u” v +u v" do (C u)" 1 / (cos ² x) t (sin x)" (u" v – u v") / v² c (cos x)" 0 o (tg x)" u " + v " e (ctg x) " C u " rz
Sprawdź się! (u + v)" u" + v" e (u v)" u" v + u v "to (u /v)" (u' v –u v") / v² s (x ⁿ)" n x ⁿ ⁻¹ p C" 0 o (Cu)" C u " n (sin x)" Cos x e (cos x)" - sin x n (tg x)" 1 / (cos² x) t (ctg x)" - 1 / (sin² x ) A
Wykładnik jest funkcja zasilania. Wykładnik jest funkcją, gdzie e jest podstawą logarytmów naturalnych.
1 y= e x 45° Funkcja y= e x nazywana jest „wykładnikiem” x ₀ =0; tg 45° = 1 W punkcie (0;1) nachylenie stycznej do wykresu funkcji k = tg 45° = 1 - znaczenie geometryczne pochodna wykładnika Wykładnik y = e x
Twierdzenie 1. Funkcja y = e jest różniczkowalna w każdym punkcie dziedziny definicji, oraz (e)" = e x x x Logarytm naturalny (ln) to logarytm o podstawie e: ln x = log x e Funkcja wykładnicza jest różniczkowalna w każdym punkcie dziedziny definicji oraz (a)” = a ∙ ln a x x Twierdzenie 2.
Wzory na różniczkowanie funkcji wykładniczej (e)" = e ; (e)" = k e ; (a)" = za ∙ ln za; (a)" = k za ∙ ln za. x kx + b x x x kx + b kx + b kx + b F(a x) = + C; F(e x) = mi x +C.
„Ćwiczenia rodzą mistrzostwo”. Tacyt Publiusz Korneliusz – historyk starożytnego Rzymu
Przykłady: Znajdź pochodne funkcji: 1. = 3 e. 2. (e)" = (5x)" e = 5 e. 3. (4)" = 4 ln 4. 4. (2)" = (-7 x)" 2 ∙ ln 2 = -7 ∙ 2 ∙ ln 2. 5 x 5 x x (3 e)" 5 x - 7 x x x -7 x -7 x x
Ciekawe rzeczy w pobliżu
Leonhard Euler 1707-1783 Rosyjski naukowiec - matematyk, fizyk, mechanik, astronom... Wprowadził oznaczenie liczby e. Udowodnił, że liczba e ≈ 2, 718281... jest niewymierna. Jan Napier 1550 – 1617 Szkocki matematyk, wynalazca logarytmów. Na jego cześć liczbę e nazwano „liczbą Nepera”.
Wzrost i zanik funkcji w tempie wykładniczym nazywa się wykładniczym
Cele Lekcji: stworzyć wyobrażenie o liczbie mi; udowodnić różniczkowalność funkcji w dowolnym punkcie X;rozważ dowód twierdzenia o różniczkowalności funkcji; sprawdzenie dojrzałości umiejętności i zdolności przy rozwiązywaniu przykładów ich zastosowania.
Cele Lekcji.
Edukacyjne: powtórz definicję pochodnej, zasady różniczkowania, pochodną funkcji elementarnych, zapamiętaj wykres i własności funkcji wykładniczej, rozwijaj umiejętność znajdowania pochodnej funkcji wykładniczej, sprawdź wiedzę za pomocą zadania testowego i testu test.
Rozwojowe: promują rozwój uwagi, rozwój logicznego myślenia, intuicji matematycznej, umiejętności analizowania i stosowania wiedzy w niestandardowych sytuacjach.
Edukacyjne: kultywowanie kultury informacyjnej, rozwijanie umiejętności pracy w grupie i indywidualnie.
Metody nauczania: werbalne, wizualne, aktywne.
Formy szkolenia: zbiorowe, indywidualne, grupowe.
Sprzęt : podręcznik „Algebra i początki analizy” (pod red. Kołmogorowa), wszystkie zadania grupy B „Odcinek zamknięty” pod red. A.L. Semenova, I.V. Yashchenko, projektor multimedialny.
Kroki lekcji:
- Omówienie tematu, celu i celów lekcji (2 min.).
- Przygotowanie do nauki nowego materiału poprzez powtarzanie poznanego materiału (15 min.).
- Wprowadzenie do nowego materiału (10 min.)
- Wstępne zrozumienie i utrwalenie nowej wiedzy (15 min.).
- Zadanie domowe (1 min.).
- Podsumowanie (2 min.).
Podczas zajęć
1. Moment organizacyjny.
Ogłasza się temat lekcji: „Pochodna funkcji wykładniczej. Liczba e.”, cele, cele. Slajd 1. Prezentacja
2. Aktywizacja wiedzy wspierającej.
Aby to zrobić, w pierwszym etapie lekcji odpowiemy na pytania i rozwiążemy problemy z powtórkami. Slajd 2.
Przy tablicy dwójka uczniów pracuje nad kartkami, wykonując zadania takie jak B8 Unified State Examination.
Zadanie dla pierwszego ucznia:
Zadanie dla drugiego ucznia:

Pozostali uczniowie wykonują samodzielną pracę według następujących opcji:
| opcja 1 | Opcja 2 | ||
| 1. |  |
1. |  |
| 2. |  |
2. |  |
| 3. |  |
3. |  |
| 4. |  |
4. |  |
| 5. |  |
5. |  |
Pary wymieniają się rozwiązaniami i sprawdzają nawzajem swoje prace, sprawdzając odpowiedzi na slajdzie 3.
Brane są pod uwagę rozwiązania i odpowiedzi uczniów pracujących w tablicy.
Badanie Praca domowa Nr 1904. Pokazano slajd 4.
3. Aktualizacja tematu lekcji, stworzenie sytuacji problemowej.
Nauczyciel prosi o zdefiniowanie funkcji wykładniczej i podanie własności funkcji y = 2 x. Wykresy funkcji wykładniczych przedstawiono w postaci gładkich linii, do których w każdym punkcie można poprowadzić styczną. Ale istnienie stycznej do wykresu funkcji w punkcie o odciętej x 0 jest równoważne jej różniczkowalności w x 0.
Dla wykresów funkcji y = 2 x i y = 3 x rysujemy do nich styczne w punkcie o odciętej 0. Kąty nachylenia tych stycznych do osi odciętych wynoszą w przybliżeniu odpowiednio 35° i 48° . Slajd 5.
Wniosek: jeśli podstawa funkcji wykładniczej A wzrasta od 2 do np. 10, wówczas kąt pomiędzy styczną do wykresu funkcji w punkcie x = 0 a osią x stopniowo rośnie od 35° do 66,5°. Logiczne jest założenie, że istnieje powód A, dla którego odpowiedni kąt wynosi 45
Udowodniono, że istnieje liczba większa od 2 i mniejsza od 3. Zwykle oznacza się ją literą mi. W matematyce ustalono, że liczba mi– irracjonalne, tj. reprezentuje nieskończony dziesiętny ułamek nieokresowy.
e = 2,7182818284590…
Uwaga (niezbyt poważna). Slajd 6.
Na kolejnym slajdzie 7 pojawiają się portrety wielkich matematyków – Johna Napiera, Leonharda Eulera i krótka informacja o nich.
- Rozważmy własności funkcji y=e x
- Dowód twierdzenia 1. Slajd 8.
- Dowód twierdzenia 2. Slajd 9.
4. Dynamiczna pauza lub relaks dla oczu.
(Pozycja wyjściowa – siedząca, każde ćwiczenie powtarzamy 3-4 razy):
1. Odchylając się do tyłu, weź głęboki oddech, a następnie pochylając się do przodu, wykonaj wydech.
2. Opierając się na krześle, zamknij powieki, zamknij mocno oczy, nie otwierając powiek.
3. Ramiona wzdłuż ciała, okrężne ruchy barków w przód i w tył.
5. Utrwalenie badanego materiału.
5.1 Rozwiązanie ćwiczeń nr 538, nr 540, nr 544c.
5.2 Samodzielne wykorzystanie wiedzy, umiejętności i zdolności. Praca weryfikacyjna w formie testu. Czas wykonania zadania – 5 minut.
Kryteria oceny:
„5” – 3 punkty
„4” – 2 punkty
„3” - 1 punkt
6. Podsumowanie wyników pracy na lekcji.
- Odbicie.
- Cieniowanie.
- Przesyłanie zadań testowych.
7. Praca domowa: paragraf 41 (1, 2); nr 539 (a, b, d); 540 (c, d), 544 (a, b).
„Odcinek zamknięty” nr 1950, 2142.
Wykres funkcji wykładniczej jest zakrzywioną, gładką linią bez załamań, do której można poprowadzić styczną w każdym punkcie, przez który ona przechodzi. Logiczne jest założenie, że jeśli można narysować styczną, to funkcja będzie różniczkowalna w każdym punkcie swojej dziedziny definicji.
Będziemy wyświetlać w niektórych osie współrzędnych kilka wykresów funkcji y = x a, Dla a = 2; a = 2,3; a = 3; a = 3,4.
W punkcie o współrzędnych (0;1). Kąty tych stycznych będą wynosić odpowiednio około 35, 40, 48 i 51 stopni. Logiczne jest założenie, że w przedziale od 2 do 3 znajduje się liczba, przy której kąt nachylenia stycznej będzie równy 45 stopni.
Podajmy precyzyjne sformułowanie tego stwierdzenia: istnieje liczba większa od 2 i mniejsza od 3, oznaczona literą e, taka, że funkcja wykładnicza y = e x w punkcie 0 ma pochodną równą 1. Czyli: (e ∆x -1) / ∆x dąży do 1, gdy ∆x dąży do zera.
Ten numer mi jest niewymierny i jest zapisywany jako nieskończony nieokresowy ułamek dziesiętny:
e = 2,7182818284…
Ponieważ e jest dodatnie i niezerowe, istnieje logarytm o podstawie e. Ten logarytm nazywa się naturalny logarytm . Oznaczone przez ln(x) = log e (x).
Pochodna funkcji wykładniczej
Twierdzenie: Funkcja e x jest różniczkowalna w każdym punkcie swojej dziedziny definicji, oraz (e x)’ = e x.
Funkcja wykładnicza a x jest różniczkowalna w każdym punkcie swojej dziedziny definicji, oraz (a x)’ = (a x)*ln(a).
Konsekwencją tego twierdzenia jest fakt, że funkcja wykładnicza jest ciągła w dowolnym punkcie swojej dziedziny definicji.
Przykład: znajdź pochodną funkcji y = 2 x.
Korzystając ze wzoru na pochodną funkcji wykładniczej otrzymujemy:
(2 x)’ = (2 x)*ln(2).
Odpowiedź: (2 x)*ln(2).
Funkcja pierwotna funkcji wykładniczej
Dla funkcji wykładniczej a x określonej na zbiorze liczb rzeczywistych funkcją pierwotną będzie funkcja (a x)/(ln(a)).
ln(a) jest pewną stałą, wówczas (a x / ln(a))’= (1 / ln(a)) * (a x) * ln(a) = a x dla dowolnego x. Udowodniliśmy to twierdzenie.
Rozważmy przykład znalezienia funkcji pierwotnej funkcji wykładniczej.
Przykład: znajdź funkcję pierwotną funkcji f(x) = 5 x. Skorzystajmy ze wzoru podanego powyżej i zasad znajdowania funkcji pierwotnych. Otrzymujemy: F(x) = (5 x) / (ln(5)) +C.