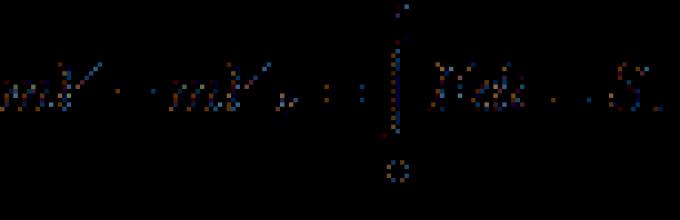(Fragmenty symfonii matematycznej)

Związek impulsu siły z podstawowym równaniem dynamiki Newtona wyraża twierdzenie o zmianie pędu punktu materialnego.

Twierdzenie. Zmiana pędu punktu materialnego w pewnym okresie czasu jest równa impulsowi siły () działającej na punkt materialny w tym samym okresie czasu. Dowód matematyczny tego twierdzenia można nazwać fragmentem symfonii matematycznej. Tutaj jest.

Różnicowy pęd punktu materialnego jest równy elementarnemu impulsowi siły działającej na punkt materialny. Mamy wyrażenie całkujące (128) dla pędu różniczkowego punktu materialnego

(129)

Twierdzenie zostało udowodnione i matematycy uważają swoją misję za zakończoną, ale inżynierowie, których przeznaczeniem jest święta wiara w matematyków, mają pytania, gdy korzystają ze sprawdzonego równania (129). Blokuje je jednak stanowczo kolejność i piękno operacji matematycznych (128 i 129), które fascynują i zachęcają do nazwania ich fragmentem symfonii matematycznej. Ileż pokoleń inżynierów zgadzało się z matematykami i zachwycało się tajemnicą ich symboli matematycznych! Ale był też inżynier, który nie zgodził się z matematykami i zadał im pytania.

Drodzy matematycy! Dlaczego żaden z Twoich podręczników mechaniki teoretycznej nie omawia procesu zastosowania Twojego symfonicznego wyniku (129) w praktyce, na przykład przy opisie procesu przyspieszania samochodu? Lewa strona równania (129) jest bardzo jasna. Samochód rozpoczyna przyspieszanie od prędkości i kończy je np. przy prędkości. Jest całkiem naturalne, że równanie (129) staje się

I od razu pojawia się pierwsze pytanie: jak z równania (130) wyznaczyć siłę, pod wpływem której samochód rozpędza się do prędkości 10 m/s? Odpowiedzi na to pytanie nie znajdziemy w żadnym z niezliczonych podręczników mechaniki teoretycznej. Idźmy dalej. Po przyspieszeniu samochód zaczyna poruszać się równomiernie z prędkością 10 m/s. Jaka siła porusza samochód???????? Nie pozostaje mi nic innego, jak zarumienić się razem z matematykami. Pierwsza zasada dynamiki Newtona mówi, że gdy samochód porusza się ruchem jednostajnym, nie działają na niego żadne siły, a samochód, mówiąc w przenośni, kicha na to prawo, zużywa benzynę i pracuje, pokonując np. odległość 100 km. Gdzie jest siła, która wykonała pracę, aby przesunąć samochód na odległość 100 km? Symfoniczne równanie matematyczne (130) milczy, ale życie toczy się dalej i domaga się odpowiedzi. Zaczynamy go szukać.

Ponieważ samochód porusza się prostoliniowo i równomiernie, siła poruszająca nim jest stała pod względem wielkości i kierunku, a równanie (130) przyjmuje postać

(131)

Zatem równanie (131) w tym przypadku opisuje przyspieszony ruch ciała. Jaka jest równa siła? Jak wyrazić jego zmianę w czasie? Matematycy wolą pominąć to pytanie i pozostawić je inżynierom, wierząc, że muszą szukać odpowiedzi na to pytanie. Inżynierom pozostaje jedno wyjście – wziąć pod uwagę, że jeśli po zakończeniu przyspieszonego ruchu ciała rozpocznie się faza równomiernego ruchu, której towarzyszy akcja stała siła przedstawiamy równanie (131) dla momentu przejścia od ruchu przyspieszonego do ruchu jednostajnego w tej postaci

(132)

Strzałka w tym równaniu nie oznacza wyniku całkowania tego równania, ale proces przejścia od jego postaci całkowej do postaci uproszczonej. Siła w tym równaniu jest równa średniej sile, która zmieniła pęd ciała od zera do wartości końcowej. Tak więc, drodzy matematycy i fizycy teoretyczni, brak waszej metody określania wielkości waszego impulsu zmusza nas do uproszczenia procedury wyznaczania siły, a brak metody określania czasu działania tej siły generalnie stawia nas w trudnej sytuacji. pozycja beznadziejna i zmuszeni jesteśmy posłużyć się wyrażeniem analizującym proces zmiany pędu ciała. W rezultacie im dłużej działa siła, tym większy jest jej impuls. Jest to wyraźnie sprzeczne z ugruntowaną od dawna koncepcją, że im krótszy czas działania, tym większy impuls siły.

Zwróćmy uwagę na fakt, że zmiana pędu punktu materialnego (impulsu siły) podczas jego przyspieszonego ruchu następuje pod wpływem siły newtonowskiej i sił oporu ruchu, w postaci sił generowanych przez opory mechaniczne i siła bezwładności. Jednak dynamika newtonowska w zdecydowanej większości zagadnień ignoruje siłę bezwładności, a mechanodynamika stwierdza, że ​​zmiana pędu ciała podczas jego ruchu przyspieszonego następuje na skutek przewagi siły newtonowskiej nad siłami oporu ruchu, do których zalicza się siła bezwładności.

Kiedy ciało porusza się w zwolnionym tempie, np. samochód z wyłączonym biegiem, nie ma siły Newtona, a zmiana pędu samochodu następuje na skutek przewagi sił oporu ruchu nad siłą bezwładność, która porusza samochód, gdy porusza się powoli.

Jak możemy teraz przywrócić wyniki zauważonych „symfonicznych” działań matematycznych (128) do głównego nurtu związków przyczynowo-skutkowych? Jest tylko jedno wyjście - znaleźć nową definicję pojęć „impuls siły” i „siła uderzenia”. Aby to zrobić, podziel obie strony równania (132) przez czas t. W efekcie będziemy mieli

. (133)

Zauważmy, że wyrażenie mV/t jest szybkością zmiany pędu (mV/t) punktu lub ciała materialnego. Jeśli weźmiemy pod uwagę, że V/t jest przyspieszeniem, to mV/t jest siłą zmieniającą pęd ciała. Ten sam wymiar po lewej i prawej stronie znaku równości daje nam prawo nazwać siłę F siłą uderzeniową i oznaczyć ją symbolem, a impuls S - impulsem uderzeniowym i oznaczyć go symbolem. Prowadzi to do nowej definicji siły uderzenia. Siła uderzenia działająca na punkt lub ciało materialne jest równa stosunkowi zmiany pędu punktu lub ciała materialnego do czasu tej zmiany.

Zwróćmy szczególną uwagę na fakt, że w powstaniu impulsu uderzeniowego (134) uczestniczy wyłącznie siła Newtona, która spowodowała zmianę prędkości samochodu z wartość zerowa do maksimum - , zatem równanie (134) należy w całości do dynamiki Newtona. Ponieważ znacznie łatwiej jest wyznaczyć wielkość prędkości doświadczalnie niż wyznaczyć przyspieszenie, wzór (134) jest bardzo wygodny do obliczeń.

Ten niezwykły wynik wynika z równania (134).

Zwróćmy uwagę, że zgodnie z nowymi prawami mechanodynamiki generatorem impulsu siły podczas przyspieszonego ruchu punktu lub ciała materialnego jest siła Newtona. Tworzy przyspieszenie ruchu punktu lub ciała, przy którym automatycznie powstaje siła bezwładności, skierowana przeciwnie do siły Newtona, a uderzenie Siła Newtona musi pokonać działanie siły bezwładności, dlatego siła bezwładności musi być przedstawiona w postaci bilans sił po lewej stronie równania (134). Ponieważ siła bezwładności jest równa masie punktu lub ciała pomnożonej przez powstałe przez nią opóźnienie, wówczas równanie (134) ma postać

(136)

Drodzy matematycy! Zobacz, jaką formę przybrał model matematyczny, opisujący impuls uderzeniowy, który przyspiesza ruch uderzanego ciała od prędkości zerowej do maksymalnej V (11). Teraz sprawdźmy jego pracę przy wyznaczaniu impulsu uderzenia, który jest równy sile uderzenia, która wystrzeliła 2. blok napędowy SShG (ryc. 120), a pozostawimy cię z bezużytecznym równaniem (132). Aby nie komplikować prezentacji, pozostawimy na razie wzór (134) w spokoju i posłużymy się wzorami, które podają średnie wartości sił. Widzisz na jakiej pozycji stawiasz inżyniera próbującego rozwiązać konkretny problem.

Zacznijmy od dynamiki Newtona. Eksperci ustalili, że drugi blok napędowy wzniósł się na wysokość 14 m. Ponieważ wzniósł się w polu grawitacyjnym, to na wysokości h=14m on energia potencjalna okazało się równe

a średnia energia kinetyczna była równa

Ryż. 120. Zdjęcie turbinowni przed katastrofą

Z równości energii kinetycznej (138) i potencjalnej (137) wynika średnia szybkość wzrostu jednostki napędowej (ryc. 121, 122)

Ryż. 121. Foton turbinowni po katastrofie

Zgodnie z nowymi prawami mechanodynamiki wzrost zespołu napędowego składał się z dwóch faz (ryc. 123): pierwszej fazy OA – przyspieszonego wzrostu i drugiej fazy AB – powolnego wzrostu, , .

Czas i odległość ich działania są w przybliżeniu równe (). Następnie równanie kinematyczne fazy przyspieszonej podnoszenia zespołu napędowego zostanie zapisane w następujący sposób:

. (140)

Ryż. 122. Widok studni bloku energetycznego i samego bloku energetycznego po katastrofie

Prawo zmiany szybkości narastania bloku energetycznego w pierwszej fazie ma postać

. (141)

Ryż. 123. Regularność zmian prędkości lotu V zespołu napędowego

Podstawiając czas z równania (140) do równania (141), mamy

. (142)

Czas podnoszenia bloku w pierwszej fazie wyznacza się ze wzoru (140)

. (143)

Wówczas całkowity czas podniesienia zespołu napędowego na wysokość 14 m będzie równy . Masa zespołu napędowego i pokrywy wynosi 2580 ton. Zgodnie z dynamiką Newtona siła, która podniosła jednostkę napędową, jest równa

Drodzy matematycy!Śledzimy Twoje symfoniczne wyniki matematyczne i zapisujemy Twój wzór (129), zgodnie z dynamiką Newtona, aby określić impuls uderzeniowy, który wystrzelił drugi zespół napędowy

i zadaj podstawowe pytanie: jak ustalić czas trwania impulsu uderzeniowego, który wystrzelił 2. blok napędowy????????????

Droga!!! Pamiętajcie, ile kredy napisały na tablicach pokolenia waszych kolegów, w zawiły sposób ucząc uczniów, jak określić impuls uderzeniowy, a nikt nie wyjaśnił, jak określić czas trwania impulsu uderzeniowego w każdym konkretnym przypadku. Powiecie, że czas trwania impulsu uderzeniowego jest równy odstępowi czasu zmiany prędkości zespołu napędowego od zera do, założymy, maksymalnej wartości 16,75 m/s (139). Jest we wzorze (143) i wynosi 0,84 s. Na razie się z Tobą zgadzamy i określamy średnią wartość impulsu uderzeniowego

Natychmiast pojawia się pytanie: dlaczego wielkość impulsu uderzeniowego (146) jest mniejsza niż siła Newtona wynosząca 50600 ton? Wy, drodzy matematycy, nie macie odpowiedzi. Idźmy dalej.

Zgodnie z dynamiką Newtona, główna siła, który oparł się wzrostowi jednostki napędowej, jest siłą grawitacji. Ponieważ siła ta jest skierowana przeciw ruchowi jednostki napędowej, generuje ona opóźnienie, które jest równe przyspieszeniu swobodny spadek. Wtedy siła grawitacji działająca na lecący w górę zespół napędowy jest równa

Dynamika Newtona nie uwzględnia innych sił, które uniemożliwiły działanie siły Newtona o masie 50 600 ton (144), a mechanodynamika stwierdza, że ​​wzrostowi zespołu napędowego przeciwstawiła się także siła bezwładności równa

Natychmiast pojawia się pytanie: jak znaleźć wielkość opóźnienia w ruchu jednostki napędowej? Dynamika Newtona milczy, ale odpowiada mechanodynamika: w momencie działania siły Newtona, która uniosła jednostkę napędową, stawiały jej opór: siła ciężkości i siła bezwładności, stąd równanie sił działających na moc jednostka w tym momencie jest zapisana w następujący sposób.

Ilość miary ruchu ruch mechaniczny, jeśli ruch mechaniczny zamienia się w mechaniczny. Na przykład mechaniczny ruch kuli bilardowej (ryc. 22) przed uderzeniem zamienia się w mechaniczny ruch kul po uderzeniu. Dla punktu pęd jest równy iloczynowi.

Miarą siły w tym przypadku jest impuls siły

. (9.1)

Pęd określa działanie siły przez pewien okres czasu . Dla punktu materialnego twierdzenie o zmianie pędu można zastosować w formie różniczkowej
(9.2) lub postać całkowa (skończona).
. (9.3)

Zmiana pędu punktu materialnego w pewnym okresie czasu jest równa impulsowi wszystkich sił przyłożonych do tego punktu w tym samym czasie.

Rysunek 22

Podczas rozwiązywania problemów Twierdzenie (9.3) jest częściej stosowane w rzutach na osie współrzędnych
;

; (9.4)

.

Korzystając z twierdzenia o zmianie pędu punktu, można rozwiązać problemy, w których na punkt lub ciało poruszające się translacyjnie działają stałe lub zmienne siły zależne od czasu, a do zadanych i poszukiwanych wielkości zalicza się czas ruchu oraz prędkości na początku i na końcu ruchu. Problemy z wykorzystaniem twierdzenia rozwiązuje się w następującej kolejności:

1. wybrać układ współrzędnych;

2. przedstawić wszystkie dane (czynne) siły i reakcje działające na punkt;

3. zapisać twierdzenie o zmianie pędu punktu w rzutach na wybrane osie współrzędnych;

4. określić wymagane ilości.

PRZYKŁAD 12.

Młotek o masie G=2t spada z wysokości h=1m na obrabiany przedmiot w czasie t=0,01s i stempluje część (rys. 23). Określ średnią siłę nacisku młotka na przedmiot obrabiany.

ROZWIĄZANIE.

1. Na obrabiany przedmiot działa siła ciężkości młotka i reakcja podłoża . Wielkość reakcji wsparcia zmienia się w czasie, dlatego rozważmy jej średnią wartość
.

2. skieruj oś współrzędnych y pionowo w dół i zastosuj twierdzenie o zmianie pędu punktu w rzucie na tę oś:
, (1) gdzie -- prędkość młota na końcu uderzenia;

- prędkość początkowa młotka w momencie kontaktu z przedmiotem.

3. Aby określić prędkość pogódźmy się równanie różniczkowe ruch młotka w rzucie na oś Y:

. (2)

Rozdzielmy zmienne i całkujmy równanie (2) dwukrotnie:
;

;

. Z warunków początkowych znajdujemy stałe całkowania C 1, C 2. Przy t=0 V y =0, wówczas C1 =0; y=0, wówczas C2=0. Dlatego młot porusza się zgodnie z prawem
, (3) a prędkość młota zmienia się zgodnie z prawem
. (4) Wyraźmy czas ruchu młotka z (3) i podstawmy go do (4)
;
. (5)

4. Rzut impulsu sił zewnętrznych na oś y wyznaczamy ze wzoru:
. (6) Zastąp (5) i (6) w (1):
, skąd znajdziemy reakcję podpory, a co za tym idzie pożądany nacisk młotka na obrabiany przedmiot
T.

Rysunek 24

 DO

gdzie M jest masą układu, Vc jest prędkością środek masy. Twierdzenie o zmianie pędu układu mechanicznego można zapisać w postaci różniczkowej i skończonej (całkowej):
;

. (9.7)

 Wielkość ruchu układu mechanicznego można zdefiniować jako sumę wielkości ruchu punktów układu
. (9.5) Pęd układu lub ciała sztywnego można wyznaczyć znając masę układu i prędkość środka masy
, (9.6)

Zmiana pędu układu mechanicznego w pewnym okresie czasu jest równa sumie impulsów sił zewnętrznych działających w tym samym czasie. Czasami wygodniej jest zastosować twierdzenie o zmianie pędu w rzucie na osie współrzędnych
; (9.8)
. (9.9)

Prawo zachowania pędu mówi, że w przypadku braku sił zewnętrznych pęd układu mechanicznego pozostaje stały. Działanie siły wewnętrzne nie może zmienić pędu układu. Z równania (9.6) wynika, że ​​kiedy
,
.

Jeśli
, To
Lub
.

D

śmigło lub śmigło, napęd odrzutowy. Kałamarnice poruszają się gwałtownie, wyrzucając wodę z worka mięśniowego niczym armata wodna (ryc. 25). Odpychana woda ma pewien ruch skierowany do tyłu. Kałamarnica otrzymuje odpowiednią prędkość ruch do przodu dzięki reaktywnej sile uciągu , ponieważ zanim kałamarnica wyskoczy z siły zrównoważony grawitacją .

Działanie prawa zachowania pędu układu mechanicznego można zilustrować na przykładzie zjawiska odrzutu lub cofania się podczas strzelania, pracy

Zastosowanie twierdzenia o zmianie pędu pozwala na wyłączenie z rozważań wszelkich sił wewnętrznych.

PRZYKŁAD 13.

Wciągarka A z bębnem o promieniu r jest zainstalowana na peronie kolejowym wolnostojącym na szynach (rys. 26). Wciągarka przeznaczona jest do przemieszczania po platformie ładunku B o masie m 1. Masa platformy z wciągarką m 2. Bęben wciągarki obraca się zgodnie z prawem
. W początkowej chwili system był mobilny. Pomijając tarcie, znajdź prawo zmiany prędkości platformy po włączeniu wciągarki.

R ROZWIĄZANIE.

1. Rozważ platformę, wciągarkę i ładunek jako pojedynczy układ mechaniczny, któremu podlega siły zewnętrzne: obciążenie grawitacyjne i platformy i reakcje I
.

2. Ponieważ wszystkie siły zewnętrzne są prostopadłe do osi x, tj.
, stosujemy zasadę zachowania pędu układu mechanicznego w rzucie na oś x:
. W początkowej chwili układ był nieruchomy, zatem

Wyraźmy wielkość ruchu układu w dowolnym momencie. Platforma porusza się do przodu z dużą prędkością ładunek podlega złożonemu ruchowi polegającemu na ruchu względnym po platformie z określoną prędkością i przenośny ruch wraz z platformą z dużą prędkością ., Gdzie
. Platforma będzie poruszać się w kierunku przeciwnym do względnego ruchu ładunku.

PRZYKŁAD 14.

M

ROZWIĄZANIE.

1. Zastosujmy twierdzenie o zmianie pędu układu mechanicznego w rzucie na oś x. Ponieważ wszystkie siły zewnętrzne działające na układ są zatem pionowe
, Następnie
, Gdzie
. (1)

2. Wyraźmy rzut pędu na oś x dla rozpatrywanego układu mechanicznego
,

 Układ mechaniczny składa się z prostokątnej pionowej płyty 1 o masie m 1 = 18 kg, poruszającej się po poziomych prowadnicach i ładunku D o masie m 2 = 6 kg. W chwili t 0 =0, gdy płyta poruszała się z prędkością u 0 =2m/s, obciążenie zaczęło przemieszczać się wzdłuż rowu zgodnie z równaniem S=AD=0,4sin( t 2) (S-w metrach, t-w sekundach), (ryc. 26). Wyznacz prędkość płyty w czasie t 1 = 1s, korzystając z twierdzenia o zmianie pędu układu mechanicznego.

Gdzie ,
- wielkość ruchu odpowiednio płyty i obciążenia.


;
, Gdzie --bezwzględna prędkość ładunku D. Z równości (1) wynika, że ​​K 1x + K 2x =C 1 lub m 1 u x +m 2 V Dx =C 1. (2) Aby wyznaczyć V Dx, należy uznać ruch ładunku D za złożony, biorąc pod uwagę jego ruch względem płyty oraz ruch samej płyty przenośnej, a następnie
, (3)
;lub w rzucie na oś x: . (4) Podstawmy (4) do (2):
. (5) Stałą całkowania C 1 wyznaczamy z warunków początkowych: przy t=0 u=u 0 ; (m 1 + m 2) u 0 = C 1. (6) Podstawiając wartość stałej C 1 do równania (5) otrzymujemy

SM.

W przypadku punktu materialnego podstawową zasadę dynamiki można przedstawić jako

Mnożąc obie strony tej relacji po lewej stronie wektorowo przez wektor promienia (ryc. 3.9), otrzymujemy

(3.32)

Po prawej stronie tego wzoru mamy moment siły względem punktu O. Lewą stronę przekształcamy stosując wzór na pochodną iloczynu wektorowego

Ale Jak produkt wektorowy wektory równoległe. Po tym otrzymujemy

(3.33)

Pierwsza pochodna po czasie momentu pędu punktu względem dowolnego środka jest równa momentowi siły względem tego samego środka.


Przykład obliczenia momentu pędu układu. Oblicz moment kinetyczny względem punktu O układu składającego się z cylindrycznego wału o masie M = 20 kg i promieniu R = 0,5 m oraz opadającego obciążenia o masie m = 60 kg (rysunek 3.12). Wał obraca się wokół osi Oz z prędkością kątową ω = 10 s -1.

Rysunek 3.12

; ;

Dla danych wejściowych moment pędu układu

Twierdzenie o zmianie momentu pędu układu. Przykładamy wypadkowe siły zewnętrzne i wewnętrzne do każdego punktu układu. Dla każdego punktu układu można zastosować twierdzenie o zmianie momentu pędu, np. w postaci (3.33)

Sumując po wszystkich punktach układu i biorąc pod uwagę, że suma pochodnych jest równa pochodnej sumy, otrzymujemy

Poprzez określenie momentu kinetycznego układu oraz właściwości sił zewnętrznych i wewnętrznych

Dlatego powstałą relację można przedstawić jako

Pierwsza pochodna momentu pędu układu względem dowolnego punktu jest równa głównemu momentowi sił zewnętrznych działających na układ względem tego samego punktu.

3.3.5. Praca siły

1) Elementarna praca siły jest równa iloczynowi skalarnemu siły i promieniowi różniczkowemu wektora punktu przyłożenia siły (ryc. 3.13)

Rysunek 3.13

Wyrażenie (3.36) można również zapisać w następujących równoważnych formach

gdzie jest rzutem siły na kierunek prędkości punktu przyłożenia siły.

2) Praca siły przy przemieszczeniu końcowym

Całkując elementarną pracę siły, otrzymujemy następujące wyrażenia na pracę siły przy końcowym przemieszczeniu z punktu A do punktu B

3) Praca stałej siły

Jeśli siła jest stała, to wynika z (3.38).

Praca stałej siły nie zależy od kształtu trajektorii, lecz zależy jedynie od wektora przemieszczenia punktu przyłożenia siły.

4) Praca siły ciężaru

Dla siły ciężaru (ryc. 3.14) i z (3.39) otrzymujemy

Rysunek 3.14

Jeśli ruch następuje z punktu B do punktu A, to

Ogólnie

Znak „+” odpowiada ruchowi punktu przyłożenia siły w dół, znak „-” – w górę.

4) Praca siły sprężystej

Niech oś sprężyny będzie skierowana wzdłuż osi x (ryc. 3.15), a koniec sprężyny przesuwa się z punktu 1 do punktu 2, a następnie z (3.38) otrzymujemy

Jeśli sztywność sprężyny wynosi Z, a następnie

A (3.41)

Jeśli koniec sprężyny przesunie się z punktu 0 do punktu 1, to w tym wyrażeniu zastępujemy , , wówczas praca siły sprężystej będzie miała postać

(3.42)

gdzie jest wydłużenie sprężyny.

Rysunek 3.15

5) Praca siły przyłożonej do obracającego się ciała. Praca chwili.

Na ryc. Rysunek 3.16 przedstawia obracający się korpus, do którego przykładana jest dowolna siła. Podczas obrotu punkt przyłożenia tej siły porusza się po okręgu.

Niech punkt materialny porusza się pod wpływem siły F. Wymagane jest określenie ruchu tego punktu względem poruszającego się układu Oksyz(patrz ruch złożony punktu materialnego), który porusza się w znany sposób względem układu stacjonarnego O 1 X 1 y 1 z 1 .

Podstawowe równanie dynamiki układu stacjonarnego

Zapiszmy bezwzględne przyspieszenie punktu, korzystając z twierdzenia Coriolisa

Gdzie A abs– przyspieszenie bezwzględne;

A wzgl– przyspieszenie względne;

A uliczka– akceleracja przenośna;

A rdzeń– Przyspieszenie Coriolisa.

Przepiszmy (25) biorąc pod uwagę (26)

Wprowadźmy notację
- przenośna siła bezwładności,
- Siła bezwładności Coriolisa. Wtedy równanie (27) przyjmuje postać

Podstawowe równanie dynamiki do badania ruchu względnego (28) zapisuje się analogicznie jak dla ruchu absolutnego, z tym że do sił działających na punkt należy dodać jedynie przeniesienie i siły bezwładności Coriolisa.

Ogólne twierdzenia o dynamice punktu materialnego

Rozwiązując wiele problemów, możesz użyć gotowych półfabrykatów uzyskanych na podstawie drugiego prawa Newtona. W tej sekcji zestawiono takie metody rozwiązywania problemów.

Twierdzenie o zmianie pędu punktu materialnego

Przedstawmy następujące charakterystyki dynamiczne:

1. Pęd punktu materialnego – wielkość wektorowa równy iloczynowi masy punktu i jego wektora prędkości


. (29)

2. Impuls siły

Elementarny impuls siły– wielkość wektora równa iloczynowi wektora siły i elementarnego przedziału czasu


(30).

Następnie pełen impuls

. (31)

Na F=stała, którą otrzymujemy S=Ft.

Impuls całkowity w skończonym czasie można obliczyć tylko w dwóch przypadkach, gdy siła działająca na punkt jest stała lub zależy od czasu. W innych przypadkach konieczne jest wyrażenie siły w funkcji czasu.

Równość wymiarów impulsu (29) i pędu (30) pozwala ustalić między nimi związek ilościowy.

Rozważmy ruch punktu materialnego M pod działaniem dowolnej siły F po dowolnej trajektorii.

O U:
. (32)

Rozdzielamy zmienne w (32) i całkujemy

. (33)

W rezultacie, biorąc pod uwagę (31), otrzymujemy

. (34)

Równanie (34) wyraża następujące twierdzenie.

Twierdzenie: Zmiana pędu punktu materialnego w pewnym okresie czasu jest równa impulsowi siły działającej na ten punkt w tym samym przedziale czasu.

Podczas rozwiązywania problemów równanie (34) należy rzutować na osie współrzędnych

Twierdzenie to jest wygodne w użyciu, gdy wśród danych i nieznanych wielkości znajduje się masa punktu, jego początkowa i prędkość końcowa, siły i czas ruchu.

Twierdzenie o zmianie momentu pędu punktu materialnego

M
moment pędu punktu materialnego względem środka jest równy iloczynowi modułu pędu punktu i ramienia, tj. najkrótsza odległość (prostopadła) od środka do linii zbiegającej się z wektor prędkości

, (36)

. (37)

Związek między momentem siły (przyczyną) a momentem pędu (skutkiem) ustala następujące twierdzenie.

Niech punkt M danej masy M porusza się pod wpływem siły F.

,
,

, (38)

. (39)

Obliczmy pochodną (39)

. (40)

Łącząc (40) i (38) ostatecznie otrzymujemy

. (41)

Równanie (41) wyraża następujące twierdzenie.

Twierdzenie: Pochodna po czasie wektora pędu punktu materialnego względem jakiegoś środka jest równa momentowi siły działającej na punkt względem tego samego środka.

Podczas rozwiązywania problemów równanie (41) należy rzutować na osie współrzędnych

W równaniach (42) momenty pędu i siły obliczane są względem osi współrzędnych.

Z (41) wynika prawo zachowania momentu pędu (prawo Keplera).

Jeżeli moment siły działający na punkt materialny względem dowolnego środka wynosi zero, wówczas moment pędu punktu względem tego środka zachowuje swoją wielkość i kierunek.

Jeśli
, To
.

Twierdzenie i prawo zachowania są używane w problemach obejmujących ruch krzywoliniowy zwłaszcza pod działaniem sił centralnych.

Wielkość ruchu układu jako wielkość wektorową wyznaczają wzory (4.12) i (4.13).

Twierdzenie. Pochodna pędu układu po czasie jest równa sumie geometrycznej wszystkich działających na niego sił zewnętrznych.

W rzutach osi kartezjańskich otrzymujemy równania skalarne.

Możesz napisać wektor

(4.28)

i równania skalarne

Które wyrażają twierdzenie o zmianie pędu układu w postaci całkowej: zmiana pędu układu w pewnym okresie czasu jest równa sumie impulsów w tym samym okresie. Przy rozwiązywaniu problemów częściej stosuje się równania (4.27).

Prawo zachowania pędu

Twierdzenie o zmianie momentu pędu

Twierdzenie o zmianie momentu pędu punktu względem środka: pochodna czasowa pędu punktu względem nieruchomego środka jest równa wektorowi momentu siły działającej na punkt względem tego samego środka.

Lub (4.30)

Porównując (4.23) i (4.30) widzimy, że momenty wektorów i są powiązane tą samą zależnością, co wektory i same siebie są ze sobą powiązane (ryc. 4.1). Jeśli rzutujemy równość na oś przechodzącą przez środek O, otrzymamy

(4.31)

Ta równość wyraża twierdzenie o momencie pędu punktu względem osi.

Ryż. 4.1.
Twierdzenie o zmianie głównego momentu pędu lub pędu układu mechanicznego względem środka: pochodna czasowa kinetycznego momentu pędu układu względem jakiegoś stałego środka jest równa sumie momentów wszystkich sił zewnętrznych względem tego samego środka.

(4.32)

Jeśli rzutujemy wyrażenie (4.32) na oś przechodzącą przez środek O, otrzymamy równość charakteryzującą twierdzenie o zmianie momentu pędu względem osi.

(4.33)

Podstawiając (4.10) do równości (4.33) możemy zapisać równanie różniczkowe obracającego się ciała sztywnego (koła, osie, wały, wirniki itp.) w trzech postaciach.

(4.34)

(4.35)

(4.36)

Wskazane jest zatem wykorzystanie twierdzenia o zmianie pędu kinetycznego do badania ruchu ciała sztywnego, co jest bardzo powszechne w technologii, jego obrotu wokół ustalonej osi.

Prawo zachowania momentu pędu układu

1. Niech wyrazi (4.32) .

Następnie z równania (4.32) wynika, że ​​tj. jeżeli suma momentów wszystkich sił zewnętrznych przyłożonych do układu względem danego środka jest równa zeru, to moment kinetyczny układu względem tego środka będzie stały numerycznie i kierunkowo.

2. Jeśli , to . Jeżeli zatem suma momentów sił zewnętrznych działających na układ względem określonej osi wynosi zero, to moment kinetyczny układu względem tej osi będzie miał wartość stałą.

Wyniki te wyrażają prawo zachowania momentu pędu.

W przypadku wirującego ciała sztywnego z równości (4.34) wynika, że ​​jeśli , to . Stąd dochodzimy do następujących wniosków:

Jeśli system jest niezmienny (absolutnie solidny), zatem ciało sztywne obraca się wokół ustalonej osi ze stałą prędkością kątową.

Jeśli system jest zmienny, to . Wraz ze wzrostem (wówczas poszczególne elementy układu oddalają się od osi obrotu) prędkość kątowa maleje, gdyż , a w miarę zmniejszania się wzrasta, zatem w przypadku układu zmiennego za pomocą sił wewnętrznych możliwa jest zmiana prędkości kątowej.

Zadanie drugie D2 praca testowa poświęcony jest twierdzeniu o zmianie momentu pędu układu względem osi.

Zadanie D2

Jednorodna pozioma platforma (okrągła o promieniu R lub prostokątna o bokach R i 2R, gdzie R = 1,2 m) o masie kg obraca się z prędkością kątową wokół pionowej osi z, oddalonej od środka masy C platformy o odległość OC = b (rys. E2.0 – D2.9, tabela D2); Wymiary wszystkich platform prostokątnych pokazano na rys. D2.0a (widok z góry).

W tym momencie ładunek D o masie kg zaczyna przemieszczać się po zsypie platformowym (pod wpływem sił wewnętrznych) zgodnie z prawem, gdzie s wyraża się w metrach, t - w sekundach. Jednocześnie para sił o momencie M (określonym w niutonometrach; w M< 0 его направление противоположно показанному на рисунках).

Wyznacz, pomijając masę wału, zależność tj. prędkość kątowa platformy w funkcji czasu.

Na wszystkich rysunkach obciążenie D jest pokazane w położeniu, w którym s > 0 (kiedy s< 0, груз находится по другую сторону от точки А). Изображая чертеж решаемой задачи, провести ось z на podana odległość OC = b od środka C.

Wskazówki. Zadanie D2 – zastosować twierdzenie o zmianie momentu pędu układu. Stosując twierdzenie do układu składającego się z platformy i ładunku, moment pędu układu względem osi z wyznacza się jako sumę momentów platformy i obciążenia. Należy wziąć pod uwagę, że prędkość bezwzględna ładunku jest sumą prędkości względnych i przenośnych, tj. . Dlatego wielkość ruchu tego ładunku . Można wówczas skorzystać z twierdzenia Varignona (statyka), zgodnie z którym ; momenty te oblicza się w taki sam sposób, jak momenty sił. Rozwiązanie wyjaśniono bardziej szczegółowo w przykładzie D2.

Przy rozwiązywaniu problemu warto przedstawić na rysunku pomocniczym widok platformy z góry (od końca z), tak jak to pokazano na ryc. D2.0, a – D2.9, a.

Moment bezwładności płyty o masie m względem osi Cz, prostopadłej do płyty i przechodzącej przez jej środek masy, wynosi: dla płyty prostokątnej o bokach i

;

Dla okrągłej płyty o promieniu R


Numer warunku B s = F(t) M
R R/2 R R/2 R R/2 R R/2 R R/2 -0,4 0,6 0,8 10 t 0,4 -0,5t -0,6t 0,8t 0,4 0,5 4t -6 -8t -9 6 -10 12

Ryż. D2.0
Ryż. D2.0a

Ryż. D2.1
Ryż. D2.1a

Ryż. D2.2
Ryż. D2.2a

Ryż. D2.3
Ryż. D2.3a

Ryż. D2.4
Ryż. D2.4a

Ryż. D2.5a
Ryż. D2.5

Ryż. D2.6
Ryż. D2.6a

Ryż. D2.7
Ryż. D2.7a

Ryż. D2.8
Ryż. D2.8a

Ryż. D2.9
Ryż. D2.9a

Ryż. D2

Przykład D2. Jednorodna pozioma platforma (prostokątna o bokach 2l i l), posiadająca masę, jest sztywno przymocowana do pionowego wału i obraca się wraz z nim wokół osi z z prędkością kątową (rys. E2a ). W pewnym momencie na wał zaczyna działać moment obrotowy M, skierowany przeciwnie ; jednocześnie ładunek D masa zlokalizowana w rowie AB w tym punkcie Z, zaczyna poruszać się po zsypie (pod wpływem sił wewnętrznych) zgodnie z prawem s = CD = F(t).

Biorąc pod uwagę: m 1 = 16 kg, t 2= 10 kg, l= 0,5 m, = 2, s = 0,4t 2 (s - w metrach, t - w sekundach), M= kt, Gdzie k=6 Nm/s. Zdefiniuj: - prawo zmiany prędkość kątowa platformy.

Rozwiązanie. Rozważmy system mechaniczny składający się z platformy i ładunku D. Aby wyznaczyć w, stosujemy twierdzenie o zmianie momentu pędu układu względem osi z:

(1)

Przedstawmy siły zewnętrzne działające na układ: siłę grawitacji reakcji oraz moment obrotowy M. Ponieważ siły i są równoległe do osi z, a reakcje przecinają tę oś, to ich momenty względem osi z są równe zero. Następnie, uznając kierunek w tej chwili za dodatni (tj. przeciwnie do ruchu wskazówek zegara), otrzymujemy a równanie (1) przyjmie tę postać.