Wyjaśnij zasadę rozwiązania problemu. Kości zostały rzucone raz. Jakie jest prawdopodobieństwo, że wyrzuci mniej niż 4 punkty? i dostałem najlepszą odpowiedź
Odpowiedź od Niezgodna[guru]
50 procent
Zasada jest niezwykle prosta. Suma wyników 6: 1,2,3,4,5,6
Spośród nich trzy spełniają warunek: 1,2,3, a trzy nie: 4,5,6. Zatem prawdopodobieństwo wynosi 3/6=1/2=0,5=50%
Odpowiedź od Jestem Supermanem[guru]
Łącznie może być sześć opcji (1,2,3,4,5,6)
A z tych opcji 1, 2 i 3 jest mniej niż cztery
Zatem 3 odpowiedzi z 6
Aby obliczyć prawdopodobieństwo, dzielimy korzystny rozkład na wszystko, tj. 3 na 6 = 0,5 lub 50%
Odpowiedź od Oriy Dovbysh[aktywny]
50%
podzielić 100% przez liczbę liczb na kostce,
a następnie pomnóż otrzymany procent przez kwotę, którą musisz znaleźć, czyli przez 3)
Odpowiedź od Iwan Panin[guru]
Nie wiem na pewno, przygotowuję się do GIA, ale nauczyciel powiedział mi dzisiaj coś, tylko o prawdopodobieństwie samochodów, ponieważ zrozumiałem, że stosunek jest pokazany jako ułamek, na górze liczba jest korzystna , a na dole moim zdaniem jest ogólnie ogólnie, no cóż, mieliśmy coś takiego o samochodach: W firmie taksówkarskiej w ten moment bezpłatne 3 czarne, 3 żółte i 14 zielonych samochodów. Jedno z aut podjechało do klienta. Znajdź prawdopodobieństwo, że przyjedzie do niego żółta taksówka. Tak więc są 3 żółte taksówki, a na ogólną liczbę samochodów jest ich 3, okazuje się, że piszemy 3 na górze ułamka, ponieważ jest to korzystna liczba samochodów, a na dole piszemy 20 , ponieważ we flocie taksówek jest w sumie 20 samochodów, więc prawdopodobieństwo 3 do 20 lub 3/20 otrzymujemy jako ułamek, cóż, tak to zrozumiałem.... Nie wiem dokładnie, jak sobie z tym poradzić kości, ale może w jakiś sposób pomogło...
Odpowiedź od 3 odpowiedzi[guru]
Cześć! Oto wybór tematów z odpowiedziami na Twoje pytanie: Wyjaśnij zasadę rozwiązania problemu. Kości zostały rzucone raz. Jakie jest prawdopodobieństwo, że wyrzuci mniej niż 4 punkty?
Zadania dla prawdopodobieństwo kości nie mniej popularne niż problemy z rzutem monetą. Warunek takiego zadania zwykle brzmi następująco: rzucając jedną lub większą liczbą kostek (2 lub 3), jakie jest prawdopodobieństwo, że suma punktów będzie równa 10, lub liczba punktów będzie wynosić 4, lub iloczyn liczby punktów lub iloczyn liczby punktów podzielony przez 2 itd.
Główną metodą rozwiązywania tego typu problemów jest zastosowanie klasycznej formuły prawdopodobieństwa.
Jedna kość, prawdopodobieństwo.
Z jedną kostką sytuacja jest dość prosta. określa się wzorem: P=m/n, gdzie m jest liczbą korzystnych dla zdarzenia wyników, a n jest liczbą wszystkich elementarnych, jednakowo możliwych wyników eksperymentu z rzuceniem kości lub sześcianu.
Zadanie 1. Kostką rzucamy raz. Jakie jest prawdopodobieństwo zdobycia parzystej liczby punktów?
Ponieważ kość jest sześcianem (lub nazywana jest również zwykłą kością, kość wyląduje na wszystkich stronach z równym prawdopodobieństwem, ponieważ jest zrównoważona), kość ma 6 boków (liczba punktów od 1 do 6, które są zwykle oznaczone kropkami), oznacza to, że problem ma całkowitą liczbę wyników: n=6. Wydarzeniu sprzyjają tylko te wyniki, w których pojawia się strona z parzystymi punktami 2,4 i 6, a kość ma boki: m=3. Teraz możemy określić pożądane prawdopodobieństwo wyrzucenia kości: P=3/6=1/2=0,5.
Zadanie 2. Kości rzucamy raz. Jakie jest prawdopodobieństwo, że zdobędziesz co najmniej 5 punktów?
Problem ten rozwiązano analogicznie do przykładu podanego powyżej. Przy rzucie kostką łączna liczba jednakowo możliwych wyników wynosi: n=6, a tylko 2 wyniki spełniają warunek zadania (co najmniej 5 wyrzuconych punktów, czyli wyrzuconych 5 lub 6 punktów), co oznacza m =2. Następnie znajdujemy wymagane prawdopodobieństwo: P=2/6=1/3=0,333.
Dwie kostki, prawdopodobieństwo.
Przy rozwiązywaniu zadań polegających na rzucie 2 kostkami bardzo wygodnie jest skorzystać ze specjalnej tabeli punktacji. Na nim liczba punktów, które wypadły na pierwszej kostce, jest wyświetlana poziomo, a liczba punktów, które wypadły na drugiej kostce, jest wyświetlana w pionie. Przedmiot obrabiany wygląda następująco:
Powstaje jednak pytanie, co będzie w pustych komórkach tabeli? To zależy od problemu, który należy rozwiązać. Jeśli problem dotyczy sumy punktów, to tam wpisuje się sumę, a jeśli chodzi o różnicę, to wpisuje się różnicę i tak dalej.
Zadanie 3. Rzucamy jednocześnie 2 kostkami. Jakie jest prawdopodobieństwo zdobycia mniej niż 5 punktów?
Najpierw musisz dowiedzieć się, jaka będzie całkowita liczba wyników eksperymentu. Wszystko było oczywiste przy rzucie jedną kostką, 6 stronami kostki – 6 wyników eksperymentu. Ale gdy są już dwie kostki, możliwe wyniki można przedstawić jako uporządkowane pary liczb w postaci (x, y), gdzie x pokazuje, ile punktów wyrzucono na pierwszych kostkach (od 1 do 6), a y - ile punktów wyrzucono na drugiej kostce (od 1 do 6). W sumie będzie takich par liczb: n=6*6=36 (w tabeli wyników odpowiadają one dokładnie 36 komórkom).
Teraz możesz wypełnić tabelę, w tym celu w każdej komórce wpisz liczbę punktów, które spadły na pierwszą i drugą kostkę. Wypełniona tabela wygląda następująco:

Korzystając z tabeli, określimy liczbę wyników sprzyjających zdarzeniu „w sumie pojawi się mniej niż 5 punktów”. Policzmy liczbę komórek, w których wartość sumy będzie mniejsza od liczby 5 (są to 2, 3 i 4). Dla wygody zamalowujemy takie komórki, będzie ich m=6:

Biorąc pod uwagę dane tabelaryczne, prawdopodobieństwo kości równa się: P=6/36=1/6.
Zadanie 4. Rzucono dwiema kostkami. Oblicz prawdopodobieństwo, że iloczyn liczby punktów będzie podzielny przez 3.
Aby rozwiązać problem, zróbmy tabelę iloczynów punktów, które wypadły na pierwszej i drugiej kostce. W nim natychmiast podkreślamy liczby, które są wielokrotnościami 3:

Zapisujemy całkowitą liczbę wyników eksperymentu n=36 (rozumowanie takie samo jak w poprzednim zadaniu) i liczbę korzystnych wyników (liczba zacienionych komórek w tabeli) m=20. Prawdopodobieństwo zdarzenia wynosi: P=20/36=5/9.
Zadanie 5. Rzucamy dwukrotnie kostkami. Jakie jest prawdopodobieństwo, że różnica punktów na pierwszej i drugiej kostce będzie wynosić od 2 do 5?
Określić prawdopodobieństwo kości Zapiszmy tabelę różnic punktowych i zaznaczmy w niej te komórki, których wartość różnicy będzie wynosić od 2 do 5:

Liczba korzystnych wyników (liczba komórek zacieniowanych w tabeli) wynosi m=10, całkowita liczba równie możliwych elementarnych wyników wyniesie n=36. Określa prawdopodobieństwo zdarzenia: P=10/36=5/18.
W przypadku prostego zdarzenia i rzucając 2 kostkami, musisz zbudować tabelę, następnie wybrać w niej niezbędne komórki i podzielić ich liczbę przez 36, zostanie to uznane za prawdopodobieństwo.
Zadanie 19 ( OGE - 2015, Jaszczenko I.V.)
Ola, Denis, Vitya, Artur i Rita rzucali losy o to, kto powinien rozpocząć grę. Znajdź prawdopodobieństwo, że Rita rozpocznie grę.
Rozwiązanie
W sumie grę może rozpocząć 5 osób.
Odpowiedź: 0,2.
Zadanie 19 ( OGE - 2015, Jaszczenko I.V.)
Misza miał w kieszeni cztery cukierki - „Grillage”, „Maska”, „Wiewiórka” i „Czerwony Kapturek” oraz klucze do mieszkania. Wyjmując klucze, Misza przypadkowo upuściła jeden cukierek. Znajdź prawdopodobieństwo, że cukierek Maska zostanie zgubiony.
Rozwiązanie
W sumie są 4 opcje.
Prawdopodobieństwo, że Misza upuścił cukierka Maska, jest równe
Odpowiedź: 0,25.
Zadanie 19 ( OGE - 2015, Jaszczenko I.V.)
Kostką (kostkami) rzucamy raz. Jakie jest prawdopodobieństwo, że wyrzucona liczba będzie nie mniejsza niż 3?
Rozwiązanie
Istnieje w sumie 6 różnych opcji zdobywania punktów na kostce.
Liczba punktów nie mniejsza niż 3 może wynosić: 3,4,5,6 – czyli 4 opcje.
Oznacza to, że prawdopodobieństwo wynosi P = 4/6 = 2/3.
Odpowiedź: 2/3.
Zadanie 19 ( OGE - 2015, Jaszczenko I.V.)
Babcia postanowiła podarować swojemu wnukowi Iljuszy na podróż losowo wybrane owoce. Miała 3 zielone jabłka, 3 zielone gruszki i 2 żółte banany. Znajdź prawdopodobieństwo, że Ilia otrzyma od swojej babci zielony owoc.
Rozwiązanie
3+3+2 = 8 - suma owoców. Spośród nich 6 jest zielonych (3 jabłka i 3 gruszki).
Wtedy prawdopodobieństwo, że Ilya otrzyma od swojej babci zielony owoc, jest równe
P = 6/8 = 3/4 = 0,75.
Odpowiedź: 0,75.
Zadanie 19 ( OGE - 2015, Jaszczenko I.V.)
Kostką rzucamy dwukrotnie. Znajdź prawdopodobieństwo, że za każdym razem wyrzucona zostanie liczba większa niż 3.
Rozwiązanie
6*6 = 36 - całkowita liczba możliwych liczb przy rzucie dwiema kostkami.
Opcje, które nam odpowiadają to:
W sumie jest 9 takich opcji.
Oznacza to, że prawdopodobieństwo, że za każdym razem wyrzucona zostanie liczba większa niż 3, jest równe
P = 9/36 = 1/4 = 0,25.
Odpowiedź: 0,25.
Zadanie 19 ( OGE - 2015, Jaszczenko I.V.)
Kostką (kostkami) rzucamy 2 razy. Znajdź prawdopodobieństwo, że raz wyrzucona zostanie liczba większa niż 3, a innym razem liczba mniejsza niż 3.
Rozwiązanie
Łączna liczba opcji: 6*6 = 36.
Pasują nam następujące wyniki:
Cele Lekcji:
Studenci powinni wiedzieć:
- określanie prawdopodobieństwa zdarzenia losowego;
- potrafić rozwiązywać problemy w celu obliczenia prawdopodobieństwa zdarzenia losowego;
- potrafi zastosować wiedzę teoretyczną w praktyce.
Cele Lekcji:
Edukacyjne: stwórz uczniom warunki do opanowania systemu wiedzy, umiejętności i zdolności z koncepcjami prawdopodobieństwa zdarzenia.
Edukacyjne: kształtowanie naukowego światopoglądu u uczniów
Rozwojowe: rozwijanie zainteresowań poznawczych uczniów, kreatywności, woli, pamięci, mowy, uwagi, wyobraźni, percepcji.
Metody organizacji zajęć edukacyjnych i poznawczych:
- wizualny,
- praktyczny,
- poprzez aktywność umysłową: indukcyjną,
- według asymilacji materiału: częściowo poszukiwawcze, reprodukcyjne,
- według stopnia samodzielności: samodzielna praca,
- stymulujące: zachęta,
- rodzaje kontroli: sprawdzanie samodzielnie rozwiązanych problemów.
Plan lekcji
- Ćwiczenia ustne
- Nauka nowego materiału
- Rozwiązywanie zadań.
- Niezależna praca.
- Podsumowanie lekcji.
- Komentowanie pracy domowej.
Sprzęt: rzutnik multimedialny (prezentacja), karty ( niezależna praca)
Podczas zajęć
I. Moment organizacyjny.
Organizacja zajęć podczas całej lekcji, gotowość uczniów do zajęć, porządek i dyscyplina.
Wyznaczanie uczniom celów uczenia się, zarówno na całą lekcję, jak i na jej poszczególne etapy.
Określ znaczenie studiowanego materiału, zarówno w tym temacie, jak iw całym kursie.
II. Powtórzenie
1. Czym jest prawdopodobieństwo?
Prawdopodobieństwo to możliwość, że coś się wydarzy lub będzie wykonalne.
2. Jaką definicję podaje twórca współczesnej teorii prawdopodobieństwa A.N. Kołmogorow?
Prawdopodobieństwo matematyczne to liczbowa charakterystyka stopnia możliwości wystąpienia określonego zdarzenia w określonych warunkach, która może się powtórzyć nieograniczoną liczbę razy.
3. Które klasyczna definicja Czy autorzy podręczników szkolnych podają prawdopodobieństwa?
Prawdopodobieństwo P(A) zdarzenia A w próbie z równie możliwymi wynikami elementarnymi jest stosunkiem liczby wyników m korzystnych dla zdarzenia A do liczby n wszystkich wyników próby.
Wniosek: w matematyce prawdopodobieństwo mierzy się liczbą.
Dzisiaj będziemy nadal rozważać model matematyczny „kości”.
Przedmiotem badań teorii prawdopodobieństwa są zdarzenia, które pojawiają się pod pewnymi warunkami i które można odtwarzać nieograniczoną liczbę razy. Każde wystąpienie tych warunków nazywa się testem.
Test polega na rzucie kostką.
Wydarzenie – wyrzucenie szóstki Lub rzucając parzystą liczbę punktów.
Przy wielokrotnym rzucie kostką prawdopodobieństwo każdej ze stron jest takie samo (kość jest sprawiedliwa).
III. Rozwiązywanie problemów ustnych.
1. Kością (kostkami) rzucono raz. Jakie jest prawdopodobieństwo, że wypadnie 4?
Rozwiązanie. Losowy eksperyment polega na rzucie kostką. Zdarzenie – liczba po stronie opuszczonej. Jest tylko sześć twarzy. Wypiszmy wszystkie zdarzenia: 1, 2, 3, 4, 5, 6. A więc P= 6. Zdarzenie A = (wyrzucone 4 punkty) jest faworyzowane przez jedno wydarzenie: 4. Zatem T= 1. Zdarzenia są równie możliwe, ponieważ zakłada się, że kość jest sprawiedliwa. Zatem P(A) = t/n= 1/6 = 0,17.
2. Kością (kostkami) rzucono raz. Jakie jest prawdopodobieństwo, że wyrzucimy nie więcej niż 4 punkty?
P= 6. Zdarzenie A = (nie więcej niż 4 punkty wyrzucone) jest faworyzowane przez 4 zdarzenia: 1, 2, 3, 4. Zatem T= 4. Zatem P(A) = t/n= 4/6 = 0,67.
3. Kością (kostkami) rzucono raz. Jakie jest prawdopodobieństwo, że wyrzuci mniej niż 4 punkty?
Rozwiązanie. Losowy eksperyment polega na rzucie kostką. Zdarzenie – liczba po stronie opuszczonej. Oznacza P= 6. Zdarzenie A = (mniej niż 4 wyrzucone punkty) jest faworyzowane przez 3 zdarzenia: 1, 2, 3. Zatem T= 3. P(A) = t/n= 3/6 = 0,5.
4. Kością (kostkami) rzucono raz. Jakie jest prawdopodobieństwo, że wyrzucona zostanie nieparzysta liczba punktów?
Rozwiązanie. Losowy eksperyment polega na rzucie kostką. Zdarzenie – liczba po stronie opuszczonej. Oznacza P= 6. Zdarzenie A = (odrzucone liczba nieparzysta punktów) faworyzuje 3 zdarzenia: 1,3,5. Dlatego T= 3. P(A) = t/n= 3/6 = 0,5.
IV. Uczyć się nowych rzeczy
Dzisiaj rozważymy problemy, gdy w losowym eksperymencie użyje się dwóch kości lub wykona dwa lub trzy rzuty.
1. W losowym eksperymencie rzucamy dwiema kostkami. Znajdź prawdopodobieństwo, że suma wylosowanych punktów wyniesie 6. Zaokrąglij odpowiedź do najbliższej setnej .
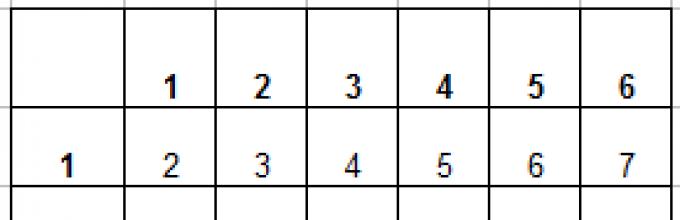
Rozwiązanie. Wynikiem tego eksperymentu jest uporządkowana para liczb. Pierwsza liczba pojawi się na pierwszej kostce, druga na drugiej. Wygodnie jest przedstawić zestaw wyników w tabeli.
Rzędy odpowiadają liczbie punktów na pierwszej kostce, kolumny na drugiej kostce. Razem zdarzenia elementarne P= 36.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Zapiszmy sumę wyrzuconych punktów w każdej komórce i pokoloruj komórki, w których suma wynosi 6.
Takich komórek jest 5. Oznacza to, że zdarzeniu A = (suma wylosowanych punktów wynosi 6) sprzyja 5 wyników. Stąd, T= 5. Zatem P(A) = 5/36 = 0,14.
2. W losowym eksperymencie rzucamy dwiema kostkami. Znajdź prawdopodobieństwo, że suma wyniesie 3 punkty. Zaokrąglij wynik do części setnych .
P= 36.
Zdarzenie A = (suma równa się 3) jest faworyzowane przez 2 wyniki. Stąd, T= 2.
Zatem P(A) = 2/36 = 0,06.
3. W losowym eksperymencie rzucamy dwiema kostkami. Znajdź prawdopodobieństwo, że suma będzie większa niż 10 punktów. Zaokrąglij wynik do części setnych .
Rozwiązanie. Wynikiem tego eksperymentu jest uporządkowana para liczb. Całkowita liczba wydarzeń P= 36.
Zdarzenie A = (w sumie zostanie przyznanych więcej niż 10 punktów) jest faworyzowane przez 3 wyniki.
Stąd, T
4. Luba rzuca dwukrotnie kostką. W sumie zdobyła 9 punktów. Znajdź prawdopodobieństwo, że jeden z rzutów zakończy się zdobyciem 5 punktów .
Rozwiązanie Wynikiem tego eksperymentu jest uporządkowana para liczb. Pierwsza liczba pojawi się przy pierwszym rzucie, druga przy drugim. Wygodnie jest przedstawić zestaw wyników w tabeli.
Wiersze odpowiadają wynikowi pierwszego rzutu, kolumny - wynikowi drugiego rzutu.
Łączna liczba zdarzeń, dla których łączny wynik wynosi 9 P= 4. Zdarzenie A = (jeden z rzutów zakończył się wynikiem 5 punktów) jest faworyzowane przez 2 wyniki. Stąd, T= 2.
Zatem P(A) = 2/4 = 0,5.
5. Sveta rzuca dwa razy kostką. W sumie zdobyła 6 punktów. Znajdź prawdopodobieństwo, że jeden z rzutów zakończy się zdobyciem 1 punktu.
Pierwszy rzut |
Drugi rzut |
Suma punktów |
||
Istnieje 5 jednakowo możliwych wyników.
Prawdopodobieństwo zdarzenia wynosi p = 2/5 = 0,4.
6. Ola rzuca dwa razy kostką. Łącznie zdobyła 5 punktów. Znajdź prawdopodobieństwo, że w pierwszym rzucie otrzymasz 3 punkty.
Pierwszy rzut |
Drugi rzut |
Suma punktów |
||
| + | = | |||
| + | = | |||
| + | = | |||
| + | = |
Istnieją 4 równie możliwe wyniki.
Korzystne wyniki – 1.
Prawdopodobieństwo zdarzenia R= 1/4 = 0,25.
7. Natasza i Vitya grają w kości. Rzucają kostką raz.
Wygrywa ten, kto rzuci więcej punktów. Jeśli liczba punktów jest równa, następuje remis. Łącznie jest 8 punktów. Znajdź prawdopodobieństwo, że Natasza wygrała.
Suma punktów |
||||
| + | = | |||
| + | = | |||
| + | = | |||
| + | = | |||
| + | = |
Istnieje 5 jednakowo możliwych wyników.
Korzystne wyniki – 2.
Prawdopodobieństwo zdarzenia R= 2/5 = 0,4.
8. Tanya i Natasza grają w kości. Rzucają kostką raz. Wygrywa ten, kto rzuci więcej punktów. Jeśli liczba punktów jest równa, następuje remis. Łącznie udało się zdobyć 6 punktów. Znajdź prawdopodobieństwo, że Tanya przegrała.
| Tanya | Natasza | Suma punktów | ||
| + | = | |||
| + | = | |||
| + | = | |||
| + | = | |||
| + | = |
Istnieje 5 jednakowo możliwych wyników.
Korzystne wyniki – 2.
Prawdopodobieństwo zdarzenia R= 2/5 = 0,4.
9. Kola i Lena grają w kości. Rzucają kostką raz. Wygrywa ten, kto rzuci więcej punktów. Jeśli liczba punktów jest równa, następuje remis. Kola rzucił jako pierwszy i zdobył 3 punkty. Znajdź prawdopodobieństwo, że Lena nie wygra.
Kola zdobył 3 punkty.
Lena ma 6 równie możliwych wyników.
Istnieją 3 korzystne wyniki przegranej (przy 1, 2 i 3).
Prawdopodobieństwo zdarzenia R= 3/6 = 0,5.
10. Masza rzuca trzy razy kostką. Jakie jest prawdopodobieństwo, że wszystkie trzy razy otrzymamy liczby parzyste?
Masza ma 6 6 6 = 216 jednakowo możliwych wyników.
Istnieje 3 · 3 · 3 = 27 korzystnych wyników przegranej.
Prawdopodobieństwo zdarzenia R= 27/216 = 1/8 = 0,125.
11. W losowym eksperymencie rzucamy trzema kostkami. Znajdź prawdopodobieństwo, że suma wyniesie 16 punktów. Zaokrąglij wynik do części setnych.
Rozwiązanie.
| Drugi | Trzeci | Suma punktów | ||||
| + | + | = | ||||
| + | + | = | ||||
| + | + | = | ||||
| + | + | = | ||||
| + | + | = | ||||
| + | + | = |
Równie możliwe wyniki – 6 6 6 = 216.
Korzystne wyniki – 6.
Prawdopodobieństwo zdarzenia R= 6/216 = 1/36 = 0,277... = 0,28. Stąd, T= 3. Dlatego P (A) = 3/36 = 0,08.
V. Samodzielna praca.
Opcja 1.
- Kostką (kostkami) rzucamy raz. Jakie jest prawdopodobieństwo, że wyrzuciłeś co najmniej 4 punkty? (Odpowiedź: 0,5)
- W losowym eksperymencie rzucamy dwiema kostkami. Znajdź prawdopodobieństwo, że suma wyniesie 5 punktów. Zaokrąglij wynik do części setnych. (Odpowiedź: 0,11)
- Anya rzuca kostką dwa razy. Łącznie zdobyła 3 punkty. Znajdź prawdopodobieństwo, że w pierwszym rzucie otrzymasz 1 punkt. (Odpowiedź: 0,5)
- Katya i Ira grają w kości. Rzucają kostką raz. Wygrywa ten, kto rzuci więcej punktów. Jeśli liczba punktów jest równa, następuje remis. Razem to 9 punktów. Znajdź prawdopodobieństwo, że Ira przegrał. (Odpowiedź: 0,5)
- W losowym eksperymencie rzucamy trzema kostkami. Znajdź prawdopodobieństwo, że suma punktów wyniesie 15. Zaokrąglij wynik do części setnych. (Odpowiedź: 0,05)
Opcja 2.
- Kostką (kostkami) rzucamy raz. Jakie jest prawdopodobieństwo, że wyrzucimy nie więcej niż 3 punkty? (Odpowiedź: 0,5)
- W losowym eksperymencie rzucamy dwiema kostkami. Znajdź prawdopodobieństwo, że suma wyniesie 10 punktów. Zaokrąglij wynik do części setnych. (Odpowiedź: 0,08)
- Żenia rzuca kostką dwa razy. Łącznie zdobyła 5 punktów. Znajdź prawdopodobieństwo, że w pierwszym rzucie otrzymasz 2 punkty. (Odpowiedź: 0,25)
- Masza i Dasza grają w kości. Rzucają kostką raz. Wygrywa ten, kto rzuci więcej punktów. Jeśli liczba punktów jest równa, następuje remis. Łącznie zdobyli 11 punktów. Znajdź prawdopodobieństwo, że Masza wygrała. (Odpowiedź: 0,5)
- W losowym eksperymencie rzucamy trzema kostkami. Znajdź prawdopodobieństwo, że suma wyniesie 17 punktów. Zaokrąglij wynik
VI. Praca domowa
- W losowym eksperymencie rzucamy trzema kostkami. Łącznie jest 12 punktów. Znajdź prawdopodobieństwo, że w pierwszym rzucie otrzymasz 5 punktów, a wynik zaokrąglij do setnych.
- Katia rzuca kostką trzy razy. Jakie jest prawdopodobieństwo, że trzykrotnie wypadną te same liczby?
VII. Podsumowanie lekcji
Co musisz wiedzieć, aby obliczyć prawdopodobieństwo zdarzenia losowego?
Aby obliczyć prawdopodobieństwo klasyczne, musisz znać wszystkie możliwe wyniki zdarzenia i korzystne wyniki.
Klasyczna definicja prawdopodobieństwa ma zastosowanie tylko do zdarzeń o równie prawdopodobnych wynikach, co ogranicza jej zakres.
Dlaczego uczymy się teorii prawdopodobieństwa w szkole?
Wiele zjawisk w otaczającym nas świecie można opisać jedynie za pomocą teorii prawdopodobieństwa.
Literatura
- Algebra i początki analizy matematycznej Klasy 10-11: podręcznik. dla ogólnokształcących instytucji edukacyjnych: poziom podstawowy / [Sh.A. Alimov, Yu.M. Kolyagin, M.V. Tkacheva itp.]. – wyd. 16, poprawione. – M.: Edukacja, 2010. – 464 s.
- Semenov A.L. Ujednolicony egzamin państwowy: 3000 problemów z odpowiedziami z matematyki. Wszystkie zadania grupy B/ – wyd. 3, poprawione. i dodatkowe – M.: Wydawnictwo „Egzamin”, 2012. – 543 s.
- Wysocki I.R., Jaszczenko I.V. Jednolity egzamin państwowy 2012. Matematyka. Zadanie B10. Teoria prawdopodobieństwa. zeszyt ćwiczeń/wyd. A.L. Semenov i I.V. Yashchenko. – M.: MCSHMO, 2012. – 48 s.