Równoległobok to czworokąt, którego przeciwne boki są równoległe parami (ryc. 233).
W przypadku dowolnego równoległoboku obowiązują następujące właściwości:
1. Przeciwne boki równoległoboku są równe.
Dowód. W równoległoboku ABCD rysujemy przekątną AC. Trójkąty ACD i AC B są równe, ponieważ mają wspólny bok AC i dwie pary równe kąty, obok:
(jak kąty poprzeczne z równoległymi liniami AD i BC). Oznacza to, i podobnie jak boki równych trójkątów leżących naprzeciw równych kątów, co należało udowodnić.

2. Przeciwne kąty równoległoboku są równe:
3. Sąsiednie kąty równoległoboku, tj. Kąty sąsiadujące z jednym bokiem, sumują się itp.
Dowód właściwości 2 i 3 uzyskuje się natychmiast z właściwości kątów dla linii równoległych.
4. Przekątne równoległoboku przecinają się w punkcie przecięcia. Innymi słowy,
Dowód. Trójkąty AOD i BOC są przystające, ponieważ ich boki AD i BC są równe (własność 1) i sąsiadujące z nimi kąty (jak kąty poprzeczne dla prostych równoległych). Z tego wynika, że odpowiednie boki tych trójkątów są równe: AO, co należało udowodnić.
Każda z tych czterech właściwości charakteryzuje równoległobok lub, jak mówią, jest jego charakterystyczną właściwością, tj. Każdy czworokąt, który ma co najmniej jedną z tych właściwości, jest równoległobokiem (a zatem ma wszystkie pozostałe trzy właściwości).
Dowód przeprowadzimy dla każdej własności osobno.
1”. Jeśli przeciwne strony czworokąta są równe parami, to jest to równoległobok.
Dowód. Niech czworokąt ABCD ma odpowiednio równe boki AD i BC, AB i CD (ryc. 233). Narysujmy przekątną AC. Trójkąty ABC i CDA będą przystające, ponieważ mają trzy pary równych boków.
Ale wtedy kąty BAC i DCA są równe i . Równoległość boków BC i AD wynika z równości kątów CAD i ACB.
2. Jeśli czworokąt ma dwie równe pary przeciwnych kątów, to jest równoległobokiem.
Dowód. Pozwalać . Od tego momentu obie strony AD i BC są równoległe (w oparciu o równoległość linii).
3. Sformułowanie i dowód pozostawiamy czytelnikowi.
4. Jeżeli przekątne czworoboku przecinają się w punkcie przecięcia na pół, to czworokąt jest równoległobokiem.
Dowód. Jeśli AO = OS, BO = OD (rys. 233), to trójkąty AOD i BOC są równe, ponieważ mają równe kąty (pionowe!) w wierzchołku O, zawarte pomiędzy parami równych boków AO i CO, BO i DO. Z równości trójkątów wnioskujemy, że boki AD i BC są równe. Boki AB i CD są również równe, a czworokąt okazuje się równoległobokiem zgodnie z charakterystyczną właściwością G.
Aby więc udowodnić, że dany czworokąt jest równoległobokiem, wystarczy sprawdzić zasadność którejkolwiek z czterech własności. Czytelnik jest proszony o samodzielne udowodnienie innej charakterystycznej właściwości równoległoboku.

5. Jeśli czworokąt ma parę równych, równoległych boków, to jest równoległobokiem.
Czasami dowolna para równoległych boków równoległoboku nazywana jest jego podstawami, a pozostałe dwa nazywane są bokami bocznymi. Odcinek prosty prostopadły do dwóch boków równoległoboku, zawarty między nimi, nazywany jest wysokością równoległoboku. Równoległobok na ryc. 234 ma wysokość h narysowaną na bokach AD i BC, jej drugą wysokość reprezentuje odcinek .
Równoległobok to czworokąt, którego przeciwne boki są równoległe, tj. leżą na liniach równoległych
Właściwości równoległoboku: 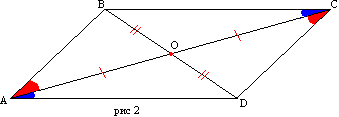 Twierdzenie 22.
Przeciwległe boki równoległoboku są równe.
Twierdzenie 22.
Przeciwległe boki równoległoboku są równe.
Dowód. W równoległoboku ABCD rysujemy przekątną AC. Trójkąty ACD i ACB są przystające, ponieważ mają wspólny bok AC i dwie pary równych kątów. sąsiadujące z nim: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (jako kąty poprzeczne z równoległymi liniami AD i BC). Oznacza to, że AB = CD i BC = AD, jako odpowiadające boki równych trójkątów itp. Równość tych trójkątów implikuje również równość odpowiednie kąty trójkąty:
Twierdzenie 23.
Przeciwległe kąty równoległoboku są równe: ∠ A=∠ C i ∠ B=∠ D.
Równość pierwszej pary wynika z równości trójkątów ABD i CBD, a drugiej - ABC i ACD.
Twierdzenie 24.
Sąsiednie kąty równoległoboku, tj. kąty przylegające do jednej strony sumują się do 180 stopni.
Dzieje się tak, ponieważ są to kąty wewnętrzne jednostronne.
Twierdzenie 25.
Przekątne równoległoboku przecinają się w punkcie przecięcia.
Dowód. Rozważmy trójkąty BOC i AOD. Zgodnie z pierwszą własnością AD=BC ∠ OAD=∠ OCB i ∠ ODA=∠ OBC leżące poprzecznie dla prostych równoległych AD i BC. Dlatego trójkąty BOC i AOD są równe pod kątem bocznym i przyległym. Oznacza to BO=OD i AO=OS, podobnie jak odpowiadające im boki równych trójkątów itp.
Znaki równoległoboku
Twierdzenie 26.
Jeżeli przeciwne strony czworokąta są równe parami, to jest to równoległobok.
Dowód. Niech czworokąt ABCD ma odpowiednio równe boki AD i BC, AB i CD (rys. 2). Narysujmy przekątną AC. Trójkąty ABC i ACD są równe z trzech stron. Wtedy kąty BAC i DCA są sobie równe, zatem AB jest równoległy do CD. Równoległość boków BC i AD wynika z równości kątów CAD i ACB.
Twierdzenie 27.
Jeśli przeciwne kąty czworokąta są równe parami, to jest to równoległobok.
Niech ∠ A=∠ C i ∠ B=∠ D. Ponieważ ∠ A+∠ B+∠ C+∠ D=360 o, następnie ∠ A+∠ B=180 o i boki AD i BC są równoległe (w oparciu o równoległość linii prostych). Udowodnimy również równoległość boków AB i CD i dochodzimy do wniosku, że ABCD jest z definicji równoległobokiem.
Twierdzenie 28.
Jeżeli sąsiednie narożniki czworoboku, tj. Kąty sąsiadujące z jednym bokiem sumują się do 180 stopni, wtedy jest to równoległobok.
Jeśli wewnętrzne kąty jednostronne sumują się do 180 stopni, wówczas linie proste są równoległe. Zatem AB jest równoległe do CD, a BC jest równoległe do AD. Z definicji czworokąt jest równoległobokiem.
Twierdzenie 29.
Jeżeli przekątne czworokąta przecinają się w punkcie przecięcia, to czworokąt jest równoległobokiem.
Dowód. Jeśli AO = OC, BO = OD, to trójkąty AOD i BOC są równe, ponieważ mają równe (pionowe) kąty w wierzchołku O, zawarte pomiędzy parami równych boków. Z równości trójkątów wnioskujemy, że AD i BC są równe. Boki AB i CD są również równe, a czworokąt okazuje się równoległobokiem zgodnie z kryterium 1.
Twierdzenie 30.
Jeśli czworokąt ma parę równych, równoległych boków, to jest równoległobokiem.
Niech boki AB i CD czworokąta ABCD będą równoległe i równe. Narysujmy przekątne AC i BD. Z równoległości tych prostych wynika, że kąty poprzeczne ABO = CDO i BAO = OCD są równe. Trójkąty ABO i CDO mają równe kąty boczne i przyległe. Zatem AO=OS, VO=ОD, tj. Przekątne dzieli się na pół w punkcie przecięcia i czworokąt okazuje się równoległobokiem zgodnie z kryterium 4.
W geometrii rozważa się szczególne przypadki równoległoboków.
Definicja
Równoległobok jest czworokątem, którego przeciwne strony są równoległe parami.
Nazywa się punkt przecięcia przekątnych równoległoboku Centrum.
Właściwości równoległoboku:
- Suma dowolnych dwóch sąsiednich kątów równoległoboku wynosi 180 $(\circ)$, a przeciwległe kąty są równe.
- Przeciwległe boki równoległoboku są równe.
- Przekątne równoległoboku przecinają się i przecinają w punkcie przecięcia.
Dowód
Niech dany będzie równoległobok $ABCD$.
1. Zauważ, że sąsiednie kąty $A$ i $B$ równoległoboku są jednostronnymi kątami wewnętrznymi z równoległymi liniami $AD$ i $BC$ oraz sieczną $AB$, czyli ich suma wynosi $180^ \circ$. Podobnie z innymi parami kątów.
Jeśli $\angle A + \angle B=180^\circ$ i $\angle C + \angle B=180^\circ$, to $\angle A = \angle C$. Podobnie $\angle B = \angle D$.
2. Rozważmy trójkąty $ABC$ i $CDA$. Z równoległości przeciwnych boków równoległoboku wynika, że $\angle BAC=\angle DCA$ i $\angle BCA=\angle DAC$. Ponieważ $AC$ jest wspólne, to trójkąty $ABC$ i $CDA$ są równe zgodnie z drugim kryterium. Z równości trójkątów wynika, że $AB=CD$ i $BC=AD$.
3. Ponieważ równoległobok jest wypukłym czworokątem, jego przekątne przecinają się. Niech $O$ będzie punktem przecięcia. Z równoległości boków $BC$ i $AD$ równoległoboku wynika, że $\angle OAD=\angle OCB$ i $\angle ODA=\angle OBC$. Biorąc pod uwagę równość $BC=AD$, otrzymujemy, że trójkąty $AOD$ i $COB$ są równe według drugiego kryterium. Dlatego $AO=CO$ i $DO=BO$, zgodnie z wymaganiami.

Znaki równoległoboku:
- Jeśli w czworokącie suma dowolnych dwóch sąsiednich kątów wynosi 180 $^(\circ)$, to ten czworokąt jest równoległobokiem.
- Jeśli w czworokącie przeciwne kąty są równe parami, wówczas ten czworokąt jest równoległobokiem.
- Jeśli w czworokącie przeciwne boki są równe parami, wówczas ten czworokąt jest równoległobokiem.
- Jeśli dwa boki czworokąta są równe i równoległe, wówczas czworokąt jest równoległobokiem.
- Jeżeli przekątne czworokąta są podzielone na pół przez ich punkt przecięcia, to czworokąt jest równoległobokiem.
Dowód
Niech $ABCD$ będzie czworokątem.
1. Zauważ, że sąsiednie kąty $A$ i $B$ są jednostronnymi kątami wewnętrznymi z prostymi $AD$ i $BC$ oraz poprzecznymi $AB$. Ponieważ ich suma wynosi 180^\circ$, zatem linie $AD$ i $BC$ są równoległe. Podobnie dla innej pary prostych, czyli $ABCD$ jest z definicji równoległobokiem.
2. Zauważ, że $\angle A + \angle B + \angle C + \angle D=360^\circ$. Jeśli $\angle A = \angle C$ i $\angle B = \angle D$, to $\angle A + \angle B=180^\circ$ i analogicznie dla pozostałych par sąsiednich kątów. Następnie używamy poprzedniego znaku.
3. Rozważmy trójkąty $ABC$ i $CDA$. Ponieważ $AC$ jest wspólne, z równości przeciwległych boków równoległoboku wynika, że trójkąty $ABC$ i $CDA$ są równe według trzeciego kryterium. Zatem $\angle BAC=\angle DCA$ i $\angle BCA=\angle DAC$, co implikuje równoległość przeciwnych stron.
4. Niech $BC$ i $AD$ będą równe i równoległe. Rozważmy trójkąty $ABC$ i $CDA$. Z równoległości prostych wynika, że $\angle BCA=\angle DAC$. Ponieważ $AC$ jest ogólne, a $BC=AD$, to trójkąty $ABC$ i $CDA$ są równe zgodnie z pierwszym kryterium. Zatem $AB=CD$. Następnie używamy poprzedniego znaku.
5. Niech $O$ będzie punktem przecięcia przekątnych oraz $AO=CO$ i $DO=BO$ Uwzględniając równość kątów pionowych otrzymujemy, że trójkąty $AOD$ i $COB$ są równe według pierwszego kryterium. Dlatego $\angle OAD=\angle OCB$, co implikuje równoległość $BC$ i $AD$. Podobnie dla drugiej pary boków.
Definicja
Nazywa się czworokąt, który ma trzy kąty proste prostokąt.
Właściwości prostokąta:
- Przekątne prostokąta są równe.
Dowód
Niech będzie dany prostokąt $ABCD$. Ponieważ prostokąt jest równoległobokiem, jego przeciwne boki są równe. Wtedy trójkąty prostokątne $ABD$ i $DCA$ są równe na dwóch nogach, co oznacza, że $BD=AC$.
Cechy prostokąta:
- Jeśli równoległobok ma kąt prosty, to ten równoległobok jest prostokątem.
- Jeżeli przekątne równoległoboku są równe, to ten równoległobok jest prostokątem.
Dowód
1. Jeżeli jeden z kątów równoległoboku jest prosty, to biorąc pod uwagę, że suma kątów przyległych wynosi 180 $(\circ)$, otrzymujemy, że pozostałe kąty są również proste.
2. Niech przekątne $AC$ i $BD$ w równoległoboku $ABCD$ będą równe. Biorąc pod uwagę równość przeciwległych boków $AB$ i $DC$, otrzymujemy, że trójkąty $ABD$ i $DCA$ są równe według trzeciego kryterium. Dlatego $\angle BAD=\angle CDA$, czyli są proste. Pozostaje użyć poprzedniego znaku.
Definicja
Nazywa się czworokąt, w którym wszystkie boki są równe diament
Właściwości rombu:
- Przekątne rombu są wzajemnie prostopadłe i stanowią dwusieczne jego kątów.
Dowód
Niech przekątne $AC$ i $BD$ rombu $ABCD$ przecinają się w punkcie $O$. Ponieważ romb jest równoległobokiem, $AO=OC$. Rozważmy Trójkąt równoramienny$ABC$. Ponieważ $AO$ to mediana narysowana do podstawy, wymagana była dwusieczna i wysokość.
Znaki diamentu:
- Jeżeli przekątne równoległoboku są wzajemnie prostopadłe, to ten równoległobok jest rombem.
- Jeśli przekątna równoległoboku jest dwusieczną jego kąta, to ten równoległobok jest rombem.
Dowód
Niech równoległobok $ABCD$ ma przekątne $AC$ i $BD$ przecinające się w punkcie $O$. Rozważmy trójkąt $ABC$.
1. Jeżeli przekątne są prostopadłe, to $BO$ jest medianą i wysokością trójkąta.
2. Jeżeli przekątna $BD$ zawiera dwusieczną kąta $ABC$, to $BO$ jest środkową i dwusieczną w trójkącie.
W obu przypadkach stwierdzamy, że trójkąt $ABC$ jest równoramienny, a w równoległoboku sąsiednie boki są równe. Dlatego jest to romb, co było wymagane.
Definicja
Nazywa się prostokąt, którego dwa sąsiednie boki są równe kwadrat.
Znaki kwadratu:
- Jeśli romb ma kąt prosty, to ten romb jest kwadratem.
- Jeśli romb ma równe przekątne, to romb jest kwadratem.
Dowód
Jeśli równoległobok ma kąt prosty lub równe przekątne, to jest prostokątem. Jeśli czworokąt jest prostokątem i rombem, to jest kwadratem.
Równoległobok to czworokąt, którego przeciwne strony są równoległe parami. Pole równoległoboku jest równe iloczynowi jego podstawy (a) i wysokości (h). Jego pole można również wyznaczyć poprzez dwa boki i kąt oraz poprzez przekątne.
Właściwości równoległoboku
1. Przeciwne strony są identyczne
Najpierw narysujmy przekątną \(AC\) . Otrzymujemy dwa trójkąty: \(ABC\) i \(ADC\).
Ponieważ \(ABCD\) jest równoległobokiem, prawdziwe jest następujące stwierdzenie:
\(AD || BC \Strzałka w prawo \kąt 1 = \kąt 2\) jak leżenie w poprzek.
\(AB || CD \Strzałka w prawo \kąt3 = \kąt 4\) jak leżenie w poprzek.
Dlatego (zgodnie z drugim kryterium: i \(AC\) jest powszechne).
I to oznacza, że \(\trójkąt ABC = \trójkąt ADC\), następnie \(AB = CD\) i \(AD = BC\) .
2. Przeciwne kąty są identyczne

Według dowodu właściwości 1 Wiemy to \(\kąt 1 = \kąt 2, \kąt 3 = \kąt 4\). Zatem suma kątów przeciwnych wynosi: \(\kąt 1 + \kąt 3 = \kąt 2 + \kąt 4\). Biorąc pod uwagę, że \(\trójkąt ABC = \trójkąt ADC\) otrzymujemy \(\angle A = \angle C \) , \(\angle B = \angle D \) .
3. Przekątne są podzielone na pół przez punkt przecięcia

Przez nieruchomość 1 wiemy, że przeciwne strony są identyczne: \(AB = CD\) . Jeszcze raz zwróć uwagę na leżące w poprzek równe kąty.
Zatem jest jasne, że \(\trójkąt AOB = \trójkąt COD\) zgodnie z drugim znakiem równości trójkątów (dwa kąty i bok między nimi). Oznacza to, że \(BO = OD\) (naprzeciwko kątów \(\kąt 2\) i \(\kąt 1\) ) i \(AO = OC\) (naprzeciwko kątów \(\kąt 3\) i \(odpowiednio \kąt 4\).
Znaki równoległoboku
Jeśli w Twoim problemie występuje tylko jedna cecha, wówczas figura jest równoległobokiem i możesz wykorzystać wszystkie właściwości tej figury.
Dla lepsze zapamiętywanie, zauważ, że test równoległoboku odpowie na następujące pytanie - „jak się dowiedzieć?”. To znaczy skąd wiesz co ustalona figura to jest równoległobok.
1. Równoległobok to czworokąt, którego dwa boki są równe i równoległe
\(AB = CD\) ; \(AB || CD \Strzałka w prawo ABCD\)- równoległobok.

Przyjrzyjmy się bliżej. Dlaczego \(AD || BC \)?
\(\trójkąt ABC = \trójkąt ADC\) Przez nieruchomość 1: \(AB = CD \) , \(\angle 1 = \angle 2 \) leżą poprzecznie, gdy \(AB \) i \(CD \) oraz sieczna \(AC \) są równoległe.
Ale jeśli \(\trójkąt ABC = \trójkąt ADC\), następnie \(\angle 3 = \angle 4 \) (leżą naprzeciwko \(AD || BC \) (\(\angle 3 \) i \(\angle 4 \) - te leżące w poprzek również są równe).
Pierwszy znak jest prawidłowy.
2. Równoległobok to czworokąt, którego przeciwne strony są równe
\(AB = CD \) , \(AD = BC \Strzałka w prawo ABCD \) jest równoległobokiem.

Rozważmy ten znak. Narysujmy ponownie przekątną \(AC\).
Przez nieruchomość 1\(\trójkąt ABC = \trójkąt ACD\).
Wynika, że: \(\kąt 1 = \angle 2 \Strzałka w prawo AD || BC \) I \(\kąt 3 = \kąt 4 \Strzałka w prawo AB || CD \), to znaczy \(ABCD\) jest równoległobokiem.
Drugi znak jest prawidłowy.
3. Równoległobok to czworokąt, którego przeciwległe kąty są równe
\(\kąt A = \kąt C\) , \(\kąt B = \kąt D \Strzałka w prawo ABCD\)- równoległobok.

\(2 \alfa + 2 \beta = 360^(\circ) \)(ponieważ \(\kąt A = \kąt C\) , \(\kąt B = \kąt D\) według warunku).
Okazało się, . Ale \(\alpha \) i \(\beta \) są wewnętrzne jednostronne w siecznej \(AB \) .
I co \(\alfa + \beta = 180^(\circ) \) mówi również, że \(AD || BC \) .
Dowód
Najpierw narysujmy przekątną AC. Otrzymujemy dwa trójkąty: ABC i ADC.

Ponieważ ABCD jest równoległobokiem, prawdziwe jest następujące stwierdzenie:
AD || BC \Strzałka w prawo \angle 1 = \angle 2 jak leżenie w poprzek.
AB || CD\Strzałka w prawo\kąt3 =\kąt 4 jak leżenie w poprzek.
Zatem \triangle ABC = \triangle ADC (według drugiego kryterium: i AC jest wspólne).
A zatem \triangle ABC = \triangle ADC, następnie AB = CD i AD = BC.
Udowodniony!
2. Przeciwne kąty są identyczne.

Dowód
Według dowodu właściwości 1 Wiemy to \angle 1 = \angle 2, \angle 3 = \angle 4. Zatem suma kątów przeciwnych wynosi: \angle 1 + \angle 3 = \angle 2 + \angle 4. Biorąc pod uwagę, że \triangle ABC = \triangle ADC otrzymujemy \angle A = \angle C , \angle B = \angle D .
Udowodniony!
3. Przekątne są podzielone na pół przez punkt przecięcia.

Dowód
Narysujmy kolejną przekątną.

Przez nieruchomość 1 wiemy, że przeciwne strony są identyczne: AB = CD. Jeszcze raz zwróć uwagę na leżące w poprzek równe kąty.
Zatem jasne jest, że \triangle AOB = \triangle COD zgodnie z drugim kryterium równości trójkątów (dwa kąty i bok między nimi). Oznacza to, że BO = OD (naprzeciwko narożników \angle 2 i \angle 1) i AO = OC (naprzeciwko odpowiednio narożników \angle 3 i \angle 4).

Udowodniony!
Znaki równoległoboku
Jeśli w Twoim problemie występuje tylko jedna cecha, wówczas figura jest równoległobokiem i możesz wykorzystać wszystkie właściwości tej figury.
Dla lepszego zapamiętywania zwróć uwagę, że znak równoległoboku odpowie na następujące pytanie: „jak się dowiedzieć?”. To znaczy, jak dowiedzieć się, że dana figura jest równoległobokiem.
1. Równoległobok to czworokąt, którego dwa boki są równe i równoległe.

AB = CD; AB || CD\Rightarrow ABCD jest równoległobokiem.
Dowód
Przyjrzyjmy się bliżej. Dlaczego AD || PNE?

\triangle ABC = \triangle ADC wg nieruchomość 1: AB = CD, AC - wspólne i \angle 1 = \angle 2 leżące poprzecznie z równoległymi AB i CD oraz sieczną AC.
Ale jeśli \triangle ABC = \triangle ADC , to \angle 3 = \angle 4 (leżą odpowiednio naprzeciw AB i CD). A zatem AD || BC (\angle 3 i \angle 4 - te leżące w poprzek też są równe).

Pierwszy znak jest prawidłowy.
2. Równoległobok to czworokąt, którego przeciwne strony są równe.

AB = CD, AD = BC \Strzałka w prawo ABCD jest równoległobokiem.
Dowód
Rozważmy ten znak. Narysujmy jeszcze raz przekątną AC.

Przez nieruchomość 1\trójkąt ABC = \trójkąt ACD .

Wynika, że: \angle 1 = \angle 2 \Strzałka w prawo AD || PNE. I \angle 3 = \angle 4 \Strzałka w prawo AB || płyta CD, czyli ABCD jest równoległobokiem.
Drugi znak jest prawidłowy.
3. Równoległobok to czworokąt, którego przeciwległe kąty są równe.

\angle A = \angle C , \angle B = \angle D \Strzałka w prawo ABCD- równoległobok.
Dowód

2 \alfa + 2 \beta = 360^(\circ)(ponieważ ABCD jest czworokątem i \angle A = \angle C , \angle B = \angle D według warunku).
Okazuje się, że \alpha + \beta = 180^(\circ) . Ale \alfa i \beta są jednostronne wewnętrzne w siecznej AB.
A fakt, że \alpha + \beta = 180^(\circ) oznacza również, że AD || PNE.
Co więcej, \alpha i \beta są jednostronne wewnętrznie w siecznej AD. A to oznacza AB || PŁYTA CD.
Trzeci znak jest prawidłowy.
4. Równoległobok to czworokąt, którego przekątne są podzielone na pół w punkcie przecięcia.

AO = OC; BO = Równoległobok OD\Strzałka w prawo.
Dowód

BO = OD; AO = OC , \angle 1 = \angle 2 w pionie \Strzałka w prawo \triangle AOB = \triangle COD, \Strzałka w prawo \kąt 3 = \kąt 4 i \Rightarrow AB || PŁYTA CD.
Podobnie BO = OD; AO = OC, \angle 5 = \angle 6 \Strzałka w prawo \triangle AOD = \triangle BOC \Strzałka w prawo \angle 7 = \angle 8 i \Rightarrow AD || PNE.
Czwarty znak jest poprawny.







