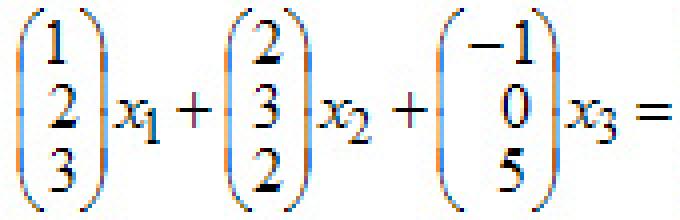Wyrażenie formy zwany liniowa kombinacja wektorów A 1 , A 2 ,...,A n z szansami λ 1, λ 2 ,..., λ n.

Wyznaczanie zależności liniowej układu wektorów

System wektorowy A 1 , A 2 ,...,A n zwany liniowo zależne, jeśli istnieje niezerowy zbiór liczb λ 1, λ 2 ,..., λ n, w którym liniowa kombinacja wektorów λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n równy wektorowi zerowemu, czyli układ równań: ma niezerowe rozwiązanie.
Zestaw liczb λ 1, λ 2 ,..., λ n jest różna od zera, jeśli co najmniej jedna z liczb λ 1, λ 2 ,..., λ n różny od zera.

Wyznaczanie liniowej niezależności układu wektorów

System wektorowy A 1 , A 2 ,...,A n zwany liniowo niezależny, jeżeli jest to kombinacja liniowa tych wektorów λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n równy wektorowi zerowemu tylko dla zerowego zbioru liczb λ 1, λ 2 ,..., λ n , czyli układ równań: A 1 x 1 +A 2 x 2 +...+A n x n =Θ ma unikalne rozwiązanie zerowe.

Przykład 29.1

Sprawdź, czy układ wektorów jest liniowo zależny

Rozwiązanie:

1. Tworzymy układ równań:

2. Rozwiązujemy to metodą Gaussa. Transformacje Jordanano układu przedstawiono w tabeli 29.1. Przy obliczeniach nie zapisuje się prawych stron układu, gdyż są one równe zeru i nie zmieniają się podczas przekształceń Jordana.

3. Z trzech ostatnich wierszy tabeli zapisz rozwiązany system równoważny oryginalnemu system:

4. Otrzymujemy rozwiązanie ogólne układu:

5. Po ustawieniu wartości zmiennej wolnej x 3 =1 według własnego uznania, otrzymujemy szczególne niezerowe rozwiązanie X=(-3,2,1).

Odpowiedź: Zatem dla niezerowego zbioru liczb (-3,2,1) liniowa kombinacja wektorów jest równa wektorowi zerowemu -3A 1 +2A 2 +1A 3 =Θ. Stąd, układ wektorowy liniowo zależny.

Właściwości układów wektorowych

Nieruchomość (1)
Jeżeli układ wektorów jest liniowo zależny, to co najmniej jeden z wektorów jest rozwijany względem pozostałych i odwrotnie, jeśli przynajmniej jeden z wektorów układu jest rozwijany względem pozostałych, to układ wektorów jest liniowo zależna.

Nieruchomość (2)
Jeśli dowolny podukład wektorów jest liniowo zależny, to cały układ jest liniowo zależny.

Nieruchomość (3)
Jeśli układ wektorów jest liniowo niezależny, to każdy z jego podukładów jest liniowo niezależny.

Nieruchomość (4)
Dowolny układ wektorów zawierający wektor zerowy jest liniowo zależny.

Nieruchomość (5)
Układ m-wymiarowych wektorów jest zawsze liniowo zależny, jeśli liczba wektorów n jest większa niż ich wymiar (n>m)

Podstawa układu wektorowego

Podstawa systemu wektorowego A 1 , A 2 ,..., An taki podsystem B 1 , B 2 ,...,B r nazywa się(każdy z wektorów B 1, B 2,..., B r jest jednym z wektorów A 1, A 2,..., An), co spełnia następujące warunki:
1. B 1 , B 2 ,..., B r liniowo niezależny układ wektorów;
2. dowolny wektor A j układ A 1 , A 2 ,..., An wyraża się liniowo poprzez wektory B 1 , B 2 ,..., B r

R— liczba wektorów zawartych w bazie.

Twierdzenie 29.1 Na bazie jednostkowej układu wektorów.

Jeżeli układ m-wymiarowych wektorów zawiera m różnych wektorów jednostkowych E 1 E 2 ,..., Em , to stanowią one podstawę układu.

Algorytm znajdowania bazy układu wektorów

Aby znaleźć bazę układu wektorów A 1 , A 2 ,...,A n należy:

  • Utwórz jednorodny układ równań odpowiadający układowi wektorów A 1 x 1 +A 2 x 2 +...+A n x n =Θ
  • Przynieś ten system

Wektory, ich właściwości i działania z nimi związane

Wektory, działania z wektorami, liniowa przestrzeń wektorowa.

Wektory są uporządkowanym zbiorem skończonej liczby liczb rzeczywistych.

Działania: 1.Mnożenie wektora przez liczbę: lambda*wektor x=(lamda*x 1, lambda*x 2 ... lambda*x n).(3,4, 0, 7)*3=(9, 12,0,21)

2. Dodawanie wektorów (należących do tej samej przestrzeni wektorowej) wektor x + wektor y = (x 1 + y 1, x 2 + y 2, ... x n + y n,)

3. Wektor 0=(0,0…0)---n E n – n-wymiarowy (przestrzeń liniowa) wektor x + wektor 0 = wektor x

Twierdzenie. Aby układ n wektorów, n-wymiarowa przestrzeń liniowa, był liniowo zależny, konieczne i wystarczające jest, aby jeden z wektorów był liniową kombinacją pozostałych.

Twierdzenie. Dowolny zbiór n+ pierwszych wektorów n-wymiarowej przestrzeni liniowej zjawisk. liniowo zależne.

Dodawanie wektorów, mnożenie wektorów przez liczby. Odejmowanie wektorów.

Suma dwóch wektorów jest wektorem skierowanym od początku wektora do końca wektora, pod warunkiem, że początek pokrywa się z końcem wektora. Jeżeli wektory są dane przez ich rozwinięcia w wektorach jednostek bazowych, to przy dodawaniu wektorów dodawane są odpowiadające im współrzędne.

Rozważmy to na przykładzie kartezjańskiego układu współrzędnych. Pozwalać

Pokażmy to

Z rysunku 3 jasno wynika, że

Sumę dowolnej skończonej liczby wektorów można obliczyć korzystając z reguły wielokąta (ryc. 4): aby skonstruować sumę skończonej liczby wektorów, wystarczy połączyć początek każdego kolejnego wektora z końcem poprzedniego i skonstruuj wektor łączący początek pierwszego wektora z końcem ostatniego.

Właściwości operacji dodawania wektorów:

W tych wyrażeniach m, n są liczbami.

Różnicę między wektorami nazywamy wektorem. Drugi człon to wektor przeciwny do wektora w kierunku, ale równy mu długości.

Zatem operację odejmowania wektorów zastępuje się operacją dodawania

Wektor, którego początek znajduje się w początku, a kończy w punkcie A (x1, y1, z1) nazywany jest wektorem promienia punktu A i jest po prostu oznaczany. Ponieważ jego współrzędne pokrywają się ze współrzędnymi punktu A, jego rozwinięcie w wektory jednostkowe ma postać

Wektor rozpoczynający się w punkcie A(x1, y1, z1) i kończący się w punkcie B(x2, y2, z2) można zapisać jako

gdzie r 2 jest wektorem promienia punktu B; r 1 - wektor promienia punktu A.

Dlatego rozwinięcie wektora w wektorach jednostkowych ma postać

Jego długość jest równa odległości między punktami A i B

MNOŻENIE

Zatem w przypadku problemu płaskiego iloczyn wektora przez a = (ax; ay) przez liczbę b oblicza się ze wzoru

a b = (ax b; ay b)

Przykład 1. Znajdź iloczyn wektora a = (1; 2) przez 3.

3 za = (3 1; 3 2) = (3; 6)

Zatem w przypadku problemu przestrzennego iloczyn wektora a = (ax; ay; az) przez liczbę b można znaleźć według wzoru

a b = (ax b; ay b; az b)

Przykład 1. Znajdź iloczyn wektora a = (1; 2; -5) przez 2.

2 za = (2 1; 2 2; 2 (-5)) = (2; 4; -10)

Iloczyn skalarny wektorów i gdzie jest kątem między wektorami i ; jeśli jedno, to

Z definicji iloczynu skalarnego wynika, że

gdzie, na przykład, jest wielkością rzutu wektora na kierunek wektora.

Skalarny kwadrat wektora:

Właściwości iloczynu skalarnego:

Iloczyn skalarny we współrzędnych

Jeśli To

Kąt między wektorami

Kąt między wektorami - kąt między kierunkami tych wektorów (najmniejszy kąt).

Iloczyn krzyżowy (Iloczyn krzyżowy dwóch wektorów.) - jest to pseudowektor prostopadły do ​​płaszczyzny zbudowanej z dwóch czynników, będący wynikiem operacji binarnej „mnożenia wektorów” po wektorach w trójwymiarowej przestrzeni euklidesowej. Iloczyn nie jest ani przemienny, ani łączny (jest antyprzemienny) i różni się od iloczynu skalarnego wektorów. W wielu zadaniach inżynierskich i fizycznych trzeba umieć skonstruować wektor prostopadły do ​​dwóch istniejących - iloczyn wektorowy zapewnia taką możliwość. Iloczyn krzyżowy jest przydatny do „pomiaru” prostopadłości wektorów - długość iloczynu krzyżowego dwóch wektorów jest równa iloczynowi ich długości, jeśli są one prostopadłe i maleje do zera, jeśli wektory są równoległe lub antyrównoległe.

Iloczyn krzyżowy definiuje się tylko w przestrzeniach trójwymiarowych i siedmiwymiarowych. Wynik iloczynu wektorowego, podobnie jak iloczynu skalarnego, zależy od metryki przestrzeni euklidesowej.

W przeciwieństwie do wzoru na obliczanie wektorów iloczynu skalarnego ze współrzędnych w trójwymiarowym prostokątnym układzie współrzędnych, wzór na iloczyn poprzeczny zależy od orientacji prostokątnego układu współrzędnych, czyli innymi słowy od jego „chiralności”

Kolinearność wektorów.

Dwa niezerowe (nierówne 0) wektory nazywane są współliniowymi, jeśli leżą na prostych równoległych lub na tej samej prostej. Dopuszczalnym, ale nie zalecanym synonimem są wektory „równoległe”. Wektory współliniowe mogą być skierowane identycznie („współkierunkowo”) lub przeciwnie (w tym drugim przypadku są czasami nazywane „antywspółliniowymi” lub „antyrównoległymi”).

Mieszany iloczyn wektorów ( a, b, c)- iloczyn skalarny wektora a oraz iloczyn wektorowy wektorów b i c:

(a,b,c)=a ⋅(b ×c)

czasami nazywa się to iloczynem potrójnej kropki wektorów, najwyraźniej dlatego, że wynikiem jest skalar (a dokładniej pseudoskalar).

Znaczenie geometryczne: moduł iloczynu zmieszanego jest liczbowo równy objętości równoległościanu utworzonego przez wektory (ABC) .

Nieruchomości

Iloczyn mieszany jest skośno-symetryczny w odniesieniu do wszystkich swoich argumentów: tj. e. przestawienie dowolnych dwóch czynników zmienia znak iloczynu. Wynika z tego, że iloczyn mieszany w prawym kartezjańskim układzie współrzędnych (w bazie ortonormalnej) jest równy wyznacznikowi macierzy złożonej z wektorów i:

Iloczyn mieszany w lewym kartezjańskim układzie współrzędnych (w bazie ortonormalnej) jest równy wyznacznikowi macierzy złożonej z wektorów i wzięty ze znakiem minus:

W szczególności,

Jeśli dowolne dwa wektory są równoległe, to z dowolnym trzecim wektorem tworzą iloczyn mieszany równy zero.

Jeśli trzy wektory są liniowo zależne (to znaczy współpłaszczyznowe, leżące w tej samej płaszczyźnie), to ich iloczyn mieszany jest równy zero.

Znaczenie geometryczne - Iloczyn mieszany jest w wartości bezwzględnej równy objętości równoległościanu (patrz rysunek) utworzonej przez wektory i; znak zależy od tego, czy ta trójka wektorów jest prawoskrętna, czy lewoskrętna.

Współpłaszczyznowość wektorów.

Trzy wektory (lub więcej) nazywane są współpłaszczyznowymi, jeśli po sprowadzeniu ich do wspólnego początku leżą w tej samej płaszczyźnie

Własności współpłaszczyznowości

Jeśli co najmniej jeden z trzech wektorów ma wartość zero, wówczas te trzy wektory są również uważane za współpłaszczyznowe.

Trójka wektorów zawierających parę współliniowych wektorów jest współpłaszczyznowa.

Iloczyn mieszany wektorów współpłaszczyznowych. Jest to kryterium współpłaszczyznowości trzech wektorów.

Wektory współpłaszczyznowe są liniowo zależne. Jest to również kryterium współpłaszczyznowości.

W przestrzeni trójwymiarowej podstawą są 3 niewspółpłaszczyznowe wektory

Wektory liniowo zależne i liniowo niezależne.

Liniowo zależne i niezależne układy wektorowe.Definicja. Nazywa się system wektorowy liniowo zależne, jeśli istnieje co najmniej jedna nietrywialna kombinacja liniowa tych wektorów równa wektorowi zerowemu. W przeciwnym razie, tj. jeśli tylko trywialna kombinacja liniowa danych wektorów jest równa wektorowi zerowemu, wektory są wywoływane liniowo niezależny.

Twierdzenie (kryterium zależności liniowej). Aby układ wektorów w przestrzeni liniowej był liniowo zależny, konieczne i wystarczające jest, aby przynajmniej jeden z tych wektorów był liniową kombinacją pozostałych.

1) Jeżeli wśród wektorów znajduje się co najmniej jeden wektor zerowy, to cały układ wektorów jest liniowo zależny.

Faktycznie, jeśli np. , to zakładając , mamy nietrywialną kombinację liniową .▲

2) Jeżeli wśród wektorów niektóre tworzą układ liniowo zależny, to cały układ jest liniowo zależny.

Rzeczywiście, niech wektory , , będą liniowo zależne. Oznacza to, że istnieje nietrywialna kombinacja liniowa równa wektorowi zerowemu. Ale wtedy, zakładając , otrzymujemy także nietrywialną kombinację liniową równą wektorowi zerowemu.

2. Podstawa i wymiar. Definicja. Układ wektorów liniowo niezależnych nazywa się przestrzeń wektorową podstawa tej przestrzeni, jeśli dowolny wektor z można przedstawić jako kombinację liniową wektorów tego układu, tj. dla każdego wektora istnieją liczby rzeczywiste tak, że zachodzi równość. Tę równość nazywamy rozkład wektorowy według podstawy i liczb są nazywane współrzędne wektora względem podstawy(Lub w podstawie) .

Twierdzenie (o jednoznaczności rozwinięcia względem bazy). Każdy wektor w przestrzeni można rozwinąć w bazę w jedyny sposób, tj. współrzędne każdego wektora w bazie są określone jednoznacznie.

W tym artykule omówimy:

  • czym są wektory współliniowe;
  • jakie są warunki kolinearności wektorów;
  • jakie istnieją właściwości wektorów współliniowych;
  • jaka jest liniowa zależność wektorów współliniowych.
Definicja 1

Wektory współliniowe to wektory, które są równoległe do jednej linii lub leżą na jednej linii.

Przykład 1

Warunki współliniowości wektorów

Dwa wektory są współliniowe, jeśli spełniony jest którykolwiek z poniższych warunków:

  • warunek 1 . Wektory aib są współliniowe, jeśli istnieje liczba λ taka, że ​​a = λ b;
  • warunek 2 . Wektory aib są współliniowe przy równych stosunkach współrzędnych:

za = (za 1 ; za 2) , b = (b 1 ; b 2) ⇒ za ∥ b ⇔ za 1 b 1 = za 2 b 2

  • warunek 3 . Wektory aib są współliniowe pod warunkiem, że iloczyn poprzeczny i wektor zerowy są równe:

za ∥ b ⇔ za, b = 0

Notatka 1

Warunek 2 nie ma zastosowania, jeśli jedna ze współrzędnych wektora wynosi zero.

Uwaga 2

Warunek 3 dotyczy tylko tych wektorów, które są określone w przestrzeni.

Przykłady problemów badania kolinearności wektorów

Przykład 1

Sprawdzamy kolinearność wektorów a = (1; 3) i b = (2; 1).

Jak rozwiązać?

W takim przypadku konieczne jest zastosowanie drugiego warunku współliniowości. Dla podanych wektorów wygląda to następująco:

Równość jest fałszywa. Z tego możemy wywnioskować, że wektory aib są niewspółliniowe.

Odpowiedź : za | | B

Przykład 2

Jaka wartość m wektora a = (1; 2) i b = (- 1; m) jest konieczna, aby wektory były współliniowe?

Jak rozwiązać?

Korzystając z drugiego warunku współliniowości, wektory będą współliniowe, jeśli ich współrzędne są proporcjonalne:

To pokazuje, że m = - 2.

Odpowiedź: m = - 2 .

Kryteria zależności liniowej i liniowej niezależności układów wektorowych

Twierdzenie

Układ wektorów w przestrzeni wektorowej jest liniowo zależny tylko wtedy, gdy jeden z wektorów układu można wyrazić w postaci pozostałych wektorów tego układu.

Dowód

Niech system e 1 , e 2 , . . . , e n jest liniowo zależne. Zapiszmy kombinację liniową tego układu równą wektorowi zerowemu:

za 1 mi 1 + za 2 mi 2 + . . . + za n mi n = 0

w którym co najmniej jeden ze współczynników kombinacji nie jest równy zero.

Niech a k ≠ 0 k ∈ 1 , 2 , . . . , N.

Obie strony równości dzielimy przez niezerowy współczynnik:

za k - 1 (ak - 1 za 1) mi 1 + (ak - 1 za k) e k + . . . + (a k - 1 za n) mi n = 0

Oznaczmy:

A k - 1 a m , gdzie m ∈ 1 , 2 , . . . , k - 1 , k + 1 , rz

W tym przypadku:

β 1 mi 1 + . . . + β k - 1 e k - 1 + β k + 1 e k + 1 + . . . + β n mi n = 0

lub mi k = (- β 1) mi 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) i n

Wynika z tego, że jeden z wektorów układu wyraża się poprzez wszystkie pozostałe wektory układu. To właśnie należało udowodnić (itp.).

Adekwatność

Niech jeden z wektorów będzie wyrażony liniowo przez wszystkie pozostałe wektory układu:

mi k = γ 1 mi 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1 + . . . + γ n mi n

Przesuwamy wektor e k na prawą stronę tej równości:

0 = γ 1 mi 1 + . . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1 + . . . + γ n mi n

Ponieważ współczynnik wektora e k jest równy - 1 ≠ 0, otrzymujemy nietrywialną reprezentację zera za pomocą układu wektorów e 1, e 2, . . . , e n , a to z kolei oznacza, że ​​ten układ wektorów jest liniowo zależny. To właśnie należało udowodnić (itp.).

Konsekwencja:

  • Układ wektorów jest liniowo niezależny, gdy żaden z jego wektorów nie może być wyrażony w postaci wszystkich innych wektorów układu.
  • Układ wektorów zawierający wektor zerowy lub dwa równe wektory jest liniowo zależny.

Własności wektorów liniowo zależnych

  1. Dla wektorów 2- i 3-wymiarowych spełniony jest warunek: dwa wektory liniowo zależne są współliniowe. Dwa współliniowe wektory są liniowo zależne.
  2. Dla wektorów trójwymiarowych spełniony jest warunek: trzy wektory liniowo zależne są współpłaszczyznowe. (3 wektory współpłaszczyznowe są liniowo zależne).
  3. Dla wektorów n-wymiarowych spełniony jest warunek: wektory n + 1 są zawsze liniowo zależne.

Przykłady rozwiązywania problemów z liniową zależnością lub liniową niezależnością wektorów

Przykład 3

Sprawdźmy wektory a = 3, 4, 5, b = - 3, 0, 5, c = 4, 4, 4, d = 3, 4, 0 pod kątem liniowej niezależności.

Rozwiązanie. Wektory są liniowo zależne, ponieważ wymiar wektorów jest mniejszy niż liczba wektorów.

Przykład 4

Sprawdźmy wektory a = 1, 1, 1, b = 1, 2, 0, c = 0, - 1, 1 pod kątem liniowej niezależności.

Rozwiązanie. Znajdujemy wartości współczynników, przy których kombinacja liniowa będzie równa wektorowi zerowemu:

x 1 za + x 2 b + x 3 do 1 = 0

Równanie wektora zapisujemy w postaci liniowej:

x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0

Rozwiązujemy ten układ metodą Gaussa:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

Od drugiej linii odejmujemy pierwszą, od trzeciej - pierwszą:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

Od pierwszej linii odejmujemy drugą, do trzeciej dodajemy drugą:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

Z rozwiązania wynika, że ​​układ ma wiele rozwiązań. Oznacza to, że istnieje niezerowa kombinacja wartości takich liczb x 1, x 2, x 3, dla których kombinacja liniowa a, b, c jest równa wektorowi zerowemu. Dlatego wektory a, b, c są liniowo zależne. ​​​​​​​

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Wprowadzony przez nas operacje liniowe na wektorach umożliwiają tworzenie różnych wyrażeń wielkości wektorowe i przekształcaj je, korzystając z właściwości ustawionych dla tych operacji.

Na podstawie danego zbioru wektorów a 1, ..., a n można utworzyć wyrażenie postaci

gdzie a 1, ... i n są dowolnymi liczbami rzeczywistymi. To wyrażenie nazywa się liniowa kombinacja wektorów a 1, ..., n. Liczby α i, i = 1, n reprezentują współczynniki kombinacji liniowej. Zbiór wektorów nazywany jest również układ wektorów.

W związku z wprowadzoną koncepcją kombinacji liniowej wektorów pojawia się problem opisania zbioru wektorów, który można zapisać jako kombinację liniową danego układu wektorów a 1, ..., a n. Poza tym naturalne są pytania o warunki, w jakich istnieje reprezentacja wektora w postaci kombinacji liniowej oraz o jednoznaczność takiej reprezentacji.

Definicja 2.1. Nazywa się wektory a 1, ... i n liniowo zależne, jeśli istnieje zbiór współczynników α 1 , ... , α n taki, że

α 1 za 1 + ... + α n а n = 0 (2.2)

i co najmniej jeden z tych współczynników jest niezerowy. Jeśli określony zbiór współczynników nie istnieje, wywoływane są wektory liniowo niezależny.

Jeśli α 1 = ... = α n = 0, to oczywiście α 1 a 1 + ... + α n a n = 0. Mając to na uwadze, możemy powiedzieć tak: wektory a 1, ... i n są liniowo niezależne, jeżeli z równości (2.2) wynika, że ​​wszystkie współczynniki α 1 , ... , α n są równe zeru.

Poniższe twierdzenie wyjaśnia, dlaczego nowe pojęcie nosi nazwę „zależność” (lub „niezależność”) i dostarcza prostego kryterium zależności liniowej.

Twierdzenie 2.1. Aby wektory a 1, ... i n, n > 1 były liniowo zależne, konieczne i wystarczające jest, aby jeden z nich był liniową kombinacją pozostałych.

◄ Konieczność. Załóżmy, że wektory a 1, ... i n są liniowo zależne. Zgodnie z definicją 2.1 zależności liniowej, w równości (2.2) po lewej stronie znajduje się co najmniej jeden niezerowy współczynnik, np. α 1. Pozostawiając pierwszy wyraz po lewej stronie równości, resztę przesuwamy na prawą stronę, jak zwykle zmieniając ich znaki. Dzieląc wynikową równość przez α 1, otrzymujemy

za 1 =-α 2 /α 1 ⋅ za 2 - ... - α n /α 1 ⋅ za n

te. reprezentacja wektora a 1 jako kombinacja liniowa pozostałych wektorów a 2, ..., an.

Adekwatność. Niech na przykład pierwszy wektor a 1 można przedstawić jako kombinację liniową pozostałych wektorów: a 1 = β 2 a 2 + ... + β n a n. Przenosząc wszystkie wyrazy z prawej strony na lewą, otrzymujemy a 1 - β 2 a 2 - ... - β n a n = 0, tj. liniowa kombinacja wektorów a 1, ..., an o współczynnikach α 1 = 1, α 2 = - β 2, ..., α n = - β n, równe wektor zerowy. W tej kombinacji liniowej nie wszystkie współczynniki wynoszą zero. Zgodnie z definicją 2.1 wektory a 1, ... i n są liniowo zależne.

Definicja i kryterium zależności liniowej są sformułowane tak, aby sugerować obecność dwóch lub więcej wektorów. Można jednak mówić także o liniowej zależności jednego wektora. Aby zrealizować tę możliwość, zamiast „wektory są liniowo zależne”, należy powiedzieć „układ wektorów jest liniowo zależny”. Łatwo zauważyć, że wyrażenie „układ jednego wektora jest liniowo zależny” oznacza, że ​​ten pojedynczy wektor ma wartość zero (w kombinacji liniowej występuje tylko jeden współczynnik i nie powinien on być równy zero).

Pojęcie zależności liniowej ma prostą interpretację geometryczną. Poniższe trzy stwierdzenia wyjaśniają tę interpretację.

Twierdzenie 2.2. Dwa wektory są liniowo zależne wtedy i tylko wtedy, gdy współliniowy.

◄ Jeśli wektory a i b są liniowo zależne, to jeden z nich, na przykład a, wyraża się przez drugi, tj. a = λb dla pewnej liczby rzeczywistej λ. Zgodnie z definicją 1.7 Pracuje wektory na liczbę, wektory aib są współliniowe.

Niech teraz wektory aib będą współliniowe. Jeśli oba mają wartość zerową, to oczywiste jest, że są one liniowo zależne, ponieważ jakakolwiek ich kombinacja liniowa jest równa wektorowi zerowemu. Niech jeden z tych wektorów nie będzie równy 0, na przykład wektor b. Oznaczmy przez λ stosunek długości wektorów: λ = |a|/|b|. Mogą być wektory współliniowe jednokierunkowy Lub skierowane przeciwnie. W tym drugim przypadku zmieniamy znak λ. Następnie sprawdzając Definicję 1.7, jesteśmy przekonani, że a = λb. Zgodnie z Twierdzeniem 2.1 wektory aib są liniowo zależne.

Uwaga 2.1. W przypadku dwóch wektorów, biorąc pod uwagę kryterium zależności liniowej, sprawdzone twierdzenie można przeformułować w następujący sposób: dwa wektory są współliniowe wtedy i tylko wtedy, gdy jeden z nich jest przedstawiony jako iloczyn drugiego przez liczbę. Jest to wygodne kryterium kolinearności dwóch wektorów.

Twierdzenie 2.3. Trzy wektory są liniowo zależne wtedy i tylko wtedy, gdy współpłaszczyznowy.

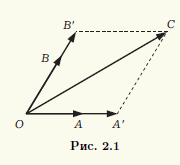
◄ Jeżeli trzy wektory a, b, c są liniowo zależne, to zgodnie z Twierdzeniem 2.1 jeden z nich, np. a, jest liniową kombinacją pozostałych: a = βb + γс. Połączmy początki wektorów b i c w punkcie A. Wtedy wektory βb, γс będą miały wspólny początek w punkcie A i wzdłuż zgodnie z zasadą równoległoboku ich suma wynosi te. wektor a będzie wektorem o początku A i koniec, który jest wierzchołkiem równoległoboku zbudowanego na wektorach składowych. Zatem wszystkie wektory leżą w tej samej płaszczyźnie, tj. Współpłaszczyznowej.

Niech wektory a, b, c będą współpłaszczyznowe. Jeśli jeden z tych wektorów ma wartość zero, to będzie to oczywiście kombinacja liniowa pozostałych. Wystarczy przyjąć wszystkie współczynniki kombinacji liniowej równe zero. Dlatego możemy założyć, że wszystkie trzy wektory nie są zerowe. Zgodny Rozpoczęty tych wektorów w wspólnym punkcie O. Niech ich końcami będą odpowiednio punkty A, B, C (ryc. 2.1). Przez punkt C rysujemy proste równoległe do prostych przechodzących przez pary punktów O, A i O, B. Wyznaczając punkty przecięcia jako A” i B”, otrzymujemy równoległobok OA”CB”, zatem OC” = OA” + OB". Wektor OA" i niezerowy wektor a = OA są współliniowe, dlatego pierwszy z nich można otrzymać mnożąc drugi przez liczbę rzeczywistą α:OA" = αOA. Podobnie OB" = βOB, β ∈ R. Otrzymujemy, że OC" = α OA + βOB, czyli wektor c jest liniową kombinacją wektorów a i b. Zgodnie z Twierdzeniem 2.1 wektory a, b, c są liniowo zależne.

Twierdzenie 2.4. Dowolne cztery wektory są liniowo zależne.

◄ Dowód przeprowadzamy według tego samego schematu, co w Twierdzeniu 2.3. Rozważmy dowolne cztery wektory a, b, cid. Jeśli jeden z czterech wektorów ma wartość zero lub są wśród nich dwa wektory współliniowe lub trzy z czterech wektorów są współpłaszczyznowe, wówczas te cztery wektory są liniowo zależne. Na przykład, jeśli wektory aib są współliniowe, to możemy utworzyć ich kombinację liniową αa + βb = 0 z niezerowymi współczynnikami, a następnie dodać pozostałe dwa wektory do tej kombinacji, przyjmując zera jako współczynniki. Otrzymujemy kombinację liniową czterech wektorów równych 0, w których występują niezerowe współczynniki.

Możemy zatem założyć, że spośród wybranych czterech wektorów żaden wektor nie jest zerowy, żadne dwa nie są współliniowe i żadne trzy nie są współpłaszczyznowe. Jako ich wspólny początek wybierzmy punkt O. Wtedy końcami wektorów a, b, c, d będą punkty A, B, C, D (rys. 2.2). Przez punkt D przeciągamy trzy płaszczyzny równoległe do płaszczyzn OBC, OCA, OAB i niech A”, B”, C” będą punktami przecięcia tych płaszczyzn z prostymi, odpowiednio OA, OB, OS. Otrzymujemy równoległościan OA" C "B" C" B"DA", a wektory a, b, c leżą na jego krawędziach wychodzących z wierzchołka O. Ponieważ czworokąt OC"DC" jest równoległobokiem, to OD = OC" + OC". Z kolei odcinek OC" jest równoległobokiem ukośnym OA"C"B", zatem OC" = OA" + OB" i OD = OA" + OB" + OC" .

Pozostaje zauważyć, że pary wektorów OA ≠ 0 i OA" , OB ≠ 0 i OB" , OC ≠ 0 i OC" są współliniowe, dlatego można tak dobrać współczynniki α, β, γ, że OA" = αOA, OB" = βOB i OC" = γOC. W końcu otrzymujemy OD = αOA + βOB + γOC. W konsekwencji wektor OD jest wyrażany przez pozostałe trzy wektory, a wszystkie cztery wektory, zgodnie z Twierdzeniem 2.1, są liniowo zależne.

Definicja 1. Liniowa kombinacja wektorów jest sumą iloczynów tych wektorów i skalarów
:

Definicja 2. System wektorowy
nazywa się układem liniowo zależnym, jeśli ich kombinacja liniowa (2.8) zanika:

i wśród liczb
istnieje co najmniej jeden, który jest różny od zera.

Definicja 3. Wektory
nazywane są liniowo niezależnymi, jeśli ich kombinacja liniowa (2.8) zanika tylko w przypadku, gdy wszystkie liczby.

Z tych definicji można uzyskać następujące wnioski.

Wniosek 1. W liniowo zależnym układzie wektorów co najmniej jeden wektor można wyrazić jako liniową kombinację pozostałych.

Dowód. Niech będzie spełniony (2.9) i dla pewności niech współczynnik
. Mamy wtedy:
. Należy pamiętać, że sytuacja odwrotna jest również prawdziwa.

Konsekwencja 2. Jeżeli układ wektorów
zawiera wektor zerowy, to układ ten jest (z konieczności) liniowo zależny - dowód jest oczywisty.

Konsekwencja 3. Jeśli wśród N wektory
każdy k(
) wektory są liniowo zależne, to wszystko N wektory są liniowo zależne (pominiemy dowód).

2 0 . Kombinacje liniowe dwóch, trzech i czterech wektorów. Rozważmy zagadnienia liniowej zależności i niezależności wektorów na prostej, płaszczyźnie i w przestrzeni. Przedstawmy odpowiednie twierdzenia.

Twierdzenie 1. Aby dwa wektory były liniowo zależne, konieczne i wystarczające jest, aby były one współliniowe.

Konieczność. Niech wektory I liniowo zależne. Oznacza to, że ich kombinacja liniowa
=0 i (dla pewności)
. Oznacza to równość
oraz (z definicji mnożenia wektora przez liczbę) wektory I współliniowy.

Adekwatność. Niech wektory I współliniowy ( ║) (zakładamy, że są one różne od wektora zerowego, w przeciwnym razie ich liniowa zależność jest oczywista).

Z Twierdzenia (2.7) (patrz §2.1, poz. 2 0) wówczas
takie, że
, Lub
– kombinacja liniowa jest równa zeru, a współczynnik przy równa się 1 – wektory I liniowo zależne.

Z tego twierdzenia wynika następujący wniosek.

Konsekwencja. Jeśli wektory I nie są współliniowe, to są liniowo niezależne.

Twierdzenie 2. Aby trzy wektory były liniowo zależne, konieczne i wystarczające jest, aby były współpłaszczyznowe.

Konieczność. Niech wektory ,I liniowo zależne. Pokażemy, że są one współpłaszczyznowe.

Z definicji liniowej zależności wektorów wynika istnienie liczb
I tak, że kombinacja liniowa
, a jednocześnie (dokładnie)
. Następnie z tej równości możemy wyrazić wektor :=
, czyli wektor równa przekątnej równoległoboku zbudowanego na wektorach po prawej stronie tej równości (ryc. 2.6). Oznacza to, że wektory ,I leżeć w tej samej płaszczyźnie.

Adekwatność. Niech wektory ,I współpłaszczyznowy. Pokażmy, że są one liniowo zależne.

Wykluczmy przypadek kolinearności dowolnej pary wektorów (ponieważ wtedy ta para jest liniowo zależna i zgodnie z wnioskiem 3 (patrz akapit 1 0) wszystkie trzy wektory są liniowo zależne). Należy zauważyć, że założenie to wyklucza również istnienie wektora zerowego wśród tych trzech.

Przesuńmy trzy współpłaszczyznowe wektory na jedną płaszczyznę i sprowadźmy je do wspólnego początku. Do końca wektora narysuj linie równoległe do wektorów I ; otrzymujemy wektory I (ryc. 2.7) - ich istnienie zapewnia fakt, że wektory I wektory, które z założenia nie są współliniowe. Wynika z tego, że wektor =+. Przepisując tę ​​równość w postaci (–1) ++=0, stwierdzamy, że wektory ,I liniowo zależne.

Ze sprawdzonego twierdzenia wynikają dwa wnioski.

Wniosek 1. Pozwalać I wektory niewspółliniowe, wektor – dowolne, leżące w płaszczyźnie określonej przez wektory I , wektor. Potem są liczby I takie, że

=+. (2.10)

Konsekwencja 2. Jeśli wektory ,I nie są współpłaszczyznowe, to są liniowo niezależne.

Twierdzenie 3. Dowolne cztery wektory są liniowo zależne.

Pominiemy dowód; z pewnymi modyfikacjami kopiuje dowód Twierdzenia 2. Podajmy wniosek z tego twierdzenia.

Konsekwencja. Dla dowolnych wektorów niewspółpłaszczyznowych ,,i dowolny wektor
I takie, że

. (2.11)

Komentarz. W przypadku wektorów w przestrzeni (trójwymiarowej) pojęcia liniowej zależności i niezależności mają, jak wynika z powyższych twierdzeń 1-3, proste znaczenie geometryczne.

Niech będą dwa wektory liniowo zależne I . W tym przypadku jeden z nich jest liniową kombinacją drugiego, to znaczy po prostu różni się od niego czynnikiem liczbowym (na przykład
). Geometrycznie oznacza to, że oba wektory leżą na wspólnej linii; mogą mieć te same lub przeciwne kierunki (ryc. 2.8 xx).

Jeżeli dwa wektory są położone względem siebie pod kątem (ryc. 2.9 xx), to w tym przypadku nie da się uzyskać jednego z nich mnożąc drugi przez liczbę - wektory takie są liniowo niezależne. Dlatego liniowa niezależność dwóch wektorów I oznacza, że ​​wektorów tych nie można ułożyć na jednej prostej.

Odkryjmy geometryczne znaczenie liniowej zależności i niezależności trzech wektorów.

Niech wektory ,I są liniowo zależne i niech (dokładnie) wektor jest liniową kombinacją wektorów I , czyli znajdujący się w płaszczyźnie zawierającej wektory I . Oznacza to, że wektory ,I leżeć w tej samej płaszczyźnie. Odwrotna sytuacja jest również prawdą: jeśli wektory ,I leżą w tej samej płaszczyźnie, to są liniowo zależne.

Zatem wektory ,I są liniowo niezależne wtedy i tylko wtedy, gdy nie leżą w tej samej płaszczyźnie.

3 0 . Pojęcie podstawy. Jednym z najważniejszych pojęć algebry liniowej i wektorowej jest pojęcie bazy. Wprowadźmy kilka definicji.

Definicja 1. Para wektorów nazywana jest uporządkowaną, jeśli określono, który wektor tej pary jest uważany za pierwszy, a który za drugi.

Definicja 2. Zamówiona para ,wektory niewspółliniowe nazywane są bazą na płaszczyźnie określonej przez dane wektory.

Twierdzenie 1. Dowolny wektor na płaszczyźnie można przedstawić jako kombinację liniową podstawowego układu wektorów ,:

(2.12)

i ta reprezentacja jest jedyna.

Dowód. Niech wektory I stanowić podstawę. Następnie dowolny wektor można przedstawić w postaci
.

Aby udowodnić niepowtarzalność, załóżmy, że istnieje jeszcze jeden rozkład
. Mamy wtedy = 0 i co najmniej jedna z różnic jest różna od zera. To ostatnie oznacza, że ​​wektory I liniowo zależny, to znaczy współliniowy; jest to sprzeczne ze stwierdzeniem, że stanowią one podstawę.

Ale potem następuje tylko rozkład.

Definicja 3. Trójkę wektorów nazywa się uporządkowaną, jeśli określono, który wektor jest uważany za pierwszy, który za drugi, a który za trzeci.

Definicja 4. Uporządkowaną trójkę wektorów niewspółpłaszczyznowych nazywa się bazą w przestrzeni.

Twierdzenie o rozkładzie i jedyności również obowiązuje tutaj.

Twierdzenie 2. Dowolny wektor można przedstawić jako kombinację liniową układu wektorów bazowych ,,:

(2.13)

i ta reprezentacja jest jednoznaczna (dowód twierdzenia pominiemy).

W rozwinięciach (2.12) i (2.13) ilości nazywane są współrzędnymi wektorowymi w danej bazie (a dokładniej współrzędnymi afinicznymi).

Ze stałą podstawą
I
Możesz pisać
.

Na przykład, jeśli podana jest podstawa
i to jest dane
, to oznacza to, że istnieje reprezentacja (rozkład)
.

4 0 . Operacje liniowe na wektorach w postaci współrzędnych. Wprowadzenie bazy pozwala na zastąpienie operacji liniowych na wektorach zwykłymi operacjami liniowymi na liczbach – współrzędnych tych wektorów.

Podajmy jakąś podstawę
. Oczywiście podanie współrzędnych wektora w tej bazie całkowicie determinuje sam wektor. Obowiązują następujące propozycje:

a) dwa wektory
I
są równe wtedy i tylko wtedy, gdy odpowiadające im współrzędne są równe:

b) przy mnożeniu wektora
na numer jego współrzędne są mnożone przez tę liczbę:

; (2.15)

c) podczas dodawania wektorów dodawane są odpowiadające im współrzędne:

Dowody tych własności pominiemy; Udowodnijmy własność b) tylko jako przykład. Mamy

==

Komentarz. W przestrzeni (na płaszczyźnie) możesz wybierać nieskończenie wiele baz.

Podajmy przykład przejścia z jednej bazy do drugiej i ustalmy relacje między współrzędnymi wektora w różnych bazach.

Przykład 1. W systemie podstawowym
podane są trzy wektory:
,
I
. W podstawie ,,wektor ma rozkład. Znajdź współrzędne wektora w podstawie
.

Rozwiązanie. Mamy rozwinięcia:
,
,
; stąd,
=
+2
+
= =
, to jest
w podstawie
.

Przykład 2. Wpuśćmy jakąś podstawę
cztery wektory są podane przez ich współrzędne:
,
,
I
.

Dowiedz się, czy wektory się tworzą
podstawa; jeśli odpowiedź jest pozytywna, znajdź rozkład wektora na tej podstawie.

Rozwiązanie. 1) wektory stanowią bazę, jeśli są liniowo niezależne. Zróbmy liniową kombinację wektorów
(
) i dowiedz się przy czym
I wychodzi na zero:
=0. Mamy:

=
+
+
=

Definiując równość wektorów w postaci współrzędnych, otrzymujemy następujący układ równań (liniowych jednorodnych algebraicznych):
;
;
, którego wyznacznik
=1
, czyli system ma (tylko) trywialne rozwiązanie
. Oznacza to liniową niezależność wektorów
i dlatego stanowią podstawę.

2) rozwiń wektor na tej podstawie. Mamy: =
lub w formie współrzędnych.

Przechodząc do równości wektorów w postaci współrzędnych, otrzymujemy układ liniowych niejednorodnych równań algebraicznych:
;
;
. Rozwiązując to (na przykład korzystając z reguły Cramera) otrzymujemy:
,
,
I (
)
. Mamy rozkład wektorowy w podstawie
:=.

5 0 . Rzut wektora na oś. Właściwości rzutów. Niech będzie jakaś oś l, czyli linię prostą z wybranym na niej kierunkiem i niech będzie podany jakiś wektor Zdefiniujmy pojęcie rzutowania wektorowego na oś l.

Definicja. Projekcja wektorowa na oś l nazywa się iloczyn modułu tego wektora i cosinusa kąta między osiami l i wektor (ryc. 2.10):

. (2.17)

Następstwem tej definicji jest stwierdzenie, że równe wektory mają równe rzuty (na tę samą oś).

Zwróćmy uwagę na właściwości rzutów.

1) rzut sumy wektorów na jakąś oś l równa sumie rzutów wyrazów wektorów na tę samą oś:

2) rzut iloczynu skalara na wektor jest równy iloczynowi tego skalara przez rzut wektora na tę samą oś:

=
. (2.19)

Konsekwencja. Rzut kombinacji liniowej wektorów na oś jest równy liniowej kombinacji ich rzutów:

Dowody własności pominiemy.

6 0 . Prostokątny kartezjański układ współrzędnych w przestrzeni.Rozkład wektora na wektory jednostkowe osi. Niech jako podstawę zostaną wybrane trzy wzajemnie prostopadłe wektory jednostkowe; wprowadzamy dla nich specjalne oznaczenia
. Umieszczając ich początki w jednym punkcie O, będziemy po nich kierować (zgodnie z ort
) osie współrzędnych Wół,Oj iO z(oś z dodatnim kierunkiem, początkiem i wybraną na niej jednostką długości nazywana jest osią współrzędnych).

Definicja. Uporządkowany układ trzech wzajemnie prostopadłych osi współrzędnych o wspólnym początku i wspólnej jednostce długości nazywany jest w przestrzeni prostokątnym kartezjańskim układem współrzędnych.

Oś Wół zwana osią odciętych, Oj– oś rzędnych uO z – aplikator osiowy.

Zajmijmy się rozwinięciem dowolnego wektora w oparciu o bazę
. Z twierdzenia (patrz §2.2, akapit 3 0, (2.13)) wynika, że
można w sposób unikalny rozszerzyć na podstawie
(tutaj zamiast wyznaczać współrzędne
używać
):

. (2.21)

B (2.21)
współrzędne wektora esencji (prostokąt kartezjański). . Znaczenie współrzędnych kartezjańskich ustala następujące twierdzenie.

Twierdzenie. Współrzędne prostokątne kartezjańskie
wektor są rzutami tego wektora odpowiednio na oś Wół,Oj iO z.

Dowód. Umieśćmy wektor do początku układu współrzędnych - punkt O. Wtedy jego koniec zbiegnie się w pewnym momencie
.

Przeciągnijmy przez punkt
trzy płaszczyzny równoległe do płaszczyzn współrzędnych Oj,Oxz I Oksy(Rys. 2.11 xx). Otrzymujemy wówczas:

. (2.22)

W (2.22) wektory
I
nazywane są składnikami wektorowymi
wzdłuż osi Wół,Oj iO z.

Przepuszczać
I kąty utworzone przez wektor są odpowiednio wskazane z ortami
. Następnie dla składników otrzymujemy następujące wzory:

=
=
,
=
=
,
=
=
(2.23)

Z (2.21), (2.22) (2.23) znajdujemy:

=
=
;=
=
;=
=
(2.23)

– współrzędne
wektor istnieją rzuty tego wektora na osie współrzędnych Wół,Oj iO z odpowiednio.

Komentarz. Liczby
nazywane są cosinusami kierunku wektora .

Moduł wektorowy (przekątna równoległościanu prostokątnego) oblicza się ze wzoru:

. (2.24)

Ze wzorów (2.23) i (2.24) wynika, że ​​cosinusy kierunkowe można obliczyć korzystając ze wzorów:

=
;
=
;
=
. (2.25)

Podnosząc obie strony każdej równości z (2.25) i dodając lewą i prawą stronę otrzymanych równości wyraz po wyrazie, otrzymujemy wzór:

– nie dowolne trzy kąty tworzą określony kierunek w przestrzeni, lecz tylko te, których cosinusy są powiązane relacją (2.26).

7 0 . Współrzędne wektora promienia i punktu.Wyznaczanie wektora przez jego początek i koniec. Wprowadźmy definicję.

Definicja. Wektor promienia (oznaczony ) jest wektorem łączącym początek O z tym punktem (ryc. 2.12 xx):

. (2.27)

Dowolnemu punktowi w przestrzeni odpowiada pewien wektor promienia (i odwrotnie). Zatem punkty w przestrzeni są reprezentowane w algebrze wektorów za pomocą wektorów ich promieni.

Oczywiście współrzędne
zwrotnica M są rzutami jego wektora promienia
na osiach współrzędnych:

(2.28’)

a zatem,

(2.28)

– wektor promienia punktu to wektor, którego rzuty na osie współrzędnych są równe współrzędnym tego punktu. Prowadzi to do dwóch wpisów:
I
.

Otrzymujemy wzory do obliczania rzutów wektorowych
według współrzędnych jego pochodzenia - pkt
i koniec – punkt
.

Narysujmy wektory promieni
i wektor
(ryc. 2.13). Rozumiemy to

=
=(2.29)

– rzuty wektora na wektory jednostek współrzędnych są równe różnicom pomiędzy odpowiednimi współrzędnymi końca i początku wektora.

8 0 . Niektóre problemy dotyczące współrzędnych kartezjańskich.

1) warunki kolinearności wektorów . Z twierdzenia (patrz §2.1, akapit 2 0, wzór (2.7)) wynika, że ​​dla współliniowości wektorów I jest konieczne i wystarczające, aby zachodziła następująca relacja: =. Z tej równości wektorów otrzymujemy trzy równości w postaci współrzędnych:, co implikuje warunek współliniowości wektorów w postaci współrzędnych:

(2.30)

– dla kolinearności wektorów I konieczne i wystarczające jest, aby odpowiadające im współrzędne były proporcjonalne.

2) odległość między punktami . Z przedstawienia (2.29) wynika, że ​​odległość
pomiędzy punktami
I
określa się na podstawie wzoru

=
=. (2.31)

3) podział odcinka w zadanym stosunku . Niech zostaną przyznane punkty
I
i postawa
. Trzeba znaleźć
– współrzędne punktu M (ryc. 2.14).

Z warunku kolinearności wektorów mamy:
, Gdzie
I

. (2.32)

Z (2.32) otrzymujemy w postaci współrzędnych:

Ze wzorów (2.32’) możemy otrzymać wzory na obliczenie współrzędnych środka odcinka
, zakładając
:

Komentarz. Będziemy liczyć segmenty
I
dodatni lub ujemny w zależności od tego, czy ich kierunek pokrywa się z kierunkiem z początku
segment do końca
, lub nie pasuje. Następnie korzystając ze wzorów (2.32) – (2.32”) można znaleźć współrzędne punktu dzielącego odcinek
zewnętrznie, to znaczy w taki sposób, że jest to punkt podziału M jest w kontynuacji segmentu
, a nie w nim. Jednocześnie oczywiście
.

4) równanie powierzchni kulistej . Utwórzmy równanie powierzchni kulistej - miejsce geometryczne punktów
, w równej odległości od jakiegoś stałego środka - punktu
. To oczywiste, że w tym przypadku
i biorąc pod uwagę wzór (2.31)

Równanie (2.33) jest równaniem pożądanej powierzchni kulistej.