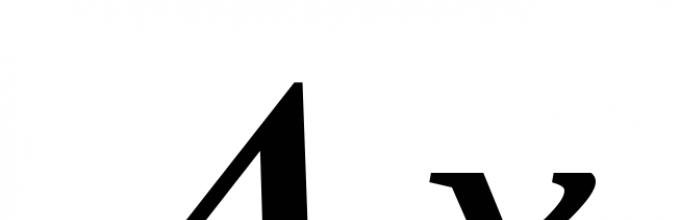Funkcja przyrostu dla manekinów. Otwarta Biblioteka – otwarta biblioteka informacji edukacyjnych. Pochodna funkcji zespolonej

Pozwalać X– argument (zmienna niezależna); y=y(x)– funkcja.

Weźmy stałą wartość argumentu x=x 0 i obliczyć wartość funkcji y 0 =y(x 0 ) . Teraz ustawmy dowolnie przyrost (zmianę) argumentu i oznacz go  X ( X może mieć dowolny znak).

Argumentem inkrementacji jest kropka X 0 +  X. Powiedzmy, że zawiera również wartość funkcji y=y(x 0 +  X)(widzieć zdjęcie).

Zatem przy dowolnej zmianie wartości argumentu uzyskuje się zmianę funkcji, która nazywa się przyrost wartości funkcji:

i nie jest dowolna, ale zależy od rodzaju funkcji i wartości
.

Argumenty i funkcje mogą być inkrementowane finał, tj. wyrażane jako liczby stałe i w takim przypadku nazywane są czasami różnicami skończonymi.

W ekonomii dość często rozważa się przyrosty skończone. Na przykład tabela pokazuje dane dotyczące długości sieci kolejowej określonego stanu. Oczywiście przyrost długości sieci oblicza się odejmując poprzednią wartość od kolejnej.

Długość sieci kolejowej rozpatrzymy jako funkcję, której argumentem będzie czas (lata).

Długość linii kolejowej na dzień 31 grudnia tys. km.	Przyrost	Średni roczny wzrost

Sam wzrost funkcji (w tym przypadku długości sieci kolejowej) nie charakteryzuje dobrze zmiany funkcji. W naszym przykładzie z faktu, że 2,5>0,9 nie można stwierdzić, że sieć rozwijała się szybciej 2000-2003 lat niż w 2004 g., ponieważ przyrost 2,5 odnosi się do okresu trzech lat, oraz 0,9 - w ciągu zaledwie jednego roku. Dlatego jest całkiem naturalne, że przyrost funkcji prowadzi do zmiany jednostki w argumencie. Przyrostem argumentu są tutaj okresy: 1996-1993=3; 2000-1996=4; 2003-2000=3; 2004-2003=1 .

Otrzymujemy to, co nazywa się w literaturze ekonomicznej średni roczny wzrost.

Można uniknąć operacji zmniejszania przyrostu jednostki zmiany argumentu, jeśli przyjmiemy wartości funkcji dla wartości argumentów różniących się o jeden, co nie zawsze jest możliwe.

W analizie matematycznej, w szczególności w rachunku różniczkowym, uwzględnia się nieskończenie małe (IM) przyrosty argumentu i funkcji.

Różniczkowanie funkcji jednej zmiennej (pochodna i różniczkowa). Pochodna funkcji

Przyrosty argumentów i funkcji w punkcie X 0 można uznać za porównywalne nieskończenie małe wielkości (patrz temat 4, porównanie BM), tj. BM jest tego samego rzędu.

Wtedy ich stosunek będzie miał skończoną granicę, którą definiujemy jako pochodną funkcji w t X 0 .

Granica stosunku przyrostu funkcji do przyrostu BM argumentu w punkcie x=x 0 zwany pochodna funkcjonuje w danym punkcie.

Symboliczne oznaczenie pochodnej kreską (a raczej cyfrą rzymską I) wprowadził Newton. Możesz także użyć indeksu dolnego, który pokazuje, z jaką zmienną obliczana jest pochodna, np. . Powszechnie stosowana jest także inna notacja zaproponowana przez twórcę rachunku pochodnych, niemieckiego matematyka Leibniza:
. Więcej o pochodzeniu tego oznaczenia dowiesz się w dalszej części rozdziału Różniczka funkcji i różnica argumentów.

Ta liczba jest szacunkowa prędkość zmiany funkcji przechodzącej przez punkt
.

Zainstalujmy znaczenie geometryczne pochodna funkcji w punkcie. W tym celu wykreślimy funkcję y=y(x) i zaznacz na nim punkty determinujące zmianę y(x) tymczasem

Styczna do wykresu funkcji w punkcie M 0
rozważymy położenie graniczne siecznej M 0 M jeśli się uwzględni
(kropka M przesuwa się wzdłuż wykresu funkcji do punktu M 0 ).

Rozważmy
. Oczywiście,
.

Jeśli chodzi o M kieruj się wzdłuż wykresu funkcji w stronę punktu M 0 , a następnie wartość
będzie dążyć do pewnej granicy, którą oznaczamy
. W której.

Ogranicz kąt  pokrywa się z kątem nachylenia stycznej narysowanej do wykresu funkcji m.in. M 0 , więc pochodna
liczbowo równe nachylenie styczne w określonym punkcie.

geometryczne znaczenie pochodnej funkcji w punkcie.

W ten sposób możemy napisać równania styczne i normalne ( normalna - jest to prosta prostopadła do stycznej) do wykresu funkcji w pewnym punkcie X 0 :

Styczna - .

Normalny -
.

Interesujące są przypadki, gdy linie te są ułożone poziomo lub pionowo (patrz Temat 3, szczególne przypadki położenia linii na płaszczyźnie). Następnie,

Jeśli
;

Jeśli
.

Definicja pochodnej nazywa się różnicowanie Funkcje.

 Jeżeli funkcja w punkcie X 0 ma skończoną pochodną, wówczas nazywa się to różniczkowalne w tym momencie. Funkcję różniczkowalną we wszystkich punktach pewnego przedziału nazywamy różniczkowalną na tym przedziale.

 Twierdzenie . Jeśli funkcja y=y(x) różniczkowalne m.in. X 0 , to jest ciągły w tym punkcie.

Zatem, ciągłość– warunek konieczny (ale niewystarczający) różniczkowalności funkcji.

Definicja 1

Jeżeli dla każdej pary $(x,y)$ wartości dwóch zmiennych niezależnych z jakiejś dziedziny przypisana jest pewna wartość $z$, to mówimy, że $z$ jest funkcją dwóch zmiennych $(x,y) $. Notacja: $z=f(x,y)$.

W odniesieniu do funkcji $z=f(x,y)$ rozważmy pojęcia przyrostu ogólnego (całkowitego) i częściowego funkcji.

Niech funkcja $z=f(x,y)$ będzie dana przez dwie niezależne zmienne $(x,y)$.

Notatka 1

Ponieważ zmienne $(x,y)$ są niezależne, jedna z nich może się zmieniać, a druga pozostaje stała.

Dajmy zmiennej $x$ przyrost $\Delta x$, pozostawiając wartość zmiennej $y$ bez zmian.

Wtedy funkcja $z=f(x,y)$ otrzyma przyrost, który nazwiemy częściowym przyrostem funkcji $z=f(x,y)$ względem zmiennej $x$. Przeznaczenie:

Podobnie nadamy zmiennej $y$ przyrost $\Delta y$, zachowując wartość zmiennej $x$ bez zmian.

Wtedy funkcja $z=f(x,y)$ otrzyma przyrost, który nazwiemy częściowym przyrostem funkcji $z=f(x,y)$ względem zmiennej $y$. Przeznaczenie:

Jeśli argumentowi $x$ zostanie podana inkrementacja $\Delta x$, a argumentowi $y$ zostanie podana inkrementacja $\Delta y$, wówczas otrzymany zostanie całkowity przyrost dana funkcja$z=f(x,y)$. Przeznaczenie:

Zatem mamy:

$\Delta _(x) z=f(x+\Delta x,y)-f(x,y)$ - częściowe zwiększenie funkcji $z=f(x,y)$ o $x$;

$\Delta _(y) z=f(x,y+\Delta y)-f(x,y)$ - częściowe zwiększenie funkcji $z=f(x,y)$ o $y$;

$\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$ - całkowity przyrost funkcji $z=f(x,y)$.

Przykład 1

Rozwiązanie:

$\Delta _(x) z=x+\Delta x+y$ - częściowy przyrost funkcji $z=f(x,y)$ powyżej $x$;

$\Delta _(y) z=x+y+\Delta y$ - częściowy przyrost funkcji $z=f(x,y)$ względem $y$.

$\Delta z=x+\Delta x+y+\Delta y$ - całkowity przyrost funkcji $z=f(x,y)$.

Przykład 2

Oblicz częściowy i całkowity przyrost funkcji $z=xy$ w punkcie $(1;2)$ dla $\Delta x=0,1;\, \, \Delta y=0,1$.

Rozwiązanie:

Z definicji przyrostu częściowego znajdujemy:

$\Delta _(x) z=(x+\Delta x)\cdot y$ - częściowy przyrost funkcji $z=f(x,y)$ ponad $x$

$\Delta _(y) z=x\cdot (y+\Delta y)$ - częściowe zwiększenie funkcji $z=f(x,y)$ o $y$;

Z definicji całkowitego przyrostu znajdujemy:

$\Delta z=(x+\Delta x)\cdot (y+\Delta y)$ - całkowity przyrost funkcji $z=f(x,y)$.

Stąd,

\[\Delta _(x) z=(1+0,1)\cdot 2=2,2\] \[\Delta _(y) z=1\cdot (2+0,1)=2,1 \] \[\Delta z= (1+0,1)\cdot (2+0,1)=1,1\cdot 2,1=2,31.\]

Uwaga 2

Całkowity przyrost danej funkcji $z=f(x,y)$ nie jest równy sumie jej przyrostów cząstkowych $\Delta _(x) z$ i $\Delta _(y) z$. Zapis matematyczny: $\Delta z\ne \Delta _(x) z+\Delta _(y) z$.

Przykład 3

Sprawdź uwagi dotyczące asercji pod kątem funkcji

Rozwiązanie:

$\Delta _(x) z=x+\Delta x+y$; $\Delta _(y) z=x+y+\Delta y$; $\Delta z=x+\Delta x+y+\Delta y$ (uzyskane w przykładzie 1)

Znajdźmy sumę przyrostów cząstkowych danej funkcji $z=f(x,y)$

\[\Delta _(x) z+\Delta _(y) z=x+\Delta x+y+(x+y+\Delta y)=2\cdot (x+y)+\Delta x+\Delta y.\]

\[\Delta _(x) z+\Delta _(y) z\ne \Delta z.\]

Definicja 2

Jeżeli dla każdej potrójnej $(x,y,z)$ wartości trzech zmiennych niezależnych z jakiejś dziedziny przypisana jest pewna wartość $w$, to mówimy, że $w$ jest funkcją trzech zmiennych $(x, y,z)$ w tym obszarze.

Notacja: $w=f(x,y,z)$.

Definicja 3

Jeżeli dla każdego zbioru $(x,y,z,...,t)$ wartości zmiennych niezależnych z pewnego obszaru przypisana jest pewna wartość $w$, to mówimy, że $w$ jest funkcją zmienne $(x,y, z,...,t)$ w tym obszarze.

Notacja: $w=f(x,y,z,...,t)$.

Dla funkcji trzech i więcej zmiennych, analogicznie jak dla funkcji dwóch zmiennych, dla każdej ze zmiennych wyznacza się przyrosty cząstkowe:

$\Delta _(z) w=f(x,y,z+\Delta z)-f(x,y,z)$ - częściowy przyrost funkcji $w=f(x,y,z,... ,t )$ o $z$;

$\Delta _(t) w=f(x,y,z,...,t+\Delta t)-f(x,y,z,...,t)$ - częściowy przyrost funkcji $w =f (x,y,z,...,t)$ o $t$.

Przykład 4

Napisz funkcje przyrostu częściowego i całkowitego

Rozwiązanie:

Z definicji przyrostu częściowego znajdujemy:

$\Delta _(x) w=((x+\Delta x)+y)\cdot z$ - częściowy przyrost funkcji $w=f(x,y,z)$ powyżej $x$

$\Delta _(y) w=(x+(y+\Delta y))\cdot z$ - częściowy przyrost funkcji $w=f(x,y,z)$ ponad $y$;

$\Delta _(z) w=(x+y)\cdot (z+\Delta z)$ - częściowy przyrost funkcji $w=f(x,y,z)$ ponad $z$;

Z definicji całkowitego przyrostu znajdujemy:

$\Delta w=((x+\Delta x)+(y+\Delta y))\cdot (z+\Delta z)$ - całkowity przyrost funkcji $w=f(x,y,z)$.

Przykład 5

Oblicz przyrost częściowy i całkowity funkcji $w=xyz$ w punkcie $(1;2;1)$ dla $\Delta x=0,1;\, \, \Delta y=0,1;\, \, \Delta z=0,1$.

Rozwiązanie:

Z definicji przyrostu częściowego znajdujemy:

$\Delta _(x) w=(x+\Delta x)\cdot y\cdot z$ - częściowy przyrost funkcji $w=f(x,y,z)$ ponad $x$

$\Delta _(y) w=x\cdot (y+\Delta y)\cdot z$ - częściowy przyrost funkcji $w=f(x,y,z)$ ponad $y$;

$\Delta _(z) w=x\cdot y\cdot (z+\Delta z)$ - częściowy przyrost funkcji $w=f(x,y,z)$ ponad $z$;

Z definicji całkowitego przyrostu znajdujemy:

$\Delta w=(x+\Delta x)\cdot (y+\Delta y)\cdot (z+\Delta z)$ - całkowity przyrost funkcji $w=f(x,y,z)$.

Stąd,

\[\Delta _(x) w=(1+0,1)\cdot 2\cdot 1=2,2\] \[\Delta _(y) w=1\cdot (2+0,1)\ cdot 1=2,1\] \[\Delta _(y) w=1\cdot 2\cdot (1+0.1)=2.2\] \[\Delta z=(1+0.1) \cdot (2+0.1)\cdot (1+0.1) =1,1\cdot 2,1\cdot 1,1=2,541.\]

Z punkt geometryczny Z punktu widzenia widzenia całkowity przyrost funkcji $z=f(x,y)$ (z definicji $\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$) jest równy przyrostowi zastosowania wykresu funkcji $z =f(x,y)$ przy przejściu od punktu $M(x,y)$ do punktu $M_(1) (x+\Delta x,y+ \Delta y)$ (ryc. 1).

Obrazek 1.

Niech x będzie dowolnym punktem w pewnym sąsiedztwie stałego punktu x 0 . różnica x – x 0 nazywana jest zwykle przyrostem zmiennej niezależnej (lub przyrostem argumentu) w punkcie x 0 i jest oznaczana Δx. Zatem,

Δx = x –x 0 ,

skąd to wynika

Przyrost funkcji – różnica między dwiema wartościami funkcji.

Niech będzie podana funkcja Na = k(x), zdefiniowany wartością argumentu równą X 0. Nadajmy argumentowi przyrost D X, ᴛ.ᴇ. rozważ wartość argumentu równą X 0+D X. Załóżmy, że ta wartość argumentu również mieści się w zakresie tej funkcji. Wtedy różnica D y = f(x 0+D X) – f(x 0) Powszechnie nazywa się to przyrostem funkcji. Przyrost funkcji F(X) W punkcie X- funkcja zwykle oznaczana Δ x f z nowej zmiennej Δ X zdefiniowana jako

Δ x f(Δ X) = F(X + Δ X) − F(X).

Znajdź przyrost argumentu i przyrost funkcji w punkcie x 0 jeśli

Przykład 2. Znajdź przyrost funkcji f(x) = x 2 jeśli x = 1, ∆x = 0,1

Rozwiązanie: f(x) = x 2, f(x+∆x) = (x+∆x) 2

Znajdźmy przyrost funkcji ∆f = f(x+∆x) - f(x) = (x+∆x) 2 - x 2 = x 2 +2x*∆x+∆x 2 - x 2 = 2x*∆x + ∆x 2 /

Zastąp wartości x=1 i ∆x= 0,1, otrzymamy ∆f = 2*1*0,1 + (0,1) 2 = 0,2+0,01 = 0,21

Znajdź przyrost argumentu i przyrost funkcji w punkcie x 0

2.f(x) = 2x 3. x 0 =3 x=2,4

3. f(x) = 2x 2 +2 x 0 =1 x=0,8

4. f(x) = 3x+4 x 0 =4 x=3,8

Definicja: Pochodna funkcji w punkcie, zwyczajowo nazywa się granicę (jeśli istnieje i jest skończona) stosunku przyrostu funkcji do przyrostu argumentu, pod warunkiem, że ten ostatni dąży do zera.

Najczęściej stosowane oznaczenia pochodne to:

Zatem,

Znalezienie pochodnej nazywa się zwykle różnicowanie . Wprowadzono definicja funkcji różniczkowalnej: Funkcję f, która ma pochodną w każdym punkcie pewnego przedziału, nazywa się zwykle różniczkowalną na tym przedziale.

Niech będzie zdefiniowana funkcja w pewnym sąsiedztwie punktu. Pochodną funkcji nazywamy zwykle taką liczbę, że funkcja w sąsiedztwie punktu U(X 0) można przedstawić jako

F(X 0 + H) = F(X 0) + Ach + o(H)

jeśli istnieje.

Wyznaczanie pochodnej funkcji w punkcie.

Niech funkcja k(x) zdefiniowany w przedziale (a;b), i są punktami tego przedziału.

Definicja. Pochodna funkcji k(x) w pewnym momencie zwyczajowo nazywa się granicę stosunku przyrostu funkcji do przyrostu argumentu w . Oznaczony przez .

Kiedy ostatnia granica nabiera określonej wartości końcowej, mówimy o istnieniu skończona pochodna w punkcie. Jeżeli granica jest nieskończona, wówczas tak mówimy pochodna jest nieskończona w danym punkcie. Jeśli granica nie istnieje, to pochodna funkcji w tym punkcie nie istnieje.

Funkcjonować k(x) mówi się, że jest różniczkowalna w punkcie, w którym ma skończoną pochodną.

W przypadku funkcji k(x) różniczkowalna w każdym punkcie pewnego przedziału (a;b), wówczas funkcję nazywamy różniczkowalną na tym przedziale. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, dowolny punkt X pomiędzy (a;b) możemy w tym miejscu dopasować wartość pochodnej funkcji, czyli mamy możliwość zdefiniowania nowej funkcji, która nazywa się pochodną funkcji k(x) na przerwie (a;b).

Operację znajdowania pochodnej nazywamy zwykle różniczkowaniem.

W życiu nie zawsze interesują nas dokładne wartości jakichkolwiek wielkości. Czasami interesujące jest poznanie zmiany tej wielkości, na przykład średniej prędkości autobusu, stosunku wielkości ruchu do okresu czasu itp. Aby porównać wartość funkcji w pewnym punkcie z wartościami tej samej funkcji w innych punktach, wygodnie jest użyć takich pojęć, jak „przyrost funkcji” i „przyrost argumentu”.

Pojęcia „przyrostu funkcji” i „przyrostu argumentu”

Powiedzmy, że x jest dowolnym punktem leżącym w pewnym sąsiedztwie punktu x0. Przyrost argumentu w punkcie x0 jest różnicą x-x0. Przyrost wyznacza się następująco: ∆x.

∆x=x-x0.

Czasami wielkość tę nazywa się także przyrostem zmiennej niezależnej w punkcie x0. Ze wzoru wynika: x = x0+∆x. W takich przypadkach mówią, że wartość początkowa zmiennej niezależnej x0 otrzymała przyrost ∆x.

Jeżeli zmienimy argument, to wartość funkcji również ulegnie zmianie.

f(x) - f(x0) = f(x0 + ∆х) - f(x0).

Przyrost funkcji f w punkcie x0, odpowiedni przyrost ∆х jest różnicą f(x0 + ∆х) - f(x0). Przyrost funkcji oznacza się następująco: ∆f. Zatem z definicji otrzymujemy:

∆f= f(x0 +∆x) - f(x0).

Czasami ∆f nazywa się także przyrostem zmiennej zależnej i ∆у stosuje się do tego oznaczenia, jeśli funkcja miała na przykład y=f(x).

Geometryczne znaczenie przyrostu

Spójrz na poniższy obrazek.

Jak widać, przyrost pokazuje zmianę rzędnej i odciętej punktu. A stosunek przyrostu funkcji do przyrostu argumentu określa kąt nachylenia siecznej przechodzącej przez początkowe i końcowe położenie punktu.

Przyjrzyjmy się przykładom zwiększania funkcji i argumentu

Przykład 1. Znajdź przyrost argumentu ∆x i przyrost funkcji ∆f w punkcie x0, jeśli f(x) = x 2, x0=2 a) x=1,9 b) x =2,1

Skorzystajmy ze wzorów podanych powyżej:

a) ∆х=х-х0 = 1,9 - 2 = -0,1;

∆f=f(1,9) - f(2) = 1,9 2 - 2 2 = -0,39;

b) ∆x=x-x0=2,1-2=0,1;

∆f=f(2,1) - f(2) = 2,1 2 - 2 2 = 0,41.

Przykład 2. Oblicz przyrost ∆f dla funkcji f(x) = 1/x w punkcie x0, jeśli przyrost argumentu jest równy ∆x.

Ponownie skorzystamy ze wzorów uzyskanych powyżej.

∆f = f(x0 + ∆x) - f(x0) =1/(x0-∆x) - 1/x0 = (x0 - (x0+∆x))/(x0*(x0+∆x)) = - ∆x/((x0*(x0+∆x)).

Definicja 1

W odniesieniu do funkcji $z=f(x,y)$ rozważmy pojęcia przyrostu ogólnego (całkowitego) i częściowego funkcji.

Niech funkcja $z=f(x,y)$ będzie dana przez dwie niezależne zmienne $(x,y)$.

Notatka 1

Ponieważ zmienne $(x,y)$ są niezależne, jedna z nich może się zmieniać, a druga pozostaje stała.

Dajmy zmiennej $x$ przyrost $\Delta x$, pozostawiając wartość zmiennej $y$ bez zmian.

Wtedy funkcja $z=f(x,y)$ otrzyma przyrost, który nazwiemy częściowym przyrostem funkcji $z=f(x,y)$ względem zmiennej $x$. Przeznaczenie:

Podobnie nadamy zmiennej $y$ przyrost $\Delta y$, zachowując wartość zmiennej $x$ bez zmian.

Wtedy funkcja $z=f(x,y)$ otrzyma przyrost, który nazwiemy częściowym przyrostem funkcji $z=f(x,y)$ względem zmiennej $y$. Przeznaczenie:

Jeśli argumentowi $x$ podano przyrost $\Delta x$, a argumentowi $y$ podano przyrost $\Delta y$, to pełny przyrost danej funkcji $z=f(x,y)$ zostaje uzyskany. Przeznaczenie:

Zatem mamy:

$\Delta _(x) z=f(x+\Delta x,y)-f(x,y)$ - częściowe zwiększenie funkcji $z=f(x,y)$ o $x$;

$\Delta _(y) z=f(x,y+\Delta y)-f(x,y)$ - częściowe zwiększenie funkcji $z=f(x,y)$ o $y$;

$\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$ - całkowity przyrost funkcji $z=f(x,y)$.

Przykład 1

Rozwiązanie:

$\Delta _(x) z=x+\Delta x+y$ - częściowy przyrost funkcji $z=f(x,y)$ powyżej $x$;

$\Delta _(y) z=x+y+\Delta y$ - częściowy przyrost funkcji $z=f(x,y)$ względem $y$.

$\Delta z=x+\Delta x+y+\Delta y$ - całkowity przyrost funkcji $z=f(x,y)$.

Przykład 2

Oblicz częściowy i całkowity przyrost funkcji $z=xy$ w punkcie $(1;2)$ dla $\Delta x=0,1;\, \, \Delta y=0,1$.

Rozwiązanie:

Z definicji przyrostu częściowego znajdujemy:

$\Delta _(x) z=(x+\Delta x)\cdot y$ - częściowy przyrost funkcji $z=f(x,y)$ ponad $x$

$\Delta _(y) z=x\cdot (y+\Delta y)$ - częściowe zwiększenie funkcji $z=f(x,y)$ o $y$;

Z definicji całkowitego przyrostu znajdujemy:

$\Delta z=(x+\Delta x)\cdot (y+\Delta y)$ - całkowity przyrost funkcji $z=f(x,y)$.

Stąd,

\[\Delta _(x) z=(1+0,1)\cdot 2=2,2\] \[\Delta _(y) z=1\cdot (2+0,1)=2,1 \] \[\Delta z= (1+0,1)\cdot (2+0,1)=1,1\cdot 2,1=2,31.\]

Uwaga 2

Całkowity przyrost danej funkcji $z=f(x,y)$ nie jest równy sumie jej przyrostów cząstkowych $\Delta _(x) z$ i $\Delta _(y) z$. Zapis matematyczny: $\Delta z\ne \Delta _(x) z+\Delta _(y) z$.

Przykład 3

Sprawdź uwagi dotyczące asercji pod kątem funkcji

Rozwiązanie:

$\Delta _(x) z=x+\Delta x+y$; $\Delta _(y) z=x+y+\Delta y$; $\Delta z=x+\Delta x+y+\Delta y$ (uzyskane w przykładzie 1)

Znajdźmy sumę przyrostów cząstkowych danej funkcji $z=f(x,y)$

\[\Delta _(x) z+\Delta _(y) z=x+\Delta x+y+(x+y+\Delta y)=2\cdot (x+y)+\Delta x+\Delta y.\]

\[\Delta _(x) z+\Delta _(y) z\ne \Delta z.\]

Definicja 2

Notacja: $w=f(x,y,z)$.

Definicja 3

Notacja: $w=f(x,y,z,...,t)$.

Dla funkcji trzech i więcej zmiennych, analogicznie jak dla funkcji dwóch zmiennych, dla każdej ze zmiennych wyznacza się przyrosty cząstkowe:

$\Delta _(z) w=f(x,y,z+\Delta z)-f(x,y,z)$ - częściowy przyrost funkcji $w=f(x,y,z,... ,t )$ o $z$;

$\Delta _(t) w=f(x,y,z,...,t+\Delta t)-f(x,y,z,...,t)$ - częściowy przyrost funkcji $w =f (x,y,z,...,t)$ o $t$.

Przykład 4

Napisz funkcje przyrostu częściowego i całkowitego

Rozwiązanie:

Z definicji przyrostu częściowego znajdujemy:

$\Delta _(x) w=((x+\Delta x)+y)\cdot z$ - częściowy przyrost funkcji $w=f(x,y,z)$ powyżej $x$

$\Delta _(y) w=(x+(y+\Delta y))\cdot z$ - częściowy przyrost funkcji $w=f(x,y,z)$ ponad $y$;

$\Delta _(z) w=(x+y)\cdot (z+\Delta z)$ - częściowy przyrost funkcji $w=f(x,y,z)$ ponad $z$;

Z definicji całkowitego przyrostu znajdujemy:

$\Delta w=((x+\Delta x)+(y+\Delta y))\cdot (z+\Delta z)$ - całkowity przyrost funkcji $w=f(x,y,z)$.

Przykład 5

Oblicz przyrost częściowy i całkowity funkcji $w=xyz$ w punkcie $(1;2;1)$ dla $\Delta x=0,1;\, \, \Delta y=0,1;\, \, \Delta z=0,1$.

Rozwiązanie:

Z definicji przyrostu częściowego znajdujemy:

$\Delta _(x) w=(x+\Delta x)\cdot y\cdot z$ - częściowy przyrost funkcji $w=f(x,y,z)$ ponad $x$

$\Delta _(y) w=x\cdot (y+\Delta y)\cdot z$ - częściowy przyrost funkcji $w=f(x,y,z)$ ponad $y$;

$\Delta _(z) w=x\cdot y\cdot (z+\Delta z)$ - częściowy przyrost funkcji $w=f(x,y,z)$ ponad $z$;

Z definicji całkowitego przyrostu znajdujemy:

$\Delta w=(x+\Delta x)\cdot (y+\Delta y)\cdot (z+\Delta z)$ - całkowity przyrost funkcji $w=f(x,y,z)$.

Stąd,

Z geometrycznego punktu widzenia całkowity przyrost funkcji $z=f(x,y)$ (z definicji $\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y) $) jest równe przyrostowi zastosowania funkcji wykresowej $z=f(x,y)$ przy przejściu od punktu $M(x,y)$ do punktu $M_(1) (x+\Delta x,y+ \Delta y)$ (ryc. 1).

Obrazek 1.