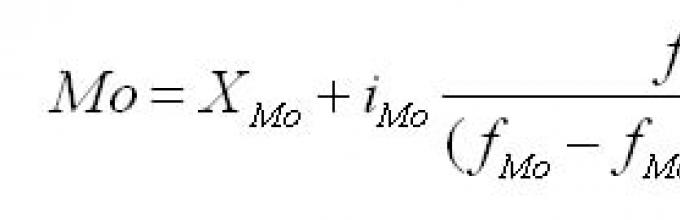Różnica modów serii danych. Charakterystyka strukturalna szeregu rozkładu wariacyjnego. Zależności między średnią arytmetyczną, medianą i modą

Mediana- jest to wartość atrybutu dzieląca uszeregowany szereg rozkładu na dwie równe części - o wartościach atrybutów mniejszych od mediany i o wartościach atrybutów większych od mediany. Aby znaleźć medianę, należy znaleźć wartość atrybutu znajdującą się w środku uporządkowanego szeregu.

Zobacz rozwiązanie problemu znalezienia formy i mediany Możesz

W seriach rankingowych, niezgrupowane dane dla znalezienie mediany sprowadzać się do poszukiwań numer seryjny mediany. Medianę można obliczyć za pomocą następującego wzoru:

gdzie Xm jest dolną granicą przedziału mediany;
im - średni przedział;
Sme to suma obserwacji zgromadzonych przed początkiem przedziału mediany;
fme to liczba obserwacji w środkowym przedziale.

Właściwości mediany

1. Mediana nie zależy od wartości atrybutów, które znajdują się po obu jej stronach.
2. Operacje analityczne na medianie są bardzo ograniczone, dlatego łącząc dwa rozkłady ze znanymi medianami, nie da się z góry przewidzieć wartości mediany nowego rozkładu.
3. Mediana ma właściwość minimalności. Jego istota polega na tym, że suma bezwzględnych odchyleń wartości x od mediany jest wartością minimalną w porównaniu z odchyleniem X od dowolnej innej wartości

Graficzna definicja mediany

Do ustalenia mediany metodą graficzną Wykorzystują zakumulowane częstotliwości, z których tworzona jest krzywa skumulowana. Wierzchołki rzędnych odpowiadających zakumulowanym częstotliwościom są połączone odcinkami prostymi. Dzieląc ostatnią rzędną na pół, co odpowiada całkowitej sumie częstotliwości, i rysując do niej prostopadłe przecięcie z krzywą skumulowaną, znajduje się rzędną pożądanej wartości mediany.

Definicja mody w statystyce

Moda – wartość atrybutu, który ma najwyższą częstotliwość w szeregu rozkładu statystycznego.

Definicja mody jest generowany na różne sposoby, a to zależy od tego, czy zmienna charakterystyka jest przedstawiona w postaci szeregu dyskretnego, czy przedziałowego.

Znalezienie mody a medianę oblicza się po prostu patrząc na kolumnę częstotliwości. W tej kolumnie znajdują największa liczba, charakteryzujący się najwyższą częstotliwością. Odpowiada pewnej wartości atrybutu, jakim jest tryb. W szeregu zmian przedziału tryb jest w przybliżeniu uważany za środkowy wariant przedziału o najwyższej częstotliwości. W takiej serii dystrybucyjnej tryb oblicza się ze wzoru:

gdzie XMo jest dolną granicą przedziału modalnego;
imo - interwał modalny;
fм0, fм0-1, fм0+1 - częstotliwości w przedziale modalnym, poprzednim i następnym.

Przedział modalny jest określony przez najwyższą częstotliwość.

Moda jest szeroko stosowana w praktyce statystycznej przy analizie popytu konsumenckiego, rejestrowaniu cen itp.

Zależności między średnią arytmetyczną, medianą i modą

W przypadku jednomodalnego szeregu symetrycznego rozkłady, mediana i moda pokrywają się. W przypadku rozkładów asymetrycznych nie są one takie same.

Dopasowanie oparte na K. Pearsonie różne rodzaje krzywych ustaliło, że dla rozkładów umiarkowanie asymetrycznych obowiązują następujące przybliżone zależności pomiędzy średnią arytmetyczną, medianą i modą:

Slepniew Paweł

Na kursie algebry w siódmej klasie podręcznik pod redakcją Telyakovsky'ego zawiera materiał ze statystyki „Średnia arytmetyczna, zakres i tryb”. Uczeń w swojej pracy podaje przykłady rozważenia tego tematu, które zasugerowali jego koledzy z klasy.

Pobierać:

Zapowiedź:

Departament Edukacji MU MO „Rejon Tarbagatai”

MBOU „Zawodska OOSH”

„Średnia arytmetyczna, zakres i tryb”

Ukończył: Slepnev Pavel, uczeń 7. klasy

Doradca naukowy:

Marina Ulakhanova Rodionowna,

nauczyciel matematyki

rok 2012

Strona wprowadzająca 3

Część główna Strona 4-9

Teoria zagadnienia s. 4-6

Miniprojekty s. 7-9

Podsumowanie Strona 9

Referencje Strona 10

Wstęp

Znaczenie

W tym rok akademicki Zaczęliśmy uczyć się dwóch przedmiotów: algebry i geometrii. Ucząc się algebry, niektóre rzeczy są mi znane z kursów 5 i 6 klasy, niektóre studiujemy dokładniej i głębiej, uczymy się wielu nowych rzeczy. Nowością w studiowaniu algebry jest zapoznanie się z pewnymi cechami statystycznymi: zakresem i modą. Ze średnią arytmetyczną zetknęliśmy się już wcześniej. Interesujące okazało się również to, że cechy te wykorzystywane są nie tylko na lekcjach matematyki, ale także w życiu, w praktyce (w produkcji, w rolnictwo w sporcie itp.).

Sformułowanie problemu

Kiedy rozwiązywaliśmy problemy do tego punktu zajęć, zrodził się pomysł, aby sami stworzyć problemy i przygotować do nich prezentacje, czyli w pewnym sensie zacząć tworzyć własną księgę problemów. Każdy wymyśla problem, robi prezentację, jakby każdy pracował nad własnym miniprojektem, a na zajęciach wspólnie wszystko rozwiązujemy i omawiamy. Jeśli zostaną popełnione błędy, poprawiamy je. A na koniec publicznie brońcie tych miniprojektów.

Cel mojej pracy: badanie statystyki.

Cele: rozpocząć opracowywanie podręcznika problemów statystycznych w formie prezentacji komputerowych.

Przedmiot badań: statystyka.

Przedmiot badań: charakterystyka statystyczna (średnia arytmetyczna, zakres, moda).

Metody badawcze:

1. Studiowanie literatury na ten temat.
2. Analiza danych.
3. Korzystanie z zasobów Internetu.
4. Korzystanie z Power Pointa.
5. Podsumowanie zebranych materiałów na ten temat.

Głównym elementem.

Teoria zagadnienia

Studiując rozdział „Charakterystyki statystyczne” zapoznaliśmy się z następującymi pojęciami: średnia arytmetyczna, zakres, tryb. Cechy te są wykorzystywane w statystykach. Ta nauka bada liczby oddzielne grupy ludność kraju i jego regionów, produkcja i konsumpcja różnego rodzaju produktów, przewóz towarów i pasażerów różnymi gałęziami transportu, Zasoby naturalne i tak dalej.

„Statystyka wie wszystko” – zapewniali Ilf i Pietrow w swojej słynnej powieści „Dwanaście krzeseł” i kontynuowali: „Wiadomo, ile jedzenia rocznie zjada przeciętny obywatel republiki... Wiadomo, ilu myśliwych, baletnic, maszyny, rowery, pomniki, jakie są w kraju, latarnie morskie i maszyny do szycia... Ileż życia, pełnego zapału, pasji i myśli, patrzy na nas ze statystycznych tablic!..” Ten ironiczny opis daje dość trafne wyobrażenie o ​statystyka (od łacińskiego status - stan) - nauka badająca, przetwarzająca i analizująca dane ilościowe dotyczące szerokiej gamy zjawisk masowych w życiu.

Statystyka gospodarcza bada zmiany cen, podaży i popytu na towary, przewiduje wzrost i spadek produkcji i konsumpcji.

Statystyka medyczna bada skuteczność różnych leków i metod leczenia, prawdopodobieństwo wystąpienia określonej choroby w zależności od wieku, płci, dziedziczności, warunków życia, złe nawyki, przewiduje rozprzestrzenianie się epidemii.

Statystyka demograficzna bada współczynnik urodzeń, wielkość populacji i jej skład (wiek, kraj, zawód).

Istnieją również statystyki finansowe, podatkowe, biologiczne i meteorologiczne.

W kurs szkolny algebrze przyglądamy się pojęciom i metodom opisowe statystyki, który zajmuje się pierwotnym przetwarzaniem informacji i obliczaniem najważniejszych cech liczbowych. Według angielskiego statystyka R. Fishera: „Statystykę można scharakteryzować jako naukę o redukcji i analizie materiału uzyskanego z obserwacji”. Cały zestaw danych liczbowych uzyskanych w próbce można (warunkowo) zastąpić kilkoma parametrami numerycznymi, z których część już rozważaliśmy na lekcjach - średnia arytmetyczna, zakres, tryb. Wyniki badań statystycznych są powszechnie wykorzystywane do wyciągania wniosków praktycznych i naukowych, dlatego ważna jest umiejętność określenia tych cech statystycznych.

Charakterystyki statystyczne można obecnie znaleźć wszędzie. Na przykład spis ludności. Dzięki temu spisowi państwo będzie wiedziało, ile pieniędzy potrzeba na budowę mieszkań, szkół, szpitali, ile osób potrzebuje mieszkań, ile dzieci jest w rodzinie, ilu jest bezrobotnych, jaki jest poziom wynagrodzeń itp. Wyniki tego spisu zostaną porównane z poprzednim, zobaczą, czy w tym czasie w kraju poprawiła się, czy sytuacja się pogorszyła, będzie można porównać dane z wynikami w innych krajach. W przemyśle bardzo ważne ma modę. Na przykład produkt, na który jest duże zapotrzebowanie, zawsze zostanie sprzedany, a fabryki będą miały dużo pieniędzy. A takich przykładów jest wiele.

Wyniki badań statystycznych są powszechnie wykorzystywane do wniosków praktycznych i naukowych.

Definicja 1. Średnia arytmetyczna ciągu liczb jest ilorazem podzielenia sumy tych liczb przez liczbę wyrazów.

Przykład: Podczas nauki obciążenie nauką Wybraliśmy grupę 12 uczniów klas 7. Poproszono ich o zanotowanie czasu (w minutach) poświęconego na wykonanie zadania w określonym dniu Praca domowa w algebrze. Otrzymaliśmy następujące dane:

23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25. Dzięki tej serii danych możesz określić, ile minut średnio uczniowie spędzają na odrabianiu zadań domowych z algebry. Aby to zrobić, musisz dodać wskazane 12 liczb i podzielić uzyskaną sumę

o 12: ==27.

Wynikowa liczba 27 nazywana jest średnią arytmetyczną rozważanego szeregu liczb.

Średnia arytmetyczna jest ważną cechą szeregu liczb, ale czasami warto wziąć pod uwagę inne przeciętny.

Definicja 2. Formą ciągu liczb jest liczba, która pojawia się w danym szeregu częściej niż inne.

Przykład: Analizując informacje o czasie spędzonym przez uczniów na odrabianiu zadań domowych z algebry, możemy interesować się nie tylko średnią arytmetyczną i zakresem uzyskanych szeregów danych, ale także innymi wskaźnikami. Ciekawostką jest na przykład to, jakie zużycie czasu charakteryzuje się wybraną grupą studentów, tj. która liczba występuje najczęściej w serii danych. Łatwo zauważyć, że w naszym przykładzie jest to liczba 25. Mówią, że liczba 25 jest modą rozpatrywanego szeregu.

Seria liczb może mieć więcej niż jeden tryb lub może nie mieć żadnego trybu. Na przykład w szeregu liczb 47, 46, 50, 47, 52, 49, 45, 43, 54, 52, 47, 52 dwie postacie to liczby 47 i 52, ponieważ każda z nich występuje trzy razy w ciągu szereg, a pozostałe liczby – mniej niż trzykrotność.

W seriach liczbowych 69, 68, 66, 70, 67, 62, 71, 74, 63, 73, 72 nie ma trybu.

Tryb serii danych zwykle znajduje się, gdy chce się zidentyfikować jakiś typowy wskaźnik. Tryb jest wskaźnikiem szeroko stosowanym w statystykach. Jednym z najczęstszych zastosowań mody jest badanie popytu. Na przykład, podejmując decyzję o tym, w jaką gramaturę opakowań zapakować masło, jakie loty otworzyć itp., najpierw bada się popyt i identyfikuje modę - najczęstsza kolejność.

Jednak znalezienie średniej arytmetycznej lub trybu nie zawsze pozwala na wyciągnięcie miarodajnych wniosków na podstawie danych statystycznych. Jeśli dysponujemy serią danych, to aby na ich podstawie wyciągnąć trafne wnioski i wiarygodne prognozy, oprócz wartości średnich musimy także wskazać, jak bardzo wykorzystywane dane różnią się od siebie. Jedną ze statystycznych miar różnicy lub rozproszenia danych jest zasięg.

Definicja 3. Rozstęp szeregu liczb to różnica pomiędzy największą i najmniejszą z tych liczb.

Przykład: W powyższym przykładzie odkryliśmy, że uczniowie spędzali średnio 27 minut na zadaniach domowych z algebry. Analiza serii danych pokazuje jednak, że czas spędzony przez część uczniów różni się istotnie od 27 minut, tj. od średniej arytmetycznej. Największe zużycie wynosi 37 minut, a najniższe 18 minut. Różnica pomiędzy najwyższym i najniższym zużyciem czasu wynosi 19 minut. W tym przypadku brana jest pod uwagę inna cecha statystyczna – zakres. Rozstęp serii wyznacza się, gdy chcemy określić, jak duży jest rozrzut danych w serii.

Mini projekty

A teraz chciałbym zaprezentować efekty naszej pracy: miniprojekty stworzenia zeszytu problemów statystycznych.

Pracuję w salonie Super-auto na stanowisku głównego kierownika działu sprzedaży. Nasz salon udostępnił samochody do udziału w zabawie z napędem na wszystkie koła. W zeszłym roku na wystawie i sprzedaży nasze samochody odniosły sukces! Wyniki sprzedaży przedstawiają się następująco:

Dział sprzedaży musi podsumować wyniki wystawy:

1. Ile samochodów sprzedawano średnio dziennie?
2. Jaki jest rozkład liczby samochodów w okresie wystawienniczo-sprzedażowym?
3. Ile samochodów sprzedawano najczęściej dziennie?

Odpowiedź: średnio sprzedawano 150 samochodów dziennie, zakres liczby sprzedanych samochodów wynosił 150, najczęściej sprzedawano 100 samochodów dziennie.

Ja, Anastasia Volochkova, została zaproszona do jury finału konkursu Lód i Ogień. Zawody odbyły się w mieście St. Petersburgu. Do finału dotarły trzy pary najsilniejszych łyżwiarzy: 1 para. Batueva Alina i Khlebodarov Kirill, druga para. Selyanskaya Julia i Kushnarev Pavel, 3 pary. Zaigraeva Anastasia i Afanasyev Dmitry. Jury: Anastasia Volochkova, Elena Malysheva, Alexey Dalmatov. Jury przyznało następującą punktację:

Znajdź średnią arytmetyczną, zakres i modę w serii oszacowań dla każdej pary.

Odpowiedź:

W tym roku odwiedziłem St. Petersburg na konkursie tańca towarzyskiego. W konkursie wzięły udział trzy piękne pary: Elena Sushentsova i Kirill Khlebodarov, Alina Batueva i Pavel Slepnev, Victoria Dzhaniashvili i Valery Tkachev.

Za swoje występy pary otrzymały następujące oceny:

Znajdź średnie oszacowanie, zakres i tryb.

Odpowiedź:

Jestem dyrektorem sklepu z modą i dodatkami „Fashion”. Sklep nieźle zarabia. Wyniki sprzedaży za ubiegły rok:

Przez pierwsze 2-3 miesiące zysk sięgał 2 milionów miesięcznie. Następnie zysk wzrósł do 4 milionów. Najbardziej udanymi miesiącami były: grudzień i maj. W maju kupowaliśmy sukienki głównie na studniówki, a w grudniu na sylwestra.

Pytanie do mojego głównego księgowego: jakie są efekty naszej pracy za ten rok?

Odpowiedź:

Zorganizowaliśmy warsztaty tuningowe „Turbo”. W pierwszym tygodniu naszej pracy zarobiliśmy: pierwszego dnia – 120 000 dolarów, drugiego dnia – 350 000 dolarów, trzeciego dnia – 99 000 dolarów, czwartego dnia – 120 000 dolarów. Oblicz, jaki jest nasz średni dzienny dochód, jaka jest różnica pomiędzy najwyższymi i najniższymi zarobkami oraz jaka kwota powtarza się najczęściej?

Odpowiedź: średnia arytmetyczna – 172 250 dolarów, zakres – 251 000 dolarów, tryb – 120 000 dolarów.

Wniosek

Podsumowując, chcę powiedzieć, że uwielbiam ten temat. Charakterystyki statystyczne są bardzo wygodne i można je stosować wszędzie. Ogólnie rzecz biorąc, porównują, dążą do postępu i pomagają poznać opinię ludzi. W trakcie pracy nad tym tematem zapoznałem się z nauką o statystyce, poznałem pewne pojęcia (średnia arytmetyczna, zakres i moda), w których można zastosować tę naukę, oraz poszerzyłem swoją wiedzę z zakresu informatyki. Myślę, że nasze problemy jako przykłady opanowania tych koncepcji przydadzą się innym! Będziemy nadal poznawać tę naukę i tworzyć własne problemy!

Tak zakończyła się moja podróż do świata matematyki, informatyki i statystyki. Ale myślę, że nie ostatni. Jest jeszcze wiele rzeczy, które chcę wiedzieć! Jak powiedział Galileo Galilei: „Natura formułuje swoje prawa w języku matematyki”. A ja chcę opanować ten język!

Bibliografia

1. Bunimowicz E.A., Bulychev V.A. « Prawdopodobieństwo i statystyka na kursie matematyki Szkoła średnia", M.: Uniwersytet Pedagogiczny„Pierwszy września”, 2005
2. Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. „Algebra, klasa 7”, M: „Prosveshcheniye”, 2009
3. Makarychev Yu.N., Mindyuk N.G. « Algebra. Elementy statystyki i rachunku prawdopodobieństwa”, klasy 7 – 9. – M.: Edukacja, 2005.

Recenzja

Przedmiotem badań studenta jest statystyka.

Przedmiotem badań są charakterystyki statystyczne (średnia arytmetyczna, rozstęp, moda).

Student zapoznał się ze źródłami naukowymi i zasobami internetowymi, aby zapoznać się z teorią zagadnienia.

Wybrany temat jest odpowiedni dla uczniów wykazujących zainteresowanie matematyką, informatyką i statystyką. Dla jego wieku przeanalizowano wystarczający materiał, wybrano dane i uogólniono. Student posiada wystarczającą wiedzę z zakresu ICT.

Praca jest wykonana zgodnie z wymaganiami.

Na zakończenie pracy wyciąga się wnioski i przedstawia praktyczny produkt: prezentacje problemów w statystyce. Cieszę się, że ktoś tak pasjonuje się matematyką.

Opiekun naukowy: Ulakhanova MR,

nauczyciel matematyki

Cele: podanie pojęć, algorytmów znajdowania średniej arytmetycznej i mediany, zakresu i postaci szeregu liczb, ukazanie znaczenia tego tematu w praktycznej działalności człowieka; nabycie praktycznych umiejętności wykonywania tych zadań; podniesienie poziomu kształcenia matematycznego wymaganego przez nowe standardy.

• wyposażenie uczniów w system wiedzy na temat „Wyznaczanie prawdopodobieństwa zdarzeń, średniej arytmetycznej i mediany zbioru liczb”;
• rozwijać umiejętności stosowania tej wiedzy przy rozwiązywaniu różnorodnych problemów o różnym stopniu złożoności;
• przygotować uczniów do zdania egzaminu państwowego;
• rozwijać umiejętności samodzielnej pracy.

Podczas zajęć

1. Część teoretyczna.

1). Znalezienie prawdopodobieństwa zdarzeń.

W Życie codzienne, w działalności praktycznej i naukowej często obserwuje się pewne zjawiska i przeprowadza się pewne eksperymenty.

W procesie obserwacji lub eksperymentu spotyka się pewne zdarzenia losowe, tj. takie zdarzenia, które mogą, ale nie muszą, nastąpić. Na przykład orzeł lub reszka przy rzucie monetą, trafienie w cel lub niecelny strzał, wygrana drużyny sportowej w spotkaniu z przeciwnikiem, przegrana lub remis – to wszystko są zdarzenia losowe.

Wzory zdarzenia losowe studiuje specjalną gałąź matematyki zwaną teoria prawdopodobieństwa. Metody teorii prawdopodobieństwa znajdują zastosowanie w wielu dziedzinach wiedzy.

Pochodzenie teorii prawdopodobieństwa nastąpiło w poszukiwaniu odpowiedzi na pytanie: jak często to lub inne zdarzenie występuje w dużej serii testów odbywających się w tych samych warunkach z losowymi wynikami.

Aby ocenić prawdopodobieństwo interesującego nas zdarzenia, konieczne jest przeprowadzenie dużej liczby eksperymentów lub obserwacji, a dopiero potem można określić prawdopodobieństwo tego zdarzenia.

Na przykład rzucanie kostką. Podczas rzucania kostką szanse, że każda liczba od 1 do 6 pojawi się na jej górnej ściance, są takie same. Mówią, że jest ich 6 równie możliwe wyniki doświadczenie w rzucaniu kostkami: rzuć 1,2,3,4,5 i 6 punktów.

Wyniki tego eksperymentu uważa się za równie możliwe, jeśli szanse ich uzyskania są równe.

Skutki, w których zachodzi jakieś zdarzenie, nazywane są korzystnymi skutkami tego zdarzenia.

Definicja: stosunek liczby korzystnych wyników N (A) zdarzenia A do liczby wszystkich równie możliwych wyników N tego zdarzenia nazywa się prawdopodobieństwem zdarzenia A.

Schemat wyznaczania prawdopodobieństwa zdarzenia.

Aby znaleźć prawdopodobieństwo zdarzenia losowego A podczas pewnego testu, należy:

• znajdź liczbę N wszystkich jednakowo możliwych wyników danego testu;
• znajdź liczbę N(A) tych korzystnych wyników próby, w której zachodzi zdarzenie A;
• znajdź stosunek N(A)/N; jest to prawdopodobieństwo zdarzenia A

Na przykład: 1 . W pudełku znajduje się 10 kul czerwonych, 7 żółtych i 3 niebieskie. Jakie jest prawdopodobieństwo, że losowo wybrana kula będzie żółta?

Rozwiązanie. Równie możliwe wyniki - (10+7+3)=20

Korzystne wyniki-7

2. W pudełku znajduje się 5 czarnych kul. Jaka jest najmniejsza liczba białych kul, które należy umieścić w tym pudełku, aby prawdopodobieństwo wylosowania czarnej kuli z pudełka było nie większe niż 0,15?

Rozwiązanie: Niech x będzie białymi kulami.

2) Wyznaczanie i znajdowanie średniej arytmetycznej i mediany ciągu liczbowego.

Definicja: średnia arytmetyczna kilku liczb to liczba równa stosunkowi sumy tych liczb do ich liczby.

Średnia arytmetyczna zbioru liczb x 1 , x 2 , x 3 , x 4 , x 5 jest zwykle oznaczana jako x.

Na przykład średnia arytmetyczna pięciu liczb zostanie zapisana w następujący sposób:

X = (x 1 + x 2 + x 3 + x 4 + x 5)/5

Przykład: znajdź średnią ocen ucznia z matematyki, jeśli w ostatnim okresie uzyskał: 3,4,4,5,3,2,4,3.

Rozwiązanie: (3+4+4+5+3+2+4+3)/8=3,5

Definicja: mediana to liczba dzieląca zbiór liczb na dwie części równych liczb, tak że po jednej stronie tej liczby wszystkie wartości są większe od mediany, a po drugiej mniejsze. Zamiast „mediana” można powiedzieć „środek”.

Schemat znajdowania mediany zbioru liczb:

Aby znaleźć medianę zbioru liczb:

• uporządkuj zbiór liczb (wpisz w kolejności rosnącej);
• jednocześnie skreślaj „największą” i „najmniejszą” liczbę ten zestaw liczby, aż pozostanie jedna liczba lub dwie liczby;
• jeśli pozostaje jedna liczba, to jest to mediana (dla nieparzystego zestawu liczb);
• jeśli pozostały dwie liczby, to mediana będzie średnią arytmetyczną dwóch pozostałych liczb (dla parzystego zbioru liczb).

Mediana jest zwykle oznaczona literą M.

Przykład: znajdź medianę zbioru liczb: 9,3,1,5,7.

Rozwiązanie: zapisz liczby w kolejności rosnącej: 1,3,5,7,9.

Skreśl 1 i 9, 3 i 7. Pozostała liczba 5 to mediana. M=5

Przykład: znajdź medianę zbioru liczb 2,3,3,5,7,10.

Rozwiązanie: skreśl 2 i 10, 3 i 7. Aby znaleźć M potrzebujesz: (3+5)/2= 4. M=4

Określanie i znajdowanie zakresu i trybu.

Definicja: Zakres szeregu liczb to różnica między największą i najmniejszą z tych liczb.

Rozstęp serii wyznacza się, gdy chcemy określić, jak duży jest rozrzut danych w serii.

Definicja: Formą ciągu liczb jest liczba, która pojawia się w danym szeregu częściej niż inne.

Seria liczb może mieć więcej niż jeden tryb lub może nie mieć żadnego trybu.

Przykład: Na lekcji wychowania fizycznego 14 uczniów skakało wzwyż, a nauczyciel zapisywał ich wyniki. Rezultatem była następująca seria danych (w cm):

125, 110, 130, 125, 120, 130, 140, 125, 110, 130, 120, 125, 120, 125.

Znajdź medianę, zakres i sposób pomiaru.

Rozwiązanie: zapisz wszystkie opcje pomiaru w kolejności rosnącej, oddzielając grupy identycznych wyników spacjami:

110, 110, 120, 120, 120, 125, 125, 125, 125, 125, 130, 130, 130, 140.

Zakres pomiarowy wynosi 140-110=30.

125 - spotkałem najwięcej razy, tj. 5 razy; jest to sposób pomiaru.

2. Część praktyczna.

1). Zadania dla niezależna decyzja na teorii prawdopodobieństwa.

1. Na każde 100 żarówek przypada średnio 4 uszkodzone. Jakie jest prawdopodobieństwo, że losowo wybrana żarówka okaże się sprawna? Odpowiedź: 0,96.

2. Na 400 płyt CD przypada średnio 8 wadliwych płyt CD. Jakie jest prawdopodobieństwo, że losowo wybrana płyta CD będzie dobra? Odpowiedź: 0,98.

3. 17 punktów z 50 ma kolor niebieski, a 13 z pozostałych punktów ma kolor pomarańczowy. Jakie jest prawdopodobieństwo, że losowo wybrany punkt zostanie pokolorowany? Odpowiedź: 0,6.

4. Ze słowa „matematyka” wybierana jest losowo jedna litera. Jakie jest prawdopodobieństwo, że wybrana litera pojawi się w tym słowie tylko raz? Odpowiedź: 0,3.

5. Ze słowa „certyfikacja” wybierana jest losowo jedna litera. Jakie jest prawdopodobieństwo, że wybraną literą będzie litera „a”? Odpowiedź: 0,2

6. Spośród 30 uczniów klas dziewiątych 4 wybrało egzamin z fizyki, 12 z nauk społecznych, 8 z języka obcego, a pozostali z literatury. Jakie jest prawdopodobieństwo, że wybrany student przystąpi do egzaminu z literatury. Odpowiedź: 0,2.

7. Test z matematyki składa się z 15 problemów: 4 problemy z geometrii, 2 problemy z teorii prawdopodobieństwa, reszta z algebry. Uczeń popełnił błąd w jednym zadaniu. Jakie jest prawdopodobieństwo, że uczeń popełnił błąd w zadaniu z algebry? Odpowiedź: 0,6.

8. Na 1000 samochodów wyprodukowanych w latach 2007-2009 150 ma uszkodzony układ hamulcowy. Jakie jest prawdopodobieństwo zakupu wadliwego samochodu? Odpowiedź: 0,15.

9. W zawodach gimnastyki artystycznej biorą udział: 3 gimnastyczki z Rosji, 3 gimnastyczki z Ukrainy i 4 gimnastyczki z Białorusi. Kolejność występów zostanie ustalona w drodze losowania. Znajdź prawdopodobieństwo, że jako pierwsza wystartuje gimnastyczka z Rosji. Odpowiedź 0,3

10. W mistrzostwach w gimnastyce artystycznej występuje 18 zawodniczek, w tym 3 gimnastyczki z Rosji i 2 gimnastyczki z Chin. Kolejność występów ustalana jest w drodze losowania. Znajdź prawdopodobieństwo, że gimnastyczka z Rosji lub Chin zajmie ostatnie miejsce? Odpowiedź: 18.05.

11. Z klasy liczącej 12 chłopców i 8 dziewcząt w drodze losowania wybiera się 1 osobę dyżurującą. Jakie jest prawdopodobieństwo, że będzie to chłopiec? Odpowiedź: 0,6.

12. Jednocześnie rzucamy 2 monetami. Jakie jest prawdopodobieństwo, że wylądują na 2 głowach? Odpowiedź to 0,25.

2)Zagadnienia znalezienia średniej i mediany arytmetycznej, zakresu i postaci zbioru liczb.

Ekipy frezujące spędziły na obróbce jednej części inny czas(w min.), prezentowane jako seria danych: 40; 37; 35; 36; 32; 42; 32; 38; 32. O ile mediana tego zbioru różni się od średniej arytmetycznej? Odpowiedź: 0.

W ogrodzie posadzono 5 sadzonek jabłoni, których wysokość w centymetrach wynosi: 168, 13, 156, 165, 144. O ile średnia arytmetyczna tego zbioru liczb różni się od jego mediany? Odpowiedź: 3, 8

6 gruszy rosnących w ogrodzie wydało plon, którego masa (w kg) każdego z drzew wynosi: 29, 35, 26, 28, 32, 36. Ile wynosi średnia arytmetyczna tego zbioru liczby różnią się od mediany? Odpowiedź: 0,5

Czas obsługi przez kasjera każdego z kilku klientów sklepu tworzył następujący ciąg danych: 2 minuty. 42 sek., 3 min. 2 sekundy, 3 minuty 7 sek., 2 min. 54 sek., 2 min. 48 sek. Znajdź średnią i medianę tej serii danych. Odpowiedź: 2 minuty. 55 sek., 2 min. 54 sek.

Czas pomiędzy siedmioma wezwaniami otrzymanymi przez taksówkę tworzył następujący ciąg danych: 34 sekundy, 45 sekund, 1 minuta. 16 sek., 38 sek., 43 sek., 52 sek. Znajdź średnią i medianę tej serii danych. Odpowiedź: 48 sek., 44 sek.

Literatura : Mordkovich, A. G., I. M. Smirnova. Poradnik dla instytucje edukacyjne(poziom podstawowy) - M.: Mnemosyne, 2009. - 164 s.

Oprócz średnich mocy w statystyce, do względnej charakterystyki wartości zmiennej cechy i wewnętrznej struktury szeregów rozkładów, stosuje się średnie strukturalne, które są głównie reprezentowane przez moda i mediana.

Moda- To najczęstszy wariant serii. Moda służy na przykład do określenia rozmiaru ubrań i butów, na które jest największe zapotrzebowanie wśród klientów. Modem dla szeregu dyskretnego jest ten o najwyższej częstotliwości. Obliczając modę dla szeregu zmian przedziału, należy najpierw wyznaczyć przedział modalny (na podstawie częstotliwości maksymalnej), a następnie wartość wartości modalnej atrybutu za pomocą wzoru:

Mediana - jest to wartość atrybutu leżącego u podstaw szeregu rankingowego i dzielącego ten szereg na dwie równe części.

Aby określić medianę w dyskretnym szeregu jeżeli częstotliwości są dostępne, należy najpierw obliczyć połowę sumy częstotliwości, a następnie określić, która wartość wariantu na nią przypada. (Jeśli posortowana seria zawiera liczba nieparzysta charakterystyki, wówczas średnią liczbę oblicza się ze wzoru:

M e = (n (liczba cech ogółem) + 1)/2,

w przypadku parzystej liczby cech mediana będzie równa średniej z dwóch cech znajdujących się w środku wiersza).

Przy obliczaniu mediany dla serii zmian przedziałowych Najpierw określ przedział mediany, w którym mieści się mediana, a następnie określ wartość mediany, korzystając ze wzoru:

Przykład. Znajdź modę i medianę.

Rozwiązanie:
W w tym przykładzie przedział modalny mieści się w przedziale wiekowym 25-30 lat, gdyż w tym przedziale występuje najwyższa częstość (1054).

Obliczmy wielkość modu:

Oznacza to, że modalny wiek studentów wynosi 27 lat.

Obliczmy medianę. Mediana interwału jest włączona Grupa wiekowa 25-30 lat, gdyż w tym przedziale istnieje opcja podziału populacji na dwie równe części (Σf i /2 = 3462/2 = 1731). Następnie podstawiamy niezbędne dane liczbowe do wzoru i otrzymujemy wartość mediany:

Oznacza to, że połowa studentów ma mniej niż 27,4 lat, a druga połowa powyżej 27,4 roku życia.

Oprócz trybu i mediany można zastosować wskaźniki takie jak kwartyle dzielące uszeregowany szereg na 4 równe części, decyle -10 części i percentyle - na 100 części.