1. Pierwsze dwa znaki równości trójkątów prostokątnych.
Aby dwa trójkąty były równe, wystarczy, że trzy elementy jednego trójkąta są równe odpowiednim elementom drugiego trójkąta, a elementy te z pewnością muszą obejmować przynajmniej jeden bok.
Ponieważ wszystkie kąty proste są sobie równe, trójkąty prostokątne mają już jeden równy element, a mianowicie jeden kąt prosty.

Wynika z tego, że trójkąty prostokątne są przystające:
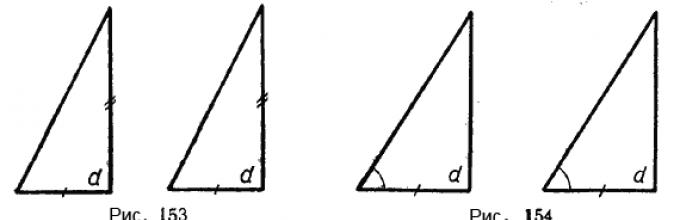
jeśli nogi jednego trójkąta są odpowiednio równe nogom innego trójkąta (ryc. 153);
jeśli noga i przyległy kąt ostry jednego trójkąta są odpowiednio równe nodze i przyległemu kątowi ostremu drugiego trójkąta (ryc. 154).
Udowodnimy teraz dwa twierdzenia ustalające dwa kolejne kryteria równości trójkątów prostokątnych.
Twierdzenia o testach równości trójkątów prostokątnych
Twierdzenie 1. Jeżeli przeciwprostokątna i kąt ostry jednego trójkąta są odpowiednio równe przeciwprostokątnej i kątowi ostremu drugiego trójkąta, to takie trójkąty prostokątne są przystające.Aby udowodnić to twierdzenie, skonstruujmy dwa kąty prostokątne ABC i A'B'C', w których kąty A i A' są równe, przeciwprostokątne AB i A'B' są również równe oraz kąty C i C' mają rację (ryc. 157) .

Nałóżmy trójkąt A’B’C’ na trójkąt ABC tak, aby wierzchołek A’ pokrywał się z wierzchołkiem A, przeciwprostokątna A’B’ pokrywała się z równą przeciwprostokątną AB. Wtedy, ze względu na równość kątów A i A’, bok A’C’ będzie przebiegał wzdłuż boku AC; noga B’C’ będzie pokrywać się z nogą BC: obie są prostopadłymi poprowadzonymi do jednej prostej AC z punktu B. Oznacza to, że wierzchołki C i C’ będą się pokrywać.
Trójkąt ABC pokrywa się z trójkątem A'B'C'.
Zatem \(\Delta\)ABC = \(\Delta\)A'B'C'.
Twierdzenie to podaje trzecie kryterium równości trójkątów prostokątnych (przez przeciwprostokątną i kąt ostry).
Twierdzenie 2. Jeżeli przeciwprostokątna i noga jednego trójkąta są odpowiednio równe przeciwprostokątnej i nodze innego trójkąta, to takie trójkąty prostokątne są przystające.
Aby to udowodnić, zbudujmy dwa prostokąty trójkąt ABC i A'B'C', w którym kąty C i C' są proste, ramiona AC i A'C' są równe, przeciwprostokątne AB i A'B' są również równe (ryc. 158).

Narysujmy prostą MN i zaznaczmy na niej punkt C, z tego punktu rysujemy prostopadłą SC do prostej MN. Następnie nałożymy kąt prosty trójkąta ABC na kąt prosty KSM tak, aby ich wierzchołki pokrywały się i ramię AC przebiegało wzdłuż półprostej SC, następnie ramię BC przebiegało wzdłuż półprostej CM. Kąt prosty trójkąta A'B'C' nałożymy na kąt prosty KCN tak, że ich wierzchołki zrównają się i noga A'C' przejdzie wzdłuż półprostej SK, następnie noga C'B' przejdzie wzdłuż półprostej CN. Wierzchołki A i A' będą się pokrywać ze względu na równość nóg AC i A'C'.
Trójkąty ABC i A'B'C' utworzą się razem Trójkąt równoramienny BAB’, w którym AC będzie wysokością i dwusieczną, a zatem osią symetrii trójkąta BAB’. Wynika z tego, że \(\Delta\)ABC = \(\Delta\)A’B’C’.
Twierdzenie to podaje czwarte kryterium równości trójkątów prostokątnych (przez przeciwprostokątną i nogę).
Zatem wszystkie znaki równości trójkątów prostokątnych:
1. Jeśli dwie nogi jednego trójkąta prostokątnego są odpowiednio równe dwóm nogom innego trójkąta prostokątnego, wówczas takie trójkąty prostokątne są równe2. Jeżeli noga i przyległy kąt ostry jednego trójkąta prostokątnego są odpowiednio równe nodze i sąsiedniemu kątowi ostremu innego trójkąta prostokątnego, to takie trójkąty prostokątne są przystające
3. Jeżeli noga i przeciwny kąt ostry jednego trójkąta prostokątnego są odpowiednio równe nodze i przeciwnemu kątowi ostremu innego trójkąta prostokątnego, to takie trójkąty prostokątne są przystające
4. Jeżeli przeciwprostokątna i kąt ostry jednego trójkąta prostokątnego są odpowiednio równe przeciwprostokątnej i kątowi ostremu innego trójkąta prostokątnego, to takie trójkąty prostokątne są przystające
5. Jeśli noga i przeciwprostokątna jednego trójkąta prostokątnego są odpowiednio równe nodze i przeciwprostokątnej innego trójkąta prostokątnego, wówczas takie trójkąty prostokątne są przystające
Aby ustalić równość trójkątów prostokątnych, wystarczy wiedzieć, że dwa elementy jednego trójkąta są odpowiednio równe dwóm elementom innego trójkąta (z wyłączeniem kąta prostego). Nie dotyczy to oczywiście równości dwóch kątów jednego trójkąta z dwoma kątami drugiego trójkąta.
Od w trójkąt prostokątny kąt między dwiema nogami jest linią prostą, a dowolne dwa kąty proste są równe, to z pierwszego znaku równości trójkątów wynika:
Jeśli nogi jednego trójkąta prostokątnego są odpowiednio równe nogom drugiego, wówczas takie trójkąty są przystające (ryc. 5).
Jeżeli noga i przyległy kąt ostry jednego trójkąta prostokątnego są odpowiednio równe nodze i kątowi przyległemu innego trójkąta, to takie trójkąty są przystające (ryc. 6).

Rozważmy jeszcze dwa znaki równości trójkątów prostokątnych.

TWIERDZENIE . Jeżeli przeciwprostokątna i kąt ostry jednego trójkąta prostokątnego są równe przeciwprostokątnej i kątowi ostremu drugiego trójkąta, to takie trójkąty są przystające (ryc. 7).
DOWÓD. Z własności 1є § wynika, że w takich trójkątach pozostałe dwa kąty ostre są również równe, dlatego trójkąty są równe zgodnie z drugim znakiem równości trójkątów, to znaczy wzdłuż boku (przeciwprostokątna) i dwóch sąsiednich kątów.
co było do okazania
TWIERDZENIE . Jeżeli przeciwprostokątna i noga jednego trójkąta prostokątnego są odpowiednio równe przeciwprostokątnej i nodze innego trójkąta, to takie trójkąty są przystające.
DOWÓD. Rozważmy trójkąty ABC i A 1 B 1 C 1 , którego kąty C i C 1 są kątami prostymi, AB = A 1 B 1 , BC = B 1 C 1 (ryc. 8).

Ponieważ< C = < C 1 , то треугольник ABC можно наложить на треугольник A 1 B 1 C 1 так, что вершина C совместится с вершиной C 1 , а стороны CA и CB наложатся соответственно на лучи C 1 A 1 и C 1 B 1 , поскольку CB = C 1 B 1 , то вершина B совместится с вершиной B 1 . Но тогда вершины A и A 1 также совместятся. В самом деле, если предположить, что точка A совместится с некоторой другой точкой A 2 луча C 1 A 1 , то получим равнобедренный треугольник A 1 B 1 A 2 , в котором углы при основании A 1 A 2 не равны (на рисунке < A 2 - острый, а < A 1 - тупой как смежный с kąt ostry B 1 Za 1 Do 1). Ale jest to niemożliwe, więc wierzchołki A i A 1 będą się pokrywać. Dlatego trójkąty ABC A 1 B 1 C 1 będą całkowicie zgodne, to znaczy są równe.
co było do okazania
twierdzenie Pitagorasa
Jego znaczenie polega na tym, że większość twierdzeń geometrii można z niego lub za jego pomocą wyprowadzić. Jedno z twierdzeń pozwala sprawdzić, że jeśli poprowadzić do niego linie prostopadłe i ukośne z punktu znajdującego się poza linią, to: a) linie ukośne są równe, jeśli ich rzuty są równe; b) ten, który jest nachylony, jest większy, co ma większy występ.
Twierdzenie Pitagorasa było pierwszym stwierdzeniem, które powiązało długości boków trójkątów. Następnie nauczyliśmy się obliczać długości boków i kąty ostre i rozwarte trójkąty. Powstała cała nauka o trygonometrii („trigon” oznacza po grecku „trójkąt”). Nauka ta znalazła zastosowanie w geodezji. Ale jeszcze wcześniej za jego pomocą nauczyli się mierzyć wyimaginowane trójkąty na niebie, których wierzchołkami były gwiazdy. Obecnie trygonometrię wykorzystuje się nawet do pomiaru odległości pomiędzy statkami kosmicznymi.
Korzystając z właściwości pól wielokątów, ustalimy teraz niezwykłą zależność pomiędzy przeciwprostokątną a ramionami trójkąta prostokątnego. Twierdzenie, które udowodnimy, nazywa się twierdzeniem Pitagorasa i jest najważniejszym twierdzeniem w geometrii.
Jeżeli dany jest nam trójkąt,
I pod kątem prostym,
To jest kwadrat przeciwprostokątnej
Zawsze możemy łatwo znaleźć:
Prostujemy nogi,
Znajdujemy sumę potęg
I to w tak prosty sposób
Dojdziemy do wyniku.
TWIERDZENIE. W trójkącie prostokątnym kwadrat przeciwprostokątnej jest równy sumie kwadratów nóg.
DOWÓD. Rozważmy trójkąt prostokątny o nogach a, b i c (ryc. 9 a).

Udowodnijmy, że do 2 = a 2 + b 2 . Zbudujmy trójkąt w kwadrat o boku a+b, jak pokazano na rysunku (ryc. 9 b).
Pole takiego kwadratu o boku a + b jest równe (a + b) 2. Z drugiej strony kwadrat ten składa się z czterech równych trójkątów prostokątnych o polu ab i kwadratu o boku c, więc
Zatem (a + b) 2 =2ab + do 2, skąd c 2 = a 2 + b 2.
co było do okazania
WNIOSEK 1 . W trójkącie prostokątnym dowolna z nóg jest krótsza od przeciwprostokątnej.
DOWÓD. Zgodnie z twierdzeniem Pitagorasa AB 2 = AC 2 + BC 2 . Ponieważ BC 2 > 0, następnie AC 2<АВ, То есть АС<АВ.
WNIOSEK 2. Dla dowolnego kąta ostrego b cosb<1.
DOWÓD. Z definicji cosinus cosб = . Ale w wniosku 1 udowodniono, że AC<АВ, Oznacza to, że ułamek jest mniejszy niż 1.
Trójkąty prostokątne, których boki są wyrażone w liczbach całkowitych, nazywane są trójkątami pitagorejskimi.
Można udowodnić, że ramiona a, b i przeciwprostokątna c takich trójkątów wyrażają się wzorami a=2kmn; b=k(m2-n2); c=k(m 2 + n 2), gdzie k, m i n są liczbami naturalnymi takimi, że m>n. Trójkąty o bokach długości 3, 4, 5 nazywane są trójkątami egipskimi, ponieważ były znane starożytnym Egipcjanom.
Odwrotność twierdzenia Pitagorasa.
Jeśli kwadrat jednego boku trójkąta jest równy sumie kwadratów dwóch pozostałych boków, to trójkąt jest prostokątny (znak trójkąta prostokątnego).
DOWÓD.
Wpuśćmy trójkąt ABC AB 2 = AC 2 + BC 2. Udowodnijmy, że kąt C jest kątem prostym. Rozważmy trójkąt prostokątny A 1 B 1 C 1 z kątem prostym C 1, w którym A 1 C 1 = AC i B 1 C 1 = BC. Według twierdzenia Pitagorasa A 1 B 1 2 = A 1 C 1 2 + B 1 C 1 2, a zatem A 1 B 1 2 = AC 2 + BC 2. Ale AC 2 + BC 2 = AB 2 zgodnie z twierdzeniem. Dlatego A 1 B 1 2 = AB 2, skąd A 1 B 1 = AB. Trójkąty ABC i A 1 B 1 C 1 są zatem równe z trzech stron< C = < C 1 , то есть треугольник ABC прямоугольный с прямым углом C.
co było do okazania
Wśród trójkątów swoje miejsce zajmują trójkąty prostokątne, a także trójkąty równoramienne i równoboczne, posiadające szczególny zespół specyficznych właściwości, charakterystycznych tylko dla tego typu trójkątów. Rozważmy kilka twierdzeń o równości trójkątów prostokątnych, co znacznie uprości rozwiązanie niektórych problemów.
Pierwszy znak równości trójkątów prostokątnych
Znaki równości trójkątów prostokątnych wywodzą się z trzech znaków równości trójkątów, ale kąt prosty zniekształca je, rozszerzając i upraszczając. Każdy ze znaków równości trójkątów prostokątnych można zastąpić jednym z trzech głównych, ale zajmie to zbyt dużo czasu, dlatego zidentyfikowano 5 właściwości i znaków równości trójkątów prostokątnych.
Bardzo często zamiast używać podstawowych znaków równości trójkątów, stosuje się metodę superpozycji, gdy dwie figury nakładają się na siebie w myślach. Nie można powiedzieć, że jest to prawda lub fałsz. Kolejna metoda dowodu do rozważenia. Nie można jednak myśleć, że jakikolwiek znak można udowodnić za pomocą zwykłej superpozycji. Dlatego rozważymy dowód znaków równości trójkątów prostokątnych poprzez trzy główne znaki równości trójkątów.
Pierwszy znak równości trójkątów prostokątnych mówi: dwa trójkąty prostokątne są równe, jeśli dwie nogi jednego trójkąta są równe dwóm bokom innego trójkąta. Krótko mówiąc, ta cecha nazywa się równością po obu stronach.

Ryż. 1. Równość po obu stronach
Udowodnienie tego znaku jest bardzo proste. Dane: dwie nogi trójkąta prostokątnego są równe. Pomiędzy nogami znajduje się kąt prosty, który jest równy 90 stopni, co oznacza, że kąt trójkątów pokrywa się. Dlatego dwa trójkąty są równe w dwóch bokach i kącie między nimi.
Drugi znak
Drugi znak brzmi następująco: dwa trójkąty prostokątne są równe, jeśli noga i przyległy kąt ostry jednego trójkąta są równe nodze i kątowi przyległemu drugiego trójkąta.
Drugi znak dowodzi się na podstawie tego samego stwierdzenia o równości kątów prostych ze sobą. Jeśli trójkąty mają równe nogi, ich kąty ostre są równe, a kąty proste z definicji są równe, to takie trójkąty są równe według drugiego znaku równości (bok i dwa sąsiednie kąty).
Trzeci znak
Dwa trójkąty prostokątne są przystające, jeśli bok i przeciwny kąt ostry są równe.

Ryż. 2. Rysunek na dowód
Suma kątów ostrych w trójkącie wynosi 90 stopni. Dla uproszczenia dowodu oznaczmy kąty małymi literami łacińskimi. Jeden kąt jest prosty, a dwa pozostałe są oznaczone literami a i b w pierwszym trójkącie; c i d w drugim trójkącie.
Kąty a i d są sobie równe zgodnie z warunkami zadania.
Odejmij kąt a od obu stron wyrażenia
Oznacza to, że jeśli w dwóch trójkątach prostokątnych dwa kąty ostre są sobie równe, to pozostałe dwa kąty ostre również będą równe i możemy użyć drugiego znaku.
W drugim i trzecim znaku należy szczególnie skupić się na kącie ostrym, ponieważ kąty proste są zawsze sobie równe.
Czwarty znak
Jeżeli przeciwprostokątna i kąt ostry jednego trójkąta prostokątnego są równe przeciwprostokątnej i kątowi ostremu drugiego trójkąta prostokątnego, to trójkąty są przystające.
Jak stwierdzono w poprzednim znaku: jeśli kąt ostry trójkąta prostokątnego jest równy odpowiadającemu mu kątowi ostremu innego trójkąta prostokątnego, wówczas druga para kątów ostrych trójkątów będzie sobie równa.
Oznacza to, że zgodnie z warunkami tego kryterium mamy równość przeciwprostokątnej i dwóch kątów ostrych trójkątów, co oznacza, że takie trójkąty będą równe w bokach i dwóch sąsiednich kątach (2. znak równości trójkątów)
Piąty znak
Jeżeli przeciwprostokątna i noga jednego trójkąta prostokątnego są odpowiednio równe przeciwprostokątnej i nodze innego trójkąta, to takie trójkąty są przystające.
Jeśli przeciwprostokątna i noga dwóch trójkątów są odpowiednio równe, wówczas drugie nogi takich trójkątów będą sobie równe. Wynika to z twierdzenia Pitagorasa.

Ryż. 3. Równość wzdłuż nogi i przeciwprostokątnej
Kwadrat przeciwprostokątnej jest równy sumie kwadratów nóg. Przeciwprostokątne są sobie równe, noga jednego trójkąta jest równa kwadratowi drugiego trójkąta, co oznacza, że suma pozostaje prawdziwa, a pozostałe dwie nogi będą sobie równe.
Czego się nauczyliśmy?
Przyjrzeliśmy się dowódowi pięciu testów na równość trójkątów poprzez podstawowe testy na równość trójkątów. Dowiedzieliśmy się, dlaczego taki dowód jest lepszy od nakładki i ustaliliśmy ścieżkę dowodu, która pozwoli w dowolnym momencie przywrócić w pamięci podstawowe pojęcia z danego tematu, bez niepotrzebnego zapamiętywania.
Testuj w temacie
Ocena artykułu
Średnia ocena: 4.6. Łączna liczba otrzymanych ocen: 100.
Przypomnijmy z materiału z poprzedniej lekcji, że trójkąt nazywamy trójkątem prostokątnym, jeśli przynajmniej jeden z jego kątów jest kątem prostym (tj. równym 90°).
Rozważmy pierwszy znak Równość trójkątów: jeśli dwie nogi jednego trójkąta prostokątnego są odpowiednio równe dwóm nogom innego trójkąta prostokątnego, to takie trójkąty są przystające.
Zilustrujmy ten przypadek:
Ryż. 1. Równe trójkąty prostokątne
Dowód:
Przypomnijmy sobie pierwszą równość dowolnych trójkątów.

Ryż. 2
Jeżeli dwa boki i kąt między nimi jednego trójkąta i odpowiadające im dwa boki i kąt między nimi drugiego trójkąta są równe, to te trójkąty są przystające. Wskazuje na to pierwszy znak równości trójkątów, czyli:

Podobny dowód następuje dla trójkątów prostokątnych:
 .
.
Trójkąty są równe według pierwszego kryterium.
Rozważmy drugi znak równości trójkątów prostokątnych. Jeżeli noga i przyległy kąt ostry jednego trójkąta prostokątnego są odpowiednio równe nodze i przyległemu kątowi ostremu innego trójkąta prostokątnego, to takie trójkąty są przystające.

Ryż. 3
Dowód:

Ryż. 4
Skorzystajmy z drugiego kryterium równości trójkątów:

Podobny dowód dla trójkątów prostokątnych:

Trójkąty są równe według drugiego kryterium.
Rozważmy trzecie kryterium równości trójkątów prostokątnych: jeśli przeciwprostokątna i kąt przyległy jednego trójkąta prostokątnego są odpowiednio równe przeciwprostokątnej i kątowi sąsiedniemu innego trójkąta, wówczas takie trójkąty są przystające.
Dowód:

Ryż. 5
Przypomnijmy drugie kryterium równości trójkątów:

Ryż. 6
Te trójkąty są równe, jeśli:

Ponieważ wiadomo, że jedna para kątów ostrych w trójkątach prostokątnych jest równa (∠A = ∠A 1), to równość drugiej pary kątów (∠B = ∠B 1) udowadnia się w następujący sposób:
Ponieważ AB = A 1 B 1 (według warunku), ∠B = ∠B 1, ∠A = ∠A 1. Dlatego trójkąty ABC i A 1 B 1 C 1 są równe zgodnie z drugim kryterium.
Rozważmy następujące kryterium równości trójkątów:
Jeśli noga i przeciwprostokątna jednego trójkąta są odpowiednio równe nodze i przeciwprostokątnej innego trójkąta, takie trójkąty prostokątne są przystające.

Ryż. 7
Dowód:
Połączmy trójkąty ABC i A 1 B 1 C 1 nakładając się na siebie. Załóżmy, że wierzchołki A i A 1 oraz C i C 1 nakładają się na siebie, ale wierzchołek B i punkt B 1 nie pokrywają się. Dokładnie tak jest w przypadku pokazanym na poniższym rysunku:

Ryż. 8
W tym przypadku możemy zauważyć trójkąt równoramienny ABV 1 (z definicji - na mocy warunku AB = AB 1). Zatem zgodnie z własnością ∠AB 1 B = ∠ABV 1. Spójrzmy na definicję kąta zewnętrznego. Narożnik zewnętrzny trójkąta to kąt przylegający do dowolnego kąta trójkąta. Jego miara stopnia jest równa sumie dwóch kątów trójkąta, które do niego nie przylegają. Rysunek pokazuje ten stosunek:

Ryż. 9
Kąt 5 jest kątem zewnętrznym trójkąta i jest równy ∠5 = ∠1 + ∠2. Wynika z tego, że kąt zewnętrzny jest większy od każdego z kątów do niego nieprzylegających.
Zatem ∠ABB 1 jest kątem zewnętrznym trójkąta ABC i jest równy sumie ∠ABB 1 = ∠CAB + ∠ACB = ∠ABC = ∠CAB + 90 o. Zatem ∠AB 1 B (który jest kątem ostrym w trójkącie prostokątnym ABC 1) nie może być równy kątowi ∠ABB 1, ponieważ zgodnie z tym, co zostało udowodnione, kąt ten jest rozwarty.
Oznacza to, że nasze założenie dotyczące położenia punktów B i B 1 okazało się błędne, zatem punkty te pokrywają się. Oznacza to, że trójkąty ABC i A 1 B 1 C 1 nakładają się na siebie. Zatem są one równe (z definicji).
Zatem funkcje te nie są wprowadzane na próżno, ponieważ można je wykorzystać do rozwiązania niektórych problemów.
- Uniwersytet Państwowy w Omsku ().
- Portal pomocy calc.ru ().
- Portal nauczyciela ().
1. nr 38. Butuzov V.F., Kadomtsev S.B., Prasolov V.V., pod red. Sadovnichy V.A. Geometria 7. M.: Edukacja. 2010
2. Na podstawie danych wskazanych na rysunku wskaż równe trójkąty, jeśli występują.

3. Na podstawie danych wskazanych na rysunku wskaż równe trójkąty, jeśli występują. Pamiętaj, że AC = AF.

4. W trójkącie prostokątnym mediana i wysokość są rysowane do przeciwprostokątnej. Kąt między nimi wynosi 20°. Określ wielkość każdego z kątów ostrych tego trójkąta prostokątnego.
Sekcje: Matematyka
Temat: „Znaki równości trójkątów prostokątnych”
Cel: utrwalenie wiedzy (właściwości trójkątów prostokątnych), zapoznanie z niektórymi znakami równości trójkątów prostokątnych.
Podczas zajęć:
I. Moment organizacyjny.II. Doustnie.
1. Odpowiedz na pytania:
- Nazwij elementy trójkąta prostokątnego.
- Jakie właściwości mają elementy trójkąta prostokątnego?
- Udowodnić, że noga trójkąta prostokątnego leżąca naprzeciw kąta 30 0 jest równa połowie przeciwprostokątnej.
- Udowodnić, że jeśli noga trójkąta prostokątnego jest równa połowie przeciwprostokątnej, to kąt leżący naprzeciw tej nogi wynosi 30 0.
- Znajdź x. Wybierz odpowiedź z trójkąta. Litery słowa znajdują się w sektorach trójkąta. Dyskusja w parach (3 min).
Obrazek 1.
Wymyślili słowo „znak”.
III. Nauka nowego materiałuBadając trójkąty, mówimy, że ma on pewne właściwości i cechy. Jakie znasz znaki równości trójkątów? Sformułowaliśmy i udowodniliśmy właściwości trójkątów prostokątnych, a dzisiaj przyjrzymy się znakom równości trójkątów prostokątnych i rozwiążemy problemy za ich pomocą.
Ile par odpowiednio równych elementów znaleziono podczas udowadniania równości trójkątów? Czy można udowodnić równość trójkątów prostokątnych wzdłuż dwóch boków?
Przed tobą dwa trójkąty prostokątne ABC i A 1 B 1 C 1, ich nogi są odpowiednio równe. Jeśli to możliwe, udowodnij ich równość.
nr 1. (Z dwóch stron)

Rysunek 2.
Dane: ABC i A 1 B 1 C 1, B=B 1 =90 0, AB = A 1 B 1, BC = B 1 C 1
Udowodnij: ABC = A 1 B 1 Do 1
Jak będzie brzmiał ten znak? (Wtedy zadanie nr 1)
Nr 2. (W zależności od nogi i przylegającego do niej kąta ostrego)

Rysunek 3.
Dane: ABC i A 1 B 1 C 1, B=B 1 =90 0, BC = B 1 C 1, C= C 1
Udowodnij: ABC = A 1 B 1 Do 1
Jak będzie brzmiał ten znak? (Wtedy zadanie nr 2)
Nr 3. (Według przeciwprostokątnej i kąta ostrego)

Rysunek 4.
Dane: ABC i A 1 B 1 C 1, B=B 1 =90 0, AC = A 1 C 1, A= A 1
Udowodnij: ABC = A 1 B 1 Do 1
Jak będzie brzmiał ten znak? (Wtedy zadanie nr 3)
Zadania. Znajdź przystające trójkąty i udowodnij ich równość.

Rysunek 5.
IV. Ugruntowanie wiedzy poznanej na lekcji.Rozwiąż następujący problem.

Rysunek 6.
Dane: ABC, A 1 B 1 C 1, DAB=CBA=90 0, AD = BD
Udowodnić: CAB=DBA.
Dyskusja w grupach czteroosobowych (3 min).
Dlaczego problem z podręcznika nr 261 z nagraniem.

Rysunek 7.
Dane: ABC – równoramienny, AD i CE – wysokość ABC
Udowodnij: AD = CE
Dowód:
V. Zadanie domowe.
P.35 (trzy znaki), nr 261 (udowodnić, że AOS jest równoramienny), nr 268 (test na równość trójkątów prostokątnych wzdłuż nogi i kąta przeciwnego).
Na następnej lekcji geometrii będziemy kontynuować naszą znajomość znaków równości trójkątów prostokątnych. Następnym razem wystawię również oceny na podstawie wyników z 2 lekcji.
Dodatkowo. Znajdź równe trójkąty.