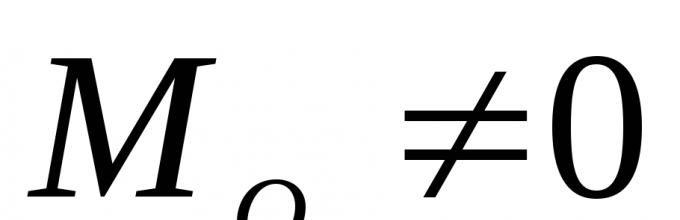Doprowadzenie płaskiego układu sił do zadanego punktu. Sprowadzenie płaskiego układu sił do środka. Sprawdzenie poprawności rozwiązania równań

Płaski układ sił arbitralnie rozmieszczonych.

Warunki równowagi par sił.

Jeżeli na ciało stałe działa kilka par sił, dowolnie rozmieszczonych w przestrzeni, to stosując sekwencyjnie regułę równoległoboku do każdych dwóch momentów par sił, dowolną liczbę par sił można zastąpić jedną równoważną parą sił , którego moment jest równy sumie momentów danych par sił.

Twierdzenie. Dla równowagi par sił działających na ciało stałe konieczne i wystarczające jest, aby suma algebraiczna rzutów momentów par sił na każdą z trzech osi współrzędnych była równa zeru.

Rozważmy przypadek przeniesienia siły do ​​dowolnego punktu, który nie leży na linii działania siły.

Weźmy siłę F przyłożoną w punkcie C. Siłę tę musimy przenieść równolegle do siebie do pewnego punktu O. Przyłóżmy w punkcie O dwie siły F” i F”, przeciwnie skierowane, równe co do wartości i równoległe do zadanej siła F, czyli F" = F" = F. Przyłożenie tych sił w punkcie O nie powoduje zmiany stanu ciała, gdyż są one wzajemnie równoważone. Powstały układ trzech sił można uznać za składający się z siły F” przyłożonej w punkcie O oraz pary sił FF” z momentem M = Fa. Ta para sił nazywa się zaanektowany, a jego ramię a jest równe ramieniu siły F względem punktu O.

Zatem, gdy siłę F doprowadza się do punktu nie leżącego na linii działania tej siły, otrzymuje się równoważny układ, składający się z siły o tej samej wielkości i kierunku co siła F oraz dołączonej pary sił, którego moment jest równy momentowi danej siły względem rzutów punktowych:

Jako przykład redukcji siły rozważmy działanie siły F na koniec C zaciśniętego pręta (ryc. 28, b). Po doprowadzeniu siły F do punktu O odcinka zaciśniętego znajdujemy w niej siłę F1 równą i równoległą do zadanej oraz moment przyłączony M równy momentowi danej siły F względem punktu redukcji O,

1.4.2 Doprowadzenie płaskiego układu sił do zadanego punktu

Opisany sposób doprowadzenia jednej siły do ​​danego punktu można zastosować do dowolnej liczby sił. Załóżmy, że w punktach ciała A, B, C i D działają siły F1, F2, F3, F4 (rys. 30).

Należy doprowadzić te siły do ​​punktu O płaszczyzny. Przedstawmy najpierw siłę F1 przyłożoną w punkcie A. Przyłóżmy w punkcie O dwie siły F1" i F1"", równoległe do niego i skierowane w przeciwne strony. W wyniku przyłożenia siły F1 otrzymamy przyłożoną siłę F1" w punkcie O i parę sił F1 "F1" z występem a1. Robiąc to samo z siłą F2 przyłożoną w punkcie B, otrzymamy siłę F2" przyłożoną w punkcie O i parę sił z występem a2, itd.

Płaski układ sił przyłożonych w punktach A, B, C i D zastąpiliśmy zbieżnymi siłami F1, F2, F3, F4 przyłożonymi w punkcie O oraz parami sił o momentach równych momentom danych sił względem punktu O :

Siły zbiegające się w jednym punkcie można zastąpić jedną siłą F”hl, równą sumie geometrycznej składników,

Siła ta, równa sumie geometrycznej danych sił, nazywa się główny wektor układu sił i oznacz F"ch.

Bazując na zasadzie dodawania par sił, można je zastąpić powstałą parą, której moment jest równy sumie algebraicznej momentów danych sił względem punktu O i nazywa się Głównym punktem względem punktu odniesienia

W rezultacie w ogólnym przypadku płaski układ sił w wyniku redukcji do danego punktu O zostaje zastąpiony układem równoważnym składającym się z jednej siły (wektor główny) i jednej pary (moment główny).

Należy zrozumieć, że wektor główny F”ch jest wypadkową danego układu sił, ponieważ układ ten nie jest równoważny jednej sile F”ch. Dopiero w szczególnym przypadku, kiedy zaniknie moment główny, wektor główny będzie wypadkową danego układu sił. Ponieważ wektor główny jest równy sumie geometrycznej sił danego układu, ani jego wielkość, ani kierunek nie zależą od wyboru środka redukcji. Wartość i znak momentu głównego Mgl zależą od położenia środka redukcji, ponieważ ramiona par składowych zależą od względnego położenia sił i punktu (środka), względem którego brane są momenty.

Mogą wystąpić następujące przypadki wprowadzenia układu sił:
1. - przypadek ogólny; układ zostaje zredukowany do wektora głównego i momentu głównego.
2. ; układ zostaje zredukowany do jednego wypadkowego równego głównemu wektorowi układu.
3. ; układ sprowadza się do pary sił, których moment jest równy momentowi głównemu.
4. ; układ jest w równowadze, to znaczy dla równowagi płaskiego układu sił konieczne i wystarczające jest, aby jego wektor główny i moment główny były jednocześnie równe zeru.

Można udowodnić, że w ogólnym przypadku zawsze istnieje punkt, wokół którego główny moment sił jest równy zeru.

Rozważmy płaski układ sił doprowadzony do punktu O, to znaczy zastąpiony wektorem głównym przyłożonym w punkcie O i momentem głównym. Dla pewności zakładamy, że moment główny jest skierowany zgodnie z ruchem wskazówek zegara, tj. . Przedstawmy ten moment główny jako parę sił FF”, których moduł zostanie wybrany równy modułowi wektora głównego, czyli przyłożymy jedną z sił tworzących parę w środku redukcji O, druga siła w punkcie C, której położenie zostanie określone na podstawie warunku: Zatem .

Ułóżmy parę sił tak, aby siła F"" była skierowana w kierunku przeciwnym do wektora głównego F"ch. W punkcie O mamy dwie równe, wzajemnie przeciwne siły F"ch i F"", skierowane wzdłuż tej samej prostej linia; można je odrzucić (zgodnie z trzecim aksjomatem). W konsekwencji, względem punktu C, moment główny rozpatrywanego układu sił jest równy zeru, a układ sprowadza się do wypadkowej.

Sprowadzenie układu sił do środka

pytania

Wykład 6

3. Warunki równowagi dla dowolnego układu sił

1. Rozważ dowolny układ sił. Wybierzmy dowolny punkt O za środkiem redukcji i korzystając z twierdzenia o równoległym przeniesieniu siły przenosimy wszystkie siły układu do danego punktu, nie zapominając o dodaniu powiązanej pary sił przy przekazywaniu każdej siły.

Zastąpmy powstały układ zbieżnych sił jedną siłą równą głównemu wektorowi pierwotnego układu sił. Układ par sił powstały podczas przenoszenia zostanie zastąpiony jedną parą o momencie równym sumie geometrycznej momentów wszystkich par sił (czyli sumie geometrycznej momentów pierwotnego układu sił względem środka O).

Ta chwila nazywa się moment główny układu sił względem środka O (ryc. 1.30).

Ryż. 1.30. Sprowadzenie układu sił do środka

Zatem każdy układ sił można zawsze zastąpić tylko dwoma współczynnikami siły - wektor główny i moment główny względem dowolnie wybranego środka redukcji . Oczywiście wektor główny układu sił nie zależy od wyboru środka redukcji (mówi się, że wektor główny jest niezmienniczy ze względu na wybór środka redukcji). Oczywiste jest również, że moment główny nie ma tej właściwości, dlatego zawsze należy wskazać, względem którego środka wyznaczany jest moment główny.

2. Doprowadzenie układu sił do najprostszej postaci

Możliwość dalszego upraszczania dowolnych układów sił zależy od wartości ich wektora głównego i momentu głównego, a także od trafnego wyboru środka redukcji. Możliwe są następujące przypadki:

A) , . W tym przypadku układ sprowadza się do pary sił z momentem, którego wartość nie zależy od wyboru środka redukcji.

B) , . System jest zredukowany do wynikowej równej , którego linia działania przechodzi przez środek O.

c) i są wzajemnie prostopadłe. Układ jest zredukowany do wynikowej równej, ale nie przechodzącej przez środek O(ryc. 1.31).

Ryż. 1.31. Doprowadzenie układu sił do wypadkowego

Zastąpmy moment główny parą sił, jak pokazano na ryc. 1.31. Zdefiniujmy R od warunku, że M 0 = R godz. Następnie, w oparciu o drugi aksjomat statyki, odrzućmy zrównoważony układ dwóch sił przyłożonych w jednym punkcie O.

d) i równoległe. Układ napędzany jest dynamiczną śrubą, której oś przechodzi przez środek O(ryc. 1.32).

Ryż. 1,32. Dynamiczna śruba

e) i nie są równe zeru, a jednocześnie wektor główny i moment główny nie są do siebie równoległe i prostopadłe. Układ napędzany jest dynamiczną śrubą, ale oś nie przechodzi przez środek O(ryc. 1.33).

Ryż. 1,33. Najbardziej ogólny przypadek redukcji układu sił

Załóżmy, że dowolny płaski układ sił sprowadza się do jednej siły równej wektorowi głównemu i przyłożonej do środka redukcji oraz do jednej pary z momentem równym momentowi głównemu
(Rysunek 57, A). Udowodnijmy, że rozważany dowolny płaski układ sił sprowadza się w tym ogólnym przypadku do siły wypadkowej
, którego linia działania przechodzi przez ten punkt A, oddalone od wybranego środka redukcji O na odległość
. Aby to zrobić, przekształcamy parę za pomocą chwili
więc ta siła I
, tworzące tę parę, okazało się równe pod względem wielkości wektorowi głównemu R”. W tym przypadku konieczne jest wybranie ramienia pary tak, aby jej moment t
pozostała równa M 0. W tym celu dźwignia pary
trzeba oczywiście znaleźć z równości

. (1)

Korzystając z faktu, że parę zawsze można przesunąć w swojej płaszczyźnie działania według uznania, przesuńmy parę
aby jej siła
został przyczepiony do ośrodka przywodzenia O i przeciwnie do wektora głównego
(Rysunek 57, B).

Rozważany dowolny płaski układ sił jest zatem równoważny tej sile
i para
. Odrzucanie sił
I
jako zrównoważony, otrzymujemy, że cały rozważany układ sił zostaje zastąpiony jedną siłą
, co jest zatem wypadkową. W tym przypadku linia działania wynikowego przejdzie przez punkt A, którego położenie względem wybranego środka redukcji określa wzór (1).

Jeżeli w wyniku sprowadzenia dowolnego płaskiego układu sił okaże się, że
, A
, to w tym konkretnym przypadku ten układ sił zostaje natychmiast zastąpiony jedną siłą, czyli wypadkową
, którego linia działania przechodzi przez wybrany środek redukcji.

Problem 7. Do punktów W I Z do ciał przykładane są siły o jednakowej wielkości i wzajemnie prostopadłych I
, oddalony od punktu O ciała w równych odległościach
. Doprowadź ten układ sił do punktu O(Rysunek 58).

Rozwiązanie. Przenieśmy siły I do pewnego stopnia równoległe do nas samych O. W wyniku tego przeniesienia uzyskujemy (Rysunek 58) siły
I
, zastosowany w tym punkcie O i pary sąsiadujące
I
, leżąc w tej samej płaszczyźnie z momentami
I
(siły tworzące te pary oznaczono na rysunku 58 kreskami). Z geometrycznego sumowania sił I , zastosowany w tym punkcie O, otrzymujemy wektor główny tego układu sił

którego moduł jest oczywiście równy

Z dodania par połączonych otrzymujemy parę wynikową, której moment jest równy momentowi głównemu
danego układu sił względem punktu O:

Dlatego ten układ dwóch sił I ma wynik

,

zastosowany w danym punkcie A, który jest oddalony od punktu O na odległość

.

;
,

tj. formy wypadkowe przy obu danych siłach I równe kąty 45 0.

Zadanie 8. Na kratownicę mostu działają siły pionowe (Rysunek 59)
t i
t odpowiednio w odległości 10 M i 40 M od lewego końca kratownicy i siłę poziomą
t na poziomie górnego pasa kratownicy wysokość kratownicy wynosi 6 M. Podaj układ sił ,I najprostsza forma.

Rozwiązanie. Rysujemy osie współrzędnych, jak pokazano na rysunku 59, przyjmując początek współrzędnych w punkcie A. Znajdźmy rzuty wektora głównego danego układu sił na oś wybranego układu współrzędnych:

gdzie znajdujemy moduł wektora głównego
:

T
.

Znajdźmy teraz moment główny danego układu sił względem początku współrzędnych A:

t m
.

W konsekwencji ten układ sił ma wypadkową
, którego moduł
T.

Znajdźmy teraz linię działania wynikowego. Wynikowy moment względem pochodzenia A zostanie określona przez formułę

,

Gdzie X I y - współrzędne punktu leżącego na linii działania wypadkowej. Ponieważ
t i
więc

.

Z z kolei z twierdzenia Varignona o momencie wypadkowej (5, § 11) mamy

Stąd,

.

Jest to równanie linii działania wypadkowej.

Zakładając w tym równaniu
, stwierdzamy, że punkt przecięcia linii działania wynikowej z górnym pasem kratownicy umieszczonym w pewnej odległości
M z lewego końca farmy. Wierzyć
M, stwierdzamy, że punkt przecięcia linii działania wynikowej z dolnym pasem kratownicy znajduje się w pewnej odległości
M z lewego końca farmy. Tak zdefiniowane połączenia są punktami przecięcia linii działania wypadkowej z górnym i dolnym pasem kratownicy w linii prostej, znajdujemy linię działania wypadkowej .

Zastąpimy płaski układ sił przyłożonych w punktach A, B, C, D:

1) siły F 1 ”, F 2 ”, F 3 ”, F 4 ”, przyłożone w punkcie O;

2) w parach sił:

fa 1 fa 1 ': M 1 = M o (F 1) = fa 1 za 1

fa 2 fa 2 ': M 2 = M o (F 2) = fa 2 za 2

F 3 F 3 ': M 3 ​​​​= M o (F 3) = F 3 za 3

fa 4 fa 4 ': M 4 = M o (F 4) = fa 4 za 4

Siły F 1 ’, F 2 ’, F 3 ’, F 4 ’ zbiegające się w punkcie O można zastąpić jedną siłą (wypadkową) F ch:

F gl = fa 1 ' + fa 2 ' + fa 3 ' + fa 4 ' = fa 1 + fa 2 + fa 3 + fa 4

F rozdz– wektor główny układu sił.

Powstałe pary sił można zastąpić powstałą parą, której moment M ch:

M gl = M 1 + M 2 + M 3 + M 4 = Σ M ja = Σ M o (F ja)

M gl - główny punkt dotyczący punktu odniesienia.

Płaski układ sił w danym punkcie O zostaje zastąpiony równoważnym układem składającym się z jednej siły (wektor główny) i jednej pary (moment główny).

Twierdzenie o momencie wypadkowej (twierdzenie Varignona)

Moment wypadkowego płaskiego układu sił względem dowolnego punktu jest równy sumie algebraicznej momentów sił składowych względem tego samego punktu.

M o (F Σ)= Σ M o (F i)

Równania równowagi dla płaskiego układu sił

FGL = 0;

M gl = ΣM o (F i) = 0.

Moduł wektora głównego można wyznaczyć poprzez rzuty na osie współrzędnych wszystkich sił układu.

F GL = (ΣF іх) 2 + (ΣF іу) 2 =0 z tego wynikają równania równowagi:

Σ F іх =0

Σ F іу =0

Σ M o (F i)=0

Inne formy równań równowagi:

Σ M A (F i) = 0

Σ М В (F і)=0 (ABC nie leżą na tym samym

Σ M do (F i) = 0 bezpośredni)

Σ M A (F i)=0 (oś x nie jest prostopadła

Σ M B (F і) = 0 bezpośrednio AB)

Σ F іх =0

Dla układu sił równoległych, wybierając jedną z osi rzutu równoległą do tych sił (oś y), a drugą prostopadłą do nich (oś x), otrzymujemy dwa równania równowagi:

Σ F іу =0

Σ M o (F i)=0

Σ M A (F i) = 0

Σ M V (F i) = 0

Algorytm rozwiązywania problemów

1. Wybierz obiekt równowagi (ciało lub punkt): rozważymy równowagę względem...

Na rysunku pokazujemy wszystkie działające siły, łącznie z reakcjami połączeń.

3. Wybierz układ współrzędnych - wskazane jest skierowanie osi współrzędnych równolegle lub prostopadle do wymaganych sił.

Układamy równania równowagi dla przedmiotu badań.

Σ F іх =0

Σ F іу =0

Σ M o (F i)=0

Z otrzymanych równań wyznaczamy nieznane wielkości (wyznaczamy reakcje).

Sprawdzamy poprawność rozwiązania równań.

Σ M p (F i) = 0

Σ M e (F i) = 0

5. Urządzenia wsporcze systemów belek

Przegubowe wsparcie

Forma zawiasowo-stała i sztywne uszczelnienie (szczypiący)

Temat:

"Środek ciężkości.

Charakterystyki geometryczne przekrojów płaskich”

Plan

1. Środek sił równoległych i jego współrzędne.
2. Środek ciężkości obszarów. Momenty statystyczne obszarów.
3. Rozwiązywanie zadań wyznaczania współrzędnych środka ciężkości płaskiej figury złożonej.
4. Biegunowe i osiowe momenty bezwładności.
5. Osiowe momenty bezwładności względem osi równoległych.
6. Wyznaczanie momentów bezwładności przekrojów zespolonych z wykorzystaniem tablic asortymentu normalnego.

1. Środek sił równoległych i jego współrzędne

Niech będzie dany układ sił równoległych F 1, F 2, F 3, ..., Fn; znane są współrzędne punktów C 1, C2, C3, ..., Cn przyłożenia tych sił (ryc. 42, b). Oznaczmy punkt przyłożenia wynikową literą C, a jego współrzędne oznaczymy xc, yc.
FΣ = F 1 + F 2 + F 3+…. + Fn = ΣF ja . (1)

FΣ xс = fa 1 x 1 + fa 2 x 2 + fa 3 x 3 +… + Fnxn = Σ fa ja x ja ,

x do = F 1 x 1 + F 2 x 2 + F 3 x 3 +… + Fnxn / FΣ = Σ F ja x i / FΣ

FΣ = F 1+ F 2+ F 3+…+ Fn= Σ F іх c =
= F 1 x 1 + F 2 x 2 + F 3 x 3 +… + Fnxn / F 1+ F 2+ F 3+…+ Fn= Σ fa ja x ja / fa ja (2)

Opisany sposób doprowadzenia jednej siły do ​​danego punktu można zastosować do dowolnej liczby sił. Załóżmy, że w punktach ciała ABC I D(Rys. 19) przyłożone siły 1 , 2 , 3 I 4 . Konieczne jest doprowadzenie tych sił do punktu O samolot. Najpierw podajmy siłę 1 , zastosowany w danym punkcie A. Zastosujmy się do tego punktu O dwie siły ’ 1 I ’’ 1 , każdy równy modułowi danej siły 1 , równolegle do niego i skierowane w przeciwne strony. W wyniku doprowadzenia siły 1 zdobędziemy władzę ’ 1 , zastosowany w tym punkcie O i kilka sił 1 ’’ 1 (siły tworzące parę zaznaczono kreskami) z ramieniem 1. Robiąc to samo z siłą 2 , zastosowany w tym punkcie W, nabieramy sił 2 , zastosowany w tym punkcie O i kilka sił 2 ’’ 2 z ramieniem 2 itp.

Płaski układ sił przyłożonych w punktach A, W, Z I D, zastąpiliśmy siłami zbiegającymi się ’ 1 , ’ 2 , ’ 3 I ’ 4 , zastosowany w tym punkcie O, oraz pary sił o momentach równych momentom danych sił względem punktu O:

M 1 = P 1 za 1 = M o ( 1); M 2 = P 2 za 2 = M o (2);

M 3 = – P 3 za 3 = M o ( 3); M 4 = – P 4 za 4 = M o (4).

Siły zbiegające się w jednym punkcie można zastąpić pojedynczą siłą " , równa sumie geometrycznej składników,

" = " 1 + " 2 + " 3 + " 4 = 1 + 2 + 3 + 4 = ja .(16)

Siła ta, równa sumie geometrycznej danych sił, nazywa się główny wektor układu sił.

W oparciu o zasadę dodawania par sił, z można zastąpić powstałą parą, której moment jest równy sumie algebraicznej momentów danych sił względem punktu O:

M o = M 1 + M 2 + M 3 + M 4 = ja = o (i).(17)

Analogicznie do wektora głównego, chwili M 0 pary równe algebraicznej sumie momentów wszystkich sił względem środka redukcji O, zwany moment główny układu względem danego środka redukcji O. Stąd, w ogólnym przypadku płaski układ sił w wyniku redukcji do danego punktu O zostaje zastąpiony układem równoważnym składającym się z jednej siły – wektora głównego – i jednej pary, której moment nazywany jest momentem głównym układu dany układ sił względem środka redukcji.

Trzeba zrozumieć, że główny wektor ’ nie jest wypadkową danego układu sił, gdyż układ ten nie jest równoważny jednej sile ’. Dopiero w szczególnym przypadku, kiedy zaniknie moment główny, wektor główny będzie wypadkową danego układu sił. Ponieważ wektor główny jest równy sumie geometrycznej sił danego układu, ani jego wielkość, ani kierunek nie zależą od wyboru środka redukcji. Wielkość i znak momentu głównego M 0 zależą od położenia środka redukcji, ponieważ ramiona par składowych zależą od względnego położenia sił i punktu (środka), względem którego brane są momenty.

Mogą wystąpić następujące przypadki wprowadzenia układu sił:

1. " ≠ 0; M o ≠ 0 - przypadek ogólny; układ zostaje zredukowany do wektora głównego i momentu głównego.

2. " ≠ 0; M o = 0; układ zostaje zredukowany do jednego wypadkowego równego głównemu wektorowi układu.

3. " = 0; M o ≠ 0; układ sprowadza się do pary sił, których moment jest równy momentowi głównemu.

4. " = 0; M o = 0; system jest w równowadze.

Można udowodnić, że w ogólnym przypadku, kiedy " ≠ 0 i M o ≠ 0, Zawsze istnieje punkt, względem którego główny moment układu sił jest równy zeru.

Rozważmy płaski układ sił zredukowany do punktu O, tj. zastąpiony wektorem głównym " ≠ 0 , zastosowany w tym punkcie O i główny punkt M o ≠ 0(ryc. 20).

Dla pewności zakładamy, że moment główny jest skierowany zgodnie z ruchem wskazówek zegara, tj. Mo< 0. Przedstawmy ten główny moment za pomocą pary sił "" , którego moduł jest równy modułowi wektora głównego " , tj. R =R '' = R '. Jedną z sił tworzących parę jest siła "" – złóż wniosek w ośrodku redukcyjnym O, inna siła – w pewnym momencie Z, którego położenie wyznacza się na podstawie warunku: M o = OS*R. Stąd,

system operacyjny =. (18)

Załóżmy kilka sił "" żeby siła "" skierowany był w kierunku przeciwnym do wektora głównego " . W punkcie O(Rys. 20) mamy dwie równe i wzajemnie przeciwne siły " I "" , skierowany wzdłuż jednej linii prostej; można je odrzucić (zgodnie z trzecim aksjomatem). Zatem w odniesieniu do punktu Z moment główny rozważanego układu sił jest równy zeru, a układ sprowadza się do wypadkowej .

§ 18. Twierdzenie o momencie wypadkowej (twierdzenie Varignona)

W ogólnym przypadku (patrz § 17) dowolny płaski układ sił jest redukowany do wektora głównego " i główny punkt M 0 względem wybranego środka redukcji, a moment główny jest równy sumie algebraicznej momentów danych sił względem punktu O

M o = o (i).(A)

Pokazano, że istnieje możliwość wyboru środka redukcji (na rys. 20 punkt Z), względem którego główny moment układu będzie równy zeru, a układ sił zostanie zredukowany do jednej wypadkowej równej wielkości wektorowi głównemu ( R = R'). Wyznaczmy moment wypadkowej względem punktu O. Biorąc pod uwagę, że ramię system operacyjny siły równe , otrzymujemy

M o () = R*OC = R = M o.(B)

Dwie wielkości, oddzielnie równe trzeciej, są sobie równe, dlatego z równań (a) i (b) znajdujemy

M o () = o ( ja).(19)

Otrzymane równanie wyraża twierdzenie Varignona: moment wypadkowego płaskiego układu sił względem dowolnego punktu jest równy sumie algebraicznej momentów sił składowych względem tego samego punktu.

Z twierdzenia Varignona wynika, że ​​moment główny płaskiego układu sił względem dowolnego punktu leżącego na linii działania jego wypadkowej jest równy zero.