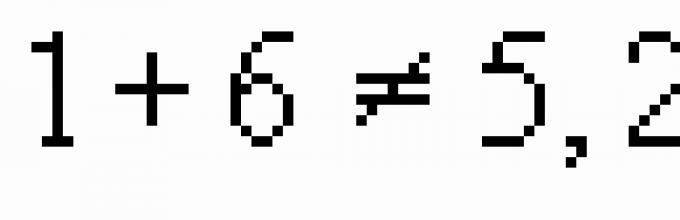Ustne rozwiązanie równań kwadratowych i twierdzenia Viety. Jak rozwiązywać równania za pomocą twierdzenia Viety w matematyce Wzór twierdzenia Viety dla przykładów równań kwadratowych

W ósmej klasie uczniowie zapoznają się z równaniami kwadratowymi i sposobami ich rozwiązywania. Jednocześnie, jak pokazuje doświadczenie, większość uczniów przy rozwiązywaniu pełnych równań kwadratowych stosuje tylko jedną metodę - wzór na pierwiastek równanie kwadratowe. Dla uczniów, którzy mają dobre umiejętności arytmetyki mentalnej, metoda ta jest wyraźnie irracjonalna. Uczniowie często muszą rozwiązywać równania kwadratowe nawet w szkole średniej, a tam po prostu szkoda tracić czas na obliczanie dyskryminatora. Moim zdaniem podczas studiowania równań kwadratowych więcej czasu i uwagi należy poświęcić zastosowaniu twierdzenia Viety (zgodnie z programem A.G. Mordkovich Algebra-8 na studiowanie tematu „Twierdzenie Viety. Rozkład kwadratu” zaplanowano tylko dwie godziny trójmian na czynniki liniowe”).

W większości podręczników do algebry twierdzenie to jest formułowane dla zredukowanego równania kwadratowego i stwierdza to jeśli równanie ma pierwiastki i , to równości , są dla nich spełnione. Następnie formułuje się stwierdzenie odwrotne do twierdzenia Viety i podaje szereg przykładów ćwiczących ten temat.

Weźmy konkretne przykłady i prześledźmy logikę rozwiązania za pomocą twierdzenia Viety.

Przykład 1. Rozwiąż równanie.

Powiedzmy, że to równanie ma pierwiastki, a mianowicie i . Wtedy, zgodnie z twierdzeniem Viety, równości muszą jednocześnie zachodzić:

Należy pamiętać, że iloczyn pierwiastków jest liczbą dodatnią. Oznacza to, że pierwiastki równania mają ten sam znak. A ponieważ suma pierwiastków jest również liczbą dodatnią, dochodzimy do wniosku, że oba pierwiastki równania są dodatnie. Wróćmy jeszcze raz do iloczynu korzeni. Załóżmy, że pierwiastki równania są dodatnimi liczbami całkowitymi. Wtedy poprawną pierwszą równość można uzyskać tylko na dwa sposoby (w zależności od kolejności czynników): lub . Sprawdźmy dla proponowanych par liczb wykonalność drugiego stwierdzenia twierdzenia Viety: . Zatem liczby 2 i 3 spełniają obie równości, a zatem są pierwiastkami danego równania.

Odpowiedź: 2; 3.

Podkreślmy główne etapy rozumowania przy rozwiązywaniu powyższego równania kwadratowego za pomocą twierdzenia Viety:

zapisz treść twierdzenia Viety

(*)

• określić znaki pierwiastków równania (Jeśli iloczyn i suma pierwiastków są dodatnie, to oba pierwiastki są liczbami dodatnimi. Jeśli iloczyn pierwiastków jest liczbą dodatnią, a suma pierwiastków jest ujemna, to oba pierwiastki są liczbami ujemnymi. Jeśli iloczyn pierwiastków jest liczbą ujemną, to pierwiastki mają różne znaki. Ponadto, jeśli suma pierwiastków jest dodatnia, to większy pierwiastek z modułu jest liczbą dodatnią, a jeśli suma pierwiastków jest mniejsza od zera, wówczas większy pierwiastek z modułu jest liczbą ujemną);
• wybierz pary liczb całkowitych, których iloczyn daje poprawną pierwszą równość w zapisie (*);
• spośród znalezionych par liczb wybierz parę, która po podstawieniu do drugiej równości w zapisie (*) da poprawną równość;
• wskaż w swojej odpowiedzi znalezione pierwiastki równania.

Podajmy więcej przykładów.

Przykład 2: Rozwiąż równanie .

Rozwiązanie.

Niech i będą pierwiastkami danego równania. Następnie, zgodnie z twierdzeniem Viety, zauważamy, że iloczyn jest dodatni, a suma jest liczbą ujemną. Oznacza to, że oba pierwiastki są liczbami ujemnymi. Wybieramy pary czynników, które dają iloczyn 10 (-1 i -10; -2 i -5). Druga para liczb sumuje się do -7. Oznacza to, że liczby -2 i -5 są pierwiastkami tego równania.

Odpowiedź: -2; -5.

Przykład 3: Rozwiąż równanie .

Rozwiązanie.

Niech i będą pierwiastkami danego równania. Następnie, zgodnie z twierdzeniem Viety, zauważamy, że iloczyn jest ujemny. Oznacza to, że korzenie mają różne znaki. Suma pierwiastków jest również liczbą ujemną. Oznacza to, że pierwiastek o największym module jest ujemny. Wybieramy pary czynników, które dają iloczyn -10 (1 i -10; 2 i -5). Druga para liczb sumuje się do -3. Oznacza to, że liczby 2 i -5 są pierwiastkami tego równania.

Odpowiedź: 2; -5.

Należy zauważyć, że twierdzenie Viety można w zasadzie sformułować dla pełnego równania kwadratowego: jeśli równanie kwadratowe ma pierwiastki i , to równości , są dla nich spełnione. Jednak zastosowanie tego twierdzenia jest dość problematyczne, ponieważ w pełnym równaniu kwadratowym przynajmniej jeden z pierwiastków (oczywiście jeśli w ogóle) jest liczba ułamkowa. A praca z wybieraniem ułamków jest długa i trudna. Ale nadal istnieje wyjście.

Rozważ pełne równanie kwadratowe . Pomnóż obie strony równania przez pierwszy współczynnik A i zapisz równanie w formie . Wprowadźmy nową zmienną i otrzymajmy zredukowane równanie kwadratowe, którego pierwiastki i (jeśli są dostępne) można znaleźć korzystając z twierdzenia Viety. Wtedy pierwiastki pierwotnego równania będą wynosić . Należy pamiętać, że utworzenie pomocniczego równania zredukowanego jest bardzo proste: drugi współczynnik zostaje zachowany, a trzeci współczynnik jest równy iloczynowi AC. Przy pewnej umiejętności uczniowie natychmiast tworzą równanie pomocnicze, znajdują jego pierwiastki korzystając z twierdzenia Viety i wskazują pierwiastki danego pełnego równania. Podajmy przykłady.

Przykład 4: Rozwiąż równanie .

Utwórzmy równanie pomocnicze i korzystając z twierdzenia Viety znajdziemy jego pierwiastki. Oznacza to, że pierwiastki pierwotnego równania .

Odpowiedź: .

Przykład 5: Rozwiąż równanie .

Równanie pomocnicze ma postać . Zgodnie z twierdzeniem Viety jego pierwiastki to . Znalezienie pierwiastków pierwotnego równania .

Odpowiedź: .

I jeszcze jeden przypadek, gdy zastosowanie twierdzenia Viety pozwala werbalnie znaleźć pierwiastki pełnego równania kwadratowego. Nie jest trudno to udowodnić liczba 1 jest pierwiastkiem równania , wtedy i tylko wtedy gdy. Drugi pierwiastek równania znajduje się na podstawie twierdzenia Viety i jest równy . Jeszcze jedno stwierdzenie: tak aby liczba –1 była pierwiastkiem równania konieczne i wystarczające. Wtedy drugi pierwiastek równania zgodnie z twierdzeniem Viety jest równy . Podobne stwierdzenia można sformułować dla zredukowanego równania kwadratowego.

Przykład 6: Rozwiąż równanie.

Należy pamiętać, że suma współczynników równania wynosi zero. Zatem pierwiastki równania .

Odpowiedź: .

Przykład 7. Rozwiąż równanie.

Współczynniki tego równania spełniają tę właściwość (w rzeczywistości 1-(-999)+(-1000)=0). Zatem pierwiastki równania .

Odpowiedź: ..

Przykłady zastosowania twierdzenia Viety

Zadanie 1. Rozwiąż podane równanie kwadratowe korzystając z twierdzenia Viety.

1.	6.	11.	16.
2.	7.	12.	17.
3.	8.	13.	18.
4.	9.	14.	19.
5.	10.	15.	20.

Zadanie 2. Rozwiąż pełne równanie kwadratowe, przechodząc do pomocniczego zredukowanego równania kwadratowego.

1.	6.	11.	16.
2.	7.	12.	17.
3.	8.	13.	18.
4.	9.	14.	19.
5.	10.	15.	20.

Zadanie 3. Rozwiąż równanie kwadratowe korzystając z własności.

Prawie każde równanie kwadratowe \można przekształcić do postaci \ Jest to jednak możliwe, jeśli początkowo podzielisz każdy wyraz przez współczynnik \przed \ Ponadto możesz wprowadzić nowy zapis:

\[(\frac (b)(a))= p\] i \[(\frac (c)(a)) = q\]

Dzięki temu będziemy mieli równanie \ zwane w matematyce zredukowanym równaniem kwadratowym. Pierwiastki tego równania i współczynniki są ze sobą powiązane, co potwierdza twierdzenie Viety.

Twierdzenie Viety: Suma pierwiastków zredukowanego równania kwadratowego \ jest równa drugiemu współczynnikowi \ wziętemu z przeciwnym znakiem, a iloczyn pierwiastków jest wyrazem wolnym \

Dla jasności rozwiążmy następujące równanie:

Rozwiążmy to równanie kwadratowe, korzystając z zapisanych zasad. Po analizie danych wyjściowych możemy stwierdzić, że równanie będzie miało dwa różne pierwiastki, gdyż:

Teraz ze wszystkich czynników liczby 15 (1 i 15, 3 i 5) wybieramy te, których różnica jest równa 2. Liczby 3 i 5 spełniają ten warunek. Przed mniejszym stawiamy znak minus numer. W ten sposób otrzymujemy pierwiastki równania \

Odpowiedź: \[ x_1= -3 i x_2 = 5\]

Gdzie mogę rozwiązać równanie za pomocą twierdzenia Viety online?

Równanie możesz rozwiązać na naszej stronie internetowej https://site. Bezpłatny solwer online pozwoli Ci rozwiązać równania online o dowolnej złożoności w ciągu kilku sekund. Wystarczy, że wprowadzisz swoje dane do solwera. Możesz także obejrzeć instrukcje wideo i dowiedzieć się, jak rozwiązać równanie na naszej stronie internetowej. A jeśli nadal masz pytania, możesz je zadać w naszej grupie VKontakte http://vk.com/pocketteacher. Dołącz do naszej grupy, zawsze chętnie Ci pomożemy.

Pomiędzy pierwiastkami i współczynnikami równania kwadratowego, oprócz wzorów pierwiastkowych, podano inne przydatne zależności Twierdzenie Viety. W tym artykule podamy sformułowanie i dowód twierdzenia Viety dla równania kwadratowego. Następnie rozważymy twierdzenie odwrotne do twierdzenia Viety. Następnie przeanalizujemy rozwiązania na najbardziej typowych przykładach. Na koniec zapisujemy wzory Vieta, które definiują relację pomiędzy pierwiastkami rzeczywistymi równanie algebraiczne stopień n i jego współczynniki.

Nawigacja strony.

Twierdzenie Viety, sformułowanie, dowód

Ze wzorów na pierwiastki równania kwadratowego a·x 2 +b·x+c=0 postaci, gdzie D=b 2 −4·a·c wynikają zależności: x 1 +x 2 =− b/a, x 1 ·x 2 = c/a . Wyniki te zostały potwierdzone Twierdzenie Viety:

Twierdzenie.

Jeśli x 1 i x 2 są pierwiastkami równania kwadratowego a x 2 +b x+c=0, wówczas suma pierwiastków jest równa stosunkowi współczynników b i a, wziętych z przeciwnym znakiem, i iloczynu pierwiastki są równe stosunkowi współczynników c i a, to znaczy .

Dowód.

Dowód twierdzenia Viety przeprowadzimy według następującego schematu: sumę i iloczyn pierwiastków równania kwadratowego układamy ze znanych wzorów na pierwiastki, następnie przekształcamy powstałe wyrażenia i upewniamy się, że są równe −b/ odpowiednio a i c/a.

Zacznijmy od sumy pierwiastków i uzupełnijmy ją. Teraz sprowadzamy ułamki do wspólnego mianownika, mamy . W liczniku powstałego ułamka, po czym:. Wreszcie po 2 otrzymujemy . Dowodzi to pierwszej zależności twierdzenia Viety dla sumy pierwiastków równania kwadratowego. Przejdźmy do drugiego.

Tworzymy iloczyn pierwiastków równania kwadratowego: . Zgodnie z zasadą mnożenia ułamków zwykłych, ostatni kawałek można zapisać jako . Teraz mnożymy nawias przez nawias w liczniku, ale szybciej jest zwinąć ten iloczyn wzór na różnicę kwadratową, Więc . Następnie pamiętając wykonujemy kolejne przejście. A ponieważ dyskryminator równania kwadratowego odpowiada wzorowi D=b 2 −4·a·c, to zamiast D w ostatnim ułamku możemy podstawić b 2 −4·a·c i otrzymamy. Po otwarciu nawiasów i rzuceniu podobne terminy dochodzimy do ułamka i jego redukcja o 4·a daje . Dowodzi to drugiej zależności twierdzenia Viety dla iloczynu pierwiastków.

Jeśli pominiemy wyjaśnienia, dowód twierdzenia Viety przyjmie lakoniczną formę:
,
.

Pozostaje tylko zauważyć, że jeśli dyskryminator jest równy zeru, równanie kwadratowe ma jeden pierwiastek. Jeśli jednak założymy, że równanie w tym przypadku ma dwa identyczne pierwiastki, to równości z twierdzenia Viety również obowiązują. Rzeczywiście, gdy D=0 pierwiastek równania kwadratowego jest równy , to i , a ponieważ D=0, czyli b 2 −4·a·c=0, skąd b 2 =4·a·c, to .

W praktyce twierdzenie Viety jest najczęściej stosowane w odniesieniu do zredukowanego równania kwadratowego (ze współczynnikiem wiodącym równym 1) postaci x 2 +p·x+q=0. Czasami formułuje się go dla równań kwadratowych właśnie tego typu, co nie ogranicza ogólności, ponieważ każde równanie kwadratowe można zastąpić równaniem równoważnym, dzieląc obie strony przez niezerową liczbę a. Podajmy odpowiednie sformułowanie twierdzenia Viety:

Twierdzenie.

Suma pierwiastków zredukowanego równania kwadratowego x 2 +p x+q=0 jest równa współczynnikowi x wziętemu z przeciwnym znakiem, a iloczyn pierwiastków jest równy członowi swobodnemu, czyli x 1 +x 2 =−p, x 1 x 2 = q.

Twierdzenie odwrotne do twierdzenia Viety

Drugie sformułowanie twierdzenia Viety podane w poprzednim akapicie wskazuje, że jeśli x 1 i x 2 są pierwiastkami zredukowanego równania kwadratowego x 2 +p x+q=0, to zależności x 1 +x 2 =−p , x 1 x 2 =q. Natomiast z zapisanych zależności x 1 +x 2 =−p, x 1 x 2 =q wynika, że ​​x 1 i x 2 są pierwiastkami równania kwadratowego x 2 +p x+q=0. Innymi słowy, odwrotność twierdzenia Viety jest prawdziwa. Sformułujmy to w formie twierdzenia i udowodnijmy.

Twierdzenie.

Jeżeli liczby x 1 i x 2 są takie, że x 1 +x 2 =−p i x 1 · x 2 =q, to ​​x 1 i x 2 są pierwiastkami zredukowanego równania kwadratowego x 2 +p · x+q =0.

Dowód.

Po zastąpieniu współczynników p i q w równaniu x 2 +p x+q=0 ich wyrażeniami poprzez x 1 i x 2 , przekształca się je w równoważne równanie.

Podstawmy liczbę x 1 zamiast x do otrzymanego równania i otrzymamy równość x 1 2 −(x 1 + x 2) x 1 + x 1 x 2 =0, co dla dowolnego x 1 i x 2 reprezentuje poprawną równość liczbową 0 = 0, ponieważ x 1 2 −(x 1 + x 2) x 1 + x 1 x 2 = x 1 2 −x 1 2 −x 2 ·x 1 +x 1 ·x 2 =0. Dlatego x 1 jest pierwiastkiem równania x 2 −(x 1 +x 2) x+x 1 x 2 =0, co oznacza, że ​​x 1 jest pierwiastkiem równoważnego równania x 2 +p·x+q=0.

Jeśli w równaniu x 2 −(x 1 +x 2) x+x 1 x 2 =0 podstaw liczbę x 2 zamiast x, otrzymamy równość x 2 2 −(x 1 +x 2) x 2 +x 1 x 2 =0. Jest to prawdziwa równość, ponieważ x 2 2 −(x 1 +x 2) x 2 +x 1 x 2 = x 2 2 −x 1 ·x 2 −x 2 2 +x 1 ·x 2 =0. Dlatego x 2 jest również pierwiastkiem równania x 2 −(x 1 +x 2) x+x 1 x 2 =0, a zatem równania x 2 +p·x+q=0.

To kończy dowód twierdzenia, odwrotność twierdzenia Vieta.

Przykłady wykorzystania twierdzenia Viety

Czas porozmawiać o praktycznym zastosowaniu twierdzenia Viety i jego twierdzenia odwrotnego. W tej sekcji przeanalizujemy rozwiązania kilku najbardziej typowych przykładów.

Zacznijmy od zastosowania twierdzenia odwrotnego do twierdzenia Viety. Wygodnie jest sprawdzić, czy dane dwie liczby są pierwiastkami danego równania kwadratowego. W tym przypadku obliczana jest ich suma i różnica, po czym sprawdzana jest ważność relacji. Jeżeli obie te zależności są spełnione, to na mocy twierdzenia odwrotnego do twierdzenia Viety dochodzi do wniosku, że liczby te są pierwiastkami równania. Jeżeli choć jedna z zależności nie jest spełniona, to liczby te nie są pierwiastkami równania kwadratowego. Podejście to można zastosować przy rozwiązywaniu równań kwadratowych w celu sprawdzenia znalezionych pierwiastków.

Przykład.

Która z par liczb 1) x 1 =−5, x 2 =3 lub 2) lub 3) jest parą pierwiastków równania kwadratowego 4 x 2 −16 x+9=0?

Rozwiązanie.

Współczynniki danego równania kwadratowego 4 x 2 −16 x+9=0 wynoszą a=4, b=−16, c=9. Zgodnie z twierdzeniem Viety suma pierwiastków równania kwadratowego powinna być równa −b/a, czyli 16/4=4, a iloczyn pierwiastków powinien być równy c/a, czyli 9 /4.

Obliczmy teraz sumę i iloczyn liczb w każdej z trzech podanych par i porównajmy je z wartościami, które właśnie uzyskaliśmy.

W pierwszym przypadku mamy x 1 +x 2 =−5+3=−2. Otrzymana wartość jest różna od 4, więc nie można przeprowadzić dalszej weryfikacji, ale korzystając z twierdzenia odwrotnego do twierdzenia Viety, można od razu stwierdzić, że pierwsza para liczb nie jest parą pierwiastków danego równania kwadratowego.

Przejdźmy do drugiego przypadku. Czyli tutaj pierwszy warunek jest spełniony. Sprawdzamy drugi warunek: otrzymana wartość różni się od 9/4. W związku z tym druga para liczb nie jest parą pierwiastków równania kwadratowego.

Został jeszcze ostatni przypadek. Tutaj i . Obydwa warunki są spełnione, więc te liczby x 1 i x 2 są pierwiastkami danego równania kwadratowego.

Odpowiedź:

Odwrotność twierdzenia Viety można zastosować w praktyce do znalezienia pierwiastków równania kwadratowego. Zwykle wybiera się pierwiastki całkowite danych równań kwadratowych o współczynnikach całkowitych, ponieważ w innych przypadkach jest to dość trudne. W tym przypadku wykorzystują fakt, że jeśli suma dwóch liczb jest równa drugiemu współczynnikowi równania kwadratowego, wziętemu ze znakiem minus, a iloczyn tych liczb jest równy wyrazowi swobodnemu, to liczby te są pierwiastki tego równania kwadratowego. Rozumiemy to na przykładzie.

Weźmy równanie kwadratowe x 2 −5 x+6=0. Aby liczby x 1 i x 2 były pierwiastkami tego równania, muszą być spełnione dwie równości: x 1 + x 2 =5 i x 1 ·x 2 =6. Pozostaje tylko wybrać takie liczby. W tym przypadku jest to dość proste: takimi liczbami są 2 i 3, gdyż 2+3=5 i 2,3=6. Zatem 2 i 3 są pierwiastkami tego równania kwadratowego.

Twierdzenie odwrotne do twierdzenia Viety jest szczególnie wygodne w użyciu do znalezienia drugiego pierwiastka danego równania kwadratowego, gdy jeden z pierwiastków jest już znany lub oczywisty. W tym przypadku drugi pierwiastek można znaleźć z dowolnej relacji.

Weźmy na przykład równanie kwadratowe 512 x 2 −509 x −3=0. Tutaj łatwo zauważyć, że pierwiastkiem równania jest jedność, ponieważ suma współczynników tego równania kwadratowego jest równa zeru. Zatem x 1 = 1. Drugi pierwiastek x 2 można znaleźć np. z zależności x 1 ·x 2 =c/a. Mamy 1 x 2 =−3/512, z czego x 2 =−3/512. W ten sposób wyznaczyliśmy oba pierwiastki równania kwadratowego: 1 i −3/512.

Oczywiste jest, że wybór korzeni jest wskazany tylko w najprostszych przypadkach. W innych przypadkach, aby znaleźć pierwiastki, można użyć wzorów na pierwiastki równania kwadratowego poprzez dyskryminator.

Inny praktyczne użycie twierdzenie, odwrotne do twierdzenia Viety, polega na ułożeniu równań kwadratowych według dane korzenie x 1 i x 2 . Aby to zrobić, wystarczy obliczyć sumę pierwiastków, co daje współczynnik dla x z przeciwnym znakiem danego równania kwadratowego, oraz iloczyn pierwiastków, co daje Wolny Członek.

Przykład.

Napisz równanie kwadratowe, którego pierwiastki to −11 i 23.

Rozwiązanie.

Oznaczmy x 1 =−11 i x 2 =23. Obliczamy sumę i iloczyn tych liczb: x 1 +x 2 =12 i x 1 ·x 2 =−253. Dlatego wskazane liczby są pierwiastkami zredukowanego równania kwadratowego z drugim współczynnikiem -12 i wolnym wyrazem -253. Oznacza to, że x 2 −12·x−253=0 jest wymaganym równaniem.

Odpowiedź:

x 2 −12·x−253=0 .

Twierdzenie Viety jest bardzo często wykorzystywane przy rozwiązywaniu problemów związanych ze znakami pierwiastków równań kwadratowych. Jak twierdzenie Viety jest powiązane ze znakami pierwiastków zredukowanego równania kwadratowego x 2 +p·x+q=0? Oto dwa istotne stwierdzenia:

• Jeśli wyraz wolny q jest liczbą dodatnią i jeśli równanie kwadratowe ma rzeczywiste pierwiastki, to albo oba są dodatnie, albo oba ujemne.
• Jeżeli wyraz wolny q jest liczbą ujemną i równanie kwadratowe ma pierwiastki rzeczywiste, to ich znaki są różne, czyli jeden pierwiastek jest dodatni, a drugi ujemny.

Stwierdzenia te wynikają ze wzoru x 1 · x 2 =q oraz z zasad dodatniego mnożenia, liczby ujemne i liczby z różnymi znakami. Spójrzmy na przykłady ich zastosowania.

Przykład.

R. to jest pozytywne. Korzystając ze wzoru dyskryminacyjnego znajdujemy D=(r+2) 2 −4 1 (r−1)= r 2 +4 r+4−4 r+4=r 2 +8, wartość wyrażenia r 2 +8 jest dodatnia dla dowolnego rzeczywistego r, zatem D > 0 dla dowolnego rzeczywistego r. W związku z tym oryginalne równanie kwadratowe ma dwa pierwiastki dla dowolnych rzeczywistych wartości parametru r.

Teraz dowiedzmy się, kiedy korzenie mają różne znaki. Jeżeli znaki pierwiastków są różne, to ich iloczyn jest ujemny i zgodnie z twierdzeniem Viety iloczyn pierwiastków zredukowanego równania kwadratowego jest równy członowi swobodnemu. Dlatego interesują nas te wartości r, dla których wolny termin r−1 jest ujemny. Zatem, aby znaleźć interesujące nas wartości r, potrzebujemy decydować nierówność liniowa r-1<0 , откуда находим r<1 .

Odpowiedź:

o godz<1 .

Formuły Vieta

Powyżej rozmawialiśmy o twierdzeniu Viety dotyczącym równania kwadratowego i analizowaliśmy zależności, jakie ono potwierdza. Ale istnieją wzory, które łączą rzeczywiste pierwiastki i współczynniki nie tylko równań kwadratowych, ale także równań sześciennych, równań czwartego stopnia i ogólnie: równania algebraiczne stopień r. Nazywają się Wzory Viety.

Zapiszmy wzór Viety na równanie algebraiczne stopnia n postaci i załóżmy, że ma ono n pierwiastków rzeczywistych x 1, x 2, ..., x n (wśród nich mogą znajdować się zbieżne):

Można otrzymać wzory Viety twierdzenie o rozkładzie wielomianu na czynniki liniowe, a także definicja równych wielomianów poprzez równość wszystkich odpowiadających im współczynników. Zatem wielomian i jego rozwinięcie na czynniki liniowe postaci są równe. Otwierając nawiasy w ostatnim iloczynu i przyrównując odpowiednie współczynniki, otrzymujemy wzory Viety.

W szczególności dla n=2 mamy już znane wzory Vieta na równanie kwadratowe.

W przypadku równania sześciennego wzory Viety mają postać

Pozostaje tylko zauważyć, że po lewej stronie formuł Viety znajdują się tak zwane elementarne wielomiany symetryczne.

Bibliografia.

• Algebra: podręcznik dla 8 klasy. ogólne wykształcenie instytucje / [Yu. N. Makaryczew, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edytowany przez SA Telyakovsky. - wyd. 16. - M.: Edukacja, 2008. - 271 s. : chory. - ISBN 978-5-09-019243-9.
• Mordkovich A. G. Algebra. 8 klasa. Za 2 godziny Część 1. Podręcznik dla uczniów szkół ogólnokształcących / A. G. Mordkovich. - wyd. 11, usunięte. - M.: Mnemosyne, 2009. - 215 s.: il. ISBN 978-5-346-01155-2.
• Algebra i początek analizy matematycznej. Klasa 10: podręcznik. dla edukacji ogólnej instytucje: podstawowe i profilowe. poziomy / [Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; edytowany przez A. B. Żyżczenko. - wyd. 3. - M.: Edukacja, 2010. - 368 s. : chory. - ISBN 978-5-09-022771-1.

W matematyce istnieją specjalne techniki, dzięki którym wiele równań kwadratowych można rozwiązać bardzo szybko i bez żadnych wyróżników. Co więcej, po odpowiednim przeszkoleniu wielu zaczyna rozwiązywać równania kwadratowe ustnie, dosłownie „od pierwszego wejrzenia”.

Niestety we współczesnym toku matematyki szkolnej takie technologie prawie się nie badają. Ale musisz wiedzieć! A dzisiaj przyjrzymy się jednej z tych technik - twierdzeniu Viety. Najpierw wprowadźmy nową definicję.

Równanie kwadratowe w postaci x 2 + bx + c = 0 nazywa się zredukowanym. Należy pamiętać, że współczynnik dla x 2 wynosi 1. Nie ma innych ograniczeń dotyczących współczynników.

1. x 2 + 7x + 12 = 0 jest zredukowanym równaniem kwadratowym;
2. x 2 − 5x + 6 = 0 - również zmniejszone;
3. 2x 2 - 6x + 8 = 0 - ale to w ogóle nie jest podane, ponieważ współczynnik x 2 jest równy 2.

Oczywiście dowolne równanie kwadratowe postaci ax 2 + bx + c = 0 można zredukować - wystarczy podzielić wszystkie współczynniki przez liczbę a. Zawsze możemy to zrobić, ponieważ z definicji równania kwadratowego wynika, że ​​a ≠ 0.

To prawda, że ​​​​te transformacje nie zawsze będą przydatne do znalezienia korzeni. Poniżej upewnimy się, że należy to zrobić tylko wtedy, gdy w równaniu końcowym danym przez kwadrat wszystkie współczynniki są liczbami całkowitymi. Na razie spójrzmy na najprostsze przykłady:

Zadanie. Przekształć równanie kwadratowe na równanie zredukowane:

1. 3x 2 - 12x + 18 = 0;
2. −4x 2 + 32x + 16 = 0;
3. 1,5x2 + 7,5x +3 = 0;
4. 2x 2 + 7x - 11 = 0.

Podzielmy każde równanie przez współczynnik zmiennej x 2. Otrzymujemy:

1. 3x 2 − 12x + 18 = 0 ⇒ x 2 − 4x + 6 = 0 - podziel wszystko przez 3;
2. −4x 2 + 32x + 16 = 0 ⇒ x 2 − 8x − 4 = 0 - podzielone przez -4;
3. 1,5x 2 + 7,5x + 3 = 0 ⇒ x 2 + 5x + 2 = 0 - podzielone przez 1,5 wszystkie współczynniki stały się liczbami całkowitymi;
4. 2x 2 + 7x - 11 = 0 ⇒ x 2 + 3,5x - 5,5 = 0 - podzielone przez 2. W tym przypadku pojawiły się współczynniki ułamkowe.

Jak widać, powyższe równania kwadratowe mogą mieć współczynniki całkowite, nawet jeśli pierwotne równanie zawierało ułamki.

Sformułujmy teraz główne twierdzenie, dla którego w rzeczywistości wprowadzono koncepcję zredukowanego równania kwadratowego:

Twierdzenie Viety. Rozważmy zredukowane równanie kwadratowe postaci x 2 + bx + c = 0. Załóżmy, że to równanie ma rzeczywiste pierwiastki x 1 i x 2. W tym przypadku prawdziwe są następujące stwierdzenia:

1. x 1 + x 2 = −b. Innymi słowy, suma pierwiastków danego równania kwadratowego jest równa współczynnikowi zmiennej x, przyjętej ze znakiem przeciwnym;
2. x 1 x 2 = do . Iloczyn pierwiastków równania kwadratowego jest równy swobodnemu współczynnikowi.

Przykłady. Dla uproszczenia rozważymy tylko powyższe równania kwadratowe, które nie wymagają dodatkowych przekształceń:

1. x 2 − 9x + 20 = 0 ⇒ x 1 + x 2 = − (−9) = 9; x 1 x 2 = 20; pierwiastki: x 1 = 4; x 2 = 5;
2. x 2 + 2x - 15 = 0 ⇒ x 1 + x 2 = -2; x 1 x 2 = −15; pierwiastki: x 1 = 3; x 2 = −5;
3. x 2 + 5x + 4 = 0 ⇒ x 1 + x 2 = −5; x 1 x 2 = 4; pierwiastki: x 1 = −1; x 2 = −4.

Twierdzenie Viety dostarcza nam dodatkowych informacji o pierwiastkach równania kwadratowego. Na pierwszy rzut oka może się to wydawać trudne, ale nawet przy minimalnym przeszkoleniu nauczysz się „widzieć” korzenie i dosłownie je odgadywać w ciągu kilku sekund.

Zadanie. Rozwiąż równanie kwadratowe:

1. x 2 - 9x + 14 = 0;
2. x 2 - 12x + 27 = 0;
3. 3x 2 + 33x + 30 = 0;
4. −7x 2 + 77x − 210 = 0.

Spróbujmy wypisać współczynniki korzystając z twierdzenia Viety i „odgadnąć” pierwiastki:

1. x 2 − 9x + 14 = 0 jest zredukowanym równaniem kwadratowym.
   Z twierdzenia Viety mamy: x 1 + x 2 = −(−9) = 9; x 1 · x 2 = 14. Łatwo zauważyć, że pierwiastkami są liczby 2 i 7;
2. x 2 − 12x + 27 = 0 - również zmniejszone.
   Według twierdzenia Viety: x 1 + x 2 = −(−12) = 12; x 1 x 2 = 27. Stąd pierwiastki: 3 i 9;
3. 3x 2 + 33x + 30 = 0 - to równanie nie jest redukowane. Ale poprawimy to teraz, dzieląc obie strony równania przez współczynnik a = 3. Otrzymujemy: x 2 + 11x + 10 = 0.
   Rozwiązujemy korzystając z twierdzenia Viety: x 1 + x 2 = −11; x 1 x 2 = 10 ⇒ pierwiastki: –10 i –1;
4. −7x 2 + 77x − 210 = 0 - znowu współczynnik dla x 2 nie jest równy 1, tj. nie podano równania. Wszystko dzielimy przez liczbę a = −7. Otrzymujemy: x 2 − 11x + 30 = 0.
   Według twierdzenia Viety: x 1 + x 2 = −(−11) = 11; x 1 x 2 = 30; Z tych równań łatwo odgadnąć pierwiastki: 5 i 6.

Z powyższego rozumowania jasno wynika, jak twierdzenie Viety upraszcza rozwiązywanie równań kwadratowych. Żadnych skomplikowanych obliczeń, żadnych pierwiastków arytmetycznych i ułamków. I nawet nie potrzebowaliśmy dyskryminatora (patrz lekcja „Rozwiązywanie równań kwadratowych”).

Oczywiście we wszystkich naszych rozważaniach wychodziliśmy z dwóch ważnych założeń, które na ogół nie zawsze spotykają się w realnych problemach:

1. Równanie kwadratowe jest zredukowane, tj. współczynnik dla x 2 wynosi 1;
2. Równanie ma dwa różne pierwiastki. Z algebraicznego punktu widzenia w tym przypadku wyróżnikiem jest D > 0 - w zasadzie początkowo zakładamy, że ta nierówność jest prawdziwa.

Jednak w typowych problemach matematycznych warunki te są spełnione. Jeśli w wyniku obliczeń wyjdzie „złe” równanie kwadratowe (współczynnik x 2 jest różny od 1), można to łatwo poprawić - spójrz na przykłady na samym początku lekcji. Generalnie milczę na temat korzeni: co to za problem, na który nie ma odpowiedzi? Oczywiście, że będą korzenie.

Zatem ogólny schemat rozwiązywania równań kwadratowych za pomocą twierdzenia Viety jest następujący:

1. Sprowadź równanie kwadratowe do podanego, jeśli nie zostało to już zrobione w opisie problemu;
2. Jeśli współczynniki w powyższym równaniu kwadratowym są ułamkowe, rozwiązujemy je za pomocą dyskryminatora. Możesz nawet wrócić do pierwotnego równania, aby pracować z bardziej „przydatnymi” liczbami;
3. W przypadku współczynników całkowitych równanie rozwiązujemy korzystając z twierdzenia Viety;
4. Jeśli nie możesz odgadnąć pierwiastków w ciągu kilku sekund, zapomnij o twierdzeniu Viety i rozwiąż za pomocą dyskryminatora.

Zadanie. Rozwiąż równanie: 5x 2 − 35x + 50 = 0.

Mamy więc przed sobą równanie, które nie jest zredukowane, ponieważ współczynnik a = 5. Podziel wszystko przez 5, otrzymamy: x 2 − 7x + 10 = 0.

Wszystkie współczynniki równania kwadratowego są liczbami całkowitymi - spróbujmy je rozwiązać korzystając z twierdzenia Viety. Mamy: x 1 + x 2 = −(−7) = 7; x 1 · x 2 = 10. W tym przypadku pierwiastki są łatwe do odgadnięcia - są to 2 i 5. Nie ma potrzeby liczenia za pomocą dyskryminatora.

Zadanie. Rozwiąż równanie: −5x 2 + 8x − 2,4 = 0.

Spójrzmy: −5x 2 + 8x − 2,4 = 0 – to równanie nie jest zredukowane, podzielmy obie strony przez współczynnik a = −5. Otrzymujemy: x 2 − 1,6x + 0,48 = 0 - równanie ze współczynnikami ułamkowymi.

Lepiej wrócić do pierwotnego równania i policzyć przez dyskryminator: −5x 2 + 8x − 2,4 = 0 ⇒ D = 8 2 − 4 · (−5) · (−2,4) = 16 ⇒ ... ⇒ x 1 = 1,2; x2 = 0,4.

Zadanie. Rozwiąż równanie: 2x 2 + 10x - 600 = 0.

Najpierw podzielmy wszystko przez współczynnik a = 2. Otrzymujemy równanie x 2 + 5x - 300 = 0.

Jest to równanie zredukowane, zgodnie z twierdzeniem Viety mamy: x 1 + x 2 = −5; x 1 x 2 = −300. Trudno w tym przypadku zgadnąć pierwiastki równania kwadratowego - osobiście poważnie utknąłem przy rozwiązywaniu tego problemu.

Będziesz musiał szukać pierwiastków poprzez dyskryminator: D = 5 2 − 4 · 1 · (−300) = 1225 = 35 2 . Jeśli nie pamiętasz pierwiastka dyskryminatora, zauważę tylko, że 1225: 25 = 49. Zatem 1225 = 25 49 = 5 2 7 2 = 35 2.

Teraz, gdy znany jest pierwiastek dyskryminatora, rozwiązanie równania nie jest trudne. Otrzymujemy: x 1 = 15; x 2 = −20.

W równaniach kwadratowych istnieje wiele zależności. Najważniejsze z nich to relacje między pierwiastkami i współczynnikami. Również w równaniach kwadratowych istnieje szereg zależności określonych przez twierdzenie Viety.

W tym temacie przedstawimy samo twierdzenie Viety i jego dowód na równanie kwadratowe, twierdzenie odwrotne do twierdzenia Viety oraz przeanalizujemy szereg przykładów rozwiązywania problemów. W materiale szczególną uwagę zwrócimy na rozważenie wzorów Viety, które definiują związek pomiędzy pierwiastkami rzeczywistymi algebraicznego równania stopnia N i jego współczynniki.

Sformułowanie i dowód twierdzenia Viety

Wzór na pierwiastki równania kwadratowego za x 2 + b x + do = 0 postaci x 1 = - b + D 2 · a, x 2 = - b - D 2 · a, gdzie re = b 2 - 4 za do, nawiązuje relacje x 1 + x 2 = - b a, x 1 x 2 = ok. Potwierdza to twierdzenie Viety.

Twierdzenie 1

W równaniu kwadratowym za x 2 + b x + do = 0, Gdzie x 1 I x 2– pierwiastki, suma pierwiastków będzie równa stosunkowi współczynników B I A, co przyjęto z przeciwnym znakiem, a iloczyn pierwiastków będzie równy stosunkowi współczynników C I A, tj. x 1 + x 2 = - b a, x 1 x 2 = ok.

Dowód 1

Oferujemy następujący schemat przeprowadzenia dowodu: weź wzór na pierwiastki, utwórz sumę i iloczyn pierwiastków równania kwadratowego, a następnie przekształć powstałe wyrażenia, aby upewnić się, że są równe - b.a I ok odpowiednio.

Zróbmy sumę pierwiastków x 1 + x 2 = - b + D 2 · a + - b - D 2 · a. Sprowadźmy ułamki do wspólnego mianownika - b + D 2 · a + - b - D 2 · a = - b + D + - b - D 2 · a. Otwórzmy nawiasy w liczniku ułamka wynikowego i przedstawmy podobne wyrazy: - b + D + - b - D 2 · a = - b + D - b - D 2 · a = - 2 · b 2 · a . Skróćmy ułamek o: 2 - b a = - b a.

W ten sposób udowodniliśmy pierwszą zależność twierdzenia Viety, które dotyczy sumy pierwiastków równania kwadratowego.

Przejdźmy teraz do drugiej relacji.

Aby to zrobić, musimy utworzyć iloczyn pierwiastków równania kwadratowego: x 1 · x 2 = - b + D 2 · a · - b - D 2 · a.

Zapamiętajmy zasadę mnożenia ułamków zwykłych i zapiszmy ostatni iloczyn następująco: - b + D · - b - D 4 · a 2.

Pomnóżmy nawias przez nawias w liczniku ułamka lub skorzystajmy ze wzoru na różnicę kwadratów, aby szybciej przekształcić ten iloczyn: - b + D · - b - D 4 · a 2 = - b 2 - D 2 4 · a 2.

Skorzystajmy z definicji pierwiastka kwadratowego, aby dokonać następującego przejścia: - b 2 - D 2 4 · a 2 = b 2 - D 4 · a 2 . Formuła re = b 2 - 4 za do odpowiada dyskryminatorowi równania kwadratowego, a zatem na ułamek zamiast D można zastąpić b 2 - 4 za do:

b 2 - re 4 za 2 = b 2 - (b 2 - 4 za do) 4 za 2

Otwórzmy nawiasy, dodajmy podobne terminy i otrzymamy: 4 · a · c 4 · a 2 . Jeśli skrócimy to do 4 a, wtedy pozostaje ok. W ten sposób udowodniliśmy drugą zależność twierdzenia Viety dla iloczynu pierwiastków.

Dowód twierdzenia Viety można zapisać w bardzo lakonicznej formie, jeśli pominiemy wyjaśnienia:

x 1 + x 2 = - b + re 2 a + - b - re 2 a = - b + re + - b - re 2 a = - 2 b 2 a = - b za , x 1 x 2 = - b + re 2 · a · - b - re 2 · a = - b + re · - b - re 4 · a 2 = - b 2 - re 2 4 · za 2 = b 2 - re 4 · a 2 = = re = b 2 - 4 · za · do = b 2 - b 2 - 4 · za · do 4 · za 2 = 4 · za · do 4 · za 2 = do za .

Gdy dyskryminator równania kwadratowego jest równy zero, równanie będzie miało tylko jeden pierwiastek. Aby móc zastosować twierdzenie Viety do takiego równania, możemy założyć, że równanie z dyskryminatorem równym zero ma dwa identyczne pierwiastki. Rzeczywiście, kiedy D=0 pierwiastkiem równania kwadratowego jest: - b 2 · a, wtedy x 1 + x 2 = - b 2 · a + - b 2 · a = - b + (- b) 2 · a = - 2 · b 2 · a = - b a i x 1 · x 2 = - b 2 · a · - b 2 · a = - b · - b 4 · a 2 = b 2 4 · a 2 , a ponieważ D = 0, czyli b 2 - 4 · a · do = 0, skąd b 2 = 4 · a · c, następnie b 2 4 · za 2 = 4 · a · do 4 · za 2 = do a.

Najczęściej w praktyce twierdzenie Viety stosuje się do zredukowanego równania kwadratowego postaci x 2 + p x + q = 0, gdzie wiodący współczynnik a jest równy 1. W związku z tym twierdzenie Viety zostało sformułowane specjalnie dla równań tego typu. Nie ogranicza to ogólności ze względu na fakt, że każde równanie kwadratowe można zastąpić równaniem równoważnym. Aby to zrobić, musisz podzielić obie jego części przez liczbę różną od zera.

Podajmy inne sformułowanie twierdzenia Viety.

Twierdzenie 2

Suma pierwiastków w danym równaniu kwadratowym x 2 + p x + q = 0 będzie równy współczynnikowi x, który jest przyjmowany z przeciwnym znakiem, iloczyn pierwiastków będzie równy członowi swobodnemu, tj. x 1 + x 2 = - p, x 1 x 2 = q.

Twierdzenie odwrotne do twierdzenia Viety

Jeśli przyjrzysz się uważnie drugiemu sformułowaniu twierdzenia Viety, zobaczysz to w przypadku pierwiastków x 1 I x 2 zredukowane równanie kwadratowe x 2 + p x + q = 0 obowiązywać będą następujące zależności: x 1 + x 2 = − p, x 1 · x 2 = q. Z tych zależności x 1 + x 2 = − p, x 1 x 2 = q wynika, że x 1 I x 2 są pierwiastkami równania kwadratowego x 2 + p x + q = 0. Dochodzimy więc do stwierdzenia, które jest odwrotnością twierdzenia Viety.

Proponujemy teraz sformalizowanie tego twierdzenia w postaci twierdzenia i przeprowadzenie jego dowodu.

Twierdzenie 3

Jeśli liczby x 1 I x 2 są takie, że x 1 + x 2 = - str I x 1 x 2 = q, To x 1 I x 2 są pierwiastkami zredukowanego równania kwadratowego x 2 + p x + q = 0.

Dowód 2

Wymiana kursów P I Q poprzez ich ekspresję x 1 I x 2 pozwala na transformację równania x 2 + p x + q = 0 w odpowiednik .

Jeśli podstawimy liczbę do powstałego równania x 1 zamiast X, wtedy otrzymamy równość x 1 2 − (x 1 + x 2) x 1 + x 1 x 2 = 0. To jest równość dla każdego x 1 I x 2 zamienia się w rzeczywistą równość liczbową 0 = 0 , ponieważ x 1 2 - (x 1 + x 2) x 1 + x 1 x 2 = x 1 2 - x 1 2 - x 2 x 1 + x 1 x 2 = 0. To znaczy, że x 1- pierwiastek równania x 2 − (x 1 + x 2) x + x 1 x 2 = 0, Więc co x 1 jest także pierwiastkiem równoważnego równania x 2 + p x + q = 0.

Podstawienie do równania x 2 − (x 1 + x 2) x + x 1 x 2 = 0 liczby x 2 zamiast x pozwala nam uzyskać równość x 2 2 − (x 1 + x 2) x 2 + x 1 x 2 = 0. Tę równość można uznać za prawdziwą, ponieważ x 2 2 − (x 1 + x 2) x 2 + x 1 x 2 = x 2 2 − x 1 x 2 − x 2 2 + x 1 x 2 = 0. Okazało się, że x 2 jest pierwiastkiem równania x 2 − (x 1 + x 2) x + x 1 x 2 = 0, i stąd równania x 2 + p x + q = 0.

Udowodniono odwrotność twierdzenia Viety.

Przykłady wykorzystania twierdzenia Viety

Zacznijmy teraz analizować najbardziej typowe przykłady na ten temat. Zacznijmy od analizy problemów wymagających zastosowania twierdzenia odwrotnego do twierdzenia Viety. Można go użyć do sprawdzenia liczb uzyskanych w wyniku obliczeń, aby sprawdzić, czy są one pierwiastkami danego równania kwadratowego. Aby to zrobić, należy obliczyć ich sumę i różnicę, a następnie sprawdzić ważność relacji x 1 + x 2 = - b a, x 1 · x 2 = a c.

Spełnienie obu zależności wskazuje, że liczby otrzymane w trakcie obliczeń są pierwiastkami równania. Jeśli widzimy, że przynajmniej jeden z warunków nie jest spełniony, to liczby te nie mogą być pierwiastkami równania kwadratowego podanego w treści zadania.

Przykład 1

Która z par liczb 1) x 1 = − 5, x 2 = 3 lub 2) x 1 = 1 - 3, x 2 = 3 + 3 lub 3) x 1 = 2 + 7 2, x 2 = 2 - 7 2 to para pierwiastków równania kwadratowego 4 x 2 - 16 x + 9 = 0?

Rozwiązanie

Znajdźmy współczynniki równania kwadratowego 4 x 2 - 16 x + 9 = 0. To jest a = 4, b = - 16, c = 9. Zgodnie z twierdzeniem Viety suma pierwiastków równania kwadratowego musi być równa - b.a, to jest, 16 4 = 4 , a iloczyn pierwiastków musi być równy ok, to jest, 9 4 .

Sprawdźmy uzyskane liczby obliczając sumę i iloczyn liczb z trzech podanych par i porównując je z uzyskanymi wartościami.

W pierwszym przypadku x 1 + x 2 = - 5 + 3 = - 2. Wartość ta jest różna od 4, zatem nie ma potrzeby kontynuowania kontroli. Zgodnie z twierdzeniem odwrotnym do twierdzenia Viety możemy od razu stwierdzić, że pierwsza para liczb nie jest pierwiastkiem tego równania kwadratowego.

W drugim przypadku x 1 + x 2 = 1 - 3 + 3 + 3 = 4. Widzimy, że pierwszy warunek jest spełniony. Ale drugi warunek nie brzmi: x 1 · x 2 = 1 - 3 · 3 + 3 = 3 + 3 - 3 · 3 - 3 = - 2 · 3. Wartość, którą otrzymaliśmy, jest inna 9 4 . Oznacza to, że druga para liczb nie jest pierwiastkiem równania kwadratowego.

Przejdźmy do rozważenia trzeciej pary. Tutaj x 1 + x 2 = 2 + 7 2 + 2 - 7 2 = 4 i x 1 x 2 = 2 + 7 2 2 - 7 2 = 2 2 - 7 2 2 = 4 - 7 4 = 16 4 - 7 4 = 9 4. Obydwa warunki są spełnione, co oznacza, że x 1 I x 2 są pierwiastkami danego równania kwadratowego.

Odpowiedź: x 1 = 2 + 7 2 , x 2 = 2 - 7 2

Możemy również skorzystać z odwrotności twierdzenia Viety, aby znaleźć pierwiastki równania kwadratowego. Najprościej jest wybrać pierwiastki całkowite podanych równań kwadratowych o współczynnikach całkowitych. Można rozważyć inne opcje. Może to jednak znacznie skomplikować obliczenia.

Do wybierania pierwiastków wykorzystujemy fakt, że jeśli suma dwóch liczb jest równa drugiemu współczynnikowi równania kwadratowego, wziętemu ze znakiem minus, a iloczyn tych liczb jest równy wyrazowi swobodnemu, to liczby te są pierwiastki tego równania kwadratowego.

Przykład 2

Jako przykład używamy równania kwadratowego x 2 - 5 x + 6 = 0. Liczby x 1 I x 2 mogą być pierwiastkami tego równania, jeśli spełnione są dwie równości x 1 + x 2 = 5 I x 1 x 2 = 6. Wybierzmy te liczby. Są to numery 2 i 3, ponieważ 2 + 3 = 5 I 2 3 = 6. Okazuje się, że 2 i 3 są pierwiastkami tego równania kwadratowego.

Odwrotność twierdzenia Viety można zastosować do znalezienia drugiego pierwiastka, gdy pierwszy jest znany lub oczywisty. W tym celu możemy skorzystać z relacji x 1 + x 2 = - b a, x 1 · x 2 = c a.

Przykład 3

Rozważmy równanie kwadratowe 512 x 2 - 509 x - 3 = 0. Konieczne jest znalezienie pierwiastków tego równania.

Rozwiązanie

Pierwszym pierwiastkiem równania jest 1, ponieważ suma współczynników tego równania kwadratowego wynosi zero. Okazało się, że x 1 = 1.

Teraz znajdźmy drugi pierwiastek. W tym celu możesz skorzystać z relacji x 1 x 2 = ok. Okazało się, że 1 x 2 = - 3512, Gdzie x 2 = - 3512.

Odpowiedź: pierwiastki równania kwadratowego podanego w opisie problemu 1 I - 3 512 .

Tylko w prostych przypadkach możliwe jest wybranie pierwiastków za pomocą twierdzenia odwrotnego do twierdzenia Viety. W innych przypadkach lepiej jest szukać według wzoru na pierwiastki równania kwadratowego poprzez dyskryminator.

Dzięki odwrotności twierdzenia Viety możemy także konstruować równania kwadratowe korzystając z istniejących pierwiastków x 1 I x 2. Aby to zrobić, musimy obliczyć sumę pierwiastków, co daje współczynnik dla X z przeciwnym znakiem danego równania kwadratowego i iloczynem pierwiastków, co daje wyraz wolny.

Przykład 4

Napisz równanie kwadratowe, którego pierwiastkami są liczby − 11 I 23 .

Rozwiązanie

Załóżmy, że x 1 = - 11 I x2 = 23. Suma i iloczyn tych liczb będzie równa: x 1 + x 2 = 12 I x 1 x 2 = - 253. Oznacza to, że drugi współczynnik wynosi 12, czyli termin wolny − 253.

Ułóżmy równanie: x 2 - 12 x - 253 = 0.

Odpowiedź: x 2 - 12 x - 253 = 0 .

Twierdzenie Viety możemy wykorzystać do rozwiązywania problemów związanych ze znakami pierwiastków równań kwadratowych. Związek twierdzenia Viety związany jest ze znakami pierwiastków zredukowanego równania kwadratowego x 2 + p x + q = 0 w następujący sposób:

• jeśli równanie kwadratowe ma rzeczywiste pierwiastki i jeśli wyraz wolny Q jest liczbą dodatnią, to pierwiastki te będą miały ten sam znak „+” lub „-”;
• jeśli równanie kwadratowe ma pierwiastki i jeśli wyraz wolny Q jest liczbą ujemną, wtedy jeden pierwiastek będzie „+”, a drugi „-”.

Obydwa stwierdzenia są konsekwencją wzoru x 1 x 2 = q oraz zasady mnożenia liczb dodatnich i ujemnych oraz liczb o różnych znakach.

Przykład 5

Są pierwiastkami równania kwadratowego x 2 - 64 x - 21 = 0 pozytywny?

Rozwiązanie

Zgodnie z twierdzeniem Viety oba pierwiastki tego równania nie mogą być dodatnie, ponieważ muszą spełniać równość x 1 x 2 = - 21. W przypadku pozytywów jest to niemożliwe x 1 I x 2.

Odpowiedź: NIE

Przykład 6

Przy jakich wartościach parametrów R równanie kwadratowe x 2 + (r + 2) x + r - 1 = 0 będzie miał dwa rzeczywiste pierwiastki o różnych znakach.

Rozwiązanie

Zacznijmy od znalezienia wartości których R, dla którego równanie będzie miało dwa pierwiastki. Znajdźmy dyskryminator i zobaczmy przy czym R będzie przyjmować wartości dodatnie. re = (r + 2) 2 - 4 1 (r - 1) = r 2 + 4 r + 4 - 4 r + 4 = r 2 + 8. Wartość wyrażenia r 2 + 8 pozytywne dla każdego prawdziwego R dlatego dyskryminator będzie większy od zera dla dowolnej liczby rzeczywistej R. Oznacza to, że oryginalne równanie kwadratowe będzie miało dwa pierwiastki dla dowolnych rzeczywistych wartości parametru R.

Zobaczmy teraz, kiedy korzenie mają różne znaki. Jest to możliwe, jeśli ich produkt jest negatywny. Zgodnie z twierdzeniem Viety iloczyn pierwiastków zredukowanego równania kwadratowego jest równy członowi swobodnemu. Oznacza to, że właściwym rozwiązaniem będą te wartości R, dla którego wolny termin r - 1 jest ujemny. Rozwiążmy nierówność liniową r − 1< 0 , получаем r < 1 .

Odpowiedź: o godz< 1 .

Formuły Vieta

Istnieje wiele wzorów, które można zastosować do wykonywania operacji na pierwiastkach i współczynnikach nie tylko równań kwadratowych, ale także sześciennych i innych typów. Nazywa się je wzorami Viety.

Dla algebraicznego równania stopnia N postaci a 0 · x n + a 1 · x n - 1 + . . . + a n - 1 x + a n = 0 uważa się, że równanie ma N prawdziwe korzenie x 1 , x 2 , … , x rz, wśród których może być taki sam:
x 1 + x 2 + x 3 + . . . + x n = - za 1 za 0 , x 1 · x 2 + x 1 · x 3 + . . . + x n - 1 · x n = za 2 za 0 , x 1 · x 2 · x 3 + x 1 · x 2 · x 4 + . . . + x n - 2 · x n - 1 · x n = - za 3 za 0 , . . . x 1 · x 2 · x 3 · . . . · x n = (- 1) n · za n za 0

Definicja 1

Wzory Viety pomagają nam uzyskać:

• twierdzenie o rozkładzie wielomianu na czynniki liniowe;
• wyznaczanie równych wielomianów poprzez równość wszystkich odpowiadających im współczynników.

Zatem wielomian a 0 · x n + a 1 · x n - 1 + . . . + a n - 1 · x + a n i jego rozwinięcie na czynniki liniowe postaci a 0 · (x - x 1) · (x - x 2) · . . . · (x - x n) są równe.

Jeśli otworzymy nawiasy w ostatnim iloczynie i zrównamy odpowiednie współczynniki, otrzymamy wzory Vieta. Przyjmując n = 2, możemy otrzymać wzór Viety na równanie kwadratowe: x 1 + x 2 = - a 1 a 0, x 1 · x 2 = a 2 a 0.

Definicja 2

Wzór Viety na równanie sześcienne:
x 1 + x 2 + x 3 = - za 1 za 0 , x 1 x 2 + x 1 x 3 + x 2 x 3 = za 2 za 0 , x 1 x 2 x 3 = - za 3 za 0

Lewa strona wzoru Viety zawiera tzw. elementarne wielomiany symetryczne.

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter