Co oznacza dzielenie z resztą? Ogólne zrozumienie dzielenia liczb naturalnych przez resztę. Pisemny podział przez liczbę dwucyfrową

Zanim szczegółowo opiszemy wszystkie kroki algorytmu dzielenia liczb naturalnych przez resztę, odpowiemy na trzy pytania: co wiemy na początku, co musimy znaleźć i na podstawie jakich rozważań to zrobimy? Początkowo znamy dzielną a i dzielnik b. Musimy znaleźć niepełny iloraz c i resztę d. Równość a = b c + d określa relację między dzielną, dzielnikiem, ilorazem częściowym i resztą. Z zapisanej równości wynika, że ​​jeśli przedstawimy dzielną a jako sumę bc + d, w której d jest mniejsze od b (ponieważ reszta jest zawsze mniejsza od dzielnika), to zobaczymy zarówno niepełny iloraz c, jak i reszta re.

Pozostaje tylko dowiedzieć się, jak przedstawić dywidendę a jako sumę b c + d. Algorytm służący do tego jest bardzo podobny do algorytmu dzielenia liczb naturalnych bez reszty. Opiszemy wszystkie kroki, a jednocześnie poprowadzimy rozwiązanie przykładu dla większej przejrzystości. Podziel 899 przez 47.

Pierwsze pięć punktów algorytmu pozwoli Ci przedstawić dywidendę jako sumę kilku warunków. Należy zauważyć, że działania z tych punktów są cyklicznie powtarzane, aż do znalezienia wszystkich warunków, które składają się na dywidendę. W ostatnim szóstym akapicie otrzymana kwota jest przeliczana na formularz b c + d (jeśli otrzymana kwota nie będzie już miała tego formularza), skąd widoczny jest poszukiwany niepełny iloraz i reszta.

Zacznijmy więc przedstawiać dywidendę 899 jako sumę kilku warunków.

Najpierw obliczamy, o ile liczba znaków w dzielnej jest większa niż liczba znaków w dzielniku, i zapamiętujemy tę liczbę.

W naszym przykładzie dywidenda ma 3 cyfry (899 - trzycyfrowy numer), a w zapisie dzielnika są dwa znaki (47 to liczba dwucyfrowa), dlatego w zapisie dzielnej jest jeszcze jeden znak i pamiętamy liczbę 1.

Teraz w rekordzie dzielnika po prawej stronie dodajemy cyfry 0 w ilości określonej przez liczbę uzyskaną w poprzednim akapicie. Co więcej, jeśli zapisana liczba jest większa niż dywidenda, wówczas 1 należy odjąć od liczby zapisanej w poprzednim akapicie.

Wróćmy do naszego przykładu. W rekordzie dzielnika 47 dodajemy jedną cyfrę 0 z prawej strony i otrzymujemy liczbę 470. Od 470<899 , то запомненное в предыдущем пункте число НЕ нужно уменьшать на 1 . Таким образом, у нас в памяти остается число 1 .

Następnie przypisujemy liczby 0 do liczby 1 po prawej stronie w ilości określonej przez liczbę zapamiętaną w poprzednim akapicie. W takim przypadku otrzymujemy jednostkę kategorii, z którą będziemy dalej pracować.

W naszym przykładzie przypisujemy 1 cyfrę 0 do liczby 1 i otrzymujemy liczbę 10, czyli będziemy pracować z cyfrą dziesiątek.

Teraz sukcesywnie mnożymy dzielnik przez 1, 2, 3, ... jednostki kategorii roboczej, aż otrzymamy liczbę większą lub równą dywidendzie.

Dowiedzieliśmy się, że w naszym przykładzie miejscem pracy jest miejsce dziesiątek. Dlatego najpierw mnożymy dzielnik przez jedną jednostkę miejsca dziesiątek, czyli mnożymy 47 przez 10, otrzymujemy 47 10 = 470. Wynikowa liczba 470 jest mniejsza niż dywidenda 899, więc przystępujemy do pomnożenia dzielnika przez dwie jednostki miejsca dziesiątek, czyli 47 jest pomnożone przez 20. Mamy 47 20 = 940. Otrzymaliśmy liczbę większą niż 899.

Liczba uzyskana w przedostatnim kroku mnożenia sekwencyjnego jest pierwszym z wymaganych wyrazów.

W rozważanym przykładzie wymaganym wyrazem jest liczba 470 (liczba ta jest równa iloczynowi 47 · 100, z tej równości skorzystamy później).

Następnie znajdujemy różnicę między dywidendą a pierwszym znalezionym terminem. Jeśli wynikowa liczba jest większa niż dzielnik, przejdź do znalezienia drugiego wyrazu. W tym celu powtarzamy wszystkie opisane kroki algorytmu, ale już otrzymaną liczbę przyjmujemy jako dywidendę. Jeżeli w tym momencie ponownie otrzymamy liczbę większą niż dzielnik, to przystępujemy do znalezienia trzeciego wyrazu, ponownie powtarzając kroki algorytmu, przyjmując wynikową liczbę jako dzielną. Idziemy więc dalej, znajdując wyrazy czwarty, piąty i kolejne, aż liczba uzyskana w tym akapicie będzie mniejsza niż dzielnik. Jak tylko to się stanie, bierzemy otrzymaną tutaj liczbę jako ostatni wymagany termin (posuwając się do przodu, powiedzmy, że jest równa reszcie) i przechodzimy do ostatniego etapu.

Wróćmy do naszego przykładu. Na tym etapie mamy 899-470 = 429. Ponieważ 429>47, bierzemy tę liczbę jako dywidendę i powtarzamy z nią wszystkie etapy algorytmu.

W zapisie liczby 429 jest o jeden znak więcej niż w zapisie liczby 47, dlatego pamiętamy liczbę 1.

Teraz w zapisie dywidendy po prawej dodajemy jedną cyfrę 0, otrzymujemy liczbę 470, która więcej numerów 429. Dlatego od liczby 1 zapamiętanej w poprzednim akapicie odejmujemy 1, otrzymujemy liczbę 0, którą pamiętamy.

Ponieważ w poprzednim akapicie zapamiętaliśmy liczbę 0, to nie ma potrzeby przypisywania pojedynczej cyfry 0 do liczby 1 po prawej stronie. W tym przypadku mamy numer 1, czyli kategorią pracy jest kategoria jedności.

Teraz kolejno mnożymy dzielnik 47 przez 1, 2, 3, ... Nie będziemy się nad tym szczegółowo rozwodzić. Powiedzmy, że 47 9 = 423<429 , а 47·10=470>429. Drugim wymaganym terminem jest liczba 423 (równa 47 · 9, której użyjemy poniżej).

Różnica między 429 a 423 wynosi 6. Ta liczba jest mniejsza niż dzielnik 47, więc jest to trzeci (i ostatni) wymagany wyraz. Teraz możemy przejść do ostatniego etapu.

Cóż, tutaj dochodzimy do ostatniego etapu. Wszystkie dotychczasowe działania miały na celu prezentację dywidendy jako sumy kilku terminów. Teraz pozostaje przekonwertować wynikową sumę na postać b c + d. W radzeniu sobie z tym zadaniem pomoże nam dystrybucyjna właściwość mnożenia względem dodawania. Po tym stanie się widoczny żądany niepełny iloraz i reszta.

W naszym przykładzie dywidenda 899 jest równa sumie trzech warunków 470, 423 i 6. Sumę 470 + 423 + 6 można przepisać jako 47 10 + 47 9 + 6 (pamiętajmy, że zwracaliśmy uwagę na równości 470 = 47 10 i 423 = 47 9). Teraz stosujemy własność mnożenia liczby naturalnej przez sumę i otrzymujemy 47 10 + 47 9 + 6 = 47 (10 + 9) + 6 = 47 19 + 6. W ten sposób dywidenda została przekształcona do postaci, której potrzebujemy 899 = 47 19 + 6, z której łatwo znaleźć niepełny iloraz 19 i resztę 6.

Tak więc 899: 47 = 19 (odpoczynek 6).

Oczywiście przy rozwiązywaniu przykładów nie będziesz tak szczegółowo opisywał procesu dzielenia z resztą.

Artykuł omawia koncepcję dzielenia liczb całkowitych przez resztę. Udowodnijmy twierdzenie o podzielności liczb całkowitych z resztą i zbadajmy związki między dzielnikami i dzielnikami, ilorazami niepełnymi i resztami. Rozważmy zasady, w których dokonuje się dzielenia liczb całkowitych przez reszty, po szczegółowym rozważeniu przykładów. Pod koniec rozwiązania dokonamy sprawdzenia.

Rozumienie dzielenia liczb całkowitych przez reszty

Dzielenie liczb całkowitych przez resztę uważa się za uogólnione dzielenie przez resztę liczb naturalnych. Dzieje się tak, ponieważ liczby naturalne są składnik cały.

Dzielenie z resztą dowolnej liczby oznacza, że ​​liczba całkowita a jest podzielna przez niezerową liczbę b. Jeśli b = 0, dzielenie reszty nie jest wykonywane.

Oprócz dzielenia liczb naturalnych przez resztę, dokonuje się również dzielenia liczb całkowitych a i b, jeśli b jest różne od zera, przez c i d. W tym przypadku a i b nazywane są dzielną i dzielnikiem, a d jest resztą z dzielenia, c jest liczbą całkowitą lub niepełnym ilorazem.

Jeśli założymy, że reszta jest nieujemną liczbą całkowitą, to jej wartość nie jest większa niż moduł liczby b. Napiszmy w ten sposób: 0 ≤ d ≤ b. Ten łańcuch nierówności jest używany przy porównywaniu 3 lub więcej liczb.

Jeśli c jest ilorazem niepełnym, to d jest resztą z dzielenia liczby całkowitej a przez b, można to krótko ustalić: a: b = c (reszta d).

Reszta przy dzieleniu liczb a przez b jest możliwa do zera, wtedy mówią, że a jest całkowicie podzielne przez b, to znaczy bez reszty. Dzielenie bez reszty jest uważane za szczególny przypadek dzielenia.

Jeśli podzielimy zero przez jakąś liczbę, w rezultacie otrzymamy zero. Pozostała część podziału również będzie wynosić zero. Można to wywieść z teorii dzielenia zera przez liczbę całkowitą.

Przyjrzyjmy się teraz znaczeniu dzielenia liczb całkowitych przez resztę.

Wiadomo, że liczby całkowite dodatnie są naturalne, to przy dzieleniu przez resztę otrzymujemy takie samo znaczenie, jak przy dzieleniu liczb naturalnych przez resztę.

Dzielenie ujemnej liczby całkowitej a przez dodatnią liczbę całkowitą b ma sens. Spójrzmy na przykład. Wyobrażamy sobie sytuację, w której mamy dług rzeczy w wysokości a, który musi spłacić b osób. Wymaga to od każdego takiego samego wkładu. Aby określić wysokość długu dla każdego, musisz zwrócić uwagę na kwotę prywatnych s. Pozostała część d mówi, że liczba pozycji po spłaceniu długów jest znana.

Weźmy przykład z jabłkami. Jeśli 2 osoby potrzebują 7 jabłek. Jeśli policzysz, że każdy musi zwrócić 4 jabłka, po pełnym przeliczeniu będą mieli 1 jabłko. Zapiszmy to w postaci równości: (- 7): 2 = - 4 (o z punktem 1).

Dzielenie dowolnej liczby a przez liczbę całkowitą nie ma sensu, ale jest możliwe jako opcja.

Twierdzenie o podzielności dla liczb całkowitych z resztą

Odkryliśmy, że a jest dzielną, następnie b jest dzielnikiem, c jest ilorazem niepełnym, a d jest resztą. Są ze sobą spokrewnieni. Pokażemy to połączenie za pomocą równości a = b c + d. Związek między nimi charakteryzuje twierdzenie o podzielności reszty.

Twierdzenie

Każda liczba całkowita może być reprezentowana tylko przez liczbę całkowitą i niezerową b w następujący sposób: a = b q + r, gdzie q i r są liczbami całkowitymi. Tutaj mamy 0 ≤ r ≤ b.

Udowodnijmy możliwość istnienia a = b q + r.

Dowód

Jeśli są dwie liczby a i b, a a jest podzielne przez b bez reszty, to z definicji wynika, że ​​istnieje liczba q, która będzie równa równości a = b q. Wtedy równość można uznać za prawdziwą: a = b q + r dla r = 0.

Następnie należy wziąć q takie, że dane przez nierówność b q< a < b · (q + 1) было верным. Необходимо вычесть b · q из всех частей выражения. Тогда придем к неравенству такого вида: 0 < a − b · q < b .

Mamy, że wartość wyrażenia a - b q jest większa od zera i nie większa od wartości liczby b, z tego wynika, że ​​r = a - b q. Otrzymujemy, że liczbę a można przedstawić w postaci a = b q + r.

Teraz należy rozważyć możliwość reprezentowania a = b q + r dla wartości ujemne b.

Wartość bezwzględna liczby okazuje się dodatnia, wtedy otrzymujemy a = b q 1 + r, gdzie wartość q 1 jest liczbą całkowitą, r jest liczbą całkowitą spełniającą warunek 0 ≤ r< b . Принимаем q = − q 1 , получим, что a = b · q + r для отрицательных b .

Dowód wyjątkowości

Załóżmy, że a = bq + r, q i r są liczbami całkowitymi z prawdziwym warunkiem 0 ≤ r< b , имеется еще одна форма записи в виде a = b · q 1 + r 1 , где q 1 oraz r 1 są jakieś liczby, gdzie q 1 ≠ q, 0 ≤ r 1< b .

Kiedy nierówność jest odejmowana od lewej i prawej strony, otrzymujemy 0 = b · (q - q 1) + r - r 1, co jest równoważne r - r 1 = b · q 1 - q. Ponieważ moduł jest używany, otrzymujemy równość r - r 1 = b q 1 - q.

Podany warunek mówi, że 0 ≤ r< b и 0 ≤ r 1 < b запишется в виде r - r 1 < b . Имеем, что Q oraz q 1- liczb całkowitych ponadto q ≠ q 1, to q 1 - q ≥ 1. Stąd mamy, że b q 1 - q ≥ b. Powstałe nierówności r - r 1< b и b · q 1 - q ≥ b указывают на то, что такое равенство в виде r - r 1 = b · q 1 - q невозможно в данном случае.

Wynika stąd, że liczby a nie można przedstawić w żaden inny sposób, chyba że za pomocą takiego zapisu a = b q + r.

Związek między dywidendą, dzielnikiem, niepełnym ilorazem i resztą

Używając równości a = b c + d, możesz znaleźć nieznaną dzielną a, gdy znasz dzielnik b z niepełnym ilorazem c i resztą d.

Przykład 1

Ustal dywidendę, jeśli w dzieleniu otrzymamy - 21, niepełny iloraz 5 i resztę 12.

Rozwiązanie

Należy obliczyć dywidendę a ze znanym dzielnikiem b = - 21, niepełnym ilorazem c = 5 i resztą d = 12. Musimy przejść do równości a = b c + d, z której otrzymujemy a = (-21) 5 + 12. Zgodnie z kolejnością wykonywania czynności mnożymy - 21 przez 5, po czym otrzymujemy (- 21) 5 + 12 = - 105 + 12 = - 93.

Odpowiedź: - 93 .

Związek między dzielnikiem a niepełnym ilorazem i resztą można wyrazić za pomocą równości: b = (a - d): c, c = (a - d): b i d = a - b c. Za ich pomocą możemy obliczyć dzielnik, iloraz cząstkowy i resztę. Sprowadza się do ciągłego znajdowania reszty po dzieleniu liczby całkowitej a przez b ze znaną dzielną, dzielnikiem i ilorazem niepełnym. Wzór ma zastosowanie d = a - b c. Rozważmy szczegółowo rozwiązanie.

Przykład 2

Znajdź resztę z dzielenia liczby całkowitej – 19 przez liczbę całkowitą 3 ze znanym niepełnym ilorazem równym – 7.

Rozwiązanie

Aby obliczyć resztę z dzielenia, zastosuj wzór w postaci d = a - b · c. Według warunku wszystkie dane są dostępne a = - 19, b = 3, c = - 7. Z tego otrzymujemy d = a - b c = - 19 - 3 (- 7) = - 19 - (- 21) = - 19 + 21 = 2 (różnica - 19 - (- 21). Ten przykład obliczana przez regułę odejmowania ujemnej liczby całkowitej.

Odpowiedź: 2 .

Wszystkie liczby całkowite dodatnie są naturalne. Wynika stąd, że dzielenie odbywa się według wszystkich reguł dzielenia z resztą liczb naturalnych. Szybkość dzielenia z resztą liczb naturalnych jest istotna, ponieważ na niej opiera się nie tylko dzielenie liczb dodatnich, ale także zasady dzielenia dowolnych liczb całkowitych.

Najwygodniejszą metodą dzielenia jest kolumna, ponieważ łatwiej i szybciej uzyskać niepełny lub tylko iloraz z resztą. Rozważmy rozwiązanie bardziej szczegółowo.

Przykład 3

Podziel 14671 przez 54.

Rozwiązanie

Ten podział należy wykonać w kolumnie:

Oznacza to, że niepełny iloraz wynosi 271, a reszta to 37.

Odpowiedź: 14 671: 54 = 271. (przystanek 37)

Zasada dzielenia z resztą dodatniej liczby całkowitej przez ujemną liczbę całkowitą, przykłady

Aby dokonać dzielenia z resztą liczby dodatniej przez liczbę całkowitą ujemną, konieczne jest sformułowanie reguły.

Definicja 1

Niepełny iloraz z dzielenia dodatniej liczby całkowitej a przez ujemną liczbę całkowitą b otrzymujemy liczbę będącą przeciwieństwem niepełnego ilorazu z dzielenia bezwzględnych wartości liczb a przez b. Wtedy reszta jest równa reszcie z dzielenia a przez b.

Stąd mamy, że niepełny iloraz dzielenia liczby całkowitej dodatniej przez liczbę całkowitą ujemną jest uważany za liczbę całkowitą niedodatnią.

Otrzymujemy algorytm:

• dzielimy moduł podzielności przez moduł dzielnika, to otrzymujemy niepełny iloraz i
• reszta;
• zapisujemy numer przeciwny do otrzymanego.

Rozważmy przykład algorytmu dzielenia dodatniej liczby całkowitej przez ujemną liczbę całkowitą.

Przykład 4

Podziel z resztą 17 przez - 5.

Rozwiązanie

Zastosujmy algorytm dzielenia z resztą dodatniej liczby całkowitej przez ujemną liczbę całkowitą. Konieczne jest podzielenie 17 przez - 5 modulo. Stąd otrzymujemy, że niepełny iloraz jest równy 3, a reszta równa się 2.

Wymaganą liczbę otrzymujemy, dzieląc 17 przez - 5 = - 3 z resztą 2.

Odpowiedź: 17: (- 5) = - 3 (odpoczynek 2).

Przykład 5

Podziel 45 przez - 15.

Rozwiązanie

Konieczne jest podzielenie liczb modulo. Podzielmy liczbę 45 przez 15, otrzymamy iloraz 3 bez reszty. Oznacza to, że liczba 45 jest podzielna przez 15 bez reszty. W odpowiedzi otrzymujemy - 3, ponieważ podział został przeprowadzony modulo.

45: (- 15) = 45: - 15 = - 45: 15 = - 3

Odpowiedź: 45: (− 15) = − 3 .

Sformułowanie reguły dzielenia z resztą jest następujące.

Definicja 2

Aby otrzymać niepełny iloraz c przy dzieleniu ujemnej liczby całkowitej a przez dodatnie b, należy zastosować przeciwieństwo podanej liczby i odjąć od niej 1, wtedy reszta d zostanie obliczona ze wzoru: d = a - pne.

Na podstawie reguły możemy wywnioskować, że dzieląc otrzymujemy nieujemną liczbę całkowitą. Dla dokładności rozwiązania stosuje się algorytm dzielenia a przez b z resztą:

• znajdź moduły dywidendy i dzielnika;
• dziel modulo;
• Napisz odwrotność podany numer i odejmij 1;
• użyj wzoru na resztę d = a - b c.

Rozważmy przykład rozwiązania, w którym zastosowano ten algorytm.

Przykład 6

Znajdź niepełny iloraz i resztę z dzielenia - 17 na 5.

Rozwiązanie

Podziel podane liczby modulo. Otrzymujemy to, dzieląc iloraz wynosi 3, a reszta to 2. Ponieważ mamy 3, odwrotnie jest 3. Musisz odjąć 1.

− 3 − 1 = − 4 .

Otrzymujemy pożądaną wartość równą - 4.

Aby obliczyć resztę, potrzebujesz a = - 17, b = 5, c = - 4, następnie d = a - b c = - 17 - 5 (- 4) = - 17 - (- 20) = - 17 + 20 = 3.

Oznacza to, że niepełny iloraz dzielenia to liczba - 4 z resztą równą 3.

Odpowiedź:(- 17): 5 = - 4 (odpoczynek 3).

Przykład 7

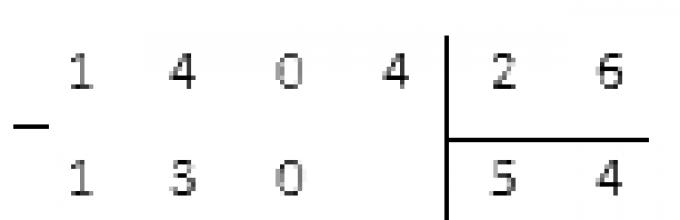
Podziel ujemną liczbę całkowitą 1404 przez dodatnią 26.

Rozwiązanie

Konieczne jest dokonanie podziału według kolumny i muła.

Otrzymaliśmy podział na wartości bezwzględne liczb bez reszty. Oznacza to, że dzielenie odbywa się bez reszty, a pożądany iloraz = - 54.

Odpowiedź: (− 1 404) : 26 = − 54 .

Reguła dzielenia z resztą ujemnych liczb całkowitych, przykłady

Konieczne jest sformułowanie reguły dzielenia z resztą liczb całkowitych liczby ujemne.

Definicja 3

Aby otrzymać niepełny iloraz c z dzielenia ujemnej liczby całkowitej a przez liczbę całkowitą ujemną b, należy wykonać obliczenia modulo, następnie dodać 1, wtedy możemy wykonać obliczenia ze wzoru d = a - b · c.

Wynika z tego, że niepełny iloraz z dzielenia liczb całkowitych ujemnych będzie liczbą dodatnią.

Sformułujmy tę zasadę w postaci algorytmu:

• znajdź moduły dywidendy i dzielnika;
• podziel moduł podzielnej przez moduł dzielnika, aby uzyskać niepełny iloraz z
• pozostała część;
• dodanie 1 do niepełnego ilorazu;
• obliczenie reszty na podstawie wzoru d = a - b · c.

Rozważmy ten algorytm na przykładzie.

Przykład 8

Znajdź niepełny iloraz i resztę podczas dzielenia - 17 przez - 5.

Rozwiązanie

Dla poprawności rozwiązania zastosujemy algorytm dzielenia z resztą. Najpierw podziel liczby modulo. Z tego otrzymujemy, że niepełny iloraz = 3, a reszta to 2. Zgodnie z regułą należy dodać niepełny iloraz i 1. Otrzymujemy, że 3 + 1 = 4. Stąd otrzymujemy, że niepełny iloraz z dzielenia danych liczb wynosi 4.

Aby obliczyć resztę, użyjemy wzoru. Hipotetycznie mamy, że a = - 17, b = - 5, c = 4, a następnie, korzystając ze wzoru, otrzymujemy d = a - b c = - 17 - (- 5) 4 = - 17 - (- 20) = - 17 + 20 = 3. Pożądana odpowiedź, czyli reszta, to 3, a niepełny iloraz to 4.

Odpowiedź:(- 17): (- 5) = 4 (odpoczynek 3).

Sprawdzanie wyniku dzielenia liczb całkowitych przez resztę

Po wykonaniu dzielenia liczb z resztą należy wykonać sprawdzenie. Ta kontrola obejmuje 2 etapy. Najpierw reszta d jest sprawdzana pod kątem nieujemności, warunek 0 ≤ d< b . При их выполнении разрешено выполнять 2 этап. Если 1 этап не выполнился, значит вычисления произведены с ошибками. Второй этап состоит из того, что равенство a = b · c + d должно быть верным. Иначе в вычисления имеется ошибка.

Rzućmy okiem na kilka przykładów.

Przykład 9

Dokonano podziału - 521 na - 12. Iloraz 44, reszta to 7. Sprawdzać.

Rozwiązanie

Ponieważ reszta jest liczbą dodatnią, jej wartość jest mniejsza niż moduł dzielnika. Dzielnik wynosi - 12, co oznacza, że ​​jego moduł wynosi 12. Możesz przejść do następnego punktu kontrolnego.

Hipotetycznie mamy, że a = - 521, b = - 12, c = 44, d = 7. Stąd obliczamy b c + d, gdzie b c + d = - 12 44 + 7 = - 528 + 7 = - 521. Stąd wynika, że ​​równość jest prawdziwa. Weryfikacja przeszła.

Przykład 10

Sprawdź podział (- 17): 5 = - 3 (reszta - 2). Czy równość jest prawdziwa?

Rozwiązanie

Punktem pierwszego etapu jest to, że konieczne jest sprawdzenie dzielenia liczb całkowitych z resztą. Z tego widać, że akcja została wykonana niepoprawnie, ponieważ podana jest reszta równa -2. Reszta nie jest ujemna.

Mamy, że drugi warunek jest spełniony, ale w tym przypadku niewystarczający.

Odpowiedź: nie.

Przykład 11

Liczba - 19 podzielona przez - 3. Niepełny iloraz to 7, a reszta to 1. Sprawdź, czy obliczenia są poprawne.

Rozwiązanie

Podana jest reszta z 1. Jest pozytywny. Wartość jest mniejsza niż moduł dzielnika, co oznacza, że ​​wykonywany jest pierwszy etap. Przejdźmy do drugiego etapu.

Obliczmy wartość wyrażenia b c + d. Hipotetycznie mamy, że b = - 3, c = 7, d = 1, stąd podstawiając wartości liczbowe, otrzymujemy b c + d = - 3 7 + 1 = - 21 + 1 = - 20. Wynika z tego, że a = b c + d równość nie jest zachowana, ponieważ warunek daje a = - 19.

Z tego wynika, że ​​podział został dokonany błędnie.

Odpowiedź: nie.

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl + Enter

Przeczytaj temat lekcji: „Podział z resztą”. Co już wiesz na ten temat?

Czy można równomiernie podzielić 8 śliwek na dwa talerze (rys. 1)?

Ryż. 1. Ilustracja na przykład

Do każdego talerza można włożyć 4 śliwki (rys. 2).

Ryż. 2. Ilustracja na przykład

Czynność, którą wykonaliśmy, można zapisać w ten sposób.

8: 2 = 4

Czy uważasz, że można równo podzielić 8 śliwek na 3 talerze (rys. 3)?

Ryż. 3. Ilustracja na przykład

Będziemy się tak zachowywać. Najpierw na każdy talerz włóż jedną śliwkę, a następnie drugą śliwkę. Pozostaną nam 2 śliwki, ale 3 talerze. Oznacza to, że nie możemy dalej równo dzielić. Do każdego talerza wkładamy 2 śliwki, zostają nam 2 śliwki (rys. 4).

Ryż. 4. Ilustracja na przykład

Kontynuujmy naszą obserwację.

Przeczytaj liczby. Wśród tych liczb znajdź te, które są podzielne przez 3.

11, 12, 13, 14, 15, 16, 17, 18, 19

Sprawdź się.

Pozostałe liczby (11, 13, 14, 16, 17, 19) nie są podzielne przez 3 lub mówią „Podziel się z resztą”.

Znajdźmy wartość ilorazu.

Dowiedz się, ile razy 3 zawiera się w liczbie 17 (ryc. 5).

Ryż. 5. Ilustracja na przykład

Widzimy, że 3 owale pasują 5 razy, a 2 owale pozostają.

Wykonaną czynność można zarejestrować w następujący sposób.

17: 3 = 5 (odpoczynek 2)

Możesz także pisać w kolumnie (ryc. 6)

Ryż. 6. Ilustracja na przykład

Rozważ rysunki. Wyjaśnij podpisy pod tymi rysunkami (rys. 7).

Ryż. 7. Ilustracja na przykład

Rozważ pierwszy rysunek (ryc. 8).

Ryż. 8. Ilustracja na przykład

Widzimy, że 15 owali podzielono przez 2, 2 powtórzono 7 razy, w pozostałych - 1 owal.

Rozważ drugą figurę (ryc. 9).

Ryż. 9. Ilustracja na przykład

Na tej figurze 15 kwadratów podzielono na 4,4 powtórzono 3 razy, w pozostałych - 3 kwadraty.

Rozważ trzecią figurę (ryc. 10).

Ryż. 10. Ilustracja na przykład

Można powiedzieć, że 15 owali podzielono na 3. Każdy z 3 powtórzono 5 razy po równo. W takich przypadkach mówi się, że reszta wynosi 0.

Zróbmy podział.

Podziel siedem kwadratów przez trzy. Dostajemy dwie grupy, a jeden kwadrat pozostanie. Zapiszmy rozwiązanie (rys. 11).

Ryż. 11. Ilustracja na przykład

Zróbmy podział.

Dowiedz się, ile razy cztery są zawarte w liczbie 10. Widzimy, że liczba 10 zawiera cztery dwa razy i pozostały 2 kwadraty. Zapiszmy rozwiązanie (rys. 12).

Ryż. 12. Ilustracja na przykład

Zróbmy podział.

Dowiedz się, ile razy dwa zawiera się w liczbie 11. Widzimy, że liczba 11 zawiera dwa na dwa 5 razy i pozostaje 1 kwadrat. Zapiszmy rozwiązanie (rys. 13).

Ryż. 13. Ilustracja na przykład

Zróbmy wniosek. Dzielenie przez resztę oznacza sprawdzenie, ile razy dzielnik jest zawarty w dzielnej i ile jednostek pozostało.

Dzielenie z resztą można również wykonać na promieniu numerycznym.

Na promieniu numerycznym zaznacz segmenty 3 podziałów i zobacz, że były trzy podziały trzy razy i jeden podział pozostał (ryc. 14).

Ryż. 14. Ilustracja na przykład

Zapiszmy rozwiązanie.

10: 3 = 3 (odpoczynek 1)

Zróbmy podział.

Na promieniu numerycznym zaznacz segmenty 3 podziałów i zobacz, że były trzy podziały trzy razy i pozostały dwa podziały (ryc. 15).

Ryż. 15. Ilustracja na przykład

Zapiszmy rozwiązanie.

11: 3 = 3 (odpoczynek 2)

Zróbmy podział.

Na promieniu numerycznym zaznacz segmenty 3 podziałów i zobacz, że otrzymaliśmy dokładnie 4 razy, reszta jest nieobecna (ryc. 16).

Ryż. 16. Ilustracja na przykład

Zapiszmy rozwiązanie.

12: 3 = 4

Dzisiaj na lekcji zapoznaliśmy się z dzieleniem z resztą, nauczyliśmy się wykonywać nazwaną akcję za pomocą obrazka i promienia liczbowego oraz przećwiczyliśmy rozwiązywanie przykładów na temat lekcji.

Bibliografia

1. MI. Moreau, mgr Bantova i inni Matematyka: Podręcznik. Ocena 3: w 2 częściach, część 1. - M .: "Edukacja", 2012.
2. MI. Moreau, mgr Bantova i inni Matematyka: Podręcznik. Ocena 3: w 2 częściach, część 2. - M .: „Edukacja”, 2012.
3. MI. Moreau. Lekcje matematyki: Wytyczne dla nauczyciela. Ocena 3. - M .: Edukacja, 2012.
4. Normatywny dokument prawny. Monitorowanie i ocena efektów uczenia się. - M .: „Edukacja”, 2011.
5. "Szkoła Rosji": Programy dla Szkoła Podstawowa... - M .: „Edukacja”, 2011.
6. SI. Wołkowa. Matematyka: Prace weryfikacyjne... Ocena 3. - M .: Edukacja, 2012.
7. V.N. Rudnickiej. Testy. - M .: „Egzamin”, 2012.

1. Nsportal.ru ().
2. Prosv.ru ().
3. Do.gendocs.ru ().

Zadanie domowe

1. Zapisz liczby podzielne przez 2 bez reszty.

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19

2. Dokonaj dzielenia z resztą używając obrazka.

3. Wykonaj dzielenie z resztą za pomocą belki liczbowej.

4. Zrób zadanie swoim kolegom z klasy na temat lekcji.

Dzielenie liczb wielocyfrowych jest najłatwiejsze w przypadku kolumny. Podział według kolumny jest również nazywany dzielenie według rogu.

Zanim zaczniesz wykonywać dzielenie długie, zastanów się szczegółowo nad samą formą zapisywania dzielenia długiego. Najpierw napisz dywidendę i umieść pionową kreskę po jej prawej stronie:

Za pionową linią, naprzeciwko dywidendy, napisz dzielnik i narysuj pod nim poziomą linię:

Poniżej poziomej linii iloraz wynikający z obliczeń będzie zapisywany etapami:

Pod dywidendą zostaną zapisane obliczenia pośrednie:

Cała forma pisania podziału kolumn wygląda następująco:

Jak podzielić przez kolumnę

Powiedzmy, że musimy podzielić 780 przez 12, zapisać akcję w kolumnie i przejść do dzielenia:

Podział długi wykonywany jest etapami. Pierwszą rzeczą, którą musimy zrobić, to określić niepełną dywidendę. Patrzymy na pierwszą cyfrę dywidendy:

ta liczba to 7, ponieważ jest mniejsza od dzielnika, to nie możemy od niej zacząć dzielenia, co oznacza, że ​​musimy wziąć jeszcze jedną cyfrę z dzielnej, liczba 78 jest większa od dzielnika, więc od niej zaczynamy dzielenie:

W naszym przypadku liczba 78 będzie niekompletna podzielna, jest nazywany niekompletnym, ponieważ jest tylko częścią dywidendy.

Po ustaleniu niepełnej dywidendy możemy dowiedzieć się, ile cyfr będzie w ilorazie, w tym celu musimy obliczyć, ile cyfr pozostało w dywidendzie po niepełnej dywidendzie, w naszym przypadku jest tylko jedna cyfra - 0, która oznacza, że ​​iloraz będzie składał się z 2 cyfr.

Po poznaniu liczby cyfr, które powinny znaleźć się w ilorazu, możesz wstawić kropki w jego miejsce. Jeśli pod koniec dzielenia liczba cyfr okazała się większa lub mniejsza niż wskazane punkty, gdzieś popełniono błąd:

Zacznijmy dzielić. Musimy określić, ile razy 12 jest zawarte w 78. Aby to zrobić, kolejno mnożymy dzielnik przez liczby naturalne 1, 2, 3, ... aż otrzymamy liczbę, która jest jak najbardziej zbliżona do niepełnej dzielnej lub równa jej, ale jej nie przekracza. W ten sposób otrzymujemy liczbę 6, zapisujemy ją pod dzielnikiem, a od 78 (zgodnie z zasadami odejmowania kolumnowego) odejmujemy 72 (12 6 = 72). Po odjęciu 72 od 78 otrzymujemy resztę z 6:

Zauważ, że pozostała część dzielenia mówi nam, czy wybraliśmy poprawną liczbę. Jeśli reszta jest równa lub większa od dzielnika, to wybraliśmy niewłaściwą liczbę i musimy wziąć większą liczbę.

Do powstałej reszty - 6, burzymy kolejną cyfrę dywidendy - 0. W rezultacie otrzymujemy niepełną dywidendę - 60. Określ, ile razy 12 jest zawarte w liczbie 60. Otrzymujemy liczbę 5, napisz ją w ilorazu po liczbie 6 i odejmij 60 od 60 ( 12 5 = 60). Reszta to zero:

Ponieważ w dywidendzie nie ma już więcej cyfr, oznacza to, że 780 zostało całkowicie podzielone przez 12. W wyniku dzielenia długiego znaleźliśmy iloraz - jest on napisany pod dzielnikiem:

Rozważmy przykład, gdy iloraz wynosi zera. Powiedzmy, że musimy podzielić 9027 przez 9.

Określ niepełną dywidendę - jest to liczba 9. Wpisz iloraz 1 i odejmij 9. Reszta wynosi zero. Zwykle, jeśli w obliczeniach pośrednich reszta okazuje się równa zero, nie jest to zapisywane:

Niszczymy kolejną cyfrę dywidendy - 0. Pamiętaj, że dzieląc zero przez dowolną liczbę, będzie zero. Piszemy w ilorazie zero (0: 9 = 0) a w obliczeniach pośrednich odejmujemy 0. Zwykle, aby nie przeciążać obliczeń pośrednich, obliczenia z zerem nie zapisujemy:

Niszczymy kolejną cyfrę dywidendy - 2. W obliczeniach pośrednich okazało się, że niepełna dywidenda (2) jest mniejsza niż dzielnik (9). W tym przypadku do ilorazu wpisywane jest zero i usuwana jest kolejna cyfra dywidendy:

Określ, ile razy 9 zawiera się w liczbie 27. Otrzymujemy liczbę 3, zapisujemy ją w ilorazie i odejmujemy 27 od 27. Reszta wynosi zero:

Ponieważ w dywidendzie nie ma już więcej cyfr, oznacza to, że liczba 9027 została całkowicie podzielona przez 9:

Rozważmy przykład, w którym dywidenda jest zakończona zerem. Powiedzmy, że musimy podzielić 3000 przez 6.

Określ niepełną dywidendę - to jest liczba 30. Piszemy w ilorazu 5 i odejmujemy 30 od 30. Reszta to zero. Jak już wspomniano, w obliczeniach pośrednich nie trzeba wpisywać reszty zera:

Niszczymy kolejną cyfrę dywidendy - 0. Ponieważ przy dzieleniu zera przez dowolną liczbę będzie zero, zapisujemy to do ilorazu zera i w obliczeniach pośrednich odejmujemy 0 od 0:

Niszczymy kolejną cyfrę dywidendy - 0. Do ilorazu zapisujemy kolejne zero, a w obliczeniach pośrednich odejmujemy 0. Ponieważ w obliczeniach pośrednich zwykle nie zapisuje się obliczenia z zerem, rekord można skrócić, pozostawiając tylko reszta - 0. Zero w reszcie na samym końcu obliczenia jest zwykle zapisywane w celu pokazania, że ​​dzielenie jest wykonywane w całości:

Ponieważ w dywidendzie nie ma już więcej cyfr, oznacza to, że 3000 jest dzielone przez 6 całkowicie:

Podział kolumny z resztą

Powiedzmy, że musimy podzielić 1340 przez 23.

Określ niepełną dywidendę - to jest liczba 134. Piszemy w ilorazu 5 i odejmujemy 115 od 134. Reszta to 19:

Niszczymy następną cyfrę dywidendy - 0. Określamy, ile razy 23 jest zawarte w liczbie 190. Otrzymujemy liczbę 8, zapisujemy ją w ilorazie i odejmujemy 184 od 190. Otrzymujemy resztę 6:

Ponieważ w dywidendzie nie ma już więcej cyfr, podział się skończył. Wynikiem jest niepełny iloraz 58, a reszta 6:

1340: 23 = 58 (pozostałe 6)

Pozostaje rozważyć przykład dzielenia przez resztę, gdy dywidenda jest mniejsza niż dzielnik. Załóżmy, że musimy podzielić 3 przez 10. Widzimy, że 10 nigdy nie jest zawarte w liczbie 3, więc zapisujemy 0 do ilorazu i odejmujemy 0 od 3 (10 · 0 = 0). Rysujemy poziomą linię i zapisujemy resztę - 3:

3: 10 = 0 (pozostałe 3)

Kalkulator dzielenia długiego

Ten kalkulator pomoże Ci wykonać długie dzielenie. Wystarczy wpisać dywidendę i dzielnik i kliknąć przycisk Oblicz.

Co robi klasa 3 z matematyki? Podział z resztą, przykłady i problemy - tego uczymy na lekcjach. W artykule zostanie omówiony podział z resztą oraz algorytm do takich obliczeń.

Osobliwości

Rozważ tematy zawarte w programie, który jest badany do klasy 3. Dzielenie z resztą jest wyróżnione w specjalnej sekcji matematyki. O czym to jest? Jeśli dywidenda nie jest podzielna równomiernie przez dzielnik, reszta pozostaje. Na przykład podziel 21 przez 6. Okazuje się, że 3, ale reszta to 3.

W przypadkach, gdy podczas dzielenia liczb naturalnych reszta wynosi zero, mówią, że dzielenie zostało całkowicie. Na przykład, jeśli 25 ma być podzielone przez 5, wynikiem jest 5. Reszta to zero.

Przykłady rozwiązań

W celu wykonania dzielenia z resztą używany jest określony rekord.

Oto przykłady z matematyki (klasa 3). Dzielenie długie z resztą można pominąć. Wystarczy wpisać w wierszu: 13:4 = 3 (reszta 1) lub 17:5 = 3 (reszta 2).

Przyjrzyjmy się wszystkim bliżej. Na przykład podzielenie 17 przez trzy daje liczbę całkowitą pięć, a resztę dwa. Jaka jest kolejność rozwiązywania takiego przykładu dla dzielenia z resztą? Najpierw musisz znaleźć maksymalną liczbę do 17, którą można podzielić przez trzy bez reszty. Największy będzie 15.

Dalej, 15 dzieli się przez liczbę trzy, wynikiem działania będzie liczba pięć. Teraz odejmujemy znalezioną liczbę od dywidendy, czyli odejmujemy 15 od 17, otrzymujemy dwa. Obowiązkowym działaniem jest pogodzenie dzielnika i reszty. Po weryfikacji należy odnotować reakcję podjętego działania. 17: 3 = 15 (pozostałe 2).

Jeśli reszta jest większa niż dzielnik, czynność została wykonana niepoprawnie. To według tego algorytmu 3. klasa dokonuje dzielenia z resztą. Przykłady są najpierw analizowane przez nauczyciela na tablicy, następnie dzieci proszone są o sprawdzenie swojej wiedzy poprzez samodzielną pracę.

Przykład mnożenia

Jednym z najtrudniejszych problemów, z jakimi borykają się klasy 3, jest dzielenie z resztą. Przykłady mogą być trudne, zwłaszcza gdy wymagane są dodatkowe obliczenia kolumnowe.

Powiedzmy, że chcesz podzielić 190 przez 27, aby uzyskać minimalne saldo. Spróbujmy rozwiązać problem za pomocą mnożenia.

Wybierzmy liczbę, która po pomnożeniu da liczbę jak najbardziej zbliżoną do 190. Jeśli pomnożymy 27 przez 6, otrzymamy liczbę 162. Odejmijmy liczbę 162 od 190, a reszta wyniesie 28 Okazało się, że jest większy niż pierwotny dzielnik. Dlatego liczba sześć nie jest odpowiednia dla naszego przykładu jako czynnik. Kontynuujmy rozwiązanie z przykładu, biorąc liczbę 7 do mnożenia.

Mnożąc 27 przez 7 otrzymujemy iloczyn 189. Następnie sprawdzimy poprawność rozwiązania, w tym celu odejmujemy wynik uzyskany od 190, czyli odejmujemy liczbę 189. Reszta będzie 1, czyli wyraźnie mniej niż 27. Dokładnie tak się rozwiązują złożone wyrażenia w szkole (klasa 3, podział z resztą). Przykłady zawsze obejmują nagranie odpowiedzi. Całe wyrażenie matematyczne można sformatować w następujący sposób: 190: 27 = 7 (reszta 1). Podobne obliczenia można wykonać w kolumnie.

W ten sposób klasa 3 dokonuje dzielenia z resztą. Podane powyżej przykłady pomogą Ci zrozumieć algorytm rozwiązywania takich problemów.

Wniosek

Aby dla studentów stopnie podstawowe ukształtowały się prawidłowe umiejętności rachunkowe, nauczyciel podczas lekcji matematyki musi zwracać uwagę na wyjaśnienie algorytmu działań dziecka przy rozwiązywaniu zadań do podziału z resztą.

Według nowego kraju związkowego standardy edukacyjne szczególną uwagę przywiązujemy do indywidualnego podejścia do treningu. Nauczyciel powinien dobierać zadania dla każdego dziecka, biorąc pod uwagę jego indywidualne możliwości. Na każdym etapie nauczania zasad podziału z resztą nauczyciel musi przeprowadzić kontrolę pośrednią. Pozwala mu zidentyfikować główne problemy, które pojawiają się przy przyswajaniu materiału dla każdego ucznia, terminowo poprawną wiedzę i umiejętności, eliminować pojawiające się problemy i uzyskać pożądany rezultat.