Równanie drgań harmonicznych
Równanie oscylacji harmonicznych ustala zależność współrzędnych ciała od czasu


Wykres cosinus w chwili początkowej ma wartość maksymalną, a wykres sinus ma w chwili początkowej wartość zerową. Jeśli zaczniemy badać oscylację od położenia równowagi, wówczas oscylacja będzie powtarzać sinusoidę. Jeżeli zaczniemy rozważać oscylację od położenia maksymalnego odchylenia, to oscylację opiszemy cosinusem. Lub takie oscylacje można opisać wzorem sinusoidalnym z fazą początkową.
Zmiana prędkości i przyspieszenia podczas oscylacji harmonicznych
Nie tylko współrzędna ciała zmienia się w czasie zgodnie z prawem sinusa lub cosinusa. Ale wielkości takie jak siła, prędkość i przyspieszenie również zmieniają się w podobny sposób. Siła i przyspieszenie są maksymalne, gdy ciało oscylacyjne znajduje się w skrajnych położeniach, w których przemieszczenie jest maksymalne, i wynoszą zero, gdy ciało przechodzi przez położenie równowagi. Natomiast prędkość w skrajnych położeniach wynosi zero, a gdy ciało przechodzi przez położenie równowagi, osiąga wartość maksymalną.
Jeśli oscylację opisuje prawo cosinusa


Jeżeli oscylację opisujemy zgodnie z prawem sinusoidalnym


Maksymalne wartości prędkości i przyspieszenia
Analizując równania zależności v(t) i a(t) możemy się domyślić, że maksymalne wartości prędkości i przyspieszenia przyjmują przypadek, gdy współczynnik trygonometryczny równe 1 lub -1. Określone przez formułę
§ 6. WIBRACJE MECHANICZNEPodstawowe formuły
Równanie harmoniczne
Gdzie X - przesunięcie punktu oscylacyjnego z położenia równowagi; T- czas; A,ω, φ - odpowiednio amplituda, częstotliwość kątowa, początkowa faza oscylacji; - faza oscylacji w danej chwili T.
Częstotliwość kątowa
gdzie ν i T są częstotliwością i okresem oscylacji.
Prędkość punktu wykonującego oscylacje harmoniczne wynosi
Przyspieszenie podczas oscylacji harmonicznych
Amplituda A wynikowe oscylacje uzyskane przez dodanie dwóch oscylacji o tych samych częstotliwościach, występujących wzdłuż jednej prostej, określa się ze wzoru
Gdzie A 1 I A 2 - amplitudy składowych drgań; φ 1 i φ 2 to ich fazy początkowe.
Fazę początkową φ wynikowych oscylacji można znaleźć ze wzoru
![]()
Częstotliwość uderzeń powstająca podczas dodawania dwóch oscylacji występujących wzdłuż jednej linii prostej o różnych, ale podobnych częstotliwościach ν 1 i ν 2,
![]()
Równanie trajektorii punktu uczestniczącego w dwóch wzajemnie prostopadłych oscylacjach o amplitudach A 1 i A 2 oraz fazach początkowych φ 1 i φ 2,
Jeżeli początkowe fazy φ 1 i φ 2 składowych drgań są takie same, to równanie trajektorii przyjmuje postać
oznacza to, że punkt porusza się po linii prostej.
W przypadku, gdy różnica faz wynosi , równanie przyjmuje postać
![]()
oznacza to, że punkt porusza się po elipsie.
Równanie różniczkowe drgań harmonicznych punktu materialnego
![]() , Lub
, Lub ![]() ,gdzie m jest masą punktu; k-
współczynnik siły quasi-sprężystej ( k=Tω 2).
,gdzie m jest masą punktu; k-
współczynnik siły quasi-sprężystej ( k=Tω 2).
Całkowita energia punktu materialnego wykonującego oscylacje harmoniczne wynosi
Okres drgań ciała zawieszonego na sprężynie (wahadło sprężyste)
![]()
Gdzie M- masa ciała; k- sztywność sprężyny. Wzór obowiązuje dla drgań sprężystych w granicach, w których spełnione jest prawo Hooke'a (przy małej masie sprężyny w porównaniu z masą ciała).
Okres drgań wahadła matematycznego
![]()
Gdzie l- długość wahadła; G- przyśpieszenie grawitacyjne. Okres drgań wahadła fizycznego
Gdzie J- moment bezwładności ciała oscylującego względem osi
wahanie; A- odległość środka masy wahadła od osi drgań;
Zmniejszona długość wahadła fizycznego.
Podane wzory są dokładne dla przypadku nieskończenie małych amplitud. W przypadku skończonych amplitud wzory te dają jedynie przybliżone wyniki. Przy amplitudach nie większych niż błąd wartości okresu nie przekracza 1%.
Okres drgań skrętnych ciała zawieszonego na elastycznej nici wynosi
![]()
Gdzie J- moment bezwładności korpusu względem osi pokrywającej się z nicią sprężystą; k- elastyczna sztywność nici, równy stosunkowi moment sprężysty powstający przy skręceniu nici do kąta, pod jakim nić jest skręcona.
Równanie różniczkowe drgań tłumionych ![]() , Lub ,
, Lub ,
Gdzie R- współczynnik oporu; δ - współczynnik tłumienia: ;ω 0 - naturalna częstotliwość kątowa drgań *
![]()
Równanie tłumionych oscylacji
Gdzie Na)- amplituda tłumionych oscylacji w danej chwili T;ω jest ich częstotliwością kątową.
Częstotliwość kątowa drgań tłumionych
![]()
О Zależność amplitudy drgań tłumionych od czasu
![]() I
I
Gdzie A 0 - amplituda oscylacji w danej chwili T=0.
Logarytmiczny dekrement oscylacji
![]()
Gdzie Na) I A(t+T)- amplitudy dwóch kolejnych oscylacji oddzielonych w czasie okresem.
Równanie różniczkowe drgań wymuszonych
gdzie jest zewnętrzną siłą okresową działającą na oscylujący punkt materialny i powodującą wymuszone oscylacje; F 0 - jego wartość amplitudy;
Amplituda drgań wymuszonych
Częstotliwość rezonansowa i amplituda rezonansowa ![]() I
I
Przykłady rozwiązywania problemów
Przykład 1. Punkt oscyluje zgodnie z prawem x(t)=![]() ,
Gdzie A=2 patrz Określ fazę początkową φ jeśli
,
Gdzie A=2 patrz Określ fazę początkową φ jeśli
X(0)=cm i X , (0)<0. Построить векторную диаграмму для мо- мента T=0.
Rozwiązanie. Skorzystajmy z równania ruchu i wyraźmy przemieszczenie w tej chwili T=0 przez fazę początkową:
![]()
Stąd znajdujemy fazę początkową:
![]()
* We wcześniej podanych wzorach na drgania harmoniczne tę samą wielkość oznaczono po prostu ω (bez indeksu 0).
Podstawmy podane wartości do tego wyrażenia X(0) i A:φ=
= ![]() . Wartość argumentu spełniają dwie wartości kąta:
. Wartość argumentu spełniają dwie wartości kąta:
Aby zdecydować, która z tych wartości kąta φ również spełnia warunek, najpierw znajdujemy:
Podstawienie wartości do tego wyrażenia T=0 i naprzemiennie wartości faz początkowych i znajdujemy
T  jak zawsze A>0 i ω>0, wówczas warunek spełnia tylko pierwsza wartość fazy początkowej. Zatem pożądana faza początkowa
jak zawsze A>0 i ω>0, wówczas warunek spełnia tylko pierwsza wartość fazy początkowej. Zatem pożądana faza początkowa
Korzystając ze znalezionej wartości φ, konstruujemy diagram wektorowy (ryc. 6.1). Przykład 2. Punkt materialny z masą T=5 g wykonuje oscylacje harmoniczne z częstotliwością ν =0,5 Hz. Amplituda oscylacji A=3 cm Wyznacz: 1) prędkość υ wskazuje na moment przemieszczenia x== 1,5 cm; 2) maksymalną siłę F max działającą na punkt; 3) Ryc. 6.1 całkowita energia mi punkt oscylacyjny.
i wzór na prędkość otrzymujemy biorąc pierwszą pochodną przemieszczenia po czasie:
Aby wyrazić prędkość poprzez przemieszczenie, należy wykluczyć czas ze wzorów (1) i (2). Aby to zrobić, podnosimy oba równania i dzielimy pierwsze przez A 2 , drugi na A 2 ω 2 i dodaj:
![]() , Lub
, Lub ![]()
Po rozwiązaniu ostatniego równania dla υ , znajdziemy
Po wykonaniu obliczeń przy użyciu tego wzoru otrzymujemy
Znak plus odpowiada przypadkowi, gdy kierunek prędkości pokrywa się z dodatnim kierunkiem osi X, znak minus - gdy kierunek prędkości pokrywa się z ujemnym kierunkiem osi X.
Przemieszczenie podczas oscylacji harmonicznych, oprócz równania (1), można również wyznaczyć za pomocą równania
Powtarzając to samo rozwiązanie z tym równaniem, otrzymujemy tę samą odpowiedź.
2. Siłę działającą na punkt wyznaczamy, korzystając z drugiego prawa Newtona:
Gdzie A - przyspieszenie punktu, które uzyskujemy biorąc pochodną prędkości od czasu:
Podstawiając wyrażenie przyspieszenia do wzoru (3), otrzymujemy
Stąd maksymalna wartość siły
![]()
Podstawiając wartości π, ν do tego równania, T I A, znajdziemy
![]()
3. Całkowita energia punktu drgającego jest sumą energii kinetycznej i potencjalnej obliczonej dla dowolnej chwili.
Energię całkowitą najłatwiej obliczyć w momencie, gdy energia kinetyczna osiąga wartość maksymalną. W tym momencie energia potencjalna wynosi zero. Zatem całkowita energia mi punkt oscylacji jest równy maksymalnej energii kinetycznej
Prędkość maksymalną wyznaczamy ze wzoru (2), wstawiając: ![]() . Podstawiając wyrażenie prędkości do wzoru (4), znajdujemy
. Podstawiając wyrażenie prędkości do wzoru (4), znajdujemy
![]()
Podstawiając wartości wielkości do tego wzoru i wykonując obliczenia, otrzymujemy
lub µJ.
Przykład 3. Na końcach cienki pręt l= 1 m i masa M 3 = 400 g wzmocnionych kuleczek z masami M 1 = 200 g I M 2 = 300g. Pręt oscyluje wokół osi poziomej, prostopadłej
prostopadle do pręta i przechodząc przez jego środek (punkt O na ryc. 6.2). Zdefiniuj okres T drgania wywoływane przez pręt.
Rozwiązanie. Okres oscylacji wahadła fizycznego, takiego jak pręt z kulkami, jest określony przez zależność
Gdzie J- T - jego masa; l Z - odległość środka masy wahadła od osi.
Moment bezwładności tego wahadła jest równy sumie momentów bezwładności kulek J 1 i J 2 i pręt J 3:
Zabieranie piłek punkty materialne, wyrazimy ich momenty bezwładności:
Ponieważ oś przechodzi przez środek pręta, jego moment bezwładności względem tej osi J 3 = =. Podstawianie otrzymanych wyrażeń J 1 , J 2 I J 3 do wzoru (2) wyznaczamy całkowity moment bezwładności wahadła fizycznego:
Po przeprowadzeniu obliczeń przy użyciu tego wzoru znajdujemy
Ryż. 6.2 Masa wahadła składa się z mas kulek i masy pręta:
Dystans l Z Środek masy wahadła od osi oscylacji znajdziemy w oparciu o następujące rozważania. Jeżeli oś X kieruj się wzdłuż pręta i zrównaj początek współrzędnych z punktem O, następnie wymaganą odległość l równa współrzędnej środka masy wahadła, tj.
Zastępowanie wartości ilości M 1 , M 2 , M, l i po wykonaniu obliczeń znajdujemy
Po wykonaniu obliczeń ze wzoru (1) otrzymujemy okres drgań wahadła fizycznego:
Przykład 4. Wahadło fizyczne to pręt o określonej długości l= 1 m i masa 3 T 1 Z przymocowany do jednego z końców obręczą o średnicy i masie T 1 . Pozioma oś Oz
wahadło przechodzi przez środek pręta prostopadle do niego (ryc. 6.3). Zdefiniuj okres T drgania takiego wahadła.
Rozwiązanie. Okres drgań wahadła fizycznego określa się ze wzoru
![]() (1)
(1)

Gdzie J- moment bezwładności wahadła względem osi drgań; T - jego masa; l C - odległość od środka masy wahadła do osi drgań.
Moment bezwładności wahadła jest równy sumie momentów bezwładności pręta J 1 i obręcz J 2:
![]() (2).
(2).
Moment bezwładności pręta względem osi prostopadłej do pręta i przechodzącej przez jego środek masy określa wzór ![]() . W tym przypadku t= 3T 1 i
. W tym przypadku t= 3T 1 i
![]()
Moment bezwładności obręczy wyznaczamy korzystając z twierdzenia Steinera ![]() ,Gdzie J-
moment bezwładności względem dowolnej osi; J 0
-
moment bezwładności względem osi przechodzącej przez środek masy równoległej do danej osi; A - odległość pomiędzy wskazanymi osiami. Stosując tę formułę do obręczy, otrzymujemy
,Gdzie J-
moment bezwładności względem dowolnej osi; J 0
-
moment bezwładności względem osi przechodzącej przez środek masy równoległej do danej osi; A - odległość pomiędzy wskazanymi osiami. Stosując tę formułę do obręczy, otrzymujemy
Zastępowanie wyrażeń J 1 i J 2 do wzoru (2) wyznaczamy moment bezwładności wahadła względem osi obrotu:
Dystans l Z od osi wahadła do środka masy jest równa
Podstawianie wyrażeń do wzoru (1) J, l s i masę wahadła wyznaczamy okres jego oscylacji:
Po obliczeniu za pomocą tego wzoru otrzymamy T=2,17 s.
Przykład 5. Dodaje się dwie oscylacje w tym samym kierunku, wyrażone równaniami; X 2 = =, gdzie A 1 = 1 cm, A 2 =2 cm, s, s, ω = =. 1. Wyznacz fazy początkowe φ 1 i φ 2 elementów oscylatora
Baniya. 2. Znajdź amplitudę A oraz początkowa faza φ powstałej oscylacji. Zapisz równanie powstałych drgań.
Rozwiązanie. 1. Równanie drgań harmonicznych ma postać
Przekształćmy równania podane w opisie problemu do tej samej postaci:

Z porównania wyrażeń (2) z równością (1) znajdujemy początkowe fazy pierwszej i drugiej oscylacji:
Cieszę się i ![]() zadowolony.
zadowolony.
2. Aby określić amplitudę A powstałych oscylacji, wygodnie jest skorzystać ze schematu wektorowego przedstawionego w Ryż. 6.4. Zgodnie z twierdzeniem cosinusa otrzymujemy
gdzie jest różnica fazowa składowych oscylacji.Od ![]() , następnie zastępując znalezione wartości φ 2 i φ 1 otrzymujemy rad.
, następnie zastępując znalezione wartości φ 2 i φ 1 otrzymujemy rad.
Zastąpmy wartości A 1 , A 2 i do wzoru (3) i wykonaj obliczenia:
A= 2,65cm.
Wyznaczmy tangens fazy początkowej φ powstałego drgania bezpośrednio z rys. 6.4: ![]() ,skąd bierze się faza początkowa?
,skąd bierze się faza początkowa?
![]()
Oscylacje nazywane są ruchami lub procesami, które charakteryzują się pewną powtarzalnością w czasie. Procesy oscylacyjne są szeroko rozpowszechnione w przyrodzie i technologii, na przykład naprzemienne wahanie wahadła zegara Elektryczność itd. Kiedy wahadło oscyluje, w tym przypadku zmienia się współrzędna jego środka masy prąd przemienny napięcie i prąd w obwodzie ulegają wahaniom. Natura fizyczna wibracje mogą być różne, dlatego występują wibracje mechaniczne, elektromagnetyczne itp. Jednak różne procesy oscylacyjne są opisane tymi samymi cechami i tymi samymi równaniami. Stąd wygoda wspólne podejście do badania wibracji o różnej naturze fizycznej.
Oscylacje nazywane są bezpłatny, jeśli popełniane są wyłącznie pod wpływem siły wewnętrzne działające pomiędzy elementami układu po wyprowadzeniu układu z położenia równowagi siły zewnętrzne i pozostawiona samej sobie. Zawsze darmowe wibracje tłumione oscylacje , ponieważ w rzeczywistych systemach straty energii są nieuniknione. W wyidealizowanym przypadku układu bez strat energii wywoływane są swobodne oscylacje (trwające tak długo, jak jest to pożądane). własny.
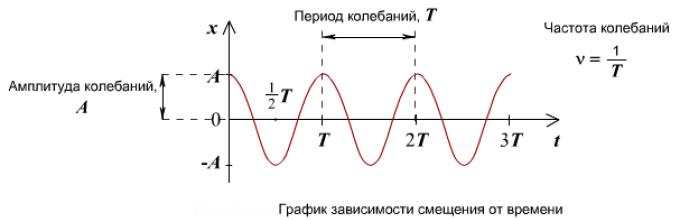
Najprostszym rodzajem swobodnych, nietłumionych oscylacji są drgania harmoniczne - oscylacje, w których wielkość oscylacyjna zmienia się w czasie zgodnie z prawem sinusa (cosinusa). Wibracje występujące w przyrodzie i technologii często mają charakter zbliżony do harmonicznego.
Oscylacje harmoniczne opisuje równanie zwane równaniem oscylacji harmonicznych:
Gdzie A- amplituda oscylacji, maksymalna wartość wielkości oscylacyjnej X; - częstotliwość kołowa (cykliczna) drgań własnych; - początkowa faza oscylacji w chwili czasu T= 0; - faza oscylacji w chwili czasu T. Faza oscylacji określa wartość wielkości oscylacyjnej w ten moment czas. Ponieważ cosinus zmienia się od +1 do -1, zatem X może przyjmować wartości od + A zanim - A.
Czas T podczas którego układ wykonuje jedno pełne oscylowanie, nazywa się okres oscylacji. Podczas T faza oscylacji jest zwiększana o 2 π , tj.
Gdzie . (14.2)
Odwrotność okresu oscylacji
tj. liczba pełnych oscylacji wykonanych w jednostce czasu nazywana jest częstotliwością oscylacji. Porównując (14.2) i (14.3) otrzymujemy
Jednostką częstotliwości jest herc (Hz): 1 Hz to częstotliwość, przy której w ciągu 1 sekundy następuje jedno pełne drganie.
Układy, w których mogą występować drgania swobodne, nazywane są układami oscylatory . Jakie właściwości musi posiadać układ, aby wystąpiły w nim drgania swobodne? Układ mechaniczny muszę mieć stabilna pozycja równowagi, po wyjściu, który się pojawi siła przywracająca skierowana w stronę położenia równowagi. Wiadomo, że ta pozycja odpowiada minimum energia potencjalna systemy. Rozważmy kilka układów oscylacyjnych spełniających wymienione właściwości.
Zmiany dowolnej wielkości opisuje się prawami sinusa lub cosinusa, wówczas takie oscylacje nazywane są harmonicznymi. Rozważmy obwód składający się z kondensatora (który został naładowany przed włączeniem do obwodu) i cewki indukcyjnej (ryc. 1).
Obrazek 1.
Równanie drgań harmonicznych można zapisać w następujący sposób:
$q=q_0cos((\omega)_0t+(\alfa )_0)$ (1)
gdzie $t$ to czas; $q$ opłata, $q_0$-- maksymalne odchylenie ładunku od jego średniej (zerowej) wartości podczas zmian; $(\omega )_0t+(\alpha )_0$- faza oscylacji; $(\alpha )_0$- faza początkowa; $(\omega )_0$ - częstotliwość cykliczna. W tym okresie faza zmienia się o 2 $\pi $.
Równanie postaci:
równanie oscylacji harmonicznych w postaci różniczkowej dla obwodu oscylacyjnego, który nie będzie zawierał czynnego oporu.
Każdy rodzaj oscylacji okresowych można dokładnie przedstawić jako sumę oscylacji harmonicznych, tzw. szereg harmoniczny.
Na okres oscylacji obwodu składającego się z cewki i kondensatora otrzymujemy wzór Thomsona:
Jeśli różniczkujemy wyrażenie (1) ze względu na czas, możemy otrzymać wzór na funkcję $I(t)$:
Napięcie na kondensatorze można znaleźć jako:
Ze wzorów (5) i (6) wynika, że natężenie prądu jest większe od napięcia na kondensatorze o $\frac(\pi )(2).$
Drgania harmoniczne można przedstawić zarówno w postaci równań, funkcji, jak i diagramów wektorowych.
Równanie (1) przedstawia swobodne, nietłumione oscylacje.
Równanie tłumionych oscylacji
Zmiana ładunku ($q$) na płytkach kondensatora w obwodzie, z uwzględnieniem rezystancji (rys. 2), zostanie opisana równaniem różniczkowym w postaci:

Rysunek 2.
Jeżeli rezystancja będąca częścią obwodu $R\
gdzie $\omega =\sqrt(\frac(1)(LC)-\frac(R^2)(4L^2))$ jest częstotliwością oscylacji cyklicznych. $\beta =\frac(R)(2L)-$współczynnik tłumienia. Amplituda tłumionych oscylacji wyraża się wzorem:
Jeśli przy $t=0$ ładunek na kondensatorze jest równy $q=q_0$ i w obwodzie nie ma prądu, to dla $A_0$ możemy napisać:
Faza oscylacji w początkowej chwili czasu ($(\alpha )_0$) jest równa:
Kiedy $R >2\sqrt(\frac(L)(C))$ zmiana ładunku nie jest oscylacją, rozładowanie kondensatora nazywa się aperiodycznym.
Przykład 1
Ćwiczenia: Maksymalna wartość opłaty wynosi $q_0=10\C$. Zmienia się harmonicznie z okresem $T= 5 s$. Określ maksymalny możliwy prąd.
Rozwiązanie:
Jako podstawę do rozwiązania problemu używamy:
Aby znaleźć aktualną siłę, wyrażenie (1.1) należy zróżnicować ze względu na czas:
gdzie maksymalna (wartość amplitudy) natężenia prądu jest wyrażeniem:
Z warunków zadania znamy wartość amplitudy ładunku ($q_0=10\C$). Powinieneś znaleźć naturalną częstotliwość oscylacji. Wyraźmy to jako:
\[(\omega )_0=\frac(2\pi )(T)\lewo(1.4\prawo).\]
W tym przypadku pożądaną wartość można znaleźć za pomocą równań (1.3) i (1.2) jako:
Ponieważ wszystkie wielkości w warunkach problemowych są przedstawione w układzie SI, obliczenia przeprowadzimy:
Odpowiedź:$I_0=12,56\A.$
Przykład 2
Ćwiczenia: Jaki jest okres drgań w obwodzie zawierającym cewkę indukcyjną $L=1$H i kondensator, jeśli natężenie prądu w obwodzie zmienia się zgodnie z prawem: $I\left(t\right)=-0,1sin20\ pi t\ \left(A \right)?$ Jaka jest pojemność kondensatora?
Rozwiązanie:
Z równania wahań prądu podanego w warunkach problemu:
widzimy, że $(\omega )_0=20\pi $, zatem możemy obliczyć okres oscylacji korzystając ze wzoru:
\ \
Zgodnie ze wzorem Thomsona dla obwodu zawierającego cewkę indukcyjną i kondensator mamy:
Obliczmy pojemność:
Odpowiedź:$T=0,1$ c, $C=2,5\cdot (10)^(-4)F.$
Przyjrzeliśmy się kilku fizycznie całkowicie różne systemy, i upewnił się, że równania ruchu są sprowadzone do tej samej postaci
Różnice pomiędzy układami fizycznymi pojawiają się jedynie w różnych definicjach wielkości oraz w różnych fizycznych znaczeniach zmiennej X: może to być współrzędna, kąt, ładunek, prąd itp. Należy zauważyć, że w tym przypadku, jak wynika z samej konstrukcji równania (1.18), wielkość ma zawsze wymiar odwrotności czasu.
Równanie (1.18) opisuje tzw drgania harmoniczne.
Równanie drgań harmonicznych (1.18) jest liniowe równanie różniczkowe drugiego rzędu (ponieważ zawiera drugą pochodną zmiennej X). Liniowość równania o tym świadczy
jeśli jakaś funkcja x(t) jest rozwiązaniem tego równania, to funkcja Cx(t) będzie również jego rozwiązaniem ( C– dowolna stała);
jeśli działa x 1(t) I x 2(t) są rozwiązaniami tego równania, to ich suma x 1 (t) + x 2 (t) będzie również rozwiązaniem tego samego równania.
Zostało to również udowodnione twierdzenie matematyczne, zgodnie z którym równanie drugiego rzędu ma dwa niezależne rozwiązania. Wszystkie pozostałe rozwiązania, zgodnie z właściwościami liniowości, można otrzymać jako ich kombinacje liniowe. Łatwo jest sprawdzić poprzez bezpośrednie różniczkowanie, że niezależne funkcje spełniają równanie (1.18). Oznacza to, że ogólne rozwiązanie tego równania ma postać:
Gdzie C 1,C 2- dowolne stałe. Rozwiązanie to można przedstawić w innej formie. Wprowadźmy wartość
|
|
i wyznacz kąt ze zależności:
|
|
Następnie rozwiązanie ogólne (1.19) zapisuje się jako
Zgodnie ze wzorami trygonometrycznymi wyrażenie w nawiasach jest równe
W końcu dochodzimy ogólne rozwiązanie równania drgań harmonicznych Jak:
Wartość nieujemna A zwany amplituda drgań, - początkowa faza oscylacji. Nazywa się cały argument cosinus – kombinacja faza oscylacji.
Wyrażenia (1.19) i (1.23) są całkowicie równoważne, więc możemy użyć dowolnego z nich, kierując się względami prostoty. Obydwa rozwiązania są funkcje okresowe czas. Rzeczywiście sinus i cosinus są okresowe z kropką . Dlatego różne stany układu wykonującego oscylacje harmoniczne powtarzają się po pewnym czasie T*, podczas którego faza oscylacji otrzymuje przyrost będący wielokrotnością :
Wynika, że
Najmniej takich czasów
zwany okres oscylacji (ryc. 1.8) i - jego cykliczny (cykliczny) częstotliwość.
Ryż. 1.8.
Oni też korzystają częstotliwość wahania
|
|
Odpowiednio częstotliwość kołowa jest równa liczbie oscylacji na sekundy
Tak więc, jeśli system na czas T charakteryzuje się wartością zmiennej x(t), wówczas zmienna będzie miała tę samą wartość po pewnym czasie (ryc. 1.9), tj
![]()
To samo znaczenie będzie naturalnie powtarzane w miarę upływu czasu 2T, ZT itp.

Ryż. 1.9. Okres oscylacji
Rozwiązanie ogólne obejmuje dwie dowolne stałe ( C1, C2 Lub A, A), których wartości muszą być określone przez dwa warunki początkowe. Zwykle (choć niekoniecznie) ich rolę pełnią początkowe wartości zmiennej x(0) i jego pochodna.
Podajmy przykład. Niech rozwiązanie (1.19) równania drgań harmonicznych opisuje ruch wahadła sprężystego. Wartości dowolnych stałych zależą od sposobu, w jaki wyprowadziliśmy wahadło ze stanu równowagi. Na przykład odciągnęliśmy sprężynę na odległość i wypuścił piłkę bez prędkości początkowej. W tym przypadku

Zastępowanie t = 0 w (1.19) znajdujemy wartość stałej C 2
![]()
Rozwiązanie wygląda zatem następująco:
Prędkość ładunku wyznaczamy różniczkując po czasie
![]()
Zastępowanie tutaj T = 0, znajdź stałą C 1:
![]()
Wreszcie
![]()
Porównując z (1.23) stwierdzamy, że jest amplitudą oscylacji, a jej faza początkowa wynosi zero: .
Wyrównoważymy teraz wahadło w inny sposób. Uderzmy ładunek tak, aby nabrał prędkości początkowej, ale praktycznie nie poruszał się podczas uderzenia. Mamy wtedy inne warunki początkowe:

![]()
nasze rozwiązanie wygląda
![]()
Prędkość ładunku zmieni się zgodnie z prawem:
![]()
Zastąpmy tutaj:
![]()