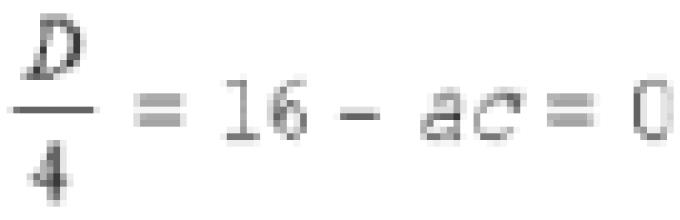Lekcja: Jak skonstruować parabolę lub funkcję kwadratową?
CZĘŚĆ TEORETYCZNA
Parabola jest wykresem funkcji opisanej wzorem ax 2 +bx+c=0.
Aby zbudować parabolę, należy postępować zgodnie z prostym algorytmem:
1) Wzór na parabolę y=ax 2 +bx+c,
Jeśli a>0 wówczas skierowane są gałęzie paraboli w górę,
w przeciwnym razie gałęzie paraboli są skierowane w dół.
Wolny Członek C punkt ten przecina parabolę z osią OY;
2), oblicza się za pomocą wzoru x=(-b)/2a, podstawiamy znaleziony x do równania paraboli i znajdujemy y;
3)Zera funkcji lub innymi słowy punkty przecięcia paraboli z osią OX, nazywane są również pierwiastkami równania. Aby znaleźć pierwiastki, przyrównujemy równanie do 0 topór 2 +bx+c=0;
Rodzaje równań:
a) Pełne równanie kwadratowe ma postać topór 2 +bx+c=0 i jest rozwiązywany przez dyskryminator;
b) Niepełne równanie kwadratowe postaci topór 2 +bx=0. Aby rozwiązać ten problem, musisz wyjąć x z nawiasów, a następnie przyrównać każdy współczynnik do 0:
topór 2 +bx=0,
x(ax+b)=0,
x=0 i ax+b=0;
c) Niepełne równanie kwadratowe postaci topór 2 +c=0. Aby go rozwiązać, musisz przesunąć niewiadome na jedną stronę, a wiadome na drugą. x =±√(c/a);
4) Znajdź kilka dodatkowych punktów, aby skonstruować funkcję.
CZĘŚĆ PRAKTYCZNA
I tak teraz na przykładzie przeanalizujemy wszystko krok po kroku:
Przykład 1:
y=x2 +4x+3
c=3 oznacza, że parabola przecina OY w punkcie x=0 y=3. Gałęzie paraboli skierowane są w górę, ponieważ a=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4- 8+3=-1 wierzchołek znajduje się w punkcie (-2;-1)
Znajdźmy pierwiastki równania x 2 +4x+3=0
Używając dyskryminatora, znajdujemy pierwiastki
a=1 b=4 c=3
D=b2-4ac=16-12=4
x=(-b±√(D))/2a
x 1 =(-4+2)/2=-1
x 2 =(-4-2)/2=-3
Weźmy kilka dowolnych punktów znajdujących się w pobliżu wierzchołka x = -2
x -4 -3 -1 0
y 3 0 0 3
Zamiast x wstaw do równania y=x 2 +4x+3 wartości
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Z wartości funkcji widać, że parabola jest symetryczna względem prostej x = -2
Przykład nr 2:
y=-x 2 +4x
c=0 oznacza, że parabola przecina OY w punkcie x=0 y=0. Gałęzie paraboli skierowane są w dół, ponieważ a=-1 -1 Znajdźmy pierwiastki równania -x 2 +4x=0
Niepełne równanie kwadratowe postaci ax 2 +bx=0. Aby rozwiązać ten problem, należy wyjąć x z nawiasów i przyrównać każdy współczynnik do 0.
x(-x+4)=0, x=0 i x=4.
Weźmy kilka dowolnych punktów znajdujących się w pobliżu wierzchołka x=2
x 0 1 3 4
y 0 3 3 0
Zamiast x wstaw do równania y=-x 2 +4x wartości
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Z wartości funkcji widać, że parabola jest symetryczna względem prostej x = 2
Przykład nr 3
y=x 2 -4
c=4 oznacza, że parabola przecina OY w punkcie x=0 y=4. Gałęzie paraboli skierowane są w górę, ponieważ a=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 wierzchołek znajduje się w punkcie (0;- 4)
Znajdźmy pierwiastki równania x 2 -4=0
Niepełne równanie kwadratowe postaci ax 2 +c=0. Aby go rozwiązać, musisz przesunąć niewiadome na jedną stronę, a wiadome na drugą. x =±√(c/a)
x2 =4
x 1 = 2
x2 =-2
Weźmy kilka dowolnych punktów znajdujących się w pobliżu wierzchołka x=0
x -2 -1 1 2
y 0 -3 -3 0
Zamiast x wstaw do równania y= x 2 -4 wartości
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Z wartości funkcji widać, że parabola jest symetryczna względem prostej x = 0
Subskrybuj na kanał na YOUTUBE aby być na bieżąco ze wszystkimi nowościami produktowymi i przygotowywać się z nami do egzaminów.
Uwagi wstępne i proste przykłady
Przykład 1. Dla jakich wartości a równanie ax 2 + 2x + 1 = 0 ma dwa różne pierwiastki?
Rozwiązanie.
To równanie jest kwadratowe w odniesieniu do zmiennej x dla a№ 0 i ma różne pierwiastki, gdy jest to dyskryminator
tj. dla< 1.
Dodatkowo, gdy a = 0, uzyskuje się równanie 2x + 1 = 0, które ma jeden pierwiastek.
Zatem a O (– `; 0) ORAZ (0; 1).
Zasada nr 1. Jeżeli współczynnik x 2 wielomianu drugiego stopnia zawiera parametr, należy przeanalizować przypadek jego zaniku.
Przykład 2. Równanie topór 2 + 8x + c = 0 ma pojedynczy pierwiastek równy 1. Ile są równe a i c?
Rozwiązanie. Zacznijmy rozwiązywać problem od szczególnego przypadku a = 0, równanie ma postać 8x + c = 0. To równanie liniowe ma rozwiązanie x 0 = 1 dla c = – 8.
Kiedy nie. Równanie kwadratowe 0 ma pojedynczy pierwiastek, jeśli ![]()
Dodatkowo podstawiając pierwiastek x 0 = 1 do równania, otrzymujemy a + 8 + c = 0.
Rozwiązanie układu dwójkowego równania liniowe, znajdujemy a = c = – 4.
Twierdzenie 1.
Dla zredukowanego trójmianu kwadratowego y = x 2 + px + q (zakładając p 2і
4q)
suma pierwiastków x 1 + x 2 = – p, iloczyn pierwiastków x 1 x 2 = q, różnica pierwiastków wynosi ![]()
i suma kwadratów pierwiastków x 1 2 + x 2 2 = p 2 – 2q.
Twierdzenie 2.
Dla trójmianu kwadratowego y = ax 2 + bx + c z dwoma pierwiastkami x 1 i x 2 mamy
rozwinięcie oś 2 + bx + c = a(x – x 1)(x – x 2), dla trójmianu z jednym pierwiastkiem x 0 – rozwinięcie
topór 2 + bx + do = a(x – x 0) 2 .
Komentarz. Często o równania kwadratowe z dyskryminatorem równym zero i mającym odpowiednio jeden pierwiastek, mówi się, że ma dwa zbieżne pierwiastki (?). Jest to związane z faktoryzacją wielomianu podanego w Twierdzeniu 2.(Właściwy sposób powiedzenia i zrozumienia w tym przypadku to „jeden pierwiastek z wielu dwóch.” – wyd.)
Zwrócimy uwagę na tę subtelność i podkreślimy przypadek pojedynczego pierwiastka krotności 2.
Przykład 3. W równaniu x 2 + ax + 12 = 0 wyznacz a w taki sposób, aby różnica pierwiastków równania była równa jeden.
Rozwiązanie. Różnica korzeni ![]()
skąd a = ± 7.
Przykład 4. Dla jakiego a suma kwadratów pierwiastków równania 2x 2 + 4x + a = 0 równa się 6?
Rozwiązanie. Zapiszmy równanie w formie ![]()
skąd x 1 2 + x 2 2 = 4 – a = 6 i a = – 2.
Przykład 5. Dla każdego a rozwiąż równanie ax 2 – 2x + 4 = 0.
Rozwiązanie. Jeśli a = 0, to x = 2. Jeśli a№
0, wówczas równanie staje się kwadratowe. Jego wyróżnik
równe D = 4 – 16a. Jeśli D< 0, т. е. a > ,
równanie nie ma rozwiązań. Jeśli D = 0, tj. a = ,
x = 4. Jeżeli D > 0, tj. a< ,
równanie ma dwa pierwiastki![]()
Położenie pierwiastków trójmianu kwadratowego
Wykres równania kwadratowego jest parabolą, a rozwiązaniami równania kwadratowego są odcięte punktów przecięcia tej paraboli z osią Wółu. Podstawą rozwiązania wszystkich problemów w tej sekcji jest zbadanie cech położenia paraboli o danych właściwościach płaszczyzna współrzędnych.
Przykład 6. Po co a pierwiastki równania x 2 – 2ax + a 2 – a – 6 = 0 mają różne znaki?
Rozwiązanie (ryc. 1).

Równanie kwadratowe albo nie ma rozwiązań (wykres jest parabolą typu D), albo ma jeden lub dwa pierwiastki dodatnie (parabola C), albo ma jeden lub dwa pierwiastki ujemne (parabola A), albo ma pierwiastki o różnych znakach (parabola B).
Łatwo zrozumieć, że ostatni typ paraboli, w odróżnieniu od innych, charakteryzuje się tym, że f(0)< 0. Таким образом, f(0) = a 2 – a – 6 < 0, откуда 0 < a < .
Rozwiązanie to pozwala na uogólnienie, które sformułujemy w postaci poniższej reguły.
Zasada 2. Aby równanie ax 2 + bx + c = 0
miał dwa różne pierwiastki x 1 i x 2 takie, że x 1< M < x 2 , необходимо и достаточно, чтобы a f(M) < 0.
Przykład 7. Dla czego a równanie x 2 – 2ax + a 2 – a – 6 = 0 ma dwa różne pierwiastki tego samego znaku?
Rozwiązanie. Interesują nas parabole typu A i C (patrz rys. 1). Charakteryzują się tym, że
skąd a O (– 6; – 2) ORAZ (3; + `` ).
Przykład 8. Dla czego a równanie x 2 – 2ax + a 2 – a – 6 = 0 ma dwa różne pierwiastki dodatnie?
Rozwiązanie. Interesują nas parabole typu C na ryc. 1.
Aby równanie miało pierwiastki, potrzebujemy![]()
Ponieważ oba pierwiastki równania muszą być dodatnie ze względu na warunek, odcięta wierzchołka paraboli leżącej między pierwiastkami jest dodatnia: x 0 = a > 0.
Współrzędna wierzchołka f(x 0)< 0 в силу того, что мы потребовали существование корней, поэтому если, кроме того, потребовать выполнение условия f(x 0) >0, wówczas ze względu na ciągłość badanej funkcji istnieje punkt x 1 O (0; x 0) tak, że f(x 1) = 0. Oczywiście jest to mniejszy pierwiastek równania.
Zatem f(0) = a 2 – a – 6 > 0 i łącząc wszystkie warunki, otrzymujemy układ
z rozwiązaniem a O (3; + `` ).
Przykład 9. Dla czego a równanie x 2 – 2ax + a 2 – a – 6 ma dwa różne pierwiastki ujemne?
Rozwiązanie. Po przestudiowaniu paraboli typu A na ryc. 1, otrzymujemy system
skąd a O (– 6; – 2).
Uogólnijmy rozwiązanie poprzednich problemów w postaci następującej reguły.
Zasada 3. Aby równanie ax 2 + bx + c = 0 miało dwa różne pierwiastki x 1 i x 2, z których każdy jest większy (mniejszy od) M, konieczne i wystarczające jest, że
Przykład 10. Funkcję f(x) podaje wzór
Znajdź wszystkie wartości parametru a, dla których równanie f(x) = 0 ma co najmniej jedno rozwiązanie.
Rozwiązanie. Wszystkie możliwe rozwiązania danego równania otrzymujemy jako rozwiązania równania kwadratowego
x 2 – (4a + 14)x + 4a 2 + 33a + 59 = 0
z dodatkowym warunkiem, że co najmniej jeden (oczywiście większy) pierwiastek x 2 ja.
Naturalnie, aby równanie miało pierwiastki, musi wynosić = – 5(a + 2) і
0,
skąd a Ј – 2.
Wykresem lewej strony wybranego równania jest parabola, której odcięta wierzchołek wynosi x 0 = 2a + 7. Rozwiązanie problemu dają dwa rodzaje paraboli (ryc. 2).
O: x 0 i a, skąd a i – 7. W tym przypadku większy pierwiastek wielomianu wynosi x 2 ja x 0 i a.
B: x 0< a, f(a)
Ј
0, skąd  .
.
W tym przypadku również większy pierwiastek wielomianu wynosi x 2 ja.
Wreszcie  .
.
Trzy rozwiązania jednej nierówności
Przykład 11. Znajdź wszystkie wartości parametru a dla których nierówność x 2 – 2ax + a 2 + 2a – 3 > 0
wykonane:
1) dla wszystkich wartości x;
2) na oczach wszystkich wartości dodatnie X;
3) dla wszystkich wartości x O [– 1; 1].
Rozwiązanie.
Pierwszy sposób.
1) Oczywiście ta nierówność zachodzi dla wszystkich x, gdy dyskryminator jest ujemny, tj.
= za 2 – (za 2 + 2a – 3) = – 2a + 3< 0,
skąd >.
2) Aby lepiej zrozumieć, co jest wymagane w opisie problemu, zastosujmy prostą technikę: narysuj kilka paraboli na płaszczyźnie współrzędnych, a następnie weź i zamknij lewą półpłaszczyznę względem osi Oy. Część paraboli, która pozostaje widoczna, musi znajdować się powyżej osi Wołu.
Warunek problemu jest spełniony w dwóch przypadkach (patrz rys. 3):
< 0, откуда a > ;
B: oba pierwiastki (może jeden, ale podwójne) równania x 2 – 2ax + a 2 + 2a – 3 = 0 znajdują się na lewo od początku układu współrzędnych. Zgodnie z regułą 3 warunek ten jest równoważny układowi nierówności Dі 0, x 0 Ј 0 i f(0) і 0.
Jednak przy rozwiązywaniu tego układu pierwszą nierówność można pominąć, gdyż nawet jeśli jakaś wartość a nie spełnia warunku Dі 0, wówczas automatycznie wpada to w rozwiązanie punktu A. W ten sposób rozwiązujemy układ
skąd a Ј – 3.
Łącząc rozwiązania punktów A i B, otrzymujemy
odpowiedź: ![]()
3) Warunek problemu jest spełniony w trzech przypadkach (patrz rys. 4):
A: wykres funkcji y = x 2 – 2ax + a 2 + 2a – 3 leży powyżej osi Wół, czyli D< 0, откуда a > ;
B: oba pierwiastki (być może jeden z wielokrotności 2) równania x 2 – 2ax + a 2 + 2a – 3 = 0 znajdują się na lewo od – 1. Warunek ten jest równoważny, jak wiemy z reguły 3, układowi nierówności Dі 0, x 0< – 1, f(– 1) > 0;
C: oba pierwiastki równania x 2 – 2ax + a 2 + 2a – 3 = 0 znajdują się na prawo od 1.
Warunek ten jest równoważny D i 0, x 0 > 1, f(1) > 0.
Jednak w punktach B i C, a także przy rozwiązywaniu poprzedniego problemu, można pominąć nierówność związaną z dyskryminatorem.
Otrzymujemy zatem dwa systemy nierówności
Po rozważeniu wszystkich przypadków otrzymujemy wynik: a >
w punkcie
w C.
Odpowiedzią na problem jest połączenie tych trzech zbiorów.
Drugi sposób. Aby warunek każdego z trzech punktów zadania był spełniony, należy podać najmniejszą wartość funkcji
y = x 2 – 2ax + a 2 + 2a – 3 w każdym z odpowiednich przedziałów musi być dodatnie.
1) Wierzchołek paraboli y = x 2 – 2ax + a 2 + 2a – 3 znajduje się w punkcie (a; 2a – 3), zatem najmniejsza wartość funkcji na całej osi liczbowej wynosi 2a – 3, oraz a > .
2) na półosi x i 0 najmniejsza wartość funkcji to f(0) = a 2 + 2a – 3, jeśli a< 0, и f(a) = 2a – 3, если a
і
0. Analizując oba przypadki, otrzymujemy ![]()
3) Najmniejszy w segmencie [– 1; 1] wartość funkcji to
Ponieważ najmniejsza wartość musi być dodatnia, otrzymujemy układy nierówności
Rozwiązaniem tych trzech układów jest zbiór
Trzeci sposób. 1) Wierzchołek paraboli y = x 2 – 2ax + a 2 + 2a – 3
znajduje się w punkcie (a; 2a – 3). Narysujmy zbiór na płaszczyźnie współrzędnych, który tworzą wierzchołki wszystkich paraboli dla różnych a (ryc. 5).
Jest to prosta y = 2x – 3. Przypomnijmy, że każdy punkt na tej prostej ma swoją wartość parametru, a z każdego punktu na tej prostej „wychodzi” parabola odpowiadająca danej wartości parametru. Parabole znajdujące się całkowicie powyżej osi Wółu charakteryzują się warunkiem 2a – 3 > 0.
2) Rozwiązaniem tego punktu są wszystkie rozwiązania pierwszego punktu i dodatkowo parabole, dla których a jest ujemne, a f(0) = a 2 + 2a – 3і 0.
3) Z ryc. 5 widać, że interesują nas parabole, dla których albo a jest ujemne, albo f(– 1) = a 2 + 4a – 2 > 0,
lub a jest dodatnie i f(1) = a 2 – 2 > 0.
Równania i nierówności sprowadzające się do równań kwadratowych
Przykład 12. Dla jakich wartości a równanie 2x 4 – 2ax 2 + a 2 – 2 = 0 nie ma rozwiązań?
Rozwiązanie. Dokonując podstawienia y = x 2 otrzymujemy równanie kwadratowe f(y) = 2y 2 – 2ay + a 2 – 2 = 0.
Otrzymane równanie nie ma rozwiązania, gdy D< 0. Кроме того, первоначальное уравнение не имеет решений, когда корни уравнения f(y) = 0 отрицательны.
Warunki te można zapisać jako zbiór
Gdzie ![]()
Przykład 13. Dla każdej wartości parametru a rozwiąż równanie cos x sin 2x = asin 3x.
Rozwiązanie. Ponieważ 2cos x grzech 2x = grzech x + grzech 3x i grzech 3x = 3sin x – 4sin 3 x,
wówczas równanie zostanie zapisane jako sin x (sin 2 x (4a – 2) – (3a – 2)) = 0.
Stąd otrzymujemy rozwiązania x = p n, n O Z dla dowolnego a. Równanie ![]()
ma rozwiązania 
nie pokrywają się z rozwiązaniami pierwszego równania, tylko pod warunkiem ![]()
Te ostatnie ograniczenia są równoważne
Odpowiedź: x = p n, n O Z dla dowolnego a; Oprócz,
Przykład 14. Znajdź wszystkie wartości parametru a, dla każdej z nich nierówność
a 2 + 2a – sin 2 x – 2acos x > 2 zachodzi dla dowolnej liczby x.
Rozwiązanie. Przekształćmy nierówność do postaci cos 2 x – 2acos x + a 2 + 2a – 3 > 0
i dokonaj zamiany t = cos x. Należy zauważyć, że parametr t ma wartość od – 1 do 1, więc problem można przeformułować w następujący sposób: znajdź wszystko takie, że
t 2 – 2at + za 2 + 2a – 3 > 0
obowiązuje dla wszystkich t O [- 1; 1]. Rozwiązaliśmy już ten problem wcześniej.
Przykład 15. Ustal, dla jakich wartości równania log 3 (9 x + 9a 3) = x ma rozwiązania i znajdź je.
Rozwiązanie. Przekształćmy równanie do postaci 9 x – 3 x + 9a 3 = 0
i dokonując zamiany y = 3 x, otrzymujemy y 2 – y + 9a 3 = 0.
Jeśli dyskryminator jest ujemny, równanie nie ma rozwiązań. Kiedy dyskryminator
D = 1 – 36a 3 = 0, równanie ma jeden pierwiastek,
oraz x = – log 3 2. Wreszcie, gdy dyskryminator jest dodatni, tj.
oryginalne równanie ma jeden pierwiastek  ,
,
i jeśli dodatkowo wyrażenie 1 jest dodatnie,
wówczas równanie ma również drugi pierwiastek ![]() .
.
Więc w końcu dostajemy 
![]() ,
,
dla pozostałych a nie ma rozwiązań.
Przykład 16. Dla każdej wartości parametru a rozwiąż równanie grzechu 4 x + sałata 4 x + grzech 2 x + a = 0.
Rozwiązanie. Ponieważ
Zapiszmy równanie w postaci sin 2 x – 2sin x – 2a – 2 = 0.
Niech y = sin 2x, wtedy y 2 – 2y – 2a – 2 = 0 (| y | J 1).
Wykres funkcji po lewej stronie równania jest parabolą z wierzchołkiem, którego odcięta wynosi y 0 = 1; wartość funkcji w punkcie y = – 1 wynosi 1 – 2a; dyskryminator równania wynosi 8a + 12. Oznacza to, że większy pierwiastek y 2 równania y 2 – 2y – 2a – 2 = 0, nawet jeśli istnieje, jest większy od 1, a odpowiadające mu równanie sin 2x = y 2 nie ma rozwiązań. 3. Dla jakich wartości a równanie 2x 2 + (3a + 1)x + a 2 + a + 2 = 0 ma co najmniej jeden pierwiastek?
4. Równanie ax 2 + bx + 5 = 0 ma pojedynczy pierwiastek równy 1. Ile wynoszą a i b?
5. Dla jakich wartości parametru a są pierwiastki równania kwadratowego 5x 2 – 7x + a = 0 powiązane jako 2 do 5?
6. W równaniu ax 2 + 8x + 3 = 0 wyznacz a tak, aby różnica między pierwiastkami równania była równa jeden.
7. Dla jakiego a suma kwadratów pierwiastków równania x 2 – 2ax + 2(a + 1) = 0 równa się 20?
8. Dla jakich b i c równanie c + bx – 2x 2 = 0 ma jeden pierwiastek dodatni i jeden ujemny?
9. Znajdź wszystkie wartości parametru a, dla których jeden pierwiastek równania x 2 – (a + 1)x + 2 = 0 jest większy od a, a drugi mniejszy od a.
10. Znajdź wszystkie wartości parametru a, dla których równanie x 2 + (a + 1)x + 2 = 0 ma dwa różne pierwiastki tego samego znaku.
11. Dla jakich wartości a wszystkie wynikowe pierwiastki równania (a – 3)x 2 – 2ax + 6a = 0 są dodatnie?
12. Dla czego a są wszystkie pierwiastki wynikowe równania (1 + a)x 2 – 3ax + 4a = 0 większe niż 1?
13. Znajdź wszystkie wartości parametru a, dla których oba różne pierwiastki równania x 2 + x + a = 0 są większe niż a.
14. Dla jakich wartości a oba pierwiastki równania 4x 2 – 2x + a = 0 zawarte są pomiędzy – 1 a 1?
15. Dla jakich wartości a równanie x 2 + 2(a – 1)x + a + 5 = 0 ma przynajmniej jeden pierwiastek dodatni?
16. Funkcję f(x) wyraża wzór
Znajdź wszystkie wartości parametru a, dla których równanie f(x) = 0 ma co najmniej jedno rozwiązanie.
17. Dla czego a jest nierówność (a 2 – 1)x 2 + 2(a – 1)x + 2 > 0 prawdziwa dla wszystkich x?
18. Dla jakich wartości parametru a obowiązuje oś nierówności 2 + 2x > 1 – 3a dla wszystkich dodatnich x?
19. Dla jakich wartości a równanie x 4 + (1 – 2a)x 2 + a 2 – 1 = 0 nie ma rozwiązań?
20. Dla jakich wartości parametru a równanie 2x 4 – 2ax 2 + a2 – 2 = 0 ma jedno lub dwa rozwiązania?
21. Dla każdej wartości a rozwiąż równanie acos x cos 2x = cos 3x.
22. Znajdź wszystkie wartości parametru a, dla każdej z nich nierówność cos 2 x + 2asin x – 2a< a 2
– 4 выполняется для любого числа x.
23. Dla każdego a rozwiąż równanie log 2 (4 x + a) = x.
24. Dla każdej wartości parametru a rozwiąż równanie sin 2 x + asin 2 2x = sin.
Wykres trójmianu kwadratowego
2019-04-19
Trójmian kwadratowy
Trójmian kwadratowy nazwaliśmy całą funkcją wymierną drugiego stopnia:
$y = topór^2 + bx + c$, (1)
gdzie $a \neq 0$. Udowodnimy, że wykresem trójmianu kwadratowego jest parabola otrzymana przez równoległe przesunięcia (w kierunkach osi współrzędnych) od paraboli $y = ax^2$. Aby to zrobić, przedstawiamy wyrażenie (1) za pomocą prostego przemiany tożsamości do głowy
$y = a(x + \alfa)^2 + \beta$. (2)
Odpowiednie przekształcenia opisane poniżej są znane jako „dokładne ekstrahowanie do kwadratu”:
$y = x^2 + bx + c = a \left (x^2 + \frac(b)(a) x \right) + c = a \left (x^2 + \frac(b)(a) x + \frac (b^2)(4a^2) \right) - \frac (b^2)(4a) + c = a \left (x + \frac(b)(2a) \right)^2 - \frac (b^2 - 4ac)(4a)$. (2")
Zredukowaliśmy trójmian kwadratowy do postaci (2); w której
$\alpha = \frac(b)(2a), \beta = - \frac (b^2 - 4ac)(4a)$
(wyrażeń tych nie należy zapamiętywać; wygodniej jest za każdym razem bezpośrednio przekształcić trójmian (1) do postaci (2).
Teraz jest jasne, że wykresem trójmianu (1) jest parabola równa paraboli $y = ax^2$ i uzyskana poprzez przesunięcie paraboli $y = ax^2$ w kierunkach osi współrzędnych o $\ alfa$ i $\beta$ (biorąc pod uwagę znak $\alpha$ i $\beta$). Wierzchołek tej paraboli znajduje się w punkcie $(- \alpha, \beta)$, jej osią jest prosta $x = - \alpha$. Dla $a > 0$ wierzchołek to najniższy punkt parabole, dla $a
Przeprowadźmy teraz badanie trójmianu kwadratowego, tj. poznamy jego właściwości w zależności od wartości liczbowych współczynników $a, b, c$ w jego wyrażeniu (1).
W równości (2") oznaczamy wartość $b^2- 4ac$ przez $d$:
$y = a \left (x + \frac(b)(2a) \right)^2 - \frac(d)(4a)$; (4)
$d = b^2 - 4ac$ nazywa się dyskryminatorem trójmianu kwadratowego. O właściwościach trójmianu (1) (i położeniu jego wykresu) decydują znaki dyskryminatora $d$ i wiodący współczynnik $a$.

1) $a > 0, d 0$; ponieważ $a > 0$, to graf znajduje się powyżej wierzchołka $O^( \prime)$; leży w górnej półpłaszczyźnie ($y > 0$ - rys. a.).
2) $za
3) $a > 0, d > 0$. Wierzchołek $O^( \prime)$ leży poniżej osi $Ox$, parabola przecina oś $Ox$ w dwóch punktach $x_1, x_2$ (ryc. c.).
4) $0 $. Wierzchołek $O^( \prime)$ leży powyżej osi $Ox$, parabola ponownie przecina oś $Ox$ w dwóch punktach $x_1, x_2$ (rys. d).
5) $a > 0, d = 0$. Wierzchołek leży na samej osi $Wół$, parabola znajduje się w górnej półpłaszczyźnie (rys. e).
6) $za
Wnioski. Jeśli $d 0$) lub mniej (jeśli $a
Jeśli $d > 0$, to funkcja jest przemienna (wykres leży częściowo poniżej, a częściowo powyżej osi $Ox$). Trójmian kwadratowy, w którym $d > 0$ ma dwa pierwiastki (zera) $x_1, x_2$. Dla $a > 0$ jest ona ujemna w przedziale między pierwiastkami (ryc. c) i dodatnia poza tym przedziałem. Przy $a
Definicja
Parabola nazywa się wykresem funkcji kwadratowej $y = ax^(2) + bx + c$, gdzie $a \neq 0$.
Wykres funkcji $y = x^2$.
Aby schematycznie wykreślić wykres funkcji $y = x^2$, znajdziemy kilka punktów spełniających tę równość. Dla wygody współrzędne tych punktów zapisujemy w formie tabeli:
Wykres funkcji $y = ax^2$.
Jeżeli współczynnik $a > 0$, to wykres $y = ax^2$ otrzymujemy z wykresu $y = x^2$ albo poprzez pionowe rozciąganie (dla $a > 1$) albo kompresję do $x$ oś (za 0,00 USD)< a < 1$). Изобразим для примера графики $y = 2x^2$ и $y = \dfrac{x^2}{2}$:
| $y = 2x^2$ | $y = \dfrac(x^2)(2)$ |
|
|
Jeśli $a< 0$, то график функции $y = ax^2$ можно получить из графика $y = |a|x^2$, отразив его симметрично относительно оси $x$. Построим графики функций $y = - x^2$, $y = -2x^2$ и $y = - \dfrac{x^2}{2}$:
| $y = - x^2$ | $y = -2x^2$ | $y = - \dfrac(x^2)(2)$ |
|
|
|
Wykres funkcji kwadratowej.
Aby wykreślić funkcję $y = ax^2 + bx + c$, musisz oddzielić $ax^2 + bx + c$ od kwadratowego trójmianu idealny kwadrat, to znaczy przedstaw to w postaci $a(x - x_0)^2 + y_0$. Wykres funkcji $y = a(x - x_0)^2 + y_0$ otrzymujemy z odpowiedniego wykresu $y = ax^2$ poprzez przesunięcie o $x_0$ wzdłuż osi $x$ i o $y_0$ wzdłuż osi $y$. W rezultacie punkt $(0;0)$ zostanie przesunięty do punktu $(x_0;y_0)$.
Definicja
Szczyt parabola $y = a(x - x_0)^2 + y_0$ jest punktem o współrzędnych $(x_0;y_0)$.
Skonstruujmy parabolę $y = 2x^2 - 4x - 6$. Wybierając cały kwadrat, otrzymujemy $y = 2(x - 1)^2 - 8$.
| Wykreślmy $y = 2x^2$ | Przesuńmy to w prawo o 1 | I w dół o 8 |
|
|
|
Rezultatem jest parabola z wierzchołkiem w punkcie $(1;-8)$.
Wykres funkcji kwadratowej $y = ax^2 + bx + c$ przecina oś $y$ w punkcie $(0; c)$ i oś $x$ w punktach $(x_(1,2) ;0)$, gdzie $ x_(1,2)$ są pierwiastkami równania kwadratowego $ax^2 + bx + c = 0$ (a jeśli równanie nie ma pierwiastków, to odpowiadająca im parabola nie przecina $ oś x$).
Na przykład parabola $y = 2x^2 - 4x - 6$ przecina osie w punktach $(0; -6)$, $(-1; 0)$ i $(3; 0)$.