Wyznaczanie przecięcia prostej i płaszczyzny. Naukowa biblioteka elektroniczna. Szczególne przypadki wzajemnej równoległości i prostopadłości prostej i płaszczyzny. szczególne przypadki wzajemnej prostopadłości dwóch płaszczyzn

Linia przecięcia dwóch płaszczyzn jest linią prostą. Rozważmy najpierw szczególny przypadek (ryc. 3.9), gdy jedna z przecinających się płaszczyzn jest równoległa do poziomej płaszczyzny rzutów (α π 1, f 0 α X). W tym przypadku linia przecięcia a, należący do samolotuα, będzie również równoległa do płaszczyzny π 1, (ryc. 3.9. a), tj. będzie pokrywać się z poziomem przecinających się płaszczyzn (a ≡ h).

Jeżeli jedna z płaszczyzn jest równoległa do przedniej płaszczyzny rzutów (rys. 3.9.b), wówczas linia przecięcia a należąca do tej płaszczyzny będzie równoległa do płaszczyzny π 2 i będzie pokrywać się z czołami przecinających się płaszczyzn (a ≡ f).

.

.

Ryż. 3.9. Szczególny przypadek przecięcie płaszczyzny położenia ogólnego z płaszczyznami: a - poziom poziomy; b - poziom czołowy

Przykład konstrukcji punktu przecięcia (K) prostej a (AB) z płaszczyzną α (DEF) pokazano na rys. 3.10. W tym celu prostą a zamyka się w dowolnej płaszczyźnie β i wyznacza się linię przecięcia płaszczyzn α i β.

W rozpatrywanym przykładzie proste AB i MN należą do tej samej płaszczyzny β i przecinają się w punkcie K, a ponieważ prosta MN należy do danej płaszczyzny α (DEF), to punkt K jest jednocześnie punktem przecięcia prostej a (AB) z płaszczyzną α. (ryc. 3.11).

.

Ryż. 3.10. Konstruowanie punktu przecięcia prostej i płaszczyzny

Aby rozwiązać taki problem na złożonym rysunku, należy znaleźć punkt przecięcia prostej w położeniu ogólnym z płaszczyzną w położeniu ogólnym.

Rozważmy przykład znalezienia punktu przecięcia prostej AB z płaszczyzną trójkąta DEF pokazanego na ryc. 3.11.

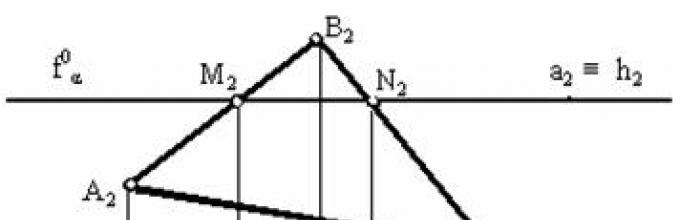
Aby znaleźć punkt przecięcia przez rzut czołowy prostej A 2 B 2, narysowano wystającą czołowo płaszczyznę β, która przecinała trójkąt w punktach M i N. Na płaszczyźnie rzutu czołowego (π 2) punkty te są reprezentowane przez rzuty M 2, N 2. Z warunku przynależności do płaszczyzny prostej na poziomej płaszczyźnie rzutów (π 1) znajdują się rzuty poziome wynikowych punktów M 1 N 1. Na przecięciu poziomych rzutów linii A 1 B 1 i M 1 N 1 powstaje poziomy rzut ich punktu przecięcia (K 1). Zgodnie z linią komunikacyjną i warunkami przynależności na czołową płaszczyznę rzutów, występuje rzut czołowy punktu przecięcia (K 2).

.

Ryż. 3.11. Przykład wyznaczania punktu przecięcia prostej i płaszczyzny

Widoczność odcinka AB względem trójkąta DEF wyznaczana jest metodą punktów konkurujących.

Na płaszczyźnie π 2 rozważane są dwa punkty NEF i 1AB. Z rzutów poziomych tych punktów można stwierdzić, że punkt N jest położony bliżej obserwatora (Y N > Y 1) niż punkt 1 (kierunek linii wzroku jest równoległy do ​​S). W konsekwencji prosta AB, czyli część prostej AB (K 1), pokrywa się z płaszczyzną DEF na płaszczyźnie π 2 (jej rzut K 2 1 2 zaznaczono linią przerywaną). Podobnie ustala się widzialność na płaszczyźnie π 1.

Pytania do samokontroli

1) Na czym polega istota metody punktów konkurencyjnych?

2) Jakie znasz właściwości linii prostej?

3) Jaki jest algorytm wyznaczania punktu przecięcia prostej i płaszczyzny?

4) Jakie zadania nazywane są pozycyjnymi?

5) Sformułuj warunki przynależności do płaszczyzny prostej.

Zwracamy uwagę na czasopisma wydawane przez wydawnictwo „Akademia Nauk Przyrodniczych”

Wiadomo, że prosta przecina płaszczyznę, jeśli nie należy do tej płaszczyzny i nie jest do niej równoległa. Postępując zgodnie z poniższym algorytmem, znajdujemy punkt przecięcia linii A z płaszczyzną rodzajową α określoną przez ślady h 0α , f 0α .

Algorytm

1. Bezpośrednio A rysujemy pomocniczą wystającą do przodu płaszczyznę γ. Rysunek pokazuje jego ślady h 0γ, f 0γ.
2. Konstruujemy rzuty prostej AB, wzdłuż której przecinają się płaszczyzny α i γ. W tym zadaniu punkt B" = h 0α ∩ h 0γ, A"" = f 0α ∩ f 0γ. Punkty A" i B"" leżą na osi x, ich położenie wyznaczają linie komunikacyjne.
3. Bezpośredni A i AB przecinają się w żądanym punkcie K. Jego rzut poziomy K” = a” ∩ A”B”. Rzut czołowy K"" leży na linii prostej a"".

Algorytm rozwiązania pozostanie taki sam, jeśli pl. α zostanie podane za pomocą równoległych, przecinających się linii, odcinka figury lub w inny możliwy sposób.

Widoczność linii a względem płaszczyzny α. Metoda konkurujących punktów

1. Zaznaczmy na rysunku rywalizujące ze sobą czołowo punkty A i C (ryc. poniżej). Zakładamy, że punkt A należy do obszaru. α i C leży na prostej a. Przednie występy A” i C” pokrywają się, ale jednocześnie punkty A i C są usuwane z płaszczyzny występów P 2 w różnych odległościach.
2. Znajdźmy rzuty poziome A” i C”. Jak widać na rysunku, punkt C” jest oddalony od płaszczyzny P 2 w większej odległości niż punkt A”, który należy do kwadratu. α. W rezultacie widoczny będzie odcinek prostej a”, znajdujący się na lewo od punktu K”. Sekcja a „” na prawo od K” jest niewidoczna. Zaznaczamy to linią przerywaną.
3. Zaznaczmy na rysunku konkurujące poziomo punkty D i E. Zakładamy, że punkt D należy do kwadratu. α, a E leży na prostej a. Rzuty poziome D” i E” pokrywają się, ale jednocześnie punkty D i E są usuwane z płaszczyzny P 1 w różnych odległościach.
4. Określmy położenie występów czołowych D"" i E"". Jak widać na rysunku, punkt D„”, znajdujący się w kwadracie. α, jest usuwany z płaszczyzny P 1 w większej odległości niż punkt E „”, należący do prostej a. W związku z tym przekrój „a” znajdujący się na prawo od punktu K” będzie niewidoczny. Zaznaczamy to linią przerywaną. Widoczna jest sekcja a „na lewo od K”.

Mając daną prostą: (1) i płaszczyznę: Ax + By + Cz + D = 0 (2).

Znajdźmy współrzędne punktu przecięcia prostej i płaszczyzny. Jeżeli prosta (1) i płaszczyzna (2) przecinają się, to współrzędne punktu przecięcia spełniają równania (1) i (2):

, .

Podstawiając znalezioną wartość t do (1), otrzymujemy współrzędne punktu przecięcia.

1) Jeśli Am + Bn + Cp = 0 i Ax 0 + By 0 + Cz 0 + D ≠ 0, to t nie istnieje, tj. linia prosta i płaszczyzna nie mają ani jednego punktu wspólnego. Są równoległe.

2) Am + Bn + Cp = 0 i Ax 0 + By 0 + Cz 0 + D = 0. W tym przypadku t może przyjmować dowolne wartości oraz , tj. linia prosta jest równoległa do płaszczyzny i ma wspólny punkt, tj. leży w samolocie.

Przykład 1. Znajdź punkt przecięcia linii z płaszczyzną 3x – 3y + 2z – 5 = 0.

3(2t – 1) – 3(4t + 3) + 2 3t – 5 = 0 => -17=0, co jest niemożliwe dla dowolnego t, tj. linia prosta i płaszczyzna nie przecinają się.

Przykład 2. Znajdź punkt przecięcia linii i płaszczyzny: x + 2y – 4z + 1 = 0.

8t + 13 + 2(2t + 1) – 4(3t + 4) + 1 = 0, 0 + 0 = 0. Dotyczy to dowolnej wartości t, tj. linia prosta leży w płaszczyźnie.

Przykład 3. Znajdź punkt przecięcia linii i płaszczyzna 3x – y + 2z – 5 = 0.

3(5t + 7) – t – 4 + 2(4t + 5) – 5 = 0, 22t + 22 = 0, t = -1, x = 5(-1) + 7 = 2, y = -1 + 4 = 3, z = 4(-1) + 5 = 1, M(2, 3, 1) – punkt przecięcia prostej i płaszczyzny.

Kąt między linią prostą a płaszczyzną. Warunki równoległości i prostopadłości prostej i płaszczyzny.

Nazywa się kąt między prostą a płaszczyzną ostry róg q pomiędzy linią prostą a jej rzutem na płaszczyznę.

Niech będzie dana prosta i płaszczyzna:

I .

Niech linia prosta przecina płaszczyznę i tworzy z nią kąt μ (). Wtedy b = 90 0 – q lub b = 90 0 + q jest kątem pomiędzy wektorem normalnym płaszczyzny a wektorem kierunkowym linii prostej. Ale . Oznacza

(3).

a) Jeśli L P, to - warunek prostopadłości prostej i płaszczyzny.

b) Jeżeli L||P, to jest warunek równoległości prostej i płaszczyzny.

c) Jeżeli prostą jest L||P i jednocześnie punkt M0(x0, y0, z0) P, to prosta leży w tej płaszczyźnie. Analitycznie:

- warunki przynależności do linii prostej i płaszczyzny.

Przykład. Biorąc pod uwagę linię prostą i punkt M 0 (1, 0, –2). Przez punkt M 0 narysuj płaszczyznę prostopadłą do tej prostej. Równania żądanej płaszczyzny szukamy w postaci: A(x – 1) + B(y – 0) + C(z + 2) = 0. W tym przypadku , ,

5(x – 1) – 5y + 5(z + 2) = 0, - x – y + z + 3 = 0.

Garść samolotów.

Belka płaszczyzn to zbiór wszystkich płaszczyzn przechodzących przez daną linię prostą – oś belki.

Aby zdefiniować wiązkę płaszczyzn wystarczy określić jej oś. Niech równanie tej prostej będzie podane w postaci ogólnej:

.

Ułożyć równanie belki oznacza ułożyć równanie, z którego można uzyskać dodatkowy warunek równanie dowolnej płaszczyzny belki, z wyjątkiem b.m. jeden. Pomnóżmy równanie II przez l i dodajmy do równania I:

A 1 x + B 1 y + C 1 z + re 1 + l(A 2 x + B 2 y + C 2 z + re 2) = 0 (1) lub

(A 1 + lA 2)x + (B 1 + lB 2)y + (C 1 + lC 2)z + (D 1 + lD 2) = 0 (2).

l – parametr – liczba, która może przyjmować wartości rzeczywiste. Dla dowolnej wybranej wartości l równania (1) i (2) mają charakter liniowy, tj. są to równania pewnej płaszczyzny.

1. Pokażmy, że ta płaszczyzna przechodzi przez oś belki L. Weźmy dowolny punkt M 0 (x 0, y 0, z 0) L. W rezultacie M 0 P 1 i M 0 P 2. Oznacza:

3x – y + 2z + 9 + 17x + 17z – 51 = 0; 20x – y + 19z – 42 = 0.

Przykład 3 (E). Napisz równanie płaszczyzny przechodzącej przez linię prostopadle do płaszczyzny x – 2y + z + 5 = 0. ; 3x – 2y + z – 3 + l(x – 2z) = 0; (3 + l)x – 2y + (1 – 2 l)z – 3 = 0; ; ; l = 8; 11x – 2y – 15z – 3 = 0.

77*. Znajdź punkt przecięcia prostej AB z płaszczyzną wyznaczoną przez trójkąt CDE (ryc. 75, a).

Rozwiązanie. Jak wiadomo, aby znaleźć punkt przecięcia prostej z płaszczyzną ogólną, należy przez tę prostą narysować płaszczyznę pomocniczą (R), skonstruować linię przecięcia tej płaszczyzny z zadaną (1-2) i znajdź

punkt przecięcia (K) podanych i skonstruowanych linii. Punkt K jest pożądanym punktem przecięcia linii z płaszczyzną (ryc. 75, b). Jako płaszczyznę pomocniczą zwykle stosuje się płaszczyznę projekcji poziomej lub czołowej.

Na ryc. 75, w c, przez prostą AB poprowadzono wystającą do przodu płaszczyznę R, której ślad R ϑ pokrywa się z literą „c”. horyzont. W tym zadaniu ślad płaszczyzny nie jest potrzebny i dlatego nie jest pokazany.

Konstruujemy linię przecięcia płaszczyzny R i płaszczyzny określonej przez trójkąt CDE (przykład takiej konstrukcji można znaleźć w Zadaniu 67). Po skonstruowaniu linii 1-2 (ryc. 75, c) znajdujemy punkt jej przecięcia z prostą AB - punkt K (k, k").

Aby wyznaczyć odcinki prostej AB, które zostaną objęte trójkątem, należy posłużyć się analizą położenia punktów na przecinających się prostych.

Przykładowo punkty 1 i 3 leżą na przecinających się (odpowiednio) liniach ED i AB. Rzuty czołowe tych punktów pokrywają się, czyli punkty 1 i 3 są jednakowo oddalone od kwadratu. N. Ale ich odległości od kwadratu. V są różne: punkt 3 jest dalej od kwadratu. V niż pkt 1. Zatem w odniesieniu do pl. V punkt 3 pokrywa się z punktem 1 (kierunek patrzenia wskazuje strzałka S). Zatem prosta AB przechodzi przed trójkątem CDE do punktu K. Zaczynając od punktu K w lewo, prosta AB jest objęta trójkątem i dlatego ten odcinek prostej zaznaczony jest linią przerywaną.

Aby zidentyfikować niewidoczny obszar na horyzoncie. rzuty linii AB, rozważmy punkty 4 i 5 leżące odpowiednio na prostych AB i CD.

Jeśli spojrzymy na te punkty w kierunku s 1, najpierw zobaczymy punkt 5. Punkt 4 pokrywa się z punktem 5. W związku z tym prosta AB w tym miejscu jest objęta trójkątem CDE, a przekrój jej rzutu z punktu k do punktu 4 należy zaznaczyć linią przerywaną. W tym przypadku punkt K znajdował się wewnątrz konturu trójkąta CDE.

Jeżeli względne położenie przecinających się elementów jest inne, możliwe jest, że punkt K znajdzie się na zewnątrz trójkąta (ryc. 75, d). Oznacza to, że prosta AB przecina płaszczyznę wyznaczoną przez trójkąt CDE poza obrysem tego trójkąta. AB staje się niewidoczny za punktem K (po lewej).

78. Znajdź punkty przecięcia prostej AB ze ścianami piramidy (ryc. 76). Ściany piramidy należy traktować jako płaszczyzny wyznaczone przez trójkąty.

79. Znajdź punkty przecięcia prostej AB ze ścianami pryzmatu (ryc. 77). Ściany pryzmatu należy traktować jako płaszczyzny wyznaczone równoległymi liniami prostymi.

80*. Znajdź punkty przecięcia prostej AB z płaszczyzną P (ryc. 78, a).

Rozwiązanie. Rysujemy wystającą czołowo płaszczyznę R przez prostą AB (ryc. 78, b) (jej ślad R ϑ pokrywa się z literą „b”) i konstruujemy linię MN przecięcia obu płaszczyzn - danych i poprowadzoną przez AB (tzw. konstrukcja jest podobna do tej wykonanej w zadaniu 70). Wymagany punkt K(k, k") przecięcia prostej AB z płaszczyzną P leży w punkcie przecięcia MN z AB.

W tym zadaniu widoczność odcinka prostego od punktu A do K jest oczywista; jednak więcej trudne przypadki na podstawie którego należy określić widoczny odcinek linii prostej

analiza położenia punktów. Przykładowo, biorąc punkt 1 (na linii AB) i punkt N (na trasie P ϑ). widzimy, że punkt 1 znajduje się dalej w stosunku do kwadratu. V niż punkt N. Zatem widoczna jest prosta AB do punktu K. Poza punktem K linia prosta jest oznaczona linią przerywaną i jest niewidoczna. Podobnie określa się widoczność po horyzont. projekcje.

81. Znajdź punkt przecięcia prostej AB z płaszczyzną P (ryc. 79).

82*. Znajdź punkt przecięcia prostej AB z płaszczyzną P (ryc. 80, a).

Rozwiązanie. Przez prostą AB rysujemy poziomo wystającą płaszczyznę R (ślad R h pokrywa się z ab) i konstruujemy linię przecięcia płaszczyzn P i R,

wykorzystując punkty M i N przecięcia ich torów o tej samej nazwie (ryc. 80, b i c). Pożądany punkt (k", k) znajduje się w punkcie przecięcia MN z AB. Na ryc. 80, d, punkt K jest konstruowany za pomocą wykresu W. Ponieważ wykres P ma rzut profilowy (ryc. 80, b).

wówczas rzut profilu k" leży w punkcie przecięcia śladu P ω z a"b". Znając k", konstruujemy k" na a"b" i k na ab. Widoczne odcinki prostej AB to określić w taki sam sposób jak w zadaniach 77 i 80.

83. Znajdź punkt przecięcia prostej AB z płaszczyzną P (ryc. 81).

84*. Znajdź punkt przecięcia prostej AB z płaszczyzną wyznaczoną przez trójkąt CDE (ryc. 82, a).

Rozwiązanie. Przez linię prostą AB rysujemy (ryc. 82, b i c) kwadrat. R, równolegle do kwadratu W. Przechodzi dany samolot wzdłuż linii prostej MN (punkty m”, n”, m i n leżą na przecięciu śladów R ϑ i R h z tymi samymi rzutami odpowiednich boków

trójkąt CDE). Ponieważ linie AB i MN są profilowe, to aby znaleźć punkt (K) ich przecięcia konstruujemy rzuty profilowe a"b" i m"n". Rzut k” znajduje się na przecięciu a „b” i m „m”. Używając k” konstruujemy k” na a „b” i k na ab.

85. Znajdź punkt przecięcia prostej EF z płaszczyzną wyznaczoną przez czworokąt ABCD (ryc. 83).