Z definicji różnicę (pierwszą różnicę) funkcji oblicza się ze wzoru  Jeśli
Jeśli  – zmienna niezależna.
– zmienna niezależna.
PRZYKŁAD.
Pokażmy, że postać pierwszej różniczki pozostaje niezmieniona (jest niezmienna) nawet w przypadku, gdy argument funkcji  samo w sobie jest funkcją, to znaczy dla złożona funkcja
samo w sobie jest funkcją, to znaczy dla złożona funkcja .
.
Pozwalać  są różniczkowalne, to z definicji
są różniczkowalne, to z definicji
Co więcej, właśnie to należało udowodnić.
PRZYKŁADY.

Udowodniona niezmienność postaci pierwszej różniczki pozwala nam to założyć  to jest pochodna jest równa stosunkowi różniczki funkcji do różnica jej argumentacji, niezależnie od tego, czy argument jest zmienną niezależną, czy funkcją.
to jest pochodna jest równa stosunkowi różniczki funkcji do różnica jej argumentacji, niezależnie od tego, czy argument jest zmienną niezależną, czy funkcją.
Różniczkowanie funkcji określonej parametrycznie
Niech funkcja If  ma na planie
ma na planie  w takim razie odwrotnie
w takim razie odwrotnie  Potem równości
Potem równości  zdefiniowany na planie
zdefiniowany na planie  funkcja określona parametrycznie,
funkcja określona parametrycznie,  –
parametr (zmienna pośrednia).
–
parametr (zmienna pośrednia).
PRZYKŁAD. Wykres funkcji  .
.

|
O 1 |
Skonstruowana krzywa nazywa się cykloida(ryc. 25) i jest trajektorią punktu na okręgu o promieniu 1, który toczy się bez przesuwania wzdłuż osi OX.
KOMENTARZ. Czasami, ale nie zawsze, parametr można wyeliminować z równań krzywej parametrycznej.
PRZYKŁADY.
 – równania parametryczne kółka, bo oczywiście
– równania parametryczne kółka, bo oczywiście 
 –parametryczne równania elipsy, ponieważ
–parametryczne równania elipsy, ponieważ 
 –równania parametryczne paraboli
–równania parametryczne paraboli 
Znajdźmy pochodną funkcji zdefiniowanej parametrycznie:

Pochodna funkcji określonej parametrycznie jest także funkcją określoną parametrycznie:  .
.
DEFINICJA. Druga pochodna funkcji jest pochodną jej pierwszej pochodnej.
Pochodna  rząd th jest pochodną pochodnej rzędu
rząd th jest pochodną pochodnej rzędu  .
.
Oznacz pochodne drugiego i  -ta kolejność w ten sposób:
-ta kolejność w ten sposób:
Z definicji drugiej pochodnej i reguły różniczkowania parametrycznie określonej funkcji wynika, że  Aby obliczyć trzecią pochodną, należy przedstawić drugą pochodną w formularzu
Aby obliczyć trzecią pochodną, należy przedstawić drugą pochodną w formularzu  i ponownie użyj wynikowej reguły. W podobny sposób oblicza się instrumenty pochodne wyższego rzędu.
i ponownie użyj wynikowej reguły. W podobny sposób oblicza się instrumenty pochodne wyższego rzędu.
PRZYKŁAD. Znajdź pochodne pierwszego i drugiego rzędu funkcji
 .
.
Podstawowe twierdzenia rachunku różniczkowego
TWIERDZENIE(Gospodarstwo rolne). Niech funkcja  ma w tym punkcie
ma w tym punkcie  ekstremum. Jeśli istnieje
ekstremum. Jeśli istnieje  , To
, To 
DOWÓD. Pozwalać  jest na przykład punktem minimalnym. Z definicji punktu minimalnego istnieje sąsiedztwo tego punktu
jest na przykład punktem minimalnym. Z definicji punktu minimalnego istnieje sąsiedztwo tego punktu  , w ramach którego
, w ramach którego  , to jest
, to jest  – przyrost
– przyrost  w tym punkcie
w tym punkcie  . A-przeorat
. A-przeorat  Obliczmy jednostronne pochodne w tym punkcie
Obliczmy jednostronne pochodne w tym punkcie  :
:
 przez twierdzenie o przejściu do granicy nierówności,
przez twierdzenie o przejściu do granicy nierówności,
ponieważ 
 , ponieważ
, ponieważ  Ale zgodnie z warunkiem
Ale zgodnie z warunkiem  istnieje, zatem lewa pochodna jest równa prawej i jest to możliwe tylko wtedy, gdy
istnieje, zatem lewa pochodna jest równa prawej i jest to możliwe tylko wtedy, gdy
Założenie, że  – punkt maksymalny prowadzi do tego samego.
– punkt maksymalny prowadzi do tego samego.
Znaczenie geometryczne twierdzenia:
TWIERDZENIE(Rola). Niech funkcja  ciągły
ciągły  , różniczkowalny
, różniczkowalny  I
I  wtedy jest
wtedy jest  takie, że
takie, że 
DOWÓD. Ponieważ  ciągły
ciągły  , to zgodnie z drugim twierdzeniem Weierstrassa dochodzi do
, to zgodnie z drugim twierdzeniem Weierstrassa dochodzi do  ich największy
ich największy  i najmniej
i najmniej  wartości albo w punktach ekstremalnych, albo na końcach segmentu.
wartości albo w punktach ekstremalnych, albo na końcach segmentu.
1. Niech  , Następnie
, Następnie
2. Niech  Ponieważ
Ponieważ  albo
albo  , Lub
, Lub  zostaje osiągnięty w punkcie ekstremalnym
zostaje osiągnięty w punkcie ekstremalnym  , ale zgodnie z twierdzeniem Fermata
, ale zgodnie z twierdzeniem Fermata  co było do okazania
co było do okazania
TWIERDZENIE(Lagrange’a). Niech funkcja  ciągły
ciągły  i różniczkowalne
i różniczkowalne  , wtedy jest
, wtedy jest  takie, że
takie, że  .
.
Znaczenie geometryczne twierdzenia:
Ponieważ  , to sieczna jest równoległa do stycznej. Zatem twierdzenie stwierdza, że istnieje styczna równoległa do siecznej przechodzącej przez punkty A i B.
, to sieczna jest równoległa do stycznej. Zatem twierdzenie stwierdza, że istnieje styczna równoległa do siecznej przechodzącej przez punkty A i B.
DOWÓD. Przez punkty A  oraz b
oraz b  Narysujmy sieczną AB. Jej równanie
Narysujmy sieczną AB. Jej równanie  Rozważ funkcję
Rozważ funkcję
 – odległość pomiędzy odpowiednimi punktami na wykresie i na siecznej AB.
– odległość pomiędzy odpowiednimi punktami na wykresie i na siecznej AB.
1.
 ciągły
ciągły  jako różnica funkcji ciągłych.
jako różnica funkcji ciągłych.
2.
 różniczkowalne
różniczkowalne  jako różnica funkcji różniczkowalnych.
jako różnica funkcji różniczkowalnych.
3.

Oznacza,  spełnia warunki twierdzenia Rolle’a, zatem istnieje
spełnia warunki twierdzenia Rolle’a, zatem istnieje  takie, że
takie, że
Twierdzenie zostało udowodnione.
KOMENTARZ. Formuła nazywa się Wzór Lagrange’a.
TWIERDZENIE(Cauchy’ego). Niech funkcje  ciągły
ciągły  , różniczkowalny
, różniczkowalny  I
I  , wtedy jest sens
, wtedy jest sens  takie, że
takie, że  .
.
DOWÓD. Pokażmy to  . Jeśli
. Jeśli  , a następnie funkcja
, a następnie funkcja  spełniałoby warunki twierdzenia Rolle’a, więc byłby sens
spełniałoby warunki twierdzenia Rolle’a, więc byłby sens  takie, że
takie, że  – sprzeczność z warunkiem. Oznacza,
– sprzeczność z warunkiem. Oznacza,  , a obie strony wzoru są zdefiniowane. Przyjrzyjmy się funkcji pomocniczej.
, a obie strony wzoru są zdefiniowane. Przyjrzyjmy się funkcji pomocniczej.
 ciągły
ciągły  , różniczkowalny
, różniczkowalny  I
I  , to jest
, to jest  spełnia warunki twierdzenia Rolle'a. Wtedy jest pewien punkt
spełnia warunki twierdzenia Rolle'a. Wtedy jest pewien punkt  , w której
, w której  , Ale
, Ale
co było do okazania
Sprawdzona formuła to tzw Formuła Cauchy’ego.
Reguła L'Hopitala(Twierdzenie L'Hopitala-Bernoulliego). Niech funkcje  ciągły
ciągły  , różniczkowalny
, różniczkowalny  ,
, I
I  . Ponadto istnieje skończone lub nieskończone
. Ponadto istnieje skończone lub nieskończone  .
.
Wtedy jest 
DOWÓD. Ponieważ według warunku  , następnie definiujemy
, następnie definiujemy  w tym punkcie
w tym punkcie  , zakładając
, zakładając  Następnie
Następnie  stanie się ciągły
stanie się ciągły  . Pokażmy to
. Pokażmy to 
 Udawajmy, że tak
Udawajmy, że tak  wtedy jest
wtedy jest  takie, że
takie, że  , ponieważ funkcja
, ponieważ funkcja  NA
NA  spełnia warunki twierdzenia Rolle'a. Ale zgodnie z warunkiem
spełnia warunki twierdzenia Rolle'a. Ale zgodnie z warunkiem  – sprzeczność. Dlatego
– sprzeczność. Dlatego 
 . Funkcje
. Funkcje  spełniają warunki twierdzenia Cauchy’ego na dowolnym przedziale
spełniają warunki twierdzenia Cauchy’ego na dowolnym przedziale  , który zawarty jest w
, który zawarty jest w  . Napiszmy wzór Cauchy'ego:
. Napiszmy wzór Cauchy'ego:
 ,
,
 .
.
Stąd mamy:  , ponieważ jeśli
, ponieważ jeśli  , To
, To  .
.
Przeprojektowując zmienną w ostatniej granicy, otrzymujemy wymagane:

NOTATKA 1. Reguła L'Hopitala pozostaje ważna nawet wtedy, gdy  I
I  . Pozwala ujawnić nie tylko niepewność typu
. Pozwala ujawnić nie tylko niepewność typu  , ale także rodzaj
, ale także rodzaj  :
:
 .
.
UWAGA 2. Jeżeli po zastosowaniu reguły L'Hopitala niepewność nie ujawni się, należy ją zastosować ponownie.
PRZYKŁAD.
KOMENTARZ 3 . Reguła L'Hopitala jest uniwersalnym sposobem ujawniania niepewności, istnieją jednak ograniczenia, które można ujawnić, stosując tylko jedną z wcześniej zbadanych poszczególnych technik.
Ale oczywiście  , ponieważ stopień licznika jest równy stopniowi mianownika i granicy równy stosunkowi współczynniki przy wyższych potęgach
, ponieważ stopień licznika jest równy stopniowi mianownika i granicy równy stosunkowi współczynniki przy wyższych potęgach 
Funkcja różnicowa
Funkcja nazywa się różniczkowalna w punkcie, ograniczające dla zestawu mi, jeśli jego przyrost wynosi Δ F(X 0), co odpowiada przyrostowi argumentu X, można przedstawić w postaci
Δ F(X 0) = A(X 0)(X - X 0) + ω (X - X 0), (1)
Gdzie ω (X - X 0) = O(X - X 0) o godz X → X 0 .
Wyświetlacz nazywa się mechanizm różnicowy Funkcje F w tym punkcie X 0 i wartość A(X 0)H - wartość różnicowa w tym momencie.
Dla wartości różnicy funkcji F przyjęte oznaczenie zm Lub zm(X 0), jeśli chcesz wiedzieć, w którym momencie zostało to obliczone. Zatem,
zm(X 0) = A(X 0)H.
Dzielenie w (1) przez X - X 0 i celowanie X Do X 0, otrzymujemy A(X 0) = F"(X 0). Dlatego mamy
zm(X 0) = F"(X 0)H. (2)
Porównując (1) i (2) widzimy, że wartość różniczki zm(X 0) (przy F"(X 0) ≠ 0) tak Głównym elementem przyrosty funkcji F w tym punkcie X 0, liniowy i jednocześnie jednorodny względem przyrostu H = X - X 0 .
Kryterium różniczkowalności funkcji
Aby spełnić funkcję F była różniczkowalna w danym punkcie X 0, konieczne i wystarczające jest, aby miał on w tym punkcie skończoną pochodną.
Niezmienniczość postaci pierwszej różniczki
Jeśli X jest zatem zmienną niezależną dx = X - X 0 (stały przyrost). W tym przypadku mamy
zm(X 0) = F"(X 0)dx. (3)
Jeśli X = φ (T) jest zatem funkcją różniczkowalną dx = φ" (T 0)dt. Stąd,
Widzieliśmy, że różniczkę funkcji można zapisać jako:
 (1),
(1),
Jeśli  istnieje zmienna niezależna. Niech to teraz
istnieje zmienna niezależna. Niech to teraz  istnieje złożona funkcja z
istnieje złożona funkcja z  , tj.
, tj.  ,
, i dlatego
i dlatego  . Jeżeli pochodne funkcji
. Jeżeli pochodne funkcji  I
I  istnieć, zatem
istnieć, zatem  , jako pochodna funkcji zespolonej. Mechanizm różnicowy
, jako pochodna funkcji zespolonej. Mechanizm różnicowy  Lub. Ale
Lub. Ale  i dlatego możemy pisać
i dlatego możemy pisać  , tj. znowu mam to wyrażenie
, tj. znowu mam to wyrażenie  jak w (1).
jak w (1).
Wniosek: wzór (1) jest poprawny jak w przypadku gdy  istnieje zmienna niezależna, tak jest w przypadku, gdy
istnieje zmienna niezależna, tak jest w przypadku, gdy  istnieje funkcja zmiennej niezależnej
istnieje funkcja zmiennej niezależnej  . W pierwszym przypadku pod
. W pierwszym przypadku pod  rozumiana jest jako różniczka zmiennej niezależnej
rozumiana jest jako różniczka zmiennej niezależnej  , w drugim – różniczka funkcji (w tym przypadku
, w drugim – różniczka funkcji (w tym przypadku  ogólnie rzecz biorąc). Ta właściwość zachowania kształtu (1) nazywa się niezmienność postaci różniczkowej.
ogólnie rzecz biorąc). Ta właściwość zachowania kształtu (1) nazywa się niezmienność postaci różniczkowej.
Niezmienniczość postaci różniczkowej zapewnia ogromne korzyści przy obliczaniu różnic funkcji złożonych.
Na przykład: trzeba obliczyć  . Niezależnie od tego, czy zmienna jest zależna czy niezależna
. Niezależnie od tego, czy zmienna jest zależna czy niezależna  , możemy to zapisać. Jeśli
, możemy to zapisać. Jeśli  - funkcja np
- funkcja np  , wtedy znajdziemy
, wtedy znajdziemy  i korzystając z niezmienności postaci różniczki, mamy prawo pisać.
i korzystając z niezmienności postaci różniczki, mamy prawo pisać.
§18. Pochodne wyższych rzędów.
Niech funkcja y = (x) będzie różniczkowalna na pewnym przedziale X (to znaczy ma skończoną pochodną y 1 = 1 (x) w każdym punkcie tego przedziału). Wtedy 1 (x) jest w X samym funkcją x. Może się okazać, że w niektórych punktach lub w ogóle x 1 (x) samo w sobie ma pochodną, tj. istnieje pochodna pochodnej (y 1) 1 =( 1 (x) 1. W tym przypadku nazywa się to pochodną drugą lub pochodną drugiego rzędu. Oznaczamy symbolami y 11, 11 (x), d 2 y/ dx 2. Jeśli to konieczne, podkreśl, że pochodna jest w t.x 0, następnie napisz
y 11 /x=x 0 lub 11 (x 0) lub d 2 y/ dx 2 /x=x 0
pochodna 1 nazywana jest pochodną pierwszego rzędu lub pierwszą pochodną.
Zatem pochodna drugiego rzędu jest pochodną pochodnej pierwszego rzędu funkcji.
Całkiem podobnie pochodna (jeśli istnieje) pochodnej drugiego rzędu nazywana jest pochodną trzeciego rzędu lub pochodną trzeciego rzędu.
Oznacz (y 11) 1 = y 111 = 111 (x)= d 3 y/ dx 3 = d 3 (x) / dx 3
Generalnie pochodną n-tego rzędu funkcji y = (x) nazywamy pochodną pochodnej (n-1) rzędu tej funkcji. (jeśli oczywiście istnieją).
Wyznaczyć
Przeczytaj: n-ta pochodna y, od (x); d n y przez d x w n-tym.
Czwarty, piąty itd. Niewygodne jest oznaczanie kolejności kreskami, dlatego liczbę należy wpisać w nawias, zamiast v (x) wpisać (5) (x).
W nawiasach, żeby nie pomylić n-tego rzędu pochodnej z n-tym stopniem funkcji.
Pochodne rzędu wyższego niż pierwszy nazywane są pochodnymi wyższego rzędu.
Z samej definicji wynika, że aby znaleźć n-tą pochodną, trzeba znaleźć po kolei wszystkie poprzednie od 1 do (n-1)-tej.
Przykłady: 1) y=x 5; y1 = 5x 4; y 11 = 20x 3;
y 111 = 60x 2; y (4) = 120x; y(5) =120; y (6) =0,…
2) y=e x; y 1 = mi x; y 11 =e x;…;
3) y=grzech; y 1 = cosх; y 11 = -sinх; y 111 = -cosх; y (4) = grzechх;…
Należy zauważyć, że druga pochodna ma pewne znaczenie mechaniczne.
Jeżeli pierwszą pochodną ścieżki po czasie jest prędkość ruchu prostoliniowego niejednostajnego
V=ds/dt, gdzie S=f(t) jest równaniem ruchu, wówczas V 1 =dV/dt= d 2 S/dt 2 jest szybkością zmiany prędkości, tj. przyspieszenie ruchu:
a= fa 11 (t)= dV/dt= d 2 S/dt 2 .
Zatem drugą pochodną ścieżki po czasie jest przyspieszenie ruchu punktu – takie jest mechaniczne znaczenie drugiej pochodnej.
W niektórych przypadkach można zapisać wyrażenie na pochodną dowolnego rzędu, z pominięciem pośrednich.
Przykłady:
y=e x; (y) (n) = (e x) (n) = mi x;
y=ax; y1 =a x lna; y11 =a x (lna) 2; y (n) = a x (lna) n;
y=x α; y1 = αx α-1; y 11 =  ; y (n) = α(α-1)… (α-n+1)x α-n, gdzie
; y (n) = α(α-1)… (α-n+1)x α-n, gdzie  =n mamy
=n mamy
y (n) = (x n) (n) = n! Wszystkie pochodne rzędu wyższego są równe zeru.
y=sinx; y 1 = cosх; y 11 = -sinх; y 111 = -cosх; y (4) = sinx;... itd.. Ponieważ
y 1 = grzech(x+  /2); y 11 = grzech(x+2
/2); y 11 = grzech(x+2  /2); y 111 = grzech(x+3
/2); y 111 = grzech(x+3  /2); itd., wówczas y (n) = (sinx) (n) = grzech (x + n
/2); itd., wówczas y (n) = (sinx) (n) = grzech (x + n  /2).
/2).
Łatwo to ustalić poprzez kolejne różniczkowanie i wzory ogólne:
1) (СU) (n) = С(U) (n) ; 2) (U±V) (n) = U (n) ± V (n)
Wzór na n-tą pochodną iloczynu dwóch funkcji (U·V) (n) okazuje się bardziej złożony. Nazywa się to formułą Leibniza.
Chodźmy po to
y=U·V; y 1 = U 1 V + UV 1; y 11 = U 11 V+ U 1 V 1 + U 1 V 1 + UV 11 = U 11 V+2U 1 V 1 + UV 11;
y 111 = U 111 V+ U 11 V 1 +2U 11 V 1 +2U 1 V 11 + U 1 V 11 + UV 111 = U 111 V+3U 11 V 1 +3 U 1 V 11 + UV 111;
Podobnie dostajemy
y (4) = U (4) V+4 U 111 V 1 +6 U 11 V 11 +4 U 1 V 111 + UV (4) itd.
Łatwo zauważyć, że prawe strony wszystkich tych wzorów przypominają rozwinięcie potęg dwumianu U + V, (U + V) 2, (U + V) 3 itd. Tylko zamiast potęg U i V występują pochodne odpowiednich rzędów. Podobieństwo będzie szczególnie kompletne, jeśli w otrzymanych wzorach zamiast U i V napiszemy U (0) i V (0), tj. 0-te pochodne funkcji U i V (same funkcje).
Rozszerzając to prawo na przypadek dowolnego n, otrzymujemy wzór ogólny
y (n) = (UV) (n) = U (n) V+ n/1! U (n-1) V 1 + n(n-1)/2! U (n-2) V (2) + n(n-1)(n-2)/3! U (n-3) V (3) +…+ n(n-1)…(n-к+1)/К! U (k) V (n-k) +…+ UV (n) - wzór Leibniza.
Przykład: znajdź (e x x) (n)
(e x) (n) =e x, x 1 =1, x 11 =0 i x (n) =0, zatem (e x x) (n) = (e x) (n) x+ n/1 ! (np. x) (n-1) x 1 = mi x x+ ne x = mi x (x+ n).
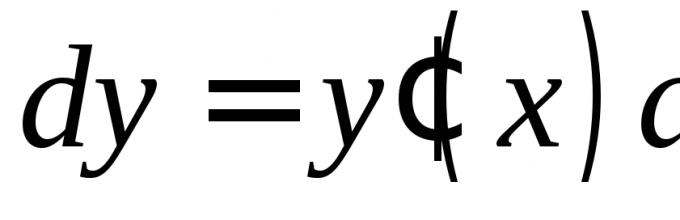
 y
y
 X
X






