Test na temat „Kinematyka” Opcja 1.
1. Odległość pomiędzy punktem początkowym i końcowym wynosi:
A) droga B) ruch C) przemieszczenie D) trajektoria
2. W którym z poniższych przypadków ruchu ciała nie można uznać za ruch? punkt materialny?
A) Ruch Ziemi wokół Słońca. B) Ruch satelity wokół Ziemi.
B) Lot samolotem z Władywostoku do Moskwy. D) Obrót obrabianej części
maszyna
3.
Które z poniższych wielkości są skalarne?
A) przemieszczenie B) droga C) prędkość
4
. Co mierzy prędkościomierz w samochodzie?
A) przyspieszenie; B) moduł prędkości chwilowej;
B) średnia prędkość; D) ruch
5.
Jaka jest podstawowa jednostka czasu? System międzynarodowy jednostki?
A) 1 godzina B) 1 minuta C) 1 s D) 1 dzień.
6.
Dwa samochody jadą po prostej autostradzie w tym samym kierunku. Jeśli skierujemy oś OX zgodnie z kierunkiem ruchu ciał po autostradzie, to jakie będą rzuty prędkości samochodów na oś OX?
7.
Samochód jeździł po Moskwie obwodnica, którego długość wynosi 109 km. Jaka jest droga przebyta l i przemieszczenie S samochodu?
A) l = 109 km; S = 0 B) l =218 km S = 109 kmV) l = 218 km; S = 0. D) l=109 km; S=218 km
8.
A ) 1 B)2 C)3 D) 4.
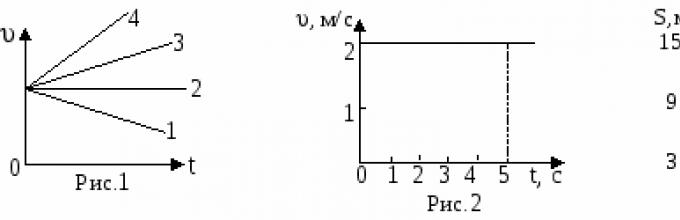
9 . Oblicz drogę przebytą przez punkt w ciągu 5 sekund. (ryc. 2).
A) 2 m B) 2,5 m C) 5 m D) 10 m.
10 .. Rysunek 3 przedstawia wykres odległości przebytej przez rowerzystę w funkcji czasu. Oblicz drogę przebytą przez rowerzystę w przedziale czasu od t 1 = 1 s do t 2 = 3 s?
11 . Jeżeli przyspieszenie wynosi 2 m/s 2 , to jest:
A) ruch jednostajny B) ruch jednostajnie zwolniony
C) ruch jednostajnie przyspieszony D) prostoliniowy
12 . Przyspieszenie charakteryzuje zmianę wektora prędkości
A) pod względem wielkości i kierunku B) w kierunku C) pod względem wielkości
13
. Samochód poruszający się po linii prostej ze stałym przyspieszeniem zwiększa swoją prędkość o:
3 m/s do 9 m/s w 6 sekund. Jak szybko jechał samochód?
A) 0 m/s 2 B) 3 m/s 2 C) 2 m/s 2 D) 1 m/s 2
14. Jaką prędkość uzyska samochód podczas hamowania z przyspieszeniem 0,5 m/s 2 10 s od rozpoczęcia hamowania, jeśli jego prędkość początkowa wynosiła 72 km/h?
A) 15 m/s B) 25 m/s C) 10 m/s D) 20 m/s.
Test na temat „Kinematyka” Opcja 2.
1
. Rowerzysta przemieszcza się z punktu A ścieżki rowerowej do punktu B po łuku AB. Nazwa
wielkość fizyczna reprezentowana przez wektor AB.
A) droga B) przemieszczenie C) prędkość
2 . Dlaczego Księżyc można uznać za punkt materialny (w stosunku do Ziemi) w obliczeniach?
A) Księżyc jest kulą B) Księżyc jest satelitą Ziemi C) Masa Księżyca jest mniejsza od masy Ziemi
D) Odległość Ziemi od Księżyca jest wielokrotnie większa niż promień Księżyca.
3.
. Wielkości fizyczne mogą być wektorami lub skalarami. Który wielkość fizyczna z powyższego jest skalarny?
A) przyspieszenie B) czas C) prędkość D) przemieszczenie
4.
. Które z poniższych wielkości są wielkościami wektorowymi:
1) ścieżka 2) ruch 3) prędkość?
A) 1 i 2 B) 2 i 3 C) 2 D) 3 i 1.
5
. Podstawowe jednostki długości w SI to:
A) metr B) kilometr C) centymetr D) milimetr
6
. Dwa samochody jadą po prostej autostradzie w przeciwnych kierunkach. Jeżeli oś OX jest skierowana zgodnie z kierunkiem ruchu pierwszego samochodu na autostradzie, to jakie będą rzuty prędkości samochodów na oś OX?
A) oba dodatnie B) oba ujemne
C) pierwszy - pozytywny, drugi - negatywny
D) pierwszy - negatywny, drugi - pozytywny
7
. Ciało rzucone pionowo sięga największa wysokość 10 m i upadł
grunt. Jaka jest droga l i przemieszczenie S w całym czasie jego ruchu?
A) l = 20 m, S = 0 m B) l = 10 m, S = 0B) l = 10 m, S = 20 m D) l = 20 m, S = 10 m.
8 . Który z wykresów odpowiada ruchowi jednostajnemu? (ryc. 1).
A ) 3 B)4 C)1 D) 2
9 . Oblicz drogę przebytą przez punkt w ciągu 3 sekund. (ryc. 2).
A) 2 m B) 6 m C) 5 m D) 1,5 m.
10. . Rysunek 3 przedstawia wykres odległości przebytej przez rowerzystę w funkcji czasu. Oblicz drogę przebytą przez rowerzystę w przedziale czasu od t 1 = 2 s do t 2 = 4 s?
A) 9 m B) 6 m C) 3 m D) 12 m
11 . Jeśli przyspieszenie wynosi -3m/s 2 , to jest:
A) ruch jednostajny B) ruch jednostajnie przyspieszony
C) ruch równomiernie zwolniony D) ruch liniowy
12
. Samochód rusza i porusza się po linii prostej ze zwiększającą się prędkością.
A) przyspieszenie wynosi 0. B) jest skierowane przeciwnie do ruchu samochodu
B) skierowane w kierunku ruchu samochodu
13. W ciągu 20 s prędkość samochodu spadła z 20 m/s do 10 m/s. Jakie jest średnie przyspieszenie samochodu?
A) 0,5 m/s 2 B) 5 m/s 2 C) -5 m/s 2 D) -0,5 m/s 2
14 . Wyznacz prędkość ciała podczas hamowania z przyspieszeniem 0,2 m/s 2 30 s od początku ruchu, jeśli jego prędkość początkowa wynosiła 2 m/s.
A) -4m B) 4m C) -6m D) 8m.
Odpowiedzi
Opcja 1 Opcja 2
1 -b 1 -b
2 - g 2 - g
3 – a 3 – b
4 – b 4 – ok
5 – w 5 – a
6 – a 6 – ok
7 - w 7 - a
8 – b 8 – zm
9 – d 9 – ur
10 – b 10 – b
11 - o 11 - o godz
12 – 12 – cali
13 – g. 13 – g
14 – b 14- a
1.13. Samochód rusza i porusza się po linii prostej ze zwiększającą się prędkością.
Jaki kierunek ma wektor przyspieszenia?
1.14. Samochód zwalnia na prostym odcinku drogi. Jaki kierunek ma znaczenie
wektor przyspieszenia?
A) przyspieszenie wynosi 0; B) skierowane przeciwko ruchowi samochodu;
B) skierowane w kierunku, w którym porusza się samochód.
1.16. Wielkości fizyczne mogą być wektorami lub skalarami. Która z poniższych wielkości fizycznych jest skalarna?
A) przyspieszenie; B) czas; B) prędkość; D) ruch.
1.18. Podstawowe jednostki długości w SI to:
A) kilometr; B) licznik; B) centymetr; D) milimetr.
1.19. Które z poniższych wielkości są wielkościami wektorowymi:
1) droga, 2) ruch, 3) prędkość?
A) 1 i 2; B) 2; B) 2 i 3; D) 3 i 1.
1,22. Poruszając się prostoliniowo, jedno ciało w ciągu sekundy pokonuje drogę 5 m, drugie - 10 m. Ruchy tych ciał są następujące: A) jednolity; B) nierówny; C) pierwszy jest nierówny, drugi jednolity; D) pierwszy jest jednolity, drugi nierówny
1 25. Moduł prędkości ciała zwiększał się 2 razy na sekundę. Które stwierdzenie byłoby poprawne?
A) przyspieszenie zmniejszyło się 2 razy; B) przyspieszenie nie uległo zmianie;
B) przyspieszenie wzrosło 2 razy
1,26. Ciało rzucone pionowo w górę osiąga maksymalną wysokość 10 m i spada
grunt. Jaka jest droga l i przemieszczenie S w całym czasie jego ruchu?
A) l = 10 m, S = 0 m; B) l = 20 m, S = 0;
B) l = 10 m, S = 20 m; D) l = 20 m, S = 10 m.
1,35. Przyspieszenie pociągu na wyjściu ze stacji wynosi 1 m/s2. Jaką drogę przejedzie pociąg w ciągu 10 s?
A) 5 m; B) 10 m; B) 50 m; D) 100 m.
1,36. Na ruch jednostajnie przyspieszony w ciągu 5 s samochód zwiększył prędkość z 10 do
15 m/s. Jaki jest moduł przyspieszenia samochodu?
A) 1 m/s2; B) 2 m/s2; B) 3 m/s2; D) 5 m/s2.
1,55. Która z podanych funkcji (v(t)) opisuje zależność modułu prędkości od
czas w mundurze prosty ruch ciało wzdłuż osi OX z prędkością 5 m/s?
A) v = 5t; B) v = t; B) v = 5; D) v = -5.
1,65. Klockowi umieszczonemu na poziomej powierzchni stołu nadano prędkość 5 m/s. Pod wpływem sił tarcia klocek porusza się z przyspieszeniem 1 m/s2. Jaka jest droga przebyta przez klocek w ciągu 6 sekund?
A) 48 m; B) 12 m; B) 40 m; D) 30 m.

13. Rysunek 3 przedstawia wykres drogi przebytej przez rowerzystę w funkcji czasu. Oblicz drogę przebytą przez rowerzystę w przedziale czasu od t 1 = 1 s do t 2 = 4 s?
A) 15 m. B) 3 m. W) 12 m. G) 9 m. D) 20 m.
14. Rysunek 3 przedstawia wykres odległości przebytej przez rowerzystę w funkcji czasu. Wyznacz prędkość rowerzysty w chwili t = 2c.
A) 2 m/s. B) 6 m/s. W) 3 m/s. G) 12 m/s. D) 8 m/s.
18. Ciało porusza się po linii prostej i zmniejsza prędkość. Gdzie skierowane jest przyspieszenie?
A) Po drodze. B) Normalnie. W) Przeciw ruchowi. G) Wzdłuż wektora promienia do danego punktu na trajektorii. D) Styczna do trajektorii
A) Księżyc jest piłką . B) Księżyc jest satelitą Ziemi. W) Masa Księżyca jest mniejsza niż masa Ziemi.
G) Odległość Ziemi od Księżyca jest wielokrotnie większa niż promień Księżyca.
D) Wśród proponowanych odpowiedzi nie ma prawidłowej odpowiedzi.
Prędkość pojazdu dla 20 s spadła z 20 m/s zanim 10 m/s . Jakie jest średnie przyspieszenie samochodu? [-0,5 m/s 2 ]
Zadanie 1.6. Znajdować graficznie ruchu i przebytej drogi T 1 = 5 z punktem materialnym, którego ruch wzdłuż osi OH opisane równaniem X = 6 – 4T + T 2, gdzie wszystkie wielkości wyrażone są w jednostkach SI.
Rozwiązanie. W zadaniu 1.5 znaleźliśmy (4) rzut prędkości na oś OH:
Wykres prędkości odpowiadający temu wyrażeniu pokazano na rysunku 1.6. Rzut ruchu na oś OH równa sumie algebraicznej pól trójkątów AOB I BCD. Ponieważ rzut prędkości w pierwszej sekcji jest ujemny, obszar trójkąta AOB weź ze znakiem minus; a rzut prędkości w drugiej części jest dodatni, to obszar trójkąta BCD weź ze znakiem plus:
Ponieważ ścieżka jest długością trajektorii i nie może się zmniejszyć, aby ją znaleźć, dodajemy obszary tych trójkątów, uznając za dodatnie obszar nie tylko trójkąta BCD, ale także trójkąt AOB:
Wcześniej (patrz zadanie 1.5) szukaliśmy tej ścieżki w inny sposób – analitycznie.
Zadanie 1.7. Na ryc. 1,7, A przedstawia wykres zależności współrzędnych jakiegoś ciała poruszającego się prostoliniowo wzdłuż osi OH, od czasu. Zakrzywione sekcje wykresu są częściami paraboli. Narysuj wykresy prędkości i przyspieszenia w funkcji czasu.
Rozwiązanie. Aby zbudować wykresy prędkości i przyspieszenia, ustawiamy zgodnie z tym wykresem (ryc. 1.7, A) charakter ruchu ciała w różnych okresach czasu.
W przedziale 0 – T 1 wykres współrzędnych jest częścią paraboli, której ramiona są skierowane w górę. Dlatego w równaniu
wyrażając w ogólnej formie zależność współrzędnej X od czasu T, współczynnik wcześniej T 2 jest dodatnie, tj. A x > 0. A ponieważ parabola jest przesunięta w prawo, oznacza to, że w 0X < 0, т.е. тело имело начальную скорость, направленную противоположно направлению оси ОХ. В течение промежутка 0 – T 1 moduł prędkości ciała najpierw maleje do zera, następnie prędkość zmienia kierunek na przeciwny i jej moduł wzrasta do określonej wartości w 1. Wykres prędkości w tej sekcji to odcinek linii prostej przechodzący pod pewnym kątem do osi T(ryc. 1.7, B), a wykres przyspieszenia jest odcinkiem poziomej linii prostej leżącej nad osią czasu (ryc. 1.7, V). Wierzchołek paraboli na rys. 1,7, A odpowiada wartości w 0X= 0 na ryc. 1,7, B.
Tymczasem T 1 – T 2 ciało poruszało się równomiernie z prędkością w 1 .
Tymczasem T 2 – T Wykres współrzędnych 3 jest częścią paraboli, której ramiona są skierowane w dół. Dlatego tutaj x < 0, скорость тела убывает до нуля к моменту времени T 3 i w międzyczasie T 3 – T 4 ciało znajduje się w spoczynku. Następnie przez pewien okres czasu T 4 – T 5 Ciało porusza się ze stałą prędkością w 2 cale Odwrotna strona. W pewnym momencie T 5 osiąga punkt początkowy i zatrzymuje się.
Uwzględniając charakter ruchu ciała, skonstruujemy odpowiednie wykresy rzutów prędkości i przyspieszenia (ryc. 1.7, pne).
Zadanie 1.8. Niech wykres prędkości będzie miał postać pokazaną na ryc. 1.8. Na podstawie tego wykresu narysuj wykres zależności drogi od czasu.
Rozwiązanie. Podzielmy cały rozpatrywany okres na trzy części: 1, 2, 3. W odcinku 1 ciało porusza się jednostajnie przyspieszonym bez prędkości początkowej. Formuła ścieżki dla tej sekcji ma postać
Gdzie A– przyspieszenie ciała.
Przyspieszenie to stosunek zmiany prędkości do okresu czasu, w którym ta zmiana nastąpiła. Jest równy stosunkowi segmentów.
W odcinku 2 ciało porusza się równomiernie z prędkością w, nabyte pod koniec sekcji 1. Ruch jednolity rozpoczął się nie w początkowej chwili czasu, ale w tej chwili T 1. W tym momencie ciało minęło już ścieżkę. Zależność drogi od czasu dla odcinka 2 ma postać:
W części 3 ruch jest równomiernie powolny. Wzór ścieżki dla tej sekcji jest następujący:
Gdzie A 1 – przyspieszenie w odcinku 3. Jest to połowa przyspieszenia A w sekcji 1, ponieważ sekcja 3 jest dwa razy dłuższa niż sekcja 1.
Wyciągnijmy wnioski. W części 1 wykres ścieżki wygląda jak parabola, w sekcji 2 - linia prosta, w sekcji 3 - również parabola, ale odwrócona (wypukłą stroną do góry) (patrz ryc. 1.9).
Wykres ścieżki nie powinien mieć załamań, jest przedstawiany jako gładka linia, to znaczy parabole są sprzężone z linią prostą. Wyjaśnia to fakt, że tangens kąta nachylenia stycznej do osi czasu określa wartość prędkości w chwili czasu T, tj. Na podstawie nachylenia stycznych do wykresu ścieżki można znaleźć prędkość ciała w tym czy innym momencie. A ponieważ wykres prędkości jest ciągły, wykres ścieżki nie ma przerw.
Ponadto wierzchołek odwróconej paraboli musi odpowiadać momentowi w czasie T 3. Wierzchołki paraboli muszą odpowiadać momentom 0 i T 3, gdyż w tych momentach prędkość ciała wynosi zero, a ścieżki styczne do wykresu muszą być dla tych punktów poziome.
Droga przebyta przez ciało w czasie T 2, numerycznie równa powierzchni figurki OABG, utworzony przez wykres prędkości na przedziale Z 2 .
Zadanie 1.9. Na ryc. Rysunek 1.10 przedstawia wykres rzutu prędkości jakiegoś ciała poruszającego się prostoliniowo wzdłuż osi OH, od czasu. Konstruuj wykresy przyspieszenia, położenia i drogi w funkcji czasu. W początkowej chwili ciało było w punkcie X 0 = –3 m. Wszystkie wartości podane są w jednostkach SI.
Rozwiązanie. Aby wykreślić zależność przyspieszenia x(T), ustalimy zgodnie z harmonogramem vx(T) charakter ruchu ciała w różnych okresach czasu. Pamiętajmy o tym z definicji
gdzie jest rzutem prędkości , .
W przedziale czasu c:
W tej sekcji i (znaki są takie same), tj. ciało porusza się ze stałym przyspieszeniem.
W przedziale czasu c:
te. i (znaki projekcyjne są przeciwne) – ruch jest równie powolny.
W części c rzut prędkości, tj. ruch następuje w dodatnim kierunku osi OH.
W części c rzut prędkości jest taki, że ciało znajduje się w spoczynku (i ).
W sekcji c:
I (znaki są takie same) – ruch jest równomiernie przyspieszany, ale od , wówczas ciało porusza się względem osi OH.
Po szóstej sekundzie ciało porusza się równomiernie () względem osi OH. wygląda jak pokazano na rys. 1.11, G.
PL 01 MATEMATYKA
Zbiór zadań do samodzielnej pracy pozalekcyjnej na temat: „Zastosowanie całki oznaczonej do rozwiązywania problemów fizycznych”.
dla specjalizacji:
100126 Usługi domowe i użyteczności publicznej
Wołogda 2013
Matematyka: Zbiór zadań do samodzielnej pracy pozalekcyjnej na temat: „Zastosowanie całki oznaczonej do rozwiązywania problemów fizycznych” dla specjalności: 100126 Usługi domowe i komunalne
Ten zbiór zadań do samodzielnej pracy pozalekcyjnej na temat: „Zastosowanie całki oznaczonej do rozwiązywania problemów fizycznych” jest pomoc nauczania w sprawie organizowania samodzielnej pracy pozalekcyjnej dla uczniów.
Zawiera zadania do samodzielnej pracy pozalekcyjnej dla sześciu opcji oraz kryteria oceny zaliczenia samodzielnej pracy.
Zestaw ma pomóc uczniom w usystematyzowaniu i utrwaleniu materiału teoretycznego zdobytego na lekcjach matematyki oraz rozwinięciu umiejętności praktycznych.
Opracował: E. A. Sevaleva – nauczyciel matematyki najwyższej kategorii w Wołogdy Construction College
2. Samodzielna praca.
3. Kryteria oceny.
4. Literatura.
Notatka wyjaśniająca
Niniejsza praca stanowi przewodnik edukacyjno-metodyczny dotyczący organizacji samodzielnej pracy pozalekcyjnej dla uczniów w dyscyplinie EN 01 „Matematyka” dla specjalności 100126 Usługi gospodarstwa domowego i użyteczności publicznej.
Cel instrukcje metodologiczne polega na zapewnieniu efektywności samodzielnej pracy, ustaleniu jej treści, ustaleniu wymagań dotyczących projektu i wyników samodzielnej pracy.
Celem samodzielnej pracy studentów w dyscyplinie EN 01 „Matematyka” jest:
· usystematyzowanie i utrwalenie zdobytej wiedzy teoretycznej i umiejętności praktycznych;
· pogłębianie i poszerzanie wiedzy teoretycznej;
· kształtowanie umiejętności korzystania z literatury przedmiotu i dodatkowej;
· rozwój zdolności poznawcze i aktywność studencka, inicjatywa twórcza, samodzielność i samoorganizacja;
· aktywizacja działalności edukacyjnej i poznawczej przyszłych specjalistów.
Samodzielna praca wykonywana jest indywidualnie w czasie wolnym od zajęć.
Student jest zobowiązany:
- przed wykonaniem samodzielnej pracy powtarzaj materiał teoretyczny omawiany na lekcjach;
- wykonać pracę zgodnie z zadaniem;
- dla każdego niezależna praca Złóż sprawozdanie nauczycielowi w formie pracy pisemnej.
Samodzielna praca na temat:
„Zastosowanie całki oznaczonej do rozwiązywania problemów fizycznych”
Cel: naucz się stosować całkę oznaczoną do rozwiązywania problemów fizycznych.
Teoria.
Obliczanie drogi przebytej przez punkt.
Droga, którą przebył punkt podczas nierównomiernego ruchu po linii prostej ze zmienną prędkością oraz odstęp czasu od do oblicza się ze wzoru
 …… (1)
…… (1)
Przykład 1. ![]() SM. Znajdź drogę przebytą przez punkt w skali 10 Z od początku ruchu.
SM. Znajdź drogę przebytą przez punkt w skali 10 Z od początku ruchu.
Rozwiązanie: Zgodnie z warunkiem ![]() , , .
, , .
Korzystając ze wzoru (1) znajdujemy:

Odpowiedź: .
Przykład 2. Prędkość punktu różni się w zależności od prawa ![]() SM. Znajdź drogę przebytą przez punkt w ciągu 4 sekund.
SM. Znajdź drogę przebytą przez punkt w ciągu 4 sekund.
Rozwiązanie: Zgodnie z warunkiem ![]() , ,
, ,
Stąd:
Odpowiedź: .
Przykład 3. Prędkość punktu różni się w zależności od prawa ![]() SM. Znajdź drogę przebytą przez punkt od początku jego ruchu do jego zatrzymania.
SM. Znajdź drogę przebytą przez punkt od początku jego ruchu do jego zatrzymania.
Rozwiązanie:
· Prędkość punktu wynosi 0 w momencie, gdy zaczyna się poruszać, i w momencie, gdy się zatrzymuje.
· Ustalmy, w którym momencie punkt się zatrzyma, w tym celu należy rozwiązać równanie: ![]()

To jest , .
· Korzystając ze wzoru (1) znajdujemy:
Odpowiedź: .
Obliczanie pracy siły.
Praca wykonywana przez zmienną siłę podczas ruchu wzdłuż osi Oh punkt materialny od x = a zanim x =, oblicza się ze wzoru:
 …… (2)
…… (2)
Często wykorzystuje się go przy rozwiązywaniu problemów polegających na obliczaniu pracy siły Prawo Hooke’a: ……(3), gdzie
Siła ( N);
X– wydłużenie bezwzględne (ściskanie) sprężyny pod wpływem siły ( M);
Współczynnik proporcjonalności ( N/m).
Przykład 4. Oblicz pracę wykonaną przez siłę, gdy sprężyna jest ściśnięta o 0,04 M, jeśli skompresować go o 0,01 M potrzebuję siły 10 N.
Rozwiązanie:
· Ponieważ x = 0,01 M przy sile =10 N

![]() , znajdujemy, tj.
, znajdujemy, tj. ![]() .
.

Odpowiedź:J.
Przykład 5. Sprężyna w spoczynku ma długość 0,2 M. Siła po 50 N rozciąga sprężynę o 0,01 M. Ile pracy należy wykonać, aby rozciągnąć sprężynę od 0,22 M do 0,32 M?
Rozwiązanie:
· Ponieważ x = 0,01 przy sile =50 N, następnie podstawiając te wartości do równości (3): , otrzymujemy:

· Teraz podstawiamy znalezioną wartość do tej samej równości ![]() , znajdujemy, tj.
, znajdujemy, tj. ![]() .
.
· Znalezienie granic całkowania: M, M.
· Znajdziemy pracę, której szukasz, korzystając ze wzoru (2): 
Gdzie X I y– w cm, a T- w wiosce Definiować trajektoria punktu, prędkość i przyspieszenie w momentach czasu t 0 =0 s, t 1 =1 s I t 2 = 5 s, a także drogę przebytą przez punkt w ciągu 5 s.
Rozwiązanie
Obliczanie trajektorii
Wyznaczamy trajektorię punktu. Mnożymy pierwsze podane równanie przez 3, drugie przez (-4), a następnie dodajemy ich lewą i prawą stronę:
3x=6t 2 +6
-4y=-6t 2 -4
————
3x-4 lata=2
Rezultatem jest równanie pierwszego stopnia - czyli równanie linii prostej ruch punktowy– prosto (rysunek 1.5).
Aby wyznaczyć współrzędne początkowego położenia punktu A 0, podstawiamy w dane równania wartości t0 =0; z pierwszego równania, które otrzymujemy x 0 = 2 cm, od drugiego y 0 = 1 cm. Dla dowolnej innej wartości t współrzędne x i y poruszającego się punktu tylko rosną, więc trajektoria punktu jest półprostą 3x-4 lata=2 z początkiem w punkcie A 0 (2; 1).

Rysunek 1.5
Obliczanie prędkości
Ustalamy to najpierw znajdując rzuty na osie współrzędnych :
![]()
Na t 0 = 0 s prędkość punktowa v 0 = 0, Na t 1 = 1 s – v 1 = 5 cm/s, Na t 2 = 5 s – v 2 = 25 cm/s.
Obliczanie przyspieszenia
Definiujemy przyspieszenie punktowe. Jego rzuty na osie współrzędnych:

Projekcje przyspieszenia nie zależą od czasu ruchu,
te. ruch punktu jest równomiernie przyspieszony, wektory prędkości i przyspieszenia pokrywają się z trajektorią punktu i są wzdłuż niej skierowane.
Z drugiej strony, ponieważ ruch punktu jest prostoliniowy, moduł przyspieszenia można wyznaczyć poprzez bezpośrednie różniczkowanie równania prędkości.