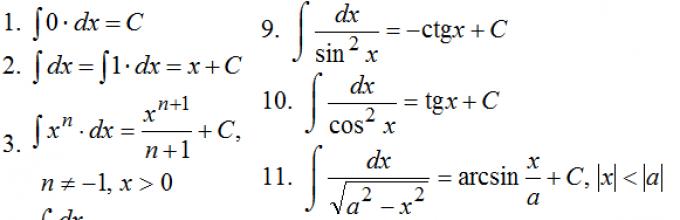Poniżej wymieniono cztery główne metody integracji.
1)
Zasada całkowania sumy lub różnicy.
.
Tutaj i poniżej u, v, w są funkcjami zmiennej całkującej x.
2)
Przesunięcie stałej poza znak całki.
Niech c będzie stałą niezależną od x. Następnie można go wyjąć ze znaku całki.
3)
Zmienna metoda wymiany.
Rozważmy całkę nieoznaczoną.
Jeśli uda nam się znaleźć taką funkcję φ (X) od x, więc
,
wówczas, zastępując zmienną t = φ(x), mamy
.
4)
Wzór na całkowanie przez części.
,
gdzie u i v są funkcjami zmiennej całkującej.
Ostateczny cel obliczeń Całki nieoznaczone- polega to na sprowadzeniu danej całki poprzez przekształcenia do najprostszych całek, które nazywane są całkami tabelarycznymi. Całki tabelaryczne wyraża się za pomocą funkcji elementarnych przy użyciu znanych wzorów.
Zobacz Tabelę całek >>>
Przykład
Oblicz całkę nieoznaczoną
Rozwiązanie
Zauważmy, że całka jest sumą i różnicą trzech wyrazów:
, I .
Stosowanie metody 1
.
Następnie zauważamy, że całki nowych całek są mnożone przez stałe 5, 4,
I 2
odpowiednio. Stosowanie metody 2
.
W tabeli całek znajdujemy wzór
.
Zakładając, że n = 2
, znajdujemy pierwszą całkę.
Przepiszmy drugą całkę w postaci
.
Zauważamy to. Następnie
Zastosujmy trzecią metodę. Zmieniamy zmienną t = φ (x) = log x.
.
W tabeli całek znajdujemy wzór
Ponieważ zmienną całkowania można oznaczyć dowolną literą
Przepiszmy trzecią całkę w postaci
.
Stosujemy wzór na całkowanie przez części.
Połóżmy to.
Następnie
;
;
;
;
.
Wreszcie mamy
.
Zbierzmy terminy z x 3
.
.
Odpowiedź
Bibliografia:
N.M. Gunther, RO Kuźmin, Zbiór problemów matematyki wyższej, „Lan”, 2003.
Całkowanie jest jedną z głównych operacji analizy matematycznej. Tablice znanych funkcji pierwotnych mogą być przydatne, ale obecnie, po pojawieniu się systemów algebry komputerowej, tracą one na znaczeniu. Poniżej znajduje się lista najpopularniejszych prymitywów.
Tabela całek podstawowych
Kolejna, kompaktowa opcja

Tabela całek funkcji trygonometrycznych
Z funkcji wymiernych
Z funkcji niewymiernych
Całki funkcji przestępnych

„C” jest dowolną stałą całkowania, którą wyznacza się, jeśli znana jest wartość całki w dowolnym punkcie. Każda funkcja ma nieskończoną liczbę funkcji pierwotnych.
Większość uczniów i studentów ma problemy z obliczaniem całek. Ta strona zawiera tabele integralne z funkcji trygonometrycznych, wymiernych, irracjonalnych i transcendentalnych, które pomogą w rozwiązaniu. Pomocna będzie również tabela instrumentów pochodnych.
Wideo - jak znaleźć całki
Jeśli nie do końca rozumiesz ten temat, obejrzyj film, który szczegółowo wszystko wyjaśnia.Tabela funkcji pierwotnych
Korzystając z własności całek nieoznaczonych i tabeli całek podstawowych,
Możesz zintegrować niektóre funkcje.
TECHNIKI INTEGRACYJNE
Metoda substytucyjna
Najpopularniejszą metodą całkowania funkcji jest metoda
podstawienie, które stosuje się, gdy szukana całka
jest tabelaryczny, ale poprzez szereg elementarnych przekształceń może taki być
zredukowane do stołu.
zmienną t zastępuje się zmienną / stosując wzór x=φ(t) i,
dlatego dx jest iloczynem φ"(t)dt.
Całkowanie przez części
Przykład: musisz znaleźć całkę
Tutaj podwójne pionowe linie obejmują wszystkie obliczenia, które
przygotowują do zastosowania formuły całkowania
Części. Wpisy przygotowawcze można wyjąć poza równanie.
OKREŚLONA CAŁKA
Zadanie. Znajdź przyrost funkcji, która jest pierwotna funkcji f(x), kiedy
przejście argumentu x z wartości a na wartość b.
Rozwiązanie. Załóżmy, że poprzez całkowanie znaleźliśmy
Jak widzimy, w wyrażeniu na przyrost funkcja pierwotna F(x) + C 1
nie ma stałej wartości C1. A ponieważ C 1 oznaczało dowolny
podany numer, wówczas uzyskany wynik prowadzi do następującego wniosku: kiedy
przejście argumentu x z wartości x=a na wartość x=b, wszystkie funkcje F(x) + C,
funkcje pierwotne dla danej funkcji f(x) mają ten sam przyrost równy
F(b)-F(a).
Przyrost ten nazywa się zwykle całką oznaczoną i oznacza
symbol
Zatem wymagana całka jest równa 6.
Znaczenie geometryczne określona całka
1. Znajdź obszar jednego łuku sinusoidalnego.
Korpus obrotu pokazano na rysunku.
Jako płaszczyznę wybiorę płaszczyznę xy.
Przykład nr 2. Znajdowanie całki oznaczonej metodą zmiany zmiennej
integracja
Przykład nr 3. Znajdowanie całki oznaczonej poprzez całkowanie po
Części.
Zależności między masą m a gęstością p:
Relacje pomiędzy ładunek elektryczny q i natężenie prądu I:
Zależność pomiędzy pojemnością cieplną c a ilością ciepła Q:
Opis ruchu lepkiej cieczy, krwi w naczyniach, rozkład
ciśnienie krwi w układzie sercowo-naczyniowym, termiczne, elektryczne,
procesy magnetyczne, optyczne związane z życiem
organizmu, wymaga zastosowania integracji.
SZKOLENIE: ROZWIĄZANIE PRZYKŁADÓW
punkty zmieniają się zgodnie z prawem v = (6t +7) m/s
Określ, jak przebyta droga zależy od czasu, jeśli prędkość materiału
punkty zmieniają się zgodnie z prawem v = (6t +7) m/s, jeśli wiadomo, że w chwili początkowej
czas (t=0), punkt materialny znajdował się w odległości s 0 = 4 m od początku
Znajdź pracę wykonaną przez sprężynę, gdy zostanie ona rozciągnięta od x 1 do x 2.
Rozwiązanie.
Aby zintegrować tę funkcję, musisz dokonać wymiany
zmienny
Ponieważ na odcinku [-1;2] jest 4 2 ≤2, to obliczamy pole S tej figury
w następujący sposób:
Rozwiązanie.
u=sinx
du = cosxdx
nowe granice całkowania: u 1 = 0 (ponieważ x 1 = 0, podstawimy tę wartość do nowego
funkcja - u = sinx, u 1 = sinx 1 = 0)
pojawienie się w nim prądu indukcyjnego,
| |
| odpowiedź: |
RÓWNANIA RÓŻNICZKOWE
Równania różniczkowe to równania zawierające wymagane
funkcje, ich pochodne różnych rzędów i zmienne niezależne.
Teoria równań różniczkowych powstała pod koniec XVII wieku pod
wpływ potrzeb mechaniki i innych dyscyplin nauk przyrodniczych,
zasadniczo jednocześnie z rachunkiem całkowym i
rachunek różniczkowy.
Najprostsze równania różniczkowe zetknęły się już w pracach I.
Newtona i G. Leibniza; termin „równania różniczkowe”
należy do Leibniza. Problem znalezienia całki nieoznaczonej F (x)
funkcje f(x) Newton rozpatrywane po prostu jako szczególny przypadek jego drugi
zadania. Takie było podejście Newtona, jako twórcy fundamentów
matematyczne nauki przyrodnicze są w pełni uzasadnione: w bardzo dużym stopniu
W wielu przypadkach prawa natury rządzące niektórymi procesami,
wyrażane są w postaci równań różniczkowych i obliczania ich przepływu
procesy sprowadzają się do rozwiązywania równań różniczkowych.
Następne dwa proste przykłady może służyć jako ilustracja
co było powiedziane.
1) Jeżeli ciało ogrzane do temperatury T zostanie umieszczone w ośrodku o temp
która jest równa zeru, to pod pewnymi warunkami możemy to założyć
przyrost ΔT (ujemny w przypadku T > 0) jego temperatury powyżej małego
przedział czasu Δt wyraża się z wystarczającą dokładnością wzorem
gdzie k jest stałym współczynnikiem. Podczas przetwarzania tego matematycznie
problem fizyczny wierzyć, że dokładnie to samo
graniczny stosunek różnic
tzn. to ma miejsce równanie różniczkowe
gdzie T oznacza pochodną nr t.
rozciągając sprężynę, przenosi ładunek
ruch. Jeśli x(t) oznacza
wielkość odchylenia ciała od
w danej chwili położenie równowagi
czas t, następnie przyspieszenie ciała
wyraża się drugą pochodną x” (t).
Siła tx” (t) działająca na ciało wynosi
z małymi odcinkami wiosny
zgodnie z prawami teorii sprężystości jest ona proporcjonalna do odchylenia x (t). To.,
otrzymujemy równanie różniczkowe
 |
| Jego rozwiązanie wygląda następująco: |