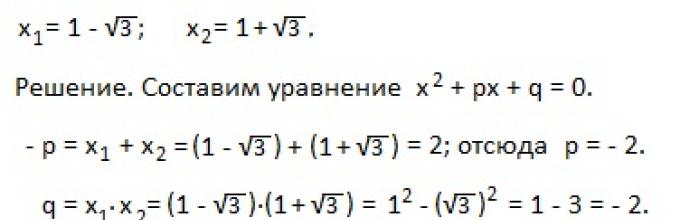Pierwsze stwierdzenie stwierdza, że suma pierwiastków tego równania jest równa wartości współczynnika zmiennej x (w tym przypadku jest to b), ale ze znakiem przeciwnym. Wizualnie wygląda to tak: x1 + x2 = −b.
Drugie stwierdzenie nie jest już związane z sumą, ale z iloczynem tych samych dwóch pierwiastków. Iloczyn ten jest przyrównywany do swobodnego współczynnika, tj. C. Lub x1 * x2 = c. Obydwa przykłady są rozwiązywane w systemie.
Twierdzenie Viety znacznie upraszcza rozwiązanie, ale ma jedno ograniczenie. Równanie kwadratowe, którego pierwiastki można znaleźć za pomocą tej techniki, należy zredukować. W powyższym równaniu współczynnik a, ten przed x2, jest równy jeden. Każde równanie można sprowadzić do podobnej postaci, dzieląc wyrażenie przez pierwszy współczynnik, ale ta operacja nie zawsze jest racjonalna.
Dowód twierdzenia
Na początek warto pamiętać, jak zgodnie z tradycją zwyczajowo szuka się korzeni równanie kwadratowe. Znaleziono pierwszy i drugi pierwiastek, a mianowicie: x1 = (-b-√D)/2, x2 = (-b+√D)/2. Ogólnie rzecz biorąc, jest ono podzielne przez 2a, ale jak już wspomniano, twierdzenie to można zastosować tylko wtedy, gdy a=1.Z twierdzenia Viety wiadomo, że suma pierwiastków jest równa drugiemu współczynnikowi ze znakiem minus. Oznacza to, że x1 + x2 = (-b-√D)/2 + (-b+√D)/2 = −2b/2 = −b.
To samo dotyczy iloczynu nieznanych pierwiastków: x1 * x2 = (-b-√D)/2 * (-b+√D)/2 = (b2-D)/4. Z kolei D = b2-4c (znowu przy a=1). Okazuje się, że wynikiem jest: x1 * x2 = (b2- b2)/4+c = c.
Z góry prosty dowód Można wyciągnąć tylko jeden wniosek: twierdzenie Viety zostało całkowicie potwierdzone.
Drugie sformułowanie i dowód
Twierdzenie Viety ma inną interpretację. Mówiąc ściślej, nie jest to interpretacja, ale sformułowanie. Faktem jest, że jeśli zostaną spełnione te same warunki, co w pierwszym przypadku: istnieją dwa różne pierwiastki rzeczywiste, wówczas twierdzenie można zapisać innym wzorem.Ta równość wygląda następująco: x2 + bx + c = (x - x1)(x - x2). Jeżeli funkcja P(x) przecina się w dwóch punktach x1 i x2, to można ją zapisać jako P(x) = (x - x1)(x - x2) * R(x). W przypadku, gdy P ma drugi stopień, a tak właśnie wygląda pierwotne wyrażenie, wówczas R jest liczbą pierwszą, czyli 1. To stwierdzenie jest prawdziwe z tego powodu, że w przeciwnym razie równość nie będzie zachowana. Współczynnik x2 przy otwieraniu nawiasów nie powinien być większy niż jeden, a wyrażenie powinno pozostać kwadratowe.
Trzy liczby 12x, x 2-5 i 4 w tej kolejności tworzą liczbę rosnącą postęp arytmetyczny https://youtu.be/U0VO_N9udpI Wybierz prawidłowe stwierdzenie MATEMATYKA ZFTSH MIPT Moskiewski Instytut Fizyki i Technologii ( Uniwersytet stanowy) Korespondencja szkoły fizycznej i technicznej. http://pin.it/9w-GqGp Znajdź wszystkie x, yiz takie, że liczby 5x + 3, y2 i 3z + 5 tworzą ciąg arytmetyczny w tej kolejności. Znajdź x i wskaż różnicę tego postępu. Rozwiązać układ równań Ujednolicony egzamin państwowy z matematyki. Lekcje wideo. Podzielność liczb całkowitych. Funkcja liniowa. Problemy z podzielnością. Twierdzenie Viety, twierdzenie odwrotne, wzory Viety. sprytny #studenci #równania #twierdzenie_vietasa #twierdzenie Następnie rozważymy twierdzenie odwrotne do twierdzenia Viety. Następnie przeanalizujemy rozwiązania na najbardziej typowych przykładach. Dowodzi to pierwszej zależności twierdzenia Viety dla sumy pierwiastków równania kwadratowego. Przejdźmy do drugiego. Jak udowodnić odwrotność twierdzenia Viety? DOK-VO: x2+px+f=0 x2-(M+N) *x+M*N=0 x2-Mx-Nx+M*N=0 x (x-N) -M (x-N) =0 (x-M ) (x-N) =0 x-M=0 x-N=0 x=M x=N CTD. Udowodniliśmy to w ten sposób klasa profilu z matematycznym nastawieniem. Odpowiedzi: pomoc w zrozumieniu twierdzenia odwrotnego do twierdzenia Viety dzięki konkretnym przykładom Twierdzenie odwrotne do twierdzenia Viety pomaga rozwiązać rozwiązanie: Jeśli współczynnik a jest liczbą, z której łatwo wyprowadzić Pierwiastek kwadratowy całość Liczba wymierna, to suma x1 i x2 będzie równa liczbie. Udowodnij twierdzenie odwrotne do twierdzenia Viety - zobacz, jak narzekać na dowód twierdzenia Viety. Sformułuj i udowodnij twierdzenie Viety oraz twierdzenie odwrotne i zastosuj je do rozwiązywania równań i problemów. Udowodnić odwrotność twierdzenia Viety. Jednolity egzamin państwowy z matematyki za 100 punktów: tajemnice, o których się nie mówi nauczyciele szkolni, problemy pochodne. Wielu kandydatów uważa, że nie muszą przygotowywać się do pierwszych czternastu problemów, myśląc, że są one bardzo łatwe, ale tak nie jest! Większość zdających popełnia proste błędy arytmetyczne, zaburzając w ten sposób wynik testu doskonałe rozwiązanie zadania części C. Takie sytuacje zdarzają się bardzo często, dlatego nie należy zaniedbywać przygotowania do pierwszych zadań, lecz przygotować się jak na treningu sportowym: jeśli Twoim celem jest zdobycie 90-100 punktów, przećwicz rozwiązywanie pierwszego bloku w 20-25 minut, jeśli za 70 -80 punktów – około 30 minut, nie więcej. Doskonałym sposobem na naukę jest rozwiązywanie w towarzystwie korepetytora, na kursach, na których zostaną postawione określone warunki: np. rozwiązujesz przed pierwszym błędem, a potem oddajesz pracę; Inną opcją jest to, że za każdy popełniony błąd przekazujesz pieniądze do kasy ogólnej. Bez względu na to, jak dziwne może się to wydawać, nie polecamy oficjalnej strony internetowej, ponieważ wszystkie testy są tak pomieszane, że nie można z niej skorzystać. Formatowanie zadań z Części C jest ważne. Jeśli rozwiązanie nie zostanie przygotowane starannie, postęp w rozwiązaniu zadania będzie niejasny, w związku z czym egzaminator na pewno znajdzie w tym błąd i obniży Twoją ocenę. Wydawać by się mogło, że rozmawialiśmy o bardzo prostych rzeczach, ale stosując się do naszych rad, zapewnisz sobie sukces zdanie jednolitego egzaminu państwowego! Tajne linki omówione w klasie mistrzowskiej można znaleźć tutaj - są to linki do kursów wideo przygotowujących do egzaminu Unified State Exam. Otrzymany wynik nazywany jest twierdzeniem Viety. Za dane trójmian kwadratowy 2 x px q Twierdzenie Viety wygląda następująco: jeśli istnieją pierwiastki, to obowiązuje również odwrotność twierdzenia Viety: jeśli liczby spełniają warunki, to te liczby są pierwiastkami równania. Dowód tego twierdzenia jest jednym z pytania testowe Zadania. Czasami dla zwięzłości oba twierdzenia Viety (bezpośrednie i odwrotne) nazywane są po prostu twierdzeniem Viety.
I. Twierdzenie Viety dla zredukowanego równania kwadratowego.
Suma pierwiastków zredukowanego równania kwadratowego x 2 +px+q=0 jest równy drugiemu współczynnikowi wziętemu z przeciwnym znakiem, a iloczyn pierwiastków jest równy członowi swobodnemu:
x 1 + x 2 = -p; x 1 ∙x 2 =q.
Znajdź pierwiastki danego równania kwadratowego, korzystając z twierdzenia Viety.
Przykład 1) x 2 -x-30=0. To jest zredukowane równanie kwadratowe ( x2 +px+q=0), drugi współczynnik p=-1, A Wolny Członek q=-30. Najpierw upewnijmy się, że to równanie ma pierwiastki i że pierwiastki (jeśli istnieją) zostaną wyrażone w liczbach całkowitych. W tym celu wystarczy, aby dyskryminator był idealny kwadrat cały numer.
Znalezienie wyróżnika D=b 2 — 4ac=(-1) 2 -4∙1∙(-30)=1+120=121= 11 2 .
Teraz, zgodnie z twierdzeniem Viety, suma pierwiastków musi być równa drugiemu współczynnikowi przyjętemu z przeciwnym znakiem, tj. ( -P), a iloczyn jest równy terminowi dowolnemu, tj. ( Q). Następnie:
x 1 + x 2 = 1; x 1 ∙x 2 =-30. Musimy wybrać dwie liczby takie, aby ich iloczyn był równy -30 , a kwota jest jednostka. To są liczby -5 I 6 . Odpowiedź: -5; 6.
Przykład 2) x 2 +6x+8=0. Mamy zredukowane równanie kwadratowe z drugim współczynnikiem p=6 i wolny członek q=8. Upewnijmy się, że istnieją pierwiastki całkowite. Znajdźmy dyskryminator D 1 D 1=3 2 -1∙8=9-8=1=1 2 . Dyskryminator D 1 jest idealnym kwadratem liczby 1 , co oznacza, że pierwiastki tego równania są liczbami całkowitymi. Wybierzmy pierwiastki korzystając z twierdzenia Viety: suma pierwiastków jest równa –р=-6, a iloczyn pierwiastków jest równy q=8. To są liczby -4 I -2 .
W rzeczywistości: -4-2=-6=-р; -4∙(-2)=8=q. Odpowiedź: -4; -2.
Przykład 3) x 2 +2x-4=0. W tym zredukowanym równaniu kwadratowym drugi współczynnik p=2 i bezpłatny członek q=-4. Znajdźmy dyskryminator D 1, ponieważ drugi współczynnik wynosi Liczba parzysta. D 1=1 2 -1∙(-4)=1+4=5. Dyskryminator nie jest idealnym kwadratem liczby, więc tak robimy wniosek: Pierwiastki tego równania nie są liczbami całkowitymi i nie można ich znaleźć za pomocą twierdzenia Viety. Oznacza to, że równanie to rozwiązujemy jak zwykle za pomocą wzorów (w tym przypadku za pomocą wzorów). Otrzymujemy:
Przykład 4). Zapisz równanie kwadratowe, korzystając z jego pierwiastków, jeśli x 1 = -7, x 2 = 4.
Rozwiązanie. Wymagane równanie zostanie zapisane w postaci: x 2 +px+q=0, oraz, w oparciu o twierdzenie Viety –p=x 1 +x 2=-7+4=-3 → p=3; q=x 1 ∙x 2=-7∙4=-28 . Wówczas równanie przyjmie postać: x2 +3x-28=0.
Przykład 5). Zapisz równanie kwadratowe, korzystając z jego pierwiastków, jeżeli:

II. Twierdzenie Viety dla pełnego równania kwadratowego topór 2 +bx+c=0.
Suma pierwiastków wynosi minus B, podzielony przez A, iloczyn pierwiastków jest równy Z, podzielony przez A:
x 1 + x 2 = -b/a; x 1 ∙x 2 =c/a.
Przykład 6). Znajdź sumę pierwiastków równania kwadratowego 2x2 -7x-11=0.
Jedną z metod rozwiązywania równania kwadratowego jest użycie formuły VIET, który został nazwany na cześć FRANCOIS VIETTE.
Był znanym prawnikiem, który służył królowi Francji w XVI wieku. W czas wolny studiował astronomię i matematykę. Ustalił związek między pierwiastkami i współczynnikami równania kwadratowego.
Zalety formuły:
1 . Stosując formułę, możesz szybko znaleźć rozwiązanie. Ponieważ nie ma potrzeby wpisywania drugiego współczynnika do kwadratu, następnie odejmij od niego 4ac, znajdź dyskryminator i podstaw jego wartość do wzoru, aby znaleźć pierwiastki.
2 . Bez rozwiązania możesz określić znaki pierwiastków i wybrać wartości pierwiastków.
3 . Po rozwiązaniu systemu dwóch rekordów znalezienie samych korzeni nie jest trudne. W powyższym równaniu kwadratowym suma pierwiastków jest równa wartości drugiego współczynnika ze znakiem minus. Iloczyn pierwiastków powyższego równania kwadratowego jest równy wartości trzeciego współczynnika.
4 . Korzystając z tych pierwiastków, zapisz równanie kwadratowe, czyli rozwiąż problem odwrotny. Na przykład tę metodę stosuje się przy rozwiązywaniu problemów z mechaniki teoretycznej.
5 . Wygodnie jest użyć wzoru, gdy współczynnik wiodący jest równy jeden.
Wady:
1
. Formuła nie jest uniwersalna.
Twierdzenie Viety 8. klasa
Formuła
Jeśli x 1 i x 2 są pierwiastkami zredukowanego równania kwadratowego x 2 + px + q = 0, to:

Przykłady
x 1 = -1; x 2 = 3 - pierwiastki równania x 2 - 2x - 3 = 0.
P = -2, q = -3.
X 1 + x 2 = -1 + 3 = 2 = -p,
X 1 x 2 = -1 3 = -3 = q.
Twierdzenie odwrotne
Formuła
Jeżeli liczby x 1, x 2, p, q są powiązane warunkami:

Wtedy x 1 i x 2 są pierwiastkami równania x 2 + px + q = 0.
Przykład
Utwórzmy równanie kwadratowe, korzystając z jego pierwiastków:
X 1 = 2 -? 3 i x 2 = 2 +? 3.
P. = x 1 + x 2 = 4; p = -4; q = x 1 x 2 = (2 - ? 3 )(2 + ? 3 ) = 4 - 3 = 1.
Wymagane równanie ma postać: x 2 - 4x + 1 = 0.
Pomiędzy pierwiastkami i współczynnikami równania kwadratowego, oprócz wzorów pierwiastkowych, podano inne przydatne zależności Twierdzenie Viety. W tym artykule podamy sformułowanie i dowód twierdzenia Viety dla równania kwadratowego. Następnie rozważymy twierdzenie odwrotne do twierdzenia Viety. Następnie przeanalizujemy rozwiązania na najbardziej typowych przykładach. Na koniec zapisujemy wzory Vieta, które definiują relację pomiędzy pierwiastkami rzeczywistymi równanie algebraiczne stopień n i jego współczynniki.
Nawigacja strony.
Twierdzenie Viety, sformułowanie, dowód
Ze wzorów na pierwiastki równania kwadratowego a·x 2 +b·x+c=0 postaci, gdzie D=b 2 −4·a·c wynikają zależności: x 1 +x 2 =− b/a, x 1 ·x 2 = c/a . Wyniki te zostały potwierdzone Twierdzenie Viety:
Twierdzenie.
Jeśli x 1 i x 2 są pierwiastkami równania kwadratowego a x 2 +b x+c=0, wówczas suma pierwiastków jest równa stosunkowi współczynników b i a, wziętych z przeciwnym znakiem, i iloczynu pierwiastki są równe stosunkowi współczynników c i a, to znaczy .
Dowód.
Dowód twierdzenia Viety przeprowadzimy według następującego schematu: sumę i iloczyn pierwiastków równania kwadratowego układamy ze znanych wzorów na pierwiastki, następnie przekształcamy powstałe wyrażenia i upewniamy się, że są równe −b/ odpowiednio a i c/a.
Zacznijmy od sumy pierwiastków i uzupełnijmy ją. Teraz sprowadzamy ułamki do wspólnego mianownika, mamy . W liczniku powstałego ułamka, po czym:. Wreszcie po 2 otrzymujemy . Dowodzi to pierwszej zależności twierdzenia Viety dla sumy pierwiastków równania kwadratowego. Przejdźmy do drugiego.
Tworzymy iloczyn pierwiastków równania kwadratowego: . Zgodnie z zasadą mnożenia ułamków zwykłych, ostatni kawałek można zapisać jako . Teraz mnożymy nawias przez nawias w liczniku, ale szybciej jest zwinąć ten iloczyn wzór na różnicę kwadratową, Więc . Następnie pamiętając wykonujemy kolejne przejście. A ponieważ dyskryminator równania kwadratowego odpowiada wzorowi D=b 2 −4·a·c, to zamiast D w ostatnim ułamku możemy podstawić b 2 −4·a·c i otrzymamy. Po otwarciu nawiasów i wprowadzeniu podobnych wyrazów dochodzimy do ułamka , a jego redukcja o 4·a daje . Dowodzi to drugiej zależności twierdzenia Viety dla iloczynu pierwiastków.
Jeśli pominiemy wyjaśnienia, dowód twierdzenia Viety przyjmie lakoniczną formę:
,
.
Pozostaje tylko zauważyć, że jeśli dyskryminator jest równy zeru, równanie kwadratowe ma jeden pierwiastek. Jeśli jednak założymy, że równanie w tym przypadku ma dwa identyczne pierwiastki, to równości z twierdzenia Viety również obowiązują. Rzeczywiście, gdy D=0 pierwiastek równania kwadratowego jest równy , to i , a ponieważ D=0, czyli b 2 −4·a·c=0, skąd b 2 =4·a·c, to .
W praktyce twierdzenie Viety jest najczęściej stosowane w odniesieniu do zredukowanego równania kwadratowego (ze współczynnikiem wiodącym równym 1) postaci x 2 +p·x+q=0. Czasami formułuje się go dla równań kwadratowych właśnie tego typu, co nie ogranicza ogólności, ponieważ każde równanie kwadratowe można zastąpić równaniem równoważnym, dzieląc obie strony przez niezerową liczbę a. Podajmy odpowiednie sformułowanie twierdzenia Viety:
Twierdzenie.
Suma pierwiastków zredukowanego równania kwadratowego x 2 +p x+q=0 jest równa współczynnikowi x wziętemu z przeciwnym znakiem, a iloczyn pierwiastków jest równy członowi swobodnemu, czyli x 1 +x 2 =−p, x 1 x 2 = q.
Twierdzenie odwrotne do twierdzenia Viety
Drugie sformułowanie twierdzenia Viety podane w poprzednim akapicie wskazuje, że jeśli x 1 i x 2 są pierwiastkami zredukowanego równania kwadratowego x 2 +p x+q=0, to zależności x 1 +x 2 =−p , x 1 x 2 =q. Natomiast z zapisanych zależności x 1 +x 2 =−p, x 1 x 2 =q wynika, że x 1 i x 2 są pierwiastkami równania kwadratowego x 2 +p x+q=0. Innymi słowy, odwrotność twierdzenia Viety jest prawdziwa. Sformułujmy to w formie twierdzenia i udowodnijmy.
Twierdzenie.
Jeżeli liczby x 1 i x 2 są takie, że x 1 +x 2 =−p i x 1 · x 2 =q, to x 1 i x 2 są pierwiastkami zredukowanego równania kwadratowego x 2 +p · x+q =0.
Dowód.
Po zastąpieniu współczynników p i q w równaniu x 2 +p x+q=0 ich wyrażeniami poprzez x 1 i x 2 , przekształca się je w równoważne równanie.
Podstawmy liczbę x 1 zamiast x do otrzymanego równania i otrzymamy równość x 1 2 −(x 1 + x 2) x 1 + x 1 x 2 =0, co dla dowolnego x 1 i x 2 reprezentuje poprawną równość liczbową 0 = 0, ponieważ x 1 2 −(x 1 + x 2) x 1 + x 1 x 2 = x 1 2 −x 1 2 −x 2 ·x 1 +x 1 ·x 2 =0. Dlatego x 1 jest pierwiastkiem równania x 2 −(x 1 +x 2) x+x 1 x 2 =0, co oznacza, że x 1 jest pierwiastkiem równoważnego równania x 2 +p·x+q=0.
Jeśli w równaniu x 2 −(x 1 +x 2) x+x 1 x 2 =0 podstaw liczbę x 2 zamiast x, otrzymamy równość x 2 2 −(x 1 +x 2) x 2 +x 1 x 2 =0. Jest to prawdziwa równość, ponieważ x 2 2 −(x 1 +x 2) x 2 +x 1 x 2 = x 2 2 −x 1 ·x 2 −x 2 2 +x 1 ·x 2 =0. Dlatego x 2 jest również pierwiastkiem równania x 2 −(x 1 +x 2) x+x 1 x 2 =0, a zatem równania x 2 +p·x+q=0.
To kończy dowód twierdzenia, odwrotność twierdzenia Vieta.
Przykłady wykorzystania twierdzenia Viety
Czas porozmawiać o praktycznym zastosowaniu twierdzenia Viety i jego twierdzenia odwrotnego. W tej sekcji przeanalizujemy rozwiązania kilku najbardziej typowych przykładów.
Zacznijmy od zastosowania twierdzenia odwrotnego do twierdzenia Viety. Wygodnie jest sprawdzić, czy dane dwie liczby są pierwiastkami danego równania kwadratowego. W tym przypadku obliczana jest ich suma i różnica, po czym sprawdzana jest ważność relacji. Jeżeli obie te zależności są spełnione, to na mocy twierdzenia odwrotnego do twierdzenia Viety dochodzi do wniosku, że liczby te są pierwiastkami równania. Jeżeli choć jedna z zależności nie jest spełniona, to liczby te nie są pierwiastkami równania kwadratowego. Podejście to można zastosować przy rozwiązywaniu równań kwadratowych w celu sprawdzenia znalezionych pierwiastków.
Przykład.
Która z par liczb 1) x 1 =−5, x 2 =3 lub 2) lub 3) jest parą pierwiastków równania kwadratowego 4 x 2 −16 x+9=0?
Rozwiązanie.
Współczynniki danego równania kwadratowego 4 x 2 −16 x+9=0 wynoszą a=4, b=−16, c=9. Zgodnie z twierdzeniem Viety suma pierwiastków równania kwadratowego powinna być równa −b/a, czyli 16/4=4, a iloczyn pierwiastków powinien być równy c/a, czyli 9 /4.
Obliczmy teraz sumę i iloczyn liczb w każdej z trzech podanych par i porównajmy je z wartościami, które właśnie uzyskaliśmy.
W pierwszym przypadku mamy x 1 +x 2 =−5+3=−2. Wynikowa wartość jest różna od 4, więc nie można dalej sprawdzać, ale korzystając z twierdzenia odwrotnego do twierdzenia Viety, można od razu stwierdzić, że pierwsza para liczb nie jest parą pierwiastków danego równania kwadratowego.
Przejdźmy do drugiego przypadku. Czyli tutaj pierwszy warunek jest spełniony. Sprawdzamy drugi warunek: otrzymana wartość różni się od 9/4. W związku z tym druga para liczb nie jest parą pierwiastków równania kwadratowego.
Został jeszcze ostatni przypadek. Tutaj i . Obydwa warunki są spełnione, więc te liczby x 1 i x 2 są pierwiastkami danego równania kwadratowego.
Odpowiedź:
Odwrotność twierdzenia Viety można zastosować w praktyce do znalezienia pierwiastków równania kwadratowego. Zwykle wybiera się pierwiastki całkowite danych równań kwadratowych o współczynnikach całkowitych, ponieważ w innych przypadkach jest to dość trudne. W tym przypadku wykorzystują fakt, że jeśli suma dwóch liczb jest równa drugiemu współczynnikowi równania kwadratowego, wziętemu ze znakiem minus, a iloczyn tych liczb jest równy wyrazowi swobodnemu, to liczby te są pierwiastki tego równania kwadratowego. Rozumiemy to na przykładzie.
Weźmy równanie kwadratowe x 2 −5 x+6=0. Aby liczby x 1 i x 2 były pierwiastkami tego równania, muszą być spełnione dwie równości: x 1 + x 2 =5 i x 1 ·x 2 =6. Pozostaje tylko wybrać takie liczby. W tym przypadku jest to dość proste: takimi liczbami są 2 i 3, gdyż 2+3=5 i 2,3=6. Zatem 2 i 3 są pierwiastkami tego równania kwadratowego.
Twierdzenie odwrotne do twierdzenia Viety jest szczególnie wygodne w użyciu do znalezienia drugiego pierwiastka danego równania kwadratowego, gdy jeden z pierwiastków jest już znany lub oczywisty. W tym przypadku drugi pierwiastek można znaleźć z dowolnej relacji.
Weźmy na przykład równanie kwadratowe 512 x 2 −509 x −3=0. Tutaj łatwo zauważyć, że pierwiastkiem równania jest jedność, ponieważ suma współczynników tego równania kwadratowego jest równa zeru. Zatem x 1 = 1. Drugi pierwiastek x 2 można znaleźć np. z zależności x 1 ·x 2 =c/a. Mamy 1 x 2 =−3/512, z czego x 2 =−3/512. W ten sposób wyznaczyliśmy oba pierwiastki równania kwadratowego: 1 i −3/512.
Oczywiste jest, że wybór korzeni jest wskazany tylko w najprostszych przypadkach. W innych przypadkach, aby znaleźć pierwiastki, można użyć wzorów na pierwiastki równania kwadratowego poprzez dyskryminator.
Inny praktyczne użycie twierdzenie, odwrotne do twierdzenia Viety, polega na ułożeniu równań kwadratowych według dane korzenie x 1 i x 2 . Aby to zrobić, wystarczy obliczyć sumę pierwiastków, która daje współczynnik x z przeciwnym znakiem danego równania kwadratowego, oraz iloczyn pierwiastków, który daje wyraz wolny.
Przykład.
Napisz równanie kwadratowe, którego pierwiastki to −11 i 23.
Rozwiązanie.
Oznaczmy x 1 =−11 i x 2 =23. Obliczamy sumę i iloczyn tych liczb: x 1 +x 2 =12 i x 1 ·x 2 =−253. Dlatego wskazane liczby są pierwiastkami zredukowanego równania kwadratowego z drugim współczynnikiem -12 i wolnym wyrazem -253. Oznacza to, że x 2 −12·x−253=0 jest wymaganym równaniem.
Odpowiedź:
x 2 −12·x−253=0 .
Twierdzenie Viety jest bardzo często wykorzystywane przy rozwiązywaniu problemów związanych ze znakami pierwiastków równań kwadratowych. Jak twierdzenie Viety jest powiązane ze znakami pierwiastków zredukowanego równania kwadratowego x 2 +p·x+q=0? Oto dwa istotne stwierdzenia:
- Jeśli wyraz wolny q jest liczbą dodatnią i jeśli równanie kwadratowe ma rzeczywiste pierwiastki, to albo oba są dodatnie, albo oba ujemne.
- Jeżeli wyraz wolny q jest liczbą ujemną i równanie kwadratowe ma pierwiastki rzeczywiste, to ich znaki są różne, czyli jeden pierwiastek jest dodatni, a drugi ujemny.
Stwierdzenia te wynikają ze wzoru x 1 · x 2 =q oraz z zasad dodatniego mnożenia, liczby ujemne i liczby z różnymi znakami. Spójrzmy na przykłady ich zastosowania.
Przykład.
R. to jest pozytywne. Korzystając ze wzoru dyskryminacyjnego znajdujemy D=(r+2) 2 −4 1 (r−1)= r 2 +4 r+4−4 r+4=r 2 +8, wartość wyrażenia r 2 +8 jest dodatnia dla dowolnego rzeczywistego r, zatem D > 0 dla dowolnego rzeczywistego r. W związku z tym oryginalne równanie kwadratowe ma dwa pierwiastki dla dowolnych rzeczywistych wartości parametru r.
Teraz dowiedzmy się, kiedy korzenie mają różne znaki. Jeżeli znaki pierwiastków są różne, to ich iloczyn jest ujemny i zgodnie z twierdzeniem Viety iloczyn pierwiastków zredukowanego równania kwadratowego jest równy członowi swobodnemu. Dlatego interesują nas te wartości r, dla których wolny termin r-1 jest ujemny. Zatem, aby znaleźć interesujące nas wartości r, potrzebujemy decydować nierówność liniowa r-1<0 , откуда находим r<1 .
Odpowiedź:
o godz<1 .
Formuły Vieta
Powyżej rozmawialiśmy o twierdzeniu Viety dotyczącym równania kwadratowego i analizowaliśmy zależności, jakie ono potwierdza. Ale istnieją wzory, które łączą rzeczywiste pierwiastki i współczynniki nie tylko równań kwadratowych, ale także równań sześciennych, równań czwartego stopnia i ogólnie: równania algebraiczne stopień r. Nazywają się Wzory Viety.
Zapiszmy wzór Viety na równanie algebraiczne stopnia n postaci i załóżmy, że ma ono n pierwiastków rzeczywistych x 1, x 2, ..., x n (wśród nich mogą znajdować się zbieżne): 
Można otrzymać wzory Viety twierdzenie o rozkładzie wielomianu na czynniki liniowe, a także definicja równych wielomianów poprzez równość wszystkich odpowiadających im współczynników. Zatem wielomian i jego rozwinięcie na czynniki liniowe postaci są równe. Otwierając nawiasy w ostatnim iloczynu i przyrównując odpowiednie współczynniki, otrzymujemy wzory Viety.
W szczególności dla n=2 mamy już znane wzory Vieta na równanie kwadratowe.
W przypadku równania sześciennego wzory Viety mają postać 
Pozostaje tylko zauważyć, że po lewej stronie formuł Viety znajdują się tak zwane elementarne wielomiany symetryczne.
Bibliografia.
- Algebra: podręcznik dla 8 klasy. ogólne wykształcenie instytucje / [Yu. N. Makaryczew, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edytowany przez SA Telyakovsky. - wyd. 16. - M.: Edukacja, 2008. - 271 s. : chory. - ISBN 978-5-09-019243-9.
- Mordkovich A. G. Algebra. 8 klasa. Za 2 godziny Część 1. Podręcznik dla uczniów szkół ogólnokształcących / A. G. Mordkovich. - wyd. 11, usunięte. - M.: Mnemosyne, 2009. - 215 s.: il. ISBN 978-5-346-01155-2.
- Algebra i początek analizy matematycznej. Klasa 10: podręcznik. dla edukacji ogólnej instytucje: podstawowe i profilowe. poziomy / [Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; edytowany przez A. B. Żyżczenko. - wyd. 3. - M.: Edukacja, 2010. - 368 s. : chory. - ISBN 978-5-09-022771-1.