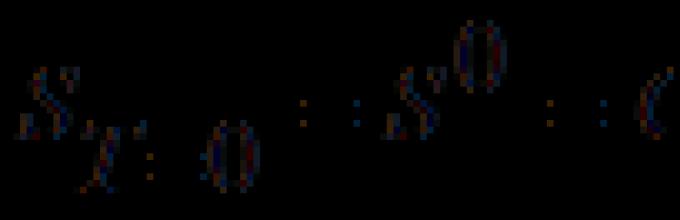Streszczenie dyscypliny: „Fizyka”
Wykonuje student Dział korespondencyjny Drugie danie (4,5)
Wydział: VT i PO Mironenko S.A.
Kazachski Uniwersytet Innowacji i Systemów Telekomunikacyjnych
ROZDZIAŁ 1: Pierwsza zasada termodynamiki
Pierwszą zasadą termodynamiki jest prawo zachowania i przemiany energii. Zgodnie z tym prawem energia izolowanego układu (równa sumie wszystkich rodzajów energii dostępnych w układzie) nie zmienia się podczas żadnych procesów zachodzących w układzie: energia nie ulega zniszczeniu ani wytworzeniu.
Pojęcie energii jest nierozerwalnie związane z ruchem materii: energia jest fizyczną miarą ruchu materii. Różnica pomiędzy poszczególnymi rodzajami energii wynika z różnic jakościowych konkretne formy ruchy ciał materialnych. Wzajemne przemiany energii ciał odzwierciedlają nieograniczoną zdolność ruchu do przechodzenia z jednej formy w drugą; Dlatego zachowanie energii wyraża fakt niezniszczalności ruchu świata materialnego.
W oparciu o prawo zachowania i przemiany energii można ustalić ilościowe zależności pomiędzy poszczególnymi rodzajami energii. Rzeczywiście, jeśli przyjąć różne rodzaje energii w takich ilościach, że każda z nich z osobna powoduje taką samą zmianę stanu danego układu, to wskazane ilości energii różnych rodzajów, ze względu na ich wzajemną wymienialność, będą równoważne.
Po Łomonosowie rosyjski akademik Hess (1840), Joule (1840), Mayer (1842), Helmholtz (1847) pracowali nad uzasadnieniem i rozwojem prawa zachowania i transformacji energii.
Pierwszym eksperymentalnym potwierdzeniem równoważności ciepła i pracy było słynne doświadczenie Joule'a. W tym eksperymencie (a dokładniej w wielu eksperymentach) praca mechaniczna pod wpływem działania sił tarcia zamieniła się w pracę, a ilość wykonanej pracy zawsze odpowiadała bardzo określonej ilości wydzielonego ciepła. W ten sposób udowodniono równoważność ciepła i pracy oraz ustalono mechaniczny równoważnik ciepła. Okazało się, że jest bardzo zbliżone do eksperymentów Joule'a współczesne znaczenie to (różnica nie przekracza 8%).
Oznaczmy przez E całkowitą energię układu termodynamicznego, niezależnie od konkretnych form, w jakich występuje ona w układzie. Zgodnie z prawem zachowania i przemiany energii całkowita energia zamkniętego lub izolowanego układu termodynamicznego nie zmienia się w czasie, tj.
Albo, co jest tym samym,
Rozważmy najpierw izolowany adiabatycznie układ zamknięty. Taki system może mechanicznie oddziaływać z otaczającymi lub zewnętrznymi ciałami i dlatego nie jest zamknięty. Przy przejściu z jednego stanu do drugiego układ ten wykonuje pracę zmiany objętości L, która zgodnie z prawem zachowania i przemiany energii jest równa spadkowi energii układu, tj.
W ogólnym przypadku nieizolowanego układu termodynamicznego, pozostającego w interakcji mechanicznej i termicznej z otaczającymi ciałami, zmiana energii układu będzie związana z pracą L wykonaną przez układ i ilością ciepła odebranego przez układ jak wynika z prawa zachowania i przemiany energii, z zależności:
W rzeczywistości niech otaczające ciała nie zmieniają swojej objętości, a zatem nie wytwarzają pracy. Wówczas rozpatrywany układ termodynamiczny wraz z otaczającymi go ciałami stanowi adiabatycznie izolowany układ złożony, a ponadto taki, że cała praca tego skomplikowany system jest wykonywana przez układ pierwotny i jest równa L. Oznaczmy energię otaczających ciał przez , a energię układu złożonego, równą sumie energii układu pierwotnego i otaczających ciał, przez E*. Następnie zgodnie z równaniem (2)
Te. ()– () = - L,
skąd wynika =– L.
Ponieważ cała praca L, zgodnie z tym, co powiedziano powyżej, wykonywana jest przez sam układ, a nie przez otaczające go ciała, strata energii otaczających ciał oznacza energię oddziaływania układu z otaczającymi ciałami, uwalnianą w innej formie z pracy, tj. w postaci ciepła. Dlatego ilość ciepła. Otrzymywany przez rozważany układ z otaczających ciał,
Zastępując różnicę w równaniu =– L przez Q, otrzymujemy równanie (3). Zgodnie z równaniem (3) zmiana energii układu termodynamicznego jest równa różnicy pomiędzy ilością ciepła Q otrzymanego przez układ a wykonaną przez niego pracą L. Równanie (3) jest ogólnym analitycznym wyrażeniem pierwsza zasada dynamiki.
Pierwszym początkiem dynamiki jest szczególny przypadek ogólne prawo zachowania energii. Powodem, dla którego w termodynamice wolą używać wyrażenia „pierwsza zasada termodynamiki” niż „prawo zachowania energii”, jest to, że konsekwencją zachowania energii jest istnienie w dowolnym układzie funkcji stanu – energii wewnętrznej (a także entalpia), która jest jedną z głównych wielkości termodynamicznych.
ROZDZIAŁ 2: Druga zasada termodynamiki
Jeśli wyjdziemy wyłącznie od pierwszej zasady termodynamiki, wówczas uprawnione jest założenie, że każdy możliwy proces, który nie jest sprzeczny z prawem zachowania energii, jest w zasadzie możliwy i mógłby zachodzić w przyrodzie.
Można by założyć np., że podczas wymiany ciepła pomiędzy dwoma ciałami o różnej temperaturze ciepło może być przekazywane zarówno z ciała o temperaturze wyższej, jak i odwrotnie, z ciała o temperaturze niższej do ciała o temperaturze wyższej. Jedynym ograniczeniem narzuconym przez pierwszą zasadę termodynamiki na ten proces jest wymóg, aby ilość ciepła oddanego przez pierwsze ciepło i otrzymanego przez drugie ciepło była równa (pod warunkiem, że nie jest wykonywana żadna przydatna praca zewnętrzna). Odpowiedź na pytanie o kierunek, w którym faktycznie następuje przekazywanie ciepła pomiędzy dwoma ciałami, a także inne rzeczywiste procesy makroskopowe, daje druga zasada termodynamiki. Różnorodność procesów wzajemnej przemiany ciepła w pracę i różne aspekty, w jakich można rozpatrywać te procesy. Wyjaśnij obecność kilku sformułowań drugiej zasady termodynamiki.
Druga zasada termodynamiki jest ważna dla teorii silników cieplnych. Silnik cieplny to urządzenie pracujące w sposób ciągły, w wyniku którego następuje zamiana ciepła na pracę. Druga zasada termodynamiki stwierdza, że w silnikach cieplnych tylko część dostarczonego ciepła może zostać przetworzona. Dlatego przydatna akcja, a co za tym idzie, sprawność silnika charakteryzuje się stosunkiem ilości ciepła zamienionego na pracę użyteczną. Do całego dostarczonego ciepła. Ten stosunek nazywa się efektywnością efektywną. silnik; te. maksymalna wartość wydajności ustala się na podstawie drugiej zasady termodynamiki.
Stosując drugą zasadę termodynamiki można, podobnie jak na podstawie pierwszej zasady termodynamiki, bazując na znanych właściwościach fizycznych substancji, przewidzieć jej pozostałe właściwości i ustalić ilościowe zależności między nimi. Takie jest fundamentalne znaczenie początku drugiej zasady termodynamiki dla badania właściwości fizycznych ciał rzeczywistych.
2.1. Pierwsze sformułowanie drugiej zasady termodynamiki
Kiedy ciepło jest wymieniane między dwoma lub większą liczbą ciał, ciepło w sposób naturalny przenosi się tylko z ciała o wyższej temperaturze do ciała o niższej temperaturze, ale nigdy odwrotnie; nieskompensowane przekazanie ciepła z ciała o temperaturze niższej do ciała o temperaturze wyższej jest niemożliwe.
Z tego stwierdzenia wynika, że nie da się w żaden sposób przeprowadzić przejścia ciepła z ciała mniej nagrzanego do ciała bardziej nagrzanego tak, aby pozostałe ciała biorące udział w procesie po zakończeniu procesu powróciły do stanu pierwotnego, tj. bez żadnych zmian resztkowych lub „kompensacyjnych” zachodzących w otaczających ciałach
(na przykład bez kosztów pracy lub wdrożenia innego odpowiednika, jeśli to możliwe, w celu uzyskania użytecznego produktu). zewnętrzna praca, proces). Wręcz przeciwnie, ciepło może samo przenosić się z nagrzanego ciała do mniej nagrzanego, tj. Nawet jeśli w tym procesie uczestniczą inne ciała, to po zakończeniu procesu mogą one powrócić do stanu pierwotnego. Wszystko to powoduje, że proces wymiany ciepła przy skończonej różnicy temperatur jest procesem ściśle jednostronnym i nieodwracalnym.
2.2. Drugie sformułowanie drugiej zasady termodynamiki
Silnik cieplny, za pomocą którego możliwe jest całkowite zamienienie ciepła otrzymanego od dowolnego ciała na pracę, a przy tym w taki sposób, że ciepło nie jest przekazywane do uczestniczących w tym procesie ciał o niższej temperaturze, nazywa się silnikiem ciągłym. maszyna ruchowa drugiego rodzaju.
Za pomocą perpetuum mobile drugiego rodzaju można by uzyskać pracę poprzez chłodzenie ciała (czyli jedynego źródła ciepła) tak, aby część ciepła oddawana przez źródło nie przechodziła do innych ciał. Ta część ciepła, która jest przekazywana ze źródła ciepła do innych ciał w procesie zamiany ciepła na pracę, stanowi „zmianę resztkową” i nazywa się „efektem kompensacyjnym” lub po prostu „kompensacją”. W tym sensie Maszyna ruchu wiecznego drugiego typu można uznać za nieskompensowany silnik cieplny.
W związku z wprowadzeniem koncepcji maszyny perpetuum mobile drugiego rodzaju, drugą zasadę termodynamiki można również sformułować w następujący sposób: maszyna perpetuum mobile drugiego rodzaju jest niemożliwa. Innymi słowy, nie da się zastosować silnika cieplnego, którego jedynym skutkiem byłoby przekształcenie ciepła dowolnego ciała w pracę bez przekazania części tego ciepła innym ciałom.
To stwierdzenie nie tylko nie zaprzecza, ale wręcz przeciwnie, jest całkowicie równoważne pierwszemu sformułowaniu drugiej zasady termodynamiki. Rzeczywiście, gdyby można było uzyskać pracę dodatnią przez ochłodzenie tylko jednego źródła ciepła i to w taki sposób, aby całe ciepło wydzielane przez to źródło zostało zamienione na pracę bez przekazywania pewnej części tego ciepła znajdującym się w nim ciałom temperaturze niższej niż temperatura źródła, a następnie zamieniając powstałą pracę w ciepło o temperaturze wyższej niż temperatura źródła, przekazalibyśmy w ten sposób ciepło ciału o wyższej temperaturze bez jakichkolwiek resztkowych zmian w stanie ciał biorących udział w procesu, co jak już wiemy jest niemożliwe.
ROZDZIAŁ 3: Trzecia zasada termodynamiki
Podczas studiowania właściwości różne substancje Na niskie temperatury, blisko zera absolutnego (T = 0), w zachowaniu substancji rzeczywistych ujawnia się następujący ważny wzór: w obszarze zera absolutnego entropia ciała w dowolnym stanie równowagi nie zależy od temperatury, objętości i innych parametrów charakteryzujące stan organizmu, tj. w (gdzie ![]() ).
).
Wynik ten, będący uogólnieniem szeregu danych eksperymentalnych i nie wynikający bezpośrednio z pierwszej ani drugiej zasady termodynamiki, stanowi treść twierdzenia termicznego Nernsta.
Z twierdzenia termicznego wynika, że w pobliżu zera absolutnego pojemności cieplne i , równe odpowiednio T i T, ze względu na równość pochodnych do zera i stają się zerowe; ogólnie rzecz biorąc, przy T = 0 pojemność cieplna dowolnego procesu jest równa zeru ![]() . W ten sam sposób, gdy pochodna (a zatem i współczynnik rozszerzalności cieplnej) również zanika, równa się zgodnie z wyrażeniem
. W ten sam sposób, gdy pochodna (a zatem i współczynnik rozszerzalności cieplnej) również zanika, równa się zgodnie z wyrażeniem ![]() pochodna
pochodna
W jakimkolwiek stanie - płynnym lub stałym, w postaci czystej substancji lub związek chemiczny– czy substancja istniała, jej entropia zgodnie z twierdzeniem termicznym at ma tę samą wartość (jeśli oczywiście substancja w każdym z tych stanów znajduje się w równowadze termodynamicznej) tak np. z entropią dowolnej substancji w cieczy i ciała stałe będą równe, a entropia mieszaniny składającej się z 1 kmol substancji A i 1 kmol substancji B będzie równa entropii 1 kmol ich związków chemicznych A i B.
Stałość entropii w oznacza, że w obszarze zera absolutnego jest ona zawsze równa zeru, tj. którakolwiek z izoterm pokrywa się z adiabatyczną. Zatem cały układ izotermiczny zachowuje się jak układ adiabatyczny i może wykonywać pracę tylko dzięki swojej energii wewnętrznej, nie pochłaniając ciepła z otaczających ciał i nie oddając im ciepła, i. wręcz przeciwnie, żaden układ adiabatyczny nie różni się w tym obszarze od układu izotermicznego.
Z tego ostatniego wynika, że nie da się osiągnąć zera absolutnego poprzez adiabatyczne rozszerzanie ciała. Podobnie nie da się osiągnąć zera absolutnego poprzez odprowadzenie ciepła z ciała, gdyż każde z ciał podczas procesu zmiany stanu zachowuje niezmienną wartość entropii, tj. przestaje oddawać ciepło do otoczenia.
Planck doszedł do wniosku, że w temperaturze zera absolutnego entropia wszystkich substancji znajdujących się w stanie równowagi, niezależnie od ciśnienia, gęstości i fazy, dąży do zera, tj. .
To stwierdzenie stanowi treść trzeciej zasady termodynamiki.
Gazy pod niezakłóconym niskim ciśnieniem skraplają się w temperaturach znacznie wyższych niż , a dopiero przy bardzo niskich ciśnieniach osiągają temperatury bliskie . Dlatego trzecia zasada termodynamiki dotyczy głównie układów skondensowanych, tj. stałych i ciała płynne(ze wszystkich substancji tylko hel2 pozostaje cieczą pod ciśnieniem rzędu 1 bara; wszystkie inne substancje przechodzą w stan stały aż do temperatury
Z trzeciej zasady termodynamiki wynika następujący ważny wniosek.
W pobliżu zera absolutnego wszystkie wielkości termodynamiczne charakteryzujące stan równowagi ciała przestają zależeć od temperatury. Oznacza to, że pochodne cząstkowe temperatury nie tylko entropii, jak zauważono wcześniej, ale także wszystkich innych funkcji termodynamicznych, na przykład energii wewnętrznej, entalpii itp., a także ciśnienia i objętości, wychodzą na zero.
Trzecia zasada termodynamiki jest manifestacją makroskopową właściwości kwantowe materiał; w tym sensie jest to prawo ścisłe.
Na podstawie trzeciej zasady termodynamiki, wykorzystując znaną pojemność cieplną, można obliczyć wartość bezwzględną funkcji termodynamicznych. Na przykład wartości entropii i entalpii ciała w danej temperaturze i ciśnieniu są określone przez równania

 ,
,
Ponadto wartość pod znakiem całki jest przyjmowana przy danym ciśnieniu.
Zgodnie z prawem Dulonga i Petita, pojemność cieplna solidny w wysokich temperaturach jest praktycznie stała i wynosi 6 cal/stopień na 1 kg ∙ atomu.
Trzecia zasada termodynamiki jest często formułowana w następujący sposób: nie da się w żaden sposób schłodzić ciała do zera absolutnego, tj. zero absolutne jest nieosiągalne. Nie oznacza to jednak możliwości uzyskania temperatur dowolnie bliskich
ROZDZIAŁ 4: Stan i potencjał termodynamiczny
4.1. Funkcje stanu
Energia wewnętrzna ciała U, jego entalpia I i entropia S są funkcjami stanu; dlatego dowolna kombinacja U, S i parametrów termicznych p, V, T będzie reprezentować funkcję stanu ciała. Ze wszystkich tych kombinacji szczególne znaczenie mają te, za pomocą których najprościej wyraża się praca wykonywana przez ciała przy zmianie ich stanu.
4.2. Maksymalna praca
Maksymalna użyteczna praca zewnętrzna reprezentuje pracę, którą system wytwarza na zewnętrznym przedmiocie pracy odizolowanym termicznie od systemu w procesie odwracalnym. 1-2 praca, którą musi wykonać zewnętrzne źródło pracy, aby przywrócić system ze stanu 2 do stanu pierwotnego. stan początkowy 1 w tych samych warunkach, t . praca procesu odwrotnego odwracalnego 2 - 1 nazywana jest pracą minimalną; w której ![]() .
.
W najbardziej ogólnym przypadku składa się z dwóch części: pracy związanej ze zmianą objętości i pracy niezwiązanej ze zmianą objętości.
Poniżej rozpatrzono dwa przypadki: 1) praca wykonywana jest przez jedno jednorodne ciało w obecności źródeł ciepła o różnych temperaturach; 2) praca jest wykonywana przez ciało. Znajduje się w środowisku, którego ciśnienie i temperatura są stałe.
4.3. Maksymalna praca ciała
Przyjmuje się, że zewnętrzny przedmiot pracy (źródło pracy) jest odizolowany termicznie od ciała, w wyniku czego oddziaływanie ciała ze źródłem pracy ma charakter wyłącznie mechaniczny; w każdym punkcie procesu odwracalnego źródło pracy wywiera nacisk na organizm. Dokładnie równe ciśnieniu ciała.
Znajdźmy wyrażenie na maksymalną pracę wykonaną przez ciało podczas przejścia ze stanu początkowego 1 do stanu końcowego 2 w warunkach, gdy jeden z parametrów termodynamicznych pozostaje niezmieniony.
Rozważmy najpierw odwracalny izentropowy proces zmiany stanu ciała, charakteryzujący się stałością entropii ciała: . W tym przypadku z pierwszej i drugiej zasady termodynamiki
lub, co jest tym samym, co tożsamość termodynamiczna
 (5)
(5)
![]() ;
; ![]() .
.
Zatem w procesie izentropowym maksymalna praca związana ze zmianą objętości jest równa utracie energii wewnętrznej, a maksymalna użyteczna praca zewnętrzna związana ze zmianą objętości jest równa utracie entalpii.
Wyznaczmy teraz maksymalną pracę wykonaną podczas procesu izotermicznego, tj. Na . W tym celu rozważmy odwracalne przejście izotermiczne ciała ze stanu początkowego 1 do stanu 2 (zarówno stan początkowy, jak i końcowy, ze względu na fakt, że rozważa się proces odwracalny). Są one równowagowe i charakteryzują się tym samym wartość temperatury), dla którego źródłem może być ciepło o tej samej temperaturze, co temperatura ciała w stanie początkowym.
Utwórzmy następujące wyrażenie z U, S, T:
F = U – TS. (6)
Funkcja stanu F nazywana jest energią Halmholtza (wcześniej nazywano ją energią swobodną).
Łatwo sprawdzić, że zmniejszenie tej funkcji, tj. różnica jest liczbowo równa maksymalnej pracy zmiany objętości wykonanej przez ciało podczas odwracalnego przejścia izometrycznego ze stanu początkowego 1 do stanu końcowego 2. Rzeczywiście, zgodnie z pierwszą zasadą termodynamiki
![]() ,
,
ale ze względu na odwracalność procesu i stałość temperatury ciała
![]() .
.
Zatem,
![]() (7)
(7)
Wyznaczmy maksymalną pracę zewnętrzną, jaką ciało może wykonać nad zewnętrznym przedmiotem pracy podczas odwracalnego procesu izometrycznego.
Ponieważ zgodnie z pierwszą zasadą termodynamiki
![]() ,
,
oraz dla odwracalnego procesu izometrycznego
Wielkość reprezentująca funkcję stanu nazywana jest energią Gibbsa (potencjałem izobarycznym) i oznaczana jest przez Ф:
Jak właśnie widzieliśmy,
![]() (9)
(9)
te. maksymalna użyteczna praca zewnętrzna podczas procesu izotermicznego jest równa utracie energii Gibbsa.
4.4. Maksymalna praca
wytwarzany przez organizm w środowisku
Jeżeli ciało znajduje się w środowisku, którego temperatura i ciśnienie są stałe i równe , to użyteczna praca zewnętrzna, jaką ciało może wykonać w procesie 1 – 2 nad zewnętrznym przedmiotem pracy, wynosi
gdzie , , to odpowiednio energia wewnętrzna, entropia i objętość ciała;
Odpowiednio energia wewnętrzna, entropia i objętość całego układu jako całości, tj. ciało i środowisko.
Największą pracę ciało wykonuje podczas procesu odwracalnego 1 – 2, gdy ; jest równa minimalnej pracy wykonanej przy przeciwnym znaku, tj.
W tym przypadku zakłada się, że wszelka praca nad zewnętrznym przedmiotem (źródłem) pracy jest wykonywana wyłącznie przez ciało; środowisko nie wchodzi w interakcję z zewnętrznym źródłem pracy i nie wykonuje zewnętrznej użytecznej pracy. Odpowiednio, wraz z odwracalną zmianą stanu środowiska, w oparciu o tożsamość termodynamiczną, mamy
Ponieważ kiedy zmienia się entropia środowiska i ciała, jest to powiązane zależnością ![]() oraz przez warunek stałości objętości całego układu jako całości
oraz przez warunek stałości objętości całego układu jako całości ![]() , to tę relację można zapisać jako
, to tę relację można zapisać jako
Wyznaczmy teraz użyteczną pracę zewnętrzną wytwarzaną przez izolowany adiabatycznie układ, z którego składa się ciało i środowisko.
Układ izolowany ma stałą objętość i dlatego cała wykonywana przez niego użyteczna praca zewnętrzna nie jest związana ze zmianą objętości.
Odwracalna zmiana stanu złożonego systemu izolowanego oznacza, co następuje. System izolowany składa się w najbardziej ogólnym przypadku z oddzielnych części, które różnią się od siebie (na przykład temperaturą, ciśnieniem, składem itp.), Które w ogólnym przypadku mogą nawet nie być ze sobą połączone. Entropia, energia wewnętrzna i objętość układu jako całości są równe odpowiednio sumie entropii, energii wewnętrznych i objętości tworzących układ części. Kiedy temperatura, ciśnienie, skład lub inne właściwości różnych części układu są różne, wówczas stan układu nie jest oczywiście stanem całkowitej równowagi termodynamicznej i musi być utrzymywany przez działanie różnych regulatorów; przegrody adiabatyczne, ściany sztywne, przegrody półprzepuszczalne itp. Jeśli regulatory działają wystarczająco wolno, tj. quasi-statycznie, tak aby w dowolnym momencie każda część układu znajdowała się w równowadze lokalnej, a całkowita entropia i objętość układu pozostały niezmienione, wówczas stan układu zmieni się w sposób odwracalny.
Podstawiając do równania (10) wartość równą, jak wspomniano powyżej, jesteśmy przekonani, że maksymalna użyteczna praca zewnętrzna układu izolowanego adiabatycznie przy odwrotnej zmianie jest równa spadkowi energii wewnętrznej układu:
Wartość reprezentuje maksymalną użyteczną pracę zewnętrzną izolowanego adiabatycznie układ zewnętrzny z odwracalną zmianą swojego stanu, gdy objętość i entropia układu pozostają niezmienione.
Z tożsamości termodynamicznej można również uzyskać wyrażenie na maksymalną użyteczną pracę zewnętrzną w przypadku, gdy przy odwrotnej zmianie stanu układu wielkości i ;
Znajdźmy teraz pracę wykonaną przez ciało podczas procesu izentropowego. Jeżeli stan ciała znajdującego się w środowisku zmienia się izentropowo, to , a zatem zgodnie z równaniem (10), maksymalna użyteczna praca zewnętrzna ciała
Jeżeli ciśnienie ciała nie zmienia się podczas procesu izentropowego i jest równe ciśnieniu otoczenia, tj. , następnie na podstawie wyrażenia (11)
![]() (15)
(15)
Wyrażenie (13) obowiązuje nawet wtedy, gdy ciśnienie ciała w stanach początkowym i końcowym jest równe ciśnieniu otoczenia , , a w stanach pośrednich, tj. ciało w stanach początkowym i końcowym znajduje się w równowadze z otoczeniem, natomiast w stanach pośrednich nie ma równowagi pomiędzy ciałem a otoczeniem.
Ponieważ ciało wraz z otoczeniem jest układem izolowanym adiabatycznie, równanie (13) określa również użyteczną pracę zewnętrzną układu izolowanego adiabatycznie pod warunkiem , .
Oczywiste jest, że gdy użyteczna praca zewnętrzna nie wiąże się ze zmianą objętości ciała, tj. równy .
Wyrażenie (14) obowiązuje także w przypadku, gdy znajduje się w stanach pośrednich i , ale w stanach końcowych i początkowych , .
Jeśli ciśnienie ciała jest stałe, a temperatura ciała jest równa temperaturze otoczenia (lub jeśli jest w stanie początkowym i końcowym, ![]() ), To
), To
![]() (17)
(17)
4,5. Maksymalna praca
kiedy organizm osiąga stan równowagi
z otoczeniem
Znajdźmy maksymalną użyteczną pracę zewnętrzną wykonaną przez ciało nad zewnętrznym przedmiotem pracy podczas przejścia ciała ze stanu początkowego 1 (który przyjmuje się za równowagę) do stanu 0 równowagi ze środowiskiem zewnętrznym o stałej temperaturze i ciśnienie. Przydatna praca zewnętrzna wykonywana podczas przejścia odwrotnego, w oparciu o pierwszą i drugą zasadę termodynamiki
![]() (18)
(18)
gdzie jest egzergia.
Egzergia nie jest jednoznaczną funkcją stanu organizmu. Rzeczywiście, w tym samym stanie Samoa, ciało będzie miało inną wartość egzergii w zależności od temperatury otoczenia. Dlatego ilość ma zasadniczo charakter pomocniczy; jego wprowadzenie wynikało jedynie z pewnej wygody w obliczeniach związanych z zastosowaniami technicznymi.
4.6. Potencjały termodynamiczne
Przez analogię do mechaniki, gdzie praca w polu sił zachowawczych jest liczbowo równa różnicy potencjałów w punkcie początkowym i końcowym, funkcje , , , , różnicę wartości w dwóch stanach reprezentują, zgodnie z wyrażeniami (5) – (17), maksymalna użyteczna praca zewnętrzna wytworzona przez układ podczas odwrotnego przejścia w odpowiednich warunkach z jednego stanu do drugiego, nazywane są potencjałami termodynamicznymi. Każdy z potencjałów termodynamicznych jest unikalną funkcją stanu układu.
W termodynamice pojęcie potencjału termodynamicznego odnosi się do całego układu jako całości (podczas gdy w fizyce zwykle chodzi o określony potencjał).
Produkt ten jest czasami nazywany „energią związaną”. Nazwa ta stanie się jasna, jeśli przypomnimy sobie, że podczas odwrotnego procesu izometrycznego cała praca jest wykonywana dzięki energii Helmholtza, a ilość - która wraz z energią wewnętrzną ciała nie jest zamieniana na pracę.
Rozdział 5: Faza równowagi i faza transformacji
5.1. Przejścia fazowe
Każda substancja może znajdować się w różnych fazach, które reprezentują różne stany agregatowe (tj. Gazowy, ciekły, krystaliczny i plazmowy) substancji, a w przypadku stanu krystalicznego także odmiany alotropowe tego ostatniego. Każda z faz stanowi jednorodny układ o identycznych właściwościach właściwości fizyczne we wszystkich jego częściach. Funkcja fazy - obecność granic oddzielających daną fazę od innych faz z nią stykających się. Właściwe przestrzenne rozgraniczenie faz pozwala na ich mechaniczne rozdzielenie.
Substancja może przejść z jednej fazy w drugą; to przejście nazywa się przejściem fazowym lub transformacją fazową.
Przejście substancji z fazy skondensowanej (tj. stałej lub ciekłej) do fazy gazowej nazywa się parowaniem lub odparowaniem (a w przypadku ciała stałego dodatkowo sublimacją lub sublimacją); przejście odwrotne nazywa się kondensacją. Przejście z fazy stałej do fazy ciekłej nazywa się topnieniem, a odwrotne przejście z fazy ciekłej do fazy stałej nazywa się krzepnięciem lub krystalizacją.
Przemianom fazowym towarzyszy absorpcja lub wydzielanie ciepła, zwane ciepłem przejścia fazowego (ciepło właściwe przejścia fazowego jest oznaczone przez ).
5.2. Ogólne warunki równowagi fazowej
Równowagowe współistnienie kilku różnych faz substancji stykających się ze sobą nazywa się równowagą fazową. Aby znaleźć warunki równowagi fazowej, rozważmy najpierw stan równowagi układu składającego się z dwóch faz tej samej substancji.
Aby istniała równowaga pomiędzy obiema stykającymi się fazami substancji, jest to konieczne w taki sam sposób, jak w przypadku ciała jednorodnego. spełnienie warunków równowagi mechanicznej i termicznej - jednakowe ciśnienie i temperatura obu faz. Jednak w odróżnieniu od ciała jednorodnego warunki te nie są wystarczające do osiągnięcia równowagi współistniejących faz, z których każda może przekształcić się w inną. Dla równowagi wymagane jest również, aby nie było preferencyjnego wzrostu jednej fazy kosztem drugiej, tj. tak aby stabilność faz w stanie równowagi była taka sama. Ten trzeci warunek znajduje się w ogólne warunki balansować.
Załóżmy, że ciśnienie i temperatura układu dwufazowego są stałe i równe i (przez ciśnienie i temperaturę układu dwufazowego rozumiemy ciśnienie i temperaturę którejkolwiek z faz, gdyż w stanie równowagi obie fazy mają ta sama wartość i ).
Gdy i są stałe, energia Hobbesa układu w stanie równowagi, zgodnie z warunkiem równowagi termodynamicznej układu przy stałym ciśnieniu i temperaturze, jest minimum energii Hobbesa F układu: , musi mieć minimum , tj. dФ=0. Ale w rozważanym przypadku układu dwufazowego
zatem, zakładając równowagę, przyjmują one następującą postać:
lub, biorąc pod uwagę to ![]() , otrzymujemy
, otrzymujemy
![]() .
.
Od tego czasu
![]() (19)
(19)
Otrzymane równanie reprezentuje pożądany trzeci warunek równowagi fazowej.
Zatem warunkiem równowagi układu dwufazowego jest równość ciśnień i temperatur obu faz oraz ich potencjałów chemicznych:; ; (20)
Bibliografia
"Termodynamika" instruktaż dla uniwersytetów, 1972 autorzy M.P. Vukalovich i I.I. Novikov
Układ termodynamiczny, zbiorowy i jego stany. Metoda zespołowa. Entropia i prawdopodobieństwo. Zespół kanoniczny Gibbsa. Rozkład kanoniczny. czynnik Gibbsa. Prawdopodobieństwa, energia swobodna i funkcja podziału.
System i podsystemy. Właściwości ogólne sumy statystyczne. Suma statystyczna cząstki testowej i kolektywu.
Gaz doskonały. Rozkład Boltzmanna. czynnik Boltzmanna. Stany kwantowe i dyskretne poziomy prostych ruchów molekularnych. Waga statystyczna poziomu (degeneracja). Kwoty według poziomów i kwoty według stanów.
Systemy zlokalizowane i zdelokalizowane. Translacyjna suma stanów, nierozróżnialność cząstek, objętość standardowa. Suma rotacyjna po poziomach cząsteczki dwuatomowej, nierozróżnialność orientacyjna i liczba symetrii. Funkcje podziału dla jednego i kilku obrotowych stopni swobody. Funkcja podziału oscylacyjnego w przybliżeniu harmonicznym. Korekta sum statystycznych prostych ruchów. Zerowy poziom drgań, skala energii molekularnej i suma molekularna stanów.
Energia swobodna A i wzory statystyczne na funkcje termodynamiczne: entropia S, ciśnienie p, energia wewnętrzna U, entalpia H, energia Gibbsa G, potencjał chemiczny m. Reakcja chemiczna oraz stała równowagi Kp w układzie gazów doskonałych.
1. Wstęp. Krótkie przypomnienie podstaw termodynamiki.
...Argumenty termodynamiczne i wyznaczone za ich pomocą funkcje stanu wygodnie jest przedstawić w postaci pojedynczej tablicy powiązanych ze sobą zmiennych. Metodę tę zaproponował Gibbs. Powiedzmy więc, że entropia, która z definicji jest funkcją stanu, przechodzi do kategorii jednej z dwóch naturalnych zmiennych kalorycznych, uzupełniając w tym zakresie temperaturę. A jeśli w jakimkolwiek procesie kalorycznym temperatura wygląda jak zmienna intensywna (siła), to entropia nabiera statusu zmiennej ekstensywnej - współrzędnej termicznej.
Tablicę tę można zawsze uzupełnić o nowe funkcje stanu lub w razie potrzeby równania stanu łączące argumenty. Liczba argumentów wymaganych do kompleksowego termodynamicznego opisu układu nazywana jest liczbą stopni swobody. Jest ona wyznaczana na podstawie podstawowych rozważań termodynamiki i można ją redukować za pomocą różnych równań sprzężenia.
W takiej pojedynczej tablicy można zamienić role argumentów i funkcji stanu. Technika ta jest szeroko stosowana w matematyce przy konstruowaniu odwrotności i funkcje ukryte. Celem takich technik logicznych i matematycznych (dość subtelnych) jest osiągnięcie maksymalnej zwartości i harmonii schematu teoretycznego.
2. Funkcje charakterystyczne. Równania różniczkowe Massiera.
Wygodnie jest uzupełnić tablicę zmiennych p, V, T funkcją stanu S. Między nimi istnieją dwa równania połączenia. Jedna z nich wyraża się w postaci postulowanej współzależności zmiennych f(p,V,T) =0. Mówiąc o „równaniu stanu”, najczęściej mamy na myśli tę zależność. Jednak każda funkcja stanu odpowiada nowemu równaniu stanu. Entropia z definicji jest funkcją stanu, tj. S=S(p,V,T). Dlatego między czterema zmiennymi istnieją dwa powiązania, a tylko dwa można zidentyfikować jako niezależne argumenty termodynamiczne, tj. Do kompleksowego termodynamicznego opisu układu wystarczą tylko dwa stopnie swobody. Jeśli ten układ zmiennych zostanie uzupełniony nową funkcją stanu, to wraz z nową zmienną pojawi się kolejne równanie sprzężenia, a zatem liczba stopni swobody nie wzrośnie.
Historycznie rzecz biorąc, pierwszą funkcją stanu była energia wewnętrzna. Dlatego przy jego udziale można utworzyć początkową tablicę zmiennych:
Tablica równań sprzężenia w tym przypadku zawiera funkcje postaci
f(p,V,T) =0, 2) U=U(p,V,T), 3) S=S(p,V,T).
Wielkości te można zamieniać rolami lub tworzyć z nich nowe funkcje stanu, ale w każdym przypadku istota sprawy nie ulegnie zmianie, a pozostaną dwie zmienne niezależne. Schemat teoretyczny nie będzie wykraczał poza dwa stopnie swobody, dopóki nie zaistnieje potrzeba uwzględnienia nowych efektów fizycznych i związanych z nimi nowych przemian energetycznych, a ich scharakteryzowanie okaże się niemożliwe bez rozszerzenia zakresu argumentacji i liczby funkcji państwowych. Wówczas liczba stopni swobody może ulec zmianie.
(2.1)3. Energia swobodna (energia Helmholtza) i jej rola.
Wskazane jest opisanie stanu układu izotermicznego o stałej objętości za pomocą energii swobodnej (funkcja Helmholtza). W tych warunkach jest to charakterystyczna funkcja i potencjał izochoryczno-izotermiczny układu.
Za pomocą częściowego zróżnicowania można z niego wydobyć inne niezbędne właściwości termodynamiczne, a mianowicie:
(3.1)Możliwe jest skonstruowanie jawnej postaci funkcji energii swobodnej dla niektórych stosunkowo prostych układów, wykorzystując metodę termodynamiki statystycznej.
4. O równowadze.
W każdym naturalnie zachodzącym procesie (spontanicznym lub swobodnym) energia swobodna układu maleje. Kiedy układ osiąga stan równowagi termodynamicznej, jego energia swobodna osiąga minimum i już w równowadze zachowuje stałą wartość. Układ można wyprowadzić ze stanu równowagi pod wpływem sił zewnętrznych, zwiększając jego energię swobodną. Taki proces nie może być już darmowy – będzie wymuszony.
Mikroskopijne ruchy cząstek nie zatrzymują się nawet w równowadze, a w układzie składającym się z ogromnej liczby cząstek i podukładów dowolnego rodzaju możliwych jest wiele różnych szczegółowych wariantów i kombinacji poszczególnych części oraz w ich obrębie, ale nie wszystkie z nich przynoszą brak równowagi w systemie.
Równowaga termodynamiczna w makrosystemie wcale nie oznacza, że w jego mikroskopijnych fragmentach zanikają wszelkie rodzaje ruchu. Wręcz przeciwnie, równowagę zapewnia dynamika właśnie tych mikroskopijnych ruchów. Dokonują ciągłego poziomowania - wygładzania zaobserwowanych znaków i właściwości makroskopowych, zapobiegając ich emisji i nadmiernym wahaniom.
5. O metodzie statystycznej.
Głównym celem metody statystycznej jest ustalenie ilościowego związku między cechami ruchy mechaniczne poszczególne cząstki tworzące równowagowy kolektyw statystyczny oraz uśrednione właściwości tego zbioru, które są dostępne do pomiarów termodynamicznych metodami makroskopowymi.
Celem jest wyprowadzenie praw ilościowych dla parametrów termodynamicznych układu w oparciu o charakterystyki mechaniczne ruchów poszczególnych mikroelementów zbioru równowagowego.
6. Równowagi i wahania. Mikrostany.
Według metody Gibbsa układ termodynamiczny jest zbiorowością - zbiorem bardzo duża liczba elementy - podsystemy tego samego typu.
Każdy podsystem z kolei może składać się także z bardzo dużej liczby innych, jeszcze mniejszych podsystemów i z kolei może pełnić rolę całkowicie niezależnego systemu.
Wszelkie naturalne wahania w układzie równowagi nie zakłócają równowagi, są one zgodne ze stabilnym stanem makroskopowym ogromnego zbioru cząstek. Po prostu redystrybuują cechy poszczególnych elementów kolektywu. Powstają różne mikrostany i wszystkie są wersjami tego samego obserwowalnego makrostanu.
Każda indywidualna kombinacja stanów elementów kolektywu generuje tylko jeden z ogromnej różnorodności możliwych mikrostanów makrosystemu. Wszystkie są równoważne w sensie fizycznym, wszystkie prowadzą do tego samego zestawu mierzalnych parametrów fizycznych układu i różnią się jedynie niektórymi szczegółami rozkładu stanów pomiędzy elementami...
Wszystkie mikrostany są zgodne z makroskopową równowagą termodynamiczną, a rozkład numeryczny poszczególnych składników energii swobodnej (jej energii i entropii) jest zjawiskiem zupełnie powszechnym. Musimy zrozumieć, że rozproszenie następuje w wyniku ciągłej wymiany energii między cząsteczkami - elementami kolektywu. Dla niektórych pierwiastków maleje, a dla innych wzrasta.
Jeśli system znajduje się w termostacie, wówczas energia jest wymieniana w sposób ciągły z otoczeniem. Naturalne energetyczne mieszanie kolektywu następuje w wyniku ciągłej wymiany pomiędzy mikrocząsteczkami kolektywu. Równowaga jest stale utrzymywana poprzez kontakt termiczny z zewnętrznym termostatem. Tak się najczęściej nazywa w statystyce. środowisko.
7. Metoda Gibbsa. Zespół statystyczny i jego elementy.
Tworzenie schemat uniwersalny mechaniki statystycznej, Gibbs zastosował zaskakująco prostą technikę.
Każdy prawdziwy system makroskopowy jest zbiorem ogromnej różnorodności elementów - podsystemów. Podsystemy mogą mieć wymiary makroskopowe i mogą być mikroskopijne, aż do atomów i cząsteczek. Wszystko zależy od rozpatrywanego problemu i poziomu badań.
W różne momenty czasie w różnych punktach układu rzeczywistego, w różnych obszarach przestrzennych makroskopowego zbiorowości, chwilowe charakterystyki jego małych elementów mogą być różne. „Niejednorodności” w zespole stale migrują.
Atomy i cząsteczki mogą znajdować się w różnych stanach kwantowych. Kolektyw jest ogromny i zawiera różne kombinacje stanów fizycznie identycznych cząstek. Na poziomie atomowo-molekularnym stany zawsze ulegają wymianie i następuje ich ciągłe mieszanie. Dzięki temu właściwości różnych fragmentów układu makroskopowego wyrównują się, a fizycznie obserwowalny stan makroskopowy układu termodynamicznego wygląda na zewnątrz niezmieniony...
Materiał z FFWiki.
| Przedmiot | Termodynamika i fizyka statystyczna | Semestr | 7-8 | Typ | wykład, seminarium | Raportowanie | egzamin | Dział | Katedra Statystyki Kwantowej i Teorii Pola |
|---|
O przedmiocie
Termodynamika i fizyka statystyczna. Pierwsze pytanie, gdy widzisz ten temat w harmonogramie, brzmi: jak to możliwe? Rzeczywiście, na pierwszym roku wykładali już fizykę molekularną, która obejmowała wszystkie 3 zasady termodynamiki, potencjałów i rozkładu Maxwella. Wydawałoby się, co jeszcze może być nowego w przyrodzie?
Okazuje się, że to, co było na pierwszym roku, to dziecinne gadanie w porównaniu z prawdziwą termodynamiką i fizyką statystyczną. Ten, za pomocą którego Landau obliczył ciekły hel i otrzymał Nagrodę Nobla.
Ważne jest, aby nie wpaść w pułapkę myślenia, że skoro na jednym wykładzie powiedzą ci to, co wiedziałeś w szkole, to tak będzie dalej. Już od połowy września będziecie świadkami niesamowitych trików z pochodnymi cząstkowymi, a pod koniec semestru jesiennego pojawią się bardzo poruszające tematy z fizyki statystycznej:
- Obliczanie sum statystycznych i rozkładów Gibbsa
- Gazy kwantowe - Gazy Fermiego i Bosego w różnych warunkach
- Przejścia fazowe i ich właściwości
- Gazy nieidealne - Łańcuchy Bogolubowa, modele plazmy i elektrolitów
Autor tych słów, mimo że na 4 dni przed egzaminami potrafił się doskonale przygotować, bardzo tego żałuje i nie radzi nikomu powtarzać takiego gwałtu na mózgu :) Zadania i pytania na egzamin znane są od dawna początku roku i bardzo przydatne jest wcześniejsze przygotowanie części materiału.
W semestrze wiosennym są zarówno proste, jak i złożone tematy. Na przykład teoria dot Ruch Browna bardzo łatwo to napisać. Ale na końcu kursu znajdują się różne równania kinetyczne, które są znacznie trudniejsze do zrozumienia.
Egzamin
Egzamin jesienny idzie całkiem nieźle, nie pozwalają na ściąganie. W większości nauczyciele nie odgrywają żadnej roli, ale nie było też żadnych zauważalnych gratisów. Trzeba znać teorię. Dyplom zawiera ocenę do egzaminu wiosennego. Egzamin wiosenny jest trudniejszy pod względem merytorycznym niż egzamin jesienny, ale zazwyczaj jest przyjmowany bardziej responsywnie. Jednak teorię również należy dobrze poznać.
Bilet na jesień i wiosnę zawiera 2 pytania teoretyczne i jedno zadanie.
Uważaj na swoje statystyki, kilka osób (liczba waha się od 2 do 10!) regularnie kończy szkołę bez zdania tego egzaminu. I to nie byle kto, ale zatwardziali studenci czwartego roku.
Materiały
Semestr jesienny
- Ulotka 7 semestr (pdf) - przydatna ulotka
- Odpowiedzi na pytania z termodynamiki (pdf) - 1 pytanie na bilet
- Odpowiedzi na pytania z fizyki statystycznej (pdf) - pytanie 2 na bilecie
- https://vk.com/doc231234703_450962027?hash=b2eb6c2220f95a7795&dl=cf7b5295f12e0fd4e0 zadania na pierwsze kolokwium
- https://vk.com/doc181113102_453848269?hash=6d6f68abc3358e2adf&dl=1606060abdd44d226e do drugiego
Semestr wiosenny
- Odpowiedzi na pytania egzaminacyjne, teoria (pdf) - odpowiedzi na pytania z egzaminu teoretycznego starannie wpisane na komputerze.
- - rozwiązywanie problemów
- Rozwiązania zadań do egzaminu (pdf) - więcej rozwiązań zadań
Literatura
Książki problemowe
- Zadania z termodynamiki i fizyki statystycznej dla studentów IV roku Wydziału Fizyki Uniwersytetu Moskiewskiego (semestr jesienny - teoria układów równowagi) (pdf)
Wykład 2.
Termodynamika, fizyka statystyczna, entropia informacyjna
1. Informacje z termodynamiki i fizyka statystyczna. Funkcja dystrybucyjna. Twierdzenie Liouville'a. Rozkład mikrokanoniczny. Pierwsza zasada termodynamiki. Procesy adiabatyczne. Entropia. Waga statystyczna. Wzór Boltzmanna. Druga zasada termodynamiki. Procesy odwracalne i nieodwracalne.
2. Entropia informacji Shannona. Kawałki, orzechy, trity itp. Związek między entropią a informacją.
Ta część należy do wykładu 1. Lepiej omówiono ją w części V („Koncepcja splątania stanów kwantowych”).
LE CNOT jest przedstawiany jako:
Wartość (qu)bit przechowujemy przez chwilę (qu)bit b zmienia się zgodnie z prawem XOR:
fragment B(target = target) zmienia swój stan wtedy i tylko wtedy, gdy stan bitu kontrolnego A pasuje 1; Jednocześnie stan bitu sterującego nie ulega zmianie.
Operacja logiczna XOR (CNOT) ilustruje, dlaczego klasyczne dane można klonować, ale danych kwantowych nie. Należy zauważyć, że w ogólnym przypadku przez dane kwantowe będziemy rozumieć superpozycje postaci
![]() , (1)
, (1)
gdzie i - Liczby zespolone lub amplitudy stanów i, .
Zgodnie z tablicą prawdy, jeśli XOR zostanie zastosowany do danych boolowskich, w których drugi bit jest w stanie „0” (b), a pierwszy jest w stanie „X” (a), to pierwszy bit się nie zmienia, a drugi staje się jego kopią:
U XOR (X, 0) = (X, X), gdzie X = „0” lub „1”.
W przypadku kwantowym dane oznaczone symbolem „X” należy uznać za superpozycję (1):
![]() .
.
Fizycznie dane można zakodować np. w podstawie polaryzacji |V> = 1, |H> = 0 (H,V)= (0,1):
![]() I
I ![]()
Można zauważyć, że kopiowanie stanu faktycznie ma miejsce. Twierdzenie o nieklonowaniu stwierdza, że kopiowanie jest niemożliwe arbitralny stan kwantowy. W rozpatrywanym przykładzie kopiowanie nastąpiło dlatego, że operacja została wykonana samodzielnie (|0>, |1>), tj. V prywatny przypadek stanu kwantowego.
Wydaje się, że operacji XOR można również użyć do skopiowania superpozycji dwóch stanów boolowskich, takich jak |45 0 > ? |V> + |H>:
![]()
Ale to nieprawda! Jedność ewolucji kwantowej wymaga, aby superpozycja stanów wejściowych została przekształcona w odpowiednią superpozycję stanów wyjściowych:
![]() (2)
(2)
Jest to tzw stan splątany (Ф+), w którym każdy z dwóch kubitów wyjściowych nie ma określonej wartości (w tym przypadku polaryzacji). Ten przykład to pokazuje operacje logiczne, wykonywane na obiektach kwantowych, przebiegają według innych zasad niż w klasycznych procesach obliczeniowych.
Powstaje następne pytanie: Wygląda na to, że jest w trybie wyjściowym A ponownie można przedstawić jako superpozycję ![]() , podobnie jak stan mody B. Jak pokazać, że tak nie jest, czyli że nie ma w ogóle sensu mówić o stanach trybu (bitu)? A i moda (trochę) B?
, podobnie jak stan mody B. Jak pokazać, że tak nie jest, czyli że nie ma w ogóle sensu mówić o stanach trybu (bitu)? A i moda (trochę) B?
Użyjmy analogii do polaryzacji, kiedy
![]() (3).
(3).
Istnieją dwa sposoby. Ścieżka 1 jest dłuższa, ale bardziej spójna. Konieczne jest obliczenie średnich wartości parametrów Stokesa dla obu trybów wyjściowych. Średnie są pobierane z funkcji falowej (2). Jeśli wszystko oprócz okaże się równe zeru, wówczas stan ten jest niespolaryzowany, tj. mieszane i superpozycja (3) nie ma sensu. Pracujemy w reprezentacji Heisenberga, gdy operatory są przekształcane, ale funkcja falowa nie.
Widzimy to więc w modzie A.
![]() - całkowite natężenie wiązki a,
- całkowite natężenie wiązki a,
![]() - proporcja polaryzacji pionowej,
- proporcja polaryzacji pionowej,
![]() - udział +45 0-tej polaryzacji,
- udział +45 0-tej polaryzacji,
![]() - udział prawoskrętnej polaryzacji kołowej.
- udział prawoskrętnej polaryzacji kołowej.
Funkcję falową, po której przeprowadza się uśrednianie, przyjmuje się w postaci (2):
gdzie są operatory narodzin i zniszczenia w modach A I B działać według zasad:

(Wykonaj obliczenia w Rozdziale V (patrz notatnik). Tam również oblicz prawdopodobieństwo zarejestrowania zbiegów okoliczności lub korelator postaci ![]() }
}
Ścieżka II jest bardziej wizualna, ale mniej „uczciwa”!
Znajdźmy zależność natężenia światła w trybie A od kąta obrotu polaroidu umieszczonego w tym trybie. Jest to standardowy kwantowo-optyczny sposób sprawdzania stanu (2) - natężenie nie powinno zależeć od rotacji. Jednocześnie podobna zależność liczby dopasowań ma postać
![]() . Zależności takie po raz pierwszy uzyskali E. Fry (1976) i A. Aspek (1985) i często są interpretowane jako dowód na nielokalność mechaniki kwantowej.
. Zależności takie po raz pierwszy uzyskali E. Fry (1976) i A. Aspek (1985) i często są interpretowane jako dowód na nielokalność mechaniki kwantowej.
Tak więc sytuację eksperymentalną przedstawiono na rysunku:

A-przeorat
![]()
gdzie jest operatorem anihilacji w trybie a. Wiadomo, że transformacja operatorów dwóch ortogonalnie spolaryzowanych modów x i y, gdy światło przechodzi przez polaroid zorientowany pod kątem, ma postać:
![]() .
.
(tylko pierwszy, czwarty, piąty i ósmy wyraz są różne od zera) =
(tylko pierwszy i ósmy wyraz są różne od zera) = - nie zależy od kąta?!
Fizycznie dzieje się tak, ponieważ funkcja falowa (2) nie jest rozłożona na czynniki i nie ma sensu mówić o stanach w modach A I B osobno. Nie można zatem twierdzić, że mod a jest w stanie superpozycji (3)!
Komentarz. Dokonane obliczenia (Sposób II) wcale nie dowodzą, że państwo jest w modzie A niespolaryzowany. Na przykład, jeśli w tym trybie byłoby światło spolaryzowane kołowo, wynik byłby taki sam. Rygorystyczny dowód – na przykład poprzez parametry Stokesa (w sekcji V).
Należy zauważyć, że postępując w ten sam sposób, możemy udowodnić, że stan w trybie a przed elementem CNOT jest spolaryzowany.

W tym przypadku należy przeprowadzić uśrednianie po funkcji falowej stanu początkowego (3). Wynik wygląda następująco:
![]() te. maksymalne zliczenia osiąga się przy = 45 0 .
te. maksymalne zliczenia osiąga się przy = 45 0 .
Informacja i entropia.
Nie wprowadzając na razie terminu „operacyjnego” „informacja”, będziemy się spierać językiem „potocznym”. Te. informacja to pewna wiedza o przedmiocie.
Poniższy przykład pokazuje, że pojęcia informacja i entropia są ze sobą ściśle powiązane. Rozważmy gaz doskonały będący w równowadze termodynamicznej. Gaz składa się z ogromnej liczby cząsteczek poruszających się w objętości V. Parametrami tego stanu są ciśnienie i temperatura. Liczba stanów takiego układu jest ogromna. Entropia gazu w równowadze TD jest maksymalna i jak wynika ze wzoru Boltzmanna, jest określona przez liczbę mikrostanów układu. Jednocześnie nie wiemy nic o tym, w jakim konkretnym stanie znajduje się system ten moment Nie mamy czasu – informacji jest niewiele. Powiedzmy, że jakimś cudem udało nam się za pomocą bardzo szybkiego urządzenia „podejrzeć stan systemu w danym momencie. Otrzymaliśmy więc o niej pewne informacje. Można sobie nawet wyobrazić, że sfotografowaliśmy nie tylko współrzędne cząsteczek, ale także ich prędkości (na przykład wykonując kilka zdjęć jedno po drugim). Co więcej, w każdym momencie, gdy dostępna jest nam informacja o stanie układu, entropia dąży do zera, gdyż system znajduje się tylko w jednym konkretnym stanie spośród całej ich ogromnej różnorodności, a stan ten jest wysoce nierównowagowy. Ten przykład pokazuje, że informacja i entropia rzeczywiście są w jakiś sposób powiązane, a natura tego połączenia już się ujawnia: im więcej informacji, tym mniejsza entropia.
Informacje z termodynamiki i fizyki statystycznej.
Wielkości fizyczne charakteryzujące stany makroskopowe ciał (wiele cząsteczek) nazywane są termodynamicznymi (w tym energia, objętość). Istnieją jednak wielkości, które pojawiają się w wyniku działania praw czysto statystycznych i mają znaczenie, gdy są stosowane tylko do układów makroskopowych. Takimi są na przykład entropia i temperatura.
Klasyczna statystyka
*Twierdzenie Liouville'a. Funkcja rozkładu jest stała na trajektoriach fazowych podsystemu (mówimy o podsystemach quasi-zamkniętych, więc twierdzenie obowiązuje tylko dla niezbyt długich okresów czasu, podczas których podsystem zachowuje się jak zamknięty).

Tutaj - - funkcja rozkładu lub gęstość prawdopodobieństwa. Jest wprowadzany poprzez prawdopodobieństwo w wykryć podsystem w elemencie przestrzeni fazowej w tym momencie: dw = ( P 1 ,..., ps , Q 1 ,..., pytanie ) dpdq , I
Znalezienie rozkładu statystycznego dla dowolnego podsystemu jest głównym zadaniem statystyki. Jeśli znany jest rozkład statystyczny, można obliczyć prawdopodobieństwa różnych wartości dowolnego wielkości fizyczne, w zależności od stanów tego podsystemu (czyli od wartości współrzędnych i pędów):
![]() .
.
*Rozkład mikrokanoniczny.
Rozkład dla zbioru dwóch podsystemów (zakłada się, że są one zamknięte, czyli słabo oddziałujące) jest równy. Dlatego ![]() - logarytm funkcji rozkładu - wartość przyłączeniowy. Z twierdzenia Liouville'a wynika, że dystrybuantę należy wyrazić w postaci takich kombinacji zmiennych p i q, które gdy podukład porusza się jako układ zamknięty, muszą pozostać stałe (takie wielkości nazywane są całkami ruchu). Oznacza to, że sama funkcja rozkładu jest całką ruchu. Co więcej, jego logarytm jest również całką ruchu i przyłączeniowy. W sumie w mechanice występuje siedem całek ruchu – energia, trzy składowe pędu i trzy składowe momentu pędu – (dla podukładu a: E a (P,
Q),
P
A (P,
Q), M A (P,
Q)). Jedyną addytywną kombinacją tych ilości jest
- logarytm funkcji rozkładu - wartość przyłączeniowy. Z twierdzenia Liouville'a wynika, że dystrybuantę należy wyrazić w postaci takich kombinacji zmiennych p i q, które gdy podukład porusza się jako układ zamknięty, muszą pozostać stałe (takie wielkości nazywane są całkami ruchu). Oznacza to, że sama funkcja rozkładu jest całką ruchu. Co więcej, jego logarytm jest również całką ruchu i przyłączeniowy. W sumie w mechanice występuje siedem całek ruchu – energia, trzy składowe pędu i trzy składowe momentu pędu – (dla podukładu a: E a (P,
Q),
P
A (P,
Q), M A (P,
Q)). Jedyną addytywną kombinacją tych ilości jest
Ponadto współczynniki (jest ich siedem) muszą pozostać takie same dla wszystkich podsystemów danego układu zamkniętego i dobierane są z warunków normalizacyjnych (4).
Aby warunek normalizacji (4) był spełniony konieczne jest, aby funkcja (P, Q) skontaktowałem się z punktami mi 0, P 0, M 0 do nieskończoności. Bardziej precyzyjne sformułowanie daje wyraz
Rozkład mikrokanoniczny.
Obecność funkcji - powoduje, że znikają one we wszystkich punktach przestrzeni fazowej, w których występuje co najmniej jedna z wielkości MI, R., M nie jest równa podanej (średniej) wartości mi 0, P 0, M 0 .
Z sześciu całek P I M można wyeliminować, zamykając system w solidnej obudowie, w której spoczywa.
![]() .
.
Entropia fizyczna
Ponownie używamy pojęcia gazu doskonałego.
Niech jednoatomowy gaz doskonały ma gęstość N i temperatura T nabiera objętości V. Będziemy mierzyć temperaturę w jednostkach energii - stała Boltzmanna się nie pojawi. Każdy atom gazu ma średnią energię kinetyczną ruchu termicznego równą 3T/2. Dlatego całkowita energia cieplna gazu jest równa
Wiadomo, że ciśnienie gazu jest równe P = nT. Jeżeli gaz może wymieniać ciepło ze środowiskiem zewnętrznym, wówczas prawo zachowania energii gazu wygląda następująco:
![]() . (5)
. (5)
Zatem zmiana energii wewnętrznej gazu może nastąpić zarówno w wyniku wykonanej przez niego pracy, jak i w wyniku otrzymania określonej ilości ciepła dQ z zewnątrz. Równanie to wyraża pierwszą zasadę termodynamiki, tj. prawo zachowania energii. Zakłada się, że gaz znajduje się w równowadze, tj. P = konst w całym tomie.
Jeśli założymy, że gaz również znajduje się w stanie równowagi TD, T =konst, wówczas zależność (5) można uznać za elementarny proces zmiany parametrów gazu, gdy zmieniają się one bardzo wolno, gdy równowaga TD nie jest zakłócona. Właśnie dla takich procesów pojęcie entropii S wprowadza się za pomocą zależności
Dlatego argumentuje się, że oprócz energii wewnętrznej gaz równowagowy ma inną wewnętrzną charakterystykę związaną z termicznym ruchem atomów. Zgodnie z (5, 6) przy stałej objętości dV= 0, zmiana energii jest proporcjonalna do zmiany temperatury, i to w ogólnym przypadku
![]()
Ponieważ ![]() Gdzie N =
nV =
konst jest całkowitą liczbą atomów gazu, wówczas ostatnią zależność można zapisać jako
Gdzie N =
nV =
konst jest całkowitą liczbą atomów gazu, wówczas ostatnią zależność można zapisać jako
![]()
Po całkowaniu otrzymujemy

Wyrażenie w nawiasach kwadratowych przedstawia entropię na cząstkę.
Zatem, jeśli zarówno temperatura, jak i objętość zmienią się w taki sposób, że VT 3/2 pozostaje stała, wówczas entropia S nie zmienia się. Zgodnie z (6) oznacza to, że gaz nie wymienia ciepła z otoczeniem zewnętrznym, tj. gaz jest od niego oddzielony ściankami termoizolacyjnymi. Proces ten nazywa się adiabatyczny.
Ponieważ
gdzie = 5/3 nazywa się wykładnikiem adiabatycznym. Zatem podczas procesu adiabatycznego temperatura i ciśnienie zmieniają się wraz z gęstością zgodnie z prawem
Formuła Boltzmanna
Jak wynika z twierdzenia Liouville'a, funkcja dystrybucji? ma ostre maksimum w E = E 0 (wartość średnia) i jest niezerowa tylko w pobliżu tego punktu. Jeśli podasz szerokość E krzywej (E), definiując ją jako szerokość prostokąta, którego wysokość jest równa wartości funkcji (E) w maksymalnym punkcie, a pole jest równe jedności ![]() (przy odpowiedniej normalizacji). Możemy przejść od przedziału wartości energii do liczby stanów Г z energiami należącymi do E (jest to w rzeczywistości średnia fluktuacja energii układu). Wówczas wartość Γ charakteryzuje stopień rozmycia stanu makroskopowego układu nad jego stanami mikroskopowymi. Inaczej mówiąc, za systemy klasyczneГ jest rozmiarem obszaru przestrzeni fazowej, w którym dany podsystem spędza prawie cały swój czas. W teorii półklasycznej ustala się zgodność pomiędzy objętością obszaru przestrzeni fazowej a liczbą przypadających na niego stanów kwantowych. Mianowicie: dla każdego stanu kwantowego w przestrzeni fazowej istnieje komórka o objętości, gdzie s jest liczbą stopni swobody
(przy odpowiedniej normalizacji). Możemy przejść od przedziału wartości energii do liczby stanów Г z energiami należącymi do E (jest to w rzeczywistości średnia fluktuacja energii układu). Wówczas wartość Γ charakteryzuje stopień rozmycia stanu makroskopowego układu nad jego stanami mikroskopowymi. Inaczej mówiąc, za systemy klasyczneГ jest rozmiarem obszaru przestrzeni fazowej, w którym dany podsystem spędza prawie cały swój czas. W teorii półklasycznej ustala się zgodność pomiędzy objętością obszaru przestrzeni fazowej a liczbą przypadających na niego stanów kwantowych. Mianowicie: dla każdego stanu kwantowego w przestrzeni fazowej istnieje komórka o objętości, gdzie s jest liczbą stopni swobody
Wartość Γ nazywana jest wagą statystyczną stanu makroskopowego i można ją zapisać jako:
Logarytm wagi statystycznej nazywa się entropią:
gdzie - waga statystyczna = liczba mikrostanów objętych makrostanem rozpatrywanego układu.
![]() .
.
W statystyce kwantowej pokazano, że = 1. Zatem
Gdzie przez rozumie się macierz statystyczną (gęstość). Ze względu na liniowość logarytmu funkcji rozkładu energii (*), gdzie przeprowadza się uśrednianie po funkcji rozkładu.
Ponieważ liczba stanów jest w każdym razie nie mniejsza niż jeden, entropia nie może być ujemna. S określa gęstość poziomów w widmie energii układu makroskopowego. Ze względu na addytywność entropii można powiedzieć, że średnie odległości pomiędzy poziomami ciała makroskopowego maleją wykładniczo wraz ze wzrostem jego rozmiaru (tj. liczby znajdujących się w nim cząstek). Najwyższa wartość entropia odpowiada całkowitej równowadze statystycznej.
Charakteryzując każdy stan makroskopowy układu poprzez rozkład energii pomiędzy różnymi podukładami, można powiedzieć, że liczba kolejnych stanów, przez które system przechodzi, odpowiada coraz bardziej prawdopodobnemu rozkładowi energii. Ten wzrost prawdopodobieństwa jest duży ze względu na jego wykładniczy charakter i S- wykładnik zawiera wielkość addytywną - entropię. To. procesy zachodzące w nierównowagowym układzie zamkniętym przebiegają w taki sposób, że układ w sposób ciągły przechodzi od stanów o niższej entropii do stanów o wyższej entropii. W rezultacie entropia osiąga najwyższą możliwą wartość, odpowiadającą całkowitej równowadze statystycznej.
Tak więc, jeśli układ zamknięty w pewnym momencie znajduje się w stanie makroskopowym nierównowagowym, wówczas najbardziej prawdopodobną konsekwencją w kolejnych momentach będzie monotoniczny wzrost entropii układu. Ten - druga zasada termodynamiki (R. Clausius, 1865). Jej statystyczne uzasadnienie podał L. Boltzmann w 1870 roku. Inna definicja:
jeśli w pewnym momencie entropia układu zamkniętego różni się od maksymalnej, to w kolejnych momentach entropia nie maleje. Rośnie lub w skrajnym przypadku pozostaje stała. Według tych dwóch możliwości wszystkie procesy zachodzące w ciałach makroskopowych są zwykle podzielone na nieodwracalny I odwracalny . Nieodwracalny - te procesy, którym towarzyszy wzrost entropii całego układu zamkniętego (nie mogą zachodzić procesy, które byłyby ich powtórzeniem w odwrotnej kolejności, gdyż w tym przypadku entropia musiałaby się zmniejszyć). Należy pamiętać, że spadek entropii może być spowodowany wahaniami. Odwracalny to procesy, w których entropia układu zamkniętego pozostaje stała i w związku z tym mogą zachodzić odwrotny kierunek. Proces ściśle odwracalny stanowi idealny przypadek ograniczający.
Podczas procesów adiabatycznych układ nie absorbuje ani nie oddaje ciepła ? Q = 0 .
Komentarz: (istotny). Stwierdzenie, że układ zamknięty musi przejść do stanu równowagi w odpowiednio długim czasie (dłuższym niż czas relaksacji) dotyczy tylko układu znajdującego się w stacjonarnych warunkach zewnętrznych. Przykładem jest zachowanie dużego obszaru Wszechświata dostępnego naszej obserwacji (właściwości natury nie mają nic wspólnego z właściwościami układu równowagi).
Informacja.
Rozważmy taśmę podzieloną na komórki - klasyczny rejestr. Jeśli w każdej komórce można umieścić tylko jeden z dwóch znaków, wówczas mówi się, że komórka zawiera trochę informacji. Jest oczywiste (patrz wykład 1), że w rejestrze zawierającym N zawarte komórki N trochę informacji i można w niej zapisać 2 N wiadomości. Zatem entropię informacji mierzy się w bitach:
![]() (7)
(7)
Tutaj Q N = 2 N- całkowita liczba różnych wiadomości. Z (7) wynika, że Entropia informacji jest po prostu równa minimalnej liczbie komórek binarnych, w których można zapisać pewną informację.
Definicja (7) może być przepisana inaczej. Niech będzie nas wielu Q N różne wiadomości. Znajdźmy prawdopodobieństwo, że wiadomość, której potrzebujemy, będzie zgodna z wiadomością wybraną losowo z całkowitej liczby Q N różne wiadomości. To oczywiście jest równe P N = 1/ Q N. Wówczas definicję (7) zapiszemy jako:
![]() (8)
(8)
Im większa liczba komórek N, tym mniej prawdopodobne P N i tym większa entropia informacji H.B zawarte w tej konkretnej wiadomości.
Przykład . Liczba liter alfabetu wynosi 32 (bez litery ё). Liczba 32 jest piątą potęgą dwójki 32 = 2 5. Aby dopasować każdą literę do określonej kombinacji liczb binarnych, musisz mieć 5 komórek. Dodając duże litery do małych, podwajamy liczbę znaków, które chcemy zakodować - będzie 64 = 2 6 - tj. dodano dodatkową porcję informacji H.B= 6. Tutaj H.B- ilość informacji na literę (małe lub wielkie). Jednak takie bezpośrednie obliczenie entropii informacyjnej nie jest całkowicie dokładne, ponieważ w alfabecie znajdują się litery, które są mniej powszechne lub częstsze. Literom, które występują rzadziej, można przypisać większą liczbę komórek, natomiast literom, które występują często, można zaoszczędzić pieniądze i nadać im te stany rejestrów, które zajmują mniejszą liczbę komórek. Precyzyjna definicja entropię informacji podał Shannon:
![]() (9)
(9)
Formalnie wyprowadzenie tej zależności można uzasadnić następująco.
Pokazaliśmy powyżej
ze względu na addytywność logarytmu funkcji rozkładu i jej liniowość w energii.
Pozwalać P- pewnego rodzaju funkcja dystrybucji wartość dyskretna fi (na przykład litery „o” w tym tekście). Jeśli korzystasz z funkcji P skonstruować funkcję rozkładu prawdopodobieństwa różnych wartości wielkości F = F 1 , F 2 ,... f N, wówczas ta funkcja będzie miała maksimum w , gdzie i (normalizacja). Wtedy p()= 1 i (ogólnie rzecz biorąc, dotyczy to klasy funkcji spełniających warunek (*))
Sumowanie odbywa się po wszystkich znakach (literach alfabetu) oraz Liczba Pi oznacza prawdopodobieństwo pojawienia się symbolu z liczbą I. Jak widać, pod tym wyrażeniem kryją się zarówno litery często używane, jak i te, których prawdopodobieństwo wystąpienia w danej wiadomości jest znikome.
Ponieważ wyrażenie (9) używa naturalny logarytm odpowiednia jednostka informacji nazywana jest „nat”.
Wyrażenie (9) można przepisać jako
gdzie nawiasy oznaczają zwykłe klasyczne uśrednianie przy użyciu funkcji rozkładu p i .
Komentarz . Na kolejnych wykładach zostanie pokazane, że dla stanów kwantowych
gdzie jest macierz gęstości. Formalnie wyrażenia (10) i (11) są takie same, ale istnieje znacząca różnica. Klasyczne uśrednianie przeprowadza się po stanach ortogonalnych (własnych) układu, natomiast w przypadku kwantowym mogą występować także stany nieortogonalne (superpozycje). Dlatego zawsze ilość H klasa H !
Wzory (8) i (9) wykorzystują logarytmy w na różnych podstawach. W (8) - w oparciu o podstawę 2 oraz w (9) - w oparciu o podstawę e. Odpowiadające tym wzorom entropie informacyjne można łatwo wyrazić poprzez siebie nawzajem. Skorzystajmy z zależności, w której M jest dowolną liczbą
![]() .
.
Następnie, biorąc to pod uwagę ![]() i otrzymujemy
i otrzymujemy
![]() - liczba bitów jest prawie półtora razy większa niż liczba nat!
- liczba bitów jest prawie półtora razy większa niż liczba nat!
Rozumując w podobny sposób, możemy otrzymać zależność pomiędzy entropiami wyrażonymi w trytach i bitach:
W technologia komputerowa użyj informacji w formacie binarnym (w bitach). Do rozumowania w fizyce wygodniej jest używać informacji Shannona (w Nat), która może charakteryzować dowolną informację dyskretną. Zawsze możesz znaleźć liczbę odpowiednich bitów.
ZWIĄZEK ENTROPII I INFORMACJI. Demon Maxwella
Paradoks ten został po raz pierwszy rozważony przez Maxwella w 1871 roku (patrz ryc. 1). Niech jakaś „nadprzyrodzona” siła otworzy i zamknie zawór w naczyniu podzielonym na dwie części i zawierającym gaz. Zawór rządzi się zasadą, że otwiera się, jeśli dotkną go szybkie cząsteczki poruszające się od prawej do lewej strony lub jeśli uderzą w niego powolne cząsteczki poruszające się w przeciwnym kierunku. W ten sposób demon wprowadza różnicę temperatur między dwiema objętościami, nie wykonując pracy, co narusza drugą zasadę termodynamiki.

Demon Maxwella. Demon ustanawia różnicę ciśnień, otwierając przepustnicę, gdy liczba cząsteczek gazu uderzających w niego z lewej strony przekracza liczbę trafień z prawej strony. Można tego dokonać w sposób całkowicie odwracalny, o ile w pamięci demona przechowywane są losowe wyniki jego obserwacji cząsteczek. Dlatego pamięć demona (lub jego głowa) nagrzewa się. Nieodwracalnym krokiem nie jest gromadzenie informacji, ale ich utrata, gdy demon później czyści pamięć. Powyżej: Wypełnianie pamięci demona fragmentami informacji jest procesem losowym. Po prawej stronie przerywanej linii znajduje się pusty obszar pamięci (wszystkie komórki są w stanie 0, po lewej stronie znajdują się losowe bity). Poniżej demon.
Podjęto wiele prób rozwiązania tego paradoksu lub wypędzenia demona. Zakładano np., że demon nie jest w stanie wydobyć informacji bez wykonania pracy lub bez zakłócenia (tj. podgrzania) gazu – okazało się jednak, że tak nie było! Inne próby sprowadzały się do tego, że druga zasada mogła zostać naruszona pod wpływem pewnych „rozsądnych” lub „myślących” sił (istot). W 1929 r Leo Szilard znacząco „zaawansował” rozwiązanie problemu, redukując je do minimalnego sformułowania i podkreślając istotne elementy. Najważniejszą rzeczą, którą Demon musi zrobić, jest ustalenie, czy pojedyncza cząsteczka znajduje się po prawej czy lewej stronie zaworu przesuwnego, co umożliwiłoby ekstrakcję ciepła. Urządzenie to nazwano silnikiem Szilarda. Jednak Szilard nie rozwiązał paradoksu, ponieważ w jego analizie nie uwzględniono, w jaki sposób pomiar, dzięki któremu demon wie, czy cząsteczka znajduje się po prawej, czy po lewej stronie, wpływa na wzrost entropii (patrz rysunek Szilard_demon.pdf). Silnik pracuje w cyklu sześciostopniowym. Silnik to cylinder z tłokami na końcach. W środku wszyta klapka. Pracę wsuwania przegrody można zredukować do zera (pokazał to Szilard). Istnieje również urządzenie pamięci (MU). Może znajdować się w jednym z trzech stanów. „Pusty”, „Cząsteczka po prawej stronie” i „Cząsteczka po lewej stronie”. Stan początkowy: UP = „Pusty”, tłoki są wciśnięte, przegroda jest wysunięta, cząsteczka ma średnią prędkość, która jest określona przez temperaturę termostatu (slajd 1).
1. Wstawia się przegrodę, pozostawiając cząsteczkę po prawej lub lewej stronie (slajd 2).
2. Urządzenie pamięci określa, gdzie znajduje się cząsteczka i przechodzi do stanu „prawego” lub „lewego”.
3. Kompresja. W zależności od stanu UE tłok przesuwa się od strony, w której nie ma cząsteczki. Ten etap nie wymaga żadnej pracy. Ponieważ próżnia jest skompresowana (slajd 3).
4. Przegroda jest usuwana. Cząsteczka zaczyna wywierać nacisk na tłok (slajd 4).
5. Skok roboczy. Cząsteczka uderza w tłok, powodując jego ruch w przeciwnym kierunku. Energia cząsteczki przekazywana jest na tłok. W miarę ruchu tłoka jego średnia prędkość powinna maleć. Tak się jednak nie dzieje, ponieważ ściany naczynia mają stałą temperaturę. Dlatego ciepło z termostatu jest przekazywane do cząsteczki, utrzymując jej stałą prędkość. W ten sposób podczas skoku roboczego energia cieplna pochodząca z termostatu zostaje zamieniona na Praca mechaniczna wykonywane przez tłok (slajd 6).
6. Oczyszczenie UE, przywrócenie go do stanu „Pusty” (slajd 7). Cykl jest zakończony (slajd 8 = slajd 1).
Zaskakujące jest, że paradoks ten został rozwiązany dopiero w latach 80. XX wieku. W tym czasie ustalono, że w zasadzie każdy proces można przeprowadzić w sposób odwracalny, tj. bez „płacenia” entropią. Wreszcie Bennett w 1982 r ustalił ostateczny związek między tym stwierdzeniem a paradoksem Maxwella. Zaproponował, że demon może faktycznie wiedzieć, gdzie znajduje się cząsteczka w silniku Szilarda, bez wykonywania pracy lub zwiększania entropii otoczenia (termostatu), a tym samym wykonać użyteczną pracę w jednym cyklu silnika. Jednakże informacja o położeniu cząsteczki musi pozostać w pamięci demona (rsi.1). Jako ukończone więcej cykli, w pamięci gromadzi się coraz więcej informacji. Aby zakończyć cykl termodynamiczny, demon musi usunąć informacje zapisane w pamięci. To właśnie tę operację wymazywania informacji należy zaliczyć do procesu zwiększania entropii otoczenia, zgodnie z wymogami drugiej zasady. Na tym kończy się zasadniczo fizyczna część demonicznego urządzenia Maxwella.
Idee te rozwinęły się w pracach D.D. Kadomcewa.
Rozważmy gaz doskonały składający się tylko z jednej cząstki (Kadomcew, „dynamika i informacja”). To nie jest absurd. Jeśli jedna cząstka zostanie zamknięta w naczyniu o objętości V, którego ścianki mają temperaturę T, to prędzej czy później dojdzie do równowagi z tymi ściankami. W każdym momencie znajduje się w bardzo konkretnym punkcie przestrzeni i z bardzo określoną prędkością. Wszystkie procesy będziemy przeprowadzać na tyle wolno, aby cząstka miała średnio czas na wypełnienie całej objętości i wielokrotną zmianę wielkości i kierunku prędkości podczas niesprężystych zderzeń ze ściankami naczynia. Zatem cząstka wywiera średni nacisk na ściany i ma temperaturę T a jego rozkład prędkości jest Maxwellowski z temperaturą T. Ten układ jednej cząstki można ściskać adiabatycznie, zmieniać jej temperaturę, dając jej możliwość osiągnięcia równowagi ze ściankami naczynia.
Średnie ciśnienie na ścianę o godz N = 1 , równa się P= T/V, a średnia gęstość n = 1/ V. Rozważmy przypadek procesu izotermicznego, gdy T =konst. Od pierwszego rozpoczęcia o godz T =konst. I P= T/V dostajemy
![]() , ponieważ
, ponieważ
Stąd dowiadujemy się, że zmiana entropii nie zależy od temperatury, więc
![]()
Tutaj wprowadzana jest stała całkowania: „wielkość cząstek”< Pracuj w procesie izotermicznym praca jest określona przez różnicę entropii. Załóżmy, że mamy idealne przegrody, które można wykorzystać do podzielenia statku na części bez marnowania energii. Podzielmy nasze naczynie na dwie równe części o objętości V/2
każdy. W tym przypadku cząstka będzie w jednej z połówek – ale nie wiemy w której. Załóżmy, że mamy urządzenie, które pozwala nam określić, w której części znajduje się cząstka, na przykład precyzyjną skalę. Następnie z symetrycznego rozkładu prawdopodobieństwa od 50% do 50% znajdującego się w dwóch połówkach otrzymujemy 100% prawdopodobieństwo dla jednej z połówek - następuje „załamanie” rozkładu prawdopodobieństwa. W związku z tym nowa entropia będzie mniejsza niż pierwotna entropia o tę kwotę Zmniejszając entropię, można wykonać pracę. Aby to zrobić, wystarczy przesunąć partycję w kierunku pustego woluminu, aż zniknie. Praca będzie równa Jeśli w świecie zewnętrznym nic się nie zmieni, to powtarzając te cykle, można zbudować maszynę perpetuum mobile drugiego rodzaju. To jest demon Maxwella w wersji Szilarda. Ale druga zasada termodynamiki zabrania wykonywania pracy wyłącznie poprzez ciepło. Oznacza to, że coś musi się dziać w świecie zewnętrznym. Co to jest? Wykrywanie cząstki w jednej z połówek zmienia informację o cząstce -
Z dwóch możliwych połówek wskazana jest tylko jedna, w której znajduje się cząstka. Wiedza ta odpowiada jednemu bitowi informacji. Proces pomiaru zmniejsza entropię cząstki (przejście do stanu nierównowagowego) i zwiększa informację o układzie (cząstce) dokładnie o tę samą wielkość. Jeśli wielokrotnie podzielisz na połowę wcześniej uzyskane połówki, ćwiartki, ósemki itp., wówczas entropia będzie stale spadać, a informacja będzie rosła! Innymi słowy Im więcej wiemy o układzie fizycznym, tym niższa jest jego entropia. Jeśli o układzie wiadomo już wszystko, oznacza to, że przenieśliśmy go do stanu wysoce nierównowagowego, gdy jego parametry są jak najbardziej odbiegające od wartości równowagi. Jeśli w naszym modelu cząstkę można umieścić w elementarnej komórce objętości V 0
, to jednocześnie S = 0
, a informacja osiąga maksymalną wartość Zatem entropia informacyjna jest miarą braku (lub stopnia niepewności) informacji o aktualnym stanie układu fizycznego. Entropia informacji Shannona: Ilość informacji
I(lub po prostu informację) o stanie układu klasycznego, uzyskaną w wyniku pomiarów przez urządzenie zewnętrzne podłączone do rozpatrywanego systemu jakimś kanałem komunikacyjnym, definiuje się jako różnicę entropii informacyjnej odpowiadającą początkowej niepewności układu państwo H 0
oraz entropia informacyjna o stanie końcowym układu po pomiarze H. Zatem, I
+
H
=
H
0
=
konst
.
W idealnym przypadku, gdy w kanale komunikacyjnym nie występują szumy i zakłócenia pochodzące ze źródeł zewnętrznych, ostateczny rozkład prawdopodobieństwa po pomiarze sprowadza się do jednej określonej wartości p.n= 1, tj. H =
0, a maksymalna wartość informacji uzyskanej podczas pomiaru zostanie określona:
Imaks =
H 0
. Zatem entropia informacyjna Shannona systemu ma znaczenie maksymalnej informacji zawartej w systemie; można to wyznaczyć w idealnych warunkach pomiaru stanu układu przy braku szumów i zakłóceń, gdy entropia stanu końcowego wynosi zero: Rozważmy klasyczny element logiczny, który może znajdować się w jednym z dwóch równie prawdopodobnych stanów logicznych „0” i „1”. Element taki wraz z otoczeniem – termostatem i sygnałem generowanym przez obiekt zewnętrzny izolowany termicznie, tworzy jeden, nierównowagowy układ zamknięty. Przejście elementu do jednego ze stanów, np. do stanu „0”, odpowiada spadkowi statystyki. waga jego stanu w porównaniu do stanu początkowego jest 2-krotna (dla układów trzypoziomowych - 3-krotna). Znajdźmy spadek entropia informacyjna Shannona, co odpowiada wzrostowi ilości informacji o elemencie o jeden, co nazywa się fragment: Dlatego entropia informacji określa liczbę bitów wymaganych do zakodowania informacji w danym systemie lub wiadomości. LITERATURA 1. D. Landau, I. Lifshits. Fizyka statystyczna. Część 1. Nauka, M 1976. 2. MA Leontovich. Wprowadzenie do termodynamiki. Fizyka statystyczna. Moskwa, Nauka, 1983. - 416 s. 3. B.B. Kadomcew. Dynamika i informacja. UFN, 164, nr 5, 449 (1994). Niech będą dwa identyczne naczynia połączone ze sobą w taki sposób, że gaz z jednego naczynia może przepływać do drugiego i niech w początkowej chwili wszystkie cząsteczki gazu znajdą się w jednym naczyniu. Po pewnym czasie nastąpi redystrybucja cząsteczek, prowadząca do powstania stanu równowagi charakteryzującego się równym prawdopodobieństwem znalezienia cząsteczek w obu naczyniach. Spontaniczne przejście do początkowego stanu nierównowagi, w którym wszystkie cząsteczki są skoncentrowane w jednym z naczyń, jest praktycznie niemożliwe. Proces przejścia ze stanu równowagi do stanu nierównowagowego okazuje się bardzo mało prawdopodobny, gdyż wielkość względnych wahań parametrów przy dużej liczbie cząstek w naczyniach jest bardzo mała. Wniosek ten odpowiada drugiej zasadzie termodynamiki, która stwierdza, że układ termodynamiczny samoistnie przechodzi ze stanu nierównowagi do stanu równowagi, natomiast proces odwrotny jest możliwy tylko pod wpływem zewnętrznych wpływów na układ. Entropia i prawdopodobieństwo Wielkość termodynamiczna charakteryzująca kierunek spontanicznych procesów termodynamicznych to entropia. Najbardziej prawdopodobny stan równowagi odpowiada maksymalnej entropii.
Niech będzie naczynie o objętości V 0
, wewnątrz którego znajduje się jedna cząsteczka. Prawdopodobieństwo, że cząstka zostanie wykryta w określonej objętości V< V
0
, przydzielone wewnątrz statku, jest równe . Jeżeli w naczyniu nie ma jednej, ale dwie cząstki, to prawdopodobieństwo ich jednoczesnego wykrycia w określonej objętości wyznacza się jako iloczyn prawdopodobieństw znalezienia każdej cząstki w tej objętości: Dla N
cząstek, prawdopodobieństwo ich jednoczesnego wykrycia w danej objętości V
będzie Jeśli w tym naczyniu wyróżnimy dwa tomy V 1
I V 2
następnie możemy zapisać współczynniki prawdopodobieństwa, że wszystkie cząsteczki znajdują się we wskazanych objętościach: Wyznaczmy przyrost entropii w procesie izotermicznym ekspansja gazu doskonałego z V 1
zanim V 2
: Korzystając ze stosunku prawdopodobieństw otrzymujemy: Otrzymane wyrażenie nie określa bezwzględnej wartości entropii w żadnym stanie, a jedynie pozwala znaleźć różnicę entropii w dwóch różnych stanach. Aby jednoznacznie określić entropię, użyj waga statystyczna G
,
którego wartość wyrażana jest jako dodatnia liczba całkowita i jest proporcjonalna do prawdopodobieństwa: G
~
P
. Waga statystyczna makrostanu
jest wielkością liczbowo równą liczbie mikrostanów równowagi, za pomocą których można zrealizować dany makrostan. Przejście do wagi statystycznej pozwala nam zapisać zależność na entropię w postaci Wzory Boltzmanna na entropię statystyczną
: Wykład 15 Zjawiska przeniesienia Przepływy termodynamiczne Przepływy termodynamiczne
związane z przeniesieniem materii, energii lub pędu z jednej części ośrodka do drugiej, powstają, gdy wartości pewnych parametrów fizycznych różnią się w objętości ośrodka. Dyfuzja
nazywany procesem samoistnego wyrównywania stężeń substancji w mieszaninach. Szybkość dyfuzji silnie zależy od stanu skupienia substancji. Dyfuzja zachodzi szybciej w gazach i bardzo wolno w ciałach stałych. Przewodność cieplna
zwane zjawiskiem prowadzącym do wyrównywania się temperatur w różnych punktach otoczenia. Wysoka przewodność cieplna metali wynika z faktu, że przenoszenie ciepła w nich odbywa się nie w wyniku chaotycznego ruchu atomów i cząsteczek, jak na przykład w gazach lub cieczach, ale przez wolne elektrony, które mają znacznie większe prędkości ruchu termicznego. Lepkość lub tarcie wewnętrzne
nazywają proces powstawania siły oporu, gdy ciało porusza się w cieczy lub gazie, oraz tłumienie fal dźwiękowych podczas ich przechodzenia przez różne ośrodki. Aby ilościowo opisać przepływ termodynamiczny, wprowadź wielkość![]() od prawdopodobieństwa min znajdź cząstkę w danej komórce jest równa V 0
/
V. Jeśli w kolejnych momentach cząstka zacznie wypełniać większą objętość, wówczas informacja zostanie utracona, a entropia wzrośnie. Podkreślamy, że za informację trzeba płacić (zgodnie z drugim prawem) zwiększeniem entropii S e układ zewnętrzny i rzeczywiście, gdyby dla jednego bitu informacji urządzenie (układ zewnętrzny) zwiększyło swoją entropię o wielkość mniejszą niż jeden bit, wówczas moglibyśmy odwrócić działanie silnika cieplnego. Mianowicie, zwiększając objętość zajmowaną przez cząstkę, zwiększylibyśmy jej entropię o tę wartość ln2
zdobywanie pracy Tln2
, a całkowita entropia układu cząstka plus urządzenie zmniejszyłaby się. Ale według drugiej zasady jest to niemożliwe. Formalnie,
od prawdopodobieństwa min znajdź cząstkę w danej komórce jest równa V 0
/
V. Jeśli w kolejnych momentach cząstka zacznie wypełniać większą objętość, wówczas informacja zostanie utracona, a entropia wzrośnie. Podkreślamy, że za informację trzeba płacić (zgodnie z drugim prawem) zwiększeniem entropii S e układ zewnętrzny i rzeczywiście, gdyby dla jednego bitu informacji urządzenie (układ zewnętrzny) zwiększyło swoją entropię o wielkość mniejszą niż jeden bit, wówczas moglibyśmy odwrócić działanie silnika cieplnego. Mianowicie, zwiększając objętość zajmowaną przez cząstkę, zwiększylibyśmy jej entropię o tę wartość ln2
zdobywanie pracy Tln2
, a całkowita entropia układu cząstka plus urządzenie zmniejszyłaby się. Ale według drugiej zasady jest to niemożliwe. Formalnie, ![]() dlatego spadkowi entropii układu (cząstki) towarzyszy wzrost entropii urządzenia.
dlatego spadkowi entropii układu (cząstki) towarzyszy wzrost entropii urządzenia.![]() , gdzie (dotyczy to systemów dwupoziomowych, np. bitów: „0” i „1”. Jeśli wymiar jest N, To H =
log nr.
Tak dla N
= 3, N =dziennik 3
i, = 3.)
, gdzie (dotyczy to systemów dwupoziomowych, np. bitów: „0” i „1”. Jeśli wymiar jest N, To H =
log nr.
Tak dla N
= 3, N =dziennik 3
i, = 3.) .
. .
. .
.
 .
.![]()
 , Gdzie
, Gdzie