Geometria jako odrębny przedmiot rozpoczyna się dla uczniów w siódmej klasie. Do tego czasu się dotykają problemy geometryczne dość lekka forma i w zasadzie to, co można zobaczyć na wizualnych przykładach: powierzchnia pokoju, działka, długość i wysokość ścian w pokojach, płaskie przedmioty itp. Na początku studiowania samej geometrii pojawiają się pierwsze trudności, takie jak na przykład koncepcja linii prostej, ponieważ tej prostej nie można dotknąć rękami. Jeśli chodzi o trójkąty, jest to najprostszy typ wielokąta, zawierający tylko trzy kąty i trzy boki.

W kontakcie z

Koledzy z klasy

Motyw trójkątów jest jednym z głównych ważny i duże tematy program nauczania w klasach geometrii 7-9. Po dobrym opanowaniu można bardzo zdecydować złożone zadania. W takim przypadku możesz początkowo rozważyć zupełnie inną figurę geometryczną, a następnie dla wygody podzielić ją na odpowiednie części trójkątne.

Praca nad dowodem równości ∆ ABC I ∆A1B1C1 Musisz dokładnie zrozumieć znaki równości liczb i umieć z nich korzystać. Zanim przestudiujesz znaki, musisz się uczyć określić równość boki i kąty najprostszych wielokątów.

Aby udowodnić, że kąty trójkątów są równe, pomocne będą następujące opcje:

  1. ∠ α = ∠ β w oparciu o konstrukcję figur.
  2. Podane w warunkach zadania.
  3. Przy dwóch równoległych liniach i obecności siecznej można utworzyć zarówno wewnętrzne krzyżujące się, jak i odpowiadające sobie ∠ α = ∠ β.
  4. Dodawanie (odejmowanie) do (od) ∠ α = ∠ β równe kąty.
  5. Pionowe ∠ α i ∠ β są zawsze podobne
  6. Generał ∠ α, jednocześnie należący do ∆MNK I ∆MNH .
  7. Dwusieczna dzieli ∠ α na dwie równe części.
  8. Sąsiadujące z ∠ 90°- kąt równy pierwotnemu.
  9. Sąsiednie równe kąty są równe.
  10. Wysokość tworzy dwa sąsiadujące ze sobą ∠ 90° .
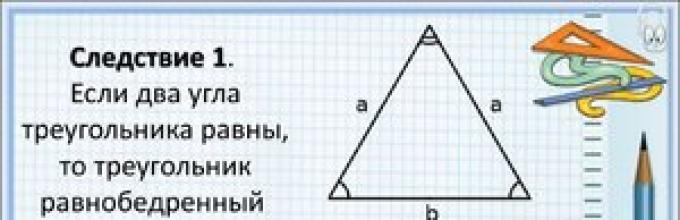
  11. W równoramiennych ∆MNK u podstawy ∠ α = ∠ β.
  12. Równy ∆MNK I ∆SDH odpowiedni ∠ α = ∠ β.
  13. Wcześniej udowodniona równość ∆MNK I ∆SDH .

To interesujące: Jak znaleźć obwód trójkąta.

3 znaki, że trójkąty są równe

Dowód równości ∆ ABC I ∆A1B1C1 bardzo wygodny w produkcji, oparty na podstawowych oznaki tożsamość tych najprostszych wielokątów. Są trzy takie znaki. Są bardzo ważne w rozwiązywaniu wielu problemów geometrycznych. Każdy z nich jest wart rozważenia.

Wymienione powyżej cechy są twierdzeniami i są udowadniane metodą nałożenia jednej figury na drugą, łącząc wierzchołki odpowiednie kąty i początek promieni. Dowody na równość trójkątów w klasie 7 opisano w bardzo przystępnej formie, ale dzieciom w wieku szkolnym trudno jest uczyć się w praktyce, ponieważ zawierają duża liczba elementy oznaczone dużymi literami łacińskimi. Wielu studentom rozpoczynającym naukę tego przedmiotu nie jest to do końca znane. Nastolatki mylą nazwy boków, półprostych i kątów.

Nieco później pojawia się kolejny ważny temat„Podobieństwo trójkątów”. Już sama definicja „podobieństwa” w geometrii oznacza podobieństwo kształtu o różnych rozmiarach. Na przykład możesz wziąć dwa kwadraty, pierwszy o boku 4 cm, a drugi 10 cm.Tego rodzaju czworokąty będą podobne, a jednocześnie będą miały różnicę, ponieważ drugi będzie większy, z każdą stronę zwiększono o tę samą liczbę razy.

Rozważając temat podobieństwa, podaje się również 3 znaki:

  • Pierwsza dotyczy dwóch odpowiednio równych kątów dwóch omawianych figur trójkątnych.
  • Drugi dotyczy kąta i tworzących go boków ∆MNK, które są równe odpowiednim elementom ∆SDH .
  • Trzeci wskazuje proporcjonalność wszystkich odpowiednich boków dwóch pożądanych figur.

Jak udowodnić, że trójkąty są podobne? Wystarczy użyć jednego z powyższych znaków i poprawnie opisać cały proces udowadniania zadania. Motyw podobieństwa ∆MNK I ∆SDH jest łatwiejszy do zrozumienia dla dzieci w wieku szkolnym, ponieważ w czasie jego nauki uczniowie już swobodnie posługują się oznaczeniami elementów w konstrukcjach geometrycznych, nie mylą się w ogromnej liczbie nazw i potrafią czytać rysunki.

Kończąc fragment obszernego tematu trójkąta figury geometryczne, uczniowie powinni już doskonale wiedzieć, jak udowodnić równość ∆MNK = ∆SDH po dwóch stronach, ustaw dwa trójkąty tak, aby były równe lub nie. Biorąc pod uwagę, że wielokąt o dokładnie trzech kątach jest jedną z najważniejszych figur geometrycznych, należy poważnie potraktować materiał, zwracając szczególną uwagę na nawet najmniejsze fakty teorii.

Mówi się, że dwa trójkąty są przystające, jeśli można je połączyć, nakładając się na siebie. Rysunek 1 pokazuje równe trójkąty ABC i A 1 B 1 do 1 . Każdy z tych trójkątów można nałożyć na drugi tak, aby były całkowicie zgodne, czyli ich wierzchołki i boki były zgodne parami. Oczywiste jest, że kąty tych trójkątów będą również pasować parami.

Zatem, jeśli dwa trójkąty są przystające, wówczas elementy (tj. Boki i kąty) jednego trójkąta są odpowiednio równe elementom drugiego trójkąta. Zauważ to w równych trójkątach o odpowiednio równych bokach(tj. nakładanie się po nałożeniu) leżą równe kąty i z powrotem: Równe boki leżą naprzeciw odpowiednio równych kątów.

Na przykład w równych trójkątach ABC i A 1 B 1 C 1, pokazanych na rysunku 1, naprzeciwko równych boków AB i A 1 B 1, odpowiednio, leżą równe kąty C i C 1. Równość trójkątów ABC i A 1 B 1 C 1 będziemy oznaczać następująco: Δ ABC = Δ A 1 B 1 C 1. Okazuje się, że równość dwóch trójkątów można ustalić porównując niektóre ich elementy.

Twierdzenie 1. Pierwszy znak równości trójkątów. Jeżeli dwa boki i kąt między nimi jednego trójkąta są odpowiednio równe dwóm bokom i kątowi między nimi innego trójkąta, to takie trójkąty są przystające (ryc. 2).

Dowód. Rozważmy trójkąty ABC i A 1 B 1 C 1, w których AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 (patrz ryc. 2). Udowodnijmy, że Δ ABC = Δ A 1 B 1 do 1 .

Ponieważ ∠ A = ∠ A 1, to trójkąt ABC można nałożyć na trójkąt A 1 B 1 C 1 w taki sposób, że wierzchołek A pokrywa się z wierzchołkiem A 1, a boki AB i AC nakładają się odpowiednio na promienie A 1 B 1 i A 1 C 1 . Ponieważ AB = A 1 B 1, AC = A 1 C 1, wówczas bok AB zrówna się z bokiem A 1 B 1, a bok AC zrówna się z bokiem A 1 C 1; w szczególności punkty B i B 1, C i C 1 będą się pokrywać. W rezultacie boki BC i B 1 C 1 zrównają się. Zatem trójkąty ABC i A 1 B 1 C 1 są całkowicie zgodne, czyli równe.

Twierdzenie 2 dowodzi się w podobny sposób, stosując metodę superpozycji.

Twierdzenie 2. Drugi znak równości trójkątów. Jeżeli bok i dwa sąsiednie kąty jednego trójkąta są odpowiednio równe bokowi i dwóm sąsiednim kątom innego trójkąta, to takie trójkąty są przystające (ryc. 34).

Komentarz. Na podstawie Twierdzenia 2 ustalono Twierdzenie 3.

Twierdzenie 3. Suma dowolnych dwóch kątów wewnętrznych trójkąta jest mniejsza niż 180°.

Twierdzenie 4 wynika z ostatniego twierdzenia.

Twierdzenie 4. Kąt zewnętrzny trójkąta jest większy od dowolnego kąta wewnętrznego, który do niego nie przylega.

Twierdzenie 5. Trzeci znak równości trójkątów. Jeżeli trzy boki jednego trójkąta są odpowiednio równe trzem bokom innego trójkąta, to takie trójkąty są przystające ().

Przykład 1. W trójkątach ABC i DEF (ryc. 4)

∠ A = ∠ E, AB = 20 cm, AC = 18 cm, DE = 18 cm, EF = 20 cm Porównaj trójkąty ABC i DEF. Jaki kąt w trójkącie DEF jest równy kątowi B?

Rozwiązanie. Trójkąty te są równe zgodnie z pierwszym znakiem. Kąt F trójkąta DEF jest równy kątowi B trójkąta ABC, ponieważ kąty te leżą naprzeciw odpowiednio równych boków DE i AC.

Przykład 2. Odcinki AB i CD (rys. 5) przecinają się w punkcie O, będącym środkiem każdego z nich. Jaka jest długość odcinka BD, jeśli odcinek AC ma 6 m?

Rozwiązanie. Trójkąty AOC i BOD są równe (według pierwszego kryterium): ∠ AOC = ∠ BOD (pionowo), AO = OB, CO = OD (według warunku).
Z równości tych trójkątów wynika, że ​​ich boki są równe, czyli AC = BD. Ale ponieważ zgodnie z warunkiem AC = 6 m, wówczas BD = 6 m.

Od czasów starożytnych do dziś poszukiwanie znaków równości figur uważane jest za podstawowe zadanie, na którym opierają się podstawy geometrii; setki twierdzeń udowadnia się za pomocą testów równości. Umiejętność udowodnienia równości i podobieństwa figur jest ważnym zadaniem we wszystkich dziedzinach budownictwa.

W kontakcie z

Wdrażanie umiejętności w praktyce

Załóżmy, że mamy figurę narysowaną na kartce papieru. Jednocześnie mamy linijkę i kątomierz, za pomocą których możemy zmierzyć długości odcinków i kąty między nimi. Jak przenieść figurę tego samego rozmiaru na drugą kartkę papieru lub podwoić jej skalę.

Wiemy, że trójkąt to figura złożona z trzech odcinków zwanych bokami, które tworzą kąty. Zatem istnieje sześć parametrów – trzy boki i trzy kąty – które definiują tę figurę.

Jednak po zmierzeniu wielkości wszystkich trzech boków i kątów przeniesienie tej figury na inną powierzchnię będzie trudnym zadaniem. Poza tym warto zadać pytanie: czy nie wystarczyłaby znajomość parametrów dwóch boków i jednego kąta, czy tylko trzech boków?

Po zmierzeniu długości dwóch boków i odległości między nimi, następnie przeniesiemy ten kąt na nową kartkę papieru, abyśmy mogli całkowicie odtworzyć trójkąt. Zastanówmy się, jak to zrobić, nauczmy się udowadniać znaki, według których można je uznać za takie same, i zdecydujmy, jaką minimalną liczbę parametrów wystarczy znać, aby mieć pewność, że trójkąty są takie same.

Ważny! Figury nazywamy identycznymi, jeżeli odcinki tworzące ich boki i kąty są sobie równe. Figury podobne to te, których boki i kąty są proporcjonalne. Zatem równość to podobieństwo ze współczynnikiem proporcjonalności wynoszącym 1.

Jakie są znaki równości trójkątów? Podajmy ich definicję:

  • pierwszy znak równości: dwa trójkąty można uznać za identyczne, jeśli dwa ich boki są równe, a także kąt między nimi.
  • drugi znak równości trójkątów: dwa trójkąty będą takie same, jeśli dwa kąty będą takie same, a także odpowiedni bok między nimi.
  • trzeci znak równości trójkątów : Trójkąty można uznać za identyczne, jeśli wszystkie ich boki są równej długości.

Jak udowodnić, że trójkąty są przystające. Przedstawmy dowód równości trójkątów.

Dowód 1 znaku

Przez długi czas wśród pierwszych matematyków znak ten był uważany za aksjomat, jednak jak się okazało, można go udowodnić geometrycznie w oparciu o bardziej podstawowe aksjomaty.

Rozważ dwa trójkąty - KMN i K 1 M 1 N 1 . Strona KM ma taką samą długość jak K 1 M 1 i KN = K 1 N 1. A kąt MKN jest równy kątom KMN i M 1 K 1 N 1.

Jeśli uznamy KM i K 1 M 1, KN i K 1 N 1 za dwa promienie wychodzące z tego samego punktu, to możemy powiedzieć, że kąty pomiędzy tymi parami promieni są takie same (określa to warunek twierdzenie). Przeprowadźmy równoległe przeniesienie promieni K 1 M 1 i K 1 N 1 z punktu K 1 do punktu K. W wyniku tego przeniesienia promienie K 1 M 1 i K 1 N 1 będą całkowicie się pokrywać. Narysujmy na promieniu K 1 M 1 odcinek o długości KM, pochodzący z punktu K. Ponieważ pod warunkiem wynikowy odcinek będzie równy odcinkiowi K 1 M 1, wówczas punkty M i M 1 pokrywają się. Podobnie z odcinkami KN i K 1 N 1. Zatem przenosząc K 1 M 1 N 1 tak, że punkty K 1 i K pokrywają się, a obie strony nakładają się, uzyskujemy całkowitą zbieżność samych figur.

Ważny! W Internecie można znaleźć dowody równości trójkątów na podstawie dwóch boków i kąta za pomocą algebraicznych i tożsamości trygonometryczne z numerycznymi wartościami boków i kątów. Jednak historycznie i matematycznie to twierdzenie został sformułowany na długo przed algebrą i przed trygonometrią. Aby udowodnić tę cechę twierdzenia, niewłaściwe jest używanie czegokolwiek innego niż podstawowe aksjomaty.

Dowód 2 znaki

Udowodnimy drugi znak równości w dwóch kątach i boku, opierając się na pierwszym.

Dowód 2 znaki

Rozważmy KMN i PRS. K jest równe P, N jest równe S. Bok KN ma tę samą długość co PS. Należy wykazać, że KMN i PRS to to samo.

Odzwierciedlmy punkt M względem promienia KN. Wynikowy punkt nazwijmy L. W tym przypadku długość boku KM = KL. NKL równa się PRS. KNL równa się RSP.

Ponieważ suma kątów wynosi 180 stopni, to KLN jest równe PRS, co oznacza, że ​​PRS i KLN są takie same (podobne) po obu stronach i kącie, zgodnie z pierwszym znakiem.

Ponieważ jednak KNL jest równy KMN, wówczas KMN i PRS to dwie identyczne liczby.

Dowód 3 znaki

Jak ustalić, że trójkąty są przystające. Wynika to bezpośrednio z dowodu drugiej cechy.

Długość KN = PS. Ponieważ K = P, N = S, KL=KM i KN = KS, MN=ML, to:

Oznacza to, że obie liczby są do siebie podobne. Ale ponieważ ich boki są takie same, są również równe.

Ze znaków równości i podobieństwa wynika wiele konsekwencji. Jednym z nich jest to, że aby ustalić, czy dwa trójkąty są równe, czy nie, należy poznać ich właściwości, czy są takie same:

  • wszystkie trzy strony;
  • obie strony i kąt między nimi;
  • oba kąty i bok między nimi.

Wykorzystanie testu równości trójkątów do rozwiązywania problemów

Konsekwencje pierwszego znaku

W toku dowodu można dojść do szeregu interesujących i użytecznych konsekwencji.

  1. . Fakt, że punkt przecięcia przekątnych równoległoboku dzieli je na dwie identyczne części, jest konsekwencją znaków równości i jest całkiem łatwy do udowodnienia.Boki dodatkowego trójkąta (o konstrukcji lustrzanej, jak w dowodach które wykonaliśmy) są bokami głównego (bokami równoległoboku).
  2. Jeśli istnieją dwa trójkąty prostokątne, które mają to samo ostre rogi, to są podobne. Jeśli noga pierwszego jest równa nodze drugiego, to są one równe. Jest to dość łatwe do zrozumienia - wszystkie trójkąty prostokątne mają kąt prosty. Dlatego znaki równości są dla nich prostsze.
  3. Dwa trójkąty o kątach prostych, w których dwie nogi mają tę samą długość, można uznać za identyczne. Wynika to z faktu, że kąt między obiema nogami wynosi zawsze 90 stopni. Zatem według pierwszego kryterium (przez dwa boki i kąt między nimi) wszystkie trójkąty o kątach prostych i identycznych nogach są równe.
  4. Jeśli istnieją dwa trójkąty prostokątne, a ich jedna noga i przeciwprostokątna są równe, to trójkąty są takie same.

Udowodnijmy to proste twierdzenie.

Istnieją dwa trójkąty prostokątne. Jeden ma boki a, b, c, gdzie c jest przeciwprostokątną; a, b - nogi. Drugi ma boki n, m, l, gdzie l jest przeciwprostokątną; m, n - nogi.

Zgodnie z twierdzeniem Pitagorasa jedna z nóg jest równa:

;

.

Zatem jeśli odpowiednio n = a, l = c (równość nóg i przeciwprostokątnych), drugie nogi będą równe. Odpowiednio liczby będą równe zgodnie z trzecią cechą (z trzech stron).

Zwróćmy uwagę na jeszcze jedną ważną konsekwencję. Jeśli istnieją dwa równe trójkąty i są one podobne ze współczynnikiem podobieństwa k, to znaczy stosunki parami wszystkich ich boków są równe k, to stosunek ich pól jest równy k2.

Pierwszy znak równości trójkątów. Lekcja wideo z geometrii 7. klasa

Geometria 7 Pierwszy znak równości trójkątów

Wniosek

Temat, który omówiliśmy, pomoże każdemu uczniowi lepiej zrozumieć podstawy koncepcje geometryczne i doskonal swoje umiejętności w najciekawszy świat matematyka.

Z kurs szkolny W geometrii dobrze znany jest znak, że trójkąty są równe wzdłuż dwóch boków i kąt między nimi, a mianowicie:

Jeżeli dwa boki i kąt między nimi jednego trójkąta są odpowiednio równe dwóm bokom i kątowi między nimi innego trójkąta, to takie trójkąty są przystające (ryc. 1).

Naturalnym jest, że pojawia się pytanie, czy trójkąty będą przystające, jeśli odpowiadające im równe kąty w trójkątach nie będą zawarte pomiędzy równymi bokami. Czy prawdą jest, że jeśli dwa boki i kąt jednego trójkąta są odpowiednio równe dwóm bokom i kątowi drugiego trójkąta, to takie trójkąty są przystające?

Okazuje się, że to nieprawda. Podajmy przykład. Rozważmy okrąg i jego cięciwę AB (ryc. 2). Mając środek w punkcie A, rysujemy kolejny okrąg przecinający pierwszy okrąg w niektórych punktach C i C 1. Wtedy w trójkątach ABC i ABC 1 AB jest wspólnym bokiem, AC = AC 1,C = Ponieważ 1, jednak trójkąty ABC i ABC 1 nie są przystające.

Formułując znaki równości trójkątów, można uwzględnić nie tylko boki i kąty, ale także inne elementy trójkątów. Rozważmy kilka sformułowań kryteriów równości trójkątów przez trzy elementy, w tym boki, kąty, wysokości, dwusieczne i środkowe trójkątów. Przekonajmy się o ważności odpowiednich znaków.

Jeżeli kąt, bok przeciwny do tego kąta i wysokość opuszczona na drugi bok jednego trójkąta są odpowiednio równe kątowi, bokowi i wysokości innego trójkąta, to takie trójkąty są przystające.

Wpuść trójkąty ABC I A 1 B 1 C 1 Z = Z 1 , AB = A 1 B 1, wysokość A.H. równa wysokości A 1 H 1 (ryc. 3). Udowodnijmy, że trójkąty ABC I A 1 B 1 C 1 są równe.

Trójkąty prostokątne ABH I A 1 B 1 H 1 mają jednakową nogę i przeciwprostokątną. Oznacza, B = B 1. Biorąc pod uwagę, że Z = Z 1, mamy równość A = A 1. Zatem w trójkątach ABC I A 1 B 1 C 1

AB= A 1 B 1 , A = A 1 , B = B 1 .

Dlatego te trójkąty są równe w boku i dwóch sąsiednich kątach.

Niech kąt, bok przylegający do tego kąta i wysokość obniżona do drugiego boku przylegającego do danego kąta jednego trójkąta będą odpowiednio równe kątowi, bokowi i wysokości drugiego trójkąta (ryc. 4).

Podajmy przykład pokazujący, że równość wskazanych elementów trójkątów nie jest wystarczająca do równości samych trójkątów.

Rozważmy trójkąty prostokątne ABH I A 1 B 1 H 1 (H = H 1 = 90 o), w którym

AB = A 1 B 1 , B = B 1 , A.H. = A 1 H 1

(ryc. 5). Na kontynuacjach boków B.H. I B 1 H 1 odłóż nierówne segmenty HC I H 1 C 1. Następnie w trójkątach ABC I A 1 B 1 C 1

AB = A 1 B 1 , B = B 1 ,

wysokości A.H. I A 1 H 1 są równe, ale same trójkąty nie są równe.

Jeżeli dwa boki i mediana zawarta między nimi jednego trójkąta są odpowiednio równe dwóm bokom i środkowej drugiego trójkąta, to takie trójkąty są przystające.

Wpuść trójkąty ABC I A 1 B 1 C 1

AC= A 1 C 1 , PNE. = B 1 C 1 ,

mediana SM równy medianie C 1 M 1 (ryc. 6). Udowodnijmy, że trójkąty ABC I A 1 B 1 C 1 są równe.

Kontynuujmy środkowe i odłóżmy na bok segmenty lekarz medycyny = CM. I M 1 D 1 = C 1 M 1 (ryc. 6).

Czworoboki ACBD I A 1 Z 1 B 1 D 1 - równoległoboki. Trójkąty ACD I A 1 C 1 D

ACD = A 1 C 1 D 1 .

Podobnie trójkąty BCD I B 1 C 1 D 1 są równe z trzech stron. Stąd,

BCD = B 1 C 1 D 1 .

Oznacza, Z = Z 1 i trójkąty ABC I A 1 B 1 C 1 są równe po obu stronach i kąt między nimi.


Niech kąt, bok przylegający do tego kąta i środkowa narysowana do tego boku jednego trójkąta będą odpowiednio równe kątowi, bokowi i środkowej drugiego trójkąta (ryc. 7).


Rozważmy okrąg ze środkiem w punkcie M(ryc. 8). Narysujmy dwie średnice AB I A 1 B 1. Przez kropki A, A 1 , M narysuj kolejny okrąg i wybierz na nim punkt C, jak pokazano na obrazku. W trójkątach ABC I A 1 B 1 C

AB = A 1 B 1 , A = A 1 ,

mediana C M ABC I A 1 B 1 C nie równe.

Jeżeli bok i dwie środkowe poprowadzone do dwóch innych boków jednego trójkąta są odpowiednio równe bokowi i dwóm środkowym innego trójkąta, to takie trójkąty są przystające.

Wpuść trójkąty ABC I A 1 B 1 C 1 AB = A 1 B 1, mediana JESTEM. równy medianie A 1 M 1, mediana B.K. równy medianie B 1 K 1 (ryc. 9). Udowodnijmy, że trójkąty ABC I A 1 B 1 C 1 są równe.

Zwrotnica O I O 1, przecięcia środkowych tych trójkątów dzielą środkowe w stosunku 2:1, licząc od wierzchołka. Zatem trójkąty ABW I A 1 B 1 O 1 są równe z trzech stron. Stąd,

BAO = B 1 A 1 O 1 ,

to znaczy trójkąty A.B.M. I A 1 B 1 M 1 są równe po obu stronach i kąt między nimi. Dlatego

ABC = A 1 B 1 C 1 .

Podobnie zostało to udowodnione

BAK = B 1 A 1 C 1 .

Zatem trójkąty ABC I A 1 B 1 C 1 są równe w boku i dwóch sąsiednich kątach.


Niech kąt i dwie środkowe narysowane do jego boków jednego trójkąta będą odpowiednio równe kątowi i dwóm środkowym innego trójkąta (ryc. 10).


Podajmy przykład pokazujący, że równość wskazanych elementów nie wystarczy do równości samych trójkątów.

Aby to zrobić, rozważ dwa równe koła ze środkami w punktach O 1 i O 2 stykają się ze sobą w jednym punkcie M(ryc. 11).

Narysujmy akord w jednym z nich AB i bezpośredni JESTEM., przecinając w pewnym miejscu drugi okrąg C. Narysujmy odcinek PNE.. Otrzymujemy trójkąt ABC. Narysujmy w nim medianę CK i oznaczać O punkt dzielący go w stosunku 2:1, licząc od wierzchołka C. Narysujmy okrąg ze środkiem w punkcie O, promień OC, przecinając w tym punkcie drugi okrąg C 1. Zróbmy bezpośredni C 1 M i oznaczać A 1 jego punkt przecięcia z pierwszym okręgiem. Oznaczmy K 1 punkt przecięcia cięciwy A 1 B i proste C 1 O. W trójkątach ABC I A 1 PNE. 1 A = A 1, mediana CK I C 1 K 1 równy, mediana B.M.- ogólny. Jednak trójkąty ABC I A 1 PNE. 1 nie są równe.

Jeżeli dwa boki i dwusieczna między nimi jednego trójkąta są odpowiednio równe dwóm bokom i dwusiecznej drugiego trójkąta, to takie trójkąty są przystające.

Wpuść trójkąty ABC I A 1 B 1 C 1

AC= A 1 C 1 , PNE. = B 1 C 1 ,

dwusieczna płyta CD równy dwusiecznej Z 1 D 1. Udowodnijmy, że trójkąty ABC I A 1 B 1 C 1 są równe.

Kontynuujmy boki AC I A 1 C 1 i narysuj odcinki na ich kontynuacjach CE = PNE. I C 1 mi 1 = B 1 C 1 (ryc. 12). Następnie

Trójkąty p.n.e. I B 1 C 1 mi 1 są równe z trzech stron. Oznacza, mi = mi 1 i BYĆ = B 1 mi 1. Trójkąty ABE I A 1 B 1 mi 1 są równe po obu stronach i kąt między nimi. Oznacza, AB = A 1 B 1. Zatem trójkąty ABC I A 1 B 1 C 1 są równe z trzech stron.


Niech kąt, bok przylegający do tego kąta i dwusieczna narysowana na drugim boku sąsiadującym z danym kątem jednego trójkąta będą odpowiednio równe kątowi, bokowi i dwusiecznej innego trójkąta (ryc. 13).


Przykład trójkątów ABC I ABC 1, pokazany na rysunku 14, pokazuje, że równość wskazanych elementów nie wystarczy do równości samych trójkątów.

Rzeczywiście, w trójkątach ABC I ABC 1 B- ogólny, AB- bok wspólny, dwusieczne OGŁOSZENIE I OGŁOSZENIE 1 są równe. Jednak trójkąty ABC I ABC 1 nie są równe.

Niech bok, środkowa i wysokość narysowane do pozostałych dwóch boków jednego trójkąta będą odpowiednio równe bokowi, środkowej i wysokości drugiego trójkąta (ryc. 15).


Podajmy przykład pokazujący, że równość wskazanych elementów nie wystarczy do równości samych trójkątów.

Aby to zrobić, rozważ okrąg i kąt z wierzchołkiem w środku A ten okrąg (ryc. 16). Połóżmy segment na boku AB, o większej średnicy i przez jego środek K narysuj linię prostą równoległą do drugiej strony kąta i przecinającą okrąg w niektórych punktach M I M 1. Narysujmy linie proste B.M., B.M. 1 i odpowiednio oznaczamy punkty ich przecięcia z bokiem kąta C I C 1. Następnie w trójkątach ABC I ABC 1 strona AB- całkowita wysokość B.H.- suma, mediana JESTEM. I JESTEM. 1 są równe, ale trójkąty ABC I ABC 1 nie są równe.

Dwa trójkąty są przystające, jeśli bok, środkowa i wysokość poprowadzone na drugi bok jednego trójkąta są odpowiednio równe bokowi, środkowej i wysokości drugiego trójkąta.

Wpuść trójkąty ABC I A 1 B 1 C 1 AC = A 1 C 1, mediana CM. I C 1 M 1 równy, wysokości CH I C 1 H 1 są równe (ryc. 17). Udowodnijmy, że trójkąty ABC I A 1 B 1 C 1 są równe.

Rzeczywiście, trójkąty prostokątne ACH I A 1 C 1 H 1 mają taką samą przeciwprostokątną i nogę. Dlatego F A=F A 1 i A.H. = A 1 H 1. Trójkąty prostokątne CMH I C 1 M 1 H 1 mają taką samą przeciwprostokątną i nogę. Stąd, M.H. = M 1 H 1, skąd JESTEM. = A 1 M 1 oznacza AB = A 1 B 1. Zatem trójkąty ABC I A 1 B 1 C 1 są równe po obu stronach i kąt między nimi.


Dwa trójkąty są równe, jeśli trzy środkowe jednego trójkąta są odpowiednio równe trzem środkowym drugiego trójkąta.

Wpuść trójkąty ABC I A 1 B 1 C 1 są odpowiednio równe medianie AK I A 1 K 1 , B.L. I B 1 L 1 , CM. I C 1 M 1 (ryc. 18). Udowodnijmy, że trójkąty ABC I A 1 B 1 C 1 są równe.

Pozwalać O I O 1 - punkty przecięcia środkowych tych trójkątów. Należy pamiętać, że mediany OM I O 1 M 1 trójkąty ABW I A 1 B 1 O 1 są równe, ponieważ stanowią jedną trzecią odpowiednich środkowych tych trójkątów.

Zgodnie z kryterium równości trójkątów, które udowodniliśmy pod numerem 3, trójkąty ABW I A 1 B 1 O 1 są równe, co oznacza AB = A 1 B 1 .

Podobnie zostało to udowodnione PNE. = B 1 C 1 i AC = A 1 C 1. Zatem trójkąty ABC I A 1 B 1 C 1 są równe z trzech stron.


Dwa trójkąty są równe, jeśli trzy wysokości jednego trójkąta są odpowiednio równe trzem wysokościom drugiego trójkąta.

Wpuść trójkąty ABC I A 1 B 1 C 1 są odpowiednio równe wysokościom A.H. I A 1 H 1 , B.G. I B 1 G 1 , CF I C 1 F 1 (ryc. 19). Udowodnijmy, że trójkąty ABC I A 1 B 1 C 1 są równe.

Oznaczmy odpowiednio boki trójkątów A, B, C I A 1 , B 1 , C 1 i odpowiadające im wysokości h, b b, godz I H 1A , H 1B , H 1C. Są równości Aha = bh b = rozdz I A 1 H 1A = B 1 H 1B = C 1 H 1C. Dzieląc pierwszą równość wyraz po wyrazie na drugą, otrzymujemy równości, z których wynikają te trójkąty ABC I A 1 B 1 C 1 są podobne. Ponieważ odpowiednie wysokości tych trójkątów są równe, są one nie tylko podobne, ale także równe.