Ranga macierzy jest ważną cechą liczbową. Najbardziej typowym problemem wymagającym znalezienia rzędu macierzy jest sprawdzenie zgodności układu liniowego równania algebraiczne. W tym artykule podamy pojęcie rangi macierzy i rozważymy metody jej wyznaczania. Aby lepiej zrozumieć materiał, szczegółowo przeanalizujemy rozwiązania kilku przykładów.
Nawigacja strony.
Wyznaczanie rangi macierzy i niezbędnych pojęć dodatkowych.
Przed wyrażeniem definicji rangi macierzy powinieneś dobrze rozumieć pojęcie małoletniego, a znalezienie nieletnich macierzy implikuje umiejętność obliczenia wyznacznika. Dlatego w razie potrzeby zalecamy przypomnienie teorii artykułu, metod znajdowania wyznacznika macierzy i właściwości wyznacznika.
Weźmy macierz A rzędu . Niech k będzie jakimś Liczba naturalna, nie przekraczającej najmniejszej z liczb m i n, tj. ![]() .
.
Definicja.
Drobne k-te zamówienie macierz A jest wyznacznikiem kwadratowej macierzy rzędu, złożonej z elementów macierzy A, które znajdują się w wybranych k wierszach i k kolumnach, przy czym układ elementów macierzy A jest zachowany.
Innymi słowy, jeśli w macierzy A usuniemy (p–k) wiersze i (n–k) kolumny, a z pozostałych elementów utworzymy macierz, zachowując układ elementów macierzy A, to wyznacznik otrzymana macierz jest małoletnią rzędu k macierzy A.
Przyjrzyjmy się definicji matrycy moll na przykładzie.
Rozważ macierz  .
.
Zapiszmy kilka nieletnich pierwszego rzędu tej macierzy. Na przykład, jeśli wybierzemy trzeci wiersz i drugą kolumnę macierzy A, to nasz wybór będzie odpowiadał mollowi pierwszego rzędu ![]() . Innymi słowy, aby otrzymać ten element drugorzędny, skreśliliśmy pierwszy i drugi wiersz oraz pierwszą, trzecią i czwartą kolumnę macierzy A i z pozostałego elementu utworzyliśmy wyznacznik. Jeśli wybierzemy pierwszy wiersz i trzecią kolumnę macierzy A, to otrzymamy element drugorzędny
. Innymi słowy, aby otrzymać ten element drugorzędny, skreśliliśmy pierwszy i drugi wiersz oraz pierwszą, trzecią i czwartą kolumnę macierzy A i z pozostałego elementu utworzyliśmy wyznacznik. Jeśli wybierzemy pierwszy wiersz i trzecią kolumnę macierzy A, to otrzymamy element drugorzędny ![]() .
.
Zilustrujmy procedurę pozyskiwania rozważanych nieletnich pierwszego rzędu  I
I  .
.
Zatem nieletni pierwszego rzędu macierzy są samymi elementami macierzy.
Pokażmy kilka nieletnich drugiego rzędu. Wybierz dwa wiersze i dwie kolumny. Weźmy na przykład pierwszy i drugi wiersz oraz trzecią i czwartą kolumnę. Przy tym wyborze mamy molla drugiego rzędu  . Ten element drugorzędny można również utworzyć, usuwając trzeci wiersz, pierwszą i drugą kolumnę z macierzy A.
. Ten element drugorzędny można również utworzyć, usuwając trzeci wiersz, pierwszą i drugą kolumnę z macierzy A.
Innym drugorzędnym drugorzędnym macierzy A jest .
Zilustrujmy konstrukcję tych nieletnich drugiego rzędu  I
I  .
.
Podobnie można znaleźć nieletnich trzeciego rzędu macierzy A. Ponieważ w macierzy A są tylko trzy wiersze, wybieramy je wszystkie. Jeśli wybierzemy pierwsze trzy kolumny tych wierszy, otrzymamy moll trzeciego rzędu 
Można ją także skonstruować przekreślając ostatnią kolumnę macierzy A.
Kolejnym mollem trzeciego rzędu jest 
uzyskany poprzez usunięcie trzeciej kolumny macierzy A.
Oto zdjęcie przedstawiające budowę tych nieletnich trzeciego rzędu  I
I  .
.
Dla danej macierzy A nie ma nieletnich rzędu wyższego niż trzeci, ponieważ .
Ile nieletnich k-tego rzędu znajduje się w macierzy A rzędu ?
Liczbę nieletnich rzędu k można obliczyć jako , gdzie  I
I  - liczba kombinacji odpowiednio od p do k i od n do k.
- liczba kombinacji odpowiednio od p do k i od n do k.
Jak skonstruować wszystkie niepełnoletnie rzędu k macierzy A rzędu p przez n?
Będziemy potrzebować wielu numerów wierszy macierzy i wielu numerów kolumn. Wszystko zapisujemy kombinacje elementów p przez k(będą one odpowiadać wybranym wierszom macierzy A przy konstruowaniu molla rzędu k). Do każdej kombinacji numerów wierszy dodajemy kolejno wszystkie kombinacje n elementów k numerów kolumn. Te zestawy kombinacji numerów wierszy i numerów kolumn macierzy A pomogą w skomponowaniu wszystkich nieletnich rzędu k.
Spójrzmy na to na przykładzie.
Przykład.
Znajdź wszystkie drugorzędne drugorzędne macierzy.
Rozwiązanie.
Ponieważ rząd oryginalnej macierzy wynosi 3 na 3, suma nieletnich drugiego rzędu będzie wynosić  .
.
Zapiszmy wszystkie kombinacje od 3 do 2 numerów wierszy macierzy A: 1, 2; 1, 3 i 2, 3. Wszystkie kombinacje numerów kolumn od 3 do 2 to 1, 2; 1, 3 i 2, 3.
Weźmy pierwszy i drugi wiersz macierzy A. Wybierając pierwszą i drugą kolumnę, pierwszą i trzecią kolumnę, drugą i trzecią kolumnę dla tych wierszy, otrzymujemy odpowiednio drugorzędne 
Dla pierwszego i trzeciego wiersza mamy podobny wybór kolumn 
Pozostaje dodać pierwszą i drugą, pierwszą i trzecią, drugą i trzecią kolumnę do drugiego i trzeciego wiersza: 
Zatem znaleziono wszystkie dziewięć drugorzędnych elementów macierzy A.
Teraz możemy przystąpić do wyznaczania rangi macierzy.
Definicja.
Ranga matrycy- Ten najwyższy porządek macierz drugorzędna, różna od zera.
Rangę macierzy A określa się jako Rank(A). Można również znaleźć oznaczenia Rg(A) lub Rang(A).
Z definicji rangi macierzy i macierzy drugorzędnej wynika, że ranga macierzy zerowej jest równa zeru, a ranga macierzy niezerowej jest nie mniejsza niż jeden.
Znalezienie rangi macierzy z definicji.
Zatem pierwszą metodą znalezienia rangi macierzy jest: sposób zliczania nieletnich. Metoda ta opiera się na określeniu rangi macierzy.
Musimy znaleźć rząd macierzy A rzędu .
Opiszmy krótko algorytm rozwiązanie tego problemu poprzez wyliczenie nieletnich.
Jeżeli chociaż jeden element macierzy jest różny od zera, to stopień macierzy jest co najmniej równy jeden (ponieważ istnieje element drugorzędny pierwszego rzędu, który nie jest równy zero).
Następnie przyjrzymy się nieletnim drugiego rzędu. Jeśli wszystkie nieletnie drugiego rzędu są równe zero, wówczas rząd macierzy jest równy jeden. Jeśli istnieje co najmniej jeden niezerowy drugorzędny drugiego rzędu, to przystępujemy do wyliczania nieletnich trzeciego rzędu, a rząd macierzy jest co najmniej równy dwa.
Podobnie, jeśli wszystkie nieletnie trzeciego rzędu wynoszą zero, wówczas stopień macierzy wynosi dwa. Jeśli istnieje co najmniej jeden małoletni trzeciego rzędu różny od zera, to stopień macierzy wynosi co najmniej trzy i przechodzimy do wyliczania nieletnich czwartego rzędu.
Należy pamiętać, że rząd macierzy nie może przekraczać najmniejszej z liczb p i n.
Przykład.
Znajdź rząd macierzy  .
.
Rozwiązanie.
Ponieważ macierz jest niezerowa, jej ranga jest nie mniejsza niż jeden.
Minor drugiego rzędu  jest różna od zera, zatem rząd macierzy A wynosi co najmniej dwa. Przechodzimy do wyliczania nieletnich trzeciego rzędu. Razem z nich
jest różna od zera, zatem rząd macierzy A wynosi co najmniej dwa. Przechodzimy do wyliczania nieletnich trzeciego rzędu. Razem z nich  rzeczy.
rzeczy. 


Wszystkie nieletnie trzeciego rzędu są równe zero. Dlatego ranga macierzy wynosi dwa.
Odpowiedź:
Ranga(A) = 2 .
Wyznaczanie rangi macierzy metodą graniczących nieletnich.
Istnieją inne metody znajdowania rangi macierzy, które pozwalają uzyskać wynik przy mniejszym nakładzie pracy obliczeniowej.
Jedną z takich metod jest metoda krawędziowa.
Zajmijmy się koncepcja krawędzi drobnej.
Mówi się, że drobne M ok rzędu (k+1) macierzy A graniczy z mniejszym M rzędu k macierzy A, jeżeli macierz odpowiadająca mollowi M ok „zawiera” macierz odpowiadającą mollowi M .
Innymi słowy, macierz odpowiadającą granicznemu drobnemu M otrzymuje się z macierzy odpowiadającej ograniczającemu mniejszemu M ok poprzez usunięcie elementów jednego wiersza i jednej kolumny.
Rozważmy na przykład macierz  i weź moll drugiego rzędu. Zapiszmy wszystkich graniczących nieletnich:
i weź moll drugiego rzędu. Zapiszmy wszystkich graniczących nieletnich: 
Metodę graniczących nieletnich uzasadnia następujące twierdzenie (przedstawiamy jego sformułowanie bez dowodu).
Twierdzenie.
Jeśli wszystkie niepełnoletnie graniczące z mollem k-tego rzędu macierzy A rzędu p na n są równe zeru, to wszystkie niepełnoletnie rzędu (k+1) macierzy A są równe zeru.
Zatem, aby znaleźć rząd macierzy, nie jest konieczne przeglądanie wszystkich nieletnich, które są wystarczająco graniczne. Liczbę nieletnich graniczących z mollem k-tego rzędu macierzy A rzędu , oblicza się ze wzoru ![]() . Należy zauważyć, że na granicy molowej k-tego rzędu macierzy A nie ma więcej małoletnich rzędu (k + 1) macierzy A. Dlatego w większości przypadków zastosowanie metody graniczącej nieletnich jest bardziej opłacalne niż zwykłe wyliczenie wszystkich nieletnich.
. Należy zauważyć, że na granicy molowej k-tego rzędu macierzy A nie ma więcej małoletnich rzędu (k + 1) macierzy A. Dlatego w większości przypadków zastosowanie metody graniczącej nieletnich jest bardziej opłacalne niż zwykłe wyliczenie wszystkich nieletnich.
Przejdźmy do wyznaczania rangi macierzy metodą graniczących nieletnich. Opiszmy krótko algorytm Ta metoda.
Jeżeli macierz A jest różna od zera, to jako element drugorzędny pierwszego rzędu przyjmujemy dowolny element macierzy A różny od zera. Przyjrzyjmy się graniczącym z nim nieletnim. Jeśli wszystkie są równe zeru, wówczas rząd macierzy jest równy jeden. Jeśli istnieje co najmniej jeden niezerowy graniczący drugorzędny (jej rząd wynosi dwa), wówczas przechodzimy do rozważania graniczących z nim drugorzędnych. Jeśli wszystkie wynoszą zero, wówczas Rank(A) = 2. Jeśli co najmniej jeden graniczący drugorzędny jest różny od zera (jego rząd wynosi trzy), wówczas rozważamy jego graniczące drugorzędne. I tak dalej. W rezultacie Rank(A) = k, jeśli wszystkie sąsiadujące elementy drugorzędne (k + 1)-tego rzędu macierzy A są równe zero, lub Rank(A) = min(p, n), jeśli istnieje nie- moll zerowy graniczący z mollem rzędu (min( p, n) – 1) .
Przyjrzyjmy się metodzie graniczącej nieletnich, aby znaleźć rząd macierzy na przykładzie.
Przykład.
Znajdź rząd macierzy  metodą graniczących nieletnich.
metodą graniczących nieletnich.
Rozwiązanie.
Ponieważ element a 1 1 macierzy A jest różny od zera, traktujemy go jako element drugorzędny pierwszego rzędu. Zacznijmy szukać granicznego molla, który jest różny od zera: 
Znaleziono małą krawędź drugiego rzędu, różną od zera. Spójrzmy na graniczące z nim nieletni (ich ![]() rzeczy):
rzeczy): 
Wszystkie nieletnie graniczące z mollem drugiego rzędu są równe zeru, dlatego rząd macierzy A jest równy dwa.
Odpowiedź:
Ranga(A) = 2 .
Przykład.
Znajdź rząd macierzy  z wykorzystaniem graniczących z małoletnimi.
z wykorzystaniem graniczących z małoletnimi.
Rozwiązanie.
Jako niezerową liczbę drugorzędną pierwszego rzędu bierzemy element a 1 1 = 1 macierzy A. Otaczający moll drugiego rzędu  nie równe zeru. Ten nieletni graniczy z nieletnim trzeciego rzędu
nie równe zeru. Ten nieletni graniczy z nieletnim trzeciego rzędu  . Ponieważ nie jest ona równa zeru i nie ma dla niej ani jednego granicznego molla, rząd macierzy A jest równy trzy.
. Ponieważ nie jest ona równa zeru i nie ma dla niej ani jednego granicznego molla, rząd macierzy A jest równy trzy.
Odpowiedź:
Ranga(A) = 3 .
Wyznaczanie rangi za pomocą elementarnych przekształceń macierzy (metoda Gaussa).
Rozważmy inny sposób znalezienia rangi macierzy.
Następujące przekształcenia macierzy nazywane są elementarnymi:
- przestawianie wierszy (lub kolumn) macierzy;
- pomnożenie wszystkich elementów dowolnego wiersza (kolumny) macierzy przez dowolną liczbę k, różną od zera;
- dodanie do elementów wiersza (kolumny) odpowiednich elementów innego wiersza (kolumny) macierzy, pomnożonych przez dowolną liczbę k.
Macierz B nazywa się równoważną macierzy A, jeśli B uzyskuje się z A za pomocą skończoną liczbą elementarne przemiany. Równoważność macierzy jest oznaczona symbolem „~”, to znaczy zapisana A ~ B.
Znalezienie rangi macierzy za pomocą elementarnych przekształceń macierzy opiera się na stwierdzeniu: jeśli macierz B otrzymamy z macierzy A za pomocą skończonej liczby elementarnych przekształceń, to Ranga(A) = Ranga(B) .
Ważność tego twierdzenia wynika z własności wyznacznika macierzy:
- Podczas zmiany układu wierszy (lub kolumn) macierzy jej wyznacznik zmienia znak. Jeśli jest równa zeru, to po przestawieniu wierszy (kolumn) pozostaje równa zeru.
- Mnożąc wszystkie elementy dowolnego wiersza (kolumny) macierzy przez dowolną liczbę k różną od zera, wyznacznik otrzymanej macierzy jest równy wyznacznikowi pierwotnej macierzy pomnożonej przez k. Jeżeli wyznacznik macierzy pierwotnej jest równy zeru, to po pomnożeniu wszystkich elementów dowolnego wiersza lub kolumny przez liczbę k wyznacznik otrzymanej macierzy również będzie równy zero.
- Dodanie do elementów pewnego wiersza (kolumny) macierzy odpowiednich elementów innego wiersza (kolumny) macierzy, pomnożone przez określoną liczbę k, nie powoduje zmiany jej wyznacznika.
Istota metody przekształceń elementarnych polega na sprowadzeniu macierzy, której rząd szukamy, do macierzy trapezowej (w konkretnym przypadku do górnej trójkątnej) za pomocą przekształceń elementarnych.
Dlaczego to się robi? Znalezienie rangi macierzy tego typu jest bardzo łatwe. Jest równa liczbie wierszy zawierających co najmniej jeden element niezerowy. A ponieważ rząd macierzy nie zmienia się przy przeprowadzaniu przekształceń elementarnych, to wynikowa wartość będzie rzędem macierzy pierwotnej.
Podajemy ilustracje macierzy, z których jedną należy otrzymać po przekształceniach. Ich wygląd zależy od kolejności macierzy.

Ilustracje te są szablonami do których przekształcimy macierz A.
Opiszmy algorytm metody.
Musimy znaleźć rząd niezerowej macierzy A rzędu (p może być równe n).
Więc, . Pomnóżmy wszystkie elementy pierwszego wiersza macierzy A przez . Otrzymujemy w tym przypadku macierz równoważną, oznaczającą ją A (1): 
Do elementów drugiego rzędu wynikowej macierzy A (1) dodajemy odpowiednie elementy pierwszego rzędu pomnożone przez . Do elementów trzeciej linii dodajemy odpowiednie elementy pierwszej linii pomnożone przez . I tak dalej, aż do linii p. Uzyskajmy równoważną macierz, oznaczmy ją A (2): 
Jeżeli wszystkie elementy wynikowej macierzy znajdujące się w wierszach od drugiego do p-tego są równe zeru, wówczas ranga tej macierzy jest równa jeden, a w konsekwencji ranga macierzy pierwotnej jest równa do jednego.
Jeśli w liniach od drugiego do p-tego znajduje się co najmniej jeden element niezerowy, to kontynuujemy transformacje. Ponadto postępujemy dokładnie w ten sam sposób, tyle że z zaznaczoną na rysunku częścią macierzy A (2). 
Jeżeli , to przestawiamy wiersze i (lub) kolumny macierzy A (2) tak, aby „nowy” element stał się niezerowy.
Liczbę r nazywamy rangą macierzy A, jeżeli:
1) w macierzy A występuje małoletni rząd r, różny od zera;
2) wszystkie niepełnoletnie rzędu (r+1) i wyższe, jeśli istnieją, są równe zeru.
W przeciwnym razie rzędem macierzy jest najwyższy rząd podrzędny inny niż zero.
Oznaczenia: rangA, r A lub r.
Z definicji wynika, że r jest dodatnią liczbą całkowitą. W przypadku macierzy zerowej ranga jest uważana za zero.
Cel usługi. Kalkulator online jest przeznaczony do wyszukiwania ranga matrycy. W tym przypadku rozwiązanie jest zapisywane w formacie Word i Excel. zobacz przykładowe rozwiązanie.
Instrukcje. Wybierz wymiar macierzy i kliknij Dalej.
Definicja . Niech będzie dana macierz rangi r. Dowolny element drugorzędny macierzy różny od zera i mający rząd r nazywany jest podstawowym, a wiersze i kolumny jej składników nazywane są wierszami i kolumnami podstawowymi.
Zgodnie z tą definicją macierz A może mieć kilka nieletnich bazowych.
Ranga macierzy jednostkowej E wynosi n (liczba wierszy).
Przykład 1. Biorąc pod uwagę dwie macierze,  i ich nieletni
i ich nieletni  ,
,  . Który z nich można uznać za podstawowy?
. Który z nich można uznać za podstawowy?
Rozwiązanie. Minor M 1 =0, więc nie może być podstawą żadnej z macierzy. Minor M 2 =-9≠0 i ma rząd 2, co oznacza, że można go przyjąć za podstawę macierzy A lub / i B, pod warunkiem, że mają one rangę równą 2. Ponieważ detB=0 (jako wyznacznik z dwiema proporcjonalnymi kolumnami), to rangB=2 i M 2 można przyjąć za moll bazowy macierzy B. Ranga macierzy A wynosi 3, gdyż detA=-27≠ 0 i dlatego rząd mniejszej podstawy tej macierzy musi być równy 3, czyli M 2 nie jest podstawą macierzy A. Należy zauważyć, że macierz A ma jedną bazę mniejszą, równą wyznacznikowi macierzy A.
Twierdzenie (o podstawie mniejszej).
Dowolny wiersz (kolumna) macierzy jest liniową kombinacją jej podstawowych wierszy (kolumn).
Wnioski z twierdzenia.
- Każda (r+1) macierz kolumnowa (wierszowa) rangi r jest liniowo zależna.
- Jeśli ranga macierzy jest mniejsza niż liczba jej wierszy (kolumn), to jej wiersze (kolumny) są zależne liniowo. Jeśli rangA jest równa liczbie jej wierszy (kolumn), to wiersze (kolumny) są liniowo niezależne.
- Wyznacznik macierzy A jest równy zero wtedy i tylko wtedy, gdy jej wiersze (kolumny) są liniowo zależne.
- Jeśli do wiersza (kolumny) macierzy dodamy kolejny wiersz (kolumnę), pomnożony przez dowolną liczbę różną od zera, to ranga macierzy nie ulegnie zmianie.
- Jeśli skreślisz wiersz (kolumnę) w macierzy będącej liniową kombinacją innych wierszy (kolumn), to ranga macierzy nie ulegnie zmianie.
- Ranga macierzy jest równa maksymalnej liczbie jej liniowo niezależnych wierszy (kolumn).
- Maksymalna liczba liniowo niezależnych wierszy jest taka sama, jak maksymalna liczba liniowo niezależnych kolumn.
Przykład 2. Znajdź rząd macierzy  .
.
Rozwiązanie.
Bazując na definicji rangi macierzy, będziemy szukać molla najwyższego rzędu, różnego od zera. Najpierw przekształcamy macierz na więcej prosty widok. Aby to zrobić, pomnóż pierwszy wiersz macierzy przez (-2) i dodaj do drugiego, następnie pomnóż przez (-1) i dodaj do trzeciego.
Definicja. Ranga matrycy to maksymalna liczba liniowo niezależnych wierszy uznawanych za wektory.
Twierdzenie 1 o rzędzie macierzy. Ranga matrycy nazywa się maksymalnym rządem niezerowej części mniejszej macierzy.
Pojęcie minora omawialiśmy już na lekcji o wyznacznikach, a teraz je uogólnimy. Weźmy pewną liczbę wierszy i pewną liczbę kolumn w macierzy i to „ile” powinno być mniejsze od liczby wierszy i kolumn macierzy, a dla wierszy i kolumn to „ile” powinno być ten sam numer. Wtedy na przecięciu ilu wierszy i ilu kolumn znajdzie się macierz niższego rzędu niż nasza pierwotna macierz. Wyznacznik jest macierzą i będzie minorem k-tego rzędu, jeśli wspomniane „niektóre” (liczba wierszy i kolumn) oznaczymy przez k.
Definicja. Drobny ( R+1)rząd, w którym leży wybrany nieletni R-ty rząd nazywa się graniczącym dla danego molla.
Dwie najczęściej stosowane metody to znalezienie rangi macierzy. Ten sposób na kontakt z nieletnimi I metoda przekształceń elementarnych(metoda Gaussa).
W przypadku stosowania metody graniczących nieletnich stosuje się następujące twierdzenie.
Twierdzenie 2 o rzędzie macierzy. Jeśli małoletni może składać się z elementów matrycy R rzędu, różny od zera, wówczas stopień macierzy jest równy R.
W przypadku stosowania metody transformacji elementarnej używana jest następująca właściwość:
Jeżeli poprzez przekształcenia elementarne otrzymamy macierz trapezową równoważną macierzy pierwotnej, to rząd tej macierzy to liczba zawartych w nim linii innych niż linie składające się wyłącznie z zer.
Wyznaczanie rangi macierzy metodą graniczących nieletnich
Młodszy zamykający to małoletni wyższego rzędu w stosunku do danego, jeżeli ten małoletni wyższego rzędu zawiera danego małoletniego.
Na przykład biorąc pod uwagę macierz
Weźmy nieletniego
Nieletnimi graniczącymi będą:
Algorytm wyznaczania rangi macierzy Następny.
1. Znajdź nieletnich drugiego rzędu, które nie są równe zero. Jeśli wszystkie niepełnoletnie drugiego rzędu są równe zeru, wówczas rząd macierzy będzie równy jeden ( R =1 ).
2. Jeśli istnieje co najmniej jeden drugorzędny drugiego rzędu, który nie jest równy zero, wówczas tworzymy graniczące nieletni trzeciego rzędu. Jeśli wszystkie sąsiadujące nieletni trzeciego rzędu są równe zeru, wówczas stopień macierzy jest równy dwa ( R =2 ).
3. Jeśli co najmniej jeden z graniczących nieletnich trzeciego rzędu nie jest równy zero, wówczas tworzymy graniczące nieletnich. Jeśli wszystkie graniczące nieletni czwartego rzędu są równe zeru, wówczas stopień macierzy jest równy trzy ( R =2 ).
4. Kontynuuj w ten sposób tak długo, jak pozwala na to rozmiar matrycy.
Przykład 1. Znajdź rząd macierzy
 .
.
Rozwiązanie. Minor drugiego rzędu ![]() .
.
Granicajmy to. Będzie czterech sąsiadujących nieletnich:
 ,
,
 ,
,
Zatem wszystkie graniczące nieletni trzeciego rzędu są równe zeru, dlatego ranga tej macierzy jest równa dwa ( R =2 ).
Przykład 2. Znajdź rząd macierzy
Rozwiązanie. Ranga tej macierzy jest równa 1, ponieważ wszystkie nieletnie drugiego rzędu tej macierzy są równe zeru (w tym przypadku, podobnie jak w przypadku nieletnich graniczących w dwóch kolejnych przykładach, drodzy uczniowie proszeni są o sprawdzenie sami, być może korzystając z zasad obliczania wyznaczników), a wśród nieletnich pierwszego rzędu, czyli wśród elementów macierzy, znajdują się jedynki niezerowe.
Przykład 3. Znajdź rząd macierzy
Rozwiązanie. Moll drugiego rzędu tej macierzy to, a wszystkie minory trzeciego rzędu tej macierzy są równe zero. Dlatego ranga tej macierzy wynosi dwa.
Przykład 4. Znajdź rząd macierzy
Rozwiązanie. Ranga tej macierzy wynosi 3, ponieważ jedynym nieletnim trzeciego rzędu tej macierzy jest 3.
Wyznaczanie rzędu macierzy metodą przekształceń elementarnych (metoda Gaussa)
Już w przykładzie 1 widać, że zadanie wyznaczenia rangi macierzy metodą graniczących nieletnich wymaga obliczenia duża liczba determinanty. Istnieje jednak sposób na ograniczenie ilości obliczeń do minimum. Metoda ta opiera się na zastosowaniu elementarnych przekształceń macierzy i nazywana jest także metodą Gaussa.
Jako elementarne przekształcenia macierzy rozumie się następujące operacje:
1) pomnożenie dowolnego wiersza lub kolumny macierzy przez liczbę inną niż zero;
2) dodanie do elementów dowolnego wiersza lub kolumny macierzy odpowiednich elementów innego wiersza lub kolumny, pomnożonych przez tę samą liczbę;
3) zamiana dwóch wierszy lub kolumn macierzy;
4) usunięcie wierszy „zerowych”, czyli takich, których wszystkie elementy są równe zeru;
5) usunięcie wszystkich linii proporcjonalnych z wyjątkiem jednej.
Twierdzenie. Podczas transformacji elementarnej rząd macierzy nie ulega zmianie. Innymi słowy, jeśli zastosujemy elementarne przekształcenia z macierzy A poszedł do matrixa B, To .
Niech zostanie podana pewna macierz:
 .
.
Wybierzmy w tej macierzy  dowolne ciągi znaków i
dowolne ciągi znaków i  dowolne kolumny
dowolne kolumny  . Następnie wyznacznik
. Następnie wyznacznik  rzędu, złożonego z elementów macierzy
rzędu, złożonego z elementów macierzy  , znajdujący się na przecięciu wybranych wierszy i kolumn, nazywany jest drugorzędnym
, znajdujący się na przecięciu wybranych wierszy i kolumn, nazywany jest drugorzędnym  macierz trzeciego rzędu
macierz trzeciego rzędu  .
.
Definicja 1.13. Ranga matrycy  zwany najwyższy porządek moll tej macierzy, różny od zera.
zwany najwyższy porządek moll tej macierzy, różny od zera.
Aby obliczyć rząd macierzy, należy uwzględnić wszystkie jej molle najniższego rzędu i jeżeli chociaż jeden z nich jest różny od zera, przystąpić do uwzględnienia minorów najwyższego rzędu. Takie podejście do określania rangi macierzy nazywa się metodą graniczną (lub metodą graniczących nieletnich).
Zadanie 1.4. Korzystając z metody graniczących nieletnich, określ rangę macierzy  .
.
 .
.
Weźmy pod uwagę krawędzie pierwszego rzędu, np.  . Następnie przechodzimy do rozważenia krawędzi drugiego rzędu.
. Następnie przechodzimy do rozważenia krawędzi drugiego rzędu.
Na przykład,  .
.
Na koniec przeanalizujmy granicę trzeciego rzędu.
 .
.
Zatem najwyższym rzędem niezerowej mniejszości jest 2  .
.
Rozwiązując Problem 1.4, można zauważyć, że liczba graniczących nieletnich drugiego rzędu jest różna od zera. W tym zakresie obowiązuje następująca koncepcja.
Definicja 1.14. Moll bazowy macierzy to dowolny niezerowy minor, którego rząd jest równy rządowi macierzy.
Twierdzenie 1.2.(Podstawowe twierdzenie). Wiersze bazowe (kolumny podstawowe) są liniowo niezależne.
Należy zauważyć, że wiersze (kolumny) macierzy są liniowo zależne wtedy i tylko wtedy, gdy co najmniej jeden z nich można przedstawić jako liniową kombinację pozostałych.
Twierdzenie 1.3. Liczba liniowo niezależnych wierszy macierzy jest równa liczbie liniowo niezależnych kolumn macierzy i jest równa rangi macierzy.
Twierdzenie 1.4.(Warunek konieczny i wystarczający, aby wyznacznik był równy zero). W celu wyznacznika  -ta kolejność
-ta kolejność  była równa zeru, konieczne i wystarczające jest, aby jej wiersze (kolumny) były liniowo zależne.
była równa zeru, konieczne i wystarczające jest, aby jej wiersze (kolumny) były liniowo zależne.
Obliczanie rangi macierzy na podstawie jej definicji jest zbyt kłopotliwe. Staje się to szczególnie ważne w przypadku macierzy wysokich rzędów. W związku z tym w praktyce rangę macierzy oblicza się w oparciu o zastosowanie Twierdzeń 10.2 - 10.4, a także wykorzystanie koncepcji równoważności macierzy i przekształceń elementarnych.
Definicja 1.15. Dwie matryce  I
I  nazywane są równoważnymi, jeśli ich rangi są równe, tj.
nazywane są równoważnymi, jeśli ich rangi są równe, tj.  .
.
Jeśli macierze  I
I  są równoważne, to zanotuj
są równoważne, to zanotuj 
 .
.
Twierdzenie 1.5. Ranga macierzy nie zmienia się pod wpływem elementarnych przekształceń.
Nazwiemy je elementarnymi transformacjami macierzy  dowolna z następujących operacji na macierzy:
dowolna z następujących operacji na macierzy:
Zastępowanie wierszy kolumnami i kolumn odpowiednimi wierszami;
Przestawianie wierszy macierzy;
Przekreślenie linii, której wszystkie elementy są zerowe;
Mnożenie ciągu przez liczbę inną niż zero;
Dodanie do elementów jednej linii odpowiednich elementów drugiej linii pomnożonych przez tę samą liczbę  .
.
Wniosek z twierdzenia 1.5. Jeśli macierz  otrzymane z matrixa
otrzymane z matrixa  stosując skończoną liczbę przekształceń elementarnych, a następnie macierz
stosując skończoną liczbę przekształceń elementarnych, a następnie macierz  I
I  są równoważne.
są równoważne.
Obliczając rząd macierzy, należy ją sprowadzić do postaci trapezowej za pomocą skończonej liczby przekształceń elementarnych.
Definicja 1.16. Trapezową będziemy nazywać formą reprezentacji macierzowej, gdy w graniczącym mollu najwyższego rzędu niezerowego wszystkie elementy poniżej przekątnych znikają. Na przykład:
 .
.

Tutaj  , elementy macierzy
, elementy macierzy  iść do zera. Wtedy postać reprezentacji takiej macierzy będzie trapezowa.
iść do zera. Wtedy postać reprezentacji takiej macierzy będzie trapezowa.
Z reguły macierze są redukowane do kształtu trapezowego za pomocą algorytmu Gaussa. Ideą algorytmu Gaussa jest to, że mnożąc elementy pierwszego rzędu macierzy przez odpowiednie współczynniki, uzyskuje się to, że wszystkie elementy pierwszej kolumny znajdujące się poniżej elementu  , zmieni się na zero. Następnie mnożąc elementy drugiej kolumny przez odpowiednie współczynniki, upewniamy się, że wszystkie elementy drugiej kolumny znajdujące się poniżej elementu
, zmieni się na zero. Następnie mnożąc elementy drugiej kolumny przez odpowiednie współczynniki, upewniamy się, że wszystkie elementy drugiej kolumny znajdujące się poniżej elementu  , zmieni się na zero. Następnie postępuj w ten sam sposób.
, zmieni się na zero. Następnie postępuj w ten sam sposób.
Zadanie 1.5. Określ rząd macierzy, redukując ją do kształtu trapezu.
 .
.
Aby ułatwić korzystanie z algorytmu Gaussa, możesz zamienić pierwszą i trzecią linię.





 .
.
To oczywiste, że tutaj  . Aby jednak nadać wynikowi bardziej elegancką formę, możesz dalej przekształcać kolumny.
. Aby jednak nadać wynikowi bardziej elegancką formę, możesz dalej przekształcać kolumny.







 .
.
Rozważymy również ważne praktyczne zastosowanie tematu: badanie układu równań liniowych pod kątem spójności.
Jaki jest rząd macierzy?
Humorystyczny motto artykułu zawiera dużą ilość prawdy. Słowo „ranga” kojarzy nam się zwykle z jakąś hierarchią, najczęściej ze szczeblem kariery. Im więcej wiedzy, doświadczenia, umiejętności, powiązań itp. ma dana osoba. – im wyższa jego pozycja i zakres możliwości. W przypadku młodzieży ranga odnosi się do ogólnego stopnia „stromości”.
A nasi matematyczni bracia żyją według tych samych zasad. Zabierzmy na spacer kilka przypadkowych osób macierze zerowe:
Pomyślmy o tym, jeśli w matrixie wszystkie zera, to o jakiej randze możemy mówić? Każdy zna nieformalne wyrażenie „całkowite zero”. W społeczeństwie matryc wszystko jest dokładnie takie samo:
Ranga macierzy zerowejdowolny rozmiar jest równy zero.
Notatka : Macierz zerowa jest oznaczona grecką literą „theta”
Aby lepiej zrozumieć rangę matrycy, w dalszej części posłużę się materiałami do pomocy geometria analityczna. Rozważ zero wektor naszą trójwymiarową przestrzeń, która nie wyznacza określonego kierunku i jest bezużyteczna do budowania podstawa afiniczna. Z algebraicznego punktu widzenia współrzędne tego wektora są zapisywane matryca„jeden po trzech” i logiczne (we wskazanym sensie geometrycznym) załóżmy, że rząd tej macierzy wynosi zero.
Teraz spójrzmy na kilka niezerowy wektory kolumnowe I wektory wierszowe:
Każda instancja ma co najmniej jeden niezerowy element i to jest coś!
Ranga dowolnego niezerowego wektora wierszowego (wektora kolumnowego) jest równa jeden
I ogólnie rzecz biorąc - jeśli w matrixie dowolne rozmiary istnieje co najmniej jeden element niezerowy, to jego ranga nie mniej jednostki.
Algebraiczne wektory wierszowe i wektory kolumnowe są w pewnym stopniu abstrakcyjne, więc wróćmy ponownie do skojarzenia geometrycznego. Niezerowe wektor wyznacza bardzo określony kierunek w przestrzeni i nadaje się do konstruowania podstawa, dlatego rangę macierzy przyjmiemy jako równą jeden.
Informacje teoretyczne : V algebra liniowa wektor jest elementem Przestrzeń wektorowa(określonych poprzez 8 aksjomatów), który w szczególności może być uporządkowanym wierszem (lub kolumną) liczb rzeczywistych z określonymi dla nich operacjami dodawania i mnożenia przez prawdziwy numer. Z więcej dokładna informacja o wektorach można znaleźć w artykule Przekształcenia liniowe.
liniowo zależne(wyrażane przez siebie). Z geometrycznego punktu widzenia druga linia zawiera współrzędne wektora współliniowego ![]() , co w ogóle nie posunęło sprawy w budownictwie podstawa trójwymiarowa, będąc w tym sensie zbędnym. Zatem ranga tej macierzy jest również równa jeden.
, co w ogóle nie posunęło sprawy w budownictwie podstawa trójwymiarowa, będąc w tym sensie zbędnym. Zatem ranga tej macierzy jest również równa jeden.
Zapiszmy współrzędne wektorów w kolumnach ( transponować macierz):
Co się zmieniło jeśli chodzi o rangę? Nic. Kolumny są proporcjonalne, co oznacza, że stopień jest równy jeden. Nawiasem mówiąc, zauważ, że wszystkie trzy linie są również proporcjonalne. Można je zidentyfikować za pomocą współrzędnych trzy wektory współliniowe płaszczyzny, z czego tylko jeden przydatne do budowy „płaskiej” podstawy. I jest to całkowicie zgodne z naszym zmysł geometryczny ranga.
Z powyższego przykładu wynika ważne stwierdzenie:
Ranga macierzy w wierszach jest równa rangi macierzy w kolumnach. Wspomniałem już o tym trochę w lekcji o efektywności metody obliczania wyznacznika.
Notatka : z liniowej zależności wierszy wynika zależność liniowa kolumny (i odwrotnie). Ale żeby zaoszczędzić czas i z przyzwyczajenia, prawie zawsze będę mówił o liniowej zależności ciągów.
Kontynuujmy szkolenie naszego ukochanego zwierzaka. Dodajmy współrzędne innego wektora współliniowego do macierzy w trzecim wierszu ![]() :
:
Czy pomógł nam w skonstruowaniu trójwymiarowej podstawy? Oczywiście nie. Wszystkie trzy wektory chodzą tam i z powrotem po tej samej ścieżce, a stopień macierzy jest równy jeden. Możesz wziąć dowolną liczbę wektorów współliniowych, powiedzmy 100, umieścić ich współrzędne w macierzy „sto na trzy”, a ranga takiego drapacza chmur nadal pozostanie jedna.
Zapoznajmy się z macierzą, której wiersze liniowo niezależny. Do skonstruowania podstawy trójwymiarowej odpowiednia jest para wektorów niewspółliniowych. Ranga tej macierzy wynosi dwa.
Jaki jest rząd macierzy? Linie nie wydają się być proporcjonalne... więc teoretycznie jest ich trzy. Jednak ranga tej macierzy również wynosi dwa. Dodałem dwie pierwsze linijki i wynik zapisałem na dole, tj. wyrażone liniowo trzecią linię przez dwie pierwsze. Geometrycznie rzędy macierzy odpowiadają współrzędnym trójki wektory współpłaszczyznowe, a wśród tej trójki jest para niewspółliniowych towarzyszy.
Jak widzisz, zależność liniowa w rozważanej matrycy nie jest oczywiste, a dziś dowiemy się, jak wydobyć to na światło dzienne.
Myślę, że wiele osób jest w stanie odgadnąć, jaki jest stopień macierzy!
Rozważmy macierz, której wiersze liniowo niezależny. Formularz wektorów podstawa afiniczna, a rząd tej macierzy wynosi trzy.
Jak wiadomo, każdy czwarty, piąty, dziesiąty wektor przestrzeni trójwymiarowej będzie wyrażony liniowo w postaci wektorów bazowych. Dlatego jeśli dodasz dowolną liczbę wierszy do macierzy, wówczas jej ranga nadal będzie wynosić trzy.
Podobne rozumowanie można przeprowadzić dla macierzy o większych rozmiarach (oczywiście bez żadnego znaczenia geometrycznego).
Definicja : Ranga macierzy to maksymalna liczba liniowo niezależnych wierszy. Lub: Rząd macierzy to maksymalna liczba liniowo niezależnych kolumn. Tak, ich liczba jest zawsze taka sama.
Z powyższego wynika również ważna praktyczna wskazówka: rząd macierzy nie przekracza jej minimalnego wymiaru. Na przykład w matrixie  cztery wiersze i pięć kolumn. Minimalny wymiar to cztery, dlatego ranga tej macierzy na pewno nie przekroczy 4.
cztery wiersze i pięć kolumn. Minimalny wymiar to cztery, dlatego ranga tej macierzy na pewno nie przekroczy 4.
Oznaczenia: w teorii i praktyce świata nie ma ogólnie przyjętego standardu wyznaczania rangi macierzy, najczęściej można spotkać: - jak to mówią, Anglik pisze co innego, Niemiec co innego. Dlatego, opierając się na słynnym dowcipie o amerykańskim i rosyjskim piekle, oznaczmy rangę macierzy rodzimym słowem. Na przykład: . A jeśli macierz jest „nienazwana”, a jest ich wiele, to możesz po prostu napisać.
Jak znaleźć rangę macierzy za pomocą nieletnich?
Gdyby moja babcia miała w swojej macierzy piątą kolumnę, to musiałaby obliczyć kolejną nieletnią czwartego rzędu („niebieski”, „malinowy” + 5. kolumna).
Wniosek: maksymalny rząd niezerowej mniejszości to trzy, co oznacza .
Być może nie wszyscy w pełni zrozumieli to zdanie: małoletni czwartego rzędu jest równy zeru, ale wśród nieletnich trzeciego rzędu była jedynka niezerowa - dlatego maksymalny rząd niezerowy mniejsze i równe trzy.
Powstaje pytanie, dlaczego nie od razu obliczyć wyznacznik? Cóż, po pierwsze, w większości zadań macierz nie jest kwadratowa, a po drugie, nawet jeśli otrzymasz wartość różną od zera, zadanie najprawdopodobniej zostanie odrzucone, ponieważ zwykle obejmuje standardowe rozwiązanie „oddolne”. A w rozważanym przykładzie zerowy wyznacznik czwartego rzędu pozwala nam stwierdzić, że rząd macierzy jest tylko mniejszy niż cztery.
Przyznam, że sam wpadłem na problem, który analizowałem, żeby lepiej wyjaśnić sposób pogranicza nieletnich. W praktyce wszystko jest prostsze:
Przykład 2
Znajdź rząd macierzy, korzystając z metody drugorzędnych krawędzi 
Rozwiązanie i odpowiedź znajdują się na końcu lekcji.
Kiedy algorytm działa najszybciej? Wróćmy do tej samej macierzy cztery na cztery.  . Oczywiście rozwiązanie będzie najkrótsze w przypadku „dobrego” narożnikowi nieletni:
. Oczywiście rozwiązanie będzie najkrótsze w przypadku „dobrego” narożnikowi nieletni:
A jeśli , to , w przeciwnym razie – .
Myślenie wcale nie jest hipotetyczne – przykładów jest wiele, gdy cała sprawa ogranicza się jedynie do nieletnich kątowych.
Jednak w niektórych przypadkach inna metoda jest bardziej skuteczna i preferowana:
Jak znaleźć rząd macierzy metodą Gaussa?
Akapit przeznaczony jest dla czytelników, którzy już się z nim zapoznali Metoda Gaussa i mniej więcej wpadło w jego ręce.
Z technicznego punktu widzenia metoda nie jest nowa:
1) stosując przekształcenia elementarne sprowadzamy macierz do postaci schodkowej;
2) rząd macierzy jest równy liczbie wierszy.
To zupełnie jasne zastosowanie metody Gaussa nie powoduje zmiany rangi macierzy, a istota tutaj jest niezwykle prosta: zgodnie z algorytmem podczas elementarnych transformacji identyfikowane i usuwane są wszystkie niepotrzebne proporcjonalne (liniowo zależne) wiersze, w wyniku czego powstaje „sucha pozostałość” - maksymalna liczba liniowo niezależnych wierszy.
Przekształćmy starą, znaną macierz o współrzędne trzech współliniowych wektorów: 
(1) Pierwsza linia została dodana do drugiej linii, pomnożona przez –2. Pierwsza linia została dodana do trzeciej linii.
(2) Linie zerowe zostały usunięte.
Zatem pozostała jedna linia, stąd . Nie trzeba dodawać, że jest to znacznie szybsze niż obliczenie dziewięciu małoletnich zerowych drugiego rzędu i dopiero potem wyciągnięcie wniosków.
Przypominam, że samo w sobie macierz algebraiczna nic nie można zmienić, a przekształcenia dokonywane są wyłącznie w celu ustalenia rangi! Nawiasem mówiąc, zatrzymajmy się jeszcze raz nad pytaniem, dlaczego nie? Macierz źródłowa  niesie informację, która zasadniczo różni się od informacji zawartej w macierzy i wierszu. W niektórych modelach matematycznych (bez przesady) różnica w jednej liczbie może być sprawą życia i śmierci. ...Zapamiętany nauczyciele szkolni matematycy klas podstawowych i średnich, którzy bezlitośnie obniżają ocenę o 1-2 punkty za najmniejszą niedokładność lub odstępstwo od algorytmu. I było strasznie rozczarowujące, gdy zamiast pozornie gwarantowanego „A” wyszło „dobrze”, a nawet gorzej. Zrozumienie przyszło znacznie później – jak inaczej powierzyć człowiekowi satelity, głowice nuklearne i elektrownie? Ale nie martw się, nie pracuję w tych obszarach =)
niesie informację, która zasadniczo różni się od informacji zawartej w macierzy i wierszu. W niektórych modelach matematycznych (bez przesady) różnica w jednej liczbie może być sprawą życia i śmierci. ...Zapamiętany nauczyciele szkolni matematycy klas podstawowych i średnich, którzy bezlitośnie obniżają ocenę o 1-2 punkty za najmniejszą niedokładność lub odstępstwo od algorytmu. I było strasznie rozczarowujące, gdy zamiast pozornie gwarantowanego „A” wyszło „dobrze”, a nawet gorzej. Zrozumienie przyszło znacznie później – jak inaczej powierzyć człowiekowi satelity, głowice nuklearne i elektrownie? Ale nie martw się, nie pracuję w tych obszarach =)
Przejdźmy do bardziej znaczących zadań, gdzie między innymi zapoznamy się z ważnymi technikami obliczeniowymi Metoda Gaussa:
Przykład 3
Znajdź rząd macierzy za pomocą przekształceń elementarnych 
Rozwiązanie: podana jest macierz „cztery na pięć”, co oznacza, że jej ranga z pewnością nie jest większa niż 4.
W pierwszej kolumnie nie ma ani 1, ani –1, zatem wymagane są dodatkowe działania, aby zdobyć choć jedną jednostkę. Przez cały okres istnienia serwisu wielokrotnie zadawano mi pytanie: „Czy można przestawiać kolumny podczas elementarnych przekształceń?” Tutaj przestawiliśmy pierwszą i drugą kolumnę i wszystko jest w porządku! W większości zadań, w których jest używany Metoda Gaussa, kolumny rzeczywiście można zmienić. ALE NIE POTRZEBNE. I nie chodzi nawet o ewentualne pomieszanie ze zmiennymi, chodzi o to, że w klasycznym toku wyższej matematyki działanie to tradycyjnie nie jest brane pod uwagę, więc takie ukłon będzie odebrany BARDZO krzywo (lub nawet zmuszony do przerobienia wszystkiego).
Druga kwestia dotyczy liczb. Podejmując decyzję, warto zastosować się do następującej praktycznej zasady: przekształcenia elementarne powinny w miarę możliwości redukować liczby macierzy. W końcu znacznie łatwiej jest pracować z jednym, dwoma, trzema niż na przykład z 23, 45 i 97. A pierwsza akcja ma na celu nie tylko uzyskanie jedynki w pierwszej kolumnie, ale także wyeliminowanie liczb 7 i 11.
Najpierw kompletne rozwiązanie, potem komentarze: 
(1) Pierwsza linia została dodana do drugiej linii, pomnożona przez –2. Pierwsza linia została dodana do trzeciej linii, pomnożona przez –3. I do sterty: pierwsza linia została dodana do czwartej linii, pomnożona przez –1.
(2) Ostatnie trzy linie są proporcjonalne. Linie 3 i 4 zostały usunięte, linia druga została przesunięta na pierwsze miejsce.
(3) Pierwsza linia została dodana do drugiej linii, pomnożona przez –3.
Macierz zredukowana do postaci rzutowej ma dwa wiersze.
Odpowiedź:
Teraz twoja kolej na torturowanie matrycy cztery na cztery:
Przykład 4
Znajdź rząd macierzy za pomocą metody Gaussa 
Przypominam ci to Metoda Gaussa nie oznacza jednoznacznej sztywności, a Twoja decyzja najprawdopodobniej będzie się różnić od mojej. Krótki przykład zadania na koniec lekcji.
Jakiej metody należy użyć, aby znaleźć rząd macierzy?
W praktyce często nie jest w ogóle określone, jaką metodę należy zastosować, aby znaleźć rangę. W takiej sytuacji należy przeanalizować warunek - dla niektórych macierzy bardziej racjonalne jest rozwiązanie poprzez niepełne elementy, dla innych znacznie bardziej opłacalne jest zastosowanie elementarnych przekształceń:
Przykład 5
Znajdź rząd macierzy 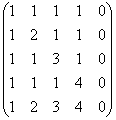
Rozwiązanie: pierwsza metoda jakoś natychmiast znika =)
Nieco wyżej radziłem nie dotykać kolumn macierzy, ale gdy jest kolumna zerowa, lub kolumny proporcjonalne/zbieżne, to i tak warto amputować: 
(1) Piąta kolumna ma wartość zero, usuń ją z macierzy. Zatem ranga macierzy jest nie większa niż cztery. Pierwsza linia została pomnożona przez –1. To kolejna charakterystyczna cecha metody Gaussa, która zamienia następującą czynność w przyjemny spacer:
(2) Do wszystkich wierszy, począwszy od drugiego, dodano wiersz pierwszy.
(3) Pierwszą linię pomnożono przez –1, trzecią linię podzielono przez 2, czwartą linię podzielono przez 3. Druga linia została dodana do piątej linii i pomnożona przez –1.
(4) Trzecia linia została dodana do piątej linii, pomnożona przez –2.
(5) Dwa ostatnie wiersze są proporcjonalne, piąty skreśla się.
Rezultatem są 4 linie.
Odpowiedź:
Standardowy pięciopiętrowy budynek do samodzielnego studiowania:
Przykład 6
Znajdź rząd macierzy
Krótkie rozwiązanie i odpowiedź na końcu lekcji.
Należy zauważyć, że wyrażenie „ranga matrycy” nie jest tak często spotykane w praktyce, a w większości problemów można się bez niego obejść. Ale jest jedno zadanie, w którym dana koncepcja jest najważniejsza aktor i na zakończenie artykułu przyjrzymy się temu praktycznemu zastosowaniu:
Jak badać układ równań liniowych pod kątem spójności?
Często oprócz rozwiązania układy równań liniowych zgodnie z warunkiem należy najpierw sprawdzić go pod kątem zgodności, to znaczy udowodnić, że w ogóle istnieje jakiekolwiek rozwiązanie. Kluczową rolę w takiej weryfikacji odgrywają Twierdzenie Kroneckera-Capelliego, które sformułuję w niezbędnej formie:
Jeśli ranga macierze systemowe równy rangi rozbudowany układ matrycowy, to system jest spójny, a jeśli podany numer pokrywa się z liczbą niewiadomych, to rozwiązanie jest unikalne.
Zatem, aby zbadać system pod kątem zgodności, konieczne jest sprawdzenie równości ![]() , Gdzie - matryca systemu(pamiętaj terminologię z lekcji Metoda Gaussa), A - rozbudowana matryca systemu(tj. macierz ze współczynnikami zmiennych + kolumna wolnych terminów).
, Gdzie - matryca systemu(pamiętaj terminologię z lekcji Metoda Gaussa), A - rozbudowana matryca systemu(tj. macierz ze współczynnikami zmiennych + kolumna wolnych terminów).








