ja = ∑r ja 2 dF i =∫r 2 dF (1.1)
W zasadzie zarówno definicja, jak i opisująca ją formuła nie są skomplikowane, a ich zapamiętanie jest znacznie łatwiejsze niż zrozumienie istoty. Ale mimo to spróbujmy dowiedzieć się, czym jest moment bezwładności i skąd się bierze.
Pojęcie momentu bezwładności zadomowiło się w wytrzymałości materiałów i mechanice strukturalnej z innej gałęzi fizyki badającej kinematykę ruchu, w szczególności ruchu obrotowego. Ale i tak zacznijmy od daleka.
Nie wiem na pewno, czy jabłko spadło na głowę Izaaka Newtona, czy spadło w pobliżu, czy też w ogóle nie spadło, teoria prawdopodobieństwa dopuszcza wszystkie te opcje (poza tym w tym jabłku jest za dużo z biblijnej legendy o drzewie poznania), ale jestem pewien, że Newton był osobą spostrzegawczą, potrafiącą wyciągać wnioski ze swoich obserwacji. Tym samym obserwacja i wyobraźnia pozwoliły Newtonowi sformułować podstawowe prawo dynamiki (drugie prawo Newtona), zgodnie z którym masa ciała M, pomnożone przez przyspieszenie A, jest równa działającej sile Q(właściwie oznaczenie F jest bardziej powszechne dla siły, ale ponieważ w dalszej części mamy do czynienia z powierzchnią, która również często jest oznaczana jako F, używam oznaczenia Q dla siły zewnętrznej, uznawanej w mechanice teoretycznej za obciążenie skupione, właściwie to się nie zmienia):
Q = mam (1.2)
Dla mnie wielkość Newtona leży w jego prostocie i przejrzystości. tę definicję. Ponadto, jeśli weźmiesz pod uwagę to, kiedy ruch jednostajnie przyspieszony przyśpieszenie A równy współczynnikowi przyrostu prędkości ΔV do pewnego okresu Δt, podczas którego zmieniała się prędkość:
a = Δv/Δt = (v - v о)/t (1.3.1)
przy Vo = 0 a = v/t (1.3.2)
wtedy można określić podstawowe parametry ruchu, takie jak odległość, prędkość, czas, a nawet pęd R, charakteryzujące wielkość ruchu:
p = mv (1.4)
Na przykład jabłko spadające z różnych wysokości pod wpływem samej grawitacji spadnie na ziemię inny czas, mają różne prędkości w momencie lądowania i odpowiednio różne impulsy. Innymi słowy, jabłko spadające z większej wysokości będzie latać dłużej i mocniej pęknie na czole nieszczęsnego obserwatora. Newton sprowadził to wszystko do prostej i zrozumiałej formuły.
Newton sformułował także prawo bezwładności (pierwsze prawo Newtona): jeśli przyspieszenie a = 0, potem w układ inercyjny punktu odniesienia nie da się określić, czy obserwowane ciało, na które nie działają siły zewnętrzne, znajduje się w spoczynku, czy też porusza się po linii prostej ze stałą prędkością. Ta właściwość ciał materialnych polegająca na utrzymywaniu ich prędkości, nawet zerowej, nazywa się bezwładnością. Miarą bezwładności jest masa bezwładności ciała. Czasami masę bezwładną nazywa się bezwładną, ale to nie zmienia istoty rzeczy. Uważa się, że masa bezwładności jest równa masie grawitacyjnej i dlatego często nie jest określone, o jaką masę chodzi, a jedynie podaje się masę ciała.
Nie mniej ważne i znaczące jest trzecie prawo Newtona, zgodnie z którym siła akcji jest równa sile reakcji, jeśli siły są skierowane w jedną linię prostą, ale w przeciwne strony. Pomimo pozornej prostoty, ten wniosek Newtona jest genialny, a znaczenie tego prawa jest trudne do przecenienia. Poniżej omówiono jedno z zastosowań tego prawa.
Jednakże postanowienia te obowiązują tylko w przypadku ciał poruszających się postępowo, tj. prostą ścieżką i jednocześnie wszystkim punkty materialne ciała takie poruszają się z tą samą prędkością i tym samym przyspieszeniem. Do ruchu krzywoliniowego, a w szczególności do ruch obrotowy np. gdy ciało obraca się wokół własnej osi symetrii, punkty materialne takiego ciała poruszają się w przestrzeni z tą samą prędkością kątową w, ale jednocześnie prędkość liniowa w różne punkty będą miały różne wartości, a ta prędkość liniowa jest wprost proporcjonalna do odległości R od osi obrotu do tego punktu:
v=wr (1.5)
w tym przypadku prędkość kątowa jest równa stosunkowi przyrostu kąta obrotu Δφ do pewnego okresu Δt, dla którego zmienił się kąt obrotu:
w = Δφ/Δt = (φ - φ о)/t (1.6.1)
przy φ o = 0 w = φ/t (1.7.2)
odpowiednio normalne przyspieszenie oraz n podczas ruchu obrotowego jest równa:
za n = v 2 /r = w 2 r (1.8)
I okazuje się, że dla ruchu obrotowego nie można bezpośrednio skorzystać ze wzoru (1.2), gdyż w ruchu obrotowym sama wartość masy ciała nie wystarczy, trzeba także znać rozkład tej masy w ciele. Okazuje się, że im bliżej osi obrotu znajdują się punkty materialne ciała, tym mniejszą siłę należy przyłożyć, aby ciało się obróciło i odwrotnie, im dalej od osi obrotu znajdują się punkty materialne ciała, tym większą siłę należy przyłożyć, aby zmusić ciało do obrotu (w tym przypadku mówimy o przyłożeniu siły w tym samym punkcie). Ponadto podczas obracania ciała wygodniej jest nie brać tego pod uwagę siła skuteczna, oraz moment obrotowy, ponieważ podczas ruchu obrotowego istnieje również punkt przyłożenia siły bardzo ważne.
Niesamowite właściwości momentu obrotowego znane są nam już od czasów Archimedesa, a jeśli pojęcie momentu obrotowego zastosujemy do ruchu obrotowego, to znaczenie momentu obrotowego M będzie tym większa, im większa będzie odległość R od osi obrotu do punktu przyłożenia siły F(w mechanice konstrukcji siła zewnętrzna często tzw R Lub Q):
M = Qr (1.9)
Z tego też niezbyt skomplikowanego wzoru wynika, że jeśli siłę przyłożymy wzdłuż osi obrotu, to nie będzie żadnego obrotu, gdyż r = 0, a jeżeli siłę przyłożymy w maksymalnej odległości od osi obrotu, to wartość chwili będzie maksymalna. A jeśli podstawimy do wzoru (1.9) wartość siły ze wzoru (1.2) oraz wartość przyspieszenia normalnego i wzór (1.8), otrzymamy równanie:
M = mw 2 r r = mw 2 r 2 (1.10)
W szczególnym przypadku, gdy ciało jest punktem materialnym o wymiarach znacznie mniejszych niż odległość tego punktu od osi obrotu, równanie (1.10) ma zastosowanie w czystej postaci. Jednakże dla ciała obracającego się wokół jednej ze swoich osi symetrii odległość od każdego punktu materialnego tworzącego to ciało jest zawsze mniejsza niż jeden z wymiarów geometrycznych ciała i dlatego rozkład masy ciała ma ogromne znaczenie, w tym przypadku należy uwzględnić te odległości osobno dla każdego punktu:
M = ∑r ja 2 w 2 m I (1.11.1)
М с = w 2 ∫r 2 dm
A potem okazuje się, że zgodnie z trzecim prawem Newtona w odpowiedzi na działanie momentu obrotowego powstanie tzw. Moment bezwładności I. W takim przypadku wartości momentu obrotowego i momentu bezwładności będą równe, a same momenty będą skierowane w przeciwne strony. Przy stałej prędkości kątowej obrotu, np. w = 1, głównymi wielkościami charakteryzującymi moment obrotowy lub moment bezwładności będzie masa punktów materialnych tworzących ciało oraz odległości tych punktów od osi obrotu. W rezultacie wzór na moment bezwładności będzie miał postać:
[- M] = ja = ∑r i 2 m I (1.12.1)
Ja do = ∫r 2 dm(1.11.2) - gdy ciało obraca się wokół osi symetrii
Gdzie I- ogólnie przyjęte oznaczenie momentu bezwładności, Ic- oznaczenie osiowego momentu bezwładności nadwozia, kg/m2. Dla jednorodnego ciała o tej samej gęstości ρ po całym ciele V Wzór na osiowy moment bezwładności ciała można zapisać następująco:
Ja do = ∫ρr 2 dV (1.13)
Zatem moment bezwładności jest miarą bezwładności ciała podczas ruchu obrotowego, tak jak masa jest miarą bezwładności ciała podczas ruchu prostoliniowego postępowego.
Koło zatoczyło koło. I tu może pojawić się pytanie, co te wszystkie prawa dynamiki i kinematyki mają wspólnego z obliczeniami statycznych konstrukcji budowlanych? Okazuje się, że żadna z tych rzeczy nie jest najbardziej bezpośrednia i natychmiastowa. Po pierwsze dlatego, że wszystkie te wzory zostały wyprowadzone przez fizyków i matematyków w tak odległych czasach, gdy takie dyscypliny jak „mechanika teoretyczna” czy „teoria wytrzymałości materiałów” po prostu nie istniały. Po drugie, ponieważ całe obliczenia konstrukcji budowlanych opierają się na wskazanych prawach i sformułowaniach oraz nieodpartym dotychczas przez nikogo stwierdzeniu o równości mas grawitacyjnych i bezwładnościowych. Ale w teorii wytrzymałości materiałów wszystko jest jeszcze prostsze, niezależnie od tego, jak paradoksalnie to brzmi.
I jest to prostsze, ponieważ przy rozwiązywaniu niektórych problemów nie można brać pod uwagę całego ciała, a jedynie jego przekrój i, jeśli to konieczne, kilka przekrojów. Ale w tych sekcjach działają te same siły fizyczne, choć o nieco innym charakterze. Zatem jeśli weźmiemy pod uwagę pewne ciało, którego długość jest stała, a samo ciało jest jednorodne, to jeśli nie weźmiemy pod uwagę stałych parametrów - długości i gęstości ( l = stała, ρ = stała) - otrzymamy model Przekrój. Dla takiego przekroju z matematycznego punktu widzenia będzie obowiązywać następujące równanie:
I р = ∫r 2 dF (2.1) → (1.1)
Gdzie IP- biegunowy moment bezwładności przekroju, m 4. W rezultacie otrzymaliśmy wzór, od którego zaczęliśmy (ale czy stał się jaśniejszy, jaki jest moment bezwładności przekroju, nie wiem).
Ponieważ w teorii wytrzymałości materiałów często uwzględnia się przekroje prostokątne, a prostokątny układ współrzędnych jest wygodniejszy, przy rozwiązywaniu problemów zwykle uwzględnia się dwa osiowe momenty bezwładności przekroju:
I z = ∫y 2 dF (2.2.1)
I y = ∫z 2 dF (2.2.2)
Obrazek 1. Wartości współrzędnych przy wyznaczaniu osiowych momentów bezwładności.
Tutaj może pojawić się pytanie, dlaczego używa się osi z I Na, a nie te bardziej znane X I Na? Tak się składa, że określenie sił w przekroju i wybór przekroju, który wytrzyma naprężenia eksploatacyjne równe przyłożonym siłom, to dwa różne zadania. Zadanie pierwsze – wyznaczanie sił – rozwiązuje mechanika konstrukcji, zadanie drugie – dobór przekrojów – rozwiązuje teoria wytrzymałości materiałów. Jednocześnie w mechanice konstrukcji jest to brane pod uwagę przy rozwiązywaniu proste zadania dość często pręt (w przypadku konstrukcji prostoliniowych) o określonej długości l, a wysokość i szerokość przekroju nie są brane pod uwagę, uważa się, że oś X precyzyjnie przechodzi przez środki ciężkości wszystkich przekrojów i tym samym przy konstruowaniu diagramów (czasami dość skomplikowanych) długość l jest precyzyjnie osadzany wzdłuż osi X i wzdłuż osi Na Wykreślane są wartości działki. Jednocześnie teoria wytrzymałości materiałów uwzględnia dokładnie przekrój poprzeczny, dla którego ważna jest szerokość i wysokość, a długość nie jest brana pod uwagę. Oczywiście przy rozwiązywaniu problemów z teorii wytrzymałości materiałów, które czasami są również dość złożone, stosuje się te same znane osie X I Na. Taki stan rzeczy nie wydaje mi się do końca prawidłowy, gdyż pomimo różnicy są to w dalszym ciągu zadania powiązane i dlatego właściwsze byłoby zastosowanie dla obliczanej konstrukcji wspólnych osi.
Wartość biegunowego momentu bezwładności w prostokątnym układzie współrzędnych będzie wynosić:
I р = ∫r 2 dF =∫y 2 dF + ∫z 2 dF (2.3)
Ponieważ w prostokątnym układzie współrzędnych promień jest przeciwprostokątną trójkąt prostokątny, a jak wiadomo, kwadrat przeciwprostokątnej jest równy sumie kwadratów nóg. Istnieje również koncepcja odśrodkowego momentu bezwładności przekroju:
I xz = ∫xzdF(2.4)
Wśród osi prostokątnego układu współrzędnych przechodzących przez środek ciężkości przekroju poprzecznego znajdują się dwie wzajemnie prostopadłe osie, względem których osiowe momenty bezwładności przyjmują wartość maksymalną i minimalną, natomiast odśrodkowy moment bezwładności przekroju Sekcja Ja zy = 0. Takie osie nazywane są głównymi środkowymi osiami przekroju, a momenty bezwładności wokół takich osi nazywane są głównymi środkowymi momentami bezwładności
Kiedy mówimy o momentach bezwładności w teorii wytrzymałości materiałów, zwykle mamy na myśli główne centralne momenty bezwładności przekroju. W przypadku przekrojów kwadratowych, prostokątnych i okrągłych główne osie będą pokrywać się z osiami symetrii. Momenty bezwładności przekroju poprzecznego nazywane są także geometrycznymi momentami bezwładności lub powierzchniowymi momentami bezwładności, ale istota pozostaje ta sama.
W zasadzie nie ma dużej potrzeby wyznaczania wartości głównych centralnych momentów bezwładności dla przekrojów najpopularniejszych kształtów geometrycznych - kwadratu, prostokąta, koła, rury, trójkąta i niektórych innych. Takie momenty bezwładności są od dawna zdefiniowane i powszechnie znane. A przy obliczaniu osiowych momentów bezwładności dla odcinków złożonych kształt geometryczny twierdzenie Huygensa-Steinera jest ważne:
ja = ja do + r 2 F (2.5)
Zatem jeśli obszary i środki ciężkości są proste figury geometryczne, tworząc złożony przekrój, wówczas określenie wartości osiowego momentu bezwładności całego przekroju nie jest trudne. Aby określić środek ciężkości złożonego przekroju, wykorzystuje się momenty statyczne przekroju. Momenty statyczne omówiono bardziej szczegółowo w innym artykule, dodam tylko tutaj. Fizyczne znaczenie momentu statycznego jest następujące: moment statyczny ciała to suma momentów punktów materialnych tworzących ciało, względem jakiegoś punktu (biegunowy moment statyczny) lub względem osi (osiowy moment statyczny) ), a ponieważ moment jest iloczynem siły i ramienia (1.9) , to moment statyczny ciała wyznacza się odpowiednio:
S = ∑M = ∑r I M I= ∫rdm (2.6)
i wówczas biegunowy moment statyczny przekroju będzie wynosić:
S р = ∫rdF (2.7)
Jak widać, definicja momentu statycznego jest podobna do definicji momentu bezwładności. Ale jest zasadnicza różnica. Moment statyczny nazywa się statycznym, ponieważ dla ciała, na które działa siła ciężkości, moment statyczny jest równy zeru względem środka ciężkości. Innymi słowy, takie ciało znajduje się w stanie równowagi, jeśli podpora zostanie przyłożona do środka ciężkości ciała. I zgodnie z pierwszym prawem Newtona takie ciało albo znajduje się w spoczynku, albo porusza się ze stałą prędkością, tj. przyspieszenie = 0. A z czysto matematycznego punktu widzenia moment statyczny może być równy zeru z prostego powodu, że przy wyznaczaniu momentu statycznego należy wziąć pod uwagę kierunek działania momentu obrotowego. Przykładowo w stosunku do osi współrzędnych przechodzących przez środek ciężkości prostokąta pola górnej i dolnej części prostokąta będą dodatnie, gdyż symbolizują one siłę ciężkości działającą w jednym kierunku. W tym przypadku odległość osi od środka ciężkości można uznać za dodatnią (warunkowo: moment od siły ciężkości górnej części prostokąta stara się obrócić przekrój zgodnie z ruchem wskazówek zegara), a do środka ciężkości dolna część - jako ujemna (warunkowo: moment od siły ciężkości dolnej części prostokąta próbuje obrócić przekrój w kierunku przeciwnym do ruchu wskazówek zegara). A ponieważ takie obszary są liczbowo równe i równe odległościom od środków ciężkości górnej części prostokąta i dolnej części prostokąta, wówczas suma działających momentów będzie pożądanym 0.
S z = ∫ydF = 0 (2.8)
To wielkie zero umożliwia również określenie reakcji podporowych konstrukcji budowlanych. Jeśli weźmiemy pod uwagę konstrukcję budynku, na którą przykładowo w pewnym punkcie przyłożone zostanie obciążenie skupione Q, to taką konstrukcję budynku można uznać za bryłę, której środek ciężkości znajduje się w miejscu przyłożenia siły, a reakcje podporowe w tym przypadku uważa się za siły przyłożone w punktach podparcia. Zatem znając wartość obciążenia skupionego Q oraz odległość od punktu przyłożenia obciążenia do podpór konstrukcji budynku, można wyznaczyć reakcje podporowe. Przykładowo dla belki swobodnie podpartej na dwóch podporach wartość reakcji podporowych będzie proporcjonalna do odległości do punktu przyłożenia siły, a suma reakcji podporowych będzie równa przyłożonemu obciążeniu. Ale z reguły przy wyznaczaniu reakcji podporowych przebiegają one jeszcze prościej: za środek ciężkości przyjmuje się jedną z podpór, a wtedy suma momentów przyłożonego obciążenia i pozostałych reakcji podporowych jest nadal równa zeru. W tym przypadku moment reakcji podporowej, względem którego sporządzane jest równanie momentu, jest równy zeru, ponieważ ramię siły = 0, co oznacza, że w sumie momentów pozostają tylko dwie siły: przyłożone obciążenie oraz nieznana reakcja podporowa (dla konstrukcji statycznie wyznaczalnych).
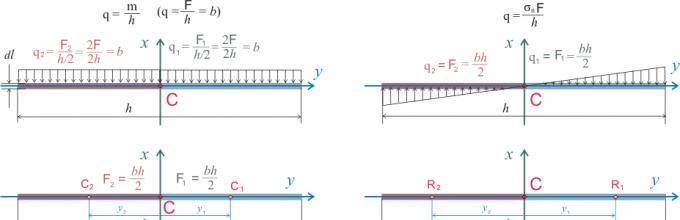
Zatem zasadnicza różnica pomiędzy momentem statycznym a momentem bezwładności polega na tym, że moment statyczny charakteryzuje przekrój, który siła ciężkości stara się przełamać na pół względem środka ciężkości lub osi symetrii, a moment bezwładność charakteryzuje ciało, którego wszystkie punkty materialne poruszają się (lub próbują poruszać się w jednym kierunku). Być może poniższe, raczej konwencjonalne schematy obliczeń dla przekroju prostokątnego pomogą Ci lepiej wyobrazić sobie tę różnicę:

Rysunek 2. Wyraźna różnica między momentem statycznym a momentem bezwładności.
Wróćmy teraz jeszcze raz do kinematyki ruchu. Jeżeli narysujemy analogie pomiędzy naprężeniami powstającymi w przekrojach konstrukcji budowlanych a różnymi rodzajami ruchu, to w elementach centralnie rozciąganych i centralnie ściskanych powstają naprężenia, które są jednakowe na całej powierzchni przekroju. Naprężenia te można porównać do działania jakiejś siły na ciało, podczas którego ciało będzie poruszać się prostoliniowo i progresywnie. A najciekawsze jest to, że przekroje elementów centralnie rozciągniętych lub centralnie ściśniętych faktycznie się poruszają, gdyż działające naprężenia powodują deformacje. Wielkość takich odkształceń można określić dla dowolnego przekroju konstrukcji. Aby to zrobić, wystarczy znać wartość naprężeń efektywnych, długość elementu, pole przekroju poprzecznego i moduł sprężystości materiału, z którego wykonana jest konstrukcja.
W przypadku elementów zginanych przekroje również nie pozostają na miejscu, ale się poruszają, a ruch przekrojów elementów zginanych jest podobny do obrotu określonego korpusu wokół określonej osi. Jak już zapewne się domyślacie moment bezwładności pozwala określić kąt nachylenia przekroju oraz przemieszczenie Δ l dla skrajnych punktów przekroju. Te skrajne punkty dla przekroju prostokątnego znajdują się w odległości równej połowie wysokości przekroju (dlaczego opisano wystarczająco szczegółowo w artykule „Podstawy wytrzymałości wytrzymałościowej. Wyznaczanie ugięcia”). A to z kolei pozwala określić ugięcie konstrukcji.
A moment bezwładności pozwala określić moment oporu przekroju. Aby to zrobić, moment bezwładności należy po prostu podzielić przez odległość od środka ciężkości przekroju do najdalszego punktu przekroju, w przypadku przekroju prostokątnego, przez h/2. A ponieważ badane przekroje nie zawsze są symetryczne, wartość momentu oporu może być różna dla różnych części przekroju.
A wszystko zaczęło się od banalnego jabłka... chociaż nie, wszystko zaczęło się od słowa.
§ 4.5. OBLICZANIE MOMENTÓW BEZWŁADNOŚCI PRZEKRÓJÓW O PROSTYM KSZTAŁCIE
Jak wskazano w § 1.5, charakterystykę geometryczną przekrojów złożonych określa się dzieląc je na szereg prostych figur, których charakterystyki geometryczne można obliczyć za pomocą odpowiednich wzorów lub określić za pomocą specjalnych tabel. Wzory te otrzymuje się w wyniku bezpośredniego całkowania wyrażeń (8.5)-(10.5). Sposoby ich uzyskania omówiono poniżej na przykładach prostokąta, trójkąta i koła.
Przekrój prostokątny
Wyznaczmy osiowy moment bezwładności prostokąta o wysokości h i szerokości b względem osi przechodzącej przez jego podstawę (ryc. 11.5, a). Wybierzmy z prostokąta o liniach równoległych do osi elementarny pasek o wysokości i szerokości b.
Powierzchnia tego paska, odległość od paska do osi jest im równa. Podstawmy te wielkości do wyrażenia na moment bezwładności (8.5):
W podobny sposób dla momentu bezwładności względem osi można otrzymać wyrażenie
Aby wyznaczyć odśrodkowy moment bezwładności, wybieramy z prostokąta z liniami równoległymi do osi (ryc.
11.5, b), elementarny obszar wielkości. Wyznaczmy najpierw odśrodkowy moment bezwładności nie całego prostokąta, a jedynie pionowego pasa o wysokości h i szerokości znajdującego się w pewnej odległości od osi
Produkt jest umieszczony poza znakiem całki, ponieważ dla wszystkich obszarów należących do rozpatrywanego paska pionowego jest stały.
Następnie scałkujmy wyrażenie w zakresie od do
Wyznaczmy teraz osiowe momenty bezwładności prostokąta względem y oraz osie przechodzące przez środek ciężkości równolegle do boków prostokąta (rys. 12.5). W tym przypadku granice całkowania będą wynosić od do
Odśrodkowy moment bezwładności prostokąta względem osi (ryc. 12.5) jest równy zeru, ponieważ osie te pokrywają się z jego osiami symetrii.
Przekrój trójkątny
Określmy osiowe momenty bezwładności trójkąta względem trzech równoległych osi przechodzących przez jego podstawę (ryc. 13.5, a), środek ciężkości (ryc. 13.5, b) i wierzchołek (ryc. 13.5, e).
W przypadku, gdy oś przechodzi przez podstawę trójkąta (ryc. 13.5, a),
W przypadku, gdy oś przechodzi przez środek ciężkości trójkąta równolegle do jego podstawy (ryc. 13.5, b),
W przypadku, gdy oś przechodzi przez wierzchołek trójkąta równolegle do jego podstawy (ryc. 13.5, c),
Moment bezwładności jest znacznie większy (trzykrotnie) od momentu bezwładności, ponieważ główna część pola trójkąta jest bardziej oddalona od osi niż od osi
Otrzymano wyrażenia (17,5) - (19,5). Trójkąt równoramienny. Jednakże dotyczą one również trójkątów innych niż równoramienne. Porównując na przykład trójkąty pokazane na ryc. 13.5, a i 13.5, d, z których pierwszy jest równoramienny, a drugi nie jest równoramienny, ustalamy, że wymiary pola i granice, w których zmienia się y (od 0 do), są takie same dla obu trójkątów. W związku z tym momenty bezwładności dla nich są również takie same. Podobnie można wykazać, że osiowe momenty bezwładności wszystkich przekrojów pokazanych na rys. 14,5 to samo. Ogólnie rzecz biorąc, przemieszczenie części przekroju równoległego do określonej osi nie wpływa na wartość osiowego momentu bezwładności względem tej osi.
Jest oczywiste, że suma osiowych momentów bezwładności trójkąta względem osi pokazanych na ryc. 13,5, a i 13,5, b powinny być równe osiowemu momentowi bezwładności prostokąta względem osi pokazanej na ryc. 11,5, o. Wynika to z faktu, że prostokąt można rozpatrywać jako dwa trójkąty, z których dla jednego oś przechodzi przez podstawę, a dla drugiego przez wierzchołek równoległy do jego podstawy (ryc. 15.5).
Rzeczywiście, zgodnie ze wzorami (17.5) i (19.5)
co pokrywa się z wyrażeniem prostokąta zgodnie ze wzorem (12.5).
Przekrój w kształcie koła
Wyznaczmy osiowy moment bezwładności okręgu względem dowolnej osi przechodzącej przez jego środek ciężkości. Z ryc. 16,5, ale powinno
Jest oczywiste, że w odniesieniu do dowolnej osi przechodzącej przez środek okręgu osiowy moment bezwładności będzie równy, a zatem
Korzystając ze wzoru (11.5) wyznaczamy biegunowy moment bezwładności okręgu względem jego środka:
Wzór na osiowy moment bezwładności okręgu można otrzymać w prostszy sposób, wyprowadzając najpierw wzór na jego biegunowy moment bezwładności względem środka (punktu O). Aby to zrobić, z koła wybieramy elementarny pierścień o grubości promienia i powierzchni (ryc. 16.5,b).
Biegunowy moment bezwładności pierścienia elementarnego względem środka koła, ponieważ wszystkie obszary elementarne, z których składa się ten pierścień, znajdują się w tej samej odległości od środka koła. Stąd,
Wynik ten jest zbieżny z uzyskanym powyżej.
Momenty bezwładności (biegunowe i osiowe) przekroju w kształcie pierścienia kołowego o średnicy zewnętrznej i wewnętrznej d (rys. 17.5) można wyznaczyć jako różnicę pomiędzy odpowiednimi momentami bezwładności okręgu zewnętrznego i wewnętrznego.
Biegunowy moment bezwładności pierścienia na podstawie wzoru (21.5)
lub, jeśli wyznaczymy
Podobnie dla osiowych momentów bezwładności pierścienia
Moment bezwładności i moment oporu
Przy określaniu przekroju konstrukcji budowlanych często konieczna jest znajomość momentu bezwładności i momentu oporu rozpatrywanego przekroju konstrukcji. Czym jest moment oporu i jaki ma on związek z momentem bezwładności opisano osobno. Ponadto w przypadku konstrukcji ściśliwych należy również znać wartość promienia bezwładności. Moment oporu i moment bezwładności, a czasem promień bezwładności dla większości przekrojów o prostym kształcie geometrycznym można wyznaczyć za pomocą dobrze znanych wzorów:
Tabela 1. Kształty przekrojów, pola przekrojów, momenty bezwładności i momenty oporu dla konstrukcji o dość prostych kształtach geometrycznych.
Zwykle te wzory są wystarczające do większości obliczeń, ale są różne przypadki i przekrój konstrukcji może nie mieć tak prostego kształtu geometrycznego lub położenia osi, wokół których potrzebny jest moment bezwładności lub moment oporu do ustalenia mogą nie być takie same, wówczas można skorzystać z następujących wzorów:
Tabela 2. Kształty przekrojów, pola przekrojów, momenty bezwładności i momenty oporu dla konstrukcji o bardziej złożonych kształtach geometrycznych

Jak widać z tabeli 2, obliczenie momentu bezwładności i momentu oporu dla nierównych kątów jest dość trudne, ale nie ma takiej potrzeby. W ofercie znajdują się asortymenty do kątowników walcowanych z kołnierzami nierównymi i równymi, a także do ceowników, dwuteowników i rur profilowanych. W asortymenty Dla każdego profilu podane są wartości momentu bezwładności i momentu oporu.
Tabela 3. Zmiany momentów bezwładności i momentów oporu w zależności od położenia osi.

Do obliczenia elementów dachu nachylonego mogą być potrzebne wzory z tabeli 3.
Byłoby miło wyjaśnić na jasnym przykładzie osobom szczególnie uzdolnionym, takim jak ja, czym jest moment bezwładności i do czego się go używa. Na wyspecjalizowanych stronach wszystko jest w jakiś sposób bardzo zagmatwane, ale Doc ma wyraźny talent do przekazywania informacji, może nie najbardziej skomplikowanych, ale bardzo kompetentnych i zrozumiałych
W zasadzie, czym jest moment bezwładności i skąd się bierze, wyjaśniono wystarczająco szczegółowo w artykule „Podstawy wytrzymałości, wzory obliczeniowe”, tutaj tylko powtórzę: „W to moment oporu przekroju poprzecznego belka, innymi słowy, powierzchnia ściśniętej lub rozciąganej części przekroju belki, pomnożona przez ramię działania siły wypadkowej.” Do obliczeń wytrzymałościowych konstrukcji należy znać moment oporu, tj. według naprężeń ostatecznych. Aby określić kąty obrotu przekroju poprzecznego i ugięcie (przemieszczenie) środka ciężkości przekroju poprzecznego, należy znać moment bezwładności, ponieważ maksymalne odkształcenia występują w najwyższych i najniższych warstwach konstrukcji zginanej, moment bezwładność można wyznaczyć mnożąc moment oporu przez odległość środka ciężkości przekrojów od warstwy górnej lub dolnej, zatem dla przekrojów prostokątnych I=Wh/2. Przy wyznaczaniu momentu bezwładności przekrojów o skomplikowanych kształtach geometrycznych najpierw dzieli się figurę złożoną na proste, następnie określa się pola przekrojów tych figur i momenty bezwładności najprostszych figur, następnie pola najprostszych liczby mnoży się przez kwadrat odległości od ogólnego środka ciężkości przekroju do środka ciężkości najprostszej figury. Moment bezwładności najprostszej figury w przekroju złożonym jest równy momentowi bezwładności figury + kwadrat odległości pomnożony przez pole. Następnie sumuje się uzyskane momenty bezwładności i otrzymuje moment bezwładności przekroju zespolonego. Ale to są najbardziej uproszczone sformułowania (choć zgadzam się, że nadal wygląda to dość skomplikowanie).
Moment bezwładności i moment oporu – dr Lom
Przy określaniu przekroju konstrukcji budowlanych często konieczna jest znajomość momentu bezwładności i momentu oporu przekroju poprzecznego konstrukcji. Moment oporu i moment energii dla zdecydowanej większości przekrojów o prostym kształcie geometrycznym można wyznaczyć za pomocą znanych od dawna wzorów
Rozdział 5. MOMENTY BEZWŁADNOŚCI PRZEKRÓJÓW PŁASKICH
Każdy przekrój płaski charakteryzuje się szeregiem cech geometrycznych: powierzchnią, współrzędnymi środka ciężkości, momentem statycznym, momentem bezwładności itp.
Momenty statyczne względem osi X I y są równe:
Momenty statyczne są zwykle wyrażane w centymetrach sześciennych lub metrach i mogą mieć zarówno wartości dodatnie, jak i wartości ujemne. Nazywa się oś, wokół której moment statyczny wynosi zero centralny. Nazywa się punkt przecięcia osi środkowych środek ciężkości sekcji. Wzory do wyznaczania współrzędnych środka ciężkości x w I y c sekcja złożona, podzielona na proste elementy, dla których znane są obszary A ja oraz położenie środka ciężkości xci I i ci,mieć formę
Wielkość momentu bezwładności charakteryzuje odporność pręta na odkształcenia (skręcanie, zginanie) w zależności od wielkości i kształtu przekroju. Istnieją momenty bezwładności:
– osiowy, określony całkami postaci
Osiowe i biegunowe momenty bezwładności są zawsze dodatnie i nie
iść do zera. Biegunowy moment bezwładności IP równy sumie osiowych momentów bezwładności ja x I I względem dowolnej pary wzajemnie prostopadłych osi X I Na:
Odśrodkowy moment bezwładności może być dodatni, ujemny lub zerowy. Wymiar momentów bezwładności wynosi cm 4 lub m 4. Wzory do wyznaczania momentów bezwładności prostych przekrojów względem osi środkowych podano w podręcznikach. Przy obliczaniu momentów bezwładności przekrojów złożonych często stosuje się wzory na przejście od osi środkowych prostych przekrojów do innych osi równoległych do osi środkowych.
gdzie są momenty bezwładności prostych przekrojów względem osi środkowych;
m, rz– odległości między osiami (rys. 18).

Ryż. 18. Aby wyznaczyć momenty bezwładności względem osi,
Ważne są główne osie środkowe przekroju. Głównymi osiami środkowymi są dwie wzajemnie prostopadłe osie przechodzące przez środek ciężkości przekroju, względem których odśrodkowy moment bezwładności wynosi zero, a osiowe momenty bezwładności mają wartości ekstremalne. Wskazano główne momenty bezwładności ja ty(maks.) i IV(min) i są określone wzorem
Położenie głównych osi określa kąt α, który wynika ze wzoru
Kąt α jest odłożony od osi z dużym, innym niż główny momentem bezwładności; wartość dodatnia- w kierunku przeciwnym do ruchu wskazówek zegara.
Jeśli przekrój ma oś symetrii, to ta oś jest główną. Druga oś główna jest prostopadła do osi symetrii. W praktyce często stosuje się profile złożone z kilku profili walcowanych (dwuteownik, ceownik, kątownik). Charakterystyki geometryczne tych profili podano w tabelach asortymentowych. W przypadku kątów nierównych i równobocznych odśrodkowy moment bezwładności względem osi środkowych równoległych do kołnierzy określa się ze wzoru
Zwróć uwagę na oznaczenie głównych osi środkowych w tabeli asortymentowej narożników. Podpisać ja xy dla narożnika zależy od jego położenia w przekroju. Rysunek 19 pokazuje możliwe położenia narożnika w przekroju i pokazuje znaki ja xy.
Ryż. 19. Możliwe położenia narożnika w przekroju
Definiować Iu, Iv oraz położenie głównych osi środkowych przekroju
Złożona sekcja składa się z dwóch walcowanych profili. Wyciąg z tabel asortymentowych (załącznik 5) pokazano na ryc. 21.
Jako pomocnicze przyjmiemy osie przechodzące wzdłuż zewnętrznego
boki kanału (oś xB, i B, patrz rys. 20).Współrzędne środka ciężkości przekroju:
(oblicz sam).

Ryż. 20. Położenie głównych środkowych osi bezwładności
U I V sekcja złożona
Jako pomocnicze można było wybrać np. osie środkowe kanału. Wtedy ilość obliczeń zostanie nieco zmniejszona.
Osiowe momenty bezwładności:
Należy pamiętać, że w przekroju znajduje się nierówny kąt
inaczej niż pokazano w tabeli asortymentowej. Oblicz wartość samodzielnie.

Nr 24 180 x 110 x 12
Ryż. 21. Wartości cech geometrycznych profili walcowanych:
A– kanał nr 24; B– narożnik nierówny 180 x 110 x 12
Odśrodkowe momenty bezwładności:
– dla kanału (są osie symetrii);
- do rogu,
znak minus – ze względu na położenie narożnika w przekroju;
– dla całego odcinka:
Postępuj zgodnie z przeznaczeniem znaków N I M. Z środkowych osi kanału przechodzimy do wspólnych środkowych osi przekroju, a zatem + m 2
Główne momenty bezwładności przekroju:
Położenie głównych osi środkowych przekroju:
; α = 55 o 48 ′;
Sprawdzenie poprawności obliczenia wielkości ja ty, IV a α jest obliczane ze wzoru
Kąt α dla tego wzoru mierzony jest od osi ty.
Rozważany przekrój ma największą odporność na zginanie względem osi ty i najmniejszy – względem osi w.
Rozdział 5. MOMENTY BEZWŁADNOŚCI PRZEKRÓJÓW PŁASKICH Każdy przekrój płaski charakteryzuje się szeregiem cech geometrycznych: powierzchnią, współrzędnymi środka ciężkości, momentem statycznym, momentem bezwładności i
Wyróżnia się następujące typy momentów bezwładności przekrojów: osiowe; odśrodkowy; polarny; centralny i główny moment bezwładności.
Odśrodkowe momenty bezwładności względne przekroje poprzeczne Na I z nazywa się całką postaci Suma osiowych momentów bezwładności przekroju względem dwóch osi współrzędnych jest równa biegunowemu momentowi bezwładności względem początku:Wymiar określonych rodzajów momentów bezwładności przekroju (długość 4), tj. m 4 lub cm 4.
Osiowe i biegunowe momenty bezwładności przekroju są wielkościami dodatnimi; odśrodkowy moment bezwładności może być dodatni, ujemny i równy zeru (dla niektórych osi będących osią symetrii).
Istnieją zależności dotyczące momentów bezwładności podczas równoległego przesunięcia i obrotu osi współrzędnych.
 Rysunek 5.4 – Równoległe przesunięcie i obrót osi współrzędnych dla dowolnego przekroju belki
Rysunek 5.4 – Równoległe przesunięcie i obrót osi współrzędnych dla dowolnego przekroju belki
Jeżeli znane są momenty bezwładności przekroju Iz, Iu, Izu względem osi z I Na, a następnie momenty bezwładności względem obróconych osi z 1 I o 1, pod kątem α względem pierwotnych osi (ryc. 5.4, B) określa się za pomocą wzorów:

Z koncepcją główne momenty bezwładności powiązać położenie głównych osi bezwładności. Główne osie bezwładności nazywane są dwiema wzajemnie prostopadłymi osiami, względem których odśrodkowy moment bezwładności jest równy zeru, a momenty osiowe przyjmują wartości ekstremalne (maksymalne i minimalne).
Jeśli główne osie przechodzą przez środek ciężkości figury, wówczas nazywa się je główne centralne osie bezwładności.
Położenie głównych osi bezwładności wyznacza się z następujących zależności:Obliczając wytrzymałość elementów konstrukcyjnych, wykorzystują koncepcję takiej cechy geometrycznej jak moduł przekroju.
Rozważmy na przykład przekrój belki (ryc. 5.5).

Rysunek 5.5 – Przykład przekroju belki
Odległość najdalszego t. A od środka ciężkości sekcji, tj. około istotne godz. 1, i odległość t. W- Poprzez godz. 2.
| (5.16) |
Praktycznym znaczeniem w obliczeniach wytrzymałościowych jest najmniejszy moment oporu przekroju W min, odpowiadający najdalszemu t. A od środka ciężkości sekcji h 1 = y maks.
Wymiary elementów oporowych (długość 3), tj. m 3, cm 3.
Tabela 5.1 – Wartości momentów bezwładności i momentów oporu najprostszych przekrojów względem osi środkowych
| Rodzaje nazw sekcji | Momenty bezwładności | Momenty oporu | ||
| Prostokąt |  | |||
| Koło |  | |
kontynuacja tabeli 5.1
Wprowadźmy kartezjański prostokątny układ współrzędnych O xy . Rozważmy dowolny przekrój (obszar zamknięty) o polu A w płaszczyźnie współrzędnych (rys. 1).
Momenty statyczne

Punkt C ze współrzędnymi (x C , y C)

zwany środek ciężkości sekcji.
Jeżeli osie współrzędnych przechodzą przez środek ciężkości przekroju, wówczas momenty statyczne przekroju są równe zeru:
Osiowe momenty bezwładności przekroje względem osi x i y nazywane są całkami postaci:

Biegunowy moment bezwładności przekrój ze względu na początek współrzędnych nazywa się całką postaci:
![]()
Odśrodkowy moment bezwładności Sekcję nazywa się całką postaci:

Główne osie bezwładności przekroju wywoływane są dwie wzajemnie prostopadłe osie, względem których I xy = 0. Jeżeli jedna z wzajemnie prostopadłych osi jest osią symetrii przekroju, to I xy =0 i dlatego te osie są głównymi. Nazywa się główne osie przechodzące przez środek ciężkości przekroju główne środkowe osie bezwładności przekroju
2. Twierdzenie Steinera-Huygensa o równoległym przesunięciu osi
Twierdzenie Steinera-Huygensa (twierdzenie Steinera).
Osiowy moment bezwładności przekroju I względem dowolnej stałej osi x jest równy sumie osiowego momentu bezwładności tego przekroju I z względną osią x * równoległą do niej, przechodzącą przez środek masy przekroju, oraz iloczyn pola przekroju poprzecznego A przez kwadrat odległości d między dwiema osiami.
![]()

Jeżeli znane są momenty bezwładności I x i I y względem osi x i y, to względem osi ν i u obróconych o kąt α osiowy i odśrodkowy moment bezwładności oblicza się ze wzorów:

Z powyższych wzorów jasno wynika, że
![]()
Te. suma osiowych momentów bezwładności przy obrocie wzajemnie prostopadłych osi nie zmienia się, tj. osie u i v, względem których odśrodkowy moment bezwładności przekroju wynosi zero, a osiowe momenty bezwładności I u i I v mają ekstremalne wartości max lub min nazywane są głównymi osiami przekroju. Nazywa się główne osie przechodzące przez środek ciężkości przekroju główne osie środkowe przekroju. W przypadku przekrojów symetrycznych ich osie symetrii są zawsze głównymi osiami środkowymi. Położenie głównych osi przekroju względem pozostałych osi określa się za pomocą zależności:

gdzie α 0 jest kątem, o który należy obrócić osie x i y, aby stały się głównymi (zwykle kąt dodatni ustawia się w kierunku przeciwnym do ruchu wskazówek zegara, kąt ujemny ustawia się zgodnie z ruchem wskazówek zegara). Nazywa się osiowe momenty bezwładności względem głównych osi główne momenty bezwładności:
Znak plus przed drugim członem odnosi się do maksymalnego momentu bezwładności, znak minus do minimum.
Osiowy (lub równikowy) moment bezwładności przekroju względem osi jest sumą iloczynów nieskończenie małych obszarów () przejętych na całym obszarze S, pomnożonych przez kwadraty odległości od nich do osi obrotu:
Biegunowy moment bezwładności przekroju jest identyfikowany względem określonego punktu (bieguna). Biegunowy moment bezwładności przekroju jest sumą iloczynów nieskończenie małych obszarów (), przejętych przez jego powierzchnię S, pomnożonych przez odległość tych obszarów od bieguna, wziętą do kwadratu:
![]()
Gdzie ![]() W przypadku osi prostopadłych, względem których znane są momenty bezwładności, biegunowy moment bezwładności względem punktu przecięcia tych osi można łatwo wyznaczyć w wyniku zsumowania osiowych momentów bezwładności:
W przypadku osi prostopadłych, względem których znane są momenty bezwładności, biegunowy moment bezwładności względem punktu przecięcia tych osi można łatwo wyznaczyć w wyniku zsumowania osiowych momentów bezwładności:
Czasami uwzględnia się odśrodkowy moment bezwładności przekroju, który określa się jako
![]()
wyrażenie (4) mówi, że odśrodkowy moment bezwładności przekroju względem wzajemnie prostopadłych osi jest sumą iloczynów obszarów elementarnych () przez odległości od nich do rozpatrywanych osi, na całym obszarze S.
Osiowe i biegunowe momenty bezwładności są zawsze dodatnie. Odśrodkowe momenty bezwładności sekcji mogą być większe lub mniejsze od zera. Odśrodkowy moment bezwładności przekroju względem osi, z których jedna lub obie pokrywają się z jego osiami symetrii, jest równy zero.
Osiowy moment bezwładności złożonego przekroju względem osi jest równy sumie osiowych momentów bezwładności części tego przekroju względem tej samej osi. Odśrodkowy moment bezwładności złożonego przekroju względem dwóch osi prostopadłych do siebie można obliczyć jako sumę odśrodkowych momentów bezwładności części względem tych samych osi. Biegunowy moment bezwładności ma tę samą właściwość. Nie jest jednak możliwe dodanie momentów bezwładności występujących względem różnych osi i punktów.
Przykłady rozwiązywania problemów
PRZYKŁAD 1
| Ćwiczenia | Wyznaczyć osiowy moment bezwładności przekroju trójkąta równoramiennego względem osi przechodzącej przez jego podstawę (rys. 1). Długość podstawy trójkąta wynosi , jego wysokość wynosi . |
| Rozwiązanie | Zróbmy rysunek. Wybierzmy prostokątny obszar elementarny na przekroju trójkątnym (patrz ryc. 1). Znajduje się w pewnej odległości od osi obrotu, długość jednego boku wynosi , drugiego boku . Z rys. 1 wynika, że:
Następnie znajdujemy obszar przydzielonej witryny jako: Moment bezwładności przekroju trójkątnego względem osi Z jest z definicji równy: |
| Odpowiedź |
PRZYKŁAD 2
| Ćwiczenia | Znajdź biegunowy moment bezwładności przekroju w kształcie okręgu względem jego środka. Promień okręgu wynosi . |
| Rozwiązanie | Najpierw znajdźmy osiowy moment bezwładności okręgu względem osi OZ (patrz ryc. 2). Wybierzmy elementarny obszar na okręgu w postaci prostokąta o bokach i . Z ryc. 2 następuje |