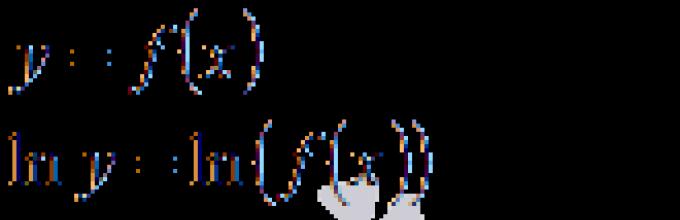Zachowanie Twojej prywatności jest dla nas ważne. Z tego powodu opracowaliśmy Politykę prywatności, która opisuje, w jaki sposób wykorzystujemy i przechowujemy Twoje dane. Zapoznaj się z naszymi praktykami dotyczącymi prywatności i daj nam znać, jeśli masz jakiekolwiek pytania.
Gromadzenie i wykorzystywanie danych osobowych
Dane osobowe to dane, które można wykorzystać do identyfikacji konkretnej osoby lub skontaktowania się z nią.
Możesz zostać poproszony o podanie swoich danych osobowych w dowolnym momencie kontaktu z nami.
Poniżej znajduje się kilka przykładów rodzajów danych osobowych, które możemy gromadzić i sposobu, w jaki możemy je wykorzystywać.
Jakie dane osobowe zbieramy:
- Kiedy składasz wniosek na stronie, możemy zbierać różne informacje, w tym Twoje imię i nazwisko, numer telefonu, adres E-mail itp.
Jak wykorzystujemy Twoje dane osobowe:
- Zebrane przez nas informacje osobiste pozwala nam kontaktować się z Tobą i informować Cię o wyjątkowych ofertach, promocjach i innych wydarzeniach oraz nadchodzących wydarzeniach.
- Od czasu do czasu możemy wykorzystywać Twoje dane osobowe do wysyłania ważnych powiadomień i komunikatów.
- Możemy również wykorzystywać dane osobowe do celów wewnętrznych, takich jak przeprowadzanie audytów, analiza danych i różnych badań w celu ulepszenia świadczonych przez nas usług i przedstawienia rekomendacji dotyczących naszych usług.
- Jeśli bierzesz udział w losowaniu nagród, konkursie lub podobnej promocji, możemy wykorzystać podane przez Ciebie informacje w celu administrowania takimi programami.
Ujawnianie informacji osobom trzecim
Nie udostępniamy otrzymanych od Państwa informacji osobom trzecim.
Wyjątki:
- Jeżeli jest to konieczne – zgodnie z prawem, procedurą sądową, postępowaniem sądowym i/lub na podstawie żądań publicznych lub żądań od agencje rządowe na terytorium Federacji Rosyjskiej – ujawnij swoje dane osobowe. Możemy również ujawnić informacje o Tobie, jeśli uznamy, że takie ujawnienie jest konieczne lub odpowiednie ze względów bezpieczeństwa, egzekwowania prawa lub innych celów ważnych dla społeczeństwa.
- W przypadku reorganizacji, fuzji lub sprzedaży możemy przekazać zebrane dane osobowe odpowiedniej następczej stronie trzeciej.
Ochrona danych osobowych
Podejmujemy środki ostrożności – w tym administracyjne, techniczne i fizyczne – aby chronić Twoje dane osobowe przed utratą, kradzieżą i niewłaściwym wykorzystaniem, a także nieuprawnionym dostępem, ujawnieniem, zmianą i zniszczeniem.
Szanowanie Twojej prywatności na poziomie firmy
Aby zapewnić bezpieczeństwo Twoich danych osobowych, przekazujemy naszym pracownikom standardy dotyczące prywatności i bezpieczeństwa oraz rygorystycznie egzekwujemy praktyki dotyczące prywatności.
Pozwalać
(1)
jest różniczkowalną funkcją zmiennej x. Najpierw przyjrzymy się temu pod kątem zbioru wartości x, dla których przyjmuje się y wartości dodatnie: . Poniżej pokażemy, że wszystkie uzyskane wyniki mają zastosowanie również dla wartości ujemnych .
W niektórych przypadkach, aby znaleźć pochodną funkcji (1), wygodnie jest ją wstępnie logarytmować
,
i następnie oblicz pochodną. Następnie, zgodnie z zasadą różniczkowania funkcji zespolonej,
.
Stąd
(2)
.
Pochodna logarytmu funkcji nazywana jest pochodną logarytmiczną:
.
Logarytmiczna pochodna funkcji y = k(x) jest pochodną naturalny logarytm ta funkcja: (lnf(x))′.
Przypadek ujemnych wartości y
Rozważmy teraz przypadek, w którym zmienna może przyjmować zarówno wartości dodatnie, jak i ujemne. W tym przypadku weź logarytm modułu i znajdź jego pochodną:
.
Stąd
(3)
.
Oznacza to, że w ogólnym przypadku musisz znaleźć pochodną logarytmu modułu funkcji.
Porównując (2) i (3) mamy:
.
Oznacza to, że formalny wynik obliczenia pochodnej logarytmicznej nie zależy od tego, czy przyjęliśmy modulo, czy nie. Dlatego też obliczając pochodną logarytmiczną nie musimy się martwić, jaki znak ma dana funkcja.
Sytuację tę można wyjaśnić za pomocą liczb zespolonych. Niech dla niektórych wartości x będzie ujemny: . Jeśli tylko rozważymy liczby rzeczywiste, to funkcja nie jest zdefiniowana. Jeśli jednak wprowadzimy pod uwagę Liczby zespolone, wówczas otrzymujemy:
.
Oznacza to, że funkcje i różnią się stałą zespoloną:
.
Zatem pochodna stałej wynosi zero
.
Własność pochodnej logarytmicznej
Z takich rozważań wynika, że pochodna logarytmiczna nie zmieni się, jeśli pomnożysz funkcję przez dowolną stałą :
.
Rzeczywiście, używając właściwości logarytmu, formuły suma pochodna I pochodna stałej, mamy:
.
Zastosowanie pochodnej logarytmicznej
Wygodnie jest używać pochodnej logarytmicznej w przypadkach, gdy pierwotna funkcja składa się z iloczynu potęgi lub funkcje wykładnicze. W tym przypadku operacja logarytmiczna zamienia iloczyn funkcji na ich sumę. Upraszcza to obliczenie pochodnej.
Przykład 1
Znajdź pochodną funkcji:
.
Rozwiązanie
Logarytmujemy pierwotną funkcję:
.
Różniczkujemy ze względu na zmienną x.
W tabeli instrumentów pochodnych znajdujemy:
.
Stosujemy zasadę różniczkowania funkcji zespolonych.
;
;
;
;
(A1.1) .
Pomnożyć przez:
.
Zatem znaleźliśmy pochodną logarytmiczną:
.
Stąd znajdujemy pochodną pierwotnej funkcji:
.
Notatka
Jeżeli chcemy posługiwać się wyłącznie liczbami rzeczywistymi, to powinniśmy przyjąć logarytm modułu pierwotnej funkcji:
.
Następnie
;
.
I otrzymaliśmy wzór (A1.1). Dlatego wynik się nie zmienił.
Odpowiedź
Przykład 2
Korzystając z pochodnej logarytmicznej, znajdź pochodną funkcji
.
Rozwiązanie
Weźmy logarytmy:
(A2.1) .
Różniczkuj ze względu na zmienną x:
;
;
;
;
;
.
Pomnożyć przez:
.
Stąd otrzymujemy pochodną logarytmiczną:
.
Pochodna pierwotnej funkcji:
.
Notatka
Tutaj oryginalna funkcja jest nieujemna: . Jest ona zdefiniowana na godz. Jeżeli nie założymy, że logarytm można zdefiniować dla ujemnych wartości argumentu, wówczas wzór (A2.1) należy zapisać w następujący sposób:
.
Ponieważ
I
,
nie będzie to miało wpływu na wynik końcowy.
Odpowiedź
Przykład 3
Znajdź pochodną
.
Rozwiązanie
Różniczkowanie wykonujemy za pomocą pochodnej logarytmicznej. Weźmy logarytm, biorąc pod uwagę, że:
(A3.1) .
Różniczkując otrzymujemy pochodną logarytmiczną.
;
;
;
(A3.2) .
Od tego czasu
.
Notatka
Obliczenia przeprowadźmy bez założenia, że logarytm można zdefiniować dla ujemnych wartości argumentu. Aby to zrobić, weź logarytm modułu pierwotnej funkcji:
.
Wtedy zamiast (A3.1) mamy:
;
.
Porównując z (A3.2) widzimy, że wynik się nie zmienił.
Przy różnicowaniu ma charakter orientacyjny funkcja zasilania lub uciążliwych wyrażeń ułamkowych, wygodnie jest użyć pochodnej logarytmicznej. W tym artykule przyjrzymy się przykładom jego zastosowania wraz ze szczegółowymi rozwiązaniami.
Dalsza prezentacja zakłada umiejętność korzystania z tabeli pochodnych, zasad różniczkowania oraz znajomość wzoru na pochodną funkcji zespolonej.
Wyprowadzenie wzoru na pochodną logarytmiczną.
Najpierw sprowadzamy logarytmy do podstawy e, upraszczamy postać funkcji, korzystając z właściwości logarytmu, a następnie znajdujemy pochodną domyślnie określonej funkcji: 
Na przykład znajdźmy pochodną wykładniczej funkcji potęgowej x do potęgi x.
Branie logarytmów daje . Zgodnie z właściwościami logarytmu. Różniczkowanie obu stron równości prowadzi do wyniku: 
Odpowiedź: ![]() .
.
Ten sam przykład można rozwiązać bez użycia pochodnej logarytmicznej. Można przeprowadzić pewne przekształcenia i przejść od różniczkowania wykładniczej funkcji potęgowej do znajdowania pochodnej funkcji zespolonej: 
Przykład.
Znajdź pochodną funkcji  .
.
Rozwiązanie.
W tym przykładzie funkcja  jest ułamkiem, a jego pochodną można znaleźć, korzystając z zasad różniczkowania. Ale ze względu na uciążliwość wyrażenia będzie to wymagało wielu przekształceń. W takich przypadkach rozsądniej jest zastosować wzór na pochodną logarytmiczną
jest ułamkiem, a jego pochodną można znaleźć, korzystając z zasad różniczkowania. Ale ze względu na uciążliwość wyrażenia będzie to wymagało wielu przekształceń. W takich przypadkach rozsądniej jest zastosować wzór na pochodną logarytmiczną ![]() . Dlaczego? Teraz zrozumiesz.
. Dlaczego? Teraz zrozumiesz.
Znajdźmy to najpierw. W przekształceniach będziemy korzystać z właściwości logarytmu (logarytm ułamka jest równy różnicy logarytmów, a logarytm iloczynu jest równy sumie logarytmów, a stopień wyrażenia pod znakiem logarytmu może wynosić wyjęty jako współczynnik przed logarytmem): 
Te przemiany doprowadziły nas do dość proste wyrażenie, którego pochodną można łatwo znaleźć: 
Otrzymany wynik podstawiamy do wzoru na pochodną logarytmiczną i otrzymujemy odpowiedź:
Aby skonsolidować materiał, podamy jeszcze kilka przykładów bez szczegółowych wyjaśnień.
Przykład.
Znajdź pochodną wykładniczej funkcji potęgowej ![]()
Czujesz, że do egzaminu zostało jeszcze dużo czasu? Czy to jest miesiąc? Dwa? Rok? Praktyka pokazuje, że uczeń najlepiej radzi sobie z egzaminem, jeśli wcześniej zacznie się do niego przygotowywać. Jest ich wiele trudne zadania, które utrudniają uczniom i przyszłym kandydatom uzyskanie najwyższych wyników. Trzeba nauczyć się pokonywać te przeszkody, a poza tym nie jest to trudne. Musisz zrozumieć zasadę pracy z różnymi zadaniami z biletów. Wtedy nie będzie problemów z nowymi.
Logarytmy na pierwszy rzut oka wydają się niezwykle złożone, ale po szczegółowej analizie sytuacja staje się znacznie prostsza. Jeśli chcesz przystąpić do egzaminu Unified State Exam najwyższa ocena, powinieneś zrozumieć daną koncepcję, co proponujemy zrobić w tym artykule.
Najpierw oddzielmy te definicje. Co to jest logarytm (log)? Jest to wskaźnik potęgi, do której należy podnieść bazę, aby uzyskać określoną liczbę. Jeśli nie jest to jasne, spójrzmy na elementarny przykład.
W takim przypadku podstawę na dole należy podnieść do drugiej potęgi, aby uzyskać liczbę 4.
Przyjrzyjmy się teraz drugiej koncepcji. Pochodna funkcji w dowolnej postaci to pojęcie charakteryzujące zmianę funkcji w danym punkcie. Jednak to program szkolny, a jeśli macie problemy z tymi pojęciami indywidualnie, warto powtórzyć temat.

Pochodna logarytmu
W Zadania z egzaminu jednolitego stanu Jako przykłady można podać kilka problemów w tym temacie. Na początek najprostsza pochodna logarytmiczna. Należy znaleźć pochodną poniższej funkcji.

Musimy znaleźć następną pochodną

Istnieje specjalna formuła.

W tym przypadku x=u, log3x=v. Podstawiamy wartości z naszej funkcji do wzoru.

Pochodna x będzie równa jeden. Logarytm jest nieco trudniejszy. Ale zrozumiesz tę zasadę, jeśli po prostu zastąpisz wartości. Przypomnijmy, że pochodna lg x jest pochodną logarytm dziesiętny, a pochodna ln x jest pochodną logarytmu naturalnego (o podstawie e).

Teraz wystarczy podłączyć uzyskane wartości do wzoru. Spróbuj sam, wtedy sprawdzimy odpowiedź.

W czym może być dla niektórych problem? Wprowadziliśmy pojęcie logarytmu naturalnego. Porozmawiajmy o tym, a jednocześnie zastanówmy się, jak rozwiązać z tym problemy. Nie zobaczysz niczego skomplikowanego, zwłaszcza gdy zrozumiesz zasadę jego działania. Należy się do tego przyzwyczaić, ponieważ jest często używany w matematyce (w wyższych instytucje edukacyjne zwłaszcza).
Pochodna logarytmu naturalnego
W swej istocie jest to pochodna logarytmu o podstawie e (tzn Liczba niewymierna, czyli około 2,7). W rzeczywistości ln jest bardzo proste, dlatego jest często używane w matematyce. Właściwie rozwiązanie problemu z nim również nie będzie problemem. Warto pamiętać, że pochodna logarytmu naturalnego o podstawie e będzie równa jedności podzielonej przez x. Rozwiązanie poniższego przykładu będzie najbardziej odkrywcze.

Wyobraźmy sobie to jako złożona funkcja, składający się z dwóch prostych.
 Wystarczy dokonać konwersji
Wystarczy dokonać konwersji

Szukamy pochodnej u po x