Na tej stronie znajdziesz wszystkie podstawowe wzory trygonometryczne, które pomogą Ci rozwiązać wiele ćwiczeń, znacznie upraszczając samo wyrażenie.
Wzory trygonometryczne - równania matematyczne dla funkcje trygonometryczne, które są wykonywane dla wszystkich prawidłowych wartości argumentów.
Wzory określają zależności pomiędzy podstawowymi funkcjami trygonometrycznymi - sinusem, cosinusem, tangensem, cotangensem.
Sinus kąta jest współrzędną y punktu (rzędnej). okrąg jednostkowy. Cosinus kąta jest współrzędną x punktu (odciętą).
Tangens i cotangens to odpowiednio stosunki sinusa do cosinusa i odwrotnie.
`sin\\alfa,\cos\\alfa`
`tg \\alpha=\frac(sin\ \alpha)(cos \\alpha),` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`ctg \ \alpha=\frac(cos\ \alpha)(sin\ \alpha),` ` \alpha\ne\pi+\pi n, \ n \in Z`
I dwa, które są używane rzadziej - sieczna, cosecans. Reprezentują one stosunek 1 do cosinusa i sinusa.
`sec \\alpha=\frac(1)(cos\ \alpha),` ` \alpha\ne\frac\pi2+\pi n,\ n \in Z`
`cosec \ \alpha=\frac(1)(sin \ \alpha),` ` \alpha\ne\pi+\pi n,\ n \in Z`
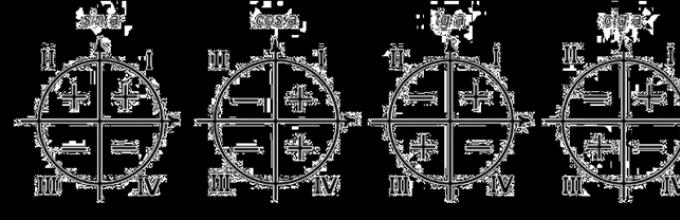
Z definicji funkcji trygonometrycznych jasno wynika, jakie znaki mają w każdej ćwiartce. Znak funkcji zależy tylko od tego, w której ćwiartce znajduje się argument.

Przy zmianie znaku argumentu z „+” na „-” jedynie funkcja cosinus nie zmienia swojej wartości. To się nazywa równo. Jego wykres jest symetryczny względem osi rzędnych.
Pozostałe funkcje (sinus, tangens, cotangens) są nieparzyste. Przy zmianie znaku argumentu z „+” na „-” ich wartość również zmienia się na ujemną. Ich wykresy są symetryczne względem początku.
`sin(-\alfa)=-sin \\alfa`
`cos(-\alfa)=cos\\alfa`
`tg(-\alfa)=-tg\\alfa`
`ctg(-\alfa)=-ctg\\alfa`
Podstawowe tożsamości trygonometryczne
Podstawowe tożsamości trygonometryczne to wzory, które ustanawiają związek między funkcjami trygonometrycznymi jednego kąta (`sin\\alpha,\cos\\alpha,\tg\\alpha,\ctg\\alpha`) i które pozwalają znaleźć wartość każda z tych funkcji poprzez dowolną znaną inną.
`sin^2 \alfa+cos^2 \alfa=1`
`tg \ \alpha \cdot ctg \ \alpha=1, \\alpha\ne\frac(\pi n) 2, \n \in Z`
`1+tg^2 \alpha=\frac 1(cos^2 \alpha)=sec^2 \alpha,` ` \alpha\ne\frac\pi2+\pi n,\n \in Z`
`1+ctg^2 \alpha=\frac 1(sin^2 \alpha)=cosec^2 \alpha,` ` \alpha\ne\pi n, \n \in Z`
Wzory na sumę i różnicę kątów funkcji trygonometrycznych
Wzory na dodawanie i odejmowanie argumentów wyrażają funkcje trygonometryczne sumy lub różnicy dwóch kątów w postaci funkcji trygonometrycznych tych kątów.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alfa+\beta)=\frac(tg \alfa+tg \\beta)(1-tg \\alfa\ tg \\beta)`
`tg(\alfa-\beta)=\frac(tg \alpha-tg \\beta)(1+tg \\alpha \ tg \\beta)`
`ctg(\alpha+\beta)=\frac(ctg \\alpha \ ctg \\beta-1)(ctg \\beta+ctg \\alpha)`
`ctg(\alpha-\beta)=\frac(ctg \\alpha\ ctg \\beta+1)(ctg \\beta-ctg \\alpha)`
Wzory na kąt podwójny
`sin \ 2\alpha=2 \ sin \alpha \cos \ \alpha=` `\frac (2 \ tg \ \alpha)(1+tg^2 \alpha)=\frac (2 \ ctg \ \alpha )(1+ctg^2 \alfa)=` `\frac 2(tg \\alfa+ctg \\alfa)`
`cos\2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \sin^2 \alpha=2 \cos^2 \alpha-1=` `\frac(1-tg^ 2\alpha)(1+tg^2\alpha)=\frac(ctg^2\alpha-1)(ctg^2\alpha+1)=` `\frac(ctg \\alpha-tg \\alpha) (ctg \ \alfa+tg \ \alfa)`
`tg \ 2\alpha=\frac(2 \ tg \ \alpha)(1-tg^2 \alpha)=` `\frac(2 \ ctg \\alpha)(ctg^2 \alpha-1)=` `\frac 2(\ctg \\alfa-tg \\alfa)`
`ctg \ 2\alpha=\frac(ctg^2 \alpha-1)(2 \ctg \ \alpha)=` `\frac (\ctg \ \alpha-tg \ \alpha)2`
Wzory na kąt potrójny
`sin \ 3\alfa=3 \ sin \ \alfa-4sin^3 \alfa`
`cos \ 3\alfa=4cos^3 \alfa-3 \ cos \\alfa`
`tg \ 3\alpha=\frac(3 \ tg \ \alpha-tg^3 \alfa)(1-3 \ tg^2 \alfa)`
`ctg \ 3\alpha=\frac(ctg^3 \alpha-3 \ ctg \ \alpha)(3 \ ctg^2 \alpha-1)`
Wzory na półkąty
`sin \ \frac \alfa 2=\pm \sqrt(\frac (1-cos \\alfa)2)`
`cos \ \frac \alfa 2=\pm \sqrt(\frac (1+cos \ \alfa)2)`
`tg \ \frac \alpha 2=\pm \sqrt(\frac (1-cos \ \alpha)(1+cos \ \alpha))=` `\frac (sin \ \alpha)(1+cos \ \ alfa)=\frac (1-cos \alfa)(sin \\alfa)`
`ctg \ \frac \alpha 2=\pm \sqrt(\frac (1+cos \ \alpha)(1-cos \ \alpha))=` `\frac (sin \ \alpha)(1-cos \ \ alfa)=\frac (1+cos \\alfa)(sin \\alfa)`
Wzory na argumenty połówkowe, podwójne i potrójne wyrażają funkcje `sin, \cos, \tg, \ctg` tych argumentów (`\frac(\alpha)2, \2\alpha, \3\alpha,... ` ) poprzez te funkcje, argument `\alpha`.
Ich wnioski można uzyskać z poprzedniej grupy (dodawanie i odejmowanie argumentów). Na przykład tożsamość podwójnego kąta można łatwo uzyskać zastępując `\beta` przez `\alpha`.
Wzory na redukcję stopni
Wzory kwadratów (sześcianów itp.) funkcji trygonometrycznych umożliwiają przejście od 2,3,... stopni do funkcji trygonometrycznych pierwszego stopnia, ale wiele kątów (`\alpha, \3\alpha, \... ` lub `2\alfa, \ 4\alfa, \...`).
`sin^2 \alpha=\frac(1-cos \ 2\alpha)2,` ` (sin^2 \frac \alpha 2=\frac(1-cos \ \alpha)2)`
`cos^2 \alpha=\frac(1+cos \ 2\alpha)2,` ` (cos^2 \frac \alpha 2=\frac(1+cos \ \alfa)2)`
`sin^3 \alpha=\frac(3sin \\alfa-sin \ 3\alfa)4`
`cos^3 \alpha=\frac(3cos \\alfa+cos \ 3\alfa)4`
`sin^4 \alpha=\frac(3-4cos \ 2\alfa+cos \ 4\alfa)8`
`cos^4 \alpha=\frac(3+4cos \ 2\alfa+cos \ 4\alfa)8`
Wzory na sumę i różnicę funkcji trygonometrycznych
Wzory są przekształceniami sumy i różnicy funkcji trygonometrycznych różnych argumentów w iloczyn.
`sin \ \alfa+sin \ \beta=` `2 \ sin \frac(\alpha+\beta)2 \ cos \frac(\alfa-\beta)2`
`sin \ \alfa-sin \ \beta=` `2 \cos \frac(\alpha+\beta)2 \sin \frac(\alfa-\beta)2`
`cos \ \alfa+cos \ \beta=` `2 \cos \frac(\alpha+\beta)2 \cos \frac(\alfa-\beta)2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac(\alpha+\beta)2 \ sin \frac(\alpha-\beta)2=` `2 \ sin \frac(\alpha+\ beta)2\sin\frac(\beta-\alfa)2`
`tg \ \alpha \pm tg \ \beta=\frac(sin(\alpha \pm \beta))(cos \ \alpha \ cos \ \beta)`
`ctg \ \alpha \pm ctg \ \beta=\frac(sin(\beta \pm \alpha))(sin \ \alpha \ sin \ \beta)`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac(cos(\alpha \mp \beta))(cos \\alpha \ sin \ \beta)`
Tutaj następuje przekształcenie dodawania i odejmowania funkcji jednego argumentu w iloczyn.
`cos \ \alfa+sin \ \alpha=\sqrt(2) \cos (\frac(\pi)4-\alfa)`
`cos \ \alpha-sin \ \alpha=\sqrt(2) \ sin (\frac(\pi)4-\alpha)`
`tg \ \alfa+ctg \ \alpha=2 \cosec \2\alpha;` `tg \ \alfa-ctg \ \alpha=-2 \ctg \2\alfa`
Poniższe wzory przekształcają sumę i różnicę jedności oraz funkcję trygonometryczną w iloczyn.
`1+cos \ \alfa=2 \cos^2 \frac(\alfa)2`
`1-cos \ \alfa=2 \ sin^2 \frac(\alfa)2`
`1+sin \ \alfa=2 \ cos^2 (\frac (\pi) 4-\frac(\alfa)2)`
`1-sin \ \alpha=2 \ sin^2 (\frac (\pi) 4-\frac(\alfa)2)`
`1 \pm tg \ \alpha=\frac(sin(\frac(\pi)4 \pm \alpha))(cos \frac(\pi)4 \cos \\alpha)=` `\frac(\sqrt (2) sin(\frac(\pi)4 \pm \alfa))(cos \\alfa)`
`1 \pm tg \ \alpha \ tg \ \beta=\frac(cos(\alpha \mp \beta))(cos \ \alpha \ cos \ \beta);` ` \ctg \ \alpha \ctg \\ beta \pm 1=\frac(cos(\alpha \mp \beta))(sin \ \alpha \ sin \ \beta)`
Wzory na przeliczanie iloczynów funkcji
Wzory na przeliczenie iloczynu funkcji trygonometrycznych z argumentami `\alfa` i `\beta` na sumę (różnicę) tych argumentów.
`sin \ \alpha \ sin \ \beta =` `\frac(cos(\alpha - \beta)-cos(\alpha + \beta))(2)`
`sin\alfa \cos\beta =` `\frac(sin(\alpha - \beta)+sin(\alfa + \beta))(2)`
`cos \ \alpha \cos \ \beta =` `\frac(cos(\alpha - \beta)+cos(\alpha + \beta))(2)`
`tg \ \alpha \ tg \ \beta =` `\frac(cos(\alpha - \beta)-cos(\alpha + \beta))(cos(\alpha - \beta)+cos(\alpha + \ beta)) =` `\frac(tg \\alpha + tg \ \beta)(ctg \ \alpha + ctg \ \beta)`
`ctg \ \alpha \ ctg \ \beta =` `\frac(cos(\alpha - \beta)+cos(\alpha + \beta))(cos(\alpha - \beta)-cos(\alpha + \ beta)) =` `\frac(ctg \\alpha + ctg \ \beta)(tg \ \alpha + tg \ \beta)`
`tg \ \alpha \ ctg \ \beta =` `\frac(sin(\alpha - \beta)+sin(\alpha + \beta))(sin(\alpha + \beta)-sin(\alpha - \ beta))`
Uniwersalne podstawienie trygonometryczne
Wzory te wyrażają funkcje trygonometryczne w postaci tangensa połówki kąta.
`sin \ \alpha= \frac(2tg\frac(\alpha)(2))(1 + tg^(2)\frac(\alpha)(2)),` ` \alpha\ne \pi +2\ pi n, n \in Z`
`cos \ \alpha= \frac(1 - tg^(2)\frac(\alpha)(2))(1 + tg^(2)\frac(\alpha)(2)),` ` \alpha \ ne \pi +2\pi n, n \in Z`
`tg \ \alpha= \frac(2tg\frac(\alpha)(2))(1 - tg^(2)\frac(\alpha)(2)),` ` \alpha \ne \pi +2\ pi n, n \in Z,` ` \alpha \ne \frac(\pi)(2)+ \pi n, n \in Z`
`ctg \ \alpha = \frac(1 - tg^(2)\frac(\alpha)(2))(2tg\frac(\alpha)(2)),` ` \alpha \ne \pi n, n \in Z,` `\alfa \ne \pi + 2\pi n, n \in Z`
Formuły redukcyjne
Wzory redukcyjne można otrzymać wykorzystując takie właściwości funkcji trygonometrycznych jak okresowość, symetria oraz właściwość przesunięcia o zadany kąt. Umożliwiają one konwersję funkcji dowolnego kąta na funkcje, których kąt mieści się w przedziale od 0 do 90 stopni.
Dla kąta (`\frac (\pi)2 \pm \alpha`) lub (`90^\circ \pm \alpha`):
`sin(\frac (\pi)2 - \alpha)=cos \ \alpha;` ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha`
`cos(\frac (\pi)2 - \alpha)=sin \ \alpha;` ` cos(\frac (\pi)2 + \alpha)=-sin \ \alfa`
`tg(\frac (\pi)2 — \alpha)=ctg \ \alpha;` ` tg(\frac (\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (\pi)2 — \alpha)=tg \ \alpha;` ` ctg(\frac (\pi)2 + \alpha)=-tg \ \alpha`
Dla kąta (`\pi \pm \alpha`) lub (`180^\circ \pm \alpha`):
`sin(\pi - \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi - \alfa)=-cos \ \alfa;` ` cos(\pi + \alfa)=-cos \ \alfa`
`tg(\pi - \alfa)=-tg \ \alfa;` ` tg(\pi + \alfa)=tg \ \alfa`
`ctg(\pi - \alfa)=-ctg \ \alfa;` ` ctg(\pi + \alfa)=ctg \ \alfa`
Dla kąta (`\frac (3\pi)2 \pm \alpha`) lub (`270^\circ \pm \alpha`):
`sin(\frac (3\pi)2 — \alpha)=-cos \ \alpha;` ` sin(\frac (3\pi)2 + \alpha)=-cos \ \alfa`
`cos(\frac (3\pi)2 — \alpha)=-sin \ \alpha;` ` cos(\frac (3\pi)2 + \alpha)=sin \ \alfa`
`tg(\frac (3\pi)2 — \alpha)=ctg \ \alpha;` ` tg(\frac (3\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (3\pi)2 — \alpha)=tg \ \alpha;` ` ctg(\frac (3\pi)2 + \alpha)=-tg \ \alpha`
Dla kąta (`2\pi \pm \alpha`) lub (`360^\circ \pm \alpha`):
`sin(2\pi - \alfa)=-sin \ \alfa;` ` sin(2\pi + \alfa)=sin \ \alfa`
`cos(2\pi - \alfa)=cos \ \alfa;` ` cos(2\pi + \alfa)=cos \ \alfa`
`tg(2\pi - \alfa)=-tg \ \alfa;` ` tg(2\pi + \alfa)=tg \ \alfa`
`ctg(2\pi - \alfa)=-ctg \ \alfa;` ` ctg(2\pi + \alfa)=ctg \ \alfa`
Wyrażanie niektórych funkcji trygonometrycznych za pomocą innych
`sin \ \alpha=\pm \sqrt(1-cos^2 \alpha)=` `\frac(tg \ \alpha)(\pm \sqrt(1+tg^2 \alpha))=\frac 1( \pm \sqrt(1+ctg^2 \alfa))`
`cos \ \alpha=\pm \sqrt(1-sin^2 \alpha)=` `\frac 1(\pm \sqrt(1+tg^2 \alpha))=\frac (ctg \\alpha)( \pm \sqrt(1+ctg^2 \alfa))`
`tg \ \alpha=\frac (sin \ \alpha)(\pm \sqrt(1-sin^2 \alpha))=` `\frac (\pm \sqrt(1-cos^2 \alpha))( cos\\alfa)=\frac 1(ctg\\alfa)`
`ctg \ \alpha=\frac (\pm \sqrt(1-sin^2 \alpha))(sin \ \alpha)=` `\frac (cos \\alpha)(\pm \sqrt(1-cos^ 2 \alfa))=\frac 1(tg \alfa)`
Trygonometria dosłownie oznacza „mierzenie trójkątów”. Zaczyna się uczyć w szkole i jest kontynuowany bardziej szczegółowo na uniwersytetach. Dlatego potrzebne są podstawowe wzory w trygonometrii począwszy od klasy 10, a także dla zdanie jednolitego egzaminu państwowego. Oznaczają połączenia między funkcjami, a ponieważ tych połączeń jest wiele, istnieje wiele samych formuł. Nie jest łatwo je wszystkie zapamiętać i nie jest to konieczne – w razie potrzeby można je wszystkie wyświetlić.
Wzory trygonometryczne są używane w rachunku całkowym, a także w uproszczeniu, obliczeniach i przekształceniach trygonometrycznych.
Ćwiczenia.
Znajdź wartość x w .
Rozwiązanie.
Znalezienie wartości argumentu funkcji, przy której jest ona równa dowolnej wartości, oznacza określenie, przy jakich argumentach wartość sinusa będzie dokładnie taka, jak wskazano w warunku.
W takim przypadku musimy dowiedzieć się, przy jakich wartościach wartość sinus będzie równa 1/2. Można to zrobić na kilka sposobów.
Na przykład użyj , za pomocą którego, aby określić, przy jakich wartościach x funkcja sinus będzie równa 1/2.
Innym sposobem jest użycie . Przypomnę, że wartości sinusów leżą na osi Oy.
Najczęstszym sposobem jest użycie , szczególnie gdy mamy do czynienia z wartościami standardowymi dla tej funkcji, takimi jak 1/2.
We wszystkich przypadkach nie należy zapominać o jednej z najważniejszych właściwości sinusa - jego okresie.
Znajdźmy w tabeli wartość 1/2 dla sinusa i zobaczmy, jakie argumenty jej odpowiadają. Argumenty, które nas interesują to Pi/6 i 5Pi/6.
Zapiszmy wszystkie pierwiastki, które spełniają dane równanie. W tym celu zapisujemy interesujący nas nieznany argument x oraz jedną z wartości argumentu otrzymanego z tabeli, czyli Pi/6. Zapisujemy dla niego, biorąc pod uwagę okres sinusa , wszystkie wartości argumentu:
![]()
Weźmy drugą wartość i wykonaj te same kroki, co w poprzednim przypadku:
![]()
Pełnym rozwiązaniem pierwotnego równania będzie: ![]() I
I ![]()
Q może przyjąć wartość dowolnej liczby całkowitej.
W trygonometrii wiele wzorów łatwiej jest wyprowadzić niż zapamiętać. Cosinus podwójnego kąta to wspaniały wzór! Pozwala uzyskać wzory na redukcje stopni i wzory na półkąty.
Potrzebujemy więc cosinusa podwójnego kąta i jednostki trygonometrycznej:
Są nawet podobne: we wzorze na cosinus podwójnego kąta jest to różnica między kwadratami cosinusa i sinusa, a w jednostce trygonometrycznej jest to ich suma. Jeśli wyrazimy cosinus z jednostki trygonometrycznej:
i podstawiamy go do cosinusa kąta podwójnego, otrzymujemy:
To kolejny wzór na cosinus podwójnego kąta:
Wzór ten jest kluczem do uzyskania wzoru redukcyjnego:
Zatem wzór na zmniejszenie stopnia sinusa jest następujący:
![]()
Jeśli w nim kąt alfa zastąpimy półkątem alfa na pół, a podwójny kąt dwa alfa zastąpimy kątem alfa, wówczas otrzymamy wzór na kąt połówkowy dla sinusa:
![]()
Teraz możemy wyrazić sinus z jednostki trygonometrycznej:
Zastąpmy to wyrażenie wzorem na cosinus podwójnego kąta:
![]()
Mamy inny wzór na cosinus kąta podwójnego:
Wzór ten jest kluczem do znalezienia wzoru na redukcję potęgi cosinusa i kąta połówkowego cosinusa.
Zatem wzór na zmniejszenie stopnia cosinusa jest następujący:
![]()
Jeśli zastąpimy α przez α/2 i 2α przez α, otrzymamy wzór na półargument dla cosinusa:
![]()
Ponieważ tangens jest stosunkiem sinusa do cosinusa, wzór na tangens jest następujący:
![]()
Cotangens to stosunek cosinusa do sinusa. Zatem wzór na cotangens wygląda następująco:
![]()
Oczywiście w procesie upraszczania wyrażenia trygonometryczne Nie ma sensu wyprowadzać wzorów na połowę kąta lub zmniejszać za każdym razem stopień. O wiele łatwiej jest położyć przed sobą kartkę papieru z wzorami. A uproszczenia będą postępować szybciej, a pamięć wzrokowa włączy zapamiętywanie.
Ale nadal warto kilka razy wyprowadzać te wzory. Będziesz wtedy mieć absolutną pewność, że podczas egzaminu, gdy nie ma możliwości skorzystania ze ściągawek, bez problemu je zdobędziesz, jeśli zajdzie taka potrzeba.