Podręcznik edukacyjno-metodyczny
przygotować się do jednolitego egzaminu państwowego z matematyki

TRYGONOMETRIA W ZASTOSOWANIU W MATEMATYCE

Celem tego samouczka jest pomoc uczniom w przygotowaniu do Jednolitego Egzaminu Państwowego z matematyki w dziale „Trygonometria”.

W podręcznik przeprowadzana jest analiza i podawane są rozwiązania typowych problemów trygonometrii oferowanych przez Instytut Moskiewski edukacja otwarta w różnych kontrolach, diagnostyce, szkoleniach, demonstracjach i arkusze egzaminacyjne z matematyki dla uczniów klas 10 i 11.

Po przeanalizowaniu każdego typowego problemu podano podobne problemy do samodzielnego rozwiązania.

Z niezbędnym informacje teoretyczne, używane do rozwiązywania problemów, można znaleźć w części „Trygonometria” w naszym „Podręczniku matematyki dla dzieci w wieku szkolnym”.

Z głównym metody rozwiązania równania trygonometryczne możesz nas spotkać w naszym podręcznik edukacyjny„Rozwiązywanie równań trygonometrycznych”.

Dla uczniów klas 10 i 11, którzy chcą dobrze się przygotować i zdać Jednolity egzamin państwowy z matematyki lub języka rosyjskiego NA wysoki wynik, Centrum edukacyjne„Resolventa” prowadzi kursy przygotowujące do Jednolitego Egzaminu Państwowego.

Organizujemy także dla uczniów

Z demo Opcje ujednoliconego egzaminu stanowego , opublikowane na oficjalnej portalu informacyjnego Jeden Egzamin państwowy, można znaleźć pod adresem

\(\blacktriangleright\) Rozważmy prostokątny układ współrzędnych, a w nim okrąg o promieniu jednostkowym i środku w początku układu współrzędnych.

Kąt w \(1^\circ\)- to jest takie kąt centralny, który opiera się na łuku, którego długość jest równa \(\dfrac1(360)\) długości całego okręgu.

\(\blacktriangleright\) Rozważymy kąty na okręgu, w którym wierzchołek znajduje się w środku okręgu, a jeden bok zawsze pokrywa się z dodatnim kierunkiem osi \(Ox\) (zaznaczonej na rysunku na czerwono) .
W ten sposób zaznaczamy narożniki \(45^\circ,\ 180^\circ,\ 240^\circ\):

Zauważ, że kąt \(0^\circ\) to kąt, którego obie strony pokrywają się z dodatnim kierunkiem osi \(Ox\) .

Punkt, w którym drugi bok takiego kąta \(\alpha\) przecina okrąg, nazwiemy \(P_(\alpha)\) .
Położenie punktu \(P_(0)\) będzie nazywane pozycją początkową.

Można zatem powiedzieć, że obracamy się po okręgu od pozycji początkowej \(P_0\) do pozycji \(P_(\alpha)\) o kąt \(\alpha\) .

\(\blacktriangleright\) Obrót w kierunku przeciwnym do ruchu wskazówek zegara jest obrotem dodatnim. Obrót w prawo jest obrotem ujemnym.

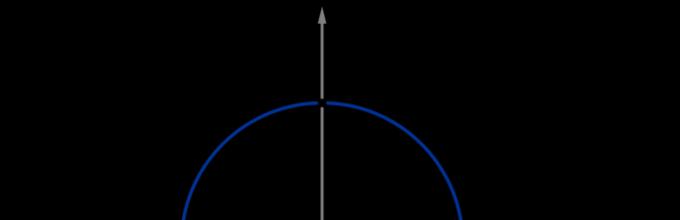
Na przykład na rysunku zaznaczono rogi \(-45^\circ, -90^\circ, -160^\circ\):

\(\blacktriangleright\) Rozważmy punkt \(P_(30^\circ)\) na okręgu. Aby obrócić się po okręgu od pozycji początkowej do punktu \(P_(30^\circ)\), należy obrócić się o kąt \(30^\circ\) (pomarańczowy). Jeśli wykonamy pełny obrót (czyli o \(360^\circ\) ) i kolejny obrót o \(30^\circ\) , to ponownie dotrzemy do tego punktu, chociaż obrót wykonaliśmy już o kąt \(390^\circ=360^\circ+30^\circ\)(niebieski). Możemy również dojść do tego punktu, skręcając w \(-330^\circ\) (zielony), do \(750^\circ=360^\circ+360^\circ+30^\circ\) itp.

Zatem każdemu punktowi na okręgu odpowiada nieskończona liczba kątów, a kąty te różnią się od siebie całkowitą liczbą pełnych obrotów ( \(n\cdot360^\circ, n\in\mathbb(Z)\)).
Na przykład kąt \(30^\circ\) jest \(360^\circ\) większy niż kąt \(-330^\circ\) i \(2\cdot 360^\circ\) mniejszy niż kąt \(750^\circ\) .

Wszystkie kąty znajdujące się w punkcie \(P_(30^\circ)\) można zapisać w postaci: \(\alpha=30^\circ+n\cdot 360^\circ, \n\in\mathbb(Z)\).

\(\czarnytrójkątprawy\) Kąt w \(1\) radianach- jest to kąt środkowy oparty na łuku, którego długość jest równa promieniowi okręgu:

Ponieważ długość całego okręgu o promieniu \(R\) jest równa \(2\pi R\), a w stopniach - \(360^\circ\), wtedy mamy \(360^\circ=2\pi \cdot 1\textbf(rad)\), Gdzie \ Jest to podstawowy wzór, za pomocą którego można przeliczać stopnie na radiany i odwrotnie.

Przykład 1. Znajdź radianową miarę kąta \(60^\circ\) .

Ponieważ \(180^\circ = \pi \Rightarrow 1^\circ = \dfrac(\pi)(180) \Rightarrow 60^\circ=\dfrac(\pi)3\)

Przykład 2. Znajdować miara stopnia kąt \(\dfrac34 \pi\) .

Ponieważ \(\pi=180^\circ \Rightarrow \dfrac34 \pi=\dfrac34 \cdot 180^\circ=135^\circ\).

Zwykle piszą na przykład nie \(\dfrac(\pi)4 \text(rad)\), ale po prostu \(\dfrac(\pi)4\) (tj. jednostka miary „rad” jest pominięta). Należy zwrócić uwagę na oznaczenie stopni podczas zapisywania kąta nie obniżaj. Zatem pisząc „kąt jest równy \(1\)” mamy na myśli, że „kąt jest równy \(1\) radianów”, a nie „kąt jest równy \(1\) stopni”.

Ponieważ \(\pi \thickokoło 3,14 \Rightarrow 180^\circ \thickokoło 3,14 \textbf(rad) \Rightarrow 1 \textbf(rad) \thickokoło 57^\circ\).
Takiego przybliżonego podstawienia nie można dokonać w przypadku problemów, ale wiedza o tym, ile \(1\) radianów w stopniach jest w przybliżeniu równe, często pomaga w rozwiązaniu niektórych problemów. Na przykład w ten sposób łatwiej jest znaleźć kąt \(5\) radianów na okręgu: jest on w przybliżeniu równy \(285^\circ\) .

\(\blacktriangleright\) Z przebiegu planimetrii (geometrii na płaszczyźnie) wiemy, że dla kątów \(0<\alpha< 90^\circ\) определены синус, косинус, тангенс и котангенс следующим образом:
jeśli dany jest trójkąt prostokątny o bokach \(a, b, c\) i kącie \(\alpha\), to:

Ponieważ na okręgu jednostkowym definiuje się dowolne kąty \(\alfa\in(-\infty;+\infty)\), musisz wyznaczyć sinus, cosinus, tangens i cotangens dla dowolnego kąta.
Rozważmy okrąg jednostkowy i znajdujący się na nim kąt \(\alpha\) i odpowiadający mu punkt \(P_(\alpha)\) :

Opuśćmy prostopadłą \(P_(\alpha)K\) z punktu \(P_(\alpha)\) do osi \(Ox\) . Otrzymujemy trójkąt prostokątny \(\triangle OP_(\alpha)K\) z którego mamy: \[\sin\alpha=\dfrac(P_(\alpha)K)(P_(\alpha)O) \qquad \cos \alpha=\dfrac(OK)(P_(\alpha)O)\] Zauważ, że odcinek \(OK\) to nic innego jak odcięta \(x_(\alpha)\) punktu \(P_(\alpha)\) , a odcinek \(P_(\alpha)K\) jest rzędną \(y_(\alpha)\) . Zauważ też, że od wzięliśmy okrąg jednostkowy, wtedy \(P_(\alpha)O=1\) jest jego promieniem.
Zatem, \[\sin\alpha=y_(\alpha), \qquad \cos \alpha=x_(\alpha)\]

Zatem jeśli punkt \(P_(\alpha)\) miał współrzędne \((x_(\alpha)\,;y_(\alpha))\), to poprzez odpowiedni kąt jego współrzędne można przepisać jako \(( \ cos\alfa\,;\sin\alfa)\) .

Definicja: 1. Sinus kąta \(\alpha\) jest rzędną punktu \(P_(\alpha)\) odpowiadającego temu kątowi na okręgu jednostkowym.

2. Cosinus kąta \(\alfa\) jest odciętą punktu \(P_(\alfa)\) odpowiadającego temu kątowi na okręgu jednostkowym.

Dlatego oś \(Oy\) nazywana jest osią sinusów, oś \(Ox\) nazywana jest osią cosinusów.

\(\blacktriangleright\) Okrąg można podzielić na \(4\) ćwiartki, jak pokazano na rysunku.

Ponieważ w ćwiartce \(I\) zarówno odcięta, jak i rzędne wszystkich punktów są dodatnie, wówczas cosinusy i sinusy wszystkich kątów z tej ćwiartki są również dodatnie.
Ponieważ w ćwiartce \(II\) rzędne wszystkich punktów są dodatnie, a odcięte są ujemne, wówczas cosinusy wszystkich kątów z tej ćwiartki są ujemne, a sinusy są dodatnie.
Podobnie możesz określić znak sinusa i cosinusa dla pozostałych ćwiartek.

Przykład 3. Ponieważ np. punkty \(P_(\frac(\pi)(6))\) i \(P_(-\frac(11\pi)6)\) pokrywają się, to ich współrzędne są równe, tj. \(\sin\dfrac(\pi)6=\sin \left(-\dfrac(11\pi)6\right),\ \cos \dfrac(\pi)6=\cos \left(-\dfrac( 11\pi)6\prawo)\).

Przykład 4. Rozważ punkty \(P_(\alpha)\) i \(P_(\pi-\alpha)\) . Niech dla wygody niech \(0<\alpha<\dfrac{\pi}2\) .

Narysujmy prostopadłe do osi \(Ox\) : \(OK\) i \(OK_1\) . Trójkąty \(OKP_(\alpha)\) i \(OK_1P_(\pi-\alpha)\) są równe pod kątem przeciwprostokątnej i kąta ( \(\kąt P_(\alfa)OK=\kąt P_(\pi-\alfa)OK_1=\alfa\)). Stąd, \(OK=OK_1, KP_(\alfa)=K_1P_(\pi-\alfa)\). Ponieważ współrzędne punktu \(P_(\alfa)=(OK;KP_(\alfa))=(\cos\alfa\,;\sin\alfa)\) i punkty \(P_(\pi-\alpha)=(-OK_1;K_1P_(\pi-\alpha))=(\cos(\pi-\alpha)\,;\sin(\pi-\alpha))\), stąd, \[\cos(\pi-\alpha)=-\cos\alpha, \qquad \sin(\pi-\alpha)=\sin\alpha\]

W ten sposób wywoływane są inne formuły formuły redukcyjne: \[(\large(\begin(array)(l|r) \hline \sin(\pi-\alpha)=\sin\alpha & \cos(\pi-\alpha)=-\cos\alpha\\ \sin(\pi+\alpha)=-\sin\alpha & \cos(\pi+\alpha)=-\cos\alpha\\ \sin(2\pi\pm\alpha)=\pm\sin\alpha & \cos (2\pi\pm\alpha)=\cos\alpha\\ \sin \left(\dfrac(\pi)2\pm\alpha\right)=\cos\alpha & \cos\left(\dfrac (\pi)2\pm\alpha\right)=\pm\sin\alpha\\ \hline \end(array)))\]

Za pomocą tych wzorów można znaleźć sinus lub cosinus dowolnego kąta, redukując tę wartość do sinusa lub cosinusa kąta z ćwiartki \(I\).

Tabela sinusów, cosinusów, stycznych i cotangensów kątów z pierwszej ćwiartki:
\[(\large(\begin(array)(|c|c|c|c|c|c|) \hline &&&&&\\[-17pt] & \quad 0 \quad (0^ \circ)& \quad \dfrac(\pi)6 \quad (30^\circ) & \quad \dfrac(\pi)4 \quad (45^\circ) & \quad \dfrac(\pi)3 \quad (60^\circ )& \quad \dfrac(\pi)2 \quad (90^\circ) \\ &&&&&\\[-17pt] \hline \sin & 0 &\frac12&\frac(\sqrt2)2&\frac(\sqrt3) 2&1\\ \hline \cos &1&\frac(\sqrt3)2&\frac(\sqrt2)2&\frac12&0\\ \hline \mathrm(tg) &0 &\frac(\sqrt3)3&1&\sqrt3&\infty\\ \hline \mathrm(ctg) &\infty &\sqrt3&1&\frac(\sqrt3)3&0\\ \hline \end(array)))\]

Należy pamiętać, że wartości te zostały wyświetlone w sekcji „Geometria na płaszczyźnie (planimetria). Część II” w temacie „Wstępne informacje o sinusie, cosinusie, tangensie i cotangensie”.

Przykład 5. Znajdź \(\sin(\dfrac(3\pi)4)\) .

Przekształćmy kąt: \(\dfrac(3\pi)4=\dfrac(4\pi-\pi)(4)=\pi-\dfrac(\pi)4\)

Zatem, \(\sin(\dfrac(3\pi)4)=\sin\left(\pi-\dfrac(\pi)4\right)=\sin\dfrac(\pi)4=\dfrac(\sqrt2) 2\).

\(\blacktriangleright\) Aby ułatwić zapamiętywanie i stosowanie wzorów redukcyjnych, możesz zastosować się do poniższej zasady.

Przypadek 1.\(n\cdot \pi\pm \alfa\) \[\sin(n\cdot \pi\pm \alpha)=\bigodot \sin\alpha\] \[\cos(n\cdot \pi\pm \alpha)=\bigodot \cos\alpha\]

Znak kąta można znaleźć, określając, w której ćwiartce się on znajduje. Korzystając z tej reguły, zakładamy, że kąt \(\alfa\) leży w kwadrancie \(I\).

Przypadek 2. Jeśli kąt można przedstawić w postaci , gdzie \(n\in\mathbb(N)\) , to \[\sin(n\cdot \pi+\dfrac(\pi)2\pm \alpha)=\bigodot \cos\alpha\] gdzie zamiast \(\bigodot\) jest znak sinusa kąta \(n\cdot \pi\pm \alpha\) . \[\cos(n\cdot \pi+\dfrac(\pi)2\pm \alpha)=\bigodot \sin\alpha\] gdzie zamiast \(\bigodot\) jest znak cosinusa kąta \(n\cdot \pi\pm \alpha\) .

Znak wyznacza się analogicznie jak w przypadku \(1\) .

Należy zauważyć, że w pierwszym przypadku funkcja pozostaje niezmieniona, a w drugim ulega zmianie (mówią, że funkcja zmienia się na kofunkcję).

Przykład 6. Znajdź \(\sin \dfrac(13\pi)(3)\) .

Przekształćmy kąt: \(\dfrac(13\pi)(3)=\dfrac(12\pi+\pi)(3)=4\pi+\dfrac(\pi)3\), stąd, \(\sin \dfrac(13\pi)(3)=\sin \left(4\pi+\dfrac(\pi)3\right)=\sin\dfrac(\pi)3=\dfrac(\sqrt3) 2\)

Przykład 7. Znajdź \(\cos \dfrac(17\pi)(6)\) .

Przekształćmy kąt: \(\dfrac(17\pi)(6)=\dfrac(18\pi-\pi)(6)=3\pi-\dfrac(\pi)6\), stąd, \(\cos \dfrac(17\pi)(6)=\cos \left(3\pi-\dfrac(\pi)6\right)=-\cos\dfrac(\pi)6=-\dfrac( \sqrt3)2\)

\(\czarnytrójkątprawy\) Zakres wartości sinus i cosinus.
Ponieważ współrzędne \(x_(\alpha)\) i \(y_(\alpha)\) dowolnego punktu \(P_(\alpha)\) na okręgu jednostkowym mieszczą się w przedziale od \(-1\) do \ (1\) i \(\cos\alpha\) i \(\sin\alpha\) są odpowiednio odciętą i rzędną tego punktu, wówczas \[(\large(-1\leq \cos\alpha\leq 1 ,\qquad -1\leq\sin\alpha\leq 1))\]

Z trójkąta prostokątnego zgodnie z twierdzeniem Pitagorasa mamy: \(x^2_(\alfa)+y^2_(\alfa)=1^2\)
Ponieważ \(x_(\alpha)=\cos\alpha,\ y_(\alpha)=\sin\alpha \Rightarrow\) \[(\large(\sin^2\alpha+\cos^2\alpha=1)) - \textbf(podstawowa tożsamość trygonometryczna (GTT))\]

\(\czarnytrójkątprawy\) Tangens i kotangens.

Ponieważ \(\mathrm(tg)\,\alpha=\dfrac(\sin\alpha)(\cos\alpha), \cos\alpha\ne 0\)

\(\mathrm(ctg)\,\alpha=\dfrac(\cos\alpha)(\sin\alpha), \sin\alpha\ne 0\), To:

1) \((\large(\mathrm(tg)\,\alpha\cdot \mathrm(ctg)\,\alpha=1, \cos\alpha\ne 0, \sin\alpha \ne 0))\)

2) tangens i cotangens są dodatnie w ćwiartkach \(I\) i \(III\), a ujemne w ćwiartkach \(II\) i \(IV\).

3) zakres wartości tangensa i cotangensa - wszystkie liczby rzeczywiste, tj. \(\mathrm(tg)\,\alpha\in\mathbb(R), \ \mathrm(ctg)\,\alpha\in\mathbb(R)\)

4) zdefiniowano także wzory redukcyjne na styczną i cotangens.

Przypadek 1. \[\mathrm(tg)\,(n\cdot \pi\pm \alpha)=\bigodot \mathrm(tg)\,\alpha\] gdzie zamiast \(\bigodot\) jest znak tangensa kąta \(n\cdot \pi\pm \alpha\) (\(\cos\alpha\ne 0\) ). \[\mathrm(ctg)\,(n\cdot \pi\pm \alpha)=\bigodot \mathrm(ctg)\,\alpha\] gdzie zamiast \(\bigodot\) jest znak kąta cotangens \(n\cdot \pi\pm \alpha\) (\(\sin\alpha\ne 0\) ).

Przypadek 2. Jeśli kąt można przedstawić jako \(n\cdot \pi+\dfrac(\pi)2\pm\alfa\), gdzie \(n\in\mathbb(N)\) , to \[\mathrm(tg)\,(n\cdot \pi+\dfrac(\pi)2\pm \alpha)=\bigodot \mathrm(ctg)\,\alpha\] gdzie w miejscu \(\bigodot\) znajduje się znak tangensa kąta \(n\cdot \pi\pm \alpha\) (\(\sin\alpha\ne 0\) ). \[\mathrm(ctg)\,(n\cdot \pi+\dfrac(\pi)2\pm \alpha)=\bigodot \mathrm(tg)\,\alpha\] gdzie zamiast \(\bigodot\) jest znak kąta cotangens \(n\cdot \pi\pm \alpha\) (\(\cos\alpha\ne 0\) ).

5) oś styczna przechodzi przez punkt \((1;0)\) równoległy do osi sinusoidy, a dodatni kierunek osi stycznej pokrywa się z dodatnim kierunkiem osi sinusoidy;
oś cotangens przechodzi przez punkt \((0;1)\) równoległy do osi cosinus, a dodatni kierunek osi cotangens pokrywa się z dodatnim kierunkiem osi cosinus.

Dowód tego faktu przedstawimy na przykładzie osi stycznej.

\(\triangle OP_(\alpha)K \sim \triangle AOB \Rightarrow \dfrac(P_(\alpha)K)(OK)=\dfrac(BA)(OB) \Rightarrow \dfrac(\sin\alpha)( \cos\alpha)=\dfrac(BA)1 \Rightarrow BA=\mathrm(tg)\,\alpha\).

Zatem jeśli punkt \(P_(\alpha)\) łączy się linią prostą ze środkiem okręgu, to ta prosta przetnie styczną w punkcie, którego wartość wynosi \(\mathrm(tg)\ ,\alfa\) .

6) z głównej tożsamości trygonometrycznej wynikają następujące wzory: \ Pierwszy wzór otrzymujemy dzieląc prawą i lewą stronę OTT przez \(\cos^2\alpha\), drugi dzieląc przez \(\sin^2\alpha\) .

Należy pamiętać, że tangens nie jest zdefiniowany dla kątów, w których cosinus wynosi zero (tzn \(\alpha=\dfrac(\pi)2+\pi n, n\in\mathbb(Z)\));
cotangens nie jest zdefiniowany dla kątów, w których sinus wynosi zero (tzn \(\alpha=\pi+\pi n, n\in\mathbb(Z)\)).

\(\czarnytrójkątprawy\) Równość cosinusa i nieparzystość sinusa, tangens, cotangens.

Przypomnijmy, że funkcja \(f(x)\) jest wywoływana nawet jeśli \(f(-x)=f(x)\) .

Funkcję nazywa się nieparzystą, jeśli \(f(-x)=-f(x)\) .

Z okręgu widać, że cosinus kąta \(\alpha\) jest równy cosinusowi kąta \(-\alpha\) dla dowolnych wartości \(\alpha\) :

Zatem cosinus jest funkcją parzystą, co oznacza, że wzór \[(\Large(\cos(-x)=\cos x))\] jest prawdziwy

Z okręgu jasno wynika, że sinus kąta \(\alpha\) jest przeciwny do sinusa kąta \(-\alpha\) dla dowolnych wartości \(\alpha\) :

Zatem sinus jest funkcją nieparzystą, co oznacza, że wzór jest poprawny \[(\Duży(\sin(-x)=-\sin x))\]

Tangens i cotangens są także funkcjami nieparzystymi: \[(\Large(\mathrm(tg)\,(-x)=-\mathrm(tg)\,x))\] \[(\Large(\mathrm(ctg)\,(-x)=-\mathrm(ctg)\,x))\]

Ponieważ \(\mathrm(tg)\,(-x)=\dfrac(\sin (-x))(\cos(-x))=\dfrac(-\sin x)(\cos x)=-\mathrm (tg)\,x \qquad \mathrm(ctg)\,(-x)=\dfrac(\cos(-x))(\sin(-x))=-\mathrm(ctg)\,x\))

Jak pokazuje praktyka, jedną z najtrudniejszych sekcji matematyki, z którą spotykają się uczniowie w ramach ujednoliconego egzaminu państwowego, jest trygonometria. Nauka o proporcjach trójkątów zaczyna się w ósmej klasie. Równania tego typu zawierają zmienną pod znakiem funkcji trygonometrycznych. Pomimo tego, że najprostsze z nich: \(sin x = a\) , \(cos x = a\) , \(tg x = a\) , \(ctg x = a\) - są znane niemal każdemu ucznia, ich realizacja jest często trudna.

Na egzaminie państwowym Unified z matematyki na poziomie profilu poprawnie rozwiązane zadanie z trygonometrii jest oceniane bardzo wysoko. Za prawidłowe wykonanie zadania z tej części uczeń może otrzymać maksymalnie 4 punkty podstawowe. W tym celu szukanie ściągawek z trygonometrii do egzaminu Unified State Exam jest prawie bezcelowe. Najrozsądniejszym rozwiązaniem jest dobre przygotowanie się do egzaminu.

Jak to zrobić?

Aby trygonometria na Jednolitym Egzaminu Państwowym z matematyki Cię nie przestraszyła, skorzystaj z naszego portalu podczas przygotowań. To wygodne, proste i skuteczne. W tej części naszego portalu edukacyjnego, dostępnej dla studentów z Moskwy i innych miast, w przystępny sposób prezentowane są materiały teoretyczne i wzory z trygonometrii do jednolitego egzaminu państwowego. Ponadto dla wszystkich definicji matematycznych wybraliśmy przykłady ze szczegółowym opisem procesu ich rozwiązywania.

Po przestudiowaniu teorii w dziale „Trygonometria” w ramach przygotowań do egzaminu Unified State Exam zalecamy przejście do „Katalogów”, aby lepiej przyswoić zdobytą wiedzę. Tutaj możesz wybrać problemy na interesujący Cię temat i wyświetlić ich rozwiązania. Zatem powtórzenie teorii trygonometrii w Unified State Examination będzie tak skuteczne, jak to tylko możliwe.

Co chcesz wiedzieć?

Przede wszystkim musisz poznać wartości \(sin\) , \(cos\) , \(tg\) , \(ctg\) kątów ostrych od \(0°\) do \(90° \) . Również przygotowując się do Jednolitego Egzaminu Państwowego w Moskwie warto pamiętać o podstawowych metodach rozwiązywania problemów trygonometrycznych. Należy zauważyć, że podczas wykonywania zadań należy sprowadzić równanie do najprostszej postaci. Możesz to zrobić w następujący sposób:

rozkład równania na czynniki;
zastąpienie zmiennej (redukcja do równań algebraicznych);
prowadzące do jednorodnego równania;
przejście do połowy rogu;
przeliczanie produktów na sumy;
poprzez wprowadzenie kąta pomocniczego;
stosując uniwersalną metodę podstawienia.

W takim przypadku najczęściej student podczas rozwiązywania musi zastosować kilka z wymienionych metod.

Powrót do przodu

Uwaga! Podglądy slajdów służą wyłącznie celom informacyjnym i mogą nie odzwierciedlać wszystkich funkcji prezentacji. Jeśli jesteś zainteresowany tą pracą, pobierz pełną wersję.

„Powiedz mi, a zapomnę,
Pokaż mi, a zapamiętam
Zaangażuj mnie, a się nauczę.”
(Chińskie przysłowie)

Matematyka już dawno stała się językiem nauki i techniki, a obecnie w coraz większym stopniu przenika do życia codziennego i języka potocznego oraz coraz częściej wprowadzana jest w obszary, które tradycyjnie wydają się od niej odległe. Intensywna matematyzacja różnych dziedzin ludzkiej działalności szczególnie nasiliła się wraz z szybkim rozwojem komputerów. Informatyzacja społeczeństwa i wprowadzenie nowoczesnych technologii informatycznych wymagają od człowieka umiejętności matematycznych w każdym miejscu pracy. Zakłada to zarówno specyficzną wiedzę matematyczną, jak i określony styl myślenia. W szczególności ważnym aspektem jest nauka trygonometrii. Badanie funkcji trygonometrycznych jest szeroko stosowane w praktyce, w badaniu wielu procesów fizycznych, w przemyśle, a nawet w medycynie. Studentom, którzy w przyszłości będą wykorzystywać matematykę w swojej działalności zawodowej, należy zapewnić wysokie przygotowanie matematyczne.

Trygonometria jest integralną częścią szkolnego kursu matematyki. Dobra wiedza i wysokie umiejętności z zakresu trygonometrii świadczą o wystarczającym poziomie kultury matematycznej i są niezbędnym warunkiem pomyślnego studiowania matematyki, fizyki i szeregu dyscyplin technicznych na uniwersytecie. Jednak znaczna część absolwentów szkół wykazuje z roku na rok bardzo słabe przygotowanie do tej ważnej części matematyki, o czym świadczą wyniki ubiegłych lat, gdyż analiza jednolitego egzaminu państwowego wykazała, że uczniowie popełniają wiele błędów przy rozwiązywaniu zadań z zakresu matematyki. tej konkretnej sekcji lub w ogóle nie bierz ich do takich zadań.

Ale nawet Grecy u zarania ludzkości uważali trygonometrię za najważniejszą z nauk, ponieważ geometria jest królową matematyki, a trygonometria jest królową geometrii. Dlatego my, nie kwestionując starożytnych Greków, uznamy trygonometrię za jedną z najważniejszych części zajęć szkolnych i ogólnie wszystkich nauk matematycznych.

Fizyka i geometria nie mogą obejść się bez trygonometrii. Egzamin ujednolicony nie może obejść się bez trygonometrii. Tylko w części B pytania dotyczące trygonometrii znajdują się w prawie jednej trzeciej typów zadań. Obejmuje to rozwiązywanie najprostszych równań trygonometrycznych w zadaniu B5 i pracę z wyrażeniami trygonometrycznymi w zadaniu B7 oraz badanie funkcji trygonometrycznych w zadaniu B14, a także zadania B12, które zawierają wzory opisujące zjawiska fizyczne i zawierają funkcje trygonometryczne. Nie sposób nie zwrócić uwagi na zadania geometryczne, przy rozwiązywaniu których wykorzystywane są definicje sinusa, cosinusa, tangensa i cotangensa kąta ostrego trójkąta prostokątnego oraz podstawowe tożsamości trygonometryczne. A to dopiero część B! Ale są też ulubione równania trygonometryczne z wyborem pierwiastków C1 i „niezbyt ulubione” zadania geometryczne C2 i C4.

W jaki sposób można szkolić uczniów w zakresie tych zagadnień? Metod można zaproponować bardzo wiele, ale najważniejsze jest to, aby dzieci nie czuły strachu i niepotrzebnego niepokoju, ze względu na ogromną różnorodność różnych zadań i formuł. W tym celu konieczne jest stworzenie pozytywnego nastroju podczas rozwiązywania tych zadań. Prezentację tę można wykorzystać do prowadzenia zajęć ze studentami oraz do wystąpień na seminariach dla matematyków przygotowujących do egzaminu Unified State Exam. Oferuje niektóre rodzaje zadań i omawia ich rozwiązania.

Dobre szkolenie może polegać nie tylko na prostym rozwiązaniu tych zadań, ale także na ich samodzielnym zestawieniu przez uczniów. W zależności od przygotowania mogą to być testy sprawdzające ograniczenia w rozwiązywaniu równań trygonometrycznych C1, a nawet same równania.

Inną aktywną metodą jest prowadzenie zajęć w formie gier intelektualnych. Myślę, że jedną z najwygodniejszych opcji jest format „Gra niestandardowa”. Ta forma gry, zwłaszcza teraz z wykorzystaniem prezentacji komputerowych, może być wykorzystywana podczas lekcji testowych, po przestudiowaniu tematów oraz w ramach przygotowań do egzaminu Unified State Exam. Proponowana praca zawiera „Twoja własna gra. Rozwiązywanie równań i nierówności trygonometrycznych.”

Wynikiem proponowanej pracy powinno być pomyślne rozwiązanie zadań Unified State Examination na temat „Trygonometria”.

Kurs wideo „Zdobądź piątkę” obejmuje wszystkie tematy niezbędne do pomyślnego zdania jednolitego egzaminu państwowego z matematyki z wynikiem 60–65 punktów. Całkowicie wszystkie zadania 1-13 z egzaminu państwowego Profile Unified z matematyki. Nadaje się również do zdania podstawowego jednolitego egzaminu państwowego z matematyki. Jeśli chcesz zdać Unified State Exam z 90-100 punktami, musisz rozwiązać część 1 w 30 minut i bez błędów!

Kurs przygotowawczy do Jednolitego Egzaminu Państwowego dla klas 10-11, a także dla nauczycieli. Wszystko, czego potrzebujesz, aby rozwiązać część 1 egzaminu państwowego Unified State Exam z matematyki (pierwsze 12 zadań) i zadanie 13 (trygonometria). A to ponad 70 punktów na egzaminie Unified State Exam i ani 100-punktowy student, ani student nauk humanistycznych nie mogą się bez nich obejść.

Cała niezbędna teoria. Szybkie rozwiązania, pułapki i tajemnice Unified State Exam. Przeanalizowano wszystkie aktualne zadania części 1 z Banku Zadań FIPI. Kurs w pełni odpowiada wymogom Unified State Exam 2018.

Kurs zawiera 5 dużych tematów, każdy po 2,5 godziny. Każdy temat jest podany od podstaw, prosto i przejrzyście.

Setki zadań z egzaminu Unified State Exam. Zadania tekstowe i teoria prawdopodobieństwa. Proste i łatwe do zapamiętania algorytmy rozwiązywania problemów. Geometria. Teoria, materiały referencyjne, analiza wszystkich typów zadań Unified State Examation. Stereometria. Podstępne rozwiązania, przydatne ściągawki, rozwój wyobraźni przestrzennej. Trygonometria od podstaw do zadania 13. Zrozumienie zamiast wkuwania. Jasne wyjaśnienia skomplikowanych pojęć. Algebra. Pierwiastki, potęgi i logarytmy, funkcja i pochodna. Podstawa do rozwiązywania złożonych problemów części 2 jednolitego egzaminu państwowego.

A) Rozwiąż równanie 2(\sin x-\cos x)=tgx-1.

B) \left[ \frac(3\pi )2;\,3\pi \right].

Pokaż rozwiązanie

Rozwiązanie

A) Otwierając nawiasy i przesuwając wszystkie wyrazy na lewą stronę, otrzymujemy równanie 1+2 \sin x-2 \cos x-tg x=0. Biorąc pod uwagę, że \cos x \neq 0, wyraz 2 \sin x można zastąpić przez 2 tan x \cos x, otrzymujemy równanie 1+2 tg x \cos x-2 \cos x-tg x=0, które poprzez grupowanie można sprowadzić do postaci (1-tg x)(1-2 \cos x)=0.

1) 1-tgx=0, tan x=1, x=\frac\pi 4+\pi n, n \in \mathbb Z;

2) 1-2 \cos x=0, \cos x=\frac12, x=\pm \frac\pi 3+2\pi n, n \in \mathbb Z.

B) Za pomocą koła liczbowego wybierz pierwiastki należące do przedziału \left[ \frac(3\pi )2;\, 3\pi \right].

x_1=\frac\pi 4+2\pi =\frac(9\pi )4,

x_2=\frac\pi 3+2\pi =\frac(7\pi )3,

x_3=-\frac\pi 3+2\pi =\frac(5\pi )3.

Odpowiedź

A) \frac\pi 4+\pi n, \pm\frac\pi 3+2\pi n, n \in \mathbb Z;

B) \frac(5\pi)3, \frac(7\pi )3, \frac(9\pi)4.

Stan

A) Rozwiązać równanie (2\sin ^24x-3\cos 4x)\cdot \sqrt (tgx)=0.

B) Wskaż pierwiastki tego równania należące do przedziału \left(0;\,\frac(3\pi )2\right] ;

Pokaż rozwiązanie

Rozwiązanie

A) OZ: \begin(cases) tgx\geqslant 0\\x\neq \frac\pi 2+\pi k,k \in \mathbb Z. \end(cases)

Oryginalne równanie na ODZ jest równoważne zbiorowi równań

\left[\!\!\begin(array)(l) 2 \sin ^2 4x-3 \cos 4x=0,\\tg x=0. \end(tablica)\right.

Rozwiążmy pierwsze równanie. W tym celu dokonamy wymiany \cos 4x=t, t \in [-1; 1]. Wtedy \sin^24x=1-t^2. Otrzymujemy:

2(1-t^2)-3t=0,

2t^2+3t-2=0,

t_1=\frac12, t_2=-2, t_2\notin [-1; 1].

\cos 4x=\frac12,

4x=\pm\frac\pi 3+2\pi n,

x=\pm \frac\pi (12)+\frac(\pi n)2, n \in \mathbb Z.

Rozwiążmy drugie równanie.

tg x=0,\, x=\pi k, k \in \mathbb Z.

Korzystając z okręgu jednostkowego, znajdujemy rozwiązania spełniające ODZ.

Znak „+” oznacza 1. i 3. ćwiartkę, w której tg x>0.

Otrzymujemy: x=\pi k, k \in \mathbb Z; x=\frac\pi (12)+\pi n, n \in \mathbb Z; x=\frac(5\pi )(12)+\pi m, m \in \mathbb Z.

B) Znajdźmy pierwiastki należące do przedziału \left(0;\,\frac(3\pi )2\right].

x=\frac\pi (12), x=\frac(5\pi )(12); x=\pi; x=\frac(13\pi )(12); x=\frac(17\pi )(12).

Odpowiedź

A) \pi k, k \in \mathbb Z; \frac\pi (12)+\pi n, n \in \mathbb Z; \frac(5\pi )(12)+\pi m, m \in \mathbb Z.

B) \Liczba Pi; \frac\pi (12); \frac(5\pi )(12); \frac(13\pi )(12); \frac(17\pi )(12).

Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu Kulabukhova.

Stan

A) Rozwiązać równanie: \cos ^2x+\cos ^2\frac\pi 6=\cos ^22x+\sin ^2\frac\pi 3;

B) Wypisz wszystkie pierwiastki należące do przedziału \left(\frac(7\pi )2;\,\frac(9\pi )2\right].

Pokaż rozwiązanie

Rozwiązanie

A) Ponieważ \sin \frac\pi 3=\cos \frac\pi 6, To \sin ^2\frac\pi 3=\cos ^2\frac\pi 6, Oznacza to, że dane równanie jest równoważne równaniu \cos^2x=\cos ^22x, które z kolei jest równoważne równaniu \cos^2x-\cos ^2 2x=0.

Ale \cos ^2x-\cos ^22x= (\cos x-\cos 2x)\cdot (\cos x+\cos 2x) I

\cos 2x=2 \cos ^2 x-1, więc równanie ma postać:

(\cos x-(2 \cos ^2 x-1))\,\cdot(\cos x+(2 \cos ^2 x-1))=0,

(2 \cos ^2 x-\cos x-1)\,\cdot (2 \cos ^2 x+\cos x-1)=0.

Wtedy albo 2 \cos ^2 x-\cos x-1=0, albo 2 \cos ^2 x+\cos x-1=0.

Rozwiązując pierwsze równanie jako równanie kwadratowe dla \cos x, otrzymujemy:

(\cos x)_(1,2)=\frac(1\pm\sqrt 9)4=\frac(1\pm3)4. Zatem albo \cos x=1 albo \cos x=-\frac12. Jeśli \cos x=1, to x=2k\pi , k \in \mathbb Z. If \cos x=-\frac12, To x=\pm \frac(2\pi )3+2s\pi , s \in \mathbb Z.

Podobnie, rozwiązując drugie równanie, otrzymujemy \cos x=-1 lub \cosx=\frac12. Jeśli \cos x=-1, to pierwiastki x=\pi +2m\pi , m \in \mathbb Z. Jeśli \cos x=\frac12, To x=\pm \frac\pi 3+2n\pi , n \in \mathbb Z.

Połączmy otrzymane rozwiązania:

x=m\pi , m \in \mathbb Z; x=\pm \frac\pi 3 +s\pi , s \in \mathbb Z.

B) Wybierzmy pierwiastki mieszczące się w danym przedziale za pomocą koła liczbowego.

Otrzymujemy: x_1 =\frac(11\pi)3, x_2=4\pi , x_3 =\frac(13\pi )3.

Odpowiedź

A) m\pi, m\in \mathbb Z; \pm \frac\pi 3 +s\pi , s \in \mathbb Z;

B) \frac(11\pi)3, 4\pi, \frac(13\pi)3.

Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu Kulabukhova.

Stan

A) Rozwiązać równanie 10\cos ^2\frac x2=\frac(11+5ctg\left(\dfrac(3\pi )2-x\right) )(1+tgx).

B) Wskaż pierwiastki tego równania należące do przedziału \left(-2\pi ; -\frac(3\pi )2\right).

Pokaż rozwiązanie

Rozwiązanie

A) 1. Zgodnie ze wzorem redukcyjnym, ctg\lewo(\frac(3\pi )2-x\prawo) =tgx. Dziedziną definicji równania będą takie wartości x, że \cos x \neq 0 i tan x \neq -1. Przekształćmy równanie, korzystając ze wzoru na cosinus podwójnego kąta 2 \cos ^2 \frac x2=1+\cos x. Otrzymujemy równanie: 5(1+\cos x) =\frac(11+5tgx)(1+tgx).

Zauważ, że \frac(11+5tgx)(1+tgx)= \frac(5(1+tgx)+6)(1+tgx)= 5+\frac(6)(1+tgx), więc równanie staje się: 5+5 \cos x=5 +\frac(6)(1+tgx). Stąd \cos x =\frac(\dfrac65)(1+tgx), \cos x+\sin x =\frac65.

2. Przekształć \sin x+\cos x korzystając ze wzoru na redukcję i wzoru na sumę cosinusów: \sin x=\cos \left(\frac\pi 2-x\right), \cos x+\sin x= \cos x+\cos \left(\frac\pi 2-x\right)= 2\cos \frac\pi 4\cos \lewo(x-\frac\pi 4\prawo)= \sqrt 2\cos \left(x-\frac\pi 4\right) = \frac65.

Stąd \cos \left(x-\frac\pi 4\right) =\frac(3\sqrt 2)5. Oznacza, x-\frac\pi 4= arc\cos \frac(3\sqrt 2)5+2\pi k, k \in \mathbb Z,

Lub x-\frac\pi 4= -arc\cos \frac(3\sqrt 2)5+2\pi t, t \in \mathbb Z.

Dlatego x=\frac\pi 4+arc\cos \frac(3\sqrt 2)5+2\pi k,k \in \mathbb Z,

Lub x =\frac\pi 4-arc\cos \frac(3\sqrt 2)5+2\pi t,t \in \mathbb Z.

Znalezione wartości x należą do domeny definicji.

B) Najpierw dowiedzmy się, gdzie pierwiastki równania znajdują się przy k=0 i t=0. Będą to odpowiednio liczby a=\frac\pi 4+arccos \frac(3\sqrt 2)5 I b=\frac\pi 4-arccos \frac(3\sqrt 2)5.

1. Udowodnijmy nierówność pomocniczą:

\frac(\sqrt 2)(2)<\frac{3\sqrt 2}2<1.

Naprawdę, \frac(\sqrt 2)(2)=\frac(5\sqrt 2)(10)<\frac{6\sqrt2}{10}=\frac{3\sqrt2}{5}.

Zauważ też, że \left(\frac(3\sqrt 2)5\right) ^2=\frac(18)(25)<1^2=1, Oznacza \frac(3\sqrt 2)5<1.

2. Z nierówności (1) Z własności arc cosinus otrzymujemy:

Arcos 1

Stąd \frac\pi 4+0<\frac\pi 4+arc\cos \frac{3\sqrt 2}5<\frac\pi 4+\frac\pi 4,

0<\frac\pi 4+arccos \frac{3\sqrt 2}5<\frac\pi 2,

Podobnie, -\frac\pi 4

0=\frac\pi 4-\frac\pi 4<\frac\pi 4-arccos \frac{3\sqrt 2}5< \frac\pi 4<\frac\pi 2,

Dla k=-1 i t=-1 otrzymujemy pierwiastki równania a-2\pi i b-2\pi.

\Bigg(a-2\pi =-\frac74\pi +arccos \frac(3\sqrt 2)5,\, b-2\pi =-\frac74\pi -arccos \frac(3\sqrt 2)5\Bigg). W której -2\pi

2\pi Oznacza to, że pierwiastki te należą do danego przedziału \left(-2\pi , -\frac(3\pi )2\right).

Dla innych wartości k i t pierwiastki równania nie należą do danego przedziału.

Rzeczywiście, jeśli k\geqslant 1 i t\geqslant 1, to pierwiastki są większe niż 2\pi. Jeśli k\leqslant -2 i t\leqslant -2, to pierwiastki są mniejsze -\frac(7\pi)2.

Odpowiedź

A) \frac\pi4\pm arccos\frac(3\sqrt2)5+2\pi k, k\in\mathbb Z;

B) -\frac(7\pi)4\pm arccos\frac(3\sqrt2)5.

Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu Kulabukhova.

Stan

A) Rozwiązać równanie \sin \left(\frac\pi 2+x\right) =\sin (-2x).

B) Znajdź wszystkie pierwiastki tego równania należące do przedziału;

Pokaż rozwiązanie

Rozwiązanie

A) Przekształćmy równanie:

\cos x =-\sin 2x,

\cos x+2 \sin x \cos x=0,

\cos x(1+2 \sin x)=0,

\cosx=0,

x =\frac\pi 2+\pi n, n\in \mathbb Z;

1+2 \sinx=0,

\sin x=-\frac12,

x=(-1)^(k+1)\cdot \frac\pi 6+\pi k, k \in \mathbb Z.

B) Pierwiastki należące do segmentu znajdujemy za pomocą okręgu jednostkowego.

Wskazany przedział zawiera pojedynczą liczbę \frac\pi 2.

Odpowiedź

A) \frac\pi 2+\pi n, n \in \mathbb Z; (-1)^(k+1)\cdot \frac\pi 6+\pi k, k \in \mathbb Z;

B) \frac\pi 2.

Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu Kulabukhova.

Stan

nie jest uwzględniony w DZ.

Oznacza, \sin x \neq 1.

Podziel obie strony równania przez współczynnik (\sin x-1), różny od zera. Otrzymujemy równanie \frac 1(1+\cos 2x)=\frac 1(1+\cos (\pi +x)), lub równanie 1+\cos 2x=1+\cos (\pi +x). Stosując wzór redukcyjny po lewej stronie i wzór redukcyjny po prawej stronie, otrzymujemy równanie 2 \cos ^2 x=1-\cos x. To równanie wynika z podstawienia \cos x=t, Gdzie -1 \leqslant t \leqslant 1 sprowadź do kwadratu: 2t^2+t-1=0, czyje korzenie t_1=-1 I t_2=\frac12. Wracając do zmiennej x, otrzymujemy \cos x = \frac12 Lub \cos x=-1, Gdzie x=\frac \pi 3+2\pi m, m \in \mathbb Z, x=-\frac \pi 3+2\pi n, n \in \mathbb Z, x=\pi +2\pi k, k \in \mathbb Z.

B) Rozwiążmy nierówności

1) -\frac(3\pi )2 \leqslant \frac(\pi )3+2\pi m \leqslant -\frac \pi 2 ,

2) -\frac(3\pi )2 \leqslant -\frac \pi 3+2\pi n \leqslant -\frac \pi (2,)

3) -\frac(3\pi )2 \leqslant \pi+2\pi k \leqslant -\frac \pi 2 , M, N, k \in \mathbb Z.

1) -\frac(3\pi )2 \leqslant \frac(\pi )3+2\pi m \leqslant -\frac \pi 2 , -\frac32\leqslant \frac13+2m \leqslant -\frac12 -\frac(11)6 \leqslant 2m\leqslant -\frac56 , -\frac(11)(12) \leqslant m \leqslant -\frac5(12).

\left [-\frac(11)(12);-\frac5(12)\right].

2) -\frac (3\pi) 2 \leqslant -\frac(\pi )3+2\pi n \leqslant -\frac(\pi )(2), -\frac32 \leqslant -\frac13 +2n \leqslant -\frac12 , -\frac76 \leqslant 2n \leqslant -\frac1(6), -\frac7(12) \leqslant n \leqslant -\frac1(12).

W zakresie nie ma liczb całkowitych \left[ -\frac7(12) ; -\frac1(12)\prawo].

3) -\frac(3\pi )2 \leqslant \pi +2\pi k\leqslant -\frac(\pi )2, -\frac32 \leqslant 1+2k\leqslant -\frac12, -\frac52 \leqslant 2k \leqslant -\frac32, -\frac54 \leqslant k \leqslant -\frac34.

Nierówność tę spełnia k=-1, a następnie x=-\pi.