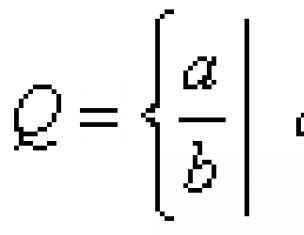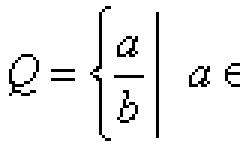Виды углов. Виды углов Углы равны то

Под редакцией Иваницкой В.П. - М.: Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1959. - 272 c.
Скачать (прямая ссылка): egnnsholaster1959.djvu Предыдущая 1 .. 11 > .. >> Следующая

Если смежные углы равны, то каждый из них называется прямым углом. Их общая сторона называется перпендикуляром к прямой, образуемой двумя другими сторонами. Можно также сказать, что биссектриса развернутого угла является перпендикуляром к прямой, образуемой его сторонами.

Теорема. Если углы равны, то равны и смежные с ними углы.

Пусть (h, k) = ^. (I, т) и пусть ^ (h!, k) и ^ (/", т)- соответствующие им смежные углы (черт. 20). Пусть, далее, / - движение, при котором ^ (h, k) отображается в (I, tri). При этом движении развернутый ^ (h, К) отобразится в развернутый (I, /"). Отсюда следует, что ^(h", k) отобразится в ^ (V, т), т. е. ^ (h!, k) = ^ (V, т).

Теорема. Существует биссектриса любого угла и притом единственная.

Пусть ^ (A, k) отличен от развернутого и внутренняя его область выпукла. Отложим на его сторонах от вершины О равные отрезки OA и OB (черт. 21, а) и соединим точки А и В. В равнобедренном треугольнике AOB А = ^B (§ 8). Соединяя середину С отрезка AB с точкой О, получим равные по первому признаку треугольники Л ОС и BOC Следовательно, AOC = ВОС, и поэтому луч ОС - биссектриса (h, k).

Если (h, k) не является выпуклым (на чертеже внутренняя область его не заштрихована), то по предыдущей

6}
t ^

теореме его биссектрисой является луч т, дополнительный к лучу /.

Из равенства треугольников ACO и BCO следует также^ что ^ ACO = BCO1 т. е. луч СО является биссектрисой развернутого угла со сторонами CA и СВ.

Пусть теперь дан раз-вернутый^(р,<7) (черт.21,6). Совершим движение, при котор ом р азвер нутый

ACB отображается в

(р, q). Луч СО отображается при этом в луч t. Так как ^ (р, t) = ^lBCO , ^BCO= ^ACO и ^ACO= = (q, t), то (р, t) = = ^(q, t), т. е. t -биссектриса (р, q).

Пусть / - биссектриса

(A, A), а Г - произвольный луч, выходящий из вершины угла и лежащий во внутренней области его. Если Г лежит во внутренней области ^ (А, /), то ^ (А, /") <^ (А, /) и ^ (А, Г) >^ (А, /). Следовательно, ^ (А, Г) <^ (А, /"). Отсюда следует, что угол имеет единственную биссектрису. Теорема доказана.

Следствие 1. Существует один и только один перпендикуляр к данной прямой, выходяищй из заданной на ней точки и лежащий в заданной полуплоскости, ограниченной этой прямой.

Следствие 2. Половины равных углов равны между собой.

Действительно, если ^ (А, А) = ^ (A", А"), то существует движение /, при котором один из них отображается в другой. По доказанной теореме их биссектрисы / и Г при данном движении также должны отобразиться одна в другую. Поэтому ^ (A, /) = ^ (A", Г).

Так как все развернутые углы равны, то частным случаем следствия 2 является предложение: все прямые углы равны между собой.

Прямые а и А, образующие при пересечении прямые углы, называются перпендикулярными (а ± Ь).

Отражение от прямой. Пусть прямая а лежит в плоскости а. Образованные при этом полуплоскости обозначим через X и р. (черт. 22). Возьмем на прямой луч А

выходящий из точки О. По свойству 6 движений (§ 7) существует единственное движение, отображающее луч h сам в себя и полуплоскость X в полуплоскость jx. Все точки этого луча по свойству 5 движений отображаются сами в себя. Все точки луча k, дополняющего до прямой луч h, тоже отображаются сами в себя.

Итак, при рассматриваемом движении все точки прямой а отображаются сами в себя. Легко, далее, видеть, что по-

Возьмем теперь точку вне прямой а.

Теорема. Через любую точку, не лежащую на прямой, проходит единственная прямая, перпендикулярная данной прямой.

Доказательство. Пусть M - точка, лежащая вне прямой а (черт. 23). Прямая а делит плоскость, определяемую этой прямой и

точкой М, на две полуплоскости: полуплоскость X, содержащую точку М, и полуплоскость jx. При отражении от прямой а точка M отображается в точку M" полуплоскости jx. Так как точки M и M" лежат в разных полуплоско-

стях, то прямые MM" и а Черт 23

пересекаются в некоторой

точке M0, которая при отражении отображается сама в себя. Отсюда следует, что прямая MM" отображается сама в себя, и поэтому углы / и 2, образованные ею с прямой а (см. черт. 23), отображаются один в другой.

луплоскость jx отображается при этом в полуплоскость X.

Рассматриваемое движение называется отражением от прямой а.

Из существования биссектрисы развернутого угла следует, что через любую точку, лежащую на прямой а, всегда можно провести прямую Ъ, перпендикулярную к прямой а.

Значит, эти углы равны, а так как они, кроме того, смежные, то MM" ± а. Пусть теперь через M проведена другая пряхмая, пересекающая прямую а в некоторой точке Af0. Она отобразится в прямую M"N0, a ^ MN0M0 отобразится в M"N0M0. Итак, ^ 3 = ^i4. Но в силу аксиомы 1 (§ 2) чки M1 N0 и M" не лежат на одной прямой, и поэтому сумма углов 3 и 4, т. е. ^ MN0M", не является развернутым углом. Отсюда вытекает, что углы 3 и 4 отличны от прямого и прямая MN0 не будет перпендикулярна прямой а. Прямая MM" является, таким образом, единственной прямой, перпендикулярной а и проходящей через точку М.

Каждый угол, в зависимости от его величины, имеет своё название:

Вид угла	Размер в градусах	Пример
Острый	Меньше 90°
Прямой	Равен 90°. На чертеже прямой угол, обычно обозначают символом , проведённым от одной стороны угла до другой.
Тупой	Больше 90°, но меньше 180°
Развёрнутый	Равен 180° Развёрнутый угол равен сумме двух прямых углов, а прямой угол составляет половину развёрнутого угла.
Выпуклый	Больше 180°, но меньше 360°
Полный	Равен 360°

Два угла называются смежными , если у них одна сторона общая, а две другие стороны составляют прямую линию:

Углы MOP и PON смежные, так как луч OP - общая сторона, а две другие стороны - OM и ON составляют прямую.

Общая сторона смежных углов называется наклонной к прямой , на которой лежат две другие стороны, только в том случае, когда смежные углы не равны между собой. Если смежные углы равны, то их общая сторона будет перпендикуляром .

Сумма смежных углов равна 180°.

Два угла называются вертикальными , если стороны одного угла дополняют до прямых линий стороны другого угла:

Углы 1 и 3, а также углы 2 и 4 - вертикальные.

Вертикальные углы равны.

Докажем, что вертикальные углы равны:

Сумма ∠1 и ∠2 составляет развёрнутый угол. И сумма ∠3 и ∠2 составляет развёрнутый угол. Значит, эти две суммы равны:

∠1 + ∠2 = ∠3 + ∠2.

В этом равенстве слева и справа есть по одинаковому слагаемому - ∠2. Равенство не нарушится, если это слагаемое в левой и в правой части опустить. Тогда мы получаем.

Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a 1 b) и (a 2 b) смежные. У них сторона b общая, а стороны a 1 и a 2 являются дополнительными полупрямыми.

Вопрос 2. Докажите, что сумма смежных углов равна 180°.
Ответ. Теорема 2.1. Сумма смежных углов равна 180°.
Доказательство. Пусть угол (a 1 b) и угол (a 2 b) - данные смежные углы (см. рис.31). Луч b проходит между сторонами a 1 и a 2 развёрнутого угла. Поэтому сумма углов (a 1 b) и (a 2 b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.

Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.

Из теоремы 2.1 следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a 1 b) и (c 1 d) равны. Нам нужно доказать, что углы (a 2 b) и (c 2 d) тоже равны.
Сумма смежных углов равна 180°. Из этого следует, что a 1 b + a 2 b = 180° и c 1 d + c 2 d = 180°. Отсюда, a 2 b = 180° - a 1 b и c 2 d = 180° - c 1 d. Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° - a 1 b = c 2 d. По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.

Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.

Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол.
Ответ. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол: x + 90° = 180°, x= 180° - 90°, x = 90°.

Вопрос 6. Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.

Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a 1 b 1) и (a 2 b 2)- данные вертикальные углы (рис. 34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т.е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.

Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.

Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».

Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3. Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.
Доказательство. Пусть a - данная прямая и A - данная точка на ней. Обозначим через a 1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.

Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Углы (a 1 b 1) и (a 1 c 1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a 1 . Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.

Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.

Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.

Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.

Углы.

Основные понятия.

Угол - это фигура, образованная двумя лучами, выходящими из одной точки.

Вершина угла - это точка, из которой выходят два луча, образующих этот угол.

Биссектриса - это луч, который выходит из вершины угла и делит угол пополам.

Развернутый угол - это угол, стороны которого лежат на одной плоскости; равен 180? и является прямой.

Прямой угол - это угол, равный половине развернутого угла; равен 90?.

Острый угол - это угол, который меньше прямого.

Тупой угол - это угол, который больше прямого, но меньше развернутого.

Угол разбивает плоскость на две части. Каждая из частей называется плоским углом .

Плоские углы с общими сторонами называются дополнительными .

Если плоский угол является частью полуплоскости, то его градусной мерой называется градусная мера обычного угла с теми же сторонами.

Если плоский угол содержит полуплоскость, то его градусная мера равна 360 º - α, где α - градусная мера дополнительного плоского угла.

Равные углы.

Это углы, которые совпадают при наложении.

Смежные углы.

Два угла называются смежными , если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

На рисунке углы (ad) и (cd) смежные. У них сторона d общая, а стороны a и c - дополнительные полупрямые.

Теорема:

Сумма смежных углов равна 180 º .

Из теоремы следует:

Если два угла равны, то смежные с ними углы равны.

Если угол не развернутый, то его градусная мера меньше 180 º .

Угол, смежный с прямым углом, есть прямой угол.

Вертикальные углы.

Два угла называются вертикальными , если стороны одного угла являются дополнительными полупрямыми сторон другого. Они созданы пересечением двух прямых и не являются прилегающими, имеют общую вершину и одинаковую градусную меру.

На рисунке углы (A 1 B 1) и (A 2 B 2) вертикальные. Стороны A 2 и B 2 второго угла являются дополнительными полупрямыми сторон A 1 и B 1 первого угла.

Теорема:

Вертикальные углы равны.

Центральный угол.

Центральным углом в окружности называется плоский угол с вершиной в ее центре (рис.1).

Часть окружности, расположенная внутри плоского угла, называется дугой окружности , соответствующей этому центральному углу (на рис.1 дуга AB является дугой окружности).

Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.

Углы, вписанные в окружность.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность (рис.2).

Свойства:

Углы при пересечении двух прямых третьей.

При пересечении прямых a и b секущей c образуется восемь углов, которые на рисунке обозначены цифрами. Некоторые пары этих углов имеют специальные названия:
соответственные углы : 1 и 5, 4 и 8, 2 и 6, 3 и 7;

накрест лежащие углы : 3 и 5, 4 и 6;
односторонние углы : 4 и 5, 3 и 6.

Признаки параллельности двух прямых

Теорема 1. Если при пересечении двух прямых секущей:

накрест лежащие углы равны, или

соответственные углы равны, или

сумма односторонних углов равна 180°, то

прямые параллельны (рис.1).

Доказательство. Ограничимся доказательством случая 1.

Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.

Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 - внешний угол треугольника АВМ, а ∠ 6 - внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.

Следствие 1 . Две различные прямые на плоскости, перпендикулярные одной и той же прямой, параллельны (рис.2).

Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное) тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду). Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.

Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.

Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).

Затем проводим через точку М прямую b перпендикулярно прямой р. Прямая b параллельна прямой а согласно следствию из теоремы 1.

Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной .

Основное свойство параллельных прямых состоит в следующем.

Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.

1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис.4).

2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).

Справедлива и следующая теорема.

Теорема 2. Если две параллельные прямые пересечены секущей, то:

накрест лежащие углы равны;

соответственные углы равны;

сумма односторонних углов равна 180°.

Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).

Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.

Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.

Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.

Решение. Пусть условию отвечает рисунок 6.