ตัวอย่างการหาอันดับของเมทริกซ์พร้อมคำตอบโดยละเอียด ค้นหาอันดับของเมทริกซ์: วิธีการและตัวอย่าง วิธีการตรวจสอบระบบสมการเชิงเส้นเพื่อความสม่ำเสมอ

อันดับของเมทริกซ์เป็นคุณลักษณะเชิงตัวเลขที่สำคัญ ปัญหาที่พบบ่อยที่สุดที่ต้องค้นหาอันดับของเมทริกซ์คือการตรวจสอบความสอดคล้องของระบบสมการพีชคณิตเชิงเส้น ในบทความนี้ เราจะให้แนวคิดเกี่ยวกับอันดับของเมทริกซ์และพิจารณาวิธีการค้นหา เพื่อการดูดซึมที่ดีขึ้นของวัสดุ เราจะวิเคราะห์รายละเอียดการแก้ปัญหาของตัวอย่างต่างๆ

การนำทางหน้า

การกำหนดอันดับของเมทริกซ์และแนวคิดเพิ่มเติมที่จำเป็น

ก่อนที่จะประกาศคำจำกัดความของอันดับของเมทริกซ์ เราควรเข้าใจแนวคิดของผู้เยาว์ให้ดีเสียก่อน และการหาค่ารองของเมทริกซ์หมายถึงความสามารถในการคำนวณดีเทอร์มีแนนต์ ดังนั้น หากจำเป็น เราแนะนำให้ระลึกถึงทฤษฎีของบทความ วิธีการหาดีเทอร์มีแนนต์ของเมทริกซ์ คุณสมบัติของดีเทอร์มีแนนต์

ใช้เมทริกซ์ A ของคำสั่ง ให้ k เป็นจำนวนธรรมชาติไม่เกินจำนวนที่น้อยที่สุดของตัวเลข m และ n นั่นคือ .

คำนิยาม.

คำสั่งรองของ kthของเมทริกซ์ A เรียกว่า ดีเทอร์มีแนนต์ของเมทริกซ์กำลังสองของลำดับ ซึ่งประกอบด้วยองค์ประกอบของเมทริกซ์ A ซึ่งอยู่ใน k แถวและคอลัมน์ k ที่เลือกไว้ล่วงหน้า และการจัดเรียงขององค์ประกอบของเมทริกซ์ A จะถูกรักษาไว้

กล่าวอีกนัยหนึ่งถ้าเราลบแถว (p – k) และ (n – k) คอลัมน์ในเมทริกซ์ A และสร้างเมทริกซ์จากองค์ประกอบที่เหลือโดยคงการจัดเรียงองค์ประกอบของเมทริกซ์ A แล้วดีเทอร์มีแนนต์ของเมทริกซ์ผลลัพธ์ เป็นตัวรองของคำสั่ง k ของเมทริกซ์ A

ลองดูคำจำกัดความของเมทริกซ์ไมเนอร์โดยใช้ตัวอย่าง

พิจารณาเมทริกซ์ .

ให้เราเขียนตัวรองอันดับหนึ่งหลายตัวของเมทริกซ์นี้ ตัวอย่างเช่น หากเราเลือกแถวที่สามและคอลัมน์ที่สองของเมทริกซ์ A ทางเลือกของเราจะสอดคล้องกับลำดับแรกรองลงมา ... กล่าวอีกนัยหนึ่ง เพื่อให้ได้ไมเนอร์นี้ เราได้ขีดฆ่าแถวที่หนึ่งและสอง เช่นเดียวกับคอลัมน์ที่หนึ่ง สาม และสี่จากเมทริกซ์ A และประกอบเป็นดีเทอร์มีแนนต์จากองค์ประกอบที่เหลือ หากเราเลือกแถวแรกและคอลัมน์ที่สามของเมทริกซ์ A เราจะได้ค่ารอง .

ให้เราอธิบายขั้นตอนการรับผู้เยาว์ที่มีลำดับแรกพิจารณา
และ .

ดังนั้น รองอันดับที่หนึ่งของเมทริกซ์จึงเป็นองค์ประกอบของเมทริกซ์เอง

เราแสดงผู้เยาว์อันดับสองหลายราย เลือกสองแถวและสองคอลัมน์ ตัวอย่างเช่น ใช้แถวแรกและแถวที่สอง และคอลัมน์ที่สามและสี่ ด้วยตัวเลือกนี้ เรามีตัวเลือกรองลงมา ... ไมเนอร์นี้ยังสามารถเกิดขึ้นได้โดยการลบแถวที่สาม คอลัมน์ที่หนึ่งและที่สองออกจากเมทริกซ์ A

รองอันดับสองของเมทริกซ์ A คือ

ให้เราอธิบายการสร้างผู้เยาว์อันดับสองเหล่านี้
และ .

ตัวรองของลำดับที่สามของเมทริกซ์ A สามารถพบได้ในทำนองเดียวกัน เนื่องจากเมทริกซ์ A มีเพียงสามแถว เราจึงเลือกทั้งหมด หากเราเลือกสามคอลัมน์แรกสำหรับแถวเหล่านี้ เราก็จะได้อันดับรองลงมา

นอกจากนี้ยังสามารถสร้างได้โดยการลบคอลัมน์สุดท้ายของเมทริกซ์ A

รองลงมาคือ

ได้จากการลบคอลัมน์ที่สามของเมทริกซ์ A

นี่คือภาพวาดที่แสดงการสร้างผู้เยาว์อันดับสามเหล่านี้
และ .

สำหรับเมทริกซ์ A ที่กำหนด ลำดับรองที่สูงกว่าลำดับที่สามจะไม่มีอยู่จริงตั้งแต่นั้นมา

ลำดับที่ k ของเมทริกซ์ A ของลำดับมีกี่ตัว

จำนวนผู้เยาว์ของคำสั่ง k สามารถคำนวณได้ดังนี้โดยที่ และ - จำนวนชุดค่าผสมจาก p ถึง k และจาก n ถึง k ตามลำดับ

วิธีสร้างผู้เยาว์ทั้งหมดของคำสั่ง k ของเมทริกซ์ A ของคำสั่ง p โดย n

เราต้องการหมายเลขแถวเมทริกซ์และหมายเลขคอลัมน์จำนวนมาก เราเขียนทุกอย่างลง การรวมกันขององค์ประกอบ p โดย k(พวกเขาจะสอดคล้องกับแถวที่เลือกของเมทริกซ์ A เมื่อสร้างลำดับรอง k) ในแต่ละชุดของหมายเลขบรรทัด เราจะเพิ่มการรวมกันขององค์ประกอบ n ทั้งหมดที่มีหมายเลขคอลัมน์ k ตามลำดับ ชุดค่าผสมของหมายเลขแถวและหมายเลขคอลัมน์ของเมทริกซ์ A เหล่านี้จะช่วยในการประกอบตัวรองทั้งหมดของลำดับ k

ลองมาดูตัวอย่างกัน

ตัวอย่าง.

หาตัวรองลำดับที่สองทั้งหมดของเมทริกซ์

สารละลาย.

เนื่องจากลำดับของเมทริกซ์ดั้งเดิมคือ 3 คูณ 3 ดังนั้นจำนวนรองทั้งหมดของลำดับที่สองจะเป็น .

ลองเขียนชุดค่าผสมทั้งหมดของตัวเลข 3 คูณ 2 ของแถวของเมทริกซ์ A: 1, 2; 1, 3 และ 2, 3 การรวมกันของหมายเลขคอลัมน์ 3 คูณ 2 คือ 1, 2; 1, 3 และ 2, 3

หาเมทริกซ์ A แถวที่หนึ่งและสอง การเลือกแถวเหล่านี้ในคอลัมน์ที่หนึ่งและสอง คอลัมน์ที่หนึ่งและสาม คอลัมน์ที่สองและสาม เราจะได้ส่วนรองตามลำดับ

สำหรับแถวที่หนึ่งและสาม โดยมีตัวเลือกคอลัมน์ที่คล้ายกัน เรามี

ยังคงต้องเพิ่มคอลัมน์ที่หนึ่งและสอง ที่หนึ่งและสาม ที่สองและสามในแถวที่สองและที่สาม:

ดังนั้น จะพบตัวรองอันดับสองทั้งหมดเก้าตัวของเมทริกซ์ A

ตอนนี้ เราสามารถดำเนินการกำหนดอันดับของเมทริกซ์

คำนิยาม.

อันดับเมทริกซ์เป็นลำดับสูงสุดของไมเนอร์ที่ไม่ใช่ศูนย์ในเมทริกซ์

อันดับของเมทริกซ์ A จะเรียกว่าอันดับ (A) คุณยังสามารถค้นหาการกำหนด Rg (A) หรือ Rang (A)

จากคำจำกัดความของอันดับของเมทริกซ์และค่ารองของเมทริกซ์ เราสามารถสรุปได้ว่าอันดับของเมทริกซ์ศูนย์มีค่าเท่ากับศูนย์ และอันดับของเมทริกซ์ที่ไม่ใช่ศูนย์คืออย่างน้อยหนึ่งรายการ

การหาอันดับของเมทริกซ์ตามนิยาม

ดังนั้น วิธีแรกในการหาอันดับของเมทริกซ์คือ วิธีเดรัจฉาน... วิธีนี้ขึ้นอยู่กับการกำหนดอันดับของเมทริกซ์

สมมติว่าเราต้องหาอันดับของเมทริกซ์ A ของลำดับ

มาอธิบายสั้นๆ อัลกอริทึมการแก้ปัญหานี้โดยการแจกแจงผู้เยาว์

หากมีองค์ประกอบอย่างน้อยหนึ่งองค์ประกอบของเมทริกซ์ที่แตกต่างจากศูนย์ ลำดับของเมทริกซ์จะเท่ากับหนึ่งเป็นอย่างน้อย (เนื่องจากมีรายการรองอันดับที่หนึ่งที่ไม่เท่ากับศูนย์)

ต่อไป เราจะวนซ้ำกับผู้เยาว์อันดับสอง หากผู้เยาว์ลำดับที่สองทั้งหมดมีค่าเท่ากับศูนย์ ลำดับของเมทริกซ์จะเท่ากับหนึ่ง หากมีผู้เยาว์อันดับสองที่ไม่ใช่ศูนย์อย่างน้อยหนึ่งราย เราจะส่งต่อไปยังการแจงนับผู้เยาว์อันดับสาม และอันดับของเมทริกซ์คืออย่างน้อยสอง

ในทำนองเดียวกัน หากผู้เยาว์ลำดับที่สามทั้งหมดเป็นศูนย์ ลำดับของเมทริกซ์จะเป็นสอง หากมีอย่างน้อยหนึ่งในลำดับรองที่สามที่ไม่ใช่ศูนย์ ลำดับของเมทริกซ์คืออย่างน้อยสาม และเราจะพิจารณาอันดับรองที่สี่

โปรดทราบว่าอันดับของเมทริกซ์ต้องไม่เกินตัวเลขที่น้อยที่สุดของ p และ n

ตัวอย่าง.

หาอันดับของเมทริกซ์ .

สารละลาย.

เนื่องจากเมทริกซ์ไม่เป็นศูนย์ ลำดับของมันคืออย่างน้อยหนึ่งอันดับ

รองลงมาของลำดับที่สอง ไม่ใช่ศูนย์ ดังนั้น ลำดับของเมทริกซ์ A อย่างน้อยสอง เราส่งต่อไปยังการแจงนับผู้เยาว์ของลำดับที่สาม ทั้งหมดนั้น สิ่งของ.

ผู้เยาว์อันดับสามทั้งหมดเป็นศูนย์ ดังนั้นอันดับของเมทริกซ์คือสอง

ตอบ:

อันดับ (A) = 2

การหาอันดับของเมทริกซ์โดยวิธี bordering minors

มีวิธีอื่นในการค้นหาอันดับของเมทริกซ์ที่ช่วยให้คุณได้ผลลัพธ์โดยใช้การคำนวณน้อยลง

วิธีหนึ่งคือ ติดขอบวิธีการรอง.

มาจัดการกับ ที่มีพรมแดนติดกับผู้เยาว์.

มีการกล่าวว่าผู้เยาว์ M ตกลงของ (k + 1) ลำดับที่ (k + 1) ของเมทริกซ์ A ล้อมรอบผู้เยาว์ M ของคำสั่ง k ของเมทริกซ์ A หากเมทริกซ์ที่สอดคล้องกับผู้เยาว์ M ตกลง "มี" เมทริกซ์ที่สอดคล้องกับผู้เยาว์ NS.

กล่าวอีกนัยหนึ่ง เมทริกซ์ที่สอดคล้องกับไมเนอร์ M ที่มีเส้นขอบ ได้มาจากเมทริกซ์ที่สอดคล้องกับไมเนอร์ M ที่มีขอบ ok โดยการลบองค์ประกอบของหนึ่งแถวและหนึ่งคอลัมน์

ตัวอย่างเช่น พิจารณาเมทริกซ์ และรับผู้เยาว์ของลำดับที่สอง มาเขียนผู้เยาว์ที่มีพรมแดนติดกันทั้งหมด:

วิธีการตีกรอบผู้เยาว์ได้รับการพิสูจน์โดยทฤษฎีบทต่อไปนี้ (เรานำเสนอสูตรโดยไม่มีการพิสูจน์)

ทฤษฎีบท.

หากผู้เยาว์ทั้งหมดที่อยู่ติดกับลำดับที่ k รองลงมาของเมทริกซ์ A ของลำดับ p คูณ n เท่ากับศูนย์ ดังนั้นตัวรองทั้งหมดของลำดับ (k + 1) ของเมทริกซ์ A จะเท่ากับศูนย์

ดังนั้น ในการหาอันดับของเมทริกซ์ ไม่จำเป็นต้องวนซ้ำกับผู้เยาว์ทั้งหมดที่มีพรมแดนติดกันเพียงพอ จำนวนผู้เยาว์ที่มีพรมแดนติดกับลำดับที่ k รองลงมาของเมทริกซ์ลำดับ A นั้นหาได้จากสูตร ... โปรดทราบว่าผู้เยาว์ที่อยู่ติดกับลำดับที่ k รองลงมาของเมทริกซ์ A นั้นไม่เกิน (k + 1) - ลำดับรองลงมาของเมทริกซ์ A ดังนั้น ในกรณีส่วนใหญ่ การใช้วิธีการของผู้เยาว์ที่มีพรมแดนติดกันนั้นให้ผลกำไรมากกว่าการแจงนับอย่างง่ายของผู้เยาว์ทั้งหมด

ให้เราดำเนินการค้นหาอันดับของเมทริกซ์โดยวิธีผู้เยาว์ที่มีพรมแดนติด มาอธิบายสั้นๆ อัลกอริทึมวิธีนี้

หากเมทริกซ์ A ไม่ใช่ศูนย์ ดังนั้นในอันดับรองลงมา เราจะนำองค์ประกอบใดๆ ของเมทริกซ์ A ที่ไม่ใช่ศูนย์ พิจารณาผู้เยาว์ที่มีพรมแดนติด หากทั้งหมดมีค่าเท่ากับศูนย์ ลำดับของเมทริกซ์จะเท่ากับหนึ่ง หากมีอย่างน้อยหนึ่งผู้เยาว์ที่ไม่มีพรมแดนติดกับ (ลำดับคือสองคน) เราจะพิจารณาผู้เยาว์ที่มีพรมแดนติดกัน หากทั้งหมดเป็นศูนย์ อันดับ (A) = 2 หากผู้เยาว์ที่มีพรมแดนติดกับอย่างน้อยหนึ่งคนไม่ใช่ศูนย์ (ลำดับคือสามคน) เราจะถือว่าผู้เยาว์ที่มีพรมแดนติดกัน เป็นต้น เป็นผลให้อันดับ (A) = k หากผู้เยาว์ที่มีพรมแดนติดกับลำดับที่ (k + 1) ของเมทริกซ์ A เท่ากับศูนย์หรืออันดับ (A) = นาที (p, n) หากไม่มีศูนย์ ผู้เยาว์ที่มีพรมแดนติดกับผู้เยาว์ของคำสั่ง (ต่ำสุด ( p, n) - 1)

ให้เราวิเคราะห์วิธี bordering minors เพื่อหาอันดับของเมทริกซ์โดยใช้ตัวอย่าง

ตัวอย่าง.

หาอันดับของเมทริกซ์ โดยวิธีการตีกรอบผู้เยาว์

สารละลาย.

เนื่องจากองค์ประกอบ a 1 1 ของเมทริกซ์ A ไม่เป็นศูนย์ เราถือว่ามันเป็นรองอันดับรองลงมา มาเริ่มมองหาผู้เยาว์ที่ไม่มีขอบเป็นศูนย์:

พบผู้เยาว์ที่มีพรมแดนติดกับลำดับที่สอง นอกเหนือจากศูนย์ มาแยกแยะผู้เยาว์ที่มีพรมแดนติดกัน ( . ของพวกเขา สิ่งของ):

ผู้เยาว์ทั้งหมดที่อยู่ติดกับลำดับรองลงมามีค่าเท่ากับศูนย์ ดังนั้น ลำดับของเมทริกซ์ A เท่ากับสอง

ตอบ:

อันดับ (A) = 2

ตัวอย่าง.

หาอันดับของเมทริกซ์ โดยใช้ผู้เยาว์ที่มีพรมแดนติด

สารละลาย.

ในฐานะที่เป็นผู้เยาว์ที่ไม่ใช่ศูนย์ของลำดับแรก เรานำองค์ประกอบ a 1 1 = 1 ของเมทริกซ์ A ผู้เยาว์ที่ขนาบข้างของคำสั่งที่สอง ไม่เป็นศูนย์ ผู้เยาว์รายนี้ล้อมรอบด้วยผู้เยาว์อันดับสาม
... เนื่องจากมันไม่เท่ากับศูนย์และไม่มีขอบรองสำหรับมัน ลำดับของเมทริกซ์ A จึงเท่ากับสาม

ตอบ:

อันดับ (A) = 3

การหาอันดับโดยใช้การแปลงเมทริกซ์เบื้องต้น (วิธีเกาส์)

พิจารณาวิธีอื่นในการหาอันดับของเมทริกซ์

การแปลงเมทริกซ์ต่อไปนี้เรียกว่าระดับประถมศึกษา:

• การเปลี่ยนแปลงของแถว (หรือคอลัมน์) ของเมทริกซ์
• การคูณองค์ประกอบทั้งหมดของแถวใดๆ (คอลัมน์) ของเมทริกซ์ด้วยตัวเลข k ใดๆ ที่ไม่ใช่ศูนย์
• การเพิ่มองค์ประกอบของแถวใด ๆ (คอลัมน์) องค์ประกอบที่สอดคล้องกันของอีกแถว (คอลัมน์) ของเมทริกซ์ คูณด้วยจำนวนโดยพลการ k

เมทริกซ์ B เรียกว่าเทียบเท่ากับเมทริกซ์ Aถ้าได้ B จาก A โดยใช้การแปลงเบื้องต้นจำนวนจำกัด ความเท่าเทียมกันของเมทริกซ์แสดงด้วยสัญลักษณ์ "~" นั่นคือเขียน A ~ B

การค้นหาอันดับของเมทริกซ์โดยใช้การแปลงเบื้องต้นของเมทริกซ์นั้นขึ้นอยู่กับคำสั่ง: หากเมทริกซ์ B ได้มาจากเมทริกซ์ A โดยใช้การแปลงเบื้องต้นจำนวนจำกัด อันดับ (A) = อันดับ (B)

ความถูกต้องของคำสั่งนี้เป็นไปตามคุณสมบัติของดีเทอร์มีแนนต์ของเมทริกซ์:

• เมื่อแถว (หรือคอลัมน์) ของเมทริกซ์ถูกจัดเรียงใหม่ ดีเทอร์มีแนนต์จะเปลี่ยนเครื่องหมาย หากมีค่าเท่ากับศูนย์ เมื่อมีการเปลี่ยนแถว (คอลัมน์) ค่าจะยังคงเท่ากับศูนย์
• เมื่อองค์ประกอบทั้งหมดของแถว (คอลัมน์) ของเมทริกซ์คูณด้วยจำนวน k ที่ไม่ใช่ศูนย์ ดีเทอร์มีแนนต์ของเมทริกซ์ที่ได้จะเท่ากับดีเทอร์มีแนนต์ของเมทริกซ์ดั้งเดิมคูณด้วย k หากดีเทอร์มีแนนต์ของเมทริกซ์ดั้งเดิมเท่ากับศูนย์ หลังจากคูณองค์ประกอบทั้งหมดของแถวหรือคอลัมน์ใดๆ ด้วยจำนวน k แล้ว ดีเทอร์มีแนนต์ของเมทริกซ์ที่ได้ก็จะเท่ากับศูนย์เช่นกัน
• การเพิ่มองค์ประกอบบางแถว (คอลัมน์) ของเมทริกซ์ องค์ประกอบที่สอดคล้องกันของอีกแถว (คอลัมน์) ของเมทริกซ์ คูณด้วยตัวเลข k บางตัวจะไม่เปลี่ยนดีเทอร์มีแนนต์

สาระสำคัญของวิธีการแปลงเบื้องต้นประกอบด้วยการลดเมทริกซ์ ซึ่งเป็นอันดับที่เราต้องหา ให้เป็นสี่เหลี่ยมคางหมู (ในบางกรณี เป็นสามเหลี่ยมบน) โดยใช้การแปลงเบื้องต้น

ทำไมถึงทำเช่นนี้? อันดับของเมทริกซ์ประเภทนี้หาได้ง่ายมาก เท่ากับจำนวนบรรทัดที่มีองค์ประกอบที่ไม่ใช่ศูนย์อย่างน้อยหนึ่งรายการ และเนื่องจากอันดับของเมทริกซ์ไม่เปลี่ยนแปลงระหว่างการแปลงเบื้องต้น ค่าที่ได้จะเป็นอันดับของเมทริกซ์ดั้งเดิม

ต่อไปนี้คือภาพประกอบของเมทริกซ์ ซึ่งหนึ่งในนั้นควรได้รับหลังจากการแปลง แบบฟอร์มขึ้นอยู่กับลำดับของเมทริกซ์

ภาพประกอบเหล่านี้เป็นเทมเพลตที่เราจะแปลงเมทริกซ์ A

มาบรรยายกัน อัลกอริธึมวิธีการ.

สมมติว่าเราต้องหาอันดับของเมทริกซ์ที่ไม่ใช่ศูนย์ A ของลำดับ (p สามารถเท่ากับ n ได้)

ดังนั้น, . ลองคูณองค์ประกอบทั้งหมดในแถวแรกของเมทริกซ์ A ด้วย ในกรณีนี้ เราได้รับเมทริกซ์ที่เทียบเท่ากัน แทนด้วย A (1):

ในองค์ประกอบของแถวที่สองของเมทริกซ์ผลลัพธ์ A (1) ให้เพิ่มองค์ประกอบที่สอดคล้องกันของแถวแรกคูณด้วย เพิ่มองค์ประกอบที่สอดคล้องกันของแถวแรกคูณด้วยองค์ประกอบในแถวที่สาม และอื่นๆ จนถึงบรรทัด p-th เราได้รับเมทริกซ์ที่เทียบเท่ากัน แทนด้วย A (2):

หากองค์ประกอบทั้งหมดของเมทริกซ์ผลลัพธ์ซึ่งอยู่ในแถวตั้งแต่วินาทีถึง p-th มีค่าเท่ากับศูนย์ ลำดับของเมทริกซ์นี้จะเท่ากับหนึ่ง ดังนั้นอันดับของเมทริกซ์ดั้งเดิมคือ เท่ากับหนึ่ง

หากมีองค์ประกอบที่ไม่ใช่ศูนย์อย่างน้อยหนึ่งรายการในแถวจากวินาทีถึง pth เราจะดำเนินการแปลงต่อไป ยิ่งกว่านั้น เราดำเนินการในลักษณะเดียวกันทั้งหมด แต่มีเฉพาะส่วนของเมทริกซ์ A ที่ทำเครื่องหมายไว้ในรูป (2)

ถ้าเราจัดเรียงแถวและ (หรือ) คอลัมน์ของเมทริกซ์ A (2) ใหม่เพื่อให้องค์ประกอบ "ใหม่" ไม่เป็นศูนย์

หมายเลข r เรียกว่าอันดับของเมทริกซ์ A หาก:
1) เมทริกซ์ A มีลำดับรอง r แตกต่างจากศูนย์
2) ลำดับรองลงมาทั้งหมด (r + 1) และสูงกว่าถ้ามีอยู่จะเท่ากับศูนย์
มิฉะนั้น ลำดับของเมทริกซ์จะเป็นลำดับสูงสุดของผู้เยาว์ที่ไม่ใช่ศูนย์
การกำหนด: rangA, r A หรือ r
จากนิยามที่ว่า r เป็นจำนวนเต็มบวก สำหรับเมทริกซ์ค่าว่าง อันดับจะถือเป็นศูนย์

วัตถุประสงค์ในการให้บริการ... เครื่องคิดเลขออนไลน์ออกแบบมาเพื่อค้นหา อันดับของเมทริกซ์... โซลูชันถูกบันทึกในรูปแบบ Word และ Excel ดูตัวอย่างการแก้ปัญหา

การเรียนการสอน. เลือกขนาดของเมทริกซ์ คลิกถัดไป

คำนิยาม . ให้เมทริกซ์ของอันดับ r ถูกกำหนด เมทริกซ์รองใดๆ ที่ไม่ใช่ศูนย์และมีลำดับ r เรียกว่า พื้นฐาน และแถวและคอลัมน์ของส่วนประกอบจะเรียกว่า แถวและคอลัมน์พื้นฐาน
ตามคำจำกัดความนี้ เมทริกซ์ A สามารถมีตัวรองพื้นฐานได้หลายตัว

อันดับของเมทริกซ์เอกลักษณ์ E คือ n (จำนวนแถว)

ตัวอย่างที่ 1 ให้เมทริกซ์สองตัว และผู้เยาว์ของพวกเขา , ... ข้อใดสามารถใช้เป็นพื้นฐานได้
สารละลาย... Minor M 1 = 0 ดังนั้นจึงไม่สามารถเป็นพื้นฐานสำหรับเมทริกซ์ใดๆ ได้ ไมเนอร์ M 2 = -9 ≠ 0 และมีลำดับที่ 2 ดังนั้นจึงสามารถใช้เป็นเมทริกซ์พื้นฐาน A หรือ / และ B ได้โดยมีอันดับเท่ากับ 2 เนื่องจาก detB = 0 (เป็นดีเทอร์มีแนนต์ที่มีคอลัมน์ตามสัดส่วนสองคอลัมน์) ดังนั้น rangB = 2 และ M 2 จึงสามารถใช้เป็นฐานรองของเมทริกซ์ B ได้ อันดับของเมทริกซ์ A คือ 3 เนื่องจาก detA = -27 ≠ 0 และ ดังนั้น ลำดับพื้นฐานรองของเมทริกซ์นี้ต้องเท่ากับ 3 นั่นคือ M 2 ไม่ใช่พื้นฐานสำหรับเมทริกซ์ A โปรดทราบว่าเมทริกซ์ A มีตัวรองพื้นฐานเพียงตัวเดียว ซึ่งเท่ากับดีเทอร์มีแนนต์ของเมทริกซ์ A

ทฤษฎีบท (บนพื้นฐานรอง) แถวใดๆ (คอลัมน์) ของเมทริกซ์เป็นการรวมกันเชิงเส้นของแถวฐาน (คอลัมน์)
ผลพวงจากทฤษฎีบท

1. คอลัมน์ (r + 1) ใดๆ (แถว) ของเมทริกซ์อันดับ r ขึ้นอยู่กับเชิงเส้น
2. หากอันดับของเมทริกซ์น้อยกว่าจำนวนแถว (คอลัมน์) แสดงว่าแถว (คอลัมน์) จะขึ้นอยู่กับเชิงเส้น หาก rangA เท่ากับจำนวนแถว (คอลัมน์) ของแถวนั้น แถว (คอลัมน์) จะเป็นอิสระเชิงเส้น
3. ดีเทอร์มีแนนต์ของเมทริกซ์ A เท่ากับศูนย์ก็ต่อเมื่อแถว (คอลัมน์) ของเมทริกซ์นั้นขึ้นอยู่กับเชิงเส้นเท่านั้น
4. หากไปที่แถว (คอลัมน์) ของเมทริกซ์ เราเพิ่มอีกแถว (คอลัมน์) คูณด้วยตัวเลขอื่นที่ไม่ใช่ศูนย์ ลำดับของเมทริกซ์จะไม่เปลี่ยนแปลง
5. หากคุณขีดฆ่าแถว (คอลัมน์) ในเมทริกซ์ ซึ่งเป็นการรวมเชิงเส้นของแถวอื่น (คอลัมน์) ลำดับของเมทริกซ์จะไม่เปลี่ยนแปลง
6. อันดับของเมทริกซ์เท่ากับจำนวนสูงสุดของแถวอิสระเชิงเส้น (คอลัมน์)
7. จำนวนแถวอิสระเชิงเส้นสูงสุดจะเท่ากับจำนวนสูงสุดของคอลัมน์อิสระเชิงเส้น

ตัวอย่างที่ 2 หาอันดับของเมทริกซ์ .
สารละลาย. ตามคำจำกัดความของอันดับของเมทริกซ์ เราจะมองหาอันดับรองลงมาของอันดับสูงสุด นอกเหนือจากศูนย์ ขั้นแรก เราแปลงเมทริกซ์ให้อยู่ในรูปแบบที่ง่ายกว่า เมื่อต้องการทำเช่นนี้ ให้คูณแถวแรกของเมทริกซ์ด้วย (-2) แล้วบวกในแถวที่สอง จากนั้นคูณด้วย (-1) แล้วบวกกับแถวที่สาม

คำนิยาม. ตามอันดับของเมทริกซ์คือจำนวนสูงสุดของเส้นอิสระเชิงเส้นที่พิจารณาว่าเป็นเวกเตอร์

ทฤษฎีบท 1 เกี่ยวกับอันดับของเมทริกซ์ ตามอันดับของเมทริกซ์คือลำดับสูงสุดของเมทริกซ์รองที่ไม่ใช่ศูนย์

เราได้วิเคราะห์แนวคิดของผู้เยาว์ในบทเรียนเกี่ยวกับดีเทอร์มิแนนต์แล้ว และตอนนี้เราจะสรุปมัน ลองพิจารณาแถวและบางคอลัมน์ในเมทริกซ์ และ "บางส่วน" นี้ควรน้อยกว่าจำนวนแถวและคอลัมน์ของเมทริกซ์ และสำหรับแถวและคอลัมน์ "บางส่วน" นี้ควรเป็นตัวเลขเดียวกัน จากนั้นที่จุดตัดของบางแถวและจำนวนคอลัมน์จะมีเมทริกซ์ที่มีลำดับต่ำกว่าเมทริกซ์ดั้งเดิมของเรากี่คอลัมน์ ดีเทอร์มีแนนต์ของเมทริกซ์นี้จะเป็นลำดับที่ k รอง ถ้า "บาง" ที่กล่าวถึง (จำนวนแถวและคอลัมน์) แทนด้วย k

คำนิยาม.ผู้เยาว์ ( NS+1) ลำดับที่ซึ่งผู้เยาว์ที่เลือกอยู่ NS-ลำดับที่ เรียกว่า bordering สำหรับผู้เยาว์ที่กำหนด

สองวิธีที่ใช้กันมากที่สุดคือ การหาอันดับของเมทริกซ์... มัน ชายแดนทางผู้เยาว์และ วิธีการแปลงเบื้องต้น(โดยวิธีเกาส์)

สำหรับวิธีการผู้เยาว์ที่มีพรมแดนติดกับจะใช้ทฤษฎีบทต่อไปนี้

ทฤษฎีบทที่ 2 เกี่ยวกับอันดับของเมทริกซ์หากจากองค์ประกอบของเมทริกซ์สามารถประกอบเป็นไมเนอร์ได้ NS- ลำดับที่ ไม่เท่ากับศูนย์ แล้วอันดับของเมทริกซ์คือ NS.

ในวิธีการแปลงเบื้องต้น ใช้คุณสมบัติต่อไปนี้:

หากโดยการแปลงเบื้องต้นได้เมทริกซ์สี่เหลี่ยมคางหมูที่เทียบเท่ากับเมทริกซ์ดั้งเดิมแล้ว อันดับของเมทริกซ์นี้คือจำนวนบรรทัดในนั้น ยกเว้นบรรทัดที่ประกอบด้วยศูนย์ทั้งหมด

การหาอันดับของเมทริกซ์โดยวิธี bordering minors method

ผู้เยาว์ที่มีพรมแดนติดกับเป็นผู้เยาว์ของลำดับที่สูงกว่าซึ่งสัมพันธ์กับผู้เยาว์ที่มีลำดับสูงกว่านี้ประกอบด้วยผู้เยาว์รายนี้

ตัวอย่างเช่น รับเมทริกซ์

มารับน้องกัน

ชายแดนจะเป็นผู้เยาว์ดังต่อไปนี้:

อัลกอริธึมในการหาอันดับของเมทริกซ์ต่อไป.

1. ค้นหาผู้เยาว์ที่ไม่ใช่ศูนย์ของลำดับที่สอง หากผู้เยาว์ลำดับที่สองทั้งหมดเท่ากับศูนย์ ลำดับของเมทริกซ์จะเท่ากับหนึ่ง ( NS =1 ).

2. หากมีอย่างน้อยหนึ่งผู้เยาว์ในลำดับที่สองที่ไม่เท่ากับศูนย์ เราจะสร้างผู้เยาว์ที่มีพรมแดนติดกับลำดับที่สาม หากผู้เยาว์ที่มีพรมแดนติดกับลำดับที่สามทั้งหมดมีค่าเท่ากับศูนย์ ลำดับของเมทริกซ์จะเท่ากับสอง ( NS =2 ).

3. หากผู้เยาว์ที่มีพรมแดนติดกับลำดับที่สามอย่างน้อยหนึ่งคนไม่เท่ากับศูนย์ เราจะสร้างผู้เยาว์ที่มีพรมแดนติดกับ หากผู้เยาว์ที่มีพรมแดนติดทั้งหมดของลำดับที่สี่มีค่าเท่ากับศูนย์ ลำดับของเมทริกซ์คือสาม ( NS =2 ).

4. ทำต่อไปตราบเท่าที่ขนาดของเมทริกซ์อนุญาต

ตัวอย่างที่ 1หาอันดับของเมทริกซ์

.

สารละลาย. รองลงมาของลำดับที่สอง .

เราใส่กรอบ จะมีผู้เยาว์ที่มีพรมแดนติดกับสี่:

,

,

ดังนั้นผู้เยาว์ที่มีพรมแดนติดกับลำดับที่สามทั้งหมดมีค่าเท่ากับศูนย์ดังนั้นอันดับของเมทริกซ์นี้จึงเท่ากับสอง ( NS =2 ).

ตัวอย่างที่ 2หาอันดับของเมทริกซ์

สารละลาย. อันดับของเมทริกซ์นี้คือ 1 เนื่องจากผู้เยาว์อันดับสองทั้งหมดของเมทริกซ์นี้มีค่าเท่ากับศูนย์ (ในกรณีนี้ เช่นเดียวกับในกรณีของผู้เยาว์ที่มีพรมแดนติดในสองตัวอย่างถัดไป นักเรียนที่รักจะได้รับเชิญให้ตรวจสอบด้วยตนเอง อาจใช้กฎในการคำนวณดีเทอร์มิแนนต์) และในกลุ่มรองอันดับหนึ่ง นั่นคือ ในบรรดาองค์ประกอบของเมทริกซ์ ไม่มีค่าเท่ากับศูนย์

ตัวอย่างที่ 3หาอันดับของเมทริกซ์

สารละลาย. ไมเนอร์ของลำดับที่สองของเมทริกซ์นี้, ในทุกไมเนอร์ของลำดับที่สามของเมทริกซ์นี้มีค่าเท่ากับศูนย์ ดังนั้นอันดับของเมทริกซ์นี้คือสอง

ตัวอย่างที่ 4หาอันดับของเมทริกซ์

สารละลาย. อันดับของเมทริกซ์นี้คือ 3 เนื่องจากเมทริกซ์อันดับสามเพียงอันดับเดียวของเมทริกซ์นี้คือ 3

การหาอันดับของเมทริกซ์โดยวิธีการแปลงเบื้องต้น (วิธีเกาส์)

ในตัวอย่างที่ 1 จะเห็นได้ว่าปัญหาในการกำหนดอันดับของเมทริกซ์โดยวิธีการล้อมรอบผู้เยาว์นั้นต้องการการคำนวณดีเทอร์มีแนนต์จำนวนมาก อย่างไรก็ตาม มีวิธีที่จะรักษาปริมาณการคำนวณให้เหลือน้อยที่สุด วิธีนี้ใช้การแปลงเมทริกซ์เบื้องต้นและเรียกอีกอย่างว่าวิธีเกาส์

การแปลงเมทริกซ์เบื้องต้นเป็นที่เข้าใจกันว่าเป็นการดำเนินการต่อไปนี้:

1) การคูณของแถวหรือคอลัมน์ใดๆ ของเมทริกซ์ด้วยตัวเลขอื่นที่ไม่ใช่ศูนย์

2) เพิ่มองค์ประกอบของแถวหรือคอลัมน์ใด ๆ ของเมทริกซ์ให้กับองค์ประกอบที่สอดคล้องกันของแถวหรือคอลัมน์อื่นคูณด้วยตัวเลขเดียวกัน

3) การสลับสองแถวหรือคอลัมน์ของเมทริกซ์

4) การลบเส้น "ศูนย์" นั่นคือองค์ประกอบทั้งหมดที่มีค่าเท่ากับศูนย์

5) การลบเส้นสัดส่วนทั้งหมดยกเว้นหนึ่งเส้น

ทฤษฎีบท.การแปลงเบื้องต้นจะไม่เปลี่ยนอันดับของเมทริกซ์ กล่าวอีกนัยหนึ่งถ้าเราใช้การแปลงเบื้องต้นจากเมทริกซ์ NSไปที่เมทริกซ์ NS, แล้ว .

ให้เมทริกซ์บางตัวได้รับ:

.

เราเลือกในเมทริกซ์นี้ เส้นโดยพลการและ คอลัมน์ตามอำเภอใจ
... แล้วดีเทอร์มีแนนต์ -ลำดับที่ประกอบด้วยองค์ประกอบเมทริกซ์
ตั้งอยู่ที่จุดตัดของแถวและคอลัมน์ที่เลือกเรียกว่าผู้เยาว์ -เมทริกซ์ลำดับที่
.

คำจำกัดความ 1.13ตามอันดับของเมทริกซ์
เรียกว่าลำดับที่ยิ่งใหญ่ที่สุดของผู้เยาว์ของเมทริกซ์นี้ นอกเหนือจากศูนย์

ในการคำนวณอันดับของเมทริกซ์ เราควรพิจารณาตัวรองทั้งหมดที่อยู่ในลำดับที่เล็กที่สุด และหากอย่างน้อยหนึ่งในนั้นไม่ใช่ศูนย์ ให้พิจารณาตัวรองที่อยู่ในลำดับสูงสุด วิธีการกำหนดอันดับของเมทริกซ์นี้เรียกว่าวิธีการสร้างขอบ (หรือวิธีผู้เยาว์ที่มีพรมแดนติด)

งาน 1.4โดยใช้วิธี bordering minors กำหนดอันดับของเมทริกซ์
.

.

พิจารณาขอบลำดับแรก ตัวอย่างเช่น
... จากนั้นเราหันไปพิจารณาเรื่องพรมแดนลำดับที่สอง

ตัวอย่างเช่น,
.

สุดท้าย มาวิเคราะห์เส้นขอบลำดับที่สามกัน

.

ดังนั้น ลำดับสูงสุดของผู้เยาว์ที่ไม่ใช่ศูนย์คือ 2 ดังนั้น
.

เมื่อแก้ปัญหา 1.4 เราสามารถสังเกตได้ว่าผู้เยาว์ที่มีพรมแดนติดกับลำดับที่สองจำนวนหนึ่งไม่ใช่ศูนย์ ในเรื่องนี้มีแนวคิดดังต่อไปนี้

คำจำกัดความ 1.14ไมเนอร์พื้นฐานของเมทริกซ์คือไมเนอร์ที่ไม่ใช่ศูนย์ใดๆ ที่มีลำดับเท่ากับอันดับของเมทริกซ์

ทฤษฎีบท 1.2(ทฤษฎีบทย่อยขั้นพื้นฐาน). แถวพื้นฐาน (คอลัมน์พื้นฐาน) มีความเป็นอิสระเชิงเส้น

โปรดทราบว่าแถว (คอลัมน์) ของเมทริกซ์จะขึ้นอยู่กับเส้นตรงถ้าหากอย่างน้อยหนึ่งแถวสามารถแสดงเป็นชุดค่าผสมเชิงเส้นของแถวอื่นๆ ได้

ทฤษฎีบท 1.3.จำนวนแถวอิสระเชิงเส้นของเมทริกซ์เท่ากับจำนวนคอลัมน์อิสระเชิงเส้นของเมทริกซ์และเท่ากับอันดับของเมทริกซ์

ทฤษฎีบท 1.4(เงื่อนไขที่จำเป็นและเพียงพอสำหรับการหายไปของดีเทอร์มีแนนต์) เพื่อเป็นตัวกำหนด -คำสั่งที่ เท่ากับศูนย์ จำเป็นและเพียงพอที่แถว (คอลัมน์) ของมันจะขึ้นกับเชิงเส้น

การคำนวณอันดับของเมทริกซ์ตามคำจำกัดความนั้นยุ่งยากเกินไป สิ่งนี้มีความสำคัญเป็นพิเศษสำหรับเมทริกซ์ของคำสั่งที่สูงกว่า ในทางปฏิบัติ ลำดับของเมทริกซ์คำนวณจากการประยุกต์ใช้ทฤษฎีบท 10.2 - 10.4 ตลอดจนการใช้แนวคิดเรื่องความเท่าเทียมกันของเมทริกซ์และการแปลงเบื้องต้น

คำจำกัดความ 1.15เมทริกซ์สองตัว
และ เรียกว่าเทียบเท่าหากอันดับของพวกเขาเท่ากันเช่น
.

ถ้าเมทริกซ์
และ เทียบเท่าแล้วหมายเหตุ
 .

ทฤษฎีบท 1.5อันดับของเมทริกซ์ไม่เปลี่ยนจากการแปลงเบื้องต้น

เราจะเรียกการแปลงเบื้องต้นของเมทริกซ์
การกระทำใดๆ ต่อไปนี้ในเมทริกซ์:

การแทนที่แถวด้วยคอลัมน์และคอลัมน์ด้วยแถวที่สอดคล้องกัน

การเปลี่ยนแปลงของแถวเมทริกซ์

การลบเส้นซึ่งองค์ประกอบทั้งหมดมีค่าเท่ากับศูนย์

การคูณสตริงด้วยจำนวนที่ไม่ใช่ศูนย์

การเพิ่มองค์ประกอบที่สอดคล้องกันของแถวอื่น ๆ ให้กับองค์ประกอบของแถวหนึ่งคูณด้วยจำนวนเดียวกัน
.

ผลพิสูจน์ทฤษฎีบท 1.5ถ้าเมทริกซ์
ที่ได้จากเมทริกซ์ โดยใช้การแปลงเบื้องต้นจำนวนจำกัด แล้วเมทริกซ์
และ มีค่าเท่ากัน

เมื่อคำนวณอันดับของเมทริกซ์ มันควรจะลดลงเป็นรูปแบบสี่เหลี่ยมคางหมูโดยใช้การแปลงเบื้องต้นจำนวนจำกัด

คำจำกัดความ 1.16เราจะเรียกรูปแบบสี่เหลี่ยมคางหมูของการแสดงเมทริกซ์เมื่อองค์ประกอบทั้งหมดที่อยู่ด้านล่างเส้นทแยงมุมหายไป ตัวอย่างเช่น:

.

ที่นี่
, องค์ประกอบของเมทริกซ์
หายตัวไป จากนั้นรูปแบบของการแสดงเมทริกซ์ดังกล่าวจะเป็นสี่เหลี่ยมคางหมู

ตามกฎแล้ว เมทริกซ์จะลดลงเป็นรูปสี่เหลี่ยมคางหมูโดยใช้อัลกอริธึมแบบเกาส์เซียน แนวคิดของอัลกอริธึมเกาส์คือการคูณองค์ประกอบของแถวแรกของเมทริกซ์ด้วยปัจจัยที่สอดคล้องกัน พวกเขาบรรลุว่าองค์ประกอบทั้งหมดของคอลัมน์แรกที่อยู่ด้านล่างองค์ประกอบ
จะหายไป จากนั้น คูณองค์ประกอบของคอลัมน์ที่สองด้วยปัจจัยที่สอดคล้องกัน เราบรรลุว่าองค์ประกอบทั้งหมดของคอลัมน์ที่สองที่อยู่ด้านล่างองค์ประกอบ
,จะหายวับไป แล้วดำเนินการในลักษณะเดียวกัน

งาน 1.5.กำหนดอันดับของเมทริกซ์โดยลดให้อยู่ในรูปสี่เหลี่ยมคางหมู

.

เพื่อความสะดวกในการใช้อัลกอริทึมเกาส์เซียน คุณสามารถสลับบรรทัดแรกและบรรทัดที่สามได้








.

แน่นอนที่นี่
... อย่างไรก็ตาม หากต้องการนำผลลัพธ์มาสู่รูปแบบที่สวยงามยิ่งขึ้น คุณสามารถทำการเปลี่ยนแปลงต่อในคอลัมน์ต่อไปได้










.

และพิจารณาการประยุกต์ใช้ธีมที่สำคัญในทางปฏิบัติด้วย: การศึกษาความเข้ากันได้ของระบบสมการเชิงเส้น.

ลำดับของเมทริกซ์คืออะไร?

บทกลอนที่ตลกขบขันของบทความมีความจริงมากมาย คำว่า "อันดับ" ที่เรามักจะเชื่อมโยงกับลำดับชั้นบางประเภท ส่วนใหญ่มักจะ กับบันไดอาชีพ ยิ่งมีความรู้ ประสบการณ์ ความสามารถ คำด่า ฯลฯ ที่บุคคลมีมากขึ้น - ยิ่งตำแหน่งและช่วงโอกาสของเขาสูงขึ้น ในแง่ของเยาวชน ยศหมายถึงระดับโดยรวมของ "ความเหนียว"

และพี่น้องคณิตศาสตร์ของเราดำเนินชีวิตด้วยหลักการเดียวกัน มาลองกันซักหน่อย เมทริกซ์ศูนย์:

ลองคิดดูว่าถ้าเมทริกซ์ หนึ่งศูนย์แล้วเราจะพูดถึงยศอะไรได้บ้าง? ทุกคนคุ้นเคยกับนิพจน์ทางการ "ศูนย์สมบูรณ์" ในสังคมเมทริกซ์ ทุกอย่างเหมือนกันหมด:

อันดับศูนย์เมทริกซ์ทุกขนาดเท่ากับศูนย์.

บันทึก : เมทริกซ์โมฆะแสดงด้วยตัวอักษรกรีก "ธีต้า"

เพื่อให้เข้าใจอันดับของเมทริกซ์ได้ดีขึ้น ต่อไปนี้ฉันจะใช้สื่อเพื่อขอความช่วยเหลือ เรขาคณิตวิเคราะห์... ถือว่าศูนย์ เวกเตอร์พื้นที่สามมิติของเราซึ่งไม่ได้กำหนดทิศทางที่แน่นอนและไม่มีประโยชน์สำหรับการก่อสร้าง แนบพื้นฐาน... จากมุมมองของพีชคณิต พิกัดของเวกเตอร์นี้เขียนเป็น เมทริกซ์"หนึ่งถึงสาม" และตรรกะ (ในความหมายทางเรขาคณิตที่ระบุ)สมมติว่าอันดับของเมทริกซ์นี้เป็นศูนย์

ลองพิจารณาดูบ้าง ไม่ใช่ศูนย์ เวกเตอร์คอลัมน์และ เวกเตอร์แถว:


แต่ละอินสแตนซ์มีองค์ประกอบที่ไม่ใช่ศูนย์อย่างน้อยหนึ่งรายการ และนั่นก็เป็นบางอย่างอยู่แล้ว!

อันดับของเวกเตอร์แถวที่ไม่ใช่ศูนย์ใดๆ (เวกเตอร์คอลัมน์) คือหนึ่ง

และโดยทั่วไปแล้วพูด - ถ้าอยู่ในเมทริกซ์ ขนาดโดยพลการมีองค์ประกอบที่ไม่ใช่ศูนย์อย่างน้อยหนึ่งตัว ตามด้วยอันดับ ไม่น้อยหน่วย.

เวกเตอร์แถวพีชคณิตและเวกเตอร์คอลัมน์ค่อนข้างเป็นนามธรรม ดังนั้นเราจึงหันไปหาการเชื่อมโยงทางเรขาคณิตอีกครั้ง ไม่ใช่ศูนย์ เวกเตอร์กำหนดทิศทางที่ชัดเจนในอวกาศและเหมาะสำหรับอาคาร พื้นฐานดังนั้นอันดับของเมทริกซ์จะถือว่าเท่ากับหนึ่ง

พื้นหลังทางทฤษฎี : ในพีชคณิตเชิงเส้น เวกเตอร์เป็นองค์ประกอบของปริภูมิเวกเตอร์ (กำหนดผ่านสัจพจน์ 8 ประการ) โดยเฉพาะอย่างยิ่ง สามารถเป็นแถวเรียง (หรือคอลัมน์) ของจำนวนจริงด้วยการดำเนินการของการบวกและการคูณด้วยจำนวนจริงที่กำหนด สำหรับพวกเขา. ข้อมูลเพิ่มเติมเกี่ยวกับเวกเตอร์สามารถพบได้ในบทความ การแปลงเชิงเส้น.

ขึ้นอยู่กับเชิงเส้น(แสดงออกผ่านกันและกัน). จากมุมมองทางเรขาคณิต บรรทัดที่สองประกอบด้วยพิกัดของเวกเตอร์คอลลิเนียร์ ที่ไม่ก้าวหน้าในเรื่องการสร้าง พื้นฐานสามมิติฟุ่มเฟือยในแง่นี้ ดังนั้นอันดับของเมทริกซ์นี้ก็เท่ากับหนึ่งเช่นกัน

ลองเขียนพิกัดของเวกเตอร์ใหม่ในคอลัมน์ ( ย้ายเมทริกซ์):

มีการเปลี่ยนแปลงอะไรในแง่ของอันดับ? ไม่มีอะไร. คอลัมน์เป็นสัดส่วน ดังนั้นอันดับจึงเป็นหนึ่ง อย่างไรก็ตาม โปรดทราบว่าทั้งสามบรรทัดเป็นสัดส่วนเช่นกัน สามารถระบุได้ด้วยพิกัด สามเวกเตอร์คอลลิเนียร์ของระนาบ ซึ่ง หนึ่งเดียวมีประโยชน์สำหรับการสร้างพื้นฐาน "แบน" และนี่สอดคล้องกับความรู้สึกทางเรขาคณิตของเราอย่างสมบูรณ์

ข้อความสำคัญดังต่อไปนี้จากตัวอย่างข้างต้น:

อันดับของเมทริกซ์ตามแถว เท่ากับอันดับของเมทริกซ์ตามคอลัมน์... ฉันได้กล่าวไปแล้วเล็กน้อยเกี่ยวกับเรื่องนี้ในบทเรียนเกี่ยวกับประสิทธิผล วิธีการคำนวณดีเทอร์มีแนนต์.

บันทึก : การพึ่งพาแถวเชิงเส้นส่งผลให้เกิดการพึ่งพาคอลัมน์เชิงเส้น (และในทางกลับกัน) แต่เพื่อเป็นการประหยัดเวลาและเพื่อให้เป็นนิสัย ฉันมักจะพูดถึงการพึ่งพาอาศัยกันเชิงเส้นของสตริง

เราจะฝึกสัตว์เลี้ยงอันเป็นที่รักของเราต่อไป เพิ่มพิกัดของเวกเตอร์ collinear อีกหนึ่งตัวให้กับเมทริกซ์ในแถวที่สาม :

เขาช่วยเราในการสร้างพื้นฐานสามมิติหรือไม่? แน่นอนไม่ เวกเตอร์ทั้งสามเดินไปมาตามเส้นทางเดียวกัน และอันดับของเมทริกซ์มีค่าเท่ากับหนึ่ง คุณสามารถใช้เวกเตอร์คอลลิเนียร์ได้มากเท่าที่ต้องการ เช่น 100 ใส่พิกัดลงในเมทริกซ์ขนาดหนึ่งร้อยคูณสาม และอันดับของตึกระฟ้าจะยังคงเป็นหน่วย

มาทำความรู้จักกับเมทริกซ์กัน ซึ่งแถวนั้น อิสระเชิงเส้น... เวกเตอร์ที่ไม่สัมพันธ์กันคู่หนึ่งเหมาะสำหรับการสร้างพื้นฐานสามมิติ อันดับของเมทริกซ์นี้คือสอง

และอันดับของเมทริกซ์คืออะไร? เส้นดูเหมือนจะเกินสัดส่วน ... ตามทฤษฎีแล้ว สามเส้น อย่างไรก็ตาม อันดับของเมทริกซ์นี้ก็เท่ากับสองเช่นกัน ฉันเพิ่มสองบรรทัดแรกและเขียนผลลัพธ์ที่ด้านล่าง นั่นคือ แสดงเชิงเส้นบรรทัดที่สามถึงสองบรรทัดแรก ในเชิงเรขาคณิต แถวของเมทริกซ์สอดคล้องกับพิกัดสาม coplanar vectorsและในหมู่สามคนนี้มีสหายที่ไม่สมรู้ร่วมคิดสองสามคน

อย่างที่เห็น ความสัมพันธ์เชิงเส้นในเมทริกซ์ที่พิจารณานั้นไม่ชัดเจนและวันนี้เราจะเรียนรู้วิธีทำให้มันเป็นจริง

ฉันคิดว่าหลายคนเดาว่าอันดับของเมทริกซ์คืออะไร!

พิจารณาเมทริกซ์ที่มีแถวเป็น อิสระเชิงเส้น... รูปแบบเวกเตอร์ แนบพื้นฐานและอันดับของเมทริกซ์นี้คือสาม

อย่างที่คุณทราบ เวกเตอร์ที่สี่ ห้า และสิบใดๆ ของปริภูมิสามมิติจะแสดงเป็นเส้นตรงในรูปของเวกเตอร์ฐาน ดังนั้น หากคุณเพิ่มจำนวนแถวลงในเมทริกซ์จำนวนเท่าใดก็ได้ ลำดับของมันคือ จะยังเท่ากับสาม.

การให้เหตุผลที่คล้ายกันสามารถทำได้สำหรับเมทริกซ์ที่ใหญ่กว่า (แน่นอน โดยไม่มีความหมายทางเรขาคณิต)

คำนิยาม : อันดับของเมทริกซ์คือจำนวนสูงสุดของแถวอิสระเชิงเส้น... หรือ: อันดับของเมทริกซ์คือจำนวนคอลัมน์อิสระเชิงเส้นสูงสุด... ใช่ จำนวนของพวกเขาจะเท่ากันเสมอ

แนวทางปฏิบัติที่สำคัญยังเป็นไปตามข้างต้น: อันดับของเมทริกซ์ไม่เกินมิติขั้นต่ำ... ตัวอย่างเช่น ในเมทริกซ์ สี่แถวและห้าคอลัมน์ มิติต่ำสุดคือสี่ ดังนั้น อันดับของเมทริกซ์นี้จะต้องไม่เกิน 4 อย่างแน่นอน

การกำหนด: ในทฤษฎีและการปฏิบัติของโลก ไม่มีมาตรฐานที่ยอมรับกันโดยทั่วไปสำหรับการกำหนดอันดับของเมทริกซ์ ส่วนใหญ่แล้วคุณจะพบว่า: - อย่างที่พวกเขาพูด ชาวอังกฤษเขียนสิ่งหนึ่ง ชาวเยอรมันเขียนอีกอย่างหนึ่ง ดังนั้น จากเกร็ดเล็กเกร็ดน้อยที่รู้จักกันดีเกี่ยวกับนรกของอเมริกาและรัสเซีย เรามาระบุอันดับของเมทริกซ์ด้วยคำพื้นเมือง ตัวอย่างเช่น: . และถ้าเมทริกซ์เป็น "นิรนาม" ซึ่งมีจำนวนมาก คุณก็สามารถเขียนลงไปได้

ฉันจะค้นหาอันดับของเมทริกซ์โดยใช้ผู้เยาว์ได้อย่างไร

ถ้าคุณยายของเรามีคอลัมน์ที่ห้าในเมทริกซ์ ก็ควรคำนวณลำดับที่ 4 รองลงมาอีกหนึ่ง ("สีน้ำเงิน", "สีแดงเข้ม" + คอลัมน์ที่ 5)

เอาท์พุต: ลำดับสูงสุดของผู้เยาว์ที่ไม่ใช่ศูนย์คือสาม ดังนั้น

บางทีอาจไม่ใช่ทุกคนที่เข้าใจวลีนี้อย่างถ่องแท้: ผู้เยาว์ในลำดับที่ 4 มีค่าเท่ากับศูนย์ แต่ในหมู่ผู้เยาว์ของลำดับที่ 3 มีลำดับที่ไม่ศูนย์ - ดังนั้นลำดับสูงสุด ไม่ใช่ศูนย์ผู้เยาว์และเท่ากับสาม

คำถามที่เกิดขึ้นทำไมไม่คำนวณดีเทอร์มีแนนต์ทันที? ประการแรก ในงานส่วนใหญ่ เมทริกซ์ไม่เป็นกำลังสอง และประการที่สอง แม้ว่าคุณจะได้รับค่าที่ไม่เป็นศูนย์ งานจะถูกปฏิเสธด้วยความน่าจะเป็นสูง เนื่องจากมักจะหมายถึงโซลูชัน "จากล่างขึ้นบน" มาตรฐาน . และในตัวอย่างที่พิจารณา ดีเทอร์มีแนนต์ศูนย์ของลำดับที่ 4 ทำให้เราสามารถยืนยันได้ว่าอันดับของเมทริกซ์นั้นน้อยกว่าสี่เท่านั้น

ฉันต้องยอมรับว่าฉันเป็นคนคิดปัญหาที่วิเคราะห์ด้วยตัวเองเพื่อที่จะอธิบายวิธีการติดผู้เยาว์ได้ดียิ่งขึ้น ในทางปฏิบัติทุกอย่างง่ายกว่า:

ตัวอย่าง 2

หาอันดับของเมทริกซ์โดยวิธี bordering minors method

คำตอบและคำตอบในตอนท้ายของบทเรียน

อัลกอริทึมจะเร็วที่สุดเมื่อใด กลับไปที่เมทริกซ์ขนาด 4 คูณ 4 ตัวเดิม ... เห็นได้ชัดว่าการแก้ปัญหาจะสั้นที่สุดในกรณีของ "ดี" ผู้เยาว์มุม:

และถ้าเป็นอย่างอื่น -.

การคิดไม่ใช่เรื่องสมมติเลย - มีตัวอย่างมากมายที่สิ่งทั้งหมดจำกัดเฉพาะผู้เยาว์เท่านั้น

อย่างไรก็ตาม ในบางกรณี วิธีอื่นมีประสิทธิภาพและดีกว่า:

ฉันจะค้นหาอันดับของเมทริกซ์โดยใช้วิธีเกาส์เซียนได้อย่างไร

ย่อหน้ามีไว้สำหรับผู้อ่านที่คุ้นเคยกับ วิธีเกาส์เซียนและยัดมือลงบนมันในระดับที่น้อยที่สุด

จากมุมมองทางเทคนิค วิธีการนี้ไม่มีความแปลกใหม่:

1) โดยใช้การแปลงเบื้องต้น เรานำเมทริกซ์ไปอยู่ในรูปแบบขั้นบันได

2) อันดับของเมทริกซ์เท่ากับจำนวนแถว

ค่อนข้างชัดเจนว่า การใช้วิธีเกาส์ไม่เปลี่ยนอันดับของเมทริกซ์และสาระสำคัญที่นี่ง่ายมาก: ตามอัลกอริทึมในระหว่างการแปลงเบื้องต้นจะมีการระบุและลบเส้นตามสัดส่วนที่ไม่จำเป็นทั้งหมด (ขึ้นอยู่กับเชิงเส้น) ซึ่งเป็นผลมาจากการที่ "สารตกค้างแห้ง" ยังคงอยู่ - จำนวนสูงสุดของ เส้นอิสระเชิงเส้น

มาแปลงเมทริกซ์เก่าที่คุ้นเคยกันด้วยพิกัดของเวกเตอร์คอลลิเนียร์สามตัวกัน:

(1) บรรทัดแรกคูณด้วย –2 ถูกเพิ่มในบรรทัดที่สอง บรรทัดแรกถูกเพิ่มในบรรทัดที่สาม

(2) ลบบรรทัดว่าง

นี่ออกจากหนึ่งบรรทัดดังนั้น จำเป็นต้องพูด วิธีนี้เร็วกว่าการคำนวณผู้เยาว์ที่ไม่มีลำดับเก้ารายมาก แล้วจึงสรุปได้

ฉันเตือนคุณว่าในตัวเอง เมทริกซ์พีชคณิตไม่มีอะไรเปลี่ยนแปลงได้ และการแปลงจะดำเนินการเพื่อจุดประสงค์ในการค้นหาอันดับเท่านั้น! โดยวิธีการที่ให้เราอาศัยอยู่อีกครั้งในคำถาม ทำไมไม่? เมทริกซ์ที่มา นำข้อมูลที่แตกต่างจากข้อมูลเมทริกซ์และแถวโดยพื้นฐาน ในแบบจำลองทางคณิตศาสตร์บางตัว (โดยไม่มีการพูดเกินจริง) ความแตกต่างในจำนวนหนึ่งอาจเป็นเรื่องของความเป็นและความตาย ... ฉันจำครูคณิตศาสตร์ของโรงเรียนในระดับประถมศึกษาและมัธยมศึกษาที่ตัดเกรดอย่างไร้ความปราณี 1-2 คะแนนสำหรับความไม่ถูกต้องหรือเบี่ยงเบนน้อยที่สุดจากอัลกอริทึม และมันก็น่ารำคาญอย่างยิ่งเมื่อแทนที่จะรับประกันว่า "ห้า" มันกลับกลายเป็น "ดี" หรือแย่กว่านั้น ความเข้าใจมาภายหลังมาก - คนอื่นจะได้รับความไว้วางใจจากดาวเทียม หัวรบนิวเคลียร์ และโรงไฟฟ้าได้อย่างไร? แต่ไม่ต้องกังวลฉันไม่ได้ทำงานในพื้นที่เหล่านี้ =)

ไปที่งานที่มีความหมายมากกว่ากัน โดยที่เราจะทำความคุ้นเคยกับเทคนิคการคำนวณที่สำคัญ วิธีเกาส์:

ตัวอย่างที่ 3

ค้นหาอันดับของเมทริกซ์โดยใช้การแปลงเบื้องต้น

สารละลาย: กำหนดเมทริกซ์ "สี่คูณห้า" ซึ่งหมายความว่าอันดับของมันไม่เกิน 4 แน่นอน

ในคอลัมน์แรก ไม่มี 1 หรือ –1 ดังนั้น จำเป็นต้องมีการดำเนินการเพิ่มเติมเพื่อให้ได้หน่วยอย่างน้อยหนึ่งหน่วย ตลอดการมีอยู่ของไซต์นี้ ฉันถูกถามคำถามซ้ำแล้วซ้ำเล่า: "เป็นไปได้ไหมที่จะจัดเรียงคอลัมน์ใหม่ในระหว่างการแปลงเบื้องต้น" ที่นี่ - จัดเรียงคอลัมน์แรกหรือคอลัมน์ที่สองใหม่และทุกอย่างเรียบร้อย! ในงานส่วนใหญ่ที่มีการใช้งาน วิธีเกาส์คอลัมน์สามารถจัดเรียงใหม่ได้ แต่ไม่จำเป็น และประเด็นก็ไม่ใช่ความสับสนที่เป็นไปได้กับตัวแปร ความจริงก็คือในหลักสูตรคลาสสิกของการสอนคณิตศาสตร์ขั้นสูง การกระทำนี้ไม่ถือเป็นธรรมเนียมปฏิบัติ ดังนั้นคำหยาบจะถูกมองว่าคดเคี้ยวมาก (หรือถูกบังคับให้ทำซ้ำทุกอย่าง) .

ประเด็นที่สองเกี่ยวกับตัวเลข เป็นประโยชน์ในการปฏิบัติตามกฎง่ายๆ ต่อไปนี้ระหว่างการตัดสินใจ: ถ้าเป็นไปได้ การแปลงเบื้องต้นควรลดจำนวนเมทริกซ์... อันที่จริง มันง่ายกว่ามากที่จะทำงานกับหนึ่งในสองในสามมากกว่าเช่นกับ 23, 45 และ 97 และการดำเนินการแรกนั้นไม่เพียงมุ่งเป้าไปที่การได้หน่วยในคอลัมน์แรกเท่านั้น แต่ยังรวมถึงการกำจัดตัวเลข 7 ด้วย และ 11

ขั้นแรกให้แก้ปัญหาโดยสมบูรณ์ จากนั้นแสดงความคิดเห็น:

(1) บรรทัดแรกคูณด้วย –2 ถูกเพิ่มในบรรทัดที่สอง บรรทัดแรกคูณด้วย –3 ถูกบวกเข้ากับบรรทัดที่สาม และไปที่กอง: บรรทัดที่ 1 คูณด้วย -1 ถูกเพิ่มในบรรทัดที่ 4

(2) สามบรรทัดสุดท้ายเป็นสัดส่วน บรรทัดที่ 3 และ 4 ถูกลบ บรรทัดที่สองถูกย้ายไปยังตำแหน่งแรก

(3) บรรทัดแรกคูณด้วย –3 ถูกเพิ่มในบรรทัดที่สอง

เมทริกซ์ถูกลดขนาดเป็นรูปแบบขั้นบันไดมีสองแถว

ตอบ:

ตอนนี้ถึงตาคุณแล้วที่จะทรมานเมทริกซ์สี่ต่อสี่:

ตัวอย่างที่ 4

ค้นหาอันดับของเมทริกซ์โดยใช้วิธีเกาส์เซียน

ฉันเตือนคุณว่า วิธีเกาส์ไม่ได้หมายความถึงความแข็งแกร่งที่ชัดเจน และการตัดสินใจของคุณมักจะแตกต่างจากการตัดสินใจของฉัน ตัวอย่างสั้นๆ เกี่ยวกับวิธีออกแบบปัญหาเมื่อจบบทเรียน

คุณควรใช้วิธีใดในการหาอันดับของเมทริกซ์

ในทางปฏิบัติมักไม่มีการกล่าวถึงว่าควรใช้วิธีใดในการหาอันดับ ในสถานการณ์เช่นนี้ เงื่อนไขควรได้รับการวิเคราะห์ - สำหรับเมทริกซ์บางตัว มีเหตุผลมากกว่าที่จะส่งต่อวิธีแก้ปัญหาผ่านตัวรอง ในขณะที่สำหรับตัวอื่น การใช้การแปลงเบื้องต้นนั้นให้ผลกำไรมากกว่ามาก:

ตัวอย่างที่ 5

หาอันดับของเมทริกซ์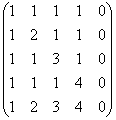

สารละลาย: วิธีแรกหายไปทันที =)

สูงขึ้นเล็กน้อย ฉันไม่แนะนำว่าอย่าแตะต้องคอลัมน์ของเมทริกซ์ แต่เมื่อมีคอลัมน์ศูนย์หรือคอลัมน์ตามสัดส่วน / สอดคล้องกัน ก็ยังคุ้มค่าที่จะทำการตัดแขนขา:

(1) คอลัมน์ที่ห้าเป็นศูนย์ เราจะลบมันออกจากเมทริกซ์ ดังนั้นอันดับของเมทริกซ์อยู่ที่สี่อย่างมากที่สุด บรรทัดแรกคูณด้วย -1 นี่เป็นอีกหนึ่งคุณลักษณะเด่นของวิธีเกาส์ ซึ่งเปลี่ยนการกระทำต่อไปนี้ให้กลายเป็นการเดินที่น่ารื่นรมย์:

(2) เพิ่มบรรทัดแรกในทุกบรรทัดโดยเริ่มจากบรรทัดที่สอง

(3) บรรทัดแรกคูณด้วย –1 บรรทัดที่สามหารด้วย 2 บรรทัดที่สี่หารด้วย 3 บรรทัดที่สองถูกบวกเข้ากับบรรทัดที่ห้า คูณด้วย –1

(4) บรรทัดที่สามคูณด้วย –2 ถูกบวกเข้ากับบรรทัดที่ห้า

(5) สองบรรทัดสุดท้ายเป็นสัดส่วน ส่วนที่ห้าจะถูกลบออก

ผลลัพธ์คือ 4 บรรทัด

ตอบ:

อาคารห้าชั้นมาตรฐานสำหรับการศึกษาด้วยตนเอง:

ตัวอย่างที่ 6

หาอันดับของเมทริกซ์

วิธีแก้ปัญหาสั้น ๆ และคำตอบในตอนท้ายของบทช่วยสอน

ควรสังเกตว่าวลี "อันดับของเมทริกซ์" นั้นไม่ได้เกิดขึ้นบ่อยนักในทางปฏิบัติ และในปัญหาส่วนใหญ่ก็สามารถทำได้โดยปราศจากมันทั้งหมด แต่มีงานหนึ่งที่แนวคิดที่เป็นปัญหาเป็นตัวแสดงหลัก และในตอนท้ายของบทความ เราจะพิจารณาการใช้งานจริงนี้:

จะตรวจสอบระบบสมการเชิงเส้นเพื่อความสม่ำเสมอได้อย่างไร?

บ่อยครั้งนอกเหนือจากการแก้ปัญหา ระบบสมการเชิงเส้นโดยเงื่อนไขนั้น ก่อนอื่นต้องตรวจสอบความเข้ากันได้ กล่าวคือ เพื่อพิสูจน์ว่ามีวิธีแก้ปัญหาใดๆ อยู่เลย มีบทบาทสำคัญในการตรวจสอบนี้โดย ทฤษฎีบทโครเนคเกอร์-คาเปลลีซึ่งฉันจะกำหนดในรูปแบบที่ต้องการ:

ถ้าอันดับ เมทริกซ์ระบบเท่ากับยศ เมทริกซ์ระบบขยายระบบก็จะสอดคล้องกัน และหากตัวเลขที่ระบุตรงกับจำนวนที่ไม่รู้จัก วิธีแก้ปัญหาก็จะไม่ซ้ำกัน

ดังนั้นเพื่อศึกษาระบบความเข้ากันได้จึงจำเป็นต้องตรวจสอบความเท่าเทียมกัน , ที่ไหน - เมทริกซ์ระบบ(จำคำศัพท์จากบทเรียน วิธีเกาส์), NS - เมทริกซ์ระบบขยาย(เช่น เมทริกซ์ที่มีค่าสัมประสิทธิ์ของตัวแปร + คอลัมน์ของเงื่อนไขอิสระ)