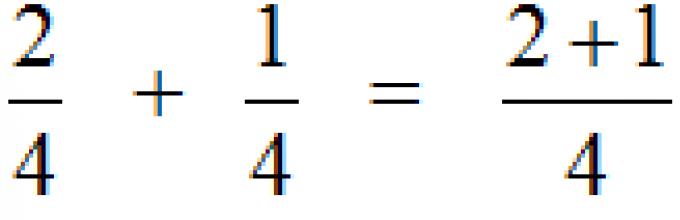Додавання дробів з однаковими знаменниками
Додавання дробів буває двох видів:
- Додавання дробів з однаковими знаменниками
- Додавання дробів з різними знаменниками
Спочатку вивчимо складання дробів з однаковими знаменниками. Тут все просто. Щоб скласти дробу з однаковими знаменниками, потрібно скласти їх чисельники, а знаменник залишити без зміни. Наприклад, складемо дроби і. Складаємо числители, а знаменник залишаємо без зміни:

Цей приклад можна легко зрозуміти, якщо згадати про піцу, яка розділена на чотири частини. Якщо до піци додати піци, то вийде піци:

Приклад 2. Скласти дроби і.

У відповіді вийшла неправильна дріб. Якщо настає кінець завдання, то від неправильних дробів прийнято позбавлятися. Щоб позбавиться від неправильного дробу, потрібно виділити в ній цілу частину. У нашому випадку ціла частина виділяється легко - два розділити на два дорівнює одиниці:

Цей приклад можна легко зрозуміти, якщо згадати про піцу, яка розділена на дві частини. Якщо до піци додати ще піци, то вийде одна ціла піца:

приклад 3. Скласти дроби і.
Знову ж складаємо числители, а знаменник залишаємо без зміни:
![]()
Цей приклад можна легко зрозуміти, якщо згадати про піцу, яка розділена на три частини. Якщо до піци додати ще піци, то вийде піци:

Приклад 4. Знайти значення виразу 
Цей приклад вирішується точно також, як і попередні. Чисельники необхідно скласти, а знаменник залишити без зміни:
Спробуємо зобразити наше рішення за допомогою малюнка. Якщо до піци додати піци і ще додати піци, то вийде 1 ціла і ще піци.

Як бачите в додаванні дробів з однаковими знаменниками нічого складного немає. Досить розуміти такі правила:
- Щоб скласти дробу з однаковими знаменника, потрібно скласти їх чисельники, а знаменник залишити без зміни;
Додавання дробів з різними знаменниками
Тепер навчимося додавати дроби з різними знаменниками. Коли складають дроби, знаменники цих дробів повинні бути однаковими. Але однаковими вони бувають не завжди.
Наприклад, дробу і скласти можна, оскільки у них однакові знаменники.
А ось дроби і відразу скласти не можна, оскільки у цих дробів різні знаменники. У таких випадках дробу потрібно приводити до однакового (загального) знаменника.
Існує кілька способів приведення дробів до однакового знаменника. Сьогодні ми розглянемо тільки один з них, оскільки інші способи можуть здатися складними для початківця.
Суть цього способу полягає в тому, що спочатку шукається (НОК) знаменників обох дробів. Потім НОК ділять на знаменник першого дробу і отримують перший додатковий множник. Аналогічно надходять і з другої дробом - НОК ділять на знаменник другого дробу і отримують другий додатковий множник.
Потім числители і знаменники дробів множаться на свої додаткові множники. В результаті цих дій, дроби у яких були різні знаменники, звертаються в дробу, у яких однакові знаменники. А як складати такі дроби ми вже знаємо.
приклад 1. Складемо дроби і
В першу чергу знаходимо найменше спільне кратне знаменників обох дробів. Знаменник першого дробу це число 3, а знаменник другого дробу - число 2. Найменше спільне кратне цих чисел дорівнює 6
НОК (2 і 3) \u003d 6
Тепер повертаємося до дробям і. Спочатку розділимо НОК на знаменник першого дробу і отримаємо перший додатковий множник. НОК це число 6, а знаменник першого дробу це число 3. Ділимо 6 на 3, отримуємо 2.
Отримане число 2 це перший додатковий множник. Записуємо його до першого дробу. Для цього робимо невелику косу лінію над дробом і записуємо над нею знайдений додатковий множник:
Аналогічно робимо і з другої дробом. Ділимо НОК на знаменник другого дробу і отримуємо другий додатковий множник. НОК це число 6, а знаменник другого дробу - число 2. Ділимо 6 на 2, отримуємо 3.
Отримане число 3 це другий додатковий множник. Записуємо його до другого дробу. Знову ж робимо невелику косу лінію над другою дробом і записуємо над нею знайдений додатковий множник:
Тепер у нас все готово для складання. Залишилося помножити числители і знаменники дробів на свої додаткові множники:

Подивіться уважно до чого ми прийшли. Ми прийшли до того, що дроби у яких були різні знаменники, перетворилися в дроби у яких однакові знаменники. А як складати такі дроби ми вже знаємо. Давайте вирішимо цей приклад до кінця:

Таким чином, приклад завершується. До додати виходить.
Спробуємо зобразити наше рішення за допомогою малюнка. Якщо до піци додати піци, то вийде одна ціла піца і ще одна шоста піци:

Зведення дробів до однакового (загального) знаменника також можна зобразити за допомогою малюнка. Привівши дроби і до спільного знаменника, ми отримали дробу і. Ці дві дробу зображатимуться тими ж шматками піц. Різниця буде лише в тому, що в цей раз вони будуть розділені на рівні частини (приведені до однакового знаменника).

Перший малюнок зображує дріб (чотири шматочки з шести), а другий малюнок зображує дріб (три шматочки з шести). Склавши ці шматочки ми отримуємо (сім шматочків з шести). Ця дріб неправильна, тому ми виділили в ній цілу частину. В результаті отримали (одну цілу піцу і ще одну шосту піци).
Відзначимо, що ми з вами розписали даний приклад занадто докладно. У навчальних закладах не прийнято писати так розгорнуто. Потрібно вміти швидко знаходити НОК обох знаменників і додаткові множники до них, а також швидко множити знайдені додаткові множники на свої числители і знаменники. Перебуваючи в школі, даний приклад нам довелося б записати наступним чином:

Але є і зворотна сторона медалі. Якщо на перших етапах вивчення математики не робити докладних записів, то починають з'являтися питання роду «А звідки ота цифра?», «Чому дробу раптом перетворюються зовсім в інші дроби? «.
Щоб легше було додавати дроби з різними знаменниками, можна скористатися наступною покроковою інструкцією:
- Знайти НОК знаменників дробів;
- Розділити НОК на знаменник кожного дробу і отримати додатковий множник для кожного дробу;
- Помножити числители і знаменники дробів на свої додаткові множники;
- Скласти дробу, у яких однакові знаменники;
- Якщо у відповіді вийшла неправильна дріб, то виділити її цілу частину;
Приклад 2. Знайти значення виразу  .
.
Скористаємося інструкцією, яка приведена вище.
Крок 1. Знайти НОК знаменників дробів
Знаходимо НОК знаменників обох дробів. Знаменники дробів це числа 2, 3 і 4

Крок 2. Розділити НОК на знаменник кожного дробу і отримати додатковий множник для кожного дробу
Ділимо НОК на знаменник першого дробу. НОК це число 12, а знаменник першого дробу це число 2. Ділимо 12 на 2, отримуємо 6. Отримали перший додатковий множник 6. Записуємо його над першою дробом:
Тепер ділимо НОК на знаменник другого дробу. НОК це число 12, а знаменник другого дробу це число 3. Ділимо 12 на 3, отримуємо 4. Отримали другий додатковий множник 4. Записуємо його над другою дробом:
Тепер ділимо НОК на знаменник третьої дробу. НОК це число 12, а знаменник третьої дробу це число 4. Ділимо 12 на 4, отримуємо 3. Отримали третій додатковий множник 3. Записуємо його над третьою дробом:
Крок 3. Помножити числители і знаменники дробів на свої додаткові множники
Множимо чисельники і знаменники на свої додаткові множники:
Крок 4. Скласти дроби у яких однакові знаменники
Ми прийшли до того, що дроби у яких були різні знаменники, перетворилися в дробу, у яких однакові (загальні) знаменники. Залишилося скласти ці дроби. складаємо:

Додавання не влізло на одному рядку, тому ми перенесли залишився вираз на наступний рядок. Це допускається в математиці. Коли вираз не поміщається на один рядок, його переносять на наступний рядок, при цьому треба обов'язково поставити знак рівності (\u003d) на кінці першого рядка і на початку нового рядка. Знак рівності на другому рядку говорить про те, що це продовження вираження, яке було на першому рядку.
Крок 5. Якщо у відповіді вийшла неправильна дріб, то виділити в ній цілу частину
У нас у відповіді вийшла неправильна дріб. Ми повинні виділити у неї цілу частину. виділяємо:

отримали відповідь
Віднімання дробів з однаковими знаменниками
Віднімання дробів буває двох видів:
- Віднімання дробів з однаковими знаменниками
- Віднімання дробів з різними знаменниками
Спочатку вивчимо віднімання дробів з однаковими знаменниками. Тут все просто. Щоб відняти від одного дробу іншу, потрібно з чисельника першого дробу відняти чисельник другого дробу, а знаменник залишити колишнім.
Наприклад, знайдемо значення виразу. Щоб вирішити це приклад, треба з чисельника першого дробу відняти чисельник другого дробу, а знаменник залишити без зміни. Так і зробимо:

Цей приклад можна легко зрозуміти, якщо згадати про піцу, яка розділена на чотири частини. Якщо від піци відрізати піци, то вийде піци:

Приклад 2. Знайти значення виразу.
Знову ж з чисельника першого дробу віднімаємо чисельник другого дробу, а знаменник залишаємо без зміни:

Цей приклад можна легко зрозуміти, якщо згадати про піцу, яка розділена на три частини. Якщо від піци відрізати піци, то вийде піци:

Приклад 3. Знайти значення виразу 
Цей приклад вирішується точно також, як і попередні. З чисельника першого дробу потрібно відняти числители інших дробів:

Як бачите в відніманні дробів з однаковими знаменниками нічого складного немає. Досить розуміти такі правила:
- Щоб відняти від одного дробу іншу, потрібно з чисельника першого дробу відняти чисельник другого дробу, а знаменник залишити без зміни;
- Якщо у відповіді вийшла неправильна дріб, то потрібно виділити в ній цілу частину.
Віднімання дробів з різними знаменниками
Наприклад, від дробу можна відняти дріб, оскільки у цих дробів однакові знаменники. А ось від дробу не можна відняти дріб, оскільки у цих дробів різні знаменники. У таких випадках дробу потрібно приводити до однакового (загального) знаменника.
Спільний знаменник знаходять за тим же принципом, яким ми користувалися при складанні дробів з різними знаменниками. В першу чергу знаходять НОК знаменників обох дробів. Потім НОК ділять на знаменник першого дробу і отримують перший додатковий множник, який записується над першою дробом. Аналогічно НОК ділять на знаменник другого дробу і отримують другий додатковий множник, який записується над другою дробом.
Потім дроби множаться на свої додаткові множники. В результаті цих операцій, дроби у яких були різні знаменники, звертаються в дробу, у яких однакові знаменники. А як віднімати такі дроби ми вже знаємо.
Приклад 1. Знайти значення виразу:
У цих дробів різні знаменники, тому потрібно привести їх до однакового (загального) знаменника.
Спочатку знаходимо НОК знаменників обох дробів. Знаменник першого дробу це число 3, а знаменник другого дробу - число 4. Найменше спільне кратне цих чисел дорівнює 12
НОК (3 і 4) \u003d 12
Тепер повертаємося до дробям і
Знайдемо додатковий множник для першого дробу. Для цього розділимо НОК на знаменник першого дробу. НОК це число 12, а знаменник першого дробу - число 3. Ділимо 12 на 3, отримуємо 4. Записуємо четвірку над першою дробом:
Аналогічно робимо і з другої дробом. Ділимо НОК на знаменник другого дробу. НОК це число 12, а знаменник другого дробу - число 4. Ділимо 12 на 4, отримуємо 3. Записуємо трійку над другою дробом:
Тепер у нас все готово для вирахування. Залишилося помножити дробу на свої додаткові множники:

Ми прийшли до того, що дроби у яких були різні знаменники, перетворилися в дроби у яких однакові знаменники. А як віднімати такі дроби ми вже знаємо. Давайте вирішимо цей приклад до кінця:

отримали відповідь
Спробуємо зобразити наше рішення за допомогою малюнка. Якщо від піци відрізати піци, то вийде піци

Це детальна версія рішення. Перебуваючи в школі, нам довелося б вирішити це приклад коротший. Виглядало б таке рішення наступним чином:

Зведення дробів і до спільного знаменника також може бути зображено за допомогою малюнка. Навівши ці дроби до спільного знаменника, ми отримали дробу і. Ці дробу зображатимуться тими ж шматочками піц, але в цей раз вони будуть розділені на рівні частини (приведені до однакового знаменника):

Перший малюнок зображує дріб (вісім шматочків з дванадцяти), а другий малюнок - дріб (три шматочки з дванадцяти). Відрізавши від восьми шматочків три шматочка ми отримуємо п'ять шматочків з дванадцяти. Дріб і описує ці п'ять шматочків.
Приклад 2. Знайти значення виразу 
У цих дробів різні знаменники, тому спочатку потрібно привести їх до однакового (загального) знаменника.
Знайдемо НОК знаменників цих дробів.
Знаменники дробів це числа 10, 3 і 5. Найменше спільне кратне цих чисел дорівнює 30
НОК (10, 3, 5) \u003d 30
Тепер знаходимо додаткові множники для кожного дробу. Для цього розділимо НОК на знаменник кожного дробу.
Знайдемо додатковий множник для першого дробу. НОК це число 30, а знаменник першого дробу - число 10. Ділимо 30 на 10, отримуємо перший додатковий множник 3. Записуємо його над першою дробом:
Тепер знаходимо додатковий множник для другого дробу. Розділимо НОК на знаменник другого дробу. НОК це число 30, а знаменник другого дробу - число 3. Ділимо 30 на 3, отримуємо другий додатковий множник 10. Записуємо його над другою дробом:
Тепер знаходимо додатковий множник для третьої дробу. Розділимо НОК на знаменник третьої дробу. НОК це число 30, а знаменник третьої дроби - число 5. Ділимо 30 на 5, отримуємо третій додатковий множник 6. Записуємо його над третьою дробом:
Тепер все готово для вирахування. Залишилося помножити дробу на свої додаткові множники:
Ми прийшли до того, що дроби у яких були різні знаменники, перетворилися в дроби у яких однакові (загальні) знаменники. А як віднімати такі дроби ми вже знаємо. Давайте вирішимо цей приклад.
Продовження прикладу не поміститься на одному рядку, тому переносимо продовження на наступний рядок. Не забуваємо про знак рівності (\u003d) на новому рядку:

У відповіді вийшла правильна дріб, і начебто нас все влаштовує, але вона надто громіздка і некрасива. Треба б зробити її простіше. А що можна зробити? Можна скоротити цей дріб.
Щоб скоротити дріб, потрібно розділити її чисельник і знаменник на (НОД) чисел 20 і 30.
Отже, знаходимо НОД чисел 20 і 30:

Тепер повертаємося до нашого прикладу і ділимо чисельник і знаменник дробу на знайдений НСД, тобто на 10

отримали відповідь
Множення дробу на число
Щоб помножити дріб на число, потрібно чисельник даної дробу помножити на це число, а знаменник залишити без змін.
приклад 1. Помножити дріб на число 1.
Помножимо чисельник дробу на число 1
![]()
Запис можна розуміти, як взяти половину 1 раз. Наприклад, якщо піци взяти 1 раз, то вийде піци

Із законів множення ми знаємо, що якщо множимое і множник поміняти місцями, то твір не зміниться. Якщо вираз, записати як, то твір, як і раніше дорівнюватиме. Знову ж спрацьовує правило множення цілого числа і дроби:
![]()
Цей запис можна розуміти, як взяття половини від одиниці. Наприклад, якщо є 1 ціла піца і ми візьмемо від неї половину, то у нас виявиться піци:

приклад 2. Знайти значення виразу
Помножимо чисельник дробу на 4
![]()
У відповіді вийшла неправильна дріб. Виділимо в ній цілу частину:
![]()
Вираз можна розуміти, як взяття двох чвертей 4 рази. Наприклад, якщо піци взяти 4 рази, то вийде дві цілі піци

А якщо поміняти множимое і множник місцями, то отримаємо вираз. Воно теж буде дорівнює 2. Цей вислів можна розуміти, як взяття двох піц від чотирьох цілих піц:

Число, яке множиться на дріб, і знаменник дробу дозволяється, якщо вони мають спільний дільник, бóльшій одиниці.
Наприклад, вираз можна обчислити двома способами.
перший спосіб. Помножити число 4 на чисельник дробу, а знаменник дробу залишити без змін:
![]()
другий спосіб. Множимо четвірку і четвірку, що знаходиться в знаменнику дробу, можна скоротити. Скоротити ці четвірки можна на 4, оскільки найбільший спільний дільник для двох четвірок є сама четвірка:

Вийшов той же результат 3. Після скорочення четвірок, на їх місці утворюються нові числа: дві одиниці. Але множення одиниці з трійкою, і далі поділ на одиницю нічого не змінює. Тому рішення можна записати коротше:
Скорочення може бути виконано навіть тоді, коли ми вирішили скористатися першим способом, але на етапі перемноження кількості 4 і чисельника 3 вирішили скористатися скороченням:

А ось наприклад вираз можна обчислити тільки першим способом - помножити 7 на знаменник дробу, а знаменник залишити без змін:
![]()
Пов'язано це з тим, що число 7 і знаменник дробу не мають спільного дільника, бóльшего одиниці, і відповідно не скорочуються.
Деякі учні помилково скорочують множиться число і чисельник дробу. Робити цього не можна. Наприклад, такий запис не є правильною:
Скорочення дробу має на увазі, що і чисельник і знаменник буде розділений на одне і теж число. У ситуації з виразом розподіл виконано тільки в чисельнику, оскільки записати це все одно, що записати. Бачимо, що розподіл виконано тільки в чисельнику, а в знаменнику ніякого поділу не відбувається.
множення дробів
Щоб перемножити дробу, потрібно перемножити їх чисельники і знаменники. Якщо у відповіді вийде неправильна дріб, потрібно виділити в ній цілу частину.
Приклад 1. Знайти значення виразу.
![]()
Отримали відповідь. Бажано скоротити дану дріб. Дріб можна скоротити на 2. Тоді остаточне рішення прийме наступний вигляд:

Вираз можна розуміти, як взяття піци від половини піци. Припустимо, у нас є половина піци:
Як взяти від цієї половини дві третини? Спочатку потрібно поділити цю половину на три рівні частини:

І взяти від цих трьох шматочків два:

У нас вийде піци. Згадайте, як виглядає піца, розділена на три частини:

Один шматок від цієї піци і взяті нами два шматочки матимуть однакові розміри:

Іншими словами, мова йде про одне й те ж розмірі піци. Тому значення виразу одно

приклад 2. Знайти значення виразу
Множимо чисельник першого дробу на числівник другого дробу, а знаменник першого дробу на знаменник другого дробу:

У відповіді вийшла неправильна дріб. Виділимо в ній цілу частину:
![]()
Приклад 3. Знайти значення виразу
Множимо чисельник першого дробу на числівник другого дробу, а знаменник першого дробу на знаменник другого дробу:
![]()
У відповіді вийшла правильна дріб, але буде добре, якщо її скоротити. Щоб скоротити цю дріб, потрібно чисельник і знаменник даної дробу розділити на найбільший спільний дільник (НСД) чисел 105 і 450.
Отже, знайдемо НОД чисел 105 і 450:

Тепер ділимо чисельник і знаменник нашої відповіді на НОД, який ми зараз знайшли, тобто на 15
Подання цілого числа у вигляді дробу
Будь-яке ціле число можна представити у вигляді дробу. Наприклад, число 5 можна представити як. Від цього п'ятірка свого значення не поміняє, оскільки вираз означає «число п'ять розділити на одиницю», а це, як відомо одно п'ятірці:
Зворотні числа
Зараз ми познайомимося з дуже цікавою темою в математиці. Вона називається «зворотні числа».
Визначення. Зворотним до числаa називається число, яке при множенні наa дає одиницю.
Давайте підставимо в це визначення замість змінної a число 5 і спробуємо прочитати визначення:
Зворотним до числа 5 називається число, яке при множенні на 5 дає одиницю.
Чи можна знайти таке число, яке при множенні на 5, дає одиницю? Виявляється можна. Уявімо п'ятірку у вигляді дробу:
Потім помножити цю дріб на саму себе, тільки поміняємо місцями чисельник і знаменник. Іншими словами, помножимо дріб на саму себе, тільки перевернуту:
Що вийде в результаті цього? Якщо ми продовжимо вирішувати це приклад, то отримаємо одиницю:
![]()
Значить зворотним до числа 5, є число, оскільки при множенні 5 на виходить одиниця.
Зворотне число можна знайти також для будь-якого іншого цілого числа.
Знайти зворотне число можна також для будь-якої іншої дробу. Для цього достатньо перевернути її.
Розподіл дробу на число
Припустимо, у нас є половина піци:
Розділимо її порівну на двох. Скільки піци дістанеться кожному?

Видно, що після поділу половини піци вийшло два рівних шматочка, кожен з яких становить піци. Значить кожному дістанеться по піци.
Тепер, коли ми навчилися складати і множити окремі дроби, можна розглядати більш складні конструкції. Наприклад, що, якщо в одному завданню зустрічається і складання, і віднімання, і множення дробів?
В першу чергу, треба перевести всі дроби в неправильні. Потім послідовно виконуємо необхідні дії - в тому ж порядку, як і для звичайних чисел. А саме:
- Спочатку виконується зведення в ступінь - позбудьтеся від всіх виразів, що містять показники;
- Потім - розподіл і множення;
- Останнім кроком виконується додавання і віднімання.
Зрозуміло, якщо у виразі присутні дужки, порядок дій змінюється - все, що стоїть всередині дужок, треба вважати в першу чергу. І пам'ятайте про неправильні дроби: виділяти цілу частину треба лише тоді, коли всі інші дії вже виконані.
Переведемо всі дроби з першого виразу в неправильні, а потім виконаємо дії:

Тепер знайдемо значення другого виразу. Тут дробів з цілою частиною немає, але є дужки, тому спочатку виконуємо додавання, і лише потім - розподіл. Зауважимо, що 14 \u003d 7 · 2. тоді:
Нарешті, вважаємо третій приклад. Тут є дужки і ступінь - їх краще вважати окремо. З огляду на, що 9 \u003d 3 · 3, маємо:
Зверніть увагу на останній приклад. Щоб звести дріб в ступінь, треба окремо звести до цього степеня чисельник, і окремо - знаменник.
Можна вирішувати по-іншому. Якщо згадати визначення ступеня, завдання зведеться до звичайного множення дробів:
багатоповерхові дроби
До сих пір ми розглядали лише «чисті» дробу, коли чисельник і знаменник представляють собою звичайні числа. Це цілком відповідає визначенню числовий дробу, яке у найпершому уроці.
Але що, якщо в чисельнику або знаменнику розмістити більш складний об'єкт? Наприклад, іншу числову дріб? Такі конструкції виникають досить часто, особливо при роботі з довгими виразами. Ось пара прикладів:
Правило роботи з багатоповерховими дробом всього одне: від них треба негайно позбавлятися. Видалити «зайві» поверхи досить просто, якщо згадати, що подрібнена риса означає стандартну операцію ділення. Тому будь-яку дріб можна переписати таким чином:
Користуючись цим фактом і дотримуючись порядок дій, ми легко зведемо будь-яку багатоповерхову дріб до звичайної. Погляньте на приклади:
Завдання. Переведіть багатоповерхові дроби в звичайні:
У кожному разі перепишемо основну дріб, замінивши роздільну лінію знаком ділення. Також згадаємо, що будь-яке ціле число можна подати у вигляді дробу зі знаменником 1. Тобто 12 \u003d 12/1; 3 \u003d 3/1. отримуємо:

В останньому прикладі перед остаточним множенням дроби були скорочені.
Специфіка роботи з багатоповерховими дробом
У багатоповерхових дробах є одна тонкість, яку завжди треба пам'ятати, інакше можна отримати невірну відповідь, навіть якщо всі обчислення були правильними. Погляньте:
- У чисельнику стоїть окреме число 7, а в знаменнику - дріб 12/5;
- У чисельнику стоїть дріб 7/12, а в знаменнику - окреме число 5.
Отже, для запису отримали дві абсолютно різних інтерпретації. Якщо підрахувати, відповіді теж будуть різними:
Щоб запис завжди читалася однозначно, використовуйте просте правило: що розділяє риса основний дробу повинна бути довше, ніж риса вкладеної. Бажано - в кілька разів.
Якщо дотримуватися цього правила, то наведені вище дробу треба записати так:
Так, можливо, це некрасиво і займає надто багато місця. Зате ви будете вважати правильно. Наостанок - кілька прикладів, де дійсно виникають багатоповерхові дроби:
Завдання. Знайдіть значення виразів:
Отже, працюємо з першим прикладом. Переведемо всі дроби в неправильні, а потім виконаємо операції додавання і ділення:

Аналогічно поступимо з другим прикладом. Переведемо всі дроби в неправильні і виконаємо необхідні операції. Щоб не втомлювати читача, я опущу деякі очевидні викладки. маємо:

Завдяки тому, що в чисельнику і знаменнику основних дробів стоять суми, правило записи багатоповерхових дробів дотримується автоматично. Крім того, в останньому прикладі ми навмисно залишили число 46/1 в формі дробу, щоб виконати поділ.
Також зазначу, що в обох прикладах подрібнена риса фактично замінює дужки: насамперед ми знаходили суму, і лише потім - приватна.
Хтось скаже, що перехід до неправильних дробів в другому прикладі був явно надмірною. Можливо, так воно і є. Але цим ми страхуємо себе від помилок, адже наступного разу приклад може виявитися набагато складніше. Вибирайте самі, що важливіше: швидкість або надійність.
Множення і ділення дробів.
Увага!
До цієї теми є додаткові
матеріали в Особливому розділі 555.
Для тих, хто сильно "не дуже ..."
І для тих, хто "дуже навіть ...")
Ця операція набагато приємніше складання-віднімання! Тому що простіше. Нагадую: щоб помножити дріб на дріб, треба перемножити числители (це буде чисельник результату) і знаменники (це буде знаменник). Тобто:
наприклад:

Все гранично просто. І, будь ласка, не шукайте спільний знаменник! Не треба його тут ...
Щоб розділити дріб на дріб, треба перевернути другу(Це важливо!) Дріб і їх перемножити, тобто .:

наприклад:

Якщо попалося множення або ділення з цілими числами і дробами - нічого страшного. Як і при додаванні, робимо з цілого числа дріб з одиницею в знаменнику - і вперед! наприклад:

У старших класах часто доводиться мати справу з триповерховими (а то і чотириповерховими!) Дробом. наприклад:
Як цей дріб привести до пристойного вигляду? Та дуже просто! Використовувати розподіл через дві точки:

Але не забувайте про порядок розподілу! На відміну від множення, тут це дуже важливо! Звичайно, 4: 2, або 2: 4 ми не сплутаємо. А ось в триповерхової дробу легко помилитися. Зверніть увагу, наприклад:
У першому випадку (вираз зліва):

У другому (вираз праворуч):

Відчуваєте різницю? 4 і 1/9!
А чим задається порядок розподілу? Або дужками, або (як тут) довжиною горизонтальних рисок. Розвивайте окомір. А якщо немає ні дужок, ні рисок, типу:
то ділимо-множимо по порядочку, зліва направо!
І ще дуже простий і важливий прийом. В діях зі ступенями він вам ой як знадобиться! Поділимо одиницю на будь-яку дріб, наприклад, на 13/15:

Дріб перекинулася! І так буває завжди. При розподілі 1 на будь-яку дріб, в результаті отримуємо ту ж дріб, тільки перевернуту.
Ось і всі дії з дробами. Річ досить проста, але помилок дає більш, ніж достатньо. Звертаємо увагу практичні поради, і їх (помилок) буде менше!
Практичні поради:
1. Найголовніше при роботі з дробовими виразами - акуратність і уважність! Це не загальні слова, які не благі побажання! Це сувора необхідність! Всі обчислення на ЄДІ робіть як повноцінне завдання, зосереджено й чітко. Краще написати дві зайві рядки в чернетці, ніж накосячіть при розрахунку в розумі.
2. У прикладах з різними видами дробів - переходимо до звичайних дробів.
3. Всі дробу скорочуємо до упору.
4. Багатоповерхові дробові вирази зводимо до звичайних, використовуючи розподіл через дві точки (стежимо за порядком розподілу!).
5. Одиницю на дріб ділимо в розумі, просто перевертаючи дріб.
Ось вам завдання, які потрібно обов'язково прорешать. Відповіді дані після всіх завдань. Використовуйте матеріали цієї теми і практичні поради. Прикиньте, скільки прикладів ви змогли вирішити правильно. З першого разу! Без калькулятора! І зробіть правильні висновки ...
Пам'ятайте - правильна відповідь, отриманий з другого (тим більше - третього) рази - не рахується! Така сувора життя.
Отже, вирішуємо в режимі іспиту ! Це вже підготовка до ЄДІ, між іншим. Вирішуємо приклад, перевіряємо, вирішуємо наступний. Вирішили все - перевірили знову з першого по останній. І тільки потім дивимося відповіді.
обчислити:


Порішали?
Шукаємо відповіді, які збігаються з вашими. Я спеціально їх безладно записав, подалі від спокуси, так би мовити ... Ось вони, відповіді, через крапку з комою записані.
0; 17/22; 3/4; 2/5; 1; 25.
А тепер робимо висновки. Якщо все вийшло - радий за вас! Елементарні обчислення з дробом - не ваша проблема! Можна зайнятися більш серйозними речами. Якщо ні...
Значить, у вас одна з двох проблем. Або обидві відразу.) Брак знань і (або) неуважність. Але це які вирішуються проблеми.
Якщо Вам подобається цей сайт ...
До речі, у мене є ще парочка цікавих сайтів для Вас.)
Можна потренуватися у вирішенні прикладів і дізнатися свій рівень. Тестування з миттєвою перевіркою. Вчимося - з інтересом!)
можна познайомитися з функціями і похідними.
Дана стаття розглядає дії над дробами. Будуть сформовані і обгрунтовані правила додавання, віднімання, множення, ділення або зведення в ступінь дробів виду A B, де A і B можуть бути числами, числовими виразами або виразами зі змінними. У висновку будуть розглянуті приклади розв'язання з докладним описом.
Yandex.RTB R-A-339285-1
Правила виконання дій з числовими дробом загального вигляду
Числові дробу загального вигляду мають чисельник і знаменник, в яких є натуральні числа або числові вирази. Якщо розглянути такі дроби, як 3 5, 2, 8 4, 1 + 2 · 3 4 · (5 - 2), 3 4 +7 8 2, 3 - 0, 8, 1 2 · 2, π 1 - 2 3 + π, 2 0, 5 ln 3, то видно, що чисельник і знаменник може мати не тільки числа, а й вираження різного плану.
визначення 1
Існують правила, за якими йде виконання дій зі звичайними дробами. Воно підходить і для дробів загального вигляду:
- При відніманні дробів з однаковими знаменниками складаються тільки числители, а знаменник залишається колишнім, а саме: a d ± c d \u003d a ± c d, значення a, c і d ≠ 0 є деякими числами або числовими виразами.
- При додаванні або вирахуванні дробу при різних знаменниках, необхідно провести приведення до спільного, після чого провести додавання чи віднімання отриманих дробів з однаковими показниками. Буквено це виглядає такому чином ab ± cd \u003d a · p ± c · rs, де значення a, b ≠ 0, c, d ≠ 0, p ≠ 0, r ≠ 0, s ≠ 0 є дійсними числами, а b · p \u003d d · r \u003d s. Коли p \u003d d і r \u003d b, тоді a b ± c d \u003d a · d ± c · d b · d.
- При множенні дробів виконується дію з числителями, після чого зі знаменниками, тоді отримаємо a b · c d \u003d a · c b · d, де a, b ≠ 0, c, d ≠ 0 виступають в ролі дійсних чисел.
- При розподілі дробу на дріб першу множимо на другу зворотну, тобто виробляємо заміну місцями чисельника і знаменника: a b: c d \u003d a b · d c.
обгрунтування правил
визначення 2Існують наступні математичні моменти, на які слід спиратися при обчисленні:
- подрібнена риса означає знак ділення;
- поділ на число розглядається як множення на його зворотне значення;
- застосування властивості дій з дійсними числами;
- застосування основного властивості дробу і числових нерівностей.
З їх допомогою можна проводити перетворення виду:
a d ± c d \u003d a · d - 1 ± c · d - 1 \u003d a ± c · d - 1 \u003d a ± c d; a b ± c d \u003d a · p b · p ± c · r d · r \u003d a · p s ± c · e s \u003d a · p ± c · r s; ab · cd \u003d a · db · d · b · cb · d \u003d a · d · a · d - 1 · b · c · b · d - 1 \u003d \u003d a · d · b · c · b · d - 1 · b · d - 1 \u003d a · d · b · cb · d · b · d - 1 \u003d \u003d (a · c) · (b · d) - 1 \u003d a · cb · d
приклади
У попередньому пункті було сказано про дії з дробами. Саме після цього дріб потребує спрощення. Детально ця тема була розглянута в пункті про перетворення дробів.
Для початку розглянемо приклад додавання і віднімання дробів з однаковими знаменником.
приклад 1
Дано дробу 8 2, 7 і 1, 2, 7, то за правилом необхідно чисельник скласти, а знаменник переписати.
Рішення
Тоді отримуємо дріб виду 8 + 1 2, 7. Після виконання складання отримуємо дріб виду 8 + 1 2, 7 \u003d 9 2, 7 \u003d 90 27 \u003d 3 1 3. Значить, 8 2, 7 + 1 2, 7 \u003d 8 + 1 2, 7 \u003d 9 2, 7 \u003d 90 27 \u003d 3 1 3.
відповідь: 8 2 , 7 + 1 2 , 7 = 3 1 3
Є інший спосіб вирішення. Для початку проводиться перехід до виду звичайного дробу, після чого виконуємо спрощення. Це виглядає таким чином:
8 2 , 7 + 1 2 , 7 = 80 27 + 10 27 = 90 27 = 3 1 3
приклад 2
Зробимо віднімання з 1 - 2 3 · log 2 3 · log 2 5 + 1 дробу типу 2 3 3 · log 2 3 · log 2 5 + 1.
Так як дані рівні знаменники, значить, що ми виконуємо обчислення дробу при однаковому знаменнику. Отримаємо, що
1 - 2 3 · log 2 3 · log 2 5 + 1 - 2 3 3 · log 2 3 · log 2 5 + 1 \u003d 1 - 2 - 2 3 3 · log 2 3 · log 2 5 + 1
Є приклади обчислення дробів з різними знаменниками. Важливий пункт - це приведення до спільного знаменника. Без цього ми не зможемо виконувати подальші дії з дробами.
Процес віддалено нагадує приведення до спільного знаменника. Тобто проводиться пошук найменшого спільного дільника в знаменнику, після чого додаються відсутні множники до дробям.
Якщо складаються дробу не мають загальних множників, тоді їм може стати їхній колективний витвір.
приклад 3
Розглянемо на прикладі складання дробів 2 3 5 +1 і 1 2.
Рішення
В даному випадку спільним знаменником виступає твір знаменників. Тоді отримуємо, що 2 • 3 5 +1. Тоді при виставленні додаткових множників маємо, що до першого дробу він дорівнює 2, а до другої 3 5 +1. Після перемноження дробу наводяться до виду 4 2 × 3 5 +1. Загальна приведення 1 2 буде мати вигляд 3 5 + 1 2 • 3 5 +1. Отримані дробові вирази складаємо і отримуємо, що
2 3 5 + 1 + 1 2 \u003d 2 · 2 2 • 3 5 +1 1 • 3 5 +1 2 · 3 5 + 1 \u003d \u003d 4 2 · 3 5 + 1 + 3 5 + 1 2 • 3 5+ 1 \u003d 4 + 3 5 + 1 2 • 3 5 + 1 \u003d 5 + 3 5 2 • 3 5 + 1
відповідь: 2 3 5 + 1 + 1 2 \u003d 5 + 3 5 2 • 3 5 + 1
Коли маємо справу з дробом загального вигляду, тоді про найменшому загальному знаменнику зазвичай справа не йде. В якості знаменника нерентабельно приймати твір числителей. Для початку необхідно перевірити, чи є число, яке менше за значенням, ніж їх твір.
приклад 4
Розглянемо на прикладі 1 6 • 2 1 5 і 1 4 • 2 3 5 коли їх твір дорівнюватиме 6 • 2 1 5 · 4 • 2 3 +5 \u003d 24 • 2 4 5. Тоді як загальний знаменник беремо 12 • 2 3 5.
Розглянемо приклади умножений дробів загального вигляду.
приклад 5
Для цього необхідно провести множення 2 + 1 6 і 2 · 5 3 · 2 + 1.
Рішення
Прямую правилом, необхідно переписати і в вигляді знаменника написати твір числителей. Отримуємо, що 2 + 1 6 ∙ 2 · 5 3 · 2 + 1 2 + 1 · 2 · 5 6 ∙ 3 · 2 + 1. Коли дріб буде помножена, можна проводити скорочення для її спрощення. Тоді 5 • 3 3 2 1: 10 9 3 \u003d 5 • 3 3 2 1 · 9 3 10.
Використовуючи правило переходу від ділення до множення на зворотну дріб, отримаємо дріб, зворотний даної. Для цього чисельник і знаменник міняються місцями. Розглянемо на прикладі:
5 • 3 3 2 1: 10 9 3 \u003d 5 • 3 3 2 1 · 9 3 10
Після чого повинні виконати множення і спростити отриману дріб. Якщо необхідно, то позбутися від ірраціональності в знаменнику. Отримуємо, що
5 · 3 3 2 + 1: 10 9 3 \u003d 5 · 3 3 · 9 3 10 · 2 + 1 \u003d 5 · 2 10 · 2 + 1 \u003d 3 2 · 2 + 1 \u003d \u003d 3 · 2 - 1 2 · 2 + 1 · 2 - 1 \u003d 3 · 2 - 1 2 · 2 2 - 1 2 \u003d 3 · 2 - 1 2
відповідь: 5 · 3 3 2 + 1: 10 9 3 \u003d 3 · 2 - 1 2
Даний пункт застосуємо, коли число або числовий вираз може бути представлено у вигляді дробу, що має знаменник, рівний 1, тоді і дію з такою дробом розглядається окремим пунктом. Наприклад, вираз 1 6 ∙ 7 4 - 1 · 3 видно, що корінь з 3 може бути замінений іншим 3 1 виразом. Тоді цей запис буде виглядати як множення двох дробів виду 1 6 ∙ 7 4 - 1 · 3 \u003d 1 6 ∙ 7 4 - 1 · 3 1.
Виконання дію з дробом, що містять змінні
Правила, розглянуті в першій статті, застосовні для дій з дробами, що містять змінні. Розглянемо правило віднімання, коли знаменники однакові.
Необхідно довести, що A, C і D (D не рівне нулю) можуть бути будь-якими виразами, причому рівність A D ± C D \u003d A ± C D рівноцінно з його областю допустимих значень.
Необхідно взяти набір змінних ОДЗ. Тоді А, С, D повинні приймати відповідні значення a 0, c 0 і d 0. Підстановка виду A D ± C D призводить різниця виду a 0 d 0 ± c 0 d 0, де за правилом додавання отримуємо формулу виду a 0 ± c 0 d 0. Якщо підставити вираз A ± C D, тоді отримуємо ту ж дріб виду a 0 ± c 0 d 0. Звідси робимо висновок, що вибране значення, яке задовольняє ОДЗ, A ± C D і A D ± C D вважаються рівними.
При будь-якому значенні змінних дані вирази будуть рівні, тобто їх називають тотожно рівними. Значить це вираз вважається доводимо рівністю виду A D ± C D \u003d A ± C D.
Приклади додавання і віднімання дробів з змінними
Коли є однакові знаменники, необхідно тільки складати або віднімати числители. Така дріб може бути спрощена. Іноді доводиться працювати з дробом, які є тотожно рівними, але при першому погляді це непомітно, так як необхідно виконувати деякі перетворення. Наприклад, x 2 3 · x 1 3 +1 і x 1 3 +1 2 або 1 2 · sin 2 α і sin a · cos a. Найчастіше потрібне спрощення вихідного вираження для того, щоб побачити однакові знаменники.
приклад 6
Обчислити: 1) x 2 + 1 x + x - 2 - 5 - xx + x - 2, 2) lg 2 x + 4 x · (lgx + 2) + 4 · lgxx · (lgx + 2), x - 1 x - 1 + xx + 1.
Рішення
- Щоб зробити обчислення, необхідно відняти дроби, яким мають однакові знаменники. Тоді отримуємо, що x 2 + 1 x + x - 2 - 5 - x x + x - 2 \u003d x 2 + 1 - 5 - x x + x - 2. Після чого можна виконувати розкриття дужок з приведенням подібних доданків. Отримуємо, що x 2 + 1 - 5 - x x + x - 2 \u003d x 2 + 1 - 5 + x x + x - 2 \u003d x 2 + x - 4 x + x - 2
- Так як знаменники однакові, то залишається тільки скласти чисельники, залишивши знаменник: lg 2 x + 4 x · (lgx + 2) + 4 · lgxx · (lgx + 2) \u003d lg 2 x + 4 + 4 x · (lgx + 2)
Додавання було виконано. Видно, що можна зробити скорочення дробу. Її чисельник може бути згорнутий по формулі квадрата суми, тоді отримаємо (l g x + 2) 2 з формул скороченого множення. Тоді отримуємо, що
l g 2 x + 4 + 2 · l g x x · (l g x + 2) \u003d (l g x + 2) 2 x · (l g x + 2) \u003d l g x + 2 x - Задані дроби виду x - 1 x - 1 + x x + 1 з різними знаменниками. Після перетворення можна перейти до складання.
Розглянемо двоякий спосіб вирішення.
Перший спосіб полягає в тому, що знаменник першого дробу піддається розкладанню на множники за допомогою квадратів, причому з її подальшим скороченням. Отримаємо дріб виду
x - 1 x - 1 \u003d x - 1 (x - 1) · x + 1 \u003d 1 x + 1
Значить, x - 1 x - 1 + x x + 1 \u003d 1 x + 1 + x x + 1 \u003d 1 + x x + 1.
В такому випадку необхідно позбавлятися від ірраціональності в знаменнику.
1 + x x + 1 \u003d 1 + x · x - 1 x + 1 · x - 1 \u003d x - 1 + x · x - x x - 1
Другий спосіб полягає в множенні чисельника і знаменника другого дробу на вираз x - 1. Таким чином, ми позбавляємося від ірраціональності і переходимо до складання дробу при наявності однакового знаменника. тоді
x - 1 x - 1 + xx + 1 \u003d x - 1 x - 1 + x · x - 1 x + 1 · x - 1 \u003d \u003d x - 1 x - 1 + x · x - xx - 1 \u003d x - 1 + x · x - xx - 1
відповідь: 1) x 2 + 1 x + x - 2 - 5 - xx + x - 2 \u003d x 2 + x - 4 x + x - 2, 2) lg 2 x + 4 x · (lgx + 2) + 4 · lgxx · (lgx + 2) \u003d lgx + 2 x, 3) x - 1 x - 1 + xx + 1 \u003d x - 1 + x · x - xx - 1.
В останньому прикладі отримали, що приведення до спільного знаменника неминуче. Для цього необхідно спрощувати дробу. Для складання або віднімаючи завжди необхідно шукати спільний знаменник, який виглядає як твір знаменників з додаванням дополніетльних множників до чисельнику.
приклад 7
Обчислити значення дробів: 1) x 3 + 1 x 7 + 2 · 2, 2) x + 1 x · ln 2 (x + 1) · (2 \u200b\u200bx - 4) - sin xx 5 · ln (x + 1) · (2 x - 4), 3) 1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x
Рішення
- Ніяких складних обчислень знаменник не вимагає, тому потрібно вибрати їх твір виду 3 · x 7 + 2 · 2, тоді до першого дробу x 7 + 2 · 2 вибирають як додатковий множник, а 3 до другої. При перемножуванні отримуємо дріб виду x 3 + 1 x 7 + 2 · 2 \u003d x · x 7 + 2 · 2 3 · x 7 + 2 · 2 + 3 · 1 3 · x 7 + 2 · 2 \u003d \u003d x · x 7 + 2 · 2 + 3 3 · x 7 + 2 · 2 \u003d x · x 7 + 2 · 2 · x + 3 3 · x 7 + 2 · 2
- Видно, що знаменники представлені у вигляді твору, що означає непотрібність додаткових перетворень. Спільним знаменником буде вважатися твір виду x 5 · ln 2 x + 1 · 2 x - 4. Звідси x 4
є додатковим множником до першого дробу, а ln (x + 1)
до другої. Після чого виробляємо віднімання і отримуємо, що:
x + 1 x · ln 2 (x + 1) · 2 x - 4 - sin xx 5 · ln (x + 1) · 2 x - 4 \u003d \u003d x + 1 · x 4 x 5 · ln 2 (x + 1 ) · 2 x - 4 - sin x · ln x + 1 x 5 · ln 2 (x + 1) · (2 \u200b\u200bx - 4) \u003d \u003d x + 1 · x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · (2 \u200b\u200bx - 4) \u003d x · x 4 + x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · (2 \u200b\u200bx - 4 ) - Даний приклад має сенс при роботі зі знаменниками дробом. Необхідно застосувати формули різниці квадратів і квадрат суми, так як саме вони дадуть можливість перейти до вираження виду 1 cos x - x · cos x + x + 1 (cos x + x) 2. Видно, що дроби приводяться до спільного знаменника. Отримуємо, що cos x - x · cos x + x 2.
Після чого отримуємо, що
1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x \u003d \u003d 1 cos x - x · cos x + x + 1 cos x + x 2 \u003d \u003d cos x + x cos x - x · cos x + x 2 + cos x - x cos x - x · cos x + x 2 \u003d \u003d cos x + x + cos x - x cos x - x · cos x + x 2 \u003d 2 · cos x cos x - x · cos x + x 2
відповідь:
1) x 3 + 1 x 7 + 2 · 2 \u003d x · x 7 + 2 · 2 · x + 3 3 · x 7 + 2 · 2, 2) x + 1 x · ln 2 (x + 1) · 2 x - 4 - sin xx 5 · ln (x + 1) · 2 x - 4 \u003d \u003d x · x 4 + x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · ( 2 x - 4), 3) 1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x \u003d 2 · cos x cos x - x · cos x + x 2.
Приклади множення дробів зі змінними
При множенні дробів чисельник множиться на чисельник, а знаменник на знаменник. Тоді можна застосовувати властивість скорочення.
приклад 8
Провести множення дробів x + 2 · x x 2 · ln x 2 · ln x + 1 і 3 · x 2 1 3 · x + 1 - 2 sin 2 · x - x.
Рішення
Необхідно виконати множення. Отримуємо, що
x + 2 · xx 2 · ln x 2 · ln x + 1 · 3 · x 2 1 3 · x + 1 - 2 sin (2 · xx) \u003d \u003d x - 2 · x · 3 · x 2 1 3 · x + 1 - 2 x 2 · ln x 2 · ln x + 1 · sin (2 · x - x)
Число 3 переноситься на перше місце для зручності підрахунків, причому можна зробити скорочення дробу на x 2, тоді отримаємо вираз виду
3 · x - 2 · x · x 1 3 · x + 1 - 2 ln x 2 · ln x + 1 · sin (2 · x - x)
відповідь: x + 2 · xx 2 · ln x 2 · ln x + 1 · 3 · x 2 1 3 · x + 1 - 2 sin (2 · xx) \u003d 3 · x - 2 · x · x 1 3 · x + 1 - 2 ln x 2 · ln x + 1 · sin (2 · x - x).
розподіл
Розподіл у дробів аналогічно множенню, так як перший дріб множать на другу зворотну. Якщо взяти, наприклад, дріб x + 2 · x x 2 · ln x 2 · ln x + 1 і розділити на 3 · x 2 1 3 · x + 1 - 2 sin 2 · x - x, тоді це можна записати таким чином, як
x + 2 · xx 2 · ln x 2 · ln x + 1: 3 · x 2 1 3 · x + 1 - 2 sin (2 · xx), після чого замінити твором виду x + 2 · xx 2 · ln x 2 · ln x + 1 · 3 · x 2 1 3 · x + 1 - 2 sin (2 · x - x)
Зведення в ступінь
Перейдемо до розгляду дії з дробами загального виду з возведенням у ступінь. Якщо є ступінь з натуральним показником, тоді дія розглядають як множення однакових дробів. Але рекомендовано використовувати загальний підхід, який базується на властивостях ступенів. Будь-які висловлювання А і С, де С тотожне Не рівняється нулю, а будь-яка дійсна r на ОДЗ для вираження виду A C r справедливо рівність A C r \u003d A r C r. Результат - дріб, зведена в ступінь. Для прикладу розглянемо:
x 0, 7 - π · ln 3 x - 2 - 5 x + 1 2, 5 \u003d \u003d x 0, 7 - π · ln 3 x - 2 - 5 2, 5 x + 1 2, 5
Порядок виконання дій з дробами
Дії над дробами виконуються за певними правилами. На практиці помічаємо, що вираз може містити кілька дробів або дробових виражень. Тоді необхідно всі дії виконувати в строгому порядку: підносити до степеня, множити, ділити, після чого додавати і віднімати. При наявності дужок перша дія виконується саме в них.
приклад 9
Обчислити 1 - x cos x - 1 c o s x · 1 + 1 x.
Рішення
Бо ж маємо однаковий знаменник, то 1 - x cos x та 1 c o s x, але виробляти віднімання за правилом не можна, спочатку виконуються дії в дужках, після чого множення, а потім складання. Тоді при обчисленні отримуємо, що
1 + 1 x \u003d 1 1 + 1 x \u003d x x + 1 x \u003d x + 1 x
При підстановці виразу в вихідне отримуємо, що 1 - x cos x - 1 cos x · x + 1 x. При множенні дробів маємо: 1 cos x · x + 1 x \u003d x + 1 cos x · x. Провівши все підстановки, одержимо 1 - x cos x - x + 1 cos x · x. Тепер необхідно працювати з дробом, які мають різні знаменники. отримаємо:
x · 1 - x cos x · x - x + 1 cos x · x \u003d x · 1 - x - 1 + x cos x · x \u003d \u003d x - x - x - 1 cos x · x \u003d - x + 1 cos x · x
відповідь: 1 - x cos x - 1 c o s x · 1 + 1 x \u003d - x + 1 cos x · x.
Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl + Enter
1º. Натуральні числа- це числа, що вживаються при рахунку. Безліч всіх натуральних чисел обозначаютN, т.е.N \u003d (1, 2, 3, ...).
дробомназивається число, що складається з декількох частин одиниці. звичайної дробомназивається число виду, де натуральне число nпоказує, на скільки рівних частин поділено одиниця, а натуральне число mпоказує, скільки таких рівних частин взято. числа mі nназивають відповідно числителемі знаменникомдробу.
Якщо чисельник менше знаменника, то звичайна дріб називається правильної; якщо чисельник дорівнює знаменника або більше нього, то дріб називається неправильної. Число, що складається з цілої і дробової частин, називається змішаним числом.
наприклад,  - правильні звичайні дроби,
- правильні звичайні дроби,  - неправильні звичайні дроби, 1 змішане число.
- неправильні звичайні дроби, 1 змішане число.
2º. При виконанні дій над звичайними дробами слід пам'ятати наступні правила:
1) Основна властивість дробу. Якщо чисельник і знаменник дробу помножити або розділити на одне й те саме натуральне число, то вийде дріб, що дорівнює даної.
Наприклад, а)  ; б)
; б)  .
.
Розподіл чисельника і знаменника дробу на їх спільний дільник, відмінний від одиниці, називається скороченням дробу.
2) Щоб змішане число представити у вигляді неправильного дробу, потрібно помножити його цілу частину на знаменник дробової частини і до отриманого добутку додати чисельник дробової частини, записати отриману суму числителем дробу, а знаменник залишити колишнім.
Аналогічно будь-яке натуральне число можна записати у вигляді неправильного дробу з будь-яким знаменником.
Наприклад, а)  , так як
, так як  ; б)
; б)  і т.д.
і т.д.
3) Щоб неправильну дріб записати у вигляді змішаного числа (тобто з неправильного дробу виділити цілу частину), потрібно чисельник розділити на знаменник, частка від ділення взяти в якості цілої частини, залишок - як чисельник, знаменник залишити колишнім.
Наприклад, а)  , Так як 200: 7 \u003d 28 (ост. 4); б)
, Так як 200: 7 \u003d 28 (ост. 4); б)  , Так як 20: 5 \u003d 4 (ост. 0).
, Так як 20: 5 \u003d 4 (ост. 0).
4) Щоб привести дроби до найменшого спільного знаменника, треба знайти найменше спільне кратне (НОК) знаменників цих дробів (воно і буде їх найменшим спільним знаменником), розділити найменший спільний знаменник на знаменники даних дробів (тобто знайти додаткові множники для дробів) , помножити чисельник і знаменник кожного дробу на її додатковий множник.
Наприклад, наведемо дроби  до найменшого спільного знаменника:
до найменшого спільного знаменника:
 ,
, ,
, ;
;
630: 18 = 35, 630: 10 = 63, 630: 21 = 30.
значить,  ;
; ;
; .
.
5) Правила арифметичних дій над звичайними дробами:
a) Додавання і віднімання дробів з однаковими знаменниками виконується за правилом:
 .
.
b) Додавання і віднімання дробів з різними знаменниками виконується по правілуa), попередньо привівши дроби до найменшого спільного знаменника.
c) При додаванні і відніманні змішаних чисел можна звернути їх у неправильні дроби, а потім виконати дії по правіламa) иb),
d) При множенні дробів користуються правилом:
 .
.
e) Щоб розділити одну дріб на іншу, треба ділене помножити на число, протилежне дільнику:
 .
.
f) При множенні і діленні змішаних чисел, їх попередньо переводять в неправильні дроби, а потім користуються правіламіd) іe).
3º. При вирішенні прикладів на всі дії з дробами слід пам'ятати, що спочатку виконуються дії в дужках. Як в дужках, так і поза ними спочатку виконують множення і ділення, а потім додавання і віднімання.
Розглянемо виконання вищевикладених правил на прикладі.
Приклад 1. Обчислити:  .
.
1)  ;
;
2)  ;
;
5)  . Відповідь: 3.
. Відповідь: 3.